Energia kinetyczna pojazdu.
Siły działające na pojazd podczas hamowania.
Moment tarcia w hamulcach i jego obliczanie.
Maksymalna siła hamowania. Hamowanie
a przyczepność kół do drogi.
Przebieg hamowania. Długość drogi hamowania
i zatrzymania.
Wpływ warunków ruchu na blokowanie kół tylnych
Sytuacje krytyczne podczas hamowania. ABS

Hamowanie

Hamowanie

Energia kinetyczna pojazdu

Poruszający się pojazd posiada znaczną

energię kinetyczną (ruchu postępowego i
obrotowego),

2

2

2

2





K

K

I

m

E





która rośnie wraz z kwadratem prędkości
jazdy. Podczas hamowania energię tę należy
przekształcić w inną postać energii.
Decydujące znaczenie ma jej przekształcenie
w pracę sił tarcia w hamulcach i ogumienia po
jezdni.

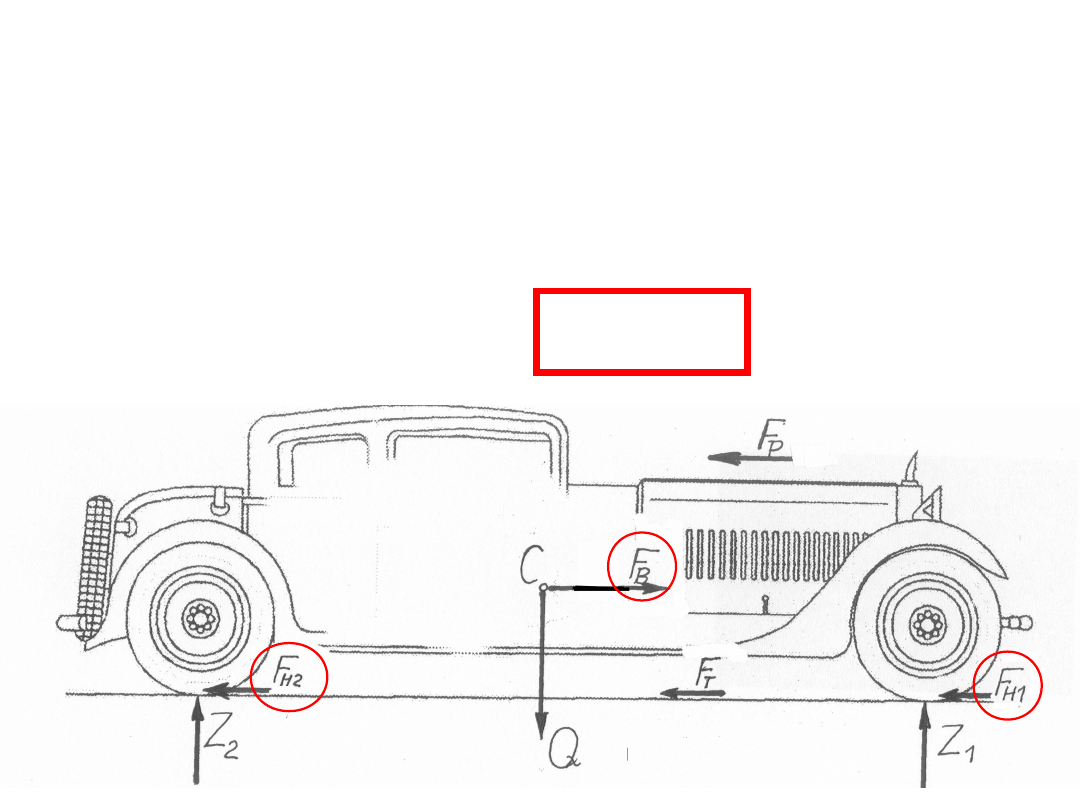
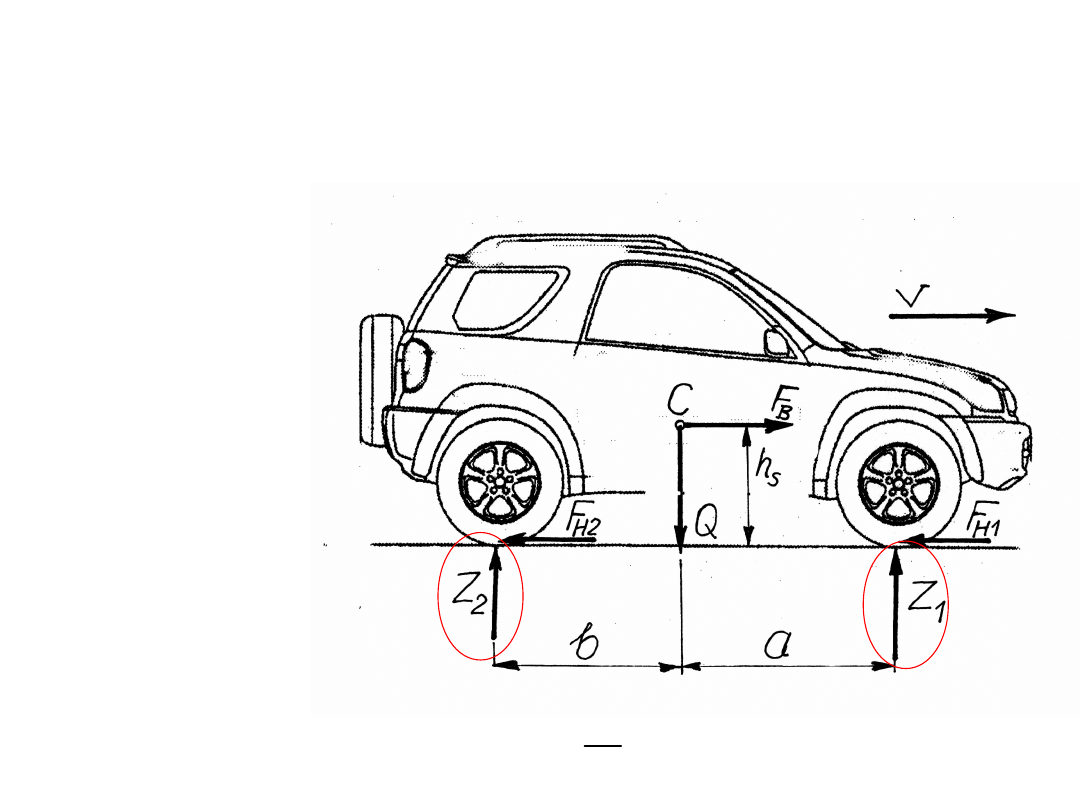
Siły działające na pojazd podczas

hamowania

Podczas hamowania konieczne jest oddziaływanie na
pojazd sił zewnętrznych, hamujących jego ruch.

Oddziaływanie reakcji

K

X

zewnętrznym od drogi na pojazd, które może spowodować
hamowanie

jest właśnie tym
oddziaływaniem

H

K

F

X 

Siły działające na pojazd podczas

hamowania, cd

poziomy mamy:

T

P

B

H

H

H

F

F

F

F

F

F











2

1

Cechą szczególną procesu hamowania jest
oddziaływanie

znacznych sił bezwładności. Z sumy rzutów sił na
kierunek

B

H

H

H

F

F

F

F







2

1

W przybliżeniu

H

B

a

g

Q

F





i

Hi

k

Hk

F

F

F

F









Na poszczególnych kołach i osiach kół jezdnych

mamy

Uwaga, -dv/dt=a

H

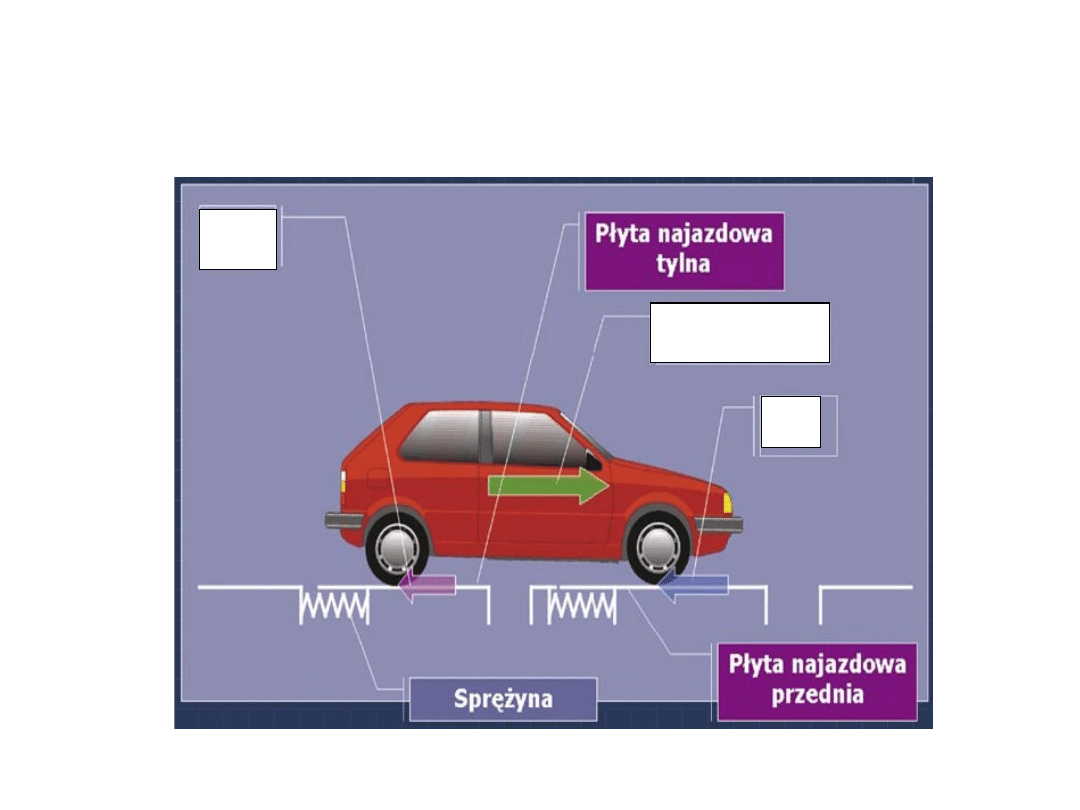
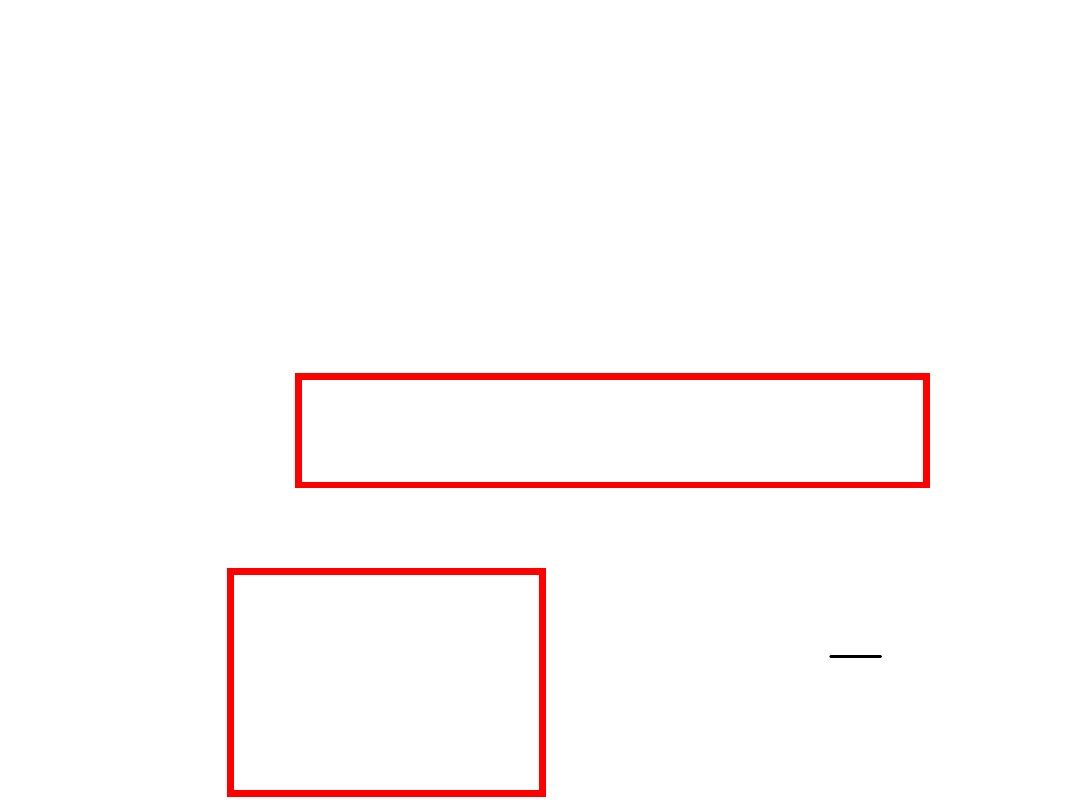
Pomiar sił hamowania na płytach
najazdowych

F

B

F

H1

F

H2

DIAGNOSTYK
A

Moment tarcia w hamulcach

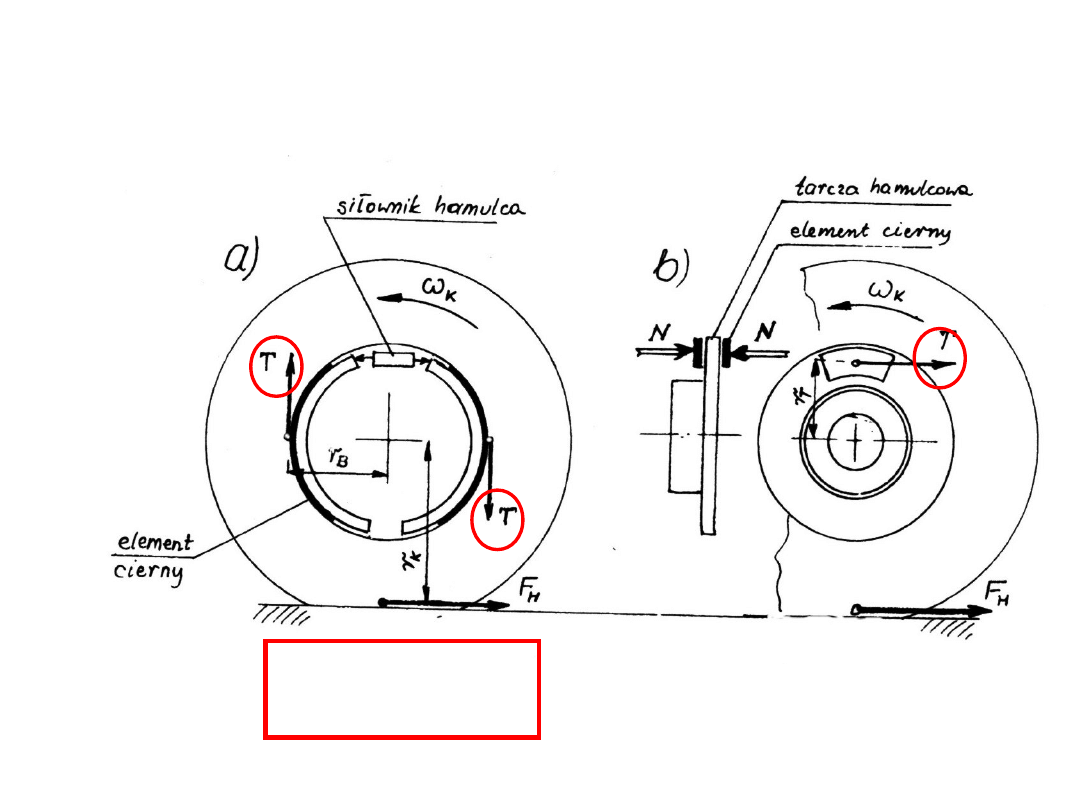
Na rysunku pokazano działanie mechanizmów
hamulcowych, zaznaczając wielkości istotne do
dalszych rozważań.

a- bębnowy mechanizm hamulcowy, b- mechanizm tarczowy

Moment tarcia w hamulcach

N

T

H





Maksymalna siła hamowania

Podczas intensywnego hamowania dla każdego koła mamy

K

K

MAX

HK

Z

F

F









,



F

F

H



Zawsze musi być spełniony warunek

Na każdej osi kół jezdnych

i

i

MAX

Hi

Z

F

F









,

W samochodzie
dwuosiowym

)

(

2

1

2

1

,

2

,

1

Z

Z

F

F

F

F

MAX

H

MAX

H

















Sumując siły hamowania na osiach kół, otrzymano
wartość maksymalnej siły hamowania samochodu w
najbardziej korzystnej sytuacji hamowania
wszystkich kół do wyczerpania ich przyczepności.

Maksymalne opóźnienie

hamowania

Dalej rozważa się sytuację najbardziej korzystnego
hamowania wszystkich kół pojazdu do wyczerpania ich
przyczepności na drodze poziomej. Zatem

Q

F

F

F

MAX

H

MAX

H

MAX

H









,

,

2

,

1

Ponieważ

B

H

F

F 

, to

MAX

H

B

MAX

H

a

g

Q

F

F

,

,







Przyjmując w procesie hamowania



1

MAX

H

a

g

Q

Q

,





,
otrzymano:

g

a

MAX

H





,

, a stąd

Hamowanie a przyczepność kół do

drogi

Pojęcie jednostkowej siły hamowania

H



Q

F

H

H





Q

Q

F

MAX

H

MAX

H









,

,







MAX

H,

Zatem

Stąd

Jednostkowa siła hamowania jest ograniczona i nie
może przekroczyć współczynnika przyczepności

pozwala

zapisa
ć



F

r

M

F

K

TK

K





i

MAX

Hi

Z

F





,



MAX

H

F

,

MAX

H

MAX

H

F

F

,

2

,

1



g

a

MAX

H





,







MAX

H,

Siła hamowania wynika z momentu tarcia w hamulcu
i jest ograniczona

na każdym kole

- maksymalna siła hamowania osi kół samochodu wynosi

a dla całego samochodu
mamy

- maksymalną wartość opóźnienia hamowania oblicza się

-

jednostkowa siła hamowania nie przekracza wartości

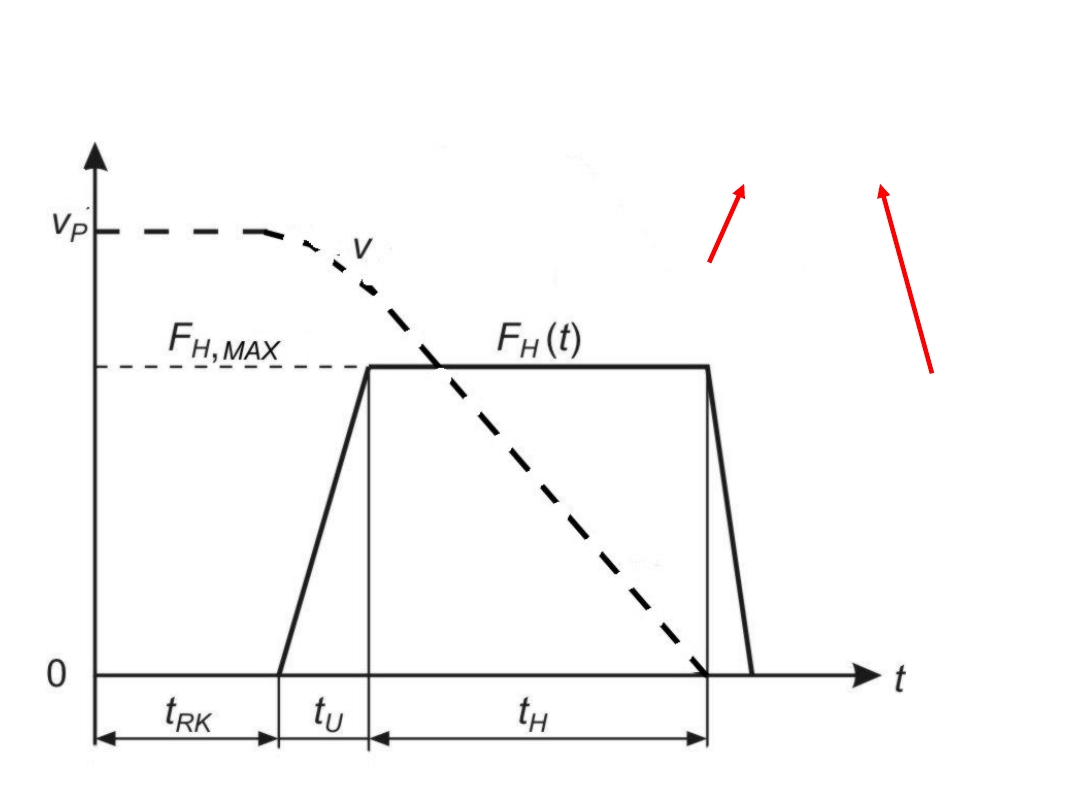
Hamowanie

i zatrzymanie

H

U

RK

Z

t

t

t

t







0,4...1,5 s

0,2...0,4
s
0,3...0,6
s

Układy
hydrauliczne

i
pneumatyczn
e

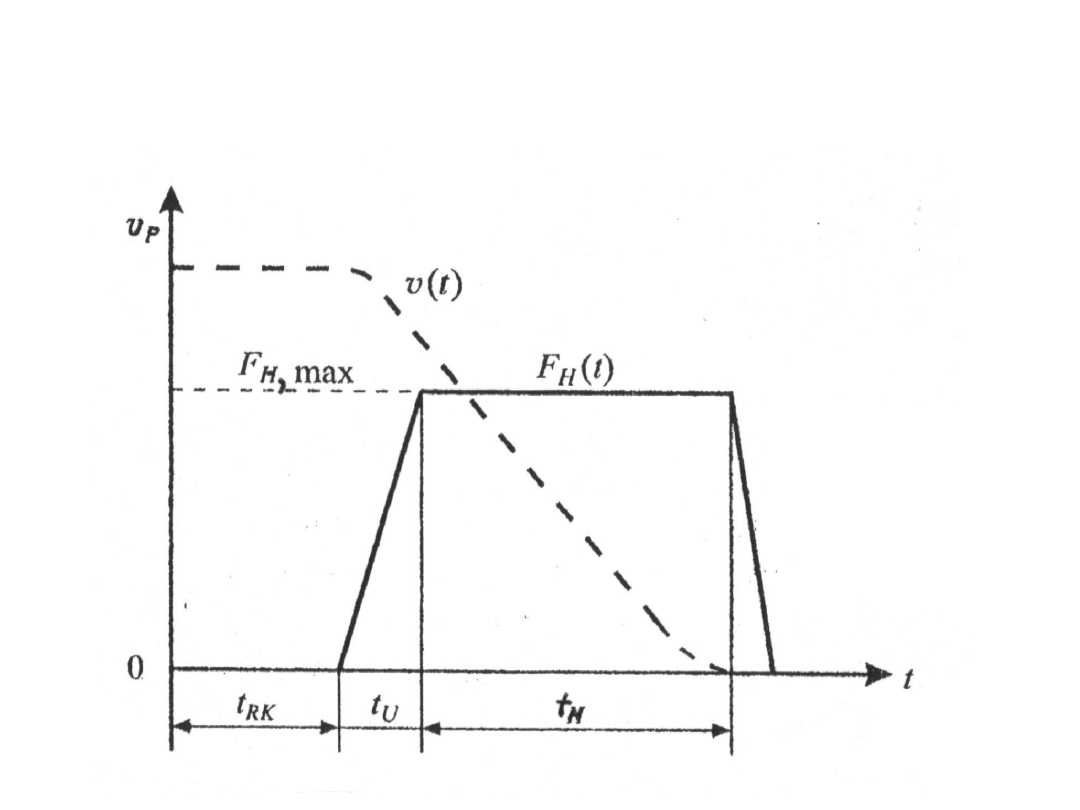
Czas zatrzymania

Przebieg hamowania

i

zatrzymania, cd

Długość drogi zatrzymania obliczono jako sumę

długości dwóch odcinków
drogi:

-

przebytej w czasie

2

U

RK

R

t

t

t





w którym zakłada się ruch jednostajny bez hamowania

H

U

t

t



2

H

a

-przebytej w czasie

jako drogi hamowania z pełną efektywnością

.

i opóźnieniem

H

P

R

Z

S

v

t

S





Zatem mamy

Długość drogi hamowania i

zatrzymania

Podczas hamowania samochód porusza się
ruchem jednostajnie opóźnionym. Drogę w ruchu
jednostajnie opóźnionym obliczamy

2

2

)

2

(

2

2

U

H

H

H

P

H

t

t

a

a

v

S







H

P

R

Z

S

v

t

S





2

P

H

2

P

P

)

2

(

2

v

)

2

(

2a

v

v

)

2

(

U

H

H

U

RK

U

RK

Z

t

t

a

t

t

t

t

S















Droga
zatrzymania

Droga
hamowania

Obliczenia długości drogi

hamowania, cd

Porównanie pracy sił hamowania i energii kinetycznej
pojazdu

F S

Q

g

H

H





2

2

2

(

)

v

v

P

K

Stąd otrzymano

H

K

P

H

gF

v

v

Q

S

2

)

(

2

2





Ważna zależność do
obliczania drogi
hamowania

Uwzględniając, że

H

B

H

ma

dt

dv

m

F

F















H

K

P

H

gma

v

v

Q

S

2

)

(

2

2

H

K

P

a

v

v

2

2

2



H

P

H

a

v

S

2

2



mamy

Hamowanie do zatrzymania

Obliczenie minimalnej długości drogi
hamowania

F

F

H

H MAX



,

S

S

H

H MIN



,

Podczas hamowania z maksymalną efektywnością, czyli przy

, mamy

.

Zatem

F

S

Q

g

H MAX

H MIN

,

,

(

)





2

2

2

v

v

P

K

S

Q

gF

H MIN

H MAX

,

,

(

)





v

v

P

K

2

2

2

Stąd

Niekiedy można
przyjmować



Q

F

MAX

H



,



g

S

MIN

H

2

v

v

2

K

2

P

,







g

S

MIN

H

2

v

2

P

,



0



K

v

Wówczas

Przy

Minimalna długość drogi
hamowania, nie
zatrzymania

Prędkość jazdy a droga

hamowania

H

P

H

a

v

S

2

2





g

S

MIN

H

2

v

2

P

,



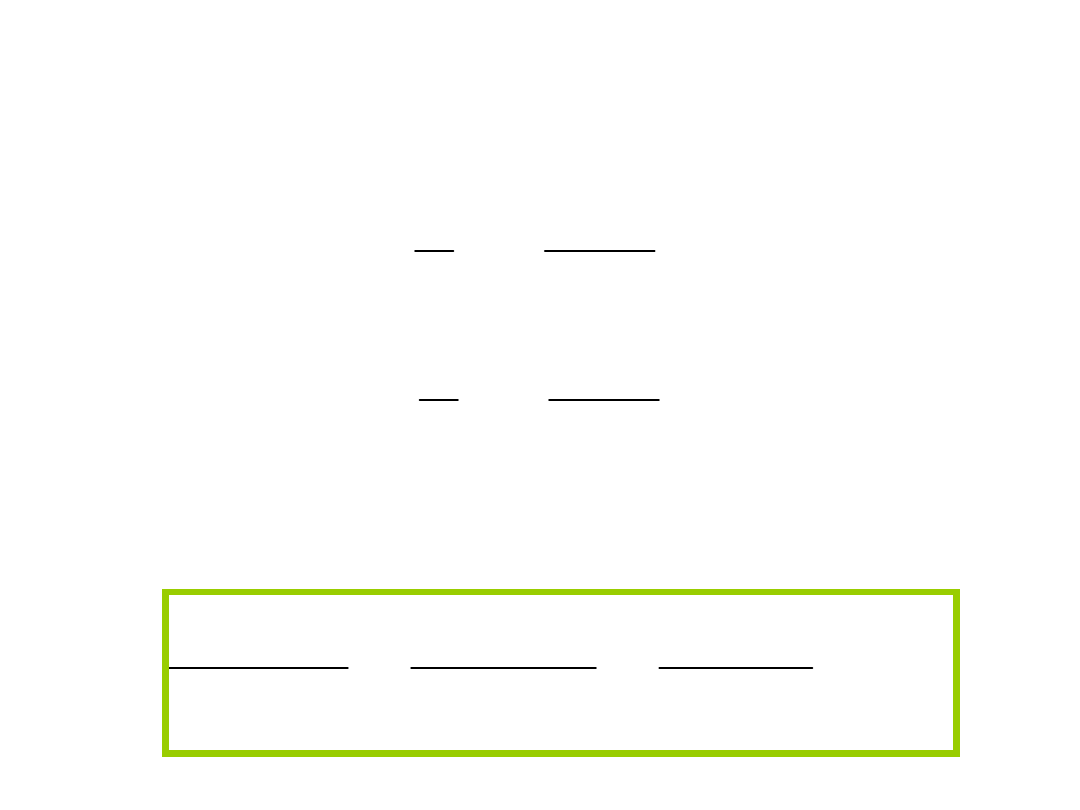
Rozkład sił hamowania

Rozkład sił hamowania na osie kół

jezdnych

Hamowanie samochodu zależy od rozkładu sił hamowania
na poszczególne osie kół jezdnych. Rozkład ten wynika z
konstrukcji układu hamulcowego. Wprowadzono
współczynnik konstrukcyjnego rozdziału sił hamowania

2

1

T

T

R

M

M





N

r

M

M

T

H

TK

Ti



4

2





Moment tarcia w hamulcach

Współczynnik rozdziału

2

1

2

1

H

H

T

T

R

F

F

M

M







gdy siły hamowania nie osiągną poziomu sił
przyczepności

wynosi

R

H

H

F

F





2

1

F

F

H

H MAX

1

1



,

F

F

H

H MAx

2

2



,

czyli

i

Rozkład sił hamowania na osie kół

jezdnych, cd

Maksymalne wartości sił hamowania zależą od nacisku kół
na drogę. Do ich obliczenia wykorzystano równania
równowagi

F h

Qb Z L

B S







1

0

F h

Qa Z L

B S







2

0

H

B

a

g

Q

F





gdzie

Rozkład sił hamowania na osie kół

jezdnych, cd 2

1





Z równań równowagi otrzymano dla

Z

Q

b

L

a h

gb

Z

Q

a

L

a h

ga

H S

H S

1

2

1

1









(

)

(

)

Są to wyrażenia
do wyznaczania
wartości nacisków
kół na drogę
podczas
hamowania

Współczynnik rozdziału wartości maksymalnych sił
hamowania obliczono

M

MAX

MAX

MAX

MAX

MAX

H

MAX

H

Z

Z

Z

Z

F

F













,

2

,

1

,

2

,

1

,

2

,

1

Regulacja sił hamowania na kołach osi

tylnej

Układ hamulcowy powinien zapewnić
dostosowanie wartości sił hamowania do
rozkładu nacisków osi kół jezdnych na drogę.

Typowy

korektor
obniża
ciśnienie w
siłownikach
hamulców kół
osi tylnej,
które podczas
hamowania są
odciążane.

Sytuacje krytyczne podczas

hamowania

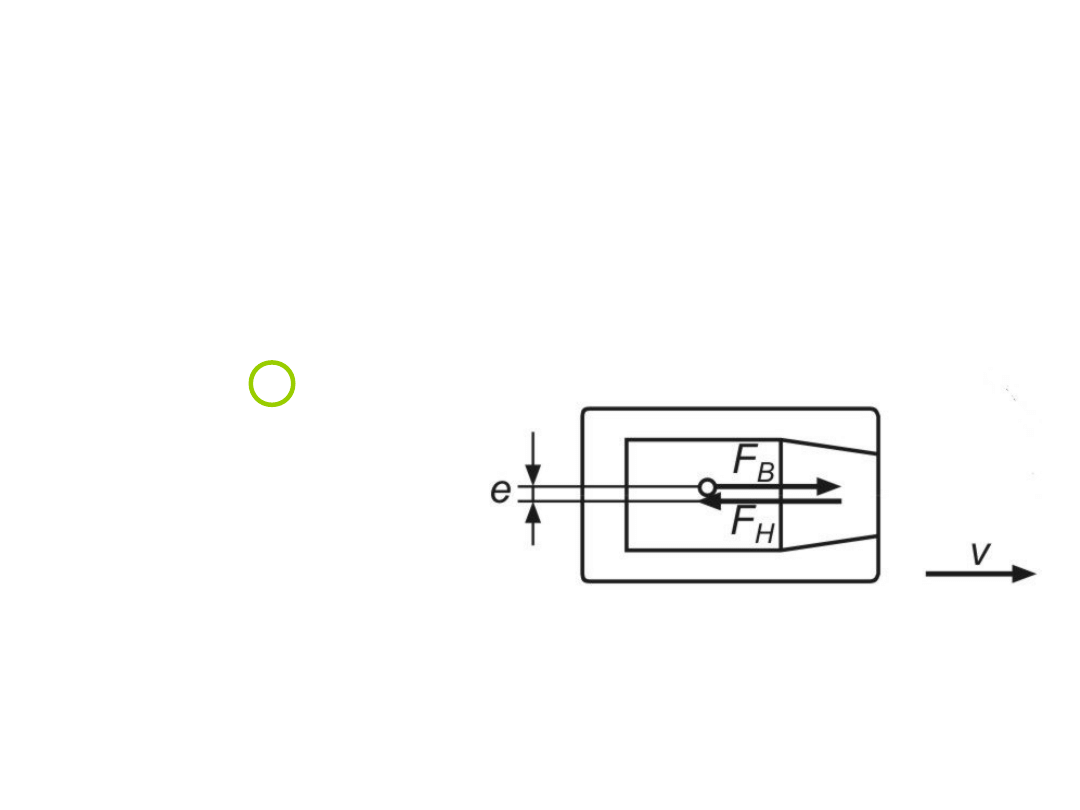
Rozważa się prostoliniowy ruch pojazdu i proces
hamowania. Analizowany jest ruch pojazdu, w którym:
- naciski kół lewej i prawej strony pojazdu nie są

równe;

-osie kół (mosty) wykazują brak wzajemnej
równoległości (zły stan techniczny pojazdu).
Podczas hamowania w takiej sytuacji linie działania siły
bezwładności (w środku masy) i wypadkowej siły
hamowania kół będą oddalone od siebie o wielkość e

będzie dążył do
obrócenia pojazdu

(moment obracający).

Utrata stateczności kierunkowej podczas
hamowania

e

F

e

F

M

H

B





0

B

H

F

F 

Powstający

przy

tym moment

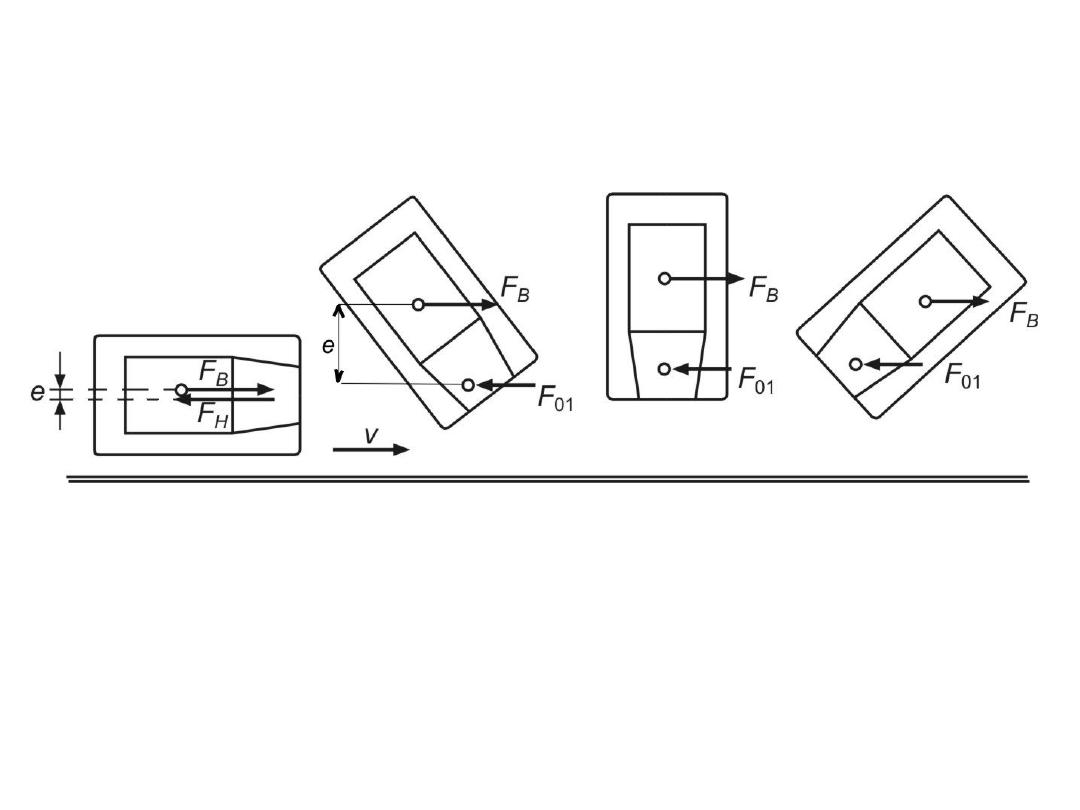
Obrót pojazdu podczas

hamowania

Podczas obrotu samochodu ramię momentu
obracającego może narastać.

Obrotowi temu

powinny przeciwdziałać reakcje styczne boczne na
kołach hamowanych.

Analiza możliwości wytworzenia reakcji

bocznych

Podczas narastania siły hamowania dysponujemy coraz
mniejszą możliwością wytworzenia reakcji stycznych
bocznych, ponieważ

Jeśli dla kół obu osi wyznaczyć różnicę

i

i

i

Z

Y

X







2

2

i

H

i

F

F 



0





Hi

i

F

F



wówczas

jest

możliwość

wytworzenia reakcji bocznej,
czyli

0



i

Y

Hi

i

F

F 



MAX

Hi

Hi

F

F

,



0



i

Y

czyli

;

koła zostały zablokowane i w konsekwencji mamy

, a dysponowana siła przyczepności
została wyczerpana w całości w kierunku
obwodowym

, to

a)

b)

Reakcja
obwodowa

Reakcja boczna

Analiza możliwości wytworzenia reakcji

bocznych, cd

Koła przednie, dociskane do drogi, osiągają wysoką

przyczepność. To zapobiega ich zablokowaniu. Jeżeli w
rezultacie intensywnego hamowania zostaną
zablokowane koła osi tylnej, to mamy następujące
wartości reakcji bocznych:

0

1



Y

0

2



Y

- koła osi przedniej

,

- koła osi tylnej

- czyli brak
zdolności do wytworzenia reakcji bocznych bo
przyczepność

kół

tylnych

została

w

całości

wyczerpana w kierunku obwodowym.

Moment obracający spowoduje boczne
przemieszczanie się tyłu samochodu (utrata
stateczności)

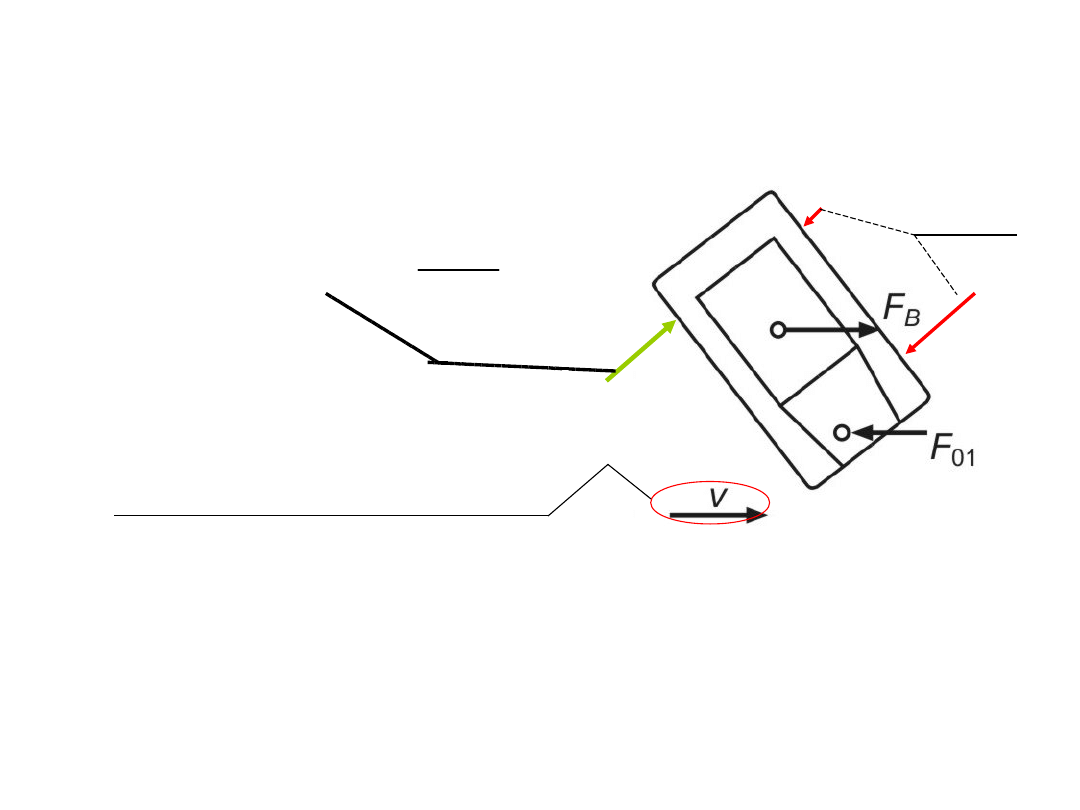
Zarzucanie samochodu w czasie

hamowania

F

Y 2

F

M

L

Y 2

0



Obecność momentu obracającego M

0

wywoła siłę

boczną

, która wynika z
zależności:

Siła ta powinna być zrównoważona przez reakcje boczne w styku
kół z drogą . Jednak na kołach tylnych mamy

0

2



Y

.

Zamierzony kierunek jazdy

Reakcje
boczne

Pojazd rozpocznie ruch obrotowy wokół środka osi kół
przednich, ponieważ te koła nie zarzucą. Dysponują one
możliwością wytworzenia reakcji stycznych bocznych

0

1



Y

Hamowanie na nawierzchni o różnej

przyczepności

Rozważania mogą dotyczyć także pojazdu, którego
hamulce są źle wyregulowane. Zakłócenie stateczności
ruchu nastąpi także podczas hamowania, przy różnej
przyczepności po lewej i prawej stronie samochodu
. Rozważono dwa przypadki:
- hamowanie z zablokowanymi kołami osi tylnej,
- hamowanie z zablokowanymi kołami osi przedniej.

split





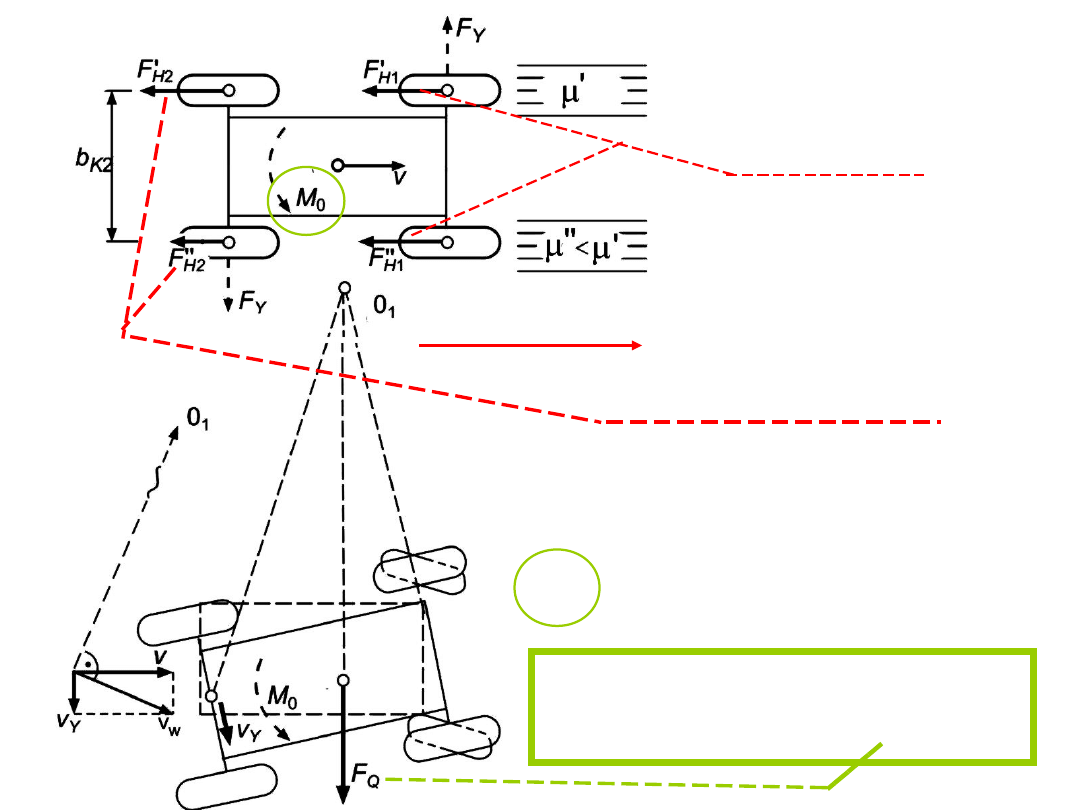
Przypadek A: hamowanie z zablokowaniem kół osi
tylnej na nawierzchni o różnej przyczepności













.

1

1

1

1

5

,

0



F

F

F

F

H

H

H















Zatem

Koła przednie nie
są zablokowane,
a więc siły są
równe

Koła tylne są zablokowane.
Zatem

MAX

H

MAX

H

F

F

,

2

,

2





















,

ponieważ

Równe siły
hamowania

Nierówne siły
hamowania

Kierunek jazdy

Na osi tylnej powstaje
moment dążący do obrócenia
pojazdu

2

,

2

,

2

0

)

(

K

MAX

H

MAX

H

b

F

F

M











Powstaje bardzo
niekorzystne
oddziaływanie siły

F

Q

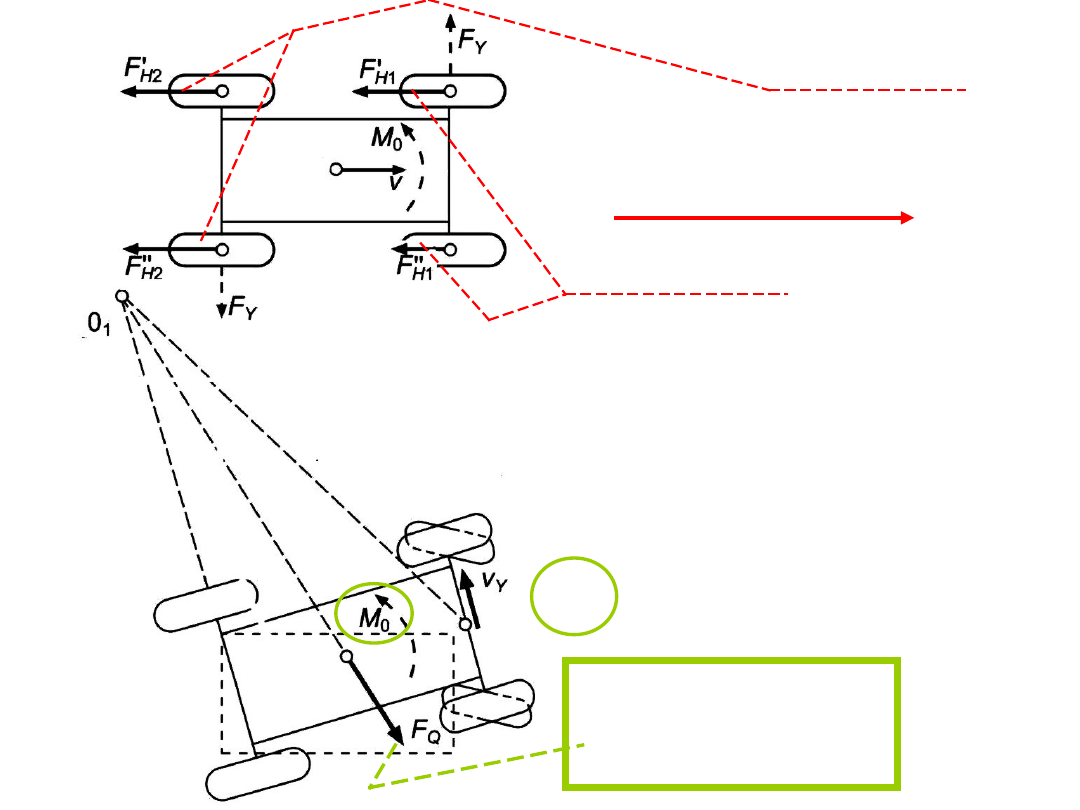
Przypadek B: hamowanie z zablokowaniem kół osi

przedniej

2

2

2

5

,

0

H

H

H

F

F

F























2

2

Z

F

Podczas tego hamowania na kołach osi tylnej (jako nie
zablokowanych) występują jednakowe siły hamowania

,

których wartości są mniejsze od siły przyczepności

,

MAX

H

MAX

H

F

F

,

1

,

1





















Koła osi przedniej zostały zablokowane .Wystąpią
zatem na nich różne wartości sił hamowania, bo
przyczepność tych kół jest różna

ponieważ

Równe siły
hamowania

Nierówne
siły
hamowania

Kierunek
jazdy

Powstanie momentu
obracającego od sił
hamowania na osi przedniej

1

,

1

,

1

0

)

(

K

MAX

H

MAX

H

b

F

F

M











Powstaje korzystne
oddziaływanie siły
odśrodkowej

Hamowanie z układem ABS

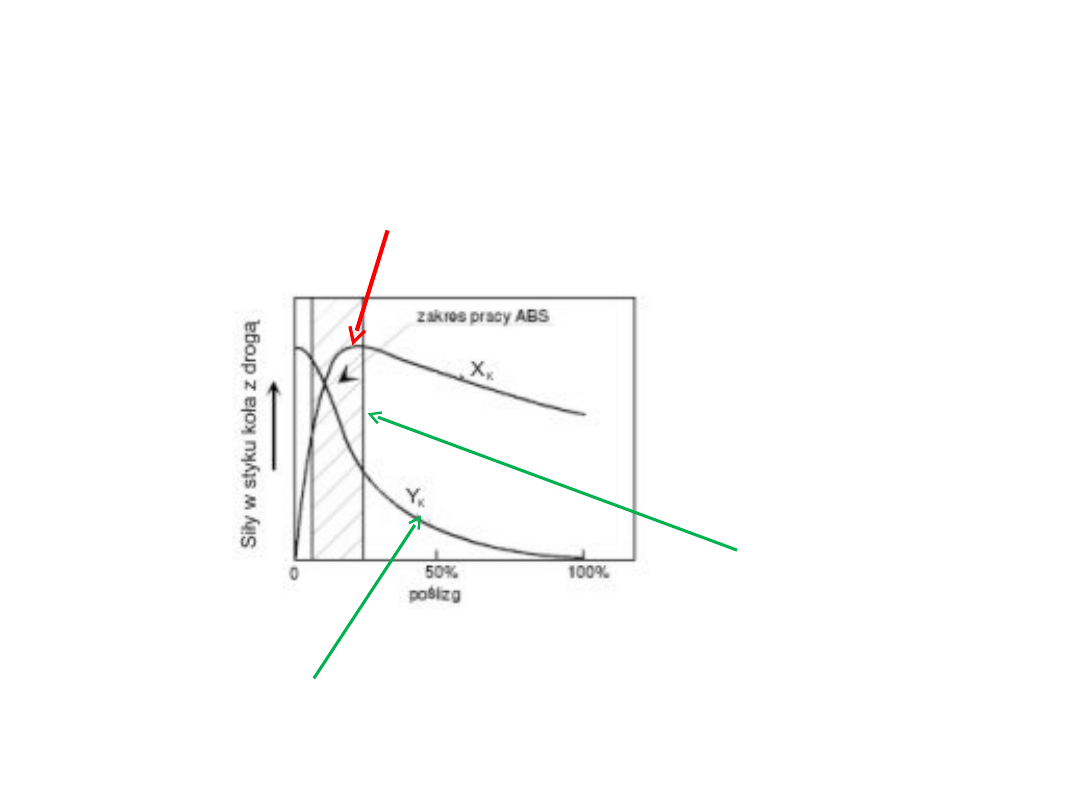
Dysponowana reakcja
styczna obwodowa na
kole

Dysponowana reakcja
styczna boczna na kole

Obszar zmian
poślizgu koła, w
którym
dysponujemy
dużą wartością
reakcji
obwodowej i dość
dużą wartością
reakcji bocznej

Zakres poślizgu, w którym powinien być
realizowany proces hamowania

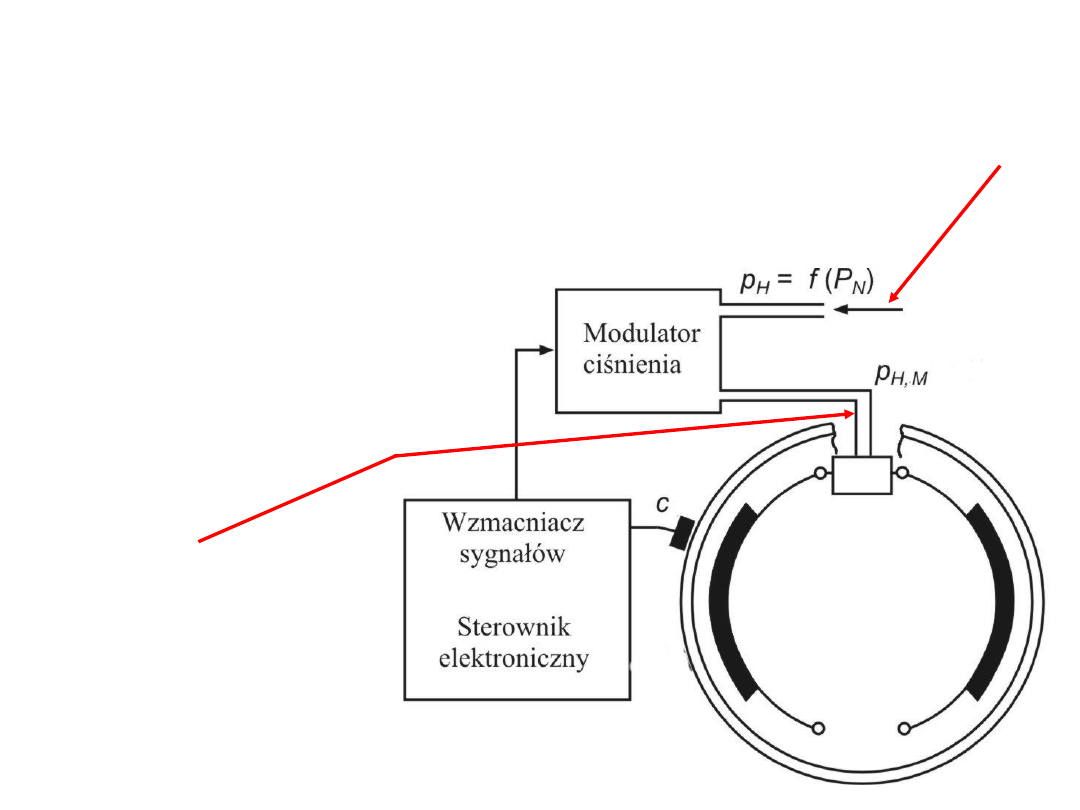
Układy regulacji poślizgu kół podczas

hamowania.

- ciśnienie w układzie uruchamiania
hamulców, zależne od nacisku

na pedał , hamulca

 - ciśnienie

w

rozpieraczu i-tego

koła

(po

modulacji)

Blokowanie kół
podczas hamowania
obniża efektywność
hamowania,
przyspiesza zużycie
opon i może być
przyczyną utraty
stateczności ruchu
(zarzucenie osi kół).

ABS

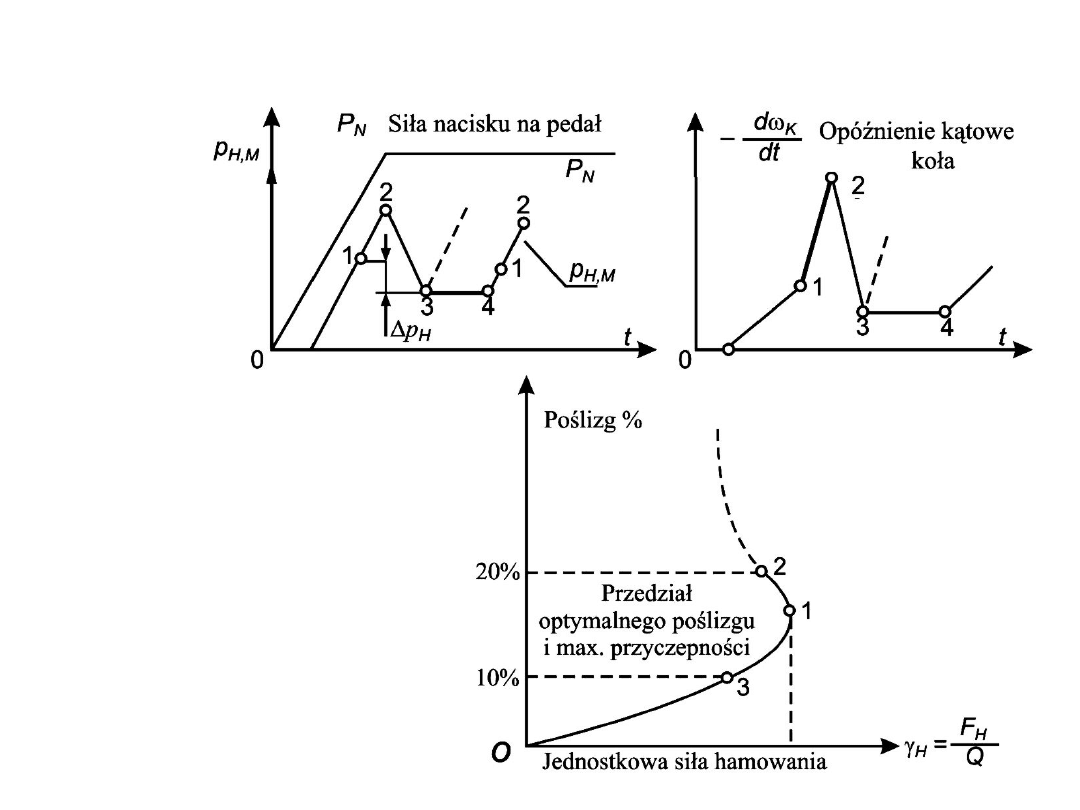
Układy regulacji poślizgu, cd

Proces
hamowania z
wykorzystanie
m ABS

37

Minimalny odstęp i hamowanie w

kolumnie

38

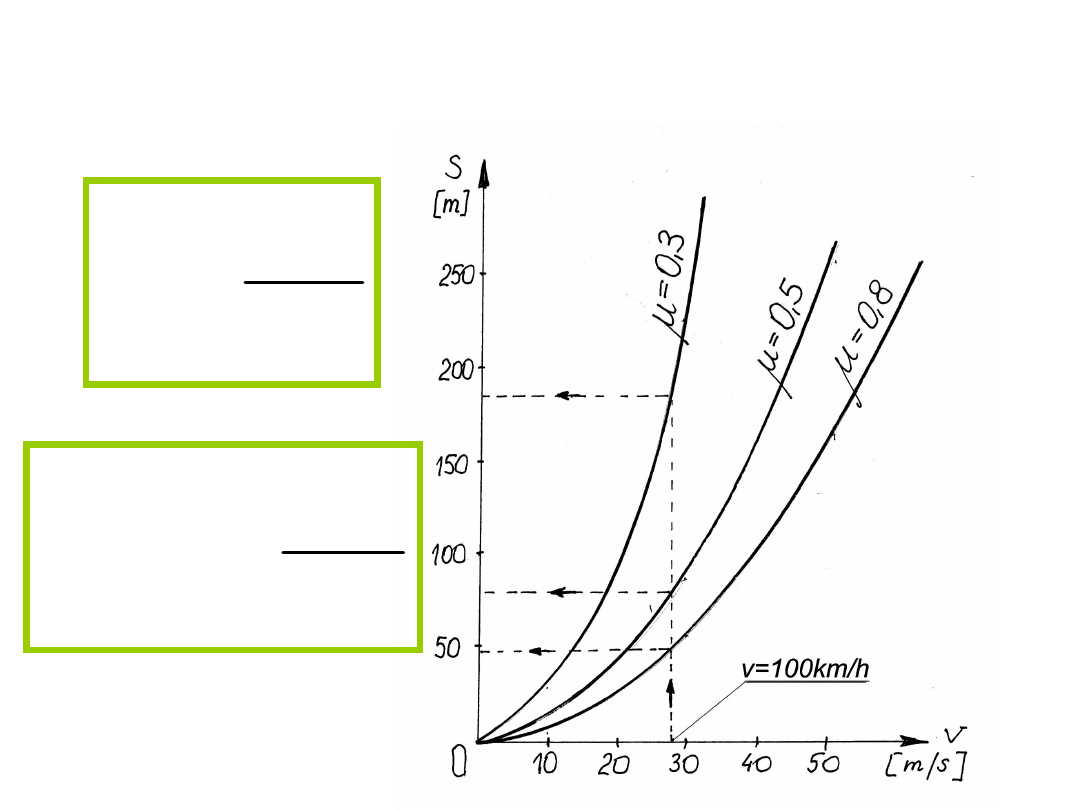
Długość drogi hamowania

39

Długość drogi zatrzymania

MIN

H

P

U

RK

Z

S

v

t

t

S

,

2





















g

v

v

S

K

P

MIN

H

2

2

2

,





Występująca w tym wyrażeniu suma została oznaczona

R

U

RK

t

t

t





2

40

Długość drogi hamowania

Samochód Golf IV, droga hamowania od prędkości
v=100km/h do zatrzymania

- ogumienie Michelin Energy MXV3A
43,8m
- ogumienie Conti Eco Contact CP
46,6m.

Samochód Audi A4, droga hamowania na nawierzchni
mokrej, jw.

- ogumienie Michelin Alpin 2
61,8m,
- ogumienie Fulda Kristall Montero
69,0m.

Samochody dostawcze, hamowanie od prędkości
v=100km/h
VW T4 48,8m
Mercedes Sprinter 412D 54,9m
Iveco Turbodaily
61,7m.

41

Jazda w kolumnie, hamowanie

Jaki odstęp należy zachować do pojazdu
poprzedzającego podczas jazdy w kolumnie?

Rozważono ruch samochodów w kolumnie
poruszającej się z prędkością

O

v

Samochód A rozpoczyna gwałtowne hamowanie z
opóźnieniem .

HA

a

Jadący za nim samochód B rozpocznie

hamowanie po upływie czasu , jaki minie
od chwili włączenia się świateł stop w
samochodzie poprzedzającym A

R

t

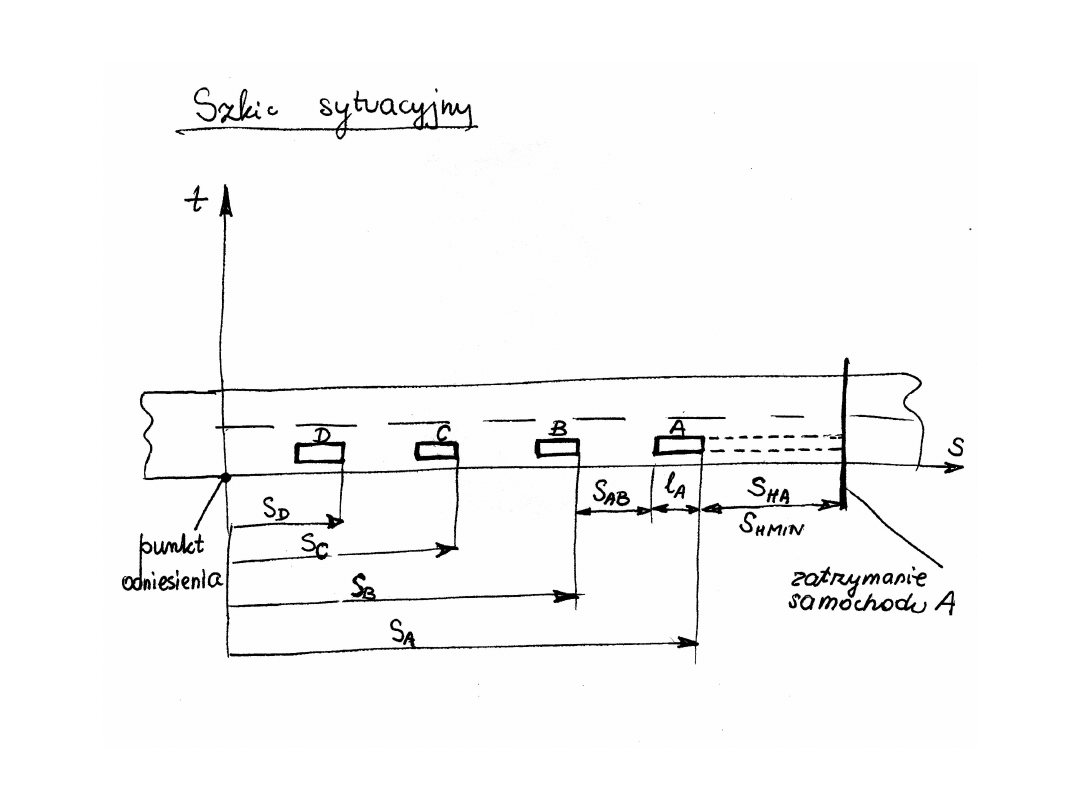
42

43

Parametry hamowania

Droga i czas hamowania samochodu A w
ruchu jednostajnie opóźnionym

HA

O

HA

a

v

S

2

2



HA

O

A

a

v

t 

Droga i czas do zatrzymania samochodu B

HB

O

U

RK

O

HB

a

v

t

t

v

S

2

)

2

(

2







HB

O

U

RK

B

a

v

t

t

t







2

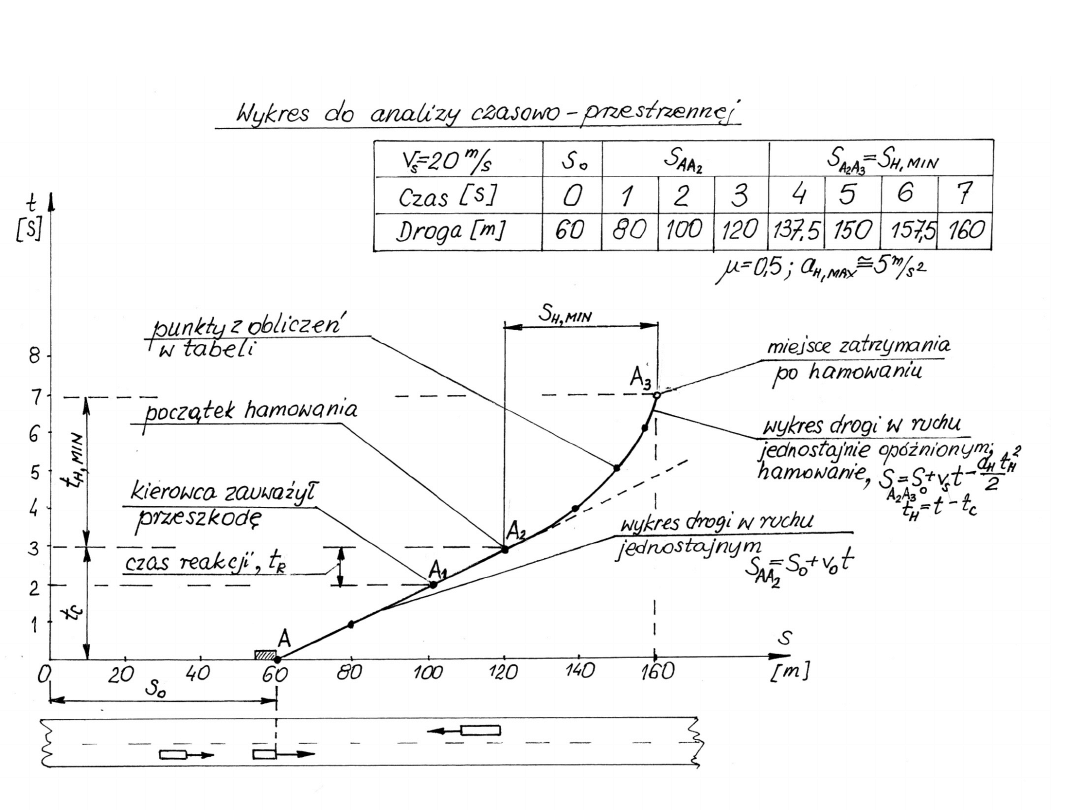
44

Obliczenia do wykresu

45

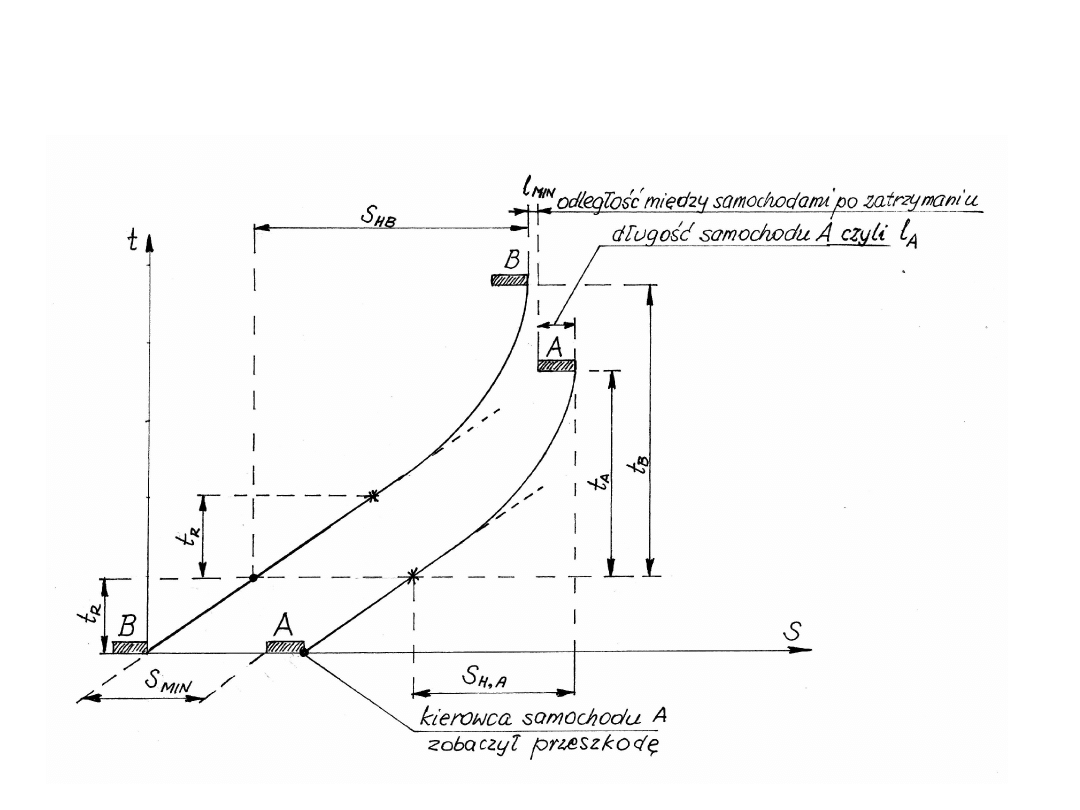
Odstęp między pojazdami

46

Minimalny odstęp między pojazdami w kolumnie,

przed rozpoczęciem hamowania, obliczono z

równości:

HA

A

MIN

A

MIN

HB

S

l

S

l

l

S











przyjmując minimalną odległość

0



MIN

l

mamy

HA

HB

MIN

S

S

S





Zakładając, że samochody osiągają takie same
wartości opóźnienia hamowania, tj.

HB

HA

a

a 

)

2

(

U

RK

O

MIN

t

t

v

S





47

Oszacowanie minimalnego

odstępu

Często w obliczeniach przyjmuje się, że
suma

sekunda

t

t

U

RK

1

2





]

[

]

[

1

]

[

m

v

s

s

m

v

S

O

O

MIN







Zatem mamy

Zatem, gdy kolumna samochodów jedzie z
prędkością 60 – 80 km/h czyli 17 – 22 m/s,
minimalny odstęp między pojazdami nie
powinien być mniejszy niż 17 – 22 m.

48

Przyjmowanie

dla różnych samochodów

i kierowców jest zbyt optymistyczne.

HB

HA

a

a 

sekunda

t

t

U

RK

1

2





Należy bardziej ostrożnie zakładać

g

a

a

HB

HA



2

.

0





s

t

RK

1



s

t

U

5

.

0



49

Praktyczne oszacowanie odległości

Kolumna samochodów jedzie z prędkością
60 – 80 km/h

m

S

MIN

34

..

25



7

.

0





m

S

MIN

38

...

28



45

.

0





m

S

MIN

50

...

36



2

.

0



