1
Fale w ośrodkach sprężystych
Fale mechaniczne
Jeśli jakimś miejscu ośrodka sprężystego wywołamy drganie,
to drgająca cząstka pociągnie za sobą kolejne cząstki i ruch drgający będzie
się przenosić od cząstki do cząstki z pewną prędkością v.
Takie rozchodzenie się drgań w ośrodku nazywamy falą.
Fale powstające w ośrodkach sprężystych (np. fale dźwiękowe) nazywamy
falami mechanicznymi
. Należy podkreślić, że poszczególne cząstki ośrodka
nie przemieszczają się, wykonują tylko drgania wokół swoich położeń
równowagi.
2
Cechą charakterystyczną fal jest to, że przenoszą energię poprzez materię
Dzięki przesuwaniu się zaburzenia w materii a nie dzięki ruchowi postępowemu
samej materii.
Do rozchodzenia się fal mechanicznych potrzebny jest ośrodek –
właściwości sprężyste ośrodka decydują o prędkości rozchodzenia się fali.
Ze względu na kierunek drgań cząstek względem kierunku rozchodzenia się
fali wyróżnia się:
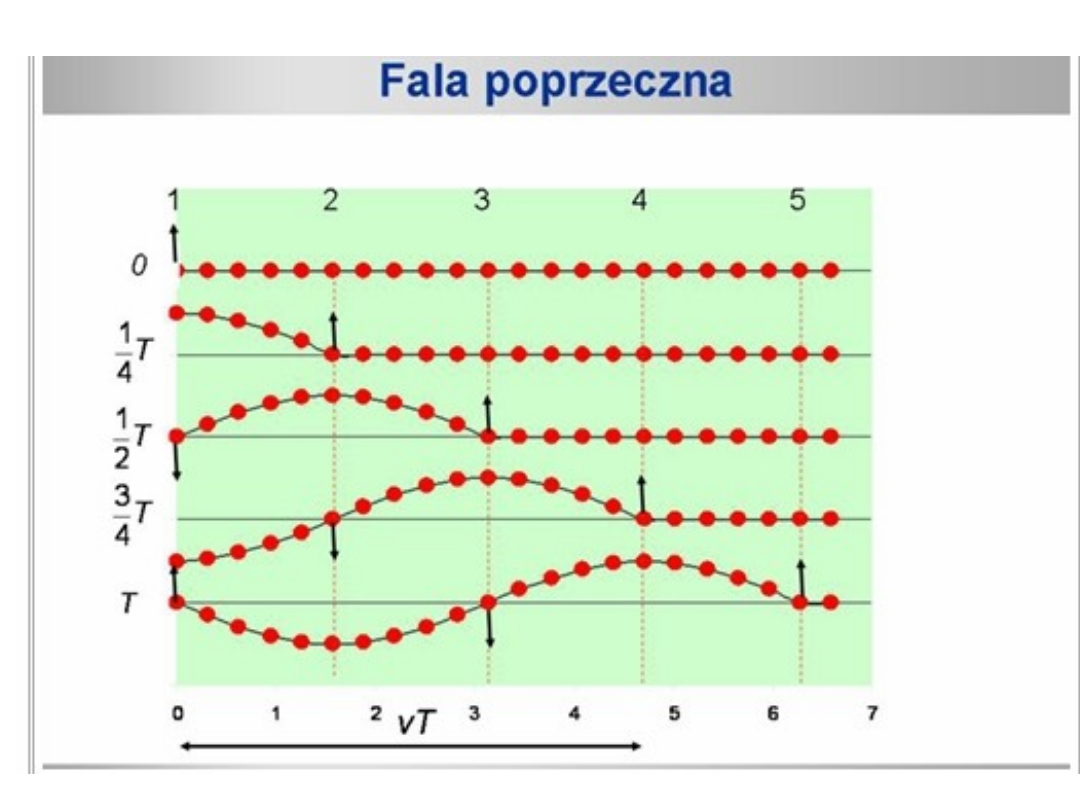
fale poprzeczne - jeśli drgania zachodzą w kierunku prostopadłym
do kierunku rozchodzenia się fali;
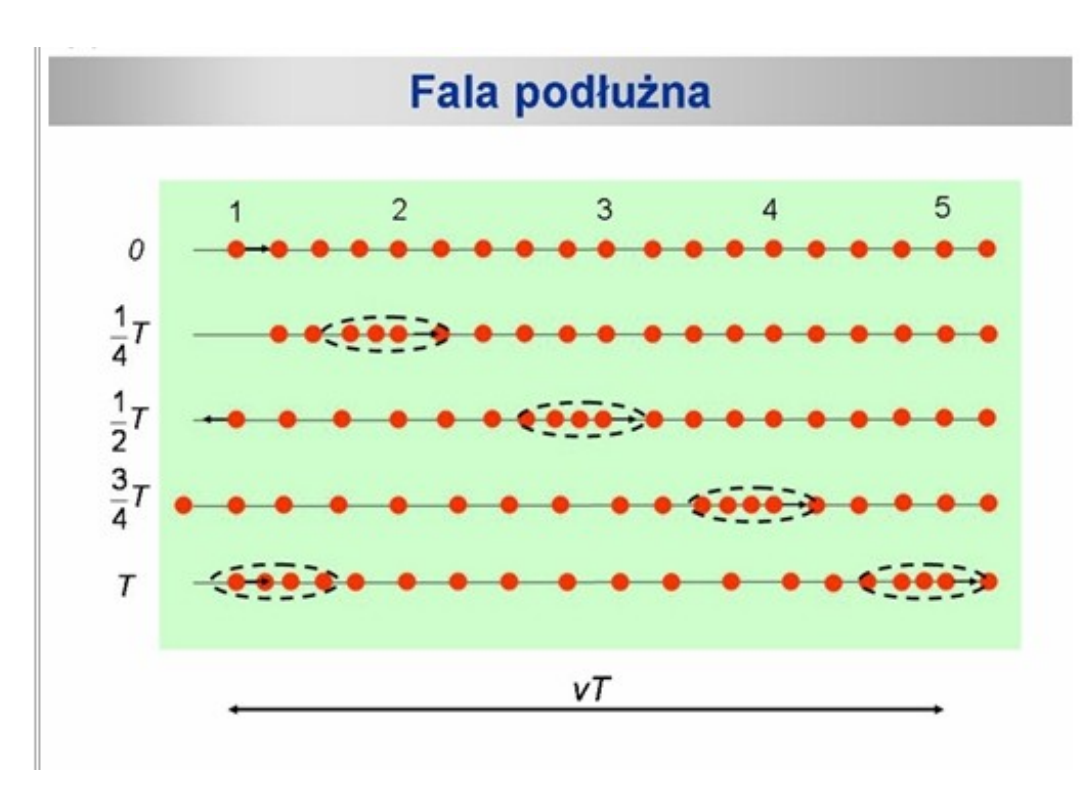
fale podłużne - jeśli drgania zachodzą w kierunku równoległym
do kierunku rozchodzenia się fali.
3
4
5
6
7
Podczas rozchodzenia się fali w drganiach biorą udział nie tylko
cząstki leżące na osi
jak na poprzednich rysunkach, lecz układ cząstek znajdujących się
w pewnej objętości
.
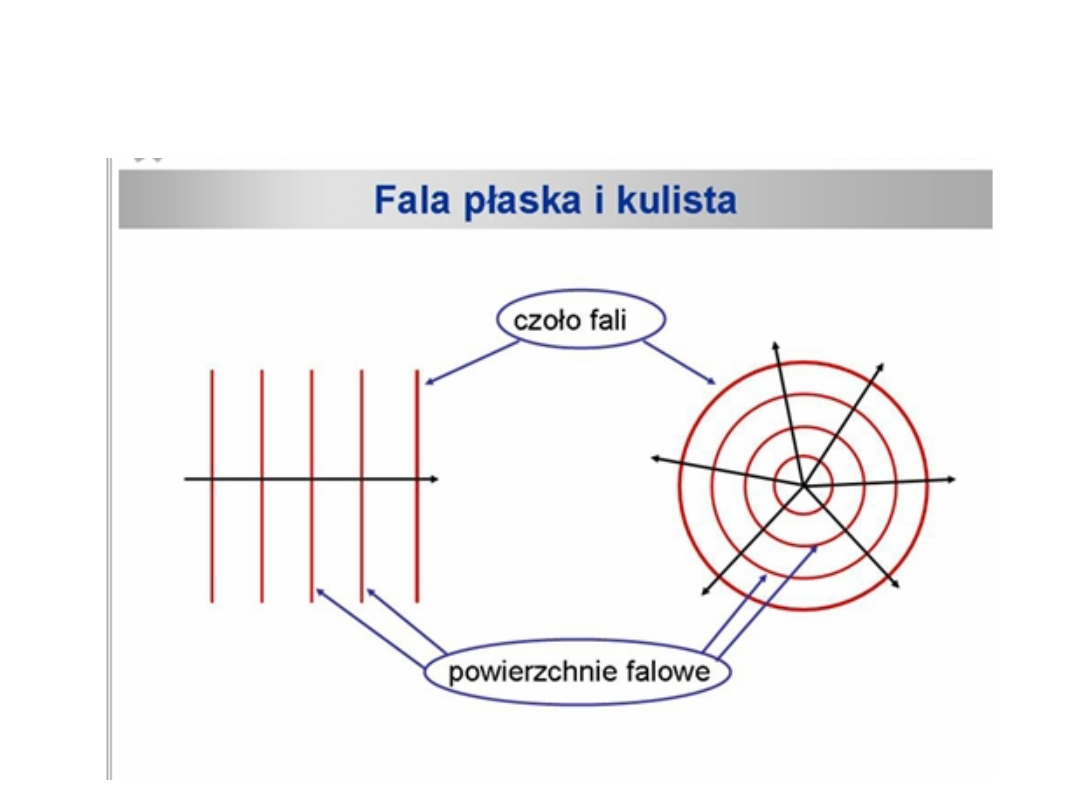
Zbiór punktów, do których fala dochodzi w danej chwili nazywamy czołem fali.
Zbiór punktów drgających w tej samej fazie nazywamy powierzchnią falową.
Przez każdy punkt biorący udział w ruchu falowym można przeprowadzić
powierzchnię falową.
Powierzchni falowych jest, więc, nieskończenie wiele,
ale czoło fali jest tylko jedno.
8
Spośród wszystkich możliwych kształtów powierzchni falowych wyróżniamy takie,
które są płaszczyznami i powierzchniami kulistymi. Fale takie nazywamy
odpowiednio falą płaską i falą kulistą.
9
10
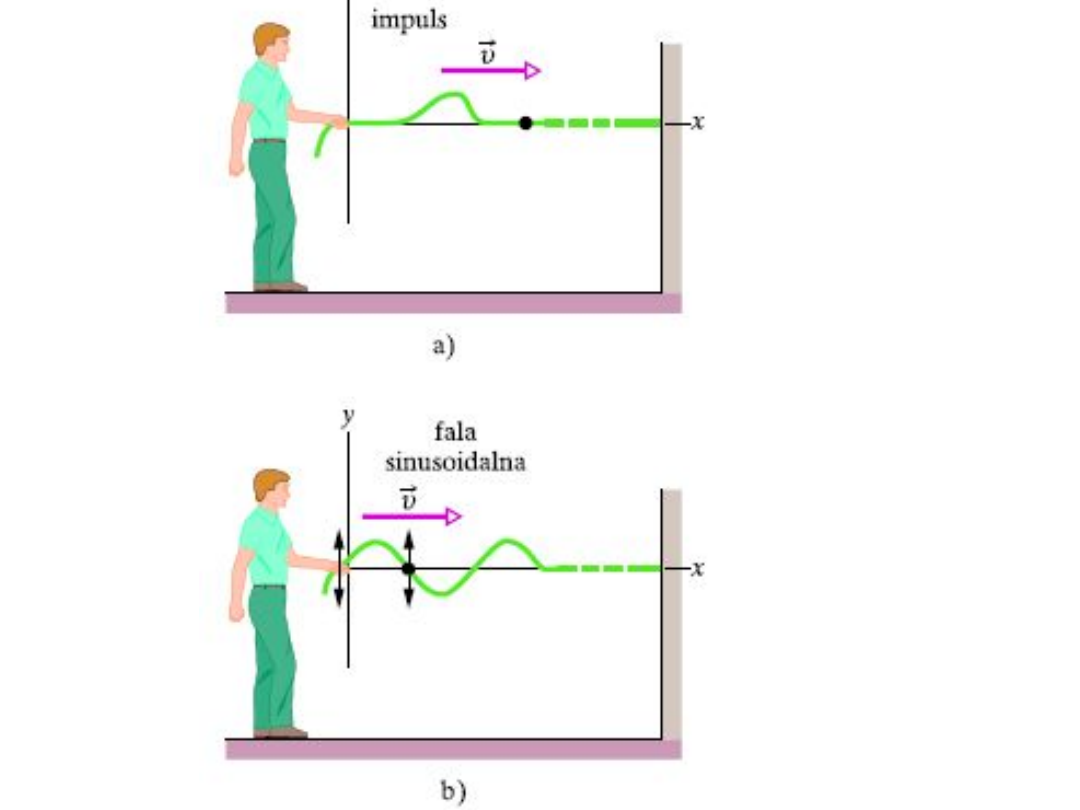
Rozważmy długi sznur naciągnięty w kierunku x, wzdłuż którego biegnie
fala poprzeczna.
W dowolnej chwili np. t = 0 kształt sznura można opisać funkcją
y = f(x),
t = 0
y – przemieszczenie cząsteczek sznura
W miarę upływu czasu fala biegnie wzdłuż sznura bez zmiany kształtu.
Po czasie t fala przesuwa się o vt w prawo (v - prędkość fali).
Zatem po czasie t równanie krzywej ma postać
y = f(x
vt)
11
Oznacza to, że w chwili t w punkcie x = vt, kształt jest taki sam jak w chwili t = 0
W punkcie x = 0.
Mamy, więc, równanie fali tylko trzeba określić funkcję f.
Jeżeli śledzimy wybraną część fali, czyli określoną fazę,
to musimy zbadać jak zmienia się w czasie wybrana wartość y
(np. maksimum - amplituda).
Chcemy, żeby y było cały czas takie samo,
więc argument x
- vt musi być taki sam, a to oznacza,
że gdy czas rośnie to musi też rosnąć x (czyli ruch w prawo).
Fala w lewo jest, więc, opisana równaniem y = f(x+vt).
Podsumowując, dla wybranej fazy mamy
x
vt = const.
12
Różniczkując względem czasu
0
d
d
v
t
x
v
t
x
d
d
To jest
prędkość fazowa
.
Zauważmy, że dla danego t mamy równanie f(x),
a dla danego miejsca sznura x mamy równanie
f(t)
13
Rozważmy teraz fale o szczególnym kształcie.
Załóżmy, że w chwili t = 0 kształt sznura jest opisany funkcją
x
A
y
2
sin
gdzie A jest maksymalnym wychyleniem
Zauważmy, że wychylenie jest takie samo w punktach x, x +
, x + 2
, x + 3
itd.,
jest długością fali (odległość między punktami o tej samej fazie).
Jeżeli fala biegnie w prawo, to po czasie t
)
(
2
sin
t
x
A
y
v
Otrzymaliśmy równanie fali biegnącej.
14
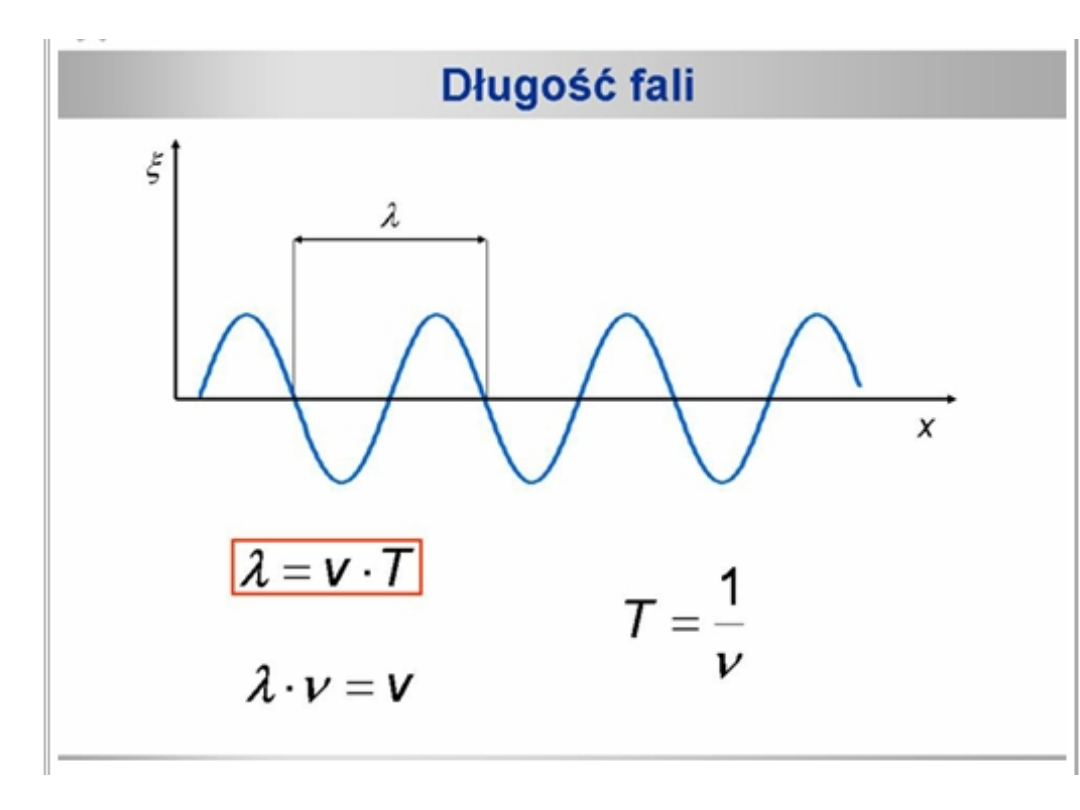
Okres T jest czasem, w którym fala przebiega odległość równą
, więc:
= vT
stąd
T
t
x
A
y
2
sin
Widać, że w danej chwili taka sama faza jest
w punktach x, x +
, x + 2
, x + 3
itd.,
oraz, że w danym miejscu faza powtarza się
w chwilach t, t + T, t +2T, itd.
15
Często wprowadza się dwie nowe wielkości:
liczbę falową k = 2/
i częstość
= 2/T
Wówczas y = Asin(kx-
t) lub y = Asin(kx+
t) dla fal biegnących
w prawo i lewo.
prędkość fazowa fali v jest dana wzorem
v =
/T =
/k
,
a dla danego x otrzymujemy równanie ruchu harmonicznego prostego.
Document Outline