Charakterystyki częstotliwościowe

Ogólnie dowolną transmitancję można przedstawić w
postaci czynnikowej:

czyli zbudowanej z członów podstawowych:

, ,
gdzie wprowadziliśmy częstość znormalizowaną
=T.
Wykresy Bodego tych członów z wykładnikiem –1
przedstawia poniższy rysunek

 





 





 























]

2

1

[

1

]

2

1

[

1

2

2

s

T

s

T

s

T

s

s

T

s

T

s

T

s

k

s

G

m

m

m

i

N

l

l

l

j

L









1

1





 j

   





1

2

2

1











j

j

l



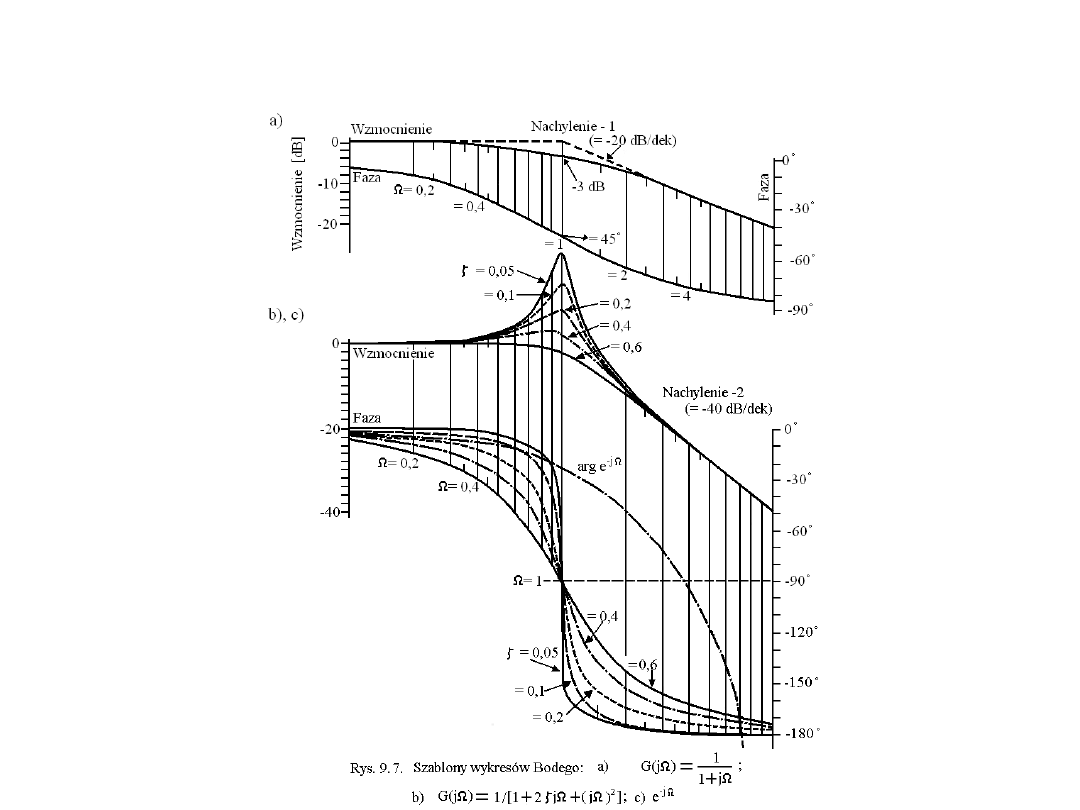
Charakterystyki częstotliwościowe

Minimalnofazowość układu

• Jak widzimy, po przekroczeniu częstości =1, charakterystyki

amplitudowe spadają w tempie –20dB/dek lub –40dB/dek.

Natomiast fazy dążą odpowiednio do: -90o oraz -180o. Mamy

więc ścisły związek pomiędzy charakterystyką fazową i

charakterystyką amplitudową. Takie układy nazywamy

minimalnofazowymi. Powyższe spostrzeżenia nie dotyczą członu

opóźniającego typu e-sT.

• Dla wykładnika +1 (czynniki w liczniku transmitancji) znaki na

osiach rzędnych zmieniają się na dodatnie. Tym samym wykresy

dla przypadku +1 oraz –1 są lustrzanymi odbiciami względem

osi 0[dB] i 0[deg].

• Układy, w których występują zera, zlokalizowane w LPP,

nazywamy układami nieminimalnofazowymi. Jak się okaże

później obiekty nieminimalnofazowe są kłopotliwe w sterowaniu.

• Niestety, sterowanie cyfrowe wprowadza dodatkowe opóźnienie

w przesyłaniu sygnału, które związane jest z z okresem

próbkowania. Tym samym układy ze sterowaniem cyfrowym

należy zaliczyć do układów nieminimalnofazowych. Opóźnienie

fazowe można ograniczyć przez zmniejszenie okresu

próbkowania.

Aproksymacja Pade

• Aproksymacja Pade stanowi bardzo dogodny do obliczeń sposób

przybliżania transmitancji członu opóźniającego przez pewną

transmitancję będącą funkcją wymierną w dowolnie szerokim (ale

skończonym) zakresie częstotliwości. Aproksymacja polega na

przedstawieniu transmitancji linii opóźniającej o

• opóźnieniu transportowym To w postaci ilorazu:

• .

• Następnie rozkłada się oddzielnie licznik i mianownik powyższego

wyrażenia w szereg potęgowy. Gdy ograniczymy się do wyrazów

liniowych, to mamy:

• Tę aproksymację nazywamy aproksymacją Pade 1-go rzędu.

Pozwala ona sprowadzić transmitancję niewymierną do

transmitancji w postaci wymiernej. Zauważmy, że aproksymacja

wprowadza zero leżące w lewej półpłaszczyźnie (LPP) zmiennej

zespolonej s. Układy, w których występują zera, zlokalizowane w

LPP, nazywamy układami nieminimalnofazowymi.

2

2

0

0

0

T

s

T

s

sT

e

e

e







2

1

2

1

0

0

0

T

s

T

s

e

sT









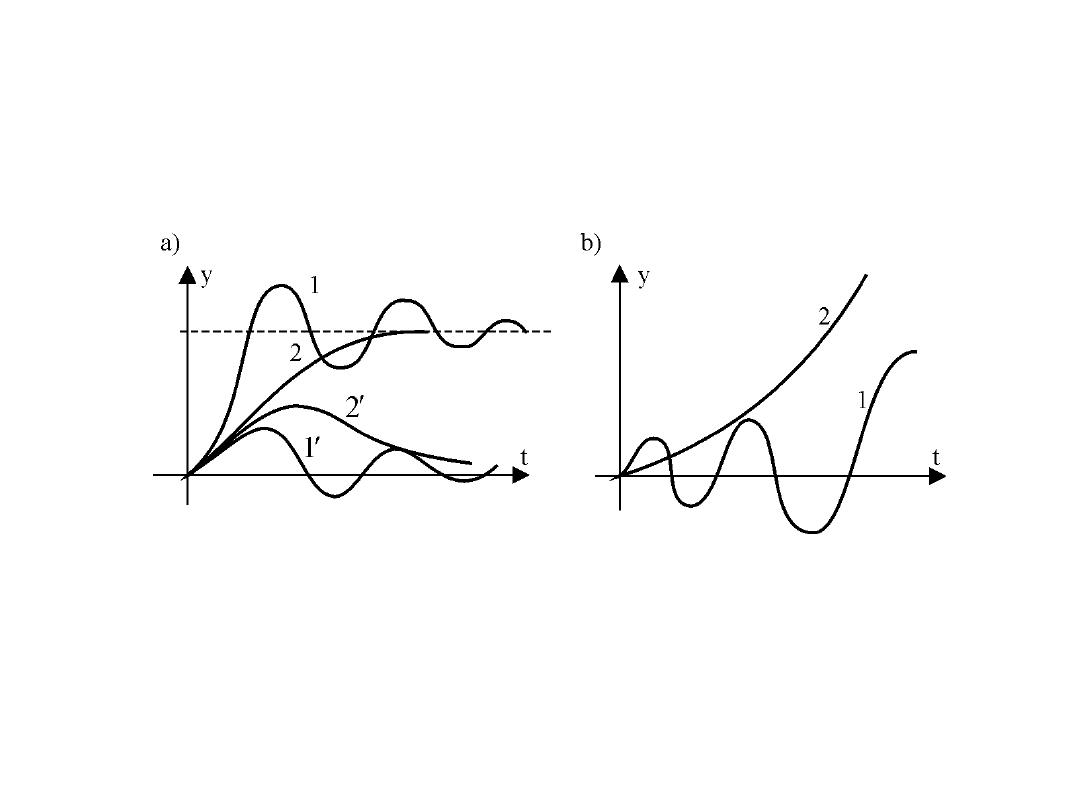
Stabilność

• Stabilność jest to własność układu dynamicznego, polegająca na powracaniu układu,

po ustaniu działania zakłócenia, do pierwotnego stanu ustalonego lub na osiąganiu

nowego stanu ustalonego, jeśli zakłócenie pozostało na stałym poziomie. Przebiegi

przejściowe tej wielkości dla układów stabilnych i niestabilnych pokazano na rysunku

• W niniejszym rozdziale ograniczymy się do pokazania metod badania stabilności

układów liniowych. Omówienie stabilności układów nieliniowych przestawione później.

• Jak pokażemy, badanie stabilności układu liniowego można sprowadzić do badania

rozwiązań równań opisujących dynamikę badanego obiektu. W epoce komputerów i

dostępnego oprogramowania jest to zadanie stosunkowo proste. Jednakże rozwiązanie

równań przeprowadza się dla ustalonego zestawu parametrów i często trudno jest na

podstawie takiego rozwiązania wyciągnąć ogólne wnioski, co do zachowania się układu

w przypadku zmiany tych parametrów oraz wnioski, co do zasad projektowania układu

sterowania dla badanego obiektu. Takie możliwości dają kryteria stabilności.

Badanie rozwiązań równań

dynamicznych

•

. Zachowanie się liniowego układu w stanie nieustalonym opisuje równanie o postaci:

•

.

•

W stanie ustalonym (stanie równowagi) pochodna jest równa zero, mamy więc:

•

.

•

Rozważmy dwa przypadki. W pierwszym zakładamy, że macierz A jest nieosobliwa. Jeśli

przyjmiemy, że nie ma wymuszenia u(t), to:

•

Ax(t)=0

.

•

Gdy A jest macierzą nieosobliwą, to aby powyższe było spełnione, musi być: x(t) =0.

•

Początek przestrzeni stanu: x=0 jest więc punktem równowagi, zwanym również punktem

osobliwym. Pozostaje oczywiście pytanie, czy jest to punkt równowagi stabilnej, to

znaczy, czy układ po wytrąceniu z tego punktu przez oddziaływania zewnętrzne z

powrotem do niego wraca po ustaniu przyczyny. Aby to ustalić rozpatrzymy układ w

stanie ustalonym, gdy działa stałe w czasie wymuszenie: u=const. Wówczas:

•
•

W tym przypadku punkt równowagi x ustalony jest przez stałą wartość u. Oczywiście, gdy

ustanie działanie sygnału u, to układ wróci do początku przestrzeni stanu: x=0 w czasie

procesu przejściowego, pod warunkiem, że układ jest stabilny.

•

W drugim przypadku, gdy macierz A jest macierzą osobliwą, to wówczas punkt: x=0 nie

jest punktem równowagi. Tym samym równaniem równowagi jest:

»

.

Ax=0

 

 

 

t

t

t

Bu

Ax

x







 

 

t

t Bu

Ax

0





)

(

1

Bu

A

x





Badanie rozwiązań równań

dynamicznych

• Jak wynika z powyższych rozważań, o stabilności decyduje

zachowanie się układu podczas procesu przejściowego. Proces

przejściowy opisuje rozwiązanie ogólne (całka ogólna)

jednorodnego równania stanu:

• dx(t)/dt=Ax(t)

Jak

wiemy rozwiązanie ogólne równania stanu ma postać:

•
• W przypadku sygnału wyjść (pomiaru), po uwzględnieniu: y=Cx,

mamy:

• .

•
• Widzimy więc, ze o przebiegu procesu przejściowego decyduje

macierz fundamentalna zbudowana z funkcji wykładniczych

postaci:

• .

• Części rzeczywiste α wykładników muszą być ujemne, aby całka

była zbieżna do zera.

 





 





x

x

A 



t

e

t

 





 





x

C

y

A 



t

e

t













sin

cos

)

(

j

e

e

a

j







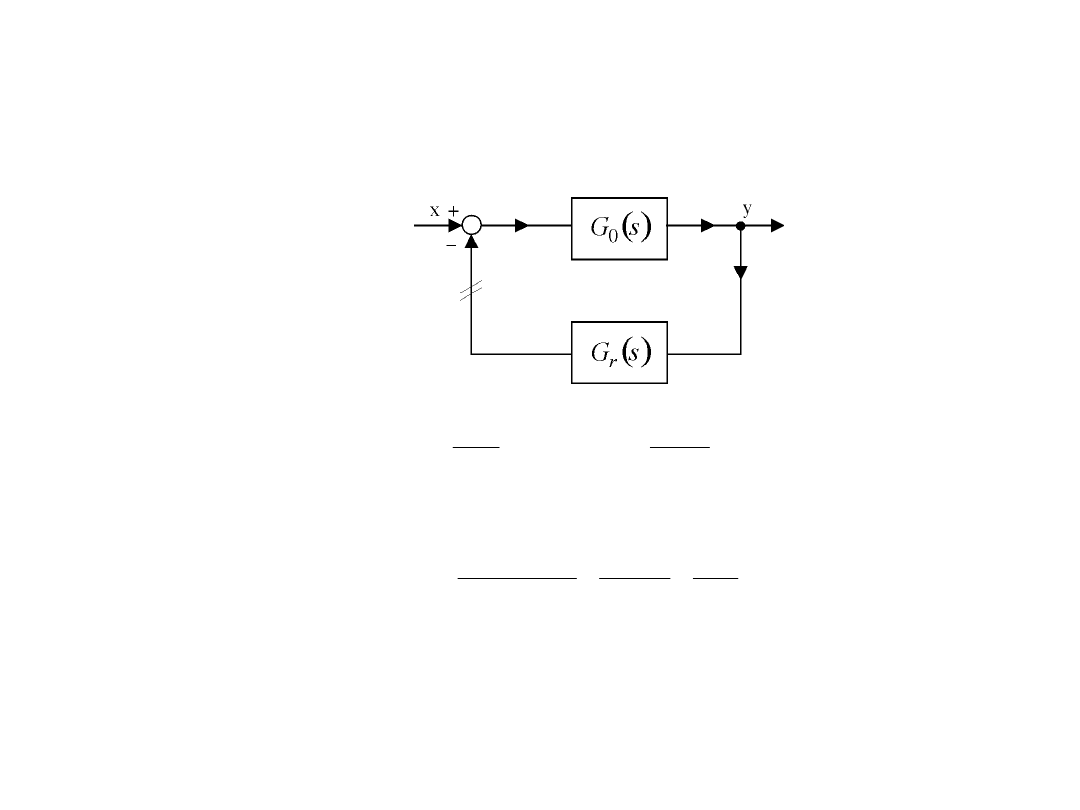
Układ otwarty i zamknięty

•

Kryterium Nyquista pozwala badać stabilność zamkniętego układu automatyki na podstawie

przebiegu charakterystyki amplitudowo-fazowej układu otwartego. Wyznaczenie

charakterystyki amplitudowo-fazowej jest możliwe zarówno poprzez analizę jak i

doświadczalnie.

•

Transmitancja operatorowa układu otwartego, otrzymanego przez przerwanie pętli sprzężenia

zwrotnego, wynosi:

•

Wielomian Mo(s) przyrównany do zera:

•

•

jest równaniem charakterystycznym n-go stopnia układu otwartego. Transmitancja operatorowa

układu zamkniętego wynosi:

•

Równanie:

•

lub

•

jest więc równaniem charakterystycznym n-tego stopnia układu zamkniętego, gdyż stopień

wielomianu Lo(s) jest mniejszy od stopnia wielomianu Mo(s) układu otwartego.

 

 

 

   

 

 

.

0

0

s

M

s

L

s

G

s

G

s

X

s

Y

s

G

o

r









 

 

   

 

 

 

 

.

'

1

1

0

0

0

s

M

s

L

s

G

s

G

s

G

s

G

s

G

s

G

r











0

)

( 

s

M

o

0

)

(

'

1

)

(







s

G

s

M

0

)

(

)

(

)

(

0

0







s

L

s

M

s

M

Warunek stabilności

• Warunek stabilności układu zamkniętego sformułujemy po

zbadaniu przyrostu argumentu funkcji dla pulsacji od zera do

nieskończoności:

• Przypadek 1 — układ otwarty jest stabilny. Jego równanie

posiada n pierwiastków w lewej półpłaszczyźnie.

• Zgodnie z kryterium Michałowa:

• Oraz

• Zmiana argumentu funkcji jest równa różnicy zmian argumentu

licznika i mianownika:

• Stąd:

 





 

 













































j

M

j

M

j

G

0

0

arg

0

'

1

arg

 

2

arg

0

0







n

j

M











 

.

2

arg

0







n

j

M











 





 

 

.

arg

arg

'

1

arg

0

0

0

0













j

M

j

M

j

G































 





.

0

2

2

'

1

arg

0

























n

n

j

G

Kryterium Nyquist’a

• Opierając się na powyższym warunku można sformułować kryterium

Nyquista.

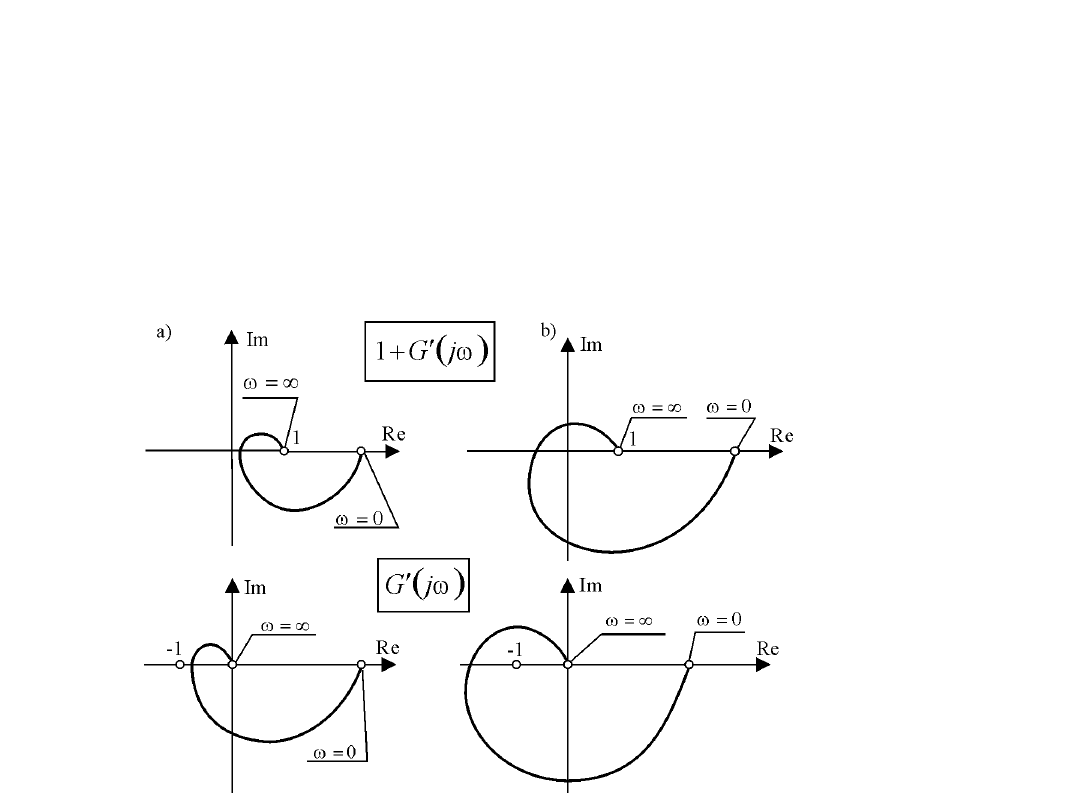
• Układ zamknięty jest stabilny, jeżeli charakterystyka amplitudowo-

fazowa układu otwartego nie obejmuje punktu dla pulsacji

zmieniającej się od 0 do . Przykładowe wykresy krzywych oraz

układów stabilnych (a) i niestabilnych (b) pokazano na rysunku.

Kryterium Nyquist’a

• Przypadek 2 - układ otwarty jest niestabilny. Jego równanie

charakterystyczne zawiera m pierwiastków w prawej półpłaszczyźnie, a

pozostałe (n-m) w lewej półpłaszczyźnie płaszczyzny pierwiastków.

• Zgodnie z kryterium Michajłowa zmiana argumentu równania

charakterystycznego układu otwartego wynosi:

• Układ zamknięty będzie stabilny, jeśli zmiana argumentu równania

charakterystycznego będzie równa:

• Warunek stabilności na podstawie zależności (10.30) można zapisać

następująco:

•
• Opierając się na powyższym warunku można sformułować kryterium

Nyquist’a dla przypadku, gdy układ otwarty jest niestabilny.

• Jeżeli otwarty układ automatyki jest niestabilny, a jego równanie

charakterystyczne posiada pierwiastków w prawej półpłaszczyźnie

płaszczyzny pierwiastków, to będzie on stabilny po zamknięciu, jeśli

charakterystyka amplitudowo – fazowa układu otwartego dla pulsacji

zmieniającej się od 0 do ∞ okrąża n-m razy punkt w kierunku dodatnim

(przeciwnym do ruchu wskazówek zegara).

 





.

2

2

0

arg

0







m

n

j

M













 

0



s

M

 

.

2

arg

0







n

j

M











 









.

2

2

2

2

2

'

1

arg

0

m

m

n

n

s

G

























Logarytmiczne kryterium

Nyguista. Zapas stabilności

• Z warunku stabilności układu

zamkniętego wynika, że wykres

nie może obejmować początku

układu współrzędnych, natomiast

nie może obejmować punktu

. Stąd:

• dla ,

• Warunek ten można zapisać:
•

 



j

G'

1

 



j

G'





0

,

1 j



 













j

G

arg

 

 

.

0

log

20











j

G

L

 

1







j

G

Zapas modułu i fazy

Zapas modułu i fazy

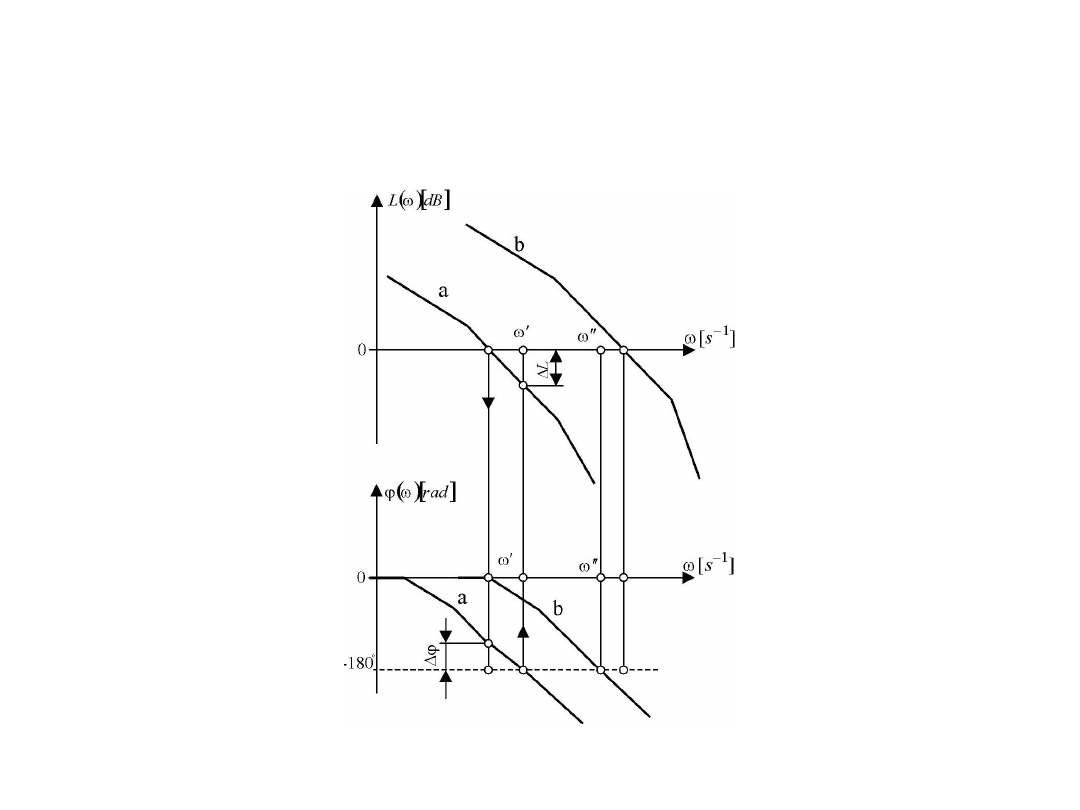
• Na podstawie powyższych warunków można sformułować

logarytmiczne kryterium Nyquista w sposób następujący.

Zamknięty układ jest stabilny, jeżeli charakterystyka

amplitudowa układu otwartego ma wartość ujemną

przy pulsacji odpowiadającej przesunięciu fazowemu

. Na powyższym rysunku przedstawiono

logarytmiczne charakterystyki amplitudowe i fazowe

układów otwartych, przy czym: a – układ zamknięty

stabilny, b – układ zamknięty niestabilny. Oznaczone na

rysunku :

• - zapas modułu [dB],

• - zapas fazy [rad],

• stanowią liczbową ocenę zapasu stabilności. Przeciętne

wartości tych parametrów w układach przemysłowych

wynoszą ,

 





0

' 



L

'



 











'

L







dB

L 6





.

4

3

2

1

rad







