
Jacek Kabziński
Automatyka i sterowanie
————————————————————————————————————————

2
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
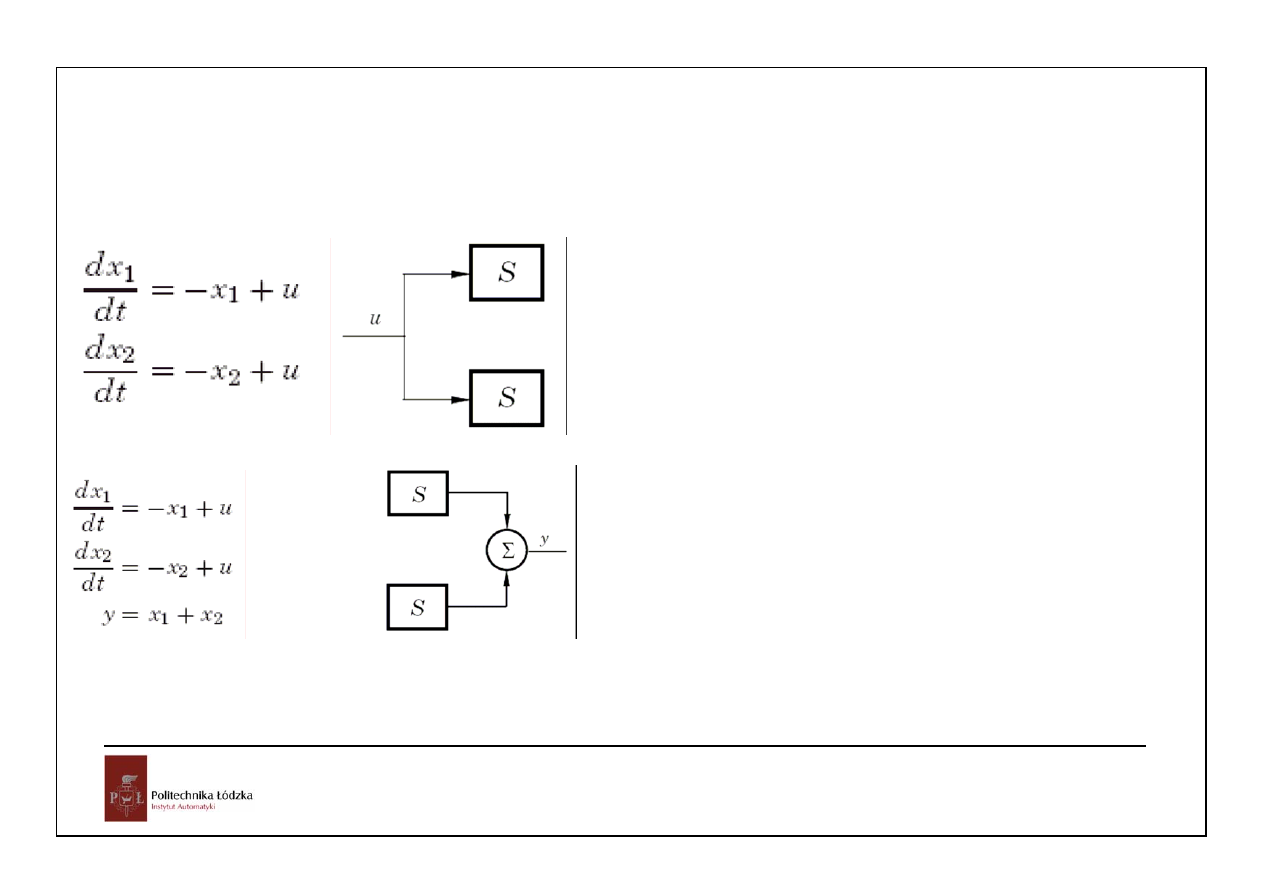
Rozważać będziemy opis układu w postaci:
równanie stanu
d
x( t ) Ax( t ) Bu( t )
dt
y( t ) Cx
równ
(
a
t )
ni
Du(
e wy ś
t )
j cia
=
+
=
+
x(t) – wektor zmiennych stanu o wymiarze nx1,
u(t) – wektor wejść/sterowań o wymiarze rx1
y(t) – wektor wyjść o wymiarze mx1
z warunkiem początkowym x(0)=x
0
lub bardziej ogólnie x(t
0
)=x
0
0
0
0
t
t
x( t )
( t t )x
( t
)Bu( )d
τ
τ τ
= Φ −
+ Φ −
∫

3
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Def.: Stan x
0
nazywać będziemy sterowalnym, jeżeli istnieje ograniczone sterowanie przeprowadzające
układ z x
0
sprowadzające wektor stanu układu z punktu x
0
do 0 w skończonym czasie. Zbiór wszystkich
stanów sterowalnych oznaczymy przez
S
.
T1. Zbiór stanów sterowalnych jest podprzestrzenią liniową przestrzeni stanów.
Dow.:
1
2
x
S , x
S ,
∈
∈
1
1
1
0
0
t
( t )x
( t
)Bu ( )d
τ
τ τ
= Φ
+ Φ −
∫
2
2
2
0
0
t
( t )x
( t
)Bu ( )d
τ
τ τ
= Φ
+ Φ −
∫
niech
2
2
1
2
2
2
1
0
u ( t ) t t
t
t , u ( t )
t
t t
≤
⎧
>
= ⎨
< ≤
⎩
1
2
2
0
0
t
( t )x
( t
)Bu ( )d
τ
τ τ
= Φ
+ Φ −
∫
(
)
(
)
1
1
2
1
2
0
0
t
( t ) ax
bx
( t
)B au ( ) bu ( ) d
τ
τ
τ
τ
= Φ
+
+ Φ −
+
∫
czyli
1
2
ax
bx
S
+
∈

4
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Lemat:
1
0
n
i
i
i
( t )
( t )A
ϕ
−
=
Φ
=
∑
Dow.:
Z definicji
2 2
3 3
0
2
3
i i
i
A t
A t
A t
( t ) I
At
!
!
i!
∞
=
Φ
= +
+
+
+
=
∑
Twierdzenie Cayley’a – Hamiltona :
Każda macierz jest spełnia swoje równie charakterystyczne, to jest jeśli
( )
1
1
1
0
det(
)
...
0
n
n
n
sI A
p s
s
b s
b s b
−
−
−
=
=
+
+ +
+
=
jest równaniem charakterystycznym macierzy A, to
0
0
1
1
1
=
+
+
+
+
−
−
I
b
A
b
A
b
A
n
n
n
(
)
1
1
1
0
n
n
n
A
b A
b A b I
−
−
= −
+ +
+
(
)
(
)
1
1
2
1
1
1
0
1
0
n
n
n
n
n
A
AA
b
b A
b A b I
b A
b A
+
−
−
−
⎡
⎤
=
= −
−
+ +
+
+ +
+
⎣
⎦
1
1
1
0
i
i
n
i
i
n
A
A
A
I
λ
λ
λ
−
−
=
+ +
+
5
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
(
)
1
1
1
0
1
1
0
0
0
0
0
i
i
i
i
i
i
i
i
n
i
i
n
n
n
i
i
i
i
t
t
t
t
( t )
A
A
A
I
A
I
i!
i!
i!
i!
λ
λ
λ
λ
λ
∞
∞
∞
∞
−
−
−
−
=
=
=
=
Φ
=
=
+ +
+
=
+ +
∑
∑
∑
∑
Tw.:
1
n
S lin B,AB, ,A B
−
⎡
⎤
=
⎣
⎦
Dow.:
1
n
S
lin B,AB, ,A B
−
⎡
⎤
⊂
⎣
⎦
0
x
S
∈
(
)
0
0
0
0
0
0
t
A t
At
e x
e
Bu( )d
τ
τ τ
−
=
+
∫
0
0
0
t
A
x
e
Bu( )d
τ
τ τ
−
= −
∫
0
0
1
1
1
0
0
0
0
0
0
i
t
t
n
n
n
i
i
i
i
i
i
i
i
i
:
x
(
)A Bu( )d
A B
(
)u( )d
A B
α
ϕ τ
τ τ
ϕ τ
τ τ
α
−
−
−
=
=
=
=−
⎛
⎞
= −
−
= −
−
=
⎜
⎟
⎝
⎠
∑
∑
∑
∫
∫
Wektor wsp. o wymiarze takim jak
wektor wejść

6
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
czyli
0
1
1
1
0
1
n
n
n
x
B,AB, ,A B
lin B,AB, ,A B
α
α
α
−
−
−
⎡
⎤
⎢
⎥
⎢
⎥
⎡
⎤
⎡
⎤
=
∈
⎣
⎦
⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
Dow.:
1
n
S
lin B,AB, ,A B
−
⎡
⎤
⊃
⎣
⎦
(szkic)
Jeśli
1
0
n
x
lin B,AB, ,A B
−
⎡
⎤
∈
⎣
⎦
, to współczynniki
0
1
1
n
α
α
α
−
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
reprezentacji
0
1
1
0
1
n
n
x
B,AB, ,A B
α
α
α
−
−
⎡
⎤
⎢
⎥
⎢
⎥
⎡
⎤
= ⎣
⎦ ⎢
⎥
⎢
⎥
⎣
⎦
są
określone. Sterowanie wyznaczamy z zależności
0
0
t
i
i
(
)u( )d
α
ϕ τ
τ τ
− =
−
∫

7
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Dokładniej: Rozważmy
0
i
i
x
A B
α
=
. Szukamy sterowania, które
0
0
0
t
i
A
i
x
A B
e
Bu( )d
τ
α
τ τ
−
=
= −
∫
. Załóżmy, że sterowanie będzie
stałe:
0
0
t
A
i
i
e
d Bu
A B
τ
τ
α
−
−
=
∫
Ten układ równań będzie miał rozwiązanie jeśli
0
0
0
0
t
t
A
A
i
i
rank
e
d B
rank
e
d B A B
τ
τ
τ
τ
α
−
−
⎡
⎤
⎡
⎤
−
=
−
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
∫
∫
i tak jest faktycznie, bo
0
0
1
1
0
0
0
0
t
t
n
n
j
i
j
j
i
j
j
j
rank
A B
(
)d
A B
rank
A B
(
)d
ϕ
τ τ
α
ϕ
τ τ
−
−
=
=
⎡
⎤
⎡
⎤
−
=
−
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
∑
∑
∫
∫
Lemat:
{
}
1
1
At
n
n
t lin e
B,AB, ,A B
lin B,AB, ,A B
−
−
⎡
⎤
⎡
⎤
∀
=
⎣
⎦
⎣
⎦
Def.: Stan x
0
nazywać będziemy osiągalnym, jeżeli istnieje ograniczone sterowanie przeprowadzające
układ z x
0
sprowadzające wektor stanu układu z punktu 0 do x
0
w skończonym czasie.
Tw. Stan x
0
jest osiągalny wtedy i tylko wtedy gdy jest sterowalny UKŁAD CIĄŁY!!.

8
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Dow.: x
0
jest sterowalny
0
0
At
e
x
−
⇔
jest sterowalny
0
0
0
0
t
At
A
e
x
e
Bu( )d
τ
τ τ
−
−
⇔
= −
∫
(
)
(
)
0
0
0
0
t
A t
x
e
B u( ) d
τ
τ
τ
−
⇔
=
−
∫
Wniosek:
Jeśli
1
2
x
S , x
S ,
∈
∈
, to istnieje ograniczone sterowanie przeprowadzające układ z x
1
do x
2
w
skończonym czasie.
Def.: Układ, w którym przestrzeń stanów sterowalnych pokrywa się z przestrzenia stanu nazywamy
całkowicie sterowalnym.
Wniosek: Koniecznym I dostatecznym warunkiem całkowitej sterowalności układu jest
1
n
rank B,AB, ,A B
n
−
⎡
⎤ =
⎣
⎦
. Dla układu jednowejściowego B=b :
1
0
n
det b,Ab, ,A b
−
⎡
⎤ ≠
⎣
⎦
1
n
S
Q
B,AB, ,A B
−
⎡
⎤
= ⎣
⎦
macierz sterowalności układu.

9
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Sterowalność a liniowe przekształcenie zmiennych stanu:
wprowadzamy nowe zmienne stanu:
0
Pq( t ) x( t ), det P
=
≠
równanie stanu
d
Pq( t ) APq( t ) Bu( t )
nowe
dt
y( t ) CPq( t ) Du( t )
now
równanie wyjś a
e
ci
=
+
=
+
1
1
równanie st
d
q( t ) P APq( t ) P Bu( t )
nowe
dt
y( t ) CPq( t ) Du( t )
anu
równanie wyjścia
nowe
−
−
=
+
=
+
1
1
d
q( t ) Aq( t ) Bu( t )
A P AP, B P B
dt
y( t ) Cq( t ) Du( t )
C CP
−
−
=
+
=
=
=
+
=
1
1
1
1
1
1
1
n
Sq
n
S
Q
P B,P AB, ,P A B
P
B,AB, ,A B
P Q
−
−
−
−
−
−
−
⎡
⎤
=
=
⎣
⎦
⎡
⎤
=
=
⎣
⎦

10
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Modalny warunek sterowalności:
Tw.: Układ o macierzach
1
1
1
1
1
2
0
0
0
0
0
0
n
n
k nk
k
s I
B
s I
B
A
B
s I
B
⎡
⎤
⎡ ⎤
⎢
⎥
⎢ ⎥
⎢
⎥
⎢ ⎥
=
=
⎢
⎥
⎢ ⎥
⎢
⎥
⎢ ⎥
⎣
⎦
⎣ ⎦
jest całkowicie sterowalny wtedy i tylko
wtedy, gdy
1
i
i
rank B
n
i
,...,k
=
=
.
Dow.:
1
1
1
1 1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
1
2
2
2
2
2
1
1
1
1
1
0
0
0
0
0
0
n
n
n
n
n
n
n
n
n
n
n
S
n
n
k
k
k
k
k
k
nk
k nk
k
nk
B
s B
B
s B
I
s I
s
I
B
s B
B
s B
I
s I
s
I
Q
B,AB, ,A B
B
s B
B
s B
I
s I
s
I
−
−
−
−
−
−
−
⎡
⎤
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎡
⎤
=
=
=
⎣
⎦ ⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
⎣
⎦

11
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Rozważmy przekształcenie układu do postaci kanonicznej diagonalnej:
1
2
0
0
0
0
0
0
n
s
s
A
s
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
,
1
1
A V AV , B V B
−
−
=
=
- ten układ będzie całkowicie sterowalny wtedy i tylko wtedy
gdy każdy z wierszy macierzy
1
B V B
−
=
będzie niezerowy, czyli
0
T
i
i w B
∀
≠ , gdzie
1
1
2
T
T
T
n
w
w
V
:W
w
−
⎡
⎤
⎢
⎥
⎢
⎥
=
=
⎢
⎥
⎢
⎥
⎣
⎦
.
Porównajmy ten warunek z postacią modalną rozwiązania równania stanu:
( )
0
0
1
1
1
0
0
i
i
i
i
t
t
n
n
n
s t
s t
s t
s
T
T
T
i
i
i
i
i
i
i
i
i
x( t )
e v w x
e
v w Bu( )d
e v w x
e
Bu( )d
τ
τ
τ τ
τ τ
−
−
=
=
=
⎡
⎤
=
+
=
+
⎢
⎥
⎣
⎦
∑
∑
∑
∫
∫
0
T
i
w B
≠ warunek sterowalności i-tego modu

12
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Inne kryteria całkowitej sterowalności:
1.
n r
rankB r rank B,AB, ,A B
n
−
⎡
⎤
=
=
⎣
⎦
2.
i
i rank s I
A B
n
⎡
⎤
∀
−
=
⎣
⎦
3.
[
]
s C rank sI
A B
n
∀ ∈
−
=
4. wiersze
At
e B
są liniowo niezależne
5. wiersze
(
)
1
sI
A
B
−
−
są liniowo niezależne
6.
( )
( )
0
T
t
A t
A t
T
t
W
e
BB e
d
τ
τ
τ
−
−
=
∫
jest dodatnio określona

13
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Sterowalność wyjść układu:
równanie stanu
d
x( t ) Ax( t ) Bu( t )
dt
y( t ) Cx
równ
(
a
t )
ni
Du(
e wy ś
t )
j cia
=
+
=
+
x(t) – wektor zmiennych stanu o wymiarze nx1,
u(t) – wektor wejść/sterowań o wymiarze rx1
y(t) – wektor wyjść o wymiarze mx1
Wyjście układu jest całkowicie sterowalne jeśli dla dowolnych y
1
y
2
można wskazać ograniczone
sterowanie przeprowadzające wektor wyjść układu z położenia y
1
do y
2
w skończonym czasie.
Warunek :
1
n
rank CB,CAB, ,CA B,D
m
−
⎡
⎤ =
⎣
⎦

14
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Sterowalność układów dyskretnych jednowejściowych
)
(
)
(
)
)
1
((
)
(
)
(
)
)
1
((
kT
bu
kT
Ax
T
k
x
kT
Bu
kT
Ax
T
k
x
+
=
+
+
=
+
Pow. układ jest całkowicie sterowalny wtedy i tylko wtedy
)
)
((
,
),
)
1
((
),
(
,
,
T
N
k
u
T
k
u
kT
u
N
x
x
d
p
+
+
∃
∀
że dla
p
x
kT
x
=
)
(
d
x
T
N
k
x
=
+
)
)
((
)
(
)
)
1
((
kT
bu
Ax
T
k
x
p
+
=
+
)
)
1
((
)
)
1
((
)
)
2
((
T
k
bu
T
k
Ax
T
k
x
+
+
+
=
+
=
)
)
1
((
)
(
2
T
k
bu
kT
Abu
x
A
p
+
+
+
=
[
]
⎥
⎦
⎤
⎢
⎣
⎡
+
+
)
(
)
)
1
((
2
kT
u
T
k
u
Ab
b
x
A
p
.....................................................................
)
)
((
)
)
((
1
0
1
T
i
k
bu
A
x
A
T
n
k
x
n
i
i
n
p
n
+
+
=
+
∑
−
=
−
−

15
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
[
]
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
−
+
+
=
+
−
)
(
)
)
1
((
)
)
1
((
)
)
((
1
kT
u
T
k
u
T
n
k
u
b
A
Ab
b
x
A
T
n
k
x
S
Q
n
p
n
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
−
+
+
=
+
)
(
)
)
1
((
)
)
1
((
)
)
((
kT
u
T
k
u
T
n
k
u
Q
x
A
T
n
k
x
S
p
n
Jeżeli
n
rankQ
S
= to układ jest sterowalny, bo N=n i można wyznaczyć sterowanie
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
−
+
+
=
)
(
)
)
1
((
)
)
1
((
kT
u
T
k
u
T
n
k
u
Q
x
A
x
S
p
n
d
(
)
p
n
d
S
x
A
x
Q
kT
u
T
k
u
T
n
k
u
−
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
−
+
−1
)
(
)
)
1
((
)
)
1
((

16
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Jeżeli układ jest sterowalny
n
rankQ
S
=
lub równoważnie
Jeżeli
n
rankQ
S
< to układ nie jest sterowalny
Dow.:
Jeżeli
n
rankQ
S
<
to istnieje i<n takie, że
b
A
c
b
A
j
i
j
j
i
∑
−
=
=
1
0
(i-ta kolumna jest liniową kombinacją
poprzednich). Wtedy
=
+
=
=
=
=
−
−
=
−
=
−
+
−
=
−
=
+
∑
∑
∑
∑
b
A
c
b
A
c
b
A
c
b
A
c
b
A
c
A
b
A
i
i
j
i
j
j
j
i
j
j
j
i
j
j
j
i
j
j
i
1
1
1
1
1
1
1
1
0
1
0
1
b
A
c
b
A
c
c
b
A
c
j
i
j
j
j
i
j
j
i
j
i
j
j
∑
∑
∑
−
=
−
=
−
−
=
−
=
+
1
0
1
0
1
1
1
1
~
,
czyli następna kolumna jest też liniową kombinacją i-1 pierwszych i każda następna postaci
b
A
N
N>i też
będzie liniową kombinacją i-1 pierwszych. Przestrzeń liniowa rozpięta na kolumnach macierzy
S
Q
(
S
linQ
) ma wymiar mniejszy od n.
Weźmy
0
=
p
x
Dowolny stan osiągalny z
0
=
p
x
ma postać

17
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
[
]
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
−
+
=
+
−
)
(
)
)
1
((
)
)
1
((
)
)
((
1
kT
u
T
k
u
T
N
k
u
b
A
Ab
b
T
N
k
x
N
S
linQ
∈
Jeżeli weźmiemy dowolny
S
d
linQ
x
∉
to nie istnieje sterowanie przeprowadzające wektor stanu z 0 do
d
x
,
czyli układ nie jest sterowalny.
Warunek modalny sterowalności
Niech
[
]
n
v
v
v
P
2
1
=
przekształca A do postaci kanonicznej diagonalnej,
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
−
T
n
T
T
w
w
w
P
2
1
1
:
18
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
n
z
z
z
A
0
0
0
0
0
~
2
1
,
b
P
b
b
b
b
n
1
2
1
~
~
~
~
−
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
=
b
w
w
w
T
n
T
T
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
2
1
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
b
w
b
w
b
w
T
n
T
T
2
1
[
]
b
A
b
A
b
Q
n
s
~
~
~
~
~
~
1
−
=
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
n
n
n
n
n
n
n
n
b
z
b
z
b
z
b
z
b
z
b
z
b
b
b
~
~
~
~
~
~
~
~
~
1
2
1
2
1
1
1
2
2
1
1
2
1
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
n
b
b
b
~
0
0
0
~
0
0
0
~
2
1
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
1
1
2
1
1
1
2
1
1
1
1
n
n
n
n
n
z
z
z
z
z
z
⇔
=
=
n
Q
rank
rankQ
s
s
~
n
i
b
i
,
,
2
,
1
0
~
=
≠
n
i
b
w
T
i
,
,
2
,
1
0
=
≠
⇔
warunek modalny sterowalności bo:
)
(kT
x
=
)
)
((
)
0
(
0
1
T
i
k
bu
A
x
A
k
i
i
k
−
+
∑
=
−
=
( )
)
0
(
1
x
w
v
z
T
j
j
n
j
k
j
∑
=
( )
)
)
((
1
0
1
T
i
k
bu
w
v
z
k
i
T
j
j
n
j
i
j
−
+
∑∑
=
=
−
=
( )
)
0
(
1
x
w
v
z
T
i
i
n
i
k
i
∑
=
( )
)
)
((
1
0
1
T
i
k
u
z
b
w
v
i
j
k
i
n
j
T
j
j
−
+
−
=
=
∑
∑

19
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Sterowalność układów dyskretnych wielowymiarowych
n
m
rankC
n
r
rankB
m
kT
y
r
kT
u
n
kT
x
kT
Cx
kT
y
kT
Bu
kT
Ax
T
k
x
≤
=
≤
=
=
=
=
=
+
=
+
,
,
)
(
dim
,
)
(
dim
,
)
(
dim
)
(
)
(
),
(
)
(
)
)
1
((
Pow. układ jest sterowalny wtedy i tylko wtedy
)
)
((
,
),
)
1
((
),
(
,
,
T
N
k
u
T
k
u
kT
u
N
x
x
d
p
+
+
∃
∀
że dla
p
x
kT
x
=
)
(
d
x
T
N
k
x
=
+
)
)
((
)
(
)
)
1
((
kT
Bu
Ax
T
k
x
p
+
=
+
)
)
1
((
)
)
1
((
)
)
2
((
T
k
Bu
T
k
Ax
T
k
x
+
+
+
=
+
=
=
)
)
1
((
)
(
2
T
k
Bu
kT
Abu
x
A
p
+
+
+
=
[
]
⎥
⎦
⎤
⎢
⎣
⎡
+
+
)
(
)
)
1
((
2
kT
u
T
k
u
AB
B
x
A
p

20
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
.....................................................................
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
−
+
⎥
⎦
⎤
⎢
⎣
⎡
+
=
+
−
)
(
)
)
1
((
)
)
1
((
)
)
((
1
kT
u
T
k
u
T
N
k
u
B
A
AB
B
x
A
T
N
k
x
r
N
r
r
p
N
„paczki” po r kolumn
Jeżeli
[
]
n
B
A
AB
B
rank
N
=
−1
to układ jest sterowalny, bo z powyższego równania można
wyznaczyć ciąg sterujący.
Wskaźnik sterowalności układu:
[
]
{
}
n
B
A
AB
B
rank
N
N
=
=
−1
:
min
:
μ
gdy we wszystkich pierwszych paczkach przybywa po r kolumn liniowo niezależnych
1
−
−
≤
≤
r
n
r
n
μ

21
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
gdy w kolejnych paczkach (drugiej, trzeciej ...) przybywa po jednej kolumnie liniowo niezależnej
Zbiór stanów N-osiągalnych:
[
]
B
A
AB
B
lin
N 1
−
Tw.
[
]
[
]
B
A
AB
B
lin
B
A
AB
B
lin
N
n
N
1
1
−
−
⊂
∀
Warunki sterowalności
[
]
n
B
A
AB
B
rank
n
=
−1
[
]
n
B
A
AB
B
rank
r
n
=
−
[
]
B
A
AB
B
Q
n
s
1
−
=
macierz sterowalności
Obserwowalność, układy ciągłe
równanie stanu
d
x( t ) Ax( t ) Bu( t )
dt
y( t ) Cx
równ
(
a
t )
ni
Du(
e wy ś
t )
j cia
=
+
=
+

22
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
x(t) – wektor zmiennych stanu o wymiarze nx1,
u(t) – wektor wejść/sterowań o wymiarze rx1
y(t) – wektor wyjść o wymiarze mx1
Układ nazywamy całkowicie obserwowalnym, jeżeli dowolny warunek początkowy x
0
może być
odtworzony na podstawie pomiarów wyjść i znajomości wejść w skończonym czasie.
0
0
0
t
t
x( t )
( t t )x
( t
)Bu( )d
τ
τ τ
= Φ −
+ Φ −
∫
0
0
0
t
t
y( t ) C ( t t )x
C
( t
)Bu( )d
Du( t )
τ
τ τ
= Φ −
+
Φ −
+
∫
Wystarczy rozważyć układ:

23
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
d
x( t ) Ax( t )
dt
y( t ) Cx( t )
=
=
0
At
y( t ) Ce x
=
1
0
n
i
i
i
( t )
( t )A
ϕ
−
=
Φ
=
∑
1
0
0
n
i
i
i
y( t ) C
( t )A x
ϕ
−
=
⎛
⎞
= ⎜
⎟
⎝
⎠
∑
Tw. Koniecznym i dostatecznym warunkiem całkowitej obserwowalności jest

24
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
1
o
n
C
CA
rankQ
rank
n
CA
−
⎡
⎤
⎢
⎥
⎢
⎥
=
=
⎢
⎥
⎢
⎥
⎣
⎦
Dow.:
Warunek konieczny: (dowód nie wprost)
Jeśli
o
rankQ
n
<
to istnieje niezerowy x
0
taki, że
0
0
0
0
1
0
0
0
0 1 2
1
i
o
n
Cx
CAx
Q x
CA x
i
, , , ,n
CA x
−
⎡
⎤
⎢
⎥
⎢
⎥
=
=
⇒
=
=
−
⎢
⎥
⎢
⎥
⎣
⎦
…
1
0
0
0
n
i
i
i
y( t )
( t )CA x
ϕ
−
=
=
=
∑
Warunek dostateczny:
25
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
0
At
y( t ) Ce x
=
0
T
T
A t
T
A t
T
At
e C y( t ) e C Ce x
=
0
0
0
0
T
T
t
t
A
T
A
T
A
W ( t )
e C y( )d
e C Ce d x
Q( t ) W ( t )x
τ
τ
τ
τ τ
τ
=
=
∫
∫
jest
nieosobliwa
dla
dowolnych
t, bo gdyby była, to dla dowolnego x:
1
1
1
0
0
0
T
t
t
T
T
A
T
A
A
x W ( t )x
x e C Ce xd
Ce x d
τ
τ
τ
τ
τ
=
=
=
∫
∫
, czyli
0
At
Ce x
=
dla dowolnych t<t
1
, a to by znaczyło
1
0
0
n
i
i
i
( t )CA x
ϕ
−
=
=
∑
, czyli
o
rankQ
n
<
.

26
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Obserwowalność a liniowe przekształcenie zmiennych stanu:
wprowadzamy nowe zmienne stanu:
0
Pq( t ) x( t ), det P
=
≠
równanie stanu
d
Pq( t ) APq( t ) Bu( t )
nowe
dt
y( t ) CPq( t ) Du( t )
now
równanie wyjś a
e
ci
=
+
=
+
1
1
równanie st
d
q( t ) P APq( t ) P Bu( t )
nowe
dt
y( t ) CPq( t ) Du( t )
anu
równanie wyjścia
nowe
−
−
=
+
=
+
1
1
d
q( t ) Aq( t ) Bu( t )
A P AP, B P B
dt
y( t ) Cq( t ) Du( t )
C CP
−
−
=
+
=
=
=
+
=
1
1
oq
o
n
n
CP
C
CAP
CA
Q
Q P
CA P
CA
−
−
⎡
⎤ ⎡
⎤
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
=
=
=
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎣
⎦
⎣
⎦

27
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Rozważmy układ w postaci kanonicznej diagonalnej:
1
2
0
0
0
0
0
0
n
s
s
A
s
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
,
1
A V AV ,C CV
−
=
=
- ten układ będzie całkowicie sterowalny wtedy i tylko wtedy,
gdy wszystkie kolumny macierzy
C CV
=
będą niezerowe. Porównajmy z
0
0
1
1
i
i
n
n
s t
s t
T
T
i
i
i
i
i
i
y( t ) C
e v w x
e Cv w x
=
=
=
=
∑
∑
0
i
Cv
≠ warunek obserwowalności i-tego modu
Dualizm sterowalności i obserwowalności:
Para (A,B) jest sterowalna
⇔
Para (B
T
,A
T
) jest obserwowalna
Para (C,A) jest obserwowalna
⇔
Para (A
T
,B
T
) jest sterowalna

28
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Obserwowalność układów dyskretnych jednowymiarowych
)
(
)
(
)
(
kT
du
kT
cx
kT
y
+
=
)
)
1
((
)
(
)
(
)
)
1
((
)
)
1
((
)
)
1
((
T
k
du
kT
cbu
kT
cAx
T
k
du
T
k
cx
T
k
y
+
+
+
=
+
+
+
=
+
)
)
2
((
)
)
1
((
)
(
)
(
)
)
2
((
2
T
k
du
T
k
cbu
kT
cABu
kT
x
cA
T
k
y
+
+
+
+
+
=
+
=
.....................................................................
1
2
1
2
1
n
n
y(( k n
)T ) cA x( kT ) cA Bu( kT )
cbu(( k n
)T ) du(( k n
)T )
−
−
+ −
=
+
+ +
+ −
+
+ −
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
+
+
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
+
+
−
−
)
)
1
((
)
)
1
((
)
(
0
0
0
)
(
)
)
1
((
)
)
1
((
)
(
2
1
T
n
k
u
T
k
u
kT
u
d
cb
b
cA
d
cb
d
kT
x
cA
cA
c
T
n
k
y
T
k
y
kT
y
n
Q
n
O

29
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Def.
Układ jest obserwowalny jeżeli
)
)
((
,
),
)
1
((
),
(
,
T
N
k
u
T
k
u
kT
u
N
+
+
∀
∃
przy znanych
)
)
((
,
),
)
1
((
),
(
T
N
k
y
T
k
y
kT
y
+
+
można wyznaczyć
)
(kT
x
Tw.
Układ jest obserwowalny
n
rankQ
O
=
⇔
n
i
cv
i
,
,
2
,
1
0
=
≠
- warunek modalny obserwowalności bo:
)
(
)
(
kT
cx
kT
y
=
=
)
)
((
)
0
(
0
1
T
i
k
bu
A
c
x
cA
k
i
i
k
−
+
∑
=
−
=
( )
)
0
(
1
x
w
v
z
c
T
j
j
n
j
k
j
∑
=
( )
)
)
((
1
0
1
T
i
k
bu
w
v
z
c
k
i
T
j
j
n
j
i
j
−
+
∑∑
=
=
−
=
( )
)
0
(
1
x
w
v
c
z
T
i
i
n
i
k
i
∑
=
( )
)
)
((
1
0
1
T
i
k
u
z
b
w
cv
i
j
k
i
n
j
T
j
j
−
+
−
=
=
∑
∑

30
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Postać kanoniczna Kalmana równań stanu
1
0
0
1
0
0
1
0
0
0
1
s no
s no
s no/ s no
s no/ s o
s no/ ns no
s no/ ns o
s o
s o
s o/ s o
s o/ ns o
ns no
ns no/ ns no
ns no/ ns o
ns no
ns o
ns o/ ns o
A
A
A
A
x
(( k
)T )
x
( kT )
A
A
x (( k
)T )
x ( kT )
A
A
x
(( k
)T )
x
( kT
A
x
(( k
)T )
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
+
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
+
⎢
⎥
⎢
⎥ =
⎢
⎥
⎢
⎥
+
⎢
⎥
⎢
⎥
+
⎣
⎦ ⎣
⎦
0
0
s no
s o
ns o
B
B
u( kT )
)
x
( kT )
−
−
−
⎡
⎤ ⎡
⎤
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
+
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎣
⎦ ⎣
⎦
[
]
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
−
−
−
−
−
−
)
(
)
(
)
(
)
(
0
0
)
(
kT
x
kT
x
kT
x
kT
x
C
C
kT
y
o
ns
no
ns
o
s
no
s
o
ns
o
s
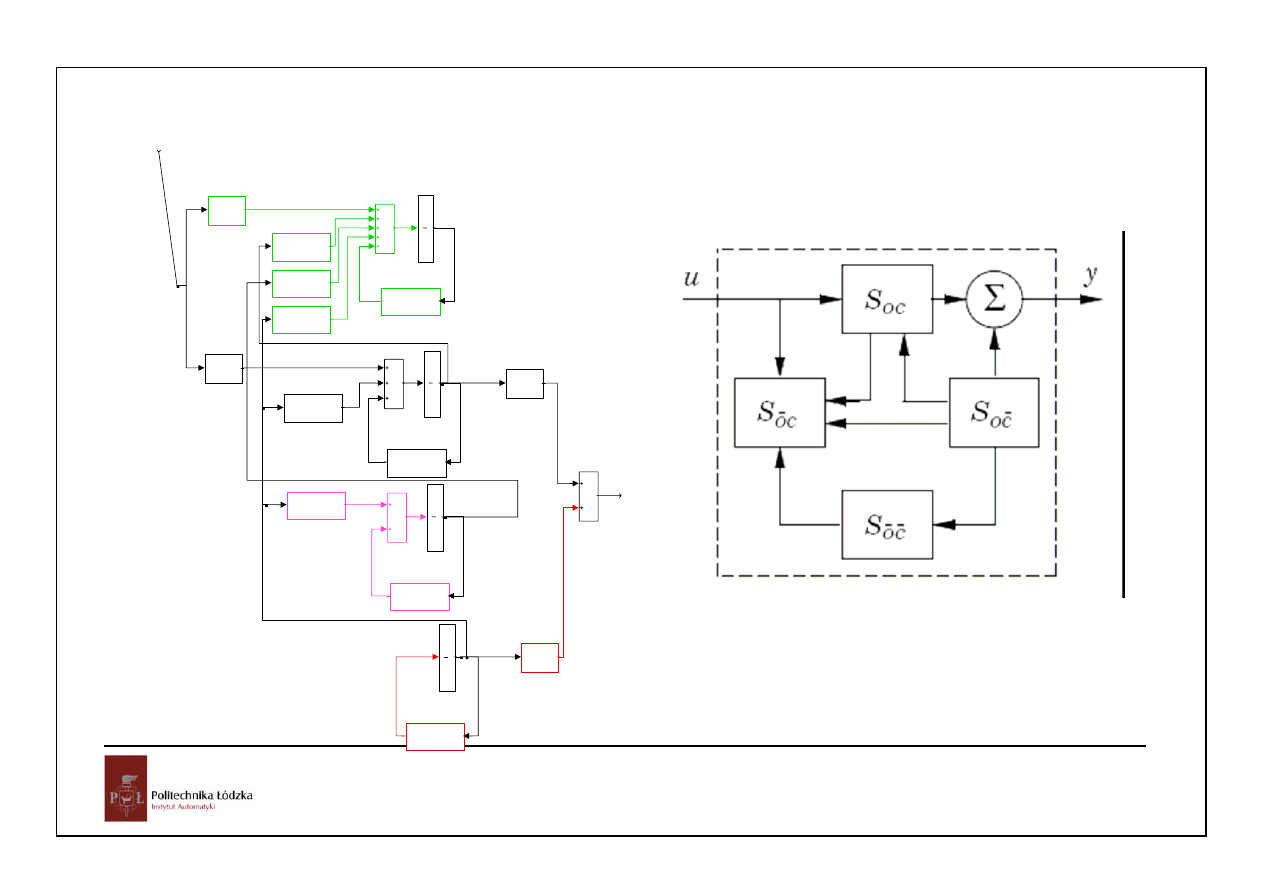
31
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
xs-no
xs-o
u
xns-no
xns-o
y
z
1
Unit Delay3
z
1
Unit Delay2
z
1
Unit Delay1
z
1
Unit Delay
Cns-o
.3
Cs-o
.2
Bs-o
.1
..5
..4
..1
Ans-o/ns-o
...9
Ans-no/ns-no
...7
Ans-no/ns-o
...6
As-o/ns-o
...5
As-no/ns-o
...4
As-no/ns-no
...3
As-no/s-o
...2
As-o/s-o
...1
As-no/s-no
...
..
Bs-no
.
32
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
−
−
1
1
1
1
1
0
0
Y
ZY
X
X
Y
Z
X
[
]
o
ns
o
s
C
C
z
G
−
−
=
0
0
)
(
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
0
0
0
0
0
0
0
0
0
1
/
/
/
/
/
/
/
/
/
o
s
no
s
o
ns
o
ns
o
ns
no
ns
no
ns
no
ns
o
ns
o
s
o
s
o
s
o
ns
no
s
no
ns
no
s
o
s
no
s
no
s
no
s
B
B
A
A
A
A
A
A
A
A
A
zI
=
[
]
o
ns
o
s
C
C
−
−
=
0
0
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
0
0
0
0
0
0
0
0
0
1
/
/
/
/
/
/
/
/
/
o
s
no
s
o
ns
o
ns
o
ns
no
ns
no
ns
no
ns
o
ns
o
s
o
s
o
s
o
ns
no
s
no
ns
no
s
o
s
no
s
no
s
no
s
B
B
A
zI
A
A
zI
A
A
zI
A
A
A
A
zI
=

33
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
[
]
o
ns
o
s
C
C
−
−
=
0
0
(
)
(
)
(
)
(
)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
0
0
0
0
0
0
0
*
*
0
*
*
*
1
/
/
1
/
1
/
1
/
o
s
no
s
o
ns
o
ns
o
ns
no
ns
no
ns
no
ns
o
s
o
s
no
s
no
s
B
B
A
zI
A
A
zI
A
zI
A
zI
[
]
o
ns
o
s
C
C
−
−
=
0
0
(
)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
0
0
*
1
/
o
s
o
s
o
s
B
A
zI
=
(
)
o
s
o
s
o
s
o
s
B
A
zI
C
−
−
−
−
−
−
1
/
(
)
o
s
o
s
o
s
o
s
B
A
zI
C
z
G
−
−
−
−
−
−
=
1
/
)
(
(
)
(
)
(
)
B
A
zI
Cadj
A
zI
B
A
zI
C
z
G
−
−
=
−
=
−
det
1
)
(
1
34
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Układ niesterowalny:
Układ nieobserwowalny:
35
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Skrócenie zer/biegunów:
36
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego

37
Automatyka i sterowanie 13 Sterowalność i obserwowalność
Układy czasu ciągłego i dyskretnego
Zadanie:
b
P( s )
s a
=
+
,
i
i
k
sk k
C( s ) k
s
s
+
= +
=
Parametry regulatora dobrano tak, by skrócić biegun obiektu i by
biegunem układu zamkniętego była wartość rzeczywista -p. Zbadać wszystkie transmitancje układu
(także dotyczące zakłóceń. Znaleźć opis w przestrzeni stanów, zbadać warunki sterowalności i
obserwowalności, także modalne warunki sterowalności i obserwowalności. Zbadać przebiegi w układzie
dla wolnego obiektu i szybkiego układu zamkniętego (np. a=0.1, p=1.0).
Wyszukiwarka
Podobne podstrony:
automatyka i sterowanie wyklad 15
automatyka i sterowanie wyklad Nieznany (8)
automatyka i sterowanie wyklad Nieznany (2)
automatyka i sterowanie wyklad 3
automatyka i sterowanie wyklad Nieznany (7)
automatyka i sterowanie wyklad Nieznany (14)
automatyka i sterowanie wyklad 16
automatyka i sterowanie wyklad Nieznany (12)
automatyka i sterowanie wyklad Nieznany (16)
automatyka i sterowanie wyklad Nieznany (5)
automatyka i sterowanie wyklad 9
automatyka i sterowanie wyklad 11
automatyka i sterowanie wyklad 4
automatyka i sterowanie wyklad 5
automatyka i sterowanie wyklad Nieznany (10)
automatyka i sterowanie wyklad Nieznany (3)
automatyka i sterowanie wyklad 8
automatyka i sterowanie wyklad 2
automatyka i sterowanie wyklad 15
więcej podobnych podstron