FUNKCJA LINIOWA

Opracował mgr Zenon Kubat

WPROWADZENIE.

POKAZ PRZEZNACZONY JEST
DLA UCZNIÓW Kl.II
GIMNAZJUM.

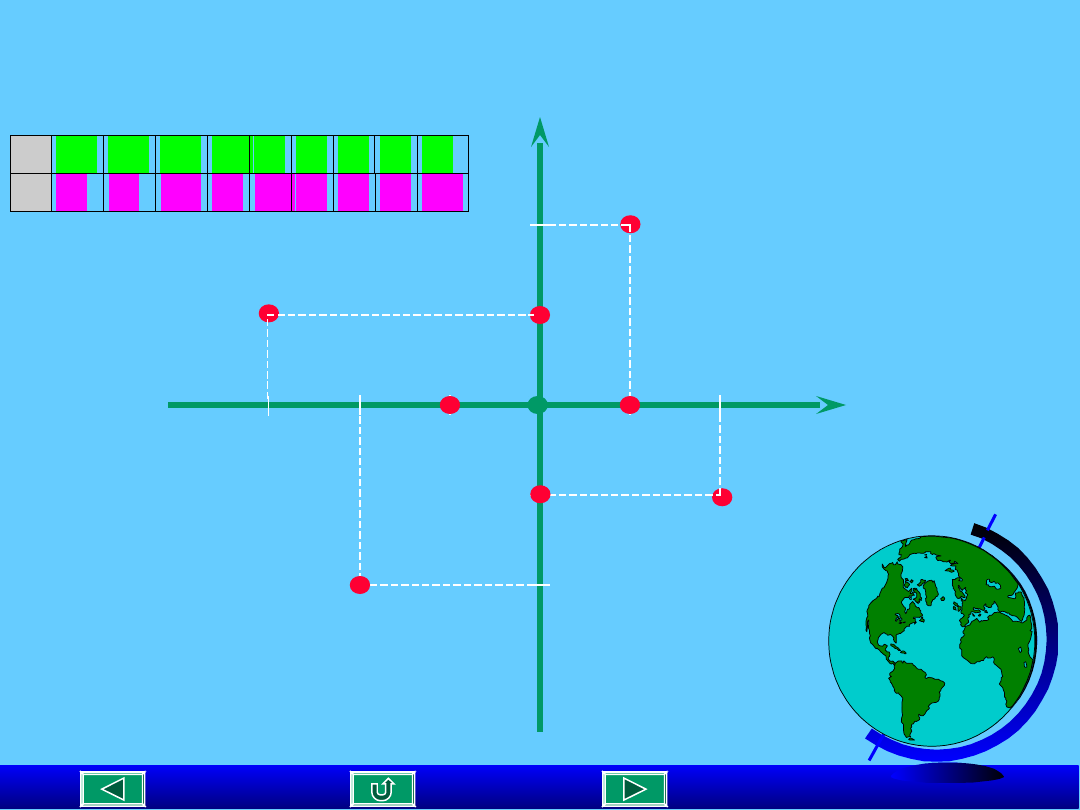
Współrzędne punktu na

płaszczyźnie.

x -3 -2 -2 -1 0 0 1 1 2
y 1 1 -2 0 -1 1 0 2 -1

-

2 -1

1

1

0

y

y

x

x

A(-2,-2)

(0,1)

(1,2)

(2,-1)

-1

-2

2

2

-
3

(-3,1)

(0,-1)

(-1,0)

(1,0)

FUNKCJA LINIOWA

jest to prosta, która opisana jest wzorem:

y= mx + b

y - wartość funkcji
m - współczynnik kierunkowy
x - argument funkcji
b - punkt przecięcia się prostej z
osią OY

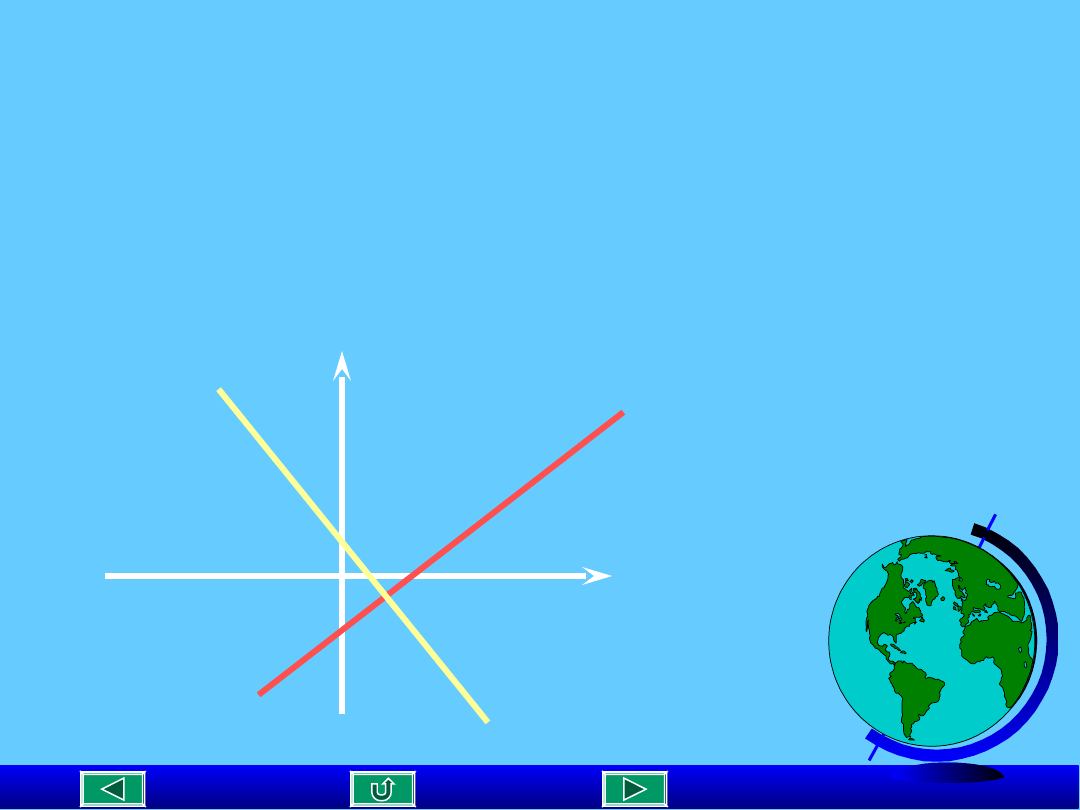
Gdy m>0 to prosta przechodzi przez I i III
ćwiartkę
układu współrzędnych.
Jeżeli m< 0 , to prosta przechodzi przez II i IV
ćwiartkę
układu współrzędnych.

I

I

II

II

III

III

IV

IV

0

X

Y

m>0

m<0

Wykresem funkcji liniowej jest prosta.

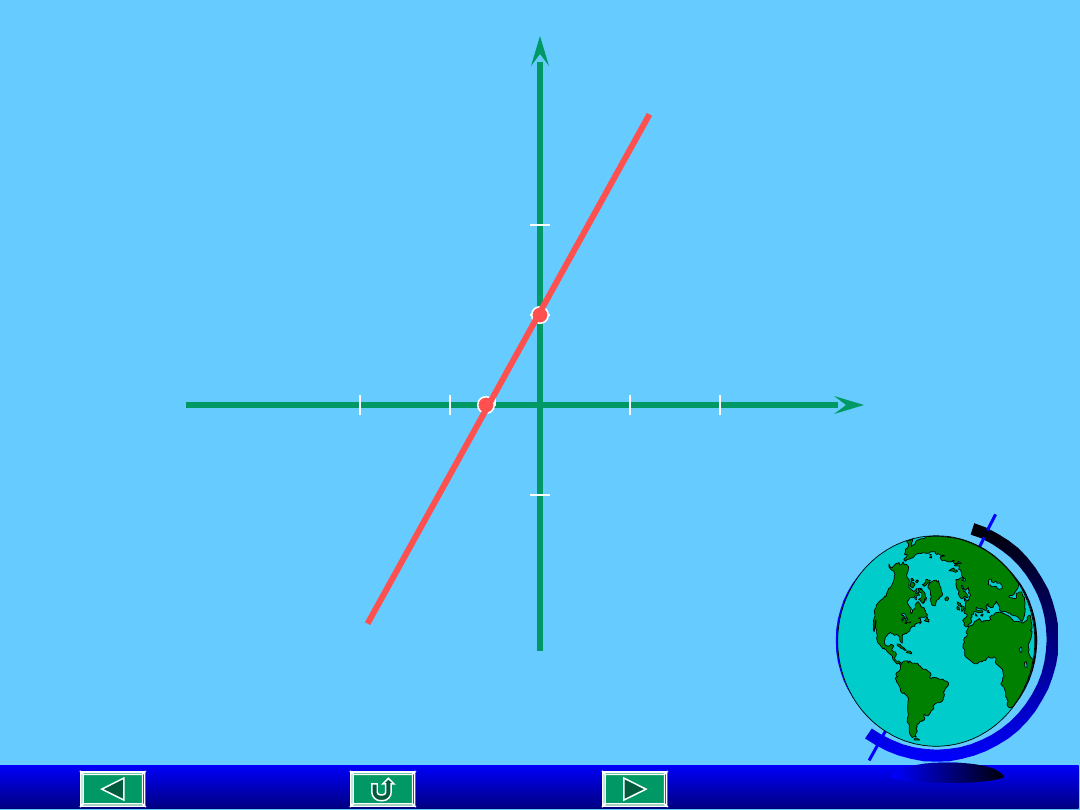
PRZYKŁAD 1

Narysuj wykres funkcji: y= 2x +1

dla y = 0 mamy : 0 = 2x + 1 czyli:
-2x = 1
2x = -1

X

= -0,5

B
(0,1)

A(-0,5;0)

Dla x = 0 mamy: y= 2*0 +1 = 1

Z zapisu funkcji wynika, że m = 2

-

1

1

1

0

y

y

x

x

-

1

B(0,1)

A(-0,5,0)

y = 2x + 1

Wykres funkcji
przechodzącej przez
punkty A(-0,5;0) i B( 0,1)

Przykład 2.

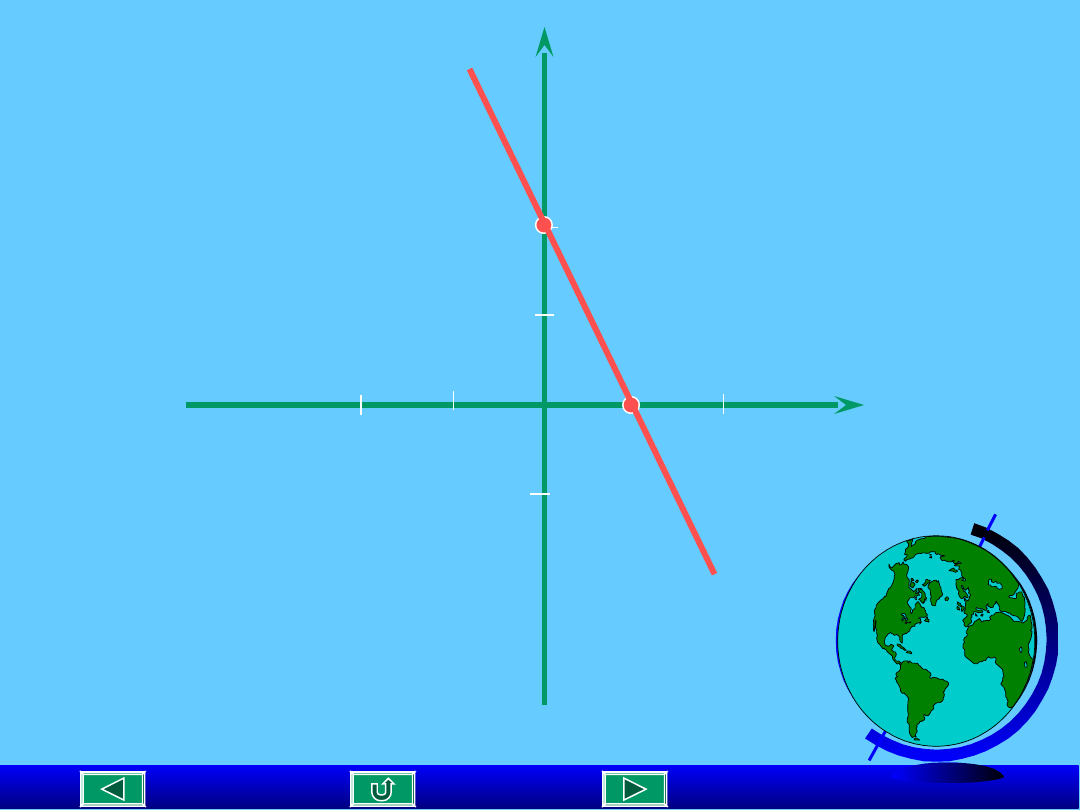
Narysuj wykres funkcji: y = - 2x + 2

z funkcji wynika,że: m<0 , gdyż :
m =- 2

Dla x = 0 , y = - 2 *0
+ 2 = 2
czyli : B( 0,2)

Dla y = 0 0 = -2x + 2
2x = 2

x = 1

czyli : A ( 1,0)

-

2 - 1

1

1 2

0

y

y

x

x

-

1

B(0,2)

A(1;0)

y = - 2x + 2

2

Wykres funkcji przechodzącej
Przez punkty A(1,0) i B(0.2)

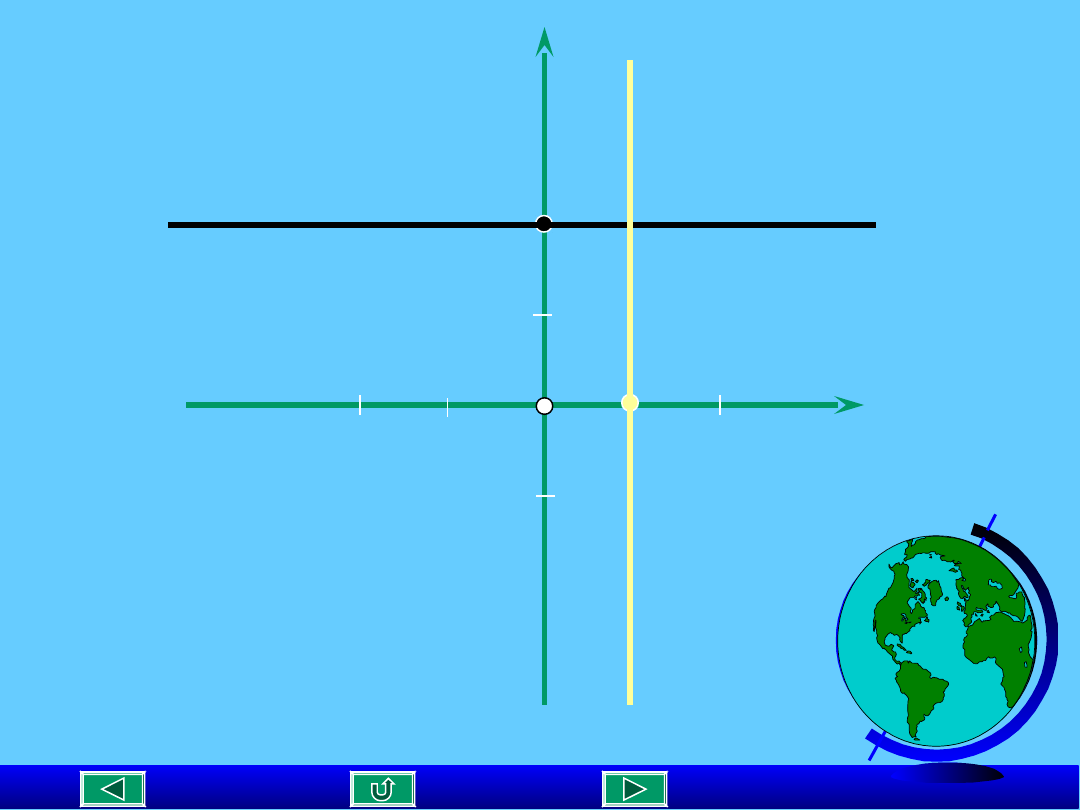
SZCZEGÓLNY PRZYPADEK
PROSTEJ.

gdy m = 0 , b= 0
wówczas y = b

prosta jest równoległa do osi 0X i przechodzi przez punkt b

gdy, dla każdego y ; x = c

wówczas prosta jest równoległa do osi OY i przechodzi
przez punkt c leżący na osi 0X.

0

y

y

x

x

B(0,b)

b

y = b

A(C,0)

x=c

Warunek równoległości

prostych.

Dowolne dwie proste są do siebie równoległe , gdy
spełniony jest warunek m

1

= m

2

np.

y = 3x + 5

y = -2x - 2

y = 3x - 2

y = - 2x + 4

m= 3

m = - 2

i

i

Warunek prostopadłości

prostych.

Dwie proste są do siebie prostopadłe, gdy zachodzi warunek:
m

1

* m

2

= - 1

Przykład.

y = 2x + 2 i y = - 0,5x - 10
gdyż, 2*(-0,5) = -1

y = -3x - 3 i y =

1

3

x + 1,5

gdyż,

-3*

1

3

= - 1

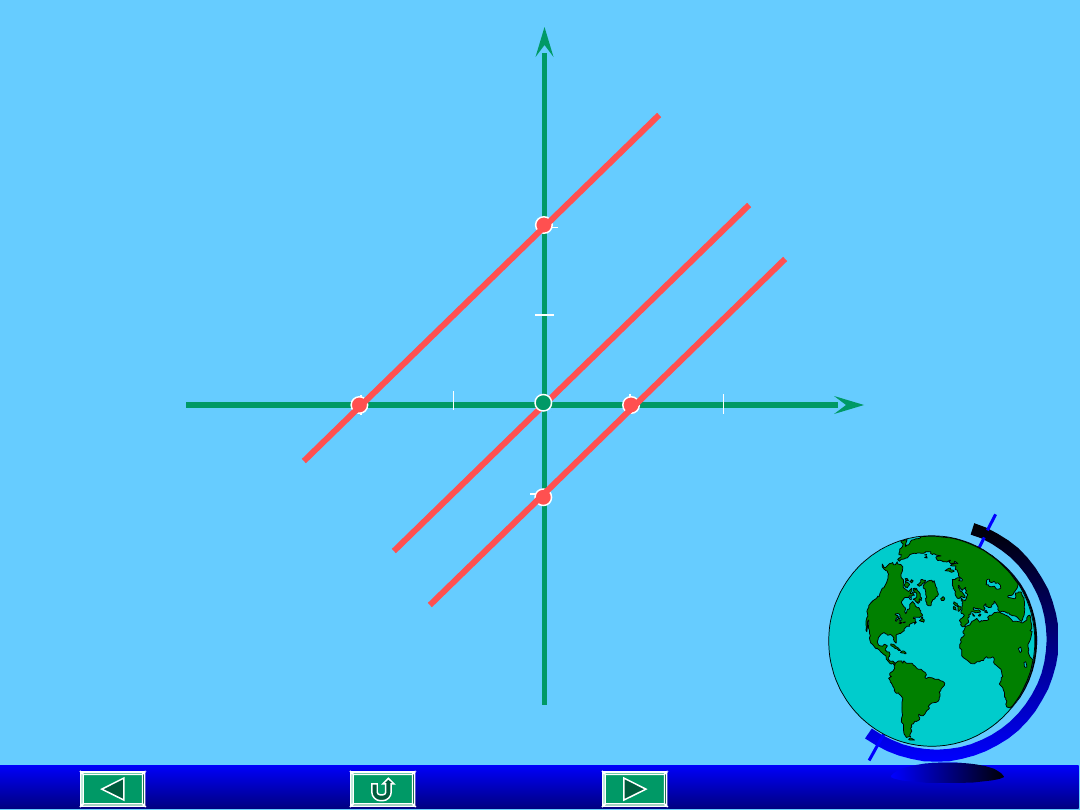
PROSTE

PROSTE

RÓWNOLEGŁE

RÓWNOLEGŁE

- 1

1

1 2

0

y

y

x

x

-

1

B(0,2)

A(-2,0)

y = 1x + 2

A

1

(1,0)

B

1

(0,-1)

y = 1x -1

y = x

2

m = 1

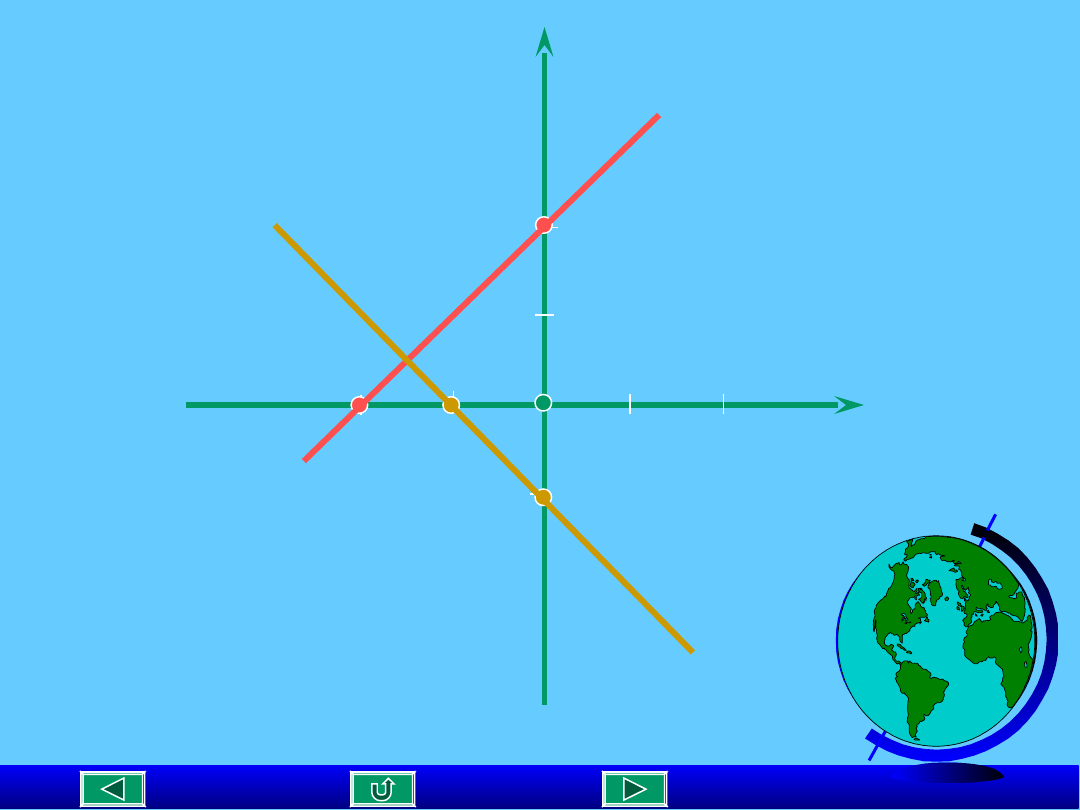
PROSTE

PROSTE

PROSTOPADŁE

PROSTOPADŁE

-

2 - 1

1

1 2

0

y

y

x

x

-

1

B

1

(0,2)

A

1

(-2,0)

y = 1x + 2

A

2

(-1,0)

B

2

(1,0)

y = - x -1

2

m

1

= 1

m

2

= -1

m

1

*m

2

= -1

RÓWNANIE PROSTEJ PRZECHODZĄCEJ

RÓWNANIE PROSTEJ PRZECHODZĄCEJ

PRZEZ PUNKTY :A(

PRZEZ PUNKTY :A(

x

x

o,

o,

y

y

o) i B(

o) i B(

x

x

1

1

,

,

y

y

1

1

)

)

Punkt A(x

o

;yo) leży na prostej y = mx + b, wtedy gdy zachodzi :

y

o=

mx

o

+

b

Prosta przechodzi przez punkty A(xo,yo) i B(x

1

,y

1

), wtedy gdy zachodzi:





y

y

y

y

x

x

x

x










0

1

0

1

0

0

PRZYKŁAD

PRZYKŁAD





y

y

y

y

x

x

x

x










0

1

0

1

0

0

Napisz równanie prostej przechodzącej przez punkty A( 2,1)
i B(-2,3)

Rozwiązanie

oznaczamy: x

o

= 2 ; y

o

= 1
x

1

= -2 ; y

1

= 3

i podstawiamy do
równania

y - 1 = -0,5 ( x -2)
y = -0,5x +2

Otrzymujemy

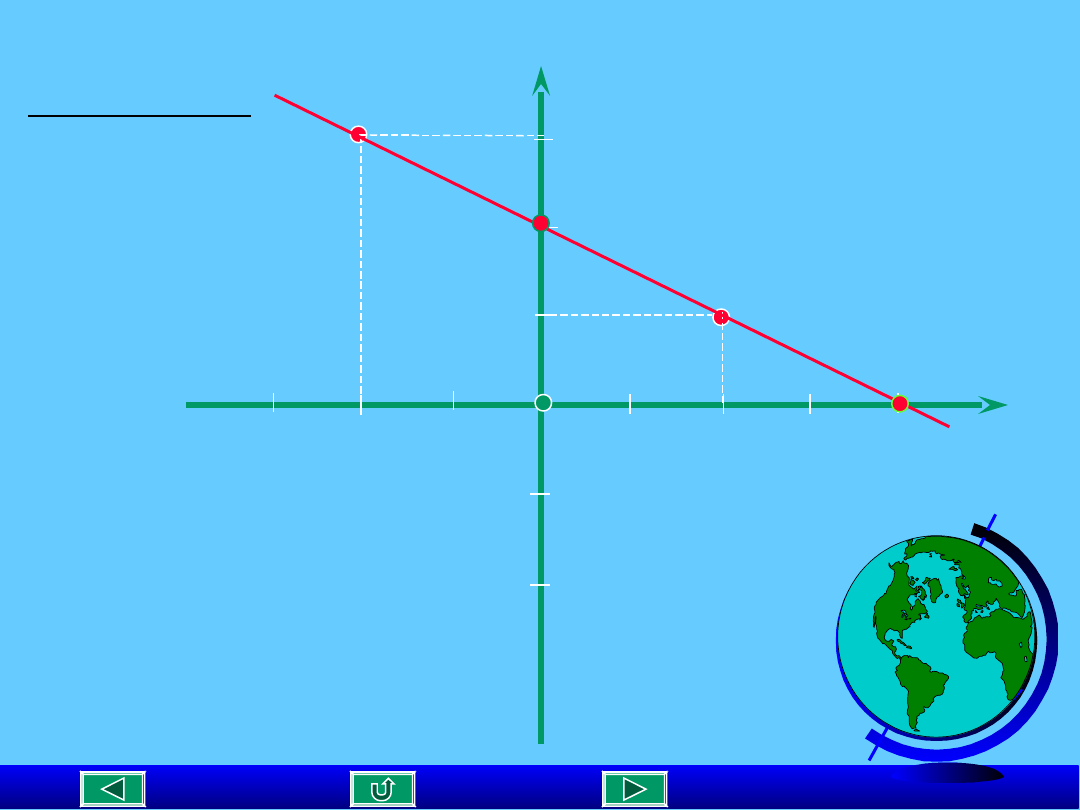
-2 - 1

1

1 2

0

y

y

x

x

-1

2

-3

-2

3

A(2,1)

B(-2,3)

3

4

y = -

0,5x

+

2

b = 2

m = - 0,5
b = 2

y = ax + b