„Wątpić we wszystko lub

wierzyć we wszystko to dwa

równie wygodne rozwiązania;

oba uwalniają od obowiązku

myślenia.”

Henri Poincare

FUNKCJA LINIOWA I JEJ

WŁASNOŚCI.

Funkcja liniowa to jedna z najprostszych
funkcji, jej wykresem jest linia prosta a wzór
nie jest skomplikowany. Funkcje liniowe mają
wiele

praktycznych

zastosowań,

mogą

opisywać

proporcjonalność

prostą

czy

posłużyć do rozwiązania układu równań,
warto więc dowiedzieć się o nich nieco więcej.

DEFINICJA FUNKCJI

LINIOWEJ.

Funkcja liniowa to funkcja określona

wzorem

y = ax + b,

gdzie a i b są liczbami rzeczywistymi.

PRZYKŁADY:
y = 2x + 3 (a = 2, b = 3)
y = -x – 4 (a = -1, b = -4)
y = 4x (a = 4, b = 0)
y = 6 (a = 0, b = 6)
Oczywiście wystarczy podać sam wzór, w
nawiasach

podaliśmy

wartości

współczynników a i b dla wyjaśnienia wzoru
ogólnego.

y = ax + b

a – współczynnik kierunkowy funkcji

liniowej.

b – wyraz wolny funkcji liniowej.

Dziedziną funkcji liniowej jest zbiór liczb

rzeczywistych.

Gdy b = 0 i jednocześnie a ≠ 0, to funkcja liniowa
przedstawia proporcjonalność prostą:

y = ax

czyli

WYKRES FUNKCJI

LINIOWEJ.

Wykresem funkcji liniowej, jak sama nazwa
wskazuje, jest linia prosta.
Do narysowania wykresu funkcji liniowej
wystarczą dwa punkty.
PRZYKŁAD
Narysuj wykres funkcji y = 2x + 2.
Wybieramy sobie dwa argumenty (x) i
obliczamy wartość funkcji, np.:
f(0) = 2 · 0 + 2 = 0 + 2 = 2
f(-1) = 2 · (-1) + 2 = -2 + 2 = 0
Zaznaczamy

oba

punkty

w

układzie

współrzędnych i rysujemy wykres.

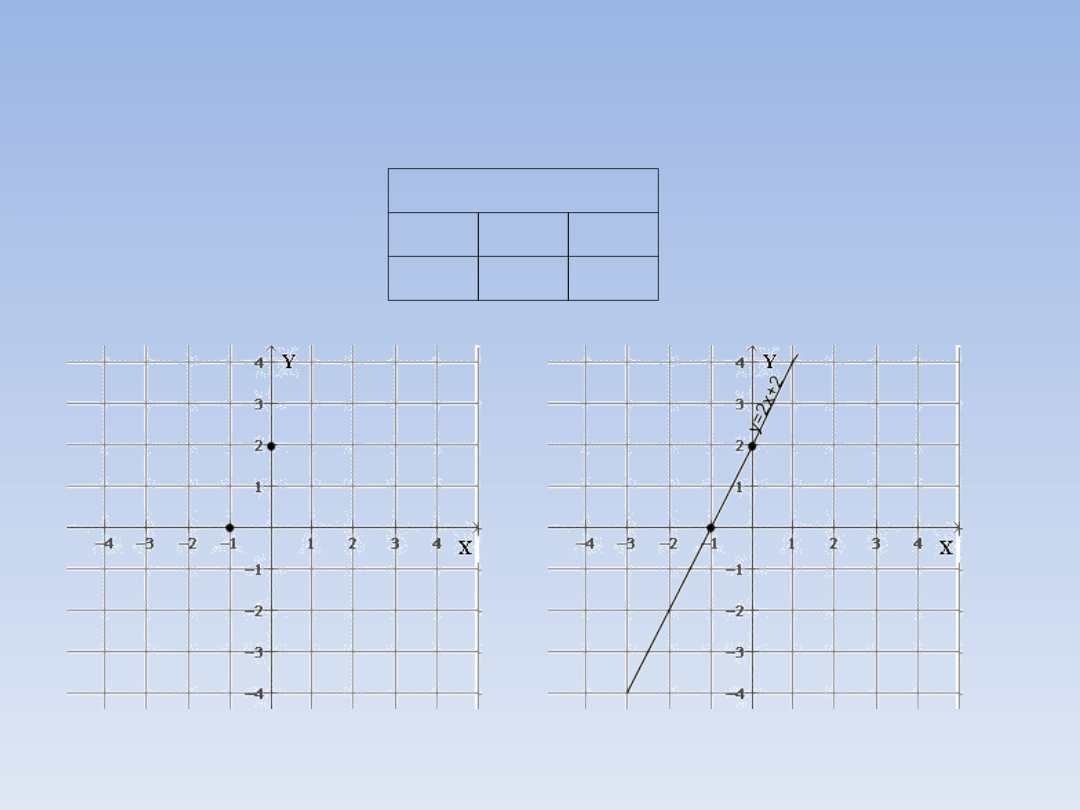
WYKRES FUNKCJI

LINIOWEJ.

y = 2x + 2

x

0

-1

y

2

0

Zaznaczamy punkty.

Rysujemy wykres.

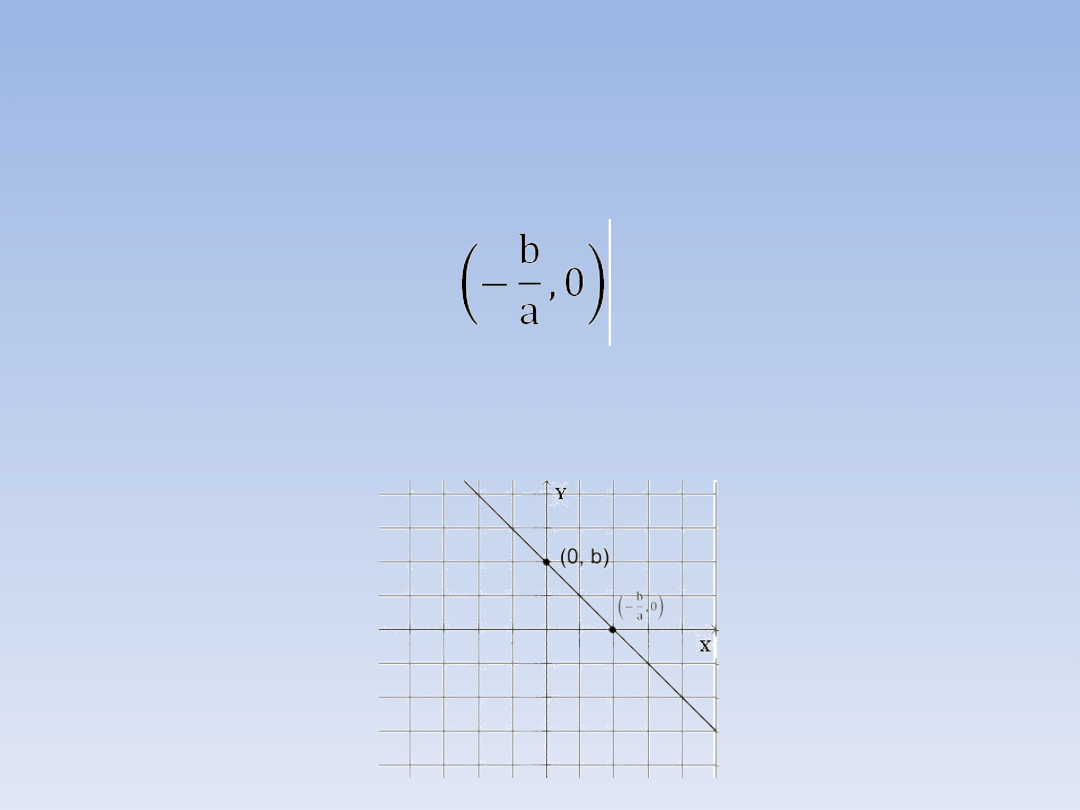
PUNKTY PRZECIĘCIA WYKRESU

FUNKCJI LINIOWEJ Z OSIAMI

UKŁADU WSPÓŁRZĘDNYCH.

Jeśli a ≠ 0, to wykres funkcji liniowej przecina
oś OX w punkcie:

Wykres funkcji liniowej przecina oś OY w
punkcie:

(0, b)

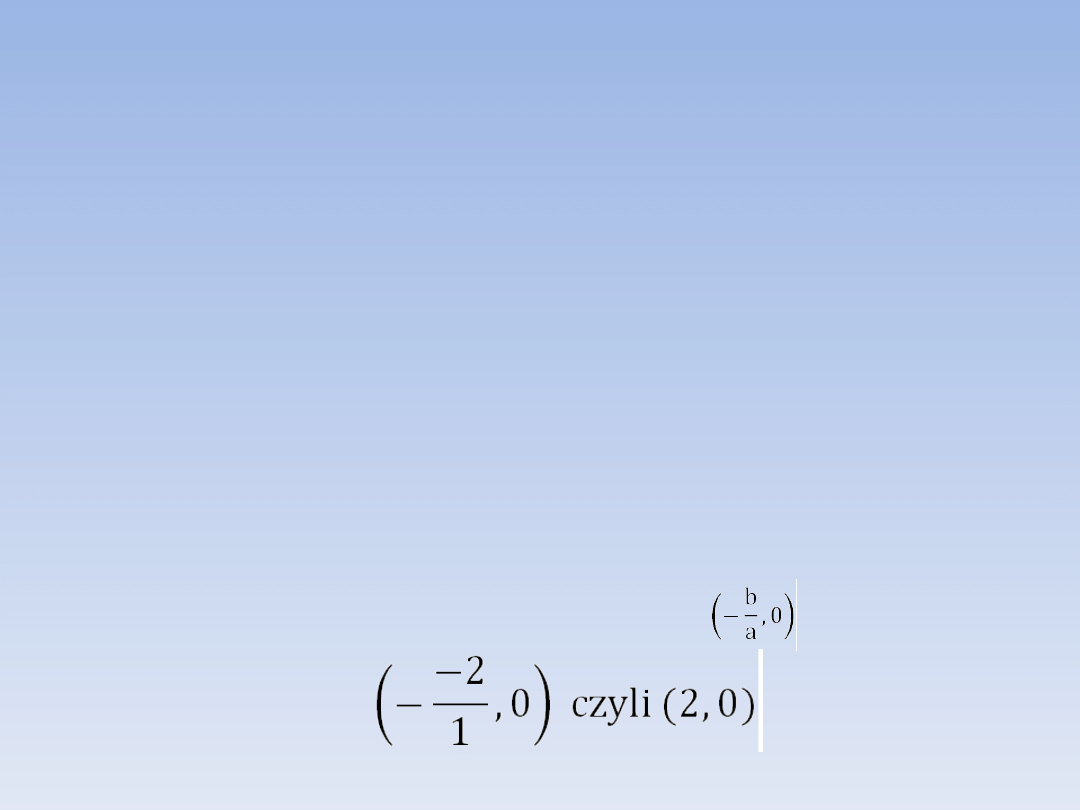
PRZYKŁAD.
Wyznacz punkty przecięcia wykresu funkcji y
= x – 2 z osiami układu współrzędnych.
Możemy narysować funkcję i odczytać
współrzędne punktów przecięcia z wykresu
lub skorzystać ze wzorów:
y = x – 2 mamy wiec a = 1 oraz b = -2.
Punkt przecięcia wykresu z osią OY to (0, b),
mamy więc

(0, -2)

Punkt przecięcia wykresu z osią OX to ,
mamy więc

PUNKTY PRZECIĘCIA WYKRESU

FUNKCJI LINIOWEJ Z OSIAMI

UKŁADU WSPÓŁRZĘDNYCH.

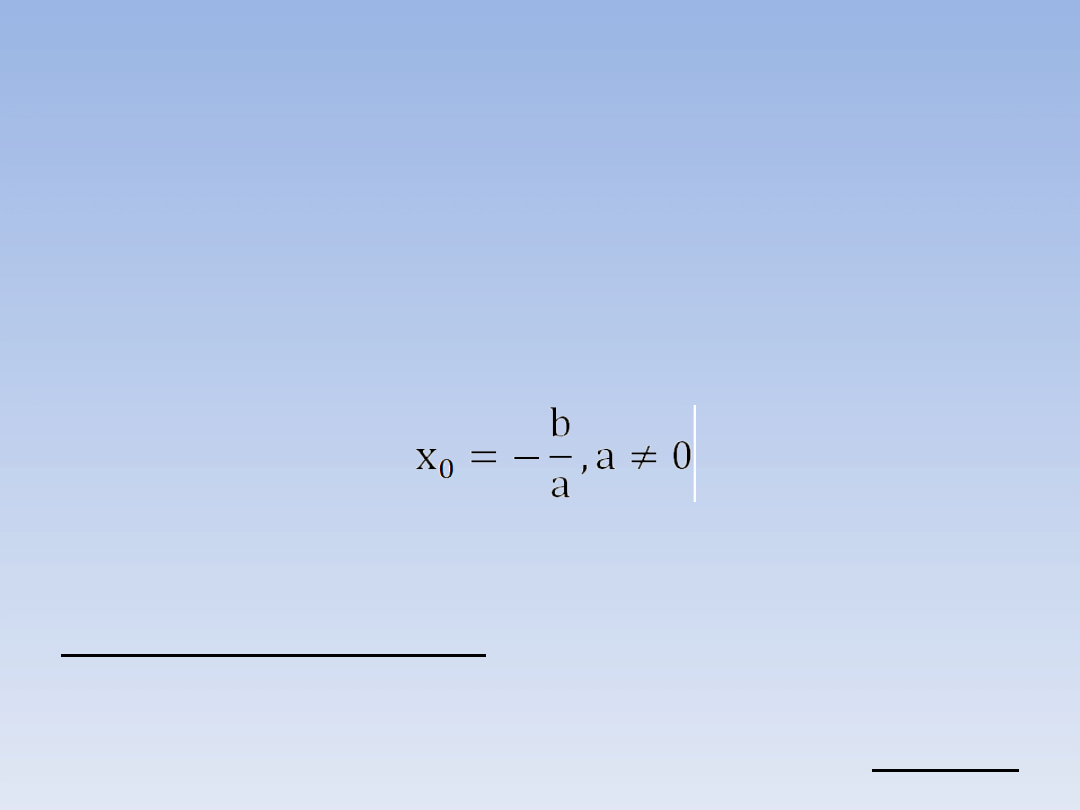
MIEJSCA ZEROWE FUNKCJI

LINIOWEJ.

Miejsce zerowe funkcji liniowej można
obliczyć tak samo jak każdej innej funkcji –
wstawiając do wzoru funkcji wartość 0 i
rozwiązując równanie. Jeśli jednak ktoś lubi
używać wzorów, miejsce zerowe funkcji
liniowej obliczy tak:

Jeśli a = 0 i b = 0, to funkcja liniowa ma
nieskończenie wiele miejsc zerowych (y = 0
czyli cała oś OX)
Jeśli a = 0 i b ≠ 0, to funkcja liniowa nie ma
miejsc zerowych (y = b czyli funkcja stała,
której wykresem jest linia równoległa do osi
OX)

MIEJSCA ZEROWE FUNKCJI

LINIOWEJ.

PRZYKŁAD.
Znajdź miejsce zerowe funkcji określonej
wzorem
y = 3x + 9.
Możemy to zrobić na kilka sposobów:
I.Narysować funkcję i odczytać miejsce
zerowe z wykresu.
II.Rozwiązać równanie wstawiając do wzoru y
= 0.
0 = 3x + 9
-3x = 9 /: (-3)
x = -3
III. Skorzystać ze wzoru.

MONOTONICZNOŚĆ FUNKCJI

LINIOWEJ.

W przypadku funkcji liniowej sprawa jest
bardzo prosta – wystarczy spojrzeć na
współczynnik a we wzorze.

WSPÓŁCZYNNI

K

KIERUNKOWY

MONOTONICZ

NOŚĆ

PRZYKŁADY

FUNKCJI

a > 0

Funkcja rosnąca

y = 2x + 5

y = 4x

y = 0,25x - 3

a < 0

Funkcja

malejąca

y = -2x

y = -x + 10

y = -0,5x + 2

a = 0

Funkcja stała

y = 9

y = -2

y = 0,3

MONOTONICZNOŚĆ FUNKCJI

LINIOWEJ.

PRZYKŁAD.
Zbadaj monotoniczność funkcji: y = 2x + 9, y
= -2, y = -8x,
y = 0,5x + 0,25, y = 1, y = x, y = -x, y = 91x
+ 102.
Obliczenia wprost z definicji byłyby bardzo
czasochłonne, na szczęście wszystkie podane
funkcję to funkcje liniowe, wystarczy więc
spojrzeć na współczynnik a (liczbę stojącą
przy x). Mamy:
- funkcje rosnące: y = 2x + 9, y = 0,5x +
0,25, y = x (a = 1),
y = 91x + 102
-funkcje malejące: y = -8x, y = -x (a = -1)
- funkcje stałe: y = -2 (a = 0), y = 1 (a = 0)

RÓWNOLEGŁOŚĆ I

PROSTOPADŁOŚĆ

WYKRESÓW FUNKCJI

LINIOWYCH.

Przykłady funkcji liniowych o wykresach
równoległych:
y = 2x || y = 2x + 2 || y = 2x – 6 || y = 2x +
18 ...
y = -x || y = -x + 4 || y = -x – 23 || y = -x +
14…
y = 0,5x || y = 0,5x +2 || y = 0,5x – 4 || y =
0,5x + 9 …

Jeśli wzory funkcji liniowych mają takie

same współczynniki kierunkowe a, to ich

wykresy są równoległe.

RÓWNOLEGŁOŚĆ I

PROSTOPADŁOŚĆ

WYKRESÓW FUNKCJI

LINIOWYCH.

Przykłady funkcji liniowych o wykresach
prostopadłych:
y = 2x + 2  y = -0,5x + 5
y = -4x – 1  y = 0,25x + 2

y = 3x + 2 

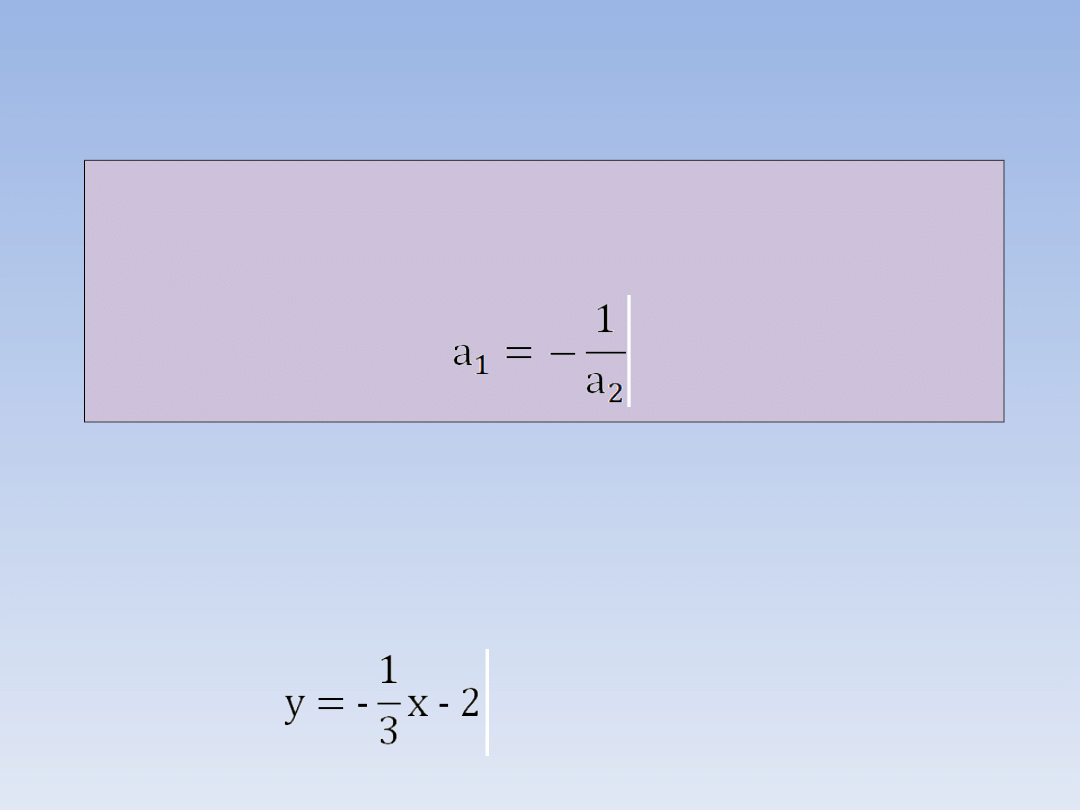
Jeśli wzory funkcji liniowych zapiszemy

następująco:

y = a

1

x + b

1

, y = a

2

x + b

2

, to wykresy

tych funkcji są prostopadłe gdy

PRZYKŁADOWE ZADANIA.

ZADANIE 1.
Dana jest funkcja liniowa y = 0,25x + 2.
a)Narysuj wykres tej funkcji.
b)Oblicz jej miejsce zerowe.
c)Sprawdź, czy punkt (100, 53) należy do
wykresu funkcji.
d)Określ, czy funkcja jest rosnąca, czy
malejąca.
e)Podaj wzór funkcji, której wykres będzie
równoległy do danej.
f)Podaj wzór funkcji, której wykres będzie
prostopadły do danej.

PRZYKŁADOWE ZADANIA.

ZADANIE 1a: narysuj wykres tej funkcji.
Rysuję tabelkę, wybieram argumenty i
obliczam wartości według wzoru.

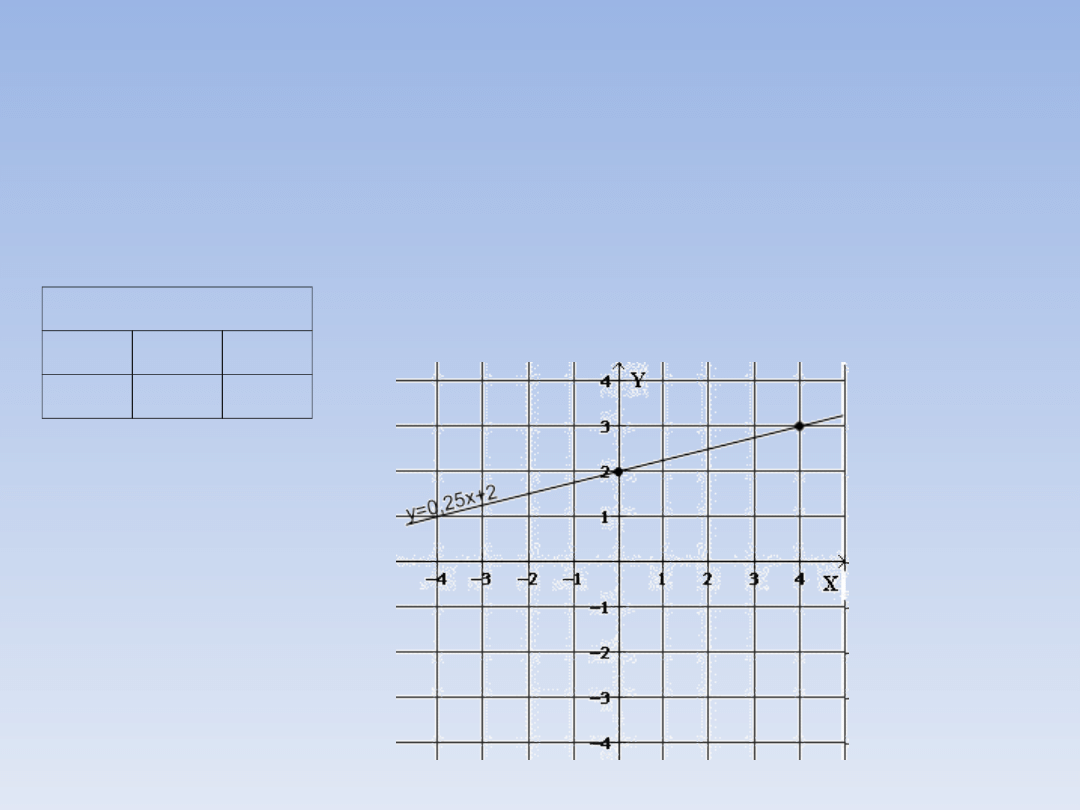
f(0) = 0,25 · 0 + 2 = 2
f(4) = 0,25 · 4 + 2 = 1 + 2 = 3

y = 0,25x + 2

x

0

4

y

y = 0,25x + 2

x

0

4

y

2

3

PRZYKŁADOWE ZADANIA.

ZADANIE 1a – ciąg dalszy.
Zaznaczam punkty w układzie
współrzędnych i rysuję linię przechodzącą
przez te punkty.

y = 0,25x + 2

x

0

4

y

2

3

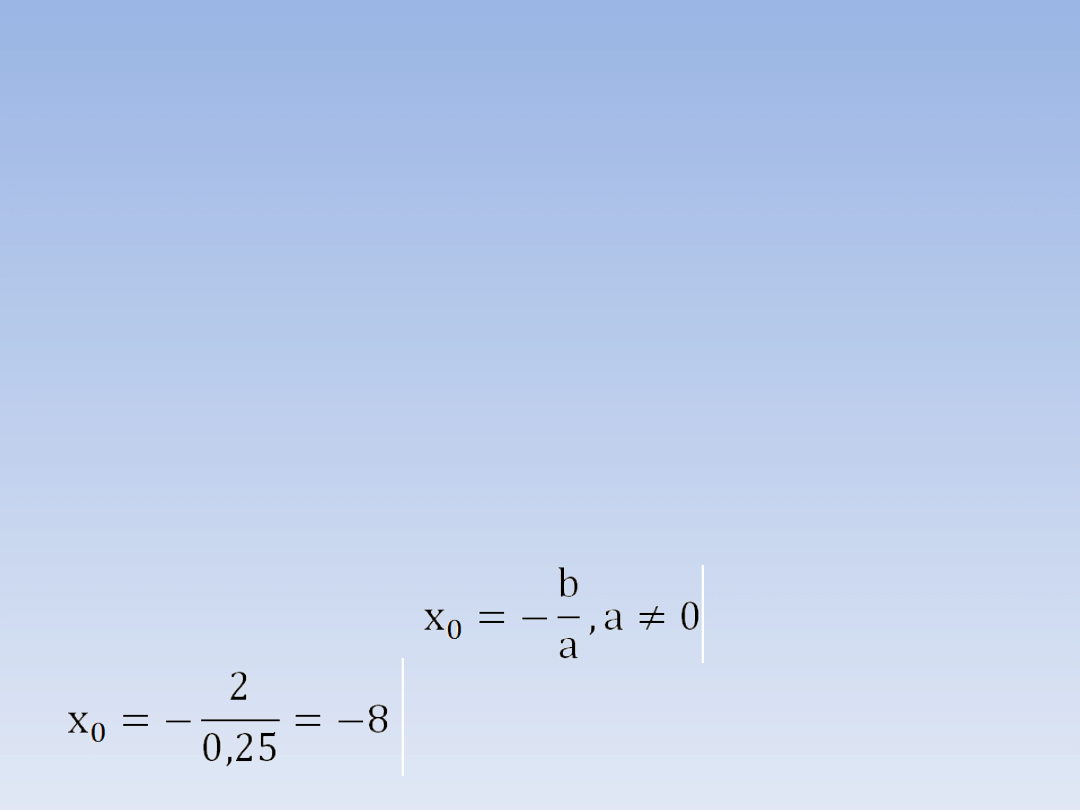
PRZYKŁADOWE ZADANIA.

ZADANIE 1b: oblicz jej miejsce zerowe.
I sposób:
Wstawiam do wzoru 0 zamiast y i rozwiązuje
równanie:
0 = 0,25x + 2
-0,25x = 2 /: (-0,25)
x = -8
Miejscem zerowym funkcji y = 0,25x + 2 jest
x

0

= -8.

II sposób:
Korzystam ze wzoru

PRZYKŁADOWE ZADANIA.

ZADANIE 1c: sprawdź, czy punkt (100, 53)
należy do wykresu funkcji.

Wstawiam x = 100 do wzoru funkcji i
sprawdzam, czy wyjdzie 53.

y = 0,25 · 100 + 2 = 25 + 2 = 27

Wyszła wartość inna niż 53 a więc punkt
(100, 53) nie należy do wykresu funkcji y =
0,25x + 2.

PRZYKŁADOWE ZADANIA.

ZADANIE 1d: określ, czy funkcja jest rosnąca,
czy malejąca.
y = 0,25x + 2
Współczynnik kierunkowy a we wzorze tej
funkcji jest większy od zera, a więc funkcja ta
jest rosnąca.

ZADANIE 1e: podaj wzór funkcji, której wykres
będzie równoległy do danej.

Wystarczy podać wzór funkcji o takim samym
współczynniku kierunkowym, np.:
y = 0,25x - 2

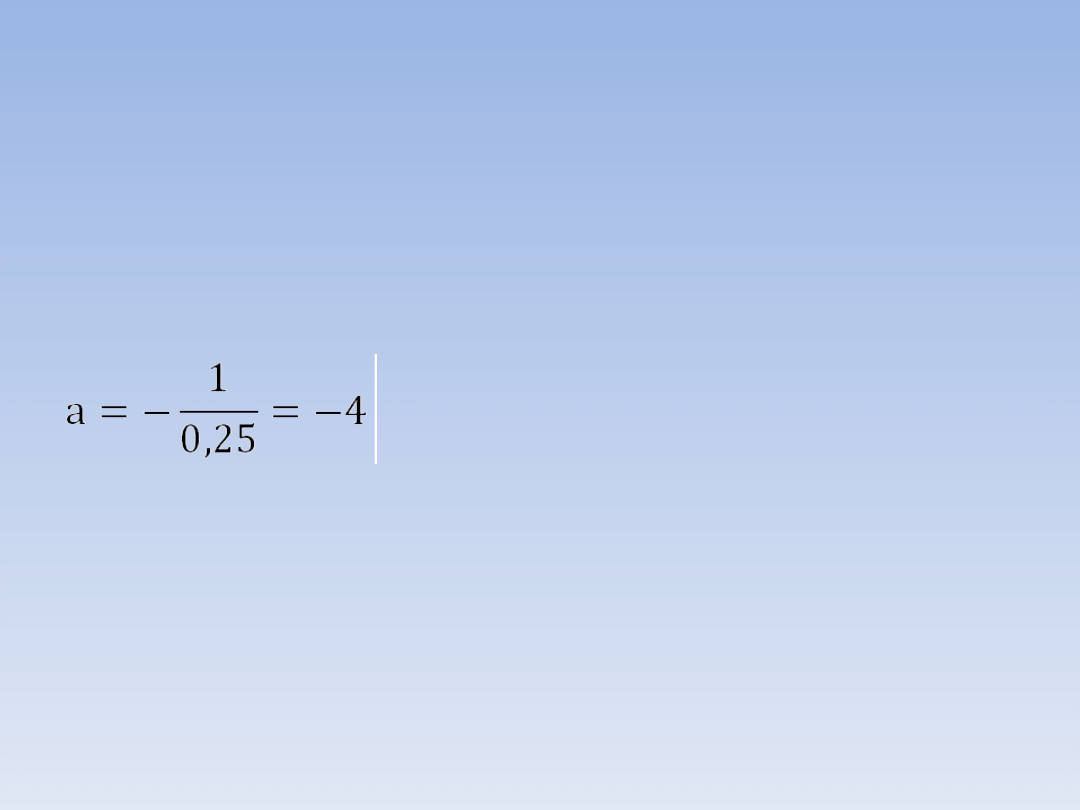
PRZYKŁADOWE ZADANIA.

ZADANIE 1f: podaj wzór funkcji, której
wykres będzie prostopadły do danej.

Wystarczy podać wzór funkcji, której
współczynnik kierunkowy będzie wynosił:

Może to być np.:
y = -4x + 12.

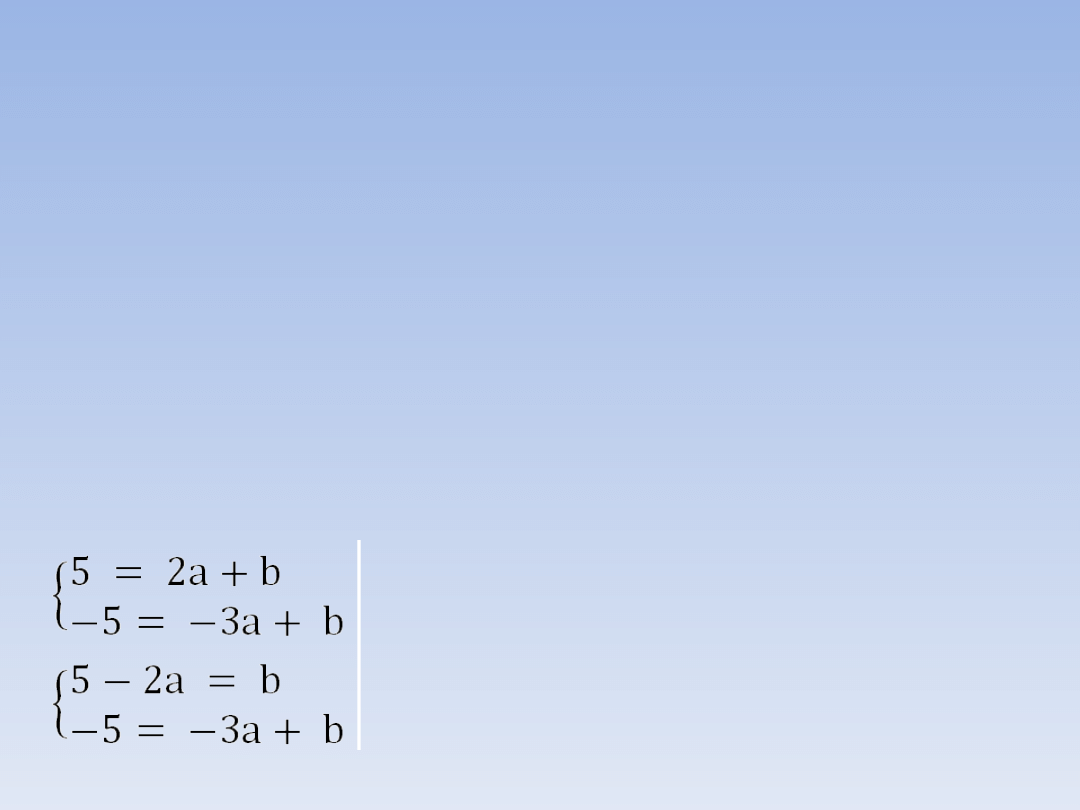
PRZYKŁADOWE ZADANIA.

ZADANIE 2.
Znajdź wzór funkcji liniowej przechodzącej
przez punkty (2, 5) oraz (-3, -5).

Musimy skorzystać ze wzoru ogólnego
funkcji liniowej
y = ax + b, podstawiając kolejno
współrzędne obu punktów otrzymamy układ
równań, z którego wyznaczymy
współczynniki a i b.

PRZYKŁADOWE ZADANIA.

ZADANIE 2.
-5 = -3a + 5 – 2a
-5 – 5 = -3a – 2a
-10 = -5a / : (-5)
a = 2
b = 5 – 2· 2 = 1
Wyliczone współczynniki wstawiamy do
wzoru ogólnego y = ax + b, otrzymując w
ten sposób wzór szukanej funkcji:

y = 2x + 1