Zadania dotyczące funkcji liniowej i jej własności

Większość z nas mając za zadanie narysowanie wykresu jakiejś funkcji przy wyznaczaniu współrzędnych punktów należących do tego wykresu, wykorzystuje tabelkę. W przypadku funkcji liniowej, wystarczy znaleźć współrzędne dwóch punktów tego wykresu i poprowadzić przez nie linię prostą.

Przykład 1

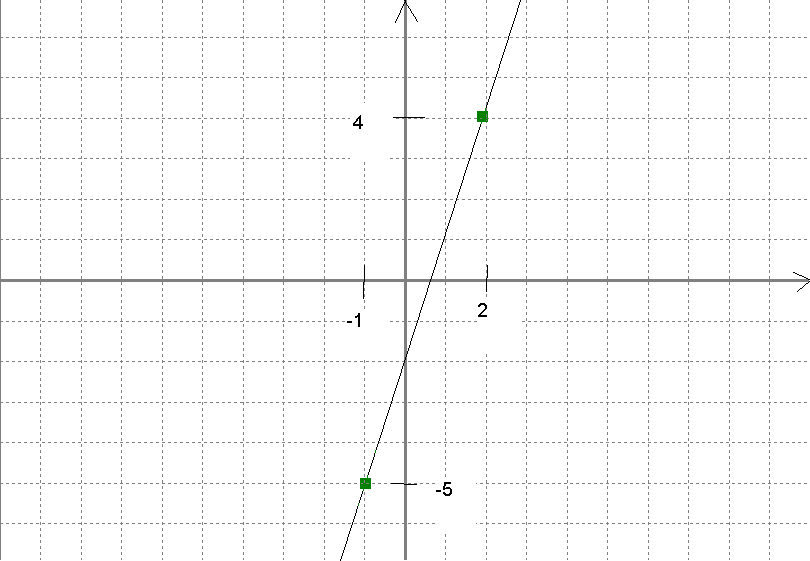
Narysuj wykres funkcji y = 3x - 2.

Rozwiązanie

Wybieramy dwie dowolne wartości argumentu x, np. x = 2 i x = -1, i dla nich wyznaczamy wartości funkcji danej w przykładzie.

Dla x = 2 otrzymujemy y = 3⋅2 - 2. Zatem dla x =2 y = 4.

Dla x = -1 otrzymujemy y = 3⋅(-1) - 2. Zatem dla x = -1 y = -5.

Otrzymane punkty (2,4), (-1,-5) zaznaczamy w układzie współrzędnych i rysujemy prostą przechodzącą przez te punkty.

Ćwiczenie 1

Rozwiąż zadanie 1 str.203 z podręcznika.

Przykład 2

(ćwiczenie C str. 200)

Podaj wzór takiej funkcji liniowej, która spełnia następujące warunki:

1. funkcja jest rosnąca, a jej wykres przecina oś y w punkcie (0,-3),

2. funkcja jest malejąca i jej wykres przecina oś y w punkcie (0,
   ),

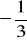
3. funkcja jest stała i do jej wykresu należy punkt (10,-20).

Rozwiązanie

1. Szukamy funkcji y = ax + b.

Jeżeli funkcja jest rosnąca, to jej współczynnik kierunkowy jest liczbą dodatnią (a>0). Ponieważ wykres funkcji przecina oś y w punkcie o współrzędnych (0,-3), więc współczynnik b = -3 i współrzędne tego punktu spełniają równanie szukanej prostej. Stąd otrzymujemy

-3 = a⋅0 + (-3)

Z powyższego równania wynika, że współczynnik a może być każdą liczba rzeczywistą dodatnią , np. dla a=2 równanie przyjmuje postać y = 2x -3.

b) Jeżeli funkcja jest malejąca, to jej współczynnik kierunkowy jest liczbą ujemną (a<0). Ponieważ wykres funkcji przecina oś y w punkcie o współrzędnych (0,
),więc współczynnik b =
i współrzędne tego punktu spełniają równanie szukanej prostej. Stąd otrzymujemy

= a⋅0 + (
)

Z powyższego równania wynika, że współczynnik a może być każdą liczba rzeczywistą ujemną , np. dla a= -2 równanie przyjmuje postać y = -2x
.

2. Jeżeli funkcja jest stała, to znaczy, że dla każdej wartości argumentu x wartość funkcji jest taka sama, a jej współczynnik kierunkowy jest równy zero. Ponieważ funkcja przechodzi przez punkt o współrzędnych (10,-20), więc szukana funkcja ma wzór y = -20.

Ćwiczenie 2

Rozwiąż zadanie 2,3 str.203 z podręcznika.

Przykład 3

Dana jest funkcja y = 7x +
.

1. dla jakich wartości argumentu funkcja ta przyjmuje wartość 3 ?

2. dla jakich argumentów wartości tej funkcji są większe od -2?

3. Wyznacz współrzędne punktów przecięcia wykresu tej funkcji z osiami układu współrzędnych.

4. Dla jakich argumentów funkcja przyjmuje wartości ujemne?

5. Znajdź wzór funkcji liniowej, której wykres jest równoległy do wykresu danej funkcji i przechodzi przez punkt (1, 3).

Rozwiązanie

1. Aby wyznaczyć szukane wartości argumentu, wystarczy rozwiązać równanie

7x +
= 3

7x = 3 -

7x =
/:7

x =

x =

x =

Dla x =
dana funkcja przyjmuje wartość 3.

2. Aby obliczyć, dla jakich argumentów wartości tej funkcji są większe od -2, wystarczy rozwiązać nierówność

7x +
> -2

7x > -2-

7x >
/: 7

x >

x >

3. Wyznaczając współrzędne punktu przecięcia wykresu z osią x wyznaczamy jednocześnie miejsce zerowe tej funkcji. Jak wiadomo, miejsce zerowe funkcji to argument, dla którego funkcja przyjmuje wartość równą zero. Zatem wystarczy przyrównać funkcję do 0 i rozwiązać równanie

7x +
= 0

7x = -
/: 7

x = -

Wyznaczając współrzędne punktu przecięcia wykresu funkcji z osią y, szukamy punktu o współrzędnych postaci (0,b), gdzie b jest współczynnikiem występującym we wzorze. Zatem nasza funkcja przecina oś x w punkcie (-
,0), a oś y w punkcie (0,
).

4. Szukamy wartości argumentów, dla których funkcja przyjmuje wartości ujemne, czyli mniejsze od 0. Zatem musimy rozwiązać nierówność

7x +
< 0

Po rozwiązaniu nierówności otrzymujemy x <-
( dla wszystkich x mniejszych od -
funkcja przyjmuje wartości ujemne).

5. Aby wykresy funkcji liniowych były równoległe ich współczynniki kierunkowe musza być takie same. Znając współczynnik kierunkowy prostej i współrzędne choć jednego punktu możemy wyznaczyć równanie prostej równoległej do danej i przechodzącej przez podany punkt.

Nasza funkcja ma równanie y = 7x +
. Jej współczynnik kierunkowy jest równy a = 7, więc współczynnik kierunkowy prostej równoległej do naszej funkcji musi być identyczny. Przyjmując, że szukany wzór ma postać

y = ax + b,

po podstawieniu wartości współczynnika kierunkowego otrzymujemy

y = 7x + b.

Ponieważ szukana prosta ma przechodzić przez punkt o współrzędnych (1,3), więc te współrzędne spełniają jej równanie. Fakt ten wykorzystujemy do wyznaczenia współczynnika b. Podstawiając odpowiednio współrzędne danego punktu do równania szukanej prostej otrzymamy

3 = 7⋅1 + b

b = 3 - 7

b = -4

Zatem prosta równoległa do prostej y = 7x +
i przechodząca przez punkt (1,3) ma równanie y = 7x - 4.

Ćwiczenie 3

Rozwiąż zadanie 8,9 str.204 oraz 12 str. 205 z podręcznika.

Przykład 4

(zadanie 11 str. 205)

1. Wyznacz współrzędne punktu przecięcia wykresów funkcji f : x
   

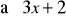
i g : x
.

Rozwiązanie

Aby wyznaczyć współrzędne punktu przecięcia wykresów dwóch funkcji wystarczy z ich równań zbudować układ i go rozwiązać.

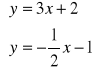
3x + 2 =

3x +
= -2 -1

/

x = -

Mając wyznaczony x podstawiamy go do jednego z równań i wyznaczamy y

y = 3⋅(-
) + 2

y = -
+ 2

y = -

Zatem wykresy funkcji f i g przecinają się w punkcie o współrzędnych (-
,-
).

Przykład 5

(zadanie 13 str. 205)

a) znajdź wzór funkcji liniowej, której wykres przechodzi przez punkty o współrzędnych (2,1) i (-2,-3).

Rozwiązanie

Szukane równanie możemy zapisać w postaci y = ax + b. Współrzędne danych punktów spełniają to równanie, zatem

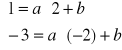
Do rozwiązania tego układu można zastosować metodę przeciwnych współczynników, gdyż przy niewiadomej a mamy liczby przeciwnych znaków.

1 - 3 = 2a - 2a + b + b

-2 = 2b /: 2

b = -1

Podstawiając do pierwszego równania wyznaczoną wartość otrzymamy

1 = 2a -1

1+ 1 = 2a /:2

a = 1

Zatem szukana prosta ma równanie y = x - 1.

Ćwiczenie 4

Rozwiąż zadanie 13 str.205 z podręcznika.

---