Elżbieta Szwajczak

Katedra Fizyki PRz

PRACA, ENERGIA, MOC

PRACA



cos

r

d

F

dW

r

d

F

dW







Siła działając na punkt materialny o masie m i
przesuwając go wykonuje pracę:

gdzie α jest kątem pomiędzy wektorem siły
F i wektorem przesunięcia elementarnego d
r
(czyli tzw. przesunięciem skierowanym).
Jednostką pracy jest [W] = N m = J.

W ruchu obrotowym:

 
 



d

M

dW





gdzie M jest momentem siły, zaś dφ jest
„skierowanym przesunięciem kątowym”.

Praca jest formą energii.

MOC

to tempo (prędkość) przekazywania
energii z układu do układu:

Jednostką mocy jest [P] J/s = W.

dt

dE

dt

dW

P





ENERGIA MECHANICZNA

Istnieją dwa rodzaje energii mechanicznej
– kinetyczna i potencjalna.

 

Energia kinetyczna

(energia ruchu)

w ruchu postępowym:

m

p

V

m

E

k

2

2

2

2





gdzie m jest masą punktu materialnego
(ciała), V jest wektorem prędkości, zaś
p=mV jest wektorem pędu.

Energia kinetyczna

w ruchu obrotowym
 

I

K

I

E

k

2

2

2

2







gdzie I jest momentem bezwładności bryły
sztywnej, ω
jest wektorem prędkości kątowej, zaś K=I ω
jest wektorem momentu pędu.

Jednostką energii kinetycznej jest [E

k

] J = (kg

m

2

)/ s

2

.

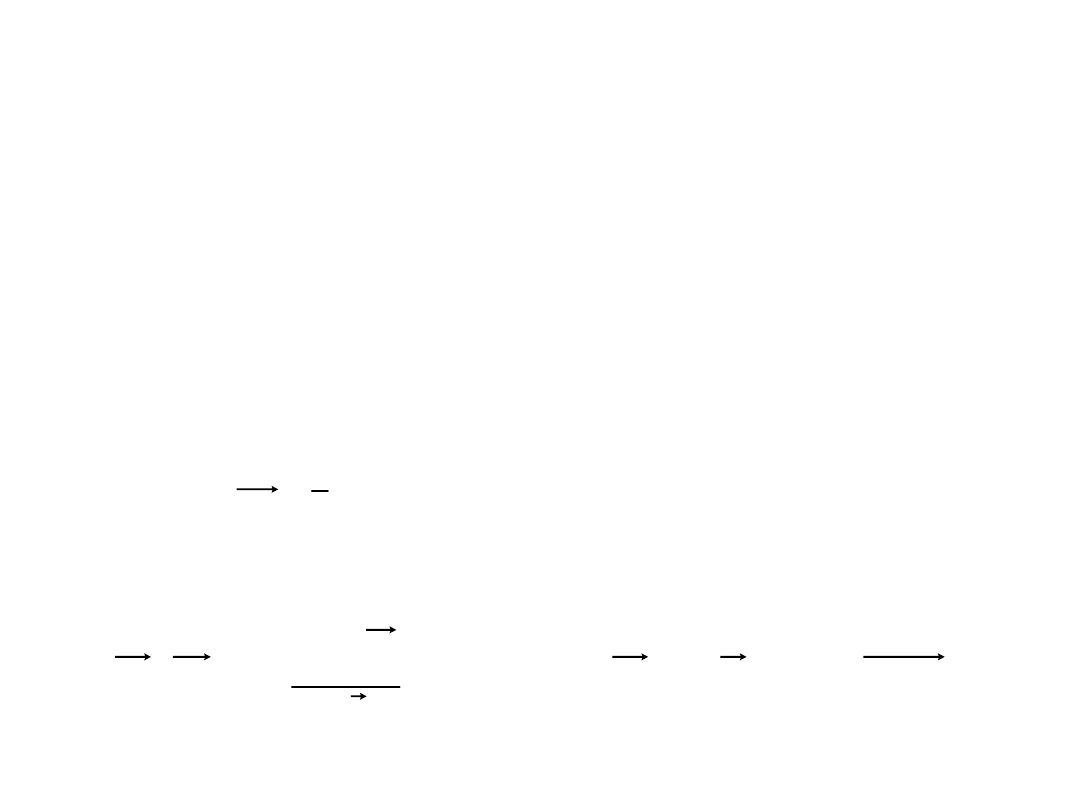
U

grad

U

F

r

d

r

dU

r

F

r

d

F

dU





















lub

)

(

)

(

lub

Energia potencjalna

Ciało ma energię potencjalną gdy jest w
polu działania sił zachowawczych. Energia
potencjalna wiąże się ze zdolnością ciała do
wykonania pracy; energia potencjalna w
danym punkcie przestrzeni jest równa pracy
wykonanej przez przyłożoną siłę przy
przeniesieniu ciała z nieskończoności do
danego punktu.

Przy czym w polu sił zachowawczych
praca nie zależy od kształtu drogi ani od
długości toru, zależy natomiast od
współrzędnych

punktu

położenia

początkowego i końcowego, tzn. praca po
torze zamkniętym wynosi zero:

0







r

d

F

Przykłady

energii

potencjalnej

 
 

Siła F
Energia U

2

4

1

4

1

2

2

2

x

k

kx

r

q

Q

r

q

Q

r

m

M

G

r

m

M

G

mgh

mg

o

o



















Przykłady energii potencjalnej cd.

1. W polu sił ciężkości
2. W polu grawitacyjnym ziemskim
3.

W

centralnym

polu

elektrostatycznym
(np. atom w modelu Bohra)
4. W polu sił sprężystych (np.
drgania
harmoniczne proste)

 

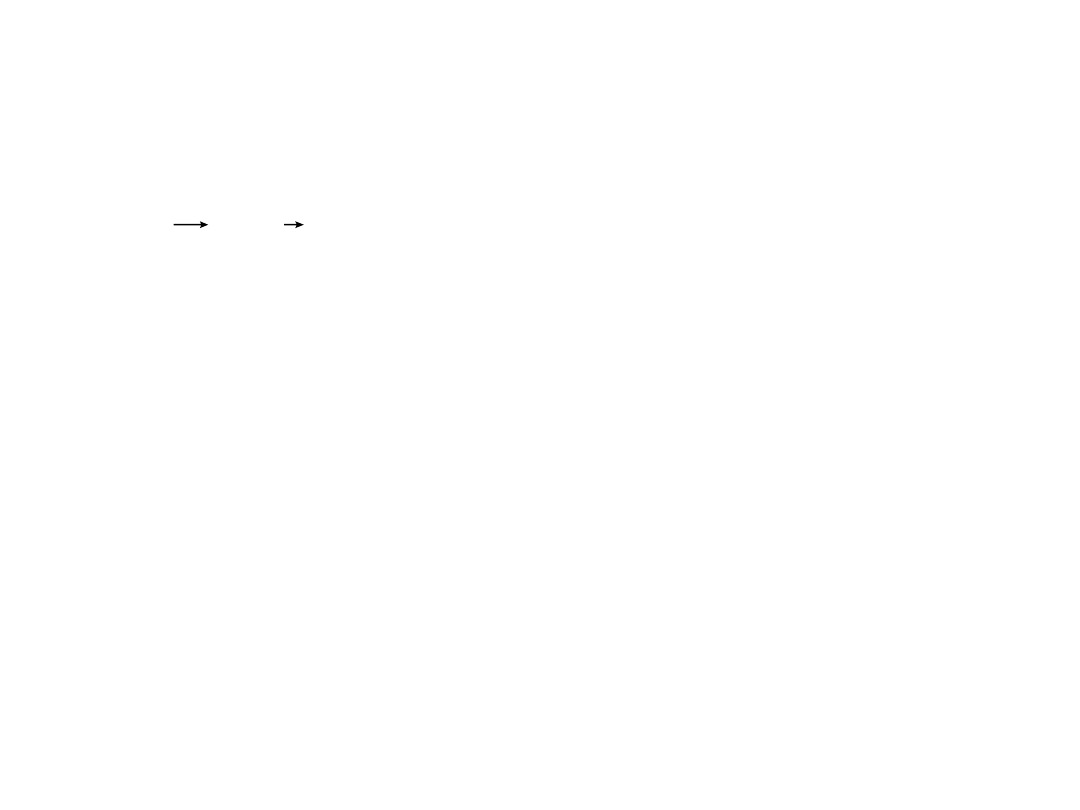
Związek praca – energia

 
Twierdzenie o pracy i energii kinetycznej:
 

Energia kinetyczna ciała rośnie dzięki pracy
wykonanej przez siłę działającą na ciało przy
jego przesunięciu
z punktu A do punktu B.

kA

B

A

kB

E

E

r

d

F









 

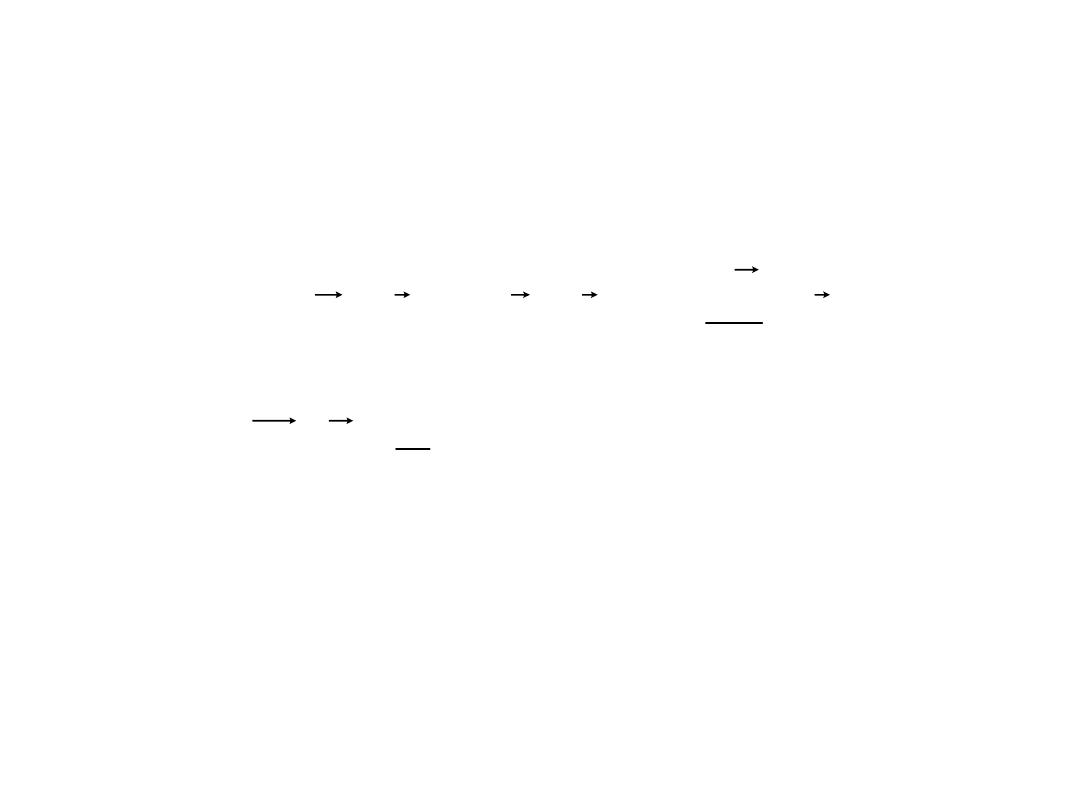
Jeśli przypomnieć drugą zasadę dynamiki
Newtona i
definicję przyspieszenia, to można wykazać, że:

 

E

W

E

E

E

V

V

m

V

d

V

m

r

d

dt

V

d

m

r

d

a

m

r

d

F

W

AB

k

kA

kB

A

B

B

A

B

A

B

A

B

A

AB









































lub

)

(

2

2

2

.

)

(

const

t

p 

0







F

F

j

j

ZASADY ZACHOWANIA

 

Zasada zachowania pędu

Całkowity pęd układu odosobnionego jest
stały w czasie:
 

Oznacza

to, że źródła wszystkich sił

znajdują się
w obrębie samego układu

.

Przy czym przez układ izolowany (zamknięty)
rozumie się
układ na który nie działają żadne siły zewnętrzne
lub działające siły równoważą się, tzn.:









i

i

i

i

i

V

m

p

p

BA

AB

F

F





Rozważmy dwu elementowy układ izolowany,
składający się z dwu ciał o masach m

A

i m

B

.

Zgodnie z trzecią zasadą dynamiki Newtona

 

Przez całkowity pęd układu rozumie
się

sumę

wektorową

pędów

wszystkich elementów układu, tj.:

lub po uwzględnieniu drugiej zasady dynamiki
Newtona:

dt

p

d

dt

p

d

B

A





Można to zapisać jako:

0

)

(









B

A

B

A

p

p

dt

d

dt

p

d

dt

p

d

.

)

(

)

(

const

t

p

t

p

B

A





co jest możliwe, gdy

Po uogólnieniu, czyli dla układu n-
elementowego

.

)

(

)

(

1

const

t

p

t

p

n

i

i









Przykłady z fizyki:
*„odrzut” karabinu przy wystrzeleniu kuli
* ruch środka masy pocisku, który
wybucha w czasie
lotu (ruch po torze zwanym torem rzutu
ukośnego).
 

Zasada zachowania momentu

pędu

.

)

(

const

t

K



i

i

i

i

i

I

K

t

K











)

(

 

gdzie całkowity moment pędu układu
jest suma wektorową momentów pędu
wszystkich elementów składowych
układu:

Całkowity moment pędu układu izolowanego nie
zmienia
się w czasie:

Przy czym przez układ odosobniony rozumie
się układ na który nie działają żadne siły
zewnętrzne lub momenty działających sił
równoważą się, tzn.:

j

j

j

j

j

F

r

M

gdzie

M

M











0

 

Przykład:
Całkowity moment pędu tancerza na
lodzie jest zachowany, zmienia się
jednak prędkość obrotów w wyniku
zmiany

momentu

bezwładności

tancerza – co jest spowodowane zmianą
rozkładu jego masy w stosunku do osi
obrotu:

.

2

const

r

m

I









 

Zasada zachowania energii

Energia mechaniczna układu izolowanego
jest stała w czasie:
 

Układ izolowany oznacza, że nie ma
wymiany ciepła z otoczeniem.
Energia mechaniczna jest suma energii
kinetycznej i energii potencjalnej; możliwa
jest zamiana energii kinetycznej w
energię potencjalną.

.

)

(

)

(

)

(

const

t

U

t

E

t

E

k







 

Istnieją także inne rodzaje energii, np.
energia cieplna, chemiczna.

W ogólności, całkowita energia układu, tj.
suma energii wszystkich rodzajów w
układzie izolowanym jest stała w czasie.