Środkowe w trójkącie

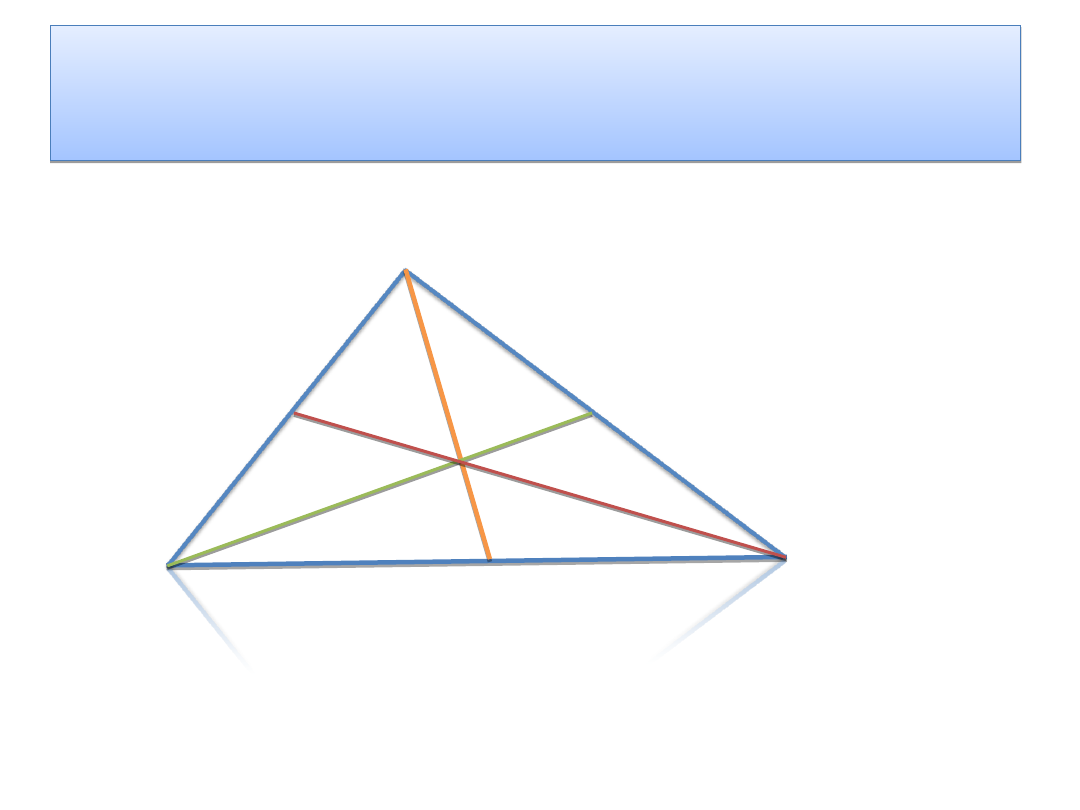
Środkową trójkąta nazywamy odcinek łączący 
wierzchołek trójkąta ze środkiem przeciwległego 
boku.

Przedstawmy tą definicję graficznie. 

B

A

C

Każdy trójkąt ma trzy środkowe.

D

E

F

| AD|=|DB| ,|AF|=|FC|, |CE|=|EB|

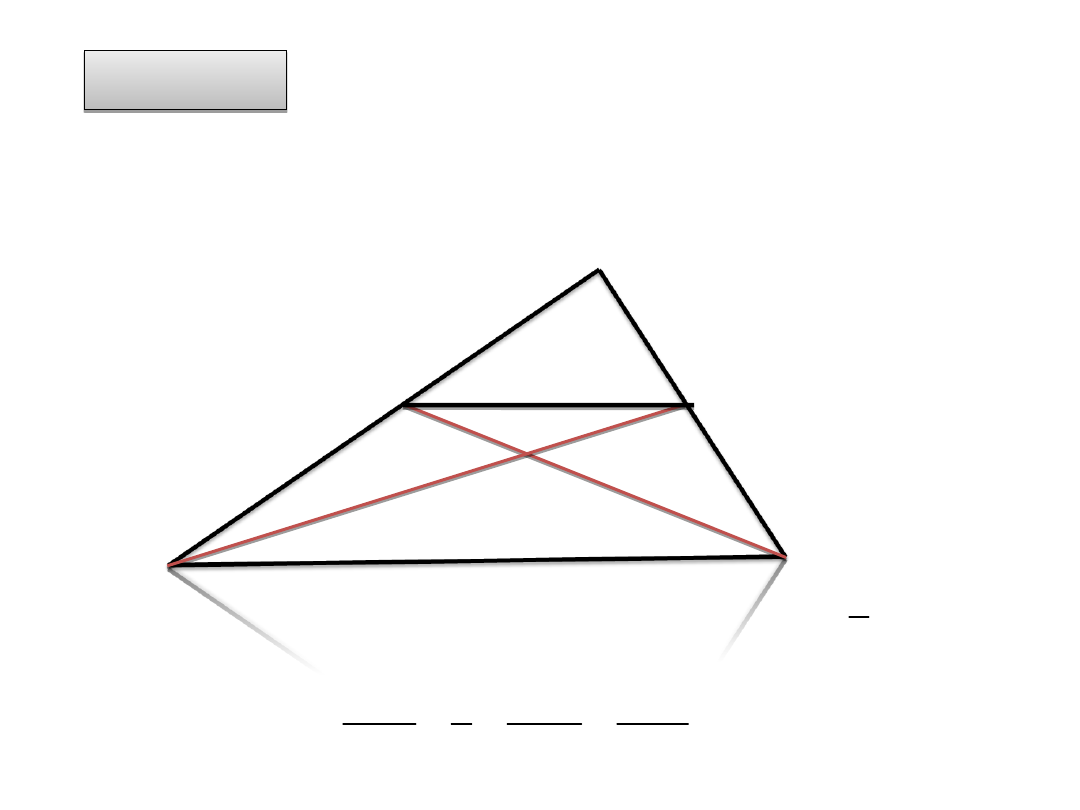
     Przykład   I 

Trójkąt ABC ma 2 środkowe :  AE i BG , które będą przecinały 

się  w punkcie 0.

  

Jak wiadomo, odcinek EG jest równoległy do odcinka BA i |EG|

=      |AB|. Zatem z twierdzenia Talesa otrzymujemy, że : 

A

B

C

G

E

O

2

1

|

|

|

|

|

|

|

|

2

1

|

|

|

|

OA

OE

OB

OG

AB

EG







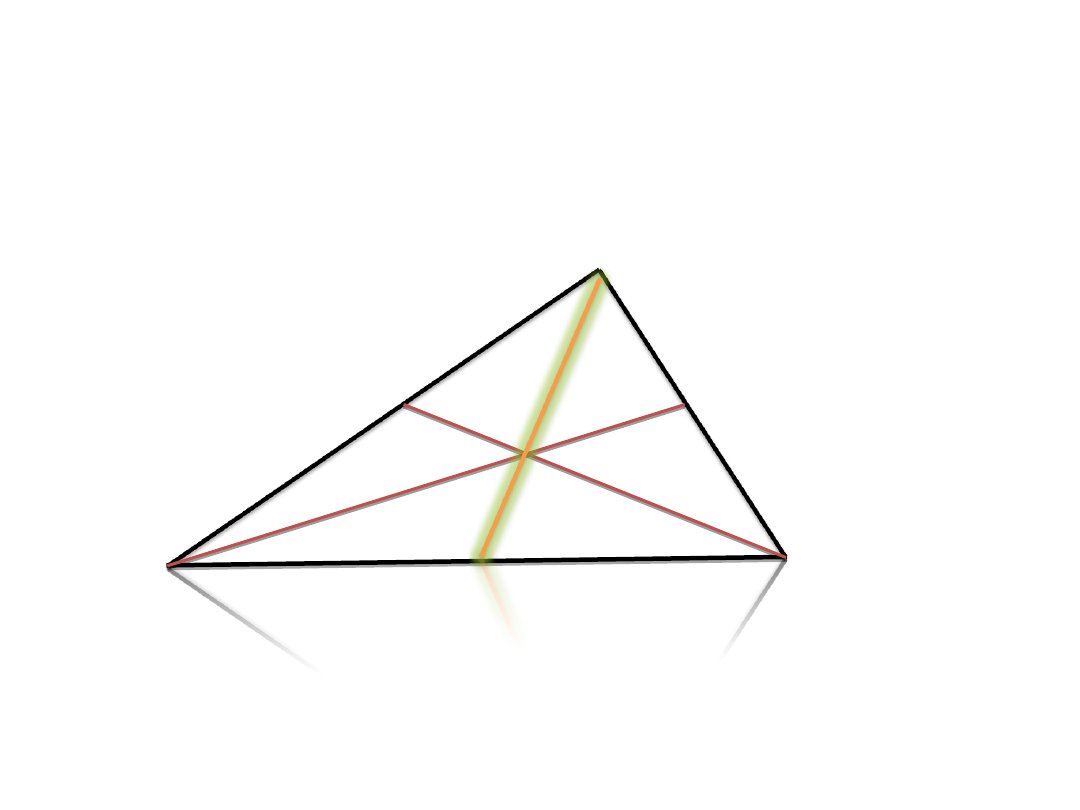
Środkowe przecięły się w punkcie 0, który podzielił je w 

stosunku 1 : 2. 

Prosto  jest więc pokazać, że trzecia środkowa (CH) przejdzie 

przez punkt 0,

który podzieli ją w stosunku 1 : 2. 

O

C

H

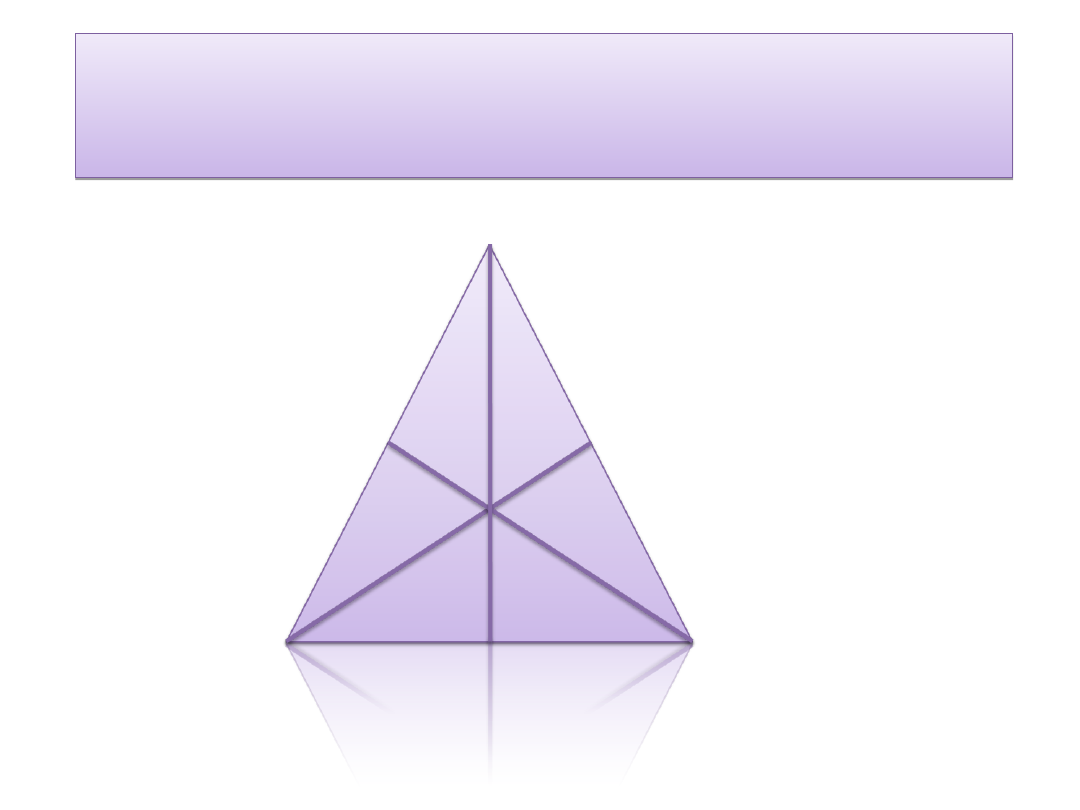
W dowolnym trójkącie trzy środkowe przecinają 
się w jednym punkcie, który dzieli każdą z nich w 
stosunku 1 : 2. 

B

A

C

Punkt przecięcia środkowych nazywamy środkiem ciężkości trójkąta.

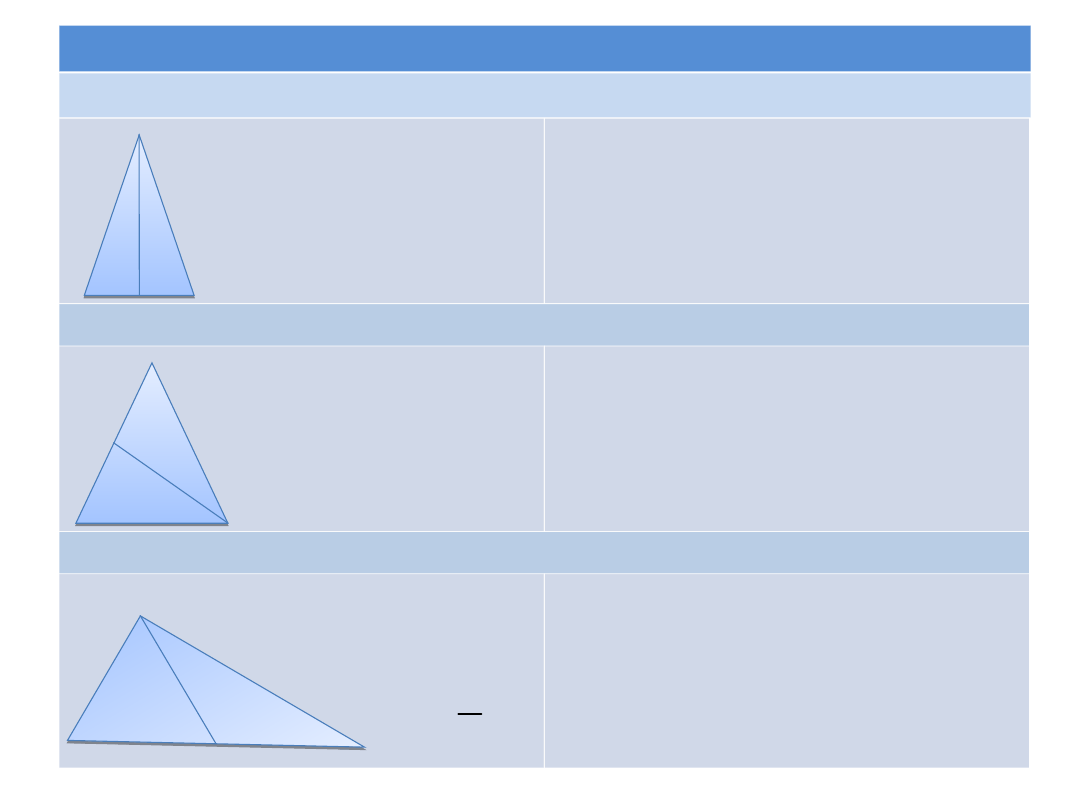
Środkowe w wybranych trójkątach

Trójkąt równoramienny

s₁- środkowa poprowadzona 

do podstawy

h₁- wysokość poprowadzona 

do podstawy

h₁ = s₁

W trójkącie równoramiennym 

środkowa poprowadzona do 

podstawy jest jednocześnie 

wysokością.

Trójkąt równoboczny

s- środkowa

h- wysokość 

h = s

W trójkącie równobocznym 

środkowe i wysokości się 

pokrywają. Dlatego wysokości w 

trójkącie równobocznym dzielą 

się w stosunku 1 : 2. 

Trójkąt prostokątny

s – środkowa poprowadzona z 

wierzchołka kąta prostego 

c – przeciwprostokątna 

W trójkącie prostokątnym 

środkową poprowadzona z 

wierzchołka kąta prostego ma 

długość połowy 

przeciwprostokątnej. 

c

s

2

1



s

s

s
₁

h₁

h

c

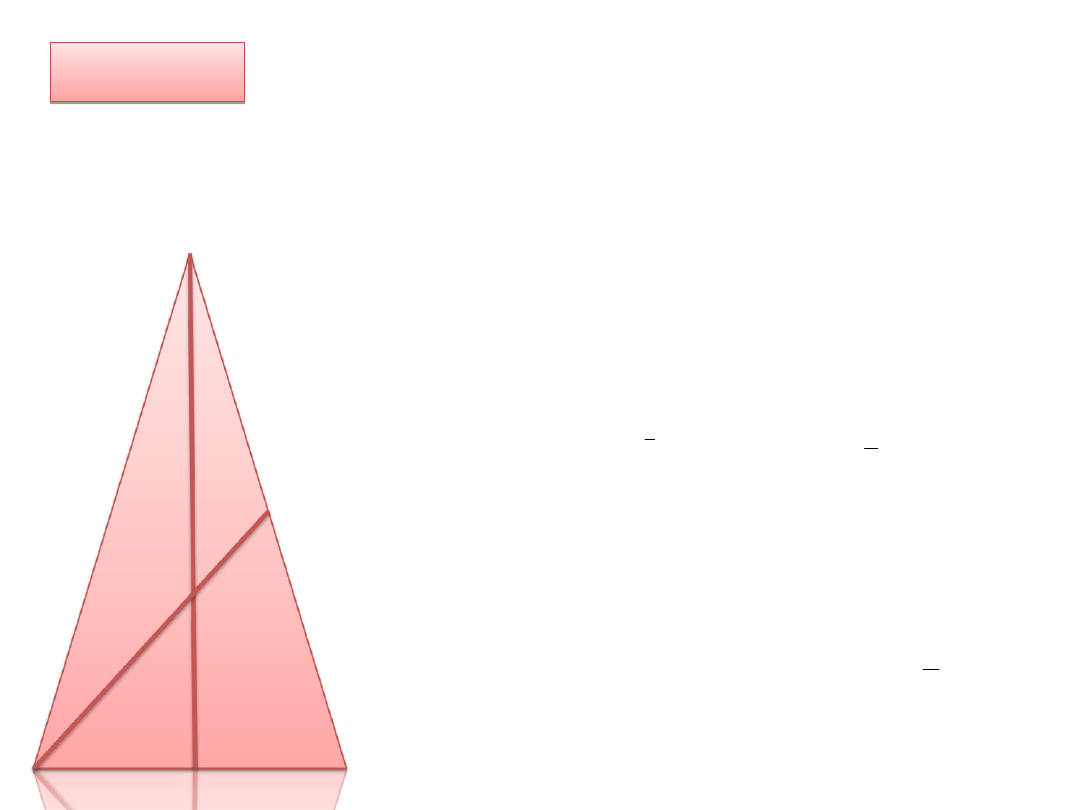
Przykład   II

W trójkącie równoramiennym ABC podstawa AB ma długość 6 cm, 

a środkowa CE ma długość 12 cm. Obliczmy długość środkowej 
AD.

C

A

B

W trójkącie ABC środkowa CE jest jednocześnie 
wysokością poprowadzoną na podstawę AB , a  punkt E 
dzieli tę podstawę na połowy :  |AE|=EB|=3cm

Punkt O przecięcia środkowych CE i AD dzieli je w 
stosunku 1 : 2.
|OE| : |CO| =1:2 , więc |OE| =    |CE|, czyli |OE| =
    

D

E

O

3

1

)

(

4

12

3

1

cm





Korzystając z twierdzenia Pitagorasa dla trójkąta 
AEO, można obliczyć długość odcinka AO: 

5

|

|

4

3

|

|

|

|

|

|

|

|

2

2

2

2

2

2











AO

AO

OE

AE

AO

Obliczamy długość środkowej AD:

|

|

2

1

|

|

|

|

|

|

|

AO

OD

i

OD

AO

AD







)

(

5

,

7

5

,

2

5

|

|

cm

AD







Michał Biros, kl. I A