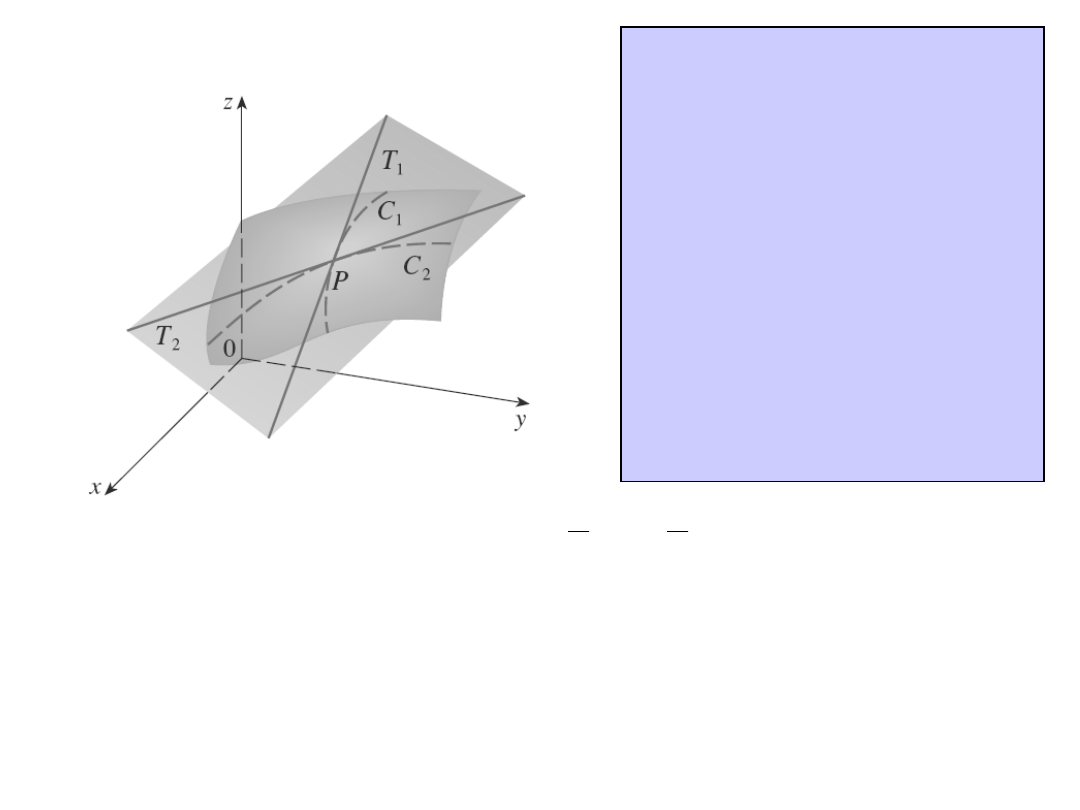
Płaszczyzna styczna

Załóżmy, że dana jest
powierzchnia S dana
równaniem z = f(x,y), gdzie f
posiada ciągłe pierwsze
pochodne cząstkowe i P(x

0

,y

0

,z

0

)

będzie punktem na S. Niech C

1

i

C

2

będą krzywymi otrzymanymi

po przecięciu powierzchni S
płaszczyznami y = y

0

i x = x

0

.

Punkt P leży na obu C

1

i C

2

.

Niech T

1

i T

2

będą liniami

stycznymi do krzywych C

1

i C

2

w

punkcie P. Powierzchnia styczna
zawiera obie proste T

1

i T

2

.

Równanie płaszczyzny
przechodzącej przez P(x

0

,y

0

,z

0

):

A(x – x

0

)+ B(y – y

0

) + C(z – z

0

)

= 0

)

,

(

)

(

)

(

)

(

0

0

0

0

0

0

0

0

y

x

f

a

y

y

x

x

a

z

z

y

y

b

x

x

a

z

z

C

B

b

C

A

a

x





























)

,

(

)

(

0

0

0

0

0

y

x

f

b

x

x

y

y

b

z

z

y











)

(

)

(

0

0

0

y

y

f

x

x

f

z

z

y

x











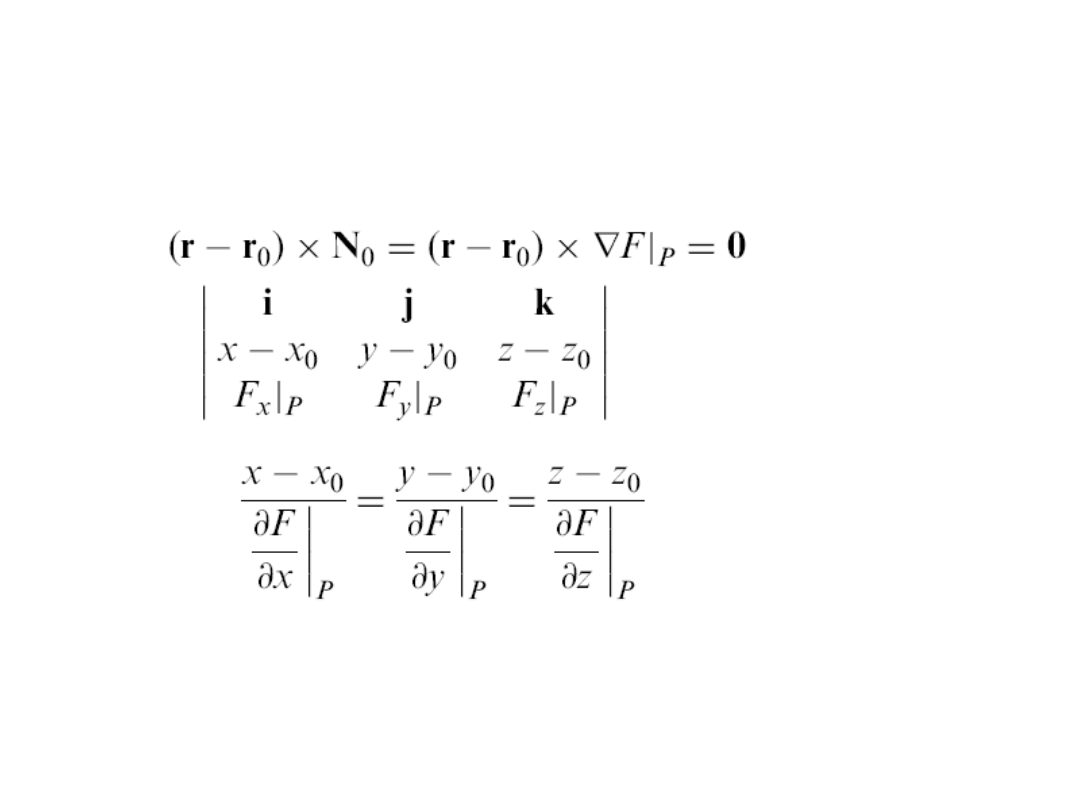
Normalna do

powierzchni

Dane powierzchnia F(x,y,z) = 0 i punkt P(x

0

,y

0

,z

0

)

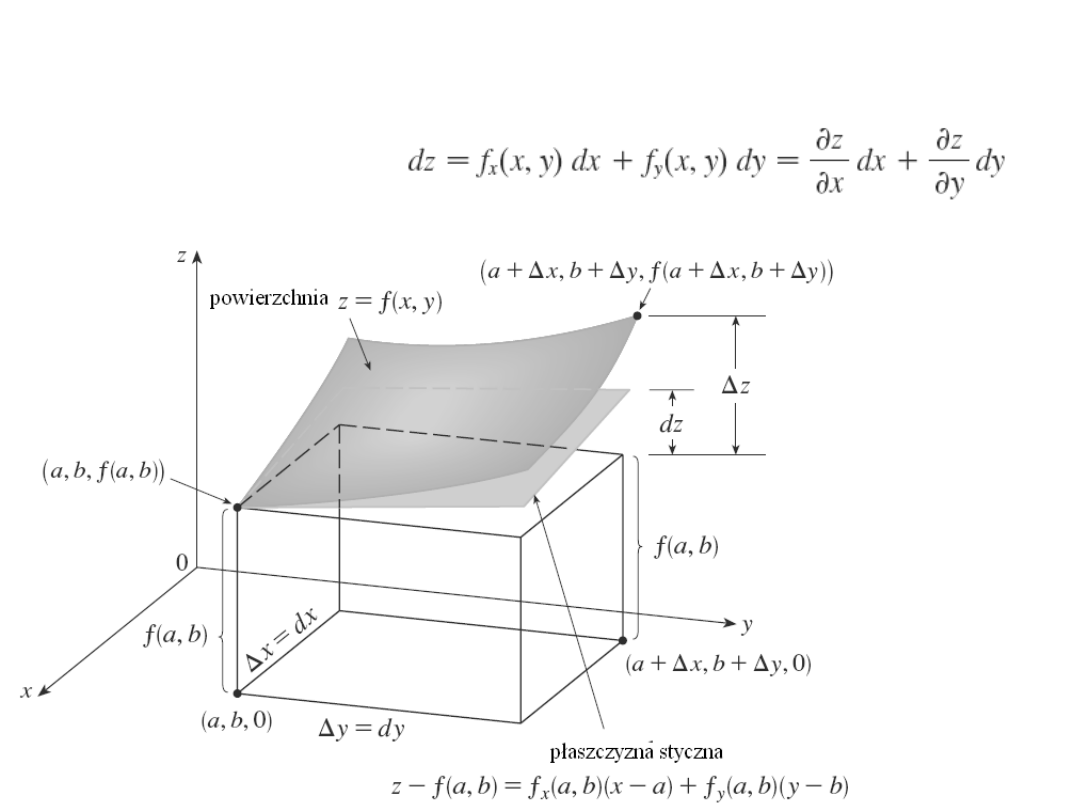
Różniczka funkcji dwóch

zmiennych

Różniczka zupełna

Różniczka funkcji wielu zmiennych

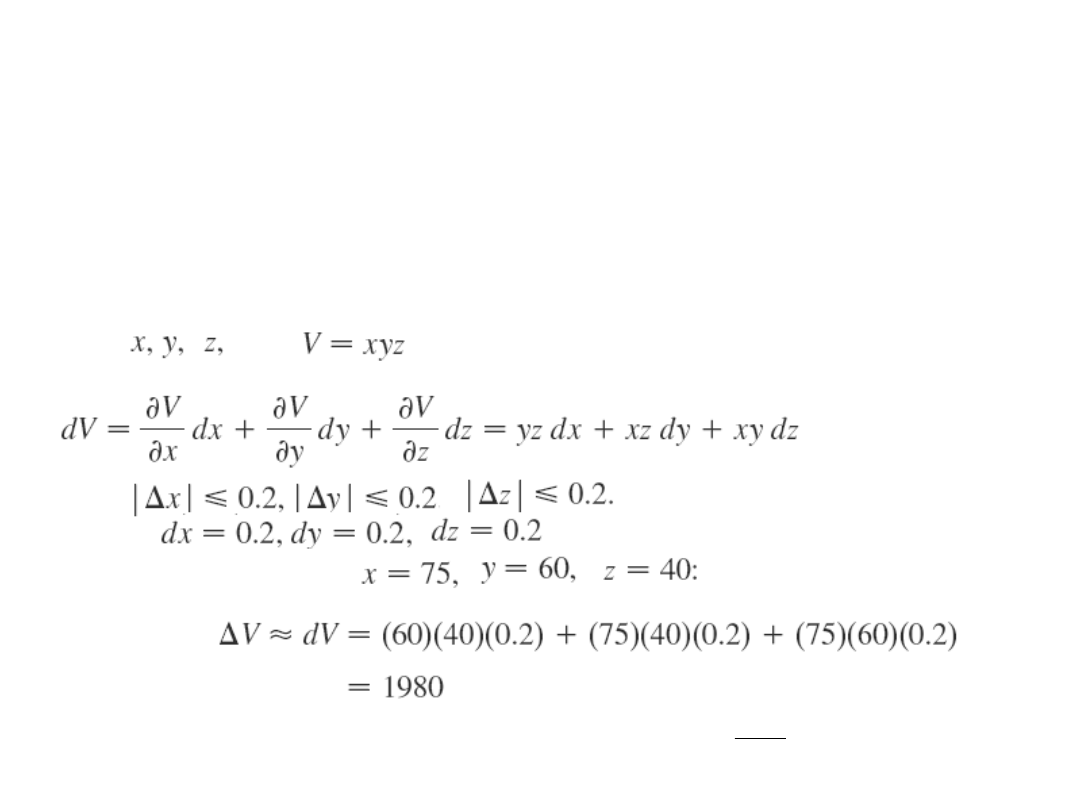
 Zmierzono krawędzie prostopadłościanu: 75 cm,
60 cm, 40 cm. Każdy z pomiarów wykonano z
dokładnością 0.2 cm. Używając różniczki oszacuj
możliwy błąd obliczonej objętości.

Przykład (analiza
błędu)

%

1





V

V

Twierdzenie Taylora

Twierdzenie Taylora

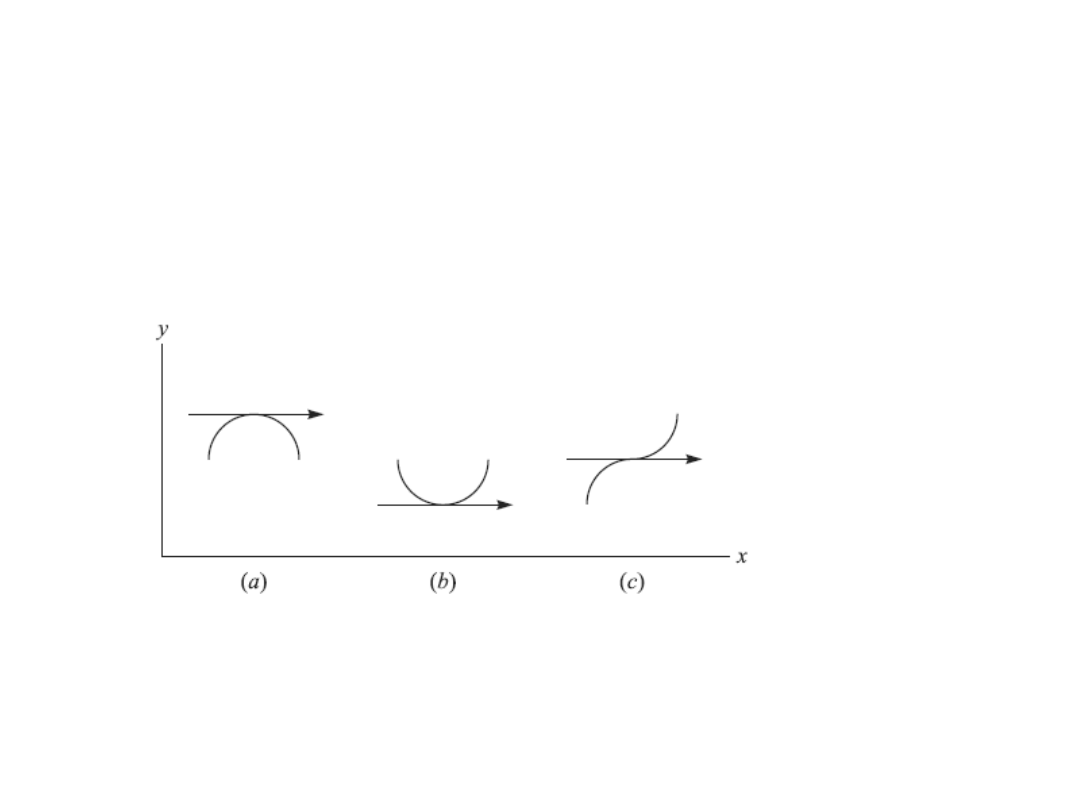
Maksimum i minimum funkcji

Funkcja jednej
zmiennej

0

0

0

)

(

)

(

0

)

(

)

(

0

0



















x

g

x

P

x

g

x

g

y

Dla

funkcji dwóch zmiennych

Przykład

Znajdź ekstrema
funkcji

20

12

3

)

,

(

3

3











y

x

y

x

y

x

f

2

gdy

0

12

3

,

1

gdy

0

3

3

2

2





















y

y

f

x

x

f

y

x

Punkty krytyczne : P(1,2), Q(-1,2), R(1,-2), S(-1.-
2)

maksimum;

jest

punkcie

;

0

)

(

0

),

2

,

1

(

punkcie

W

;

ekstremum

punkcie

w

ma

nie

0

),

2

,

1

(

punkcie

W

;

ekstremum

punkcie

w

ma

nie

0

),

2

,

1

(

punkcie

W

minimum;

jest

punkcie

;

0

)

(

0

),

2

,

1

(

punkcie

W

36

zatem

0

,

6

,

6

2











































yy

xx

yy

xx

xy

yy

xx

xy

yy

xx

f

f

P

R

Q

f

f

P

xy

f

f

f

f

y

f

x

f

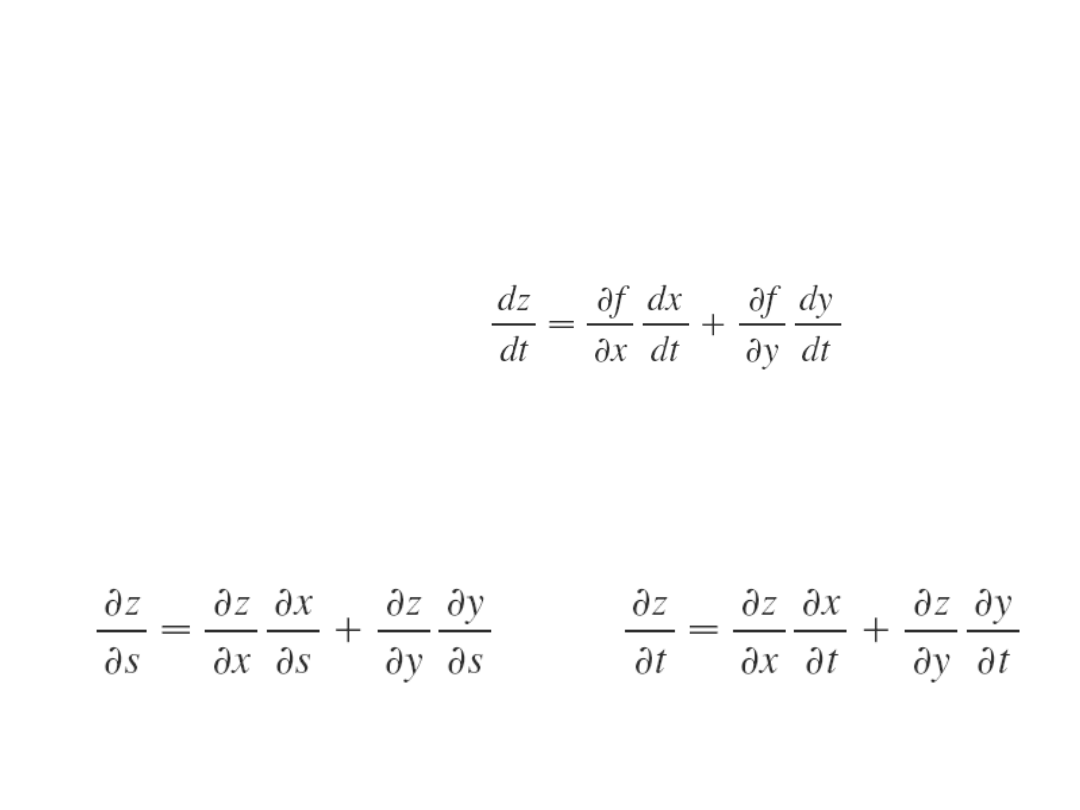
Reguła łańcucha

Twierdzen
ie

Załóżmy, że z = f(x,y) jest różniczkowalną funkcją zmiennych x
i y , gdzie x = g(t) a y = h(t) i obie te funkcje również są
różniczkowalne. Wówczas z jest różniczkowalną funkcją t i
zachodzi:

Załóżmy, że z = f(x,y) jest różniczkowalną funkcją zmiennych x
i y , gdzie x = g(s,t) a y = h(s,t) i obie te funkcje również
są różniczkowalne. Wówczas z jest różniczkowalną funkcją
s, t i zachodzi:

Twierdzenie

Załóżmy, że u = f(x

1

, x

2

,..., x

n

) jest

różniczkowalną funkcją zmiennych x

i

dla i =

1,...,n . Każda z x

1

, x

2

,..., x

n

jest funkcją

m

zmiennych t

1

, t

2

,..., t

m ..

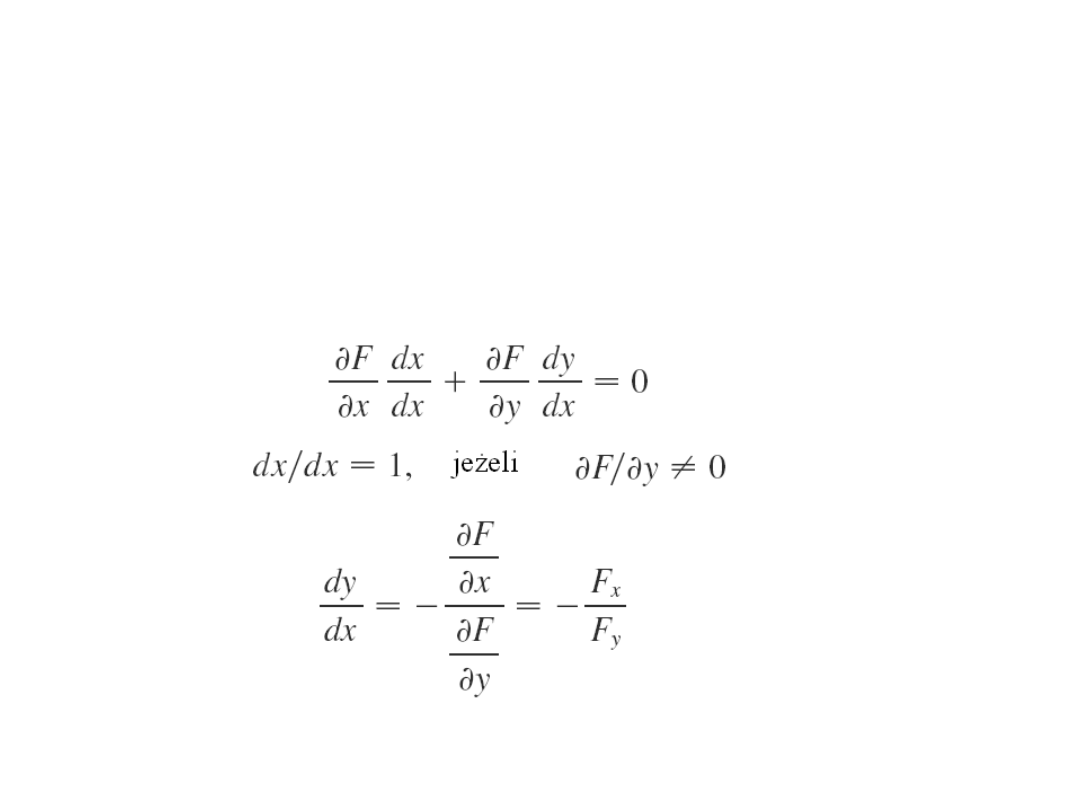
Funkcja uwikłana.

Postać
uwikłana

0

))

(

,

(

)

(

0

)

,

(







x

f

x

F

x

f

y

y

x

F

Przykład

0

))

(

,

,

(

0

)

,

,

(

)

,

(







x

f

y

x

F

z

y

x

F

y

x

f

z

Pochodna funkcji uwikłanej

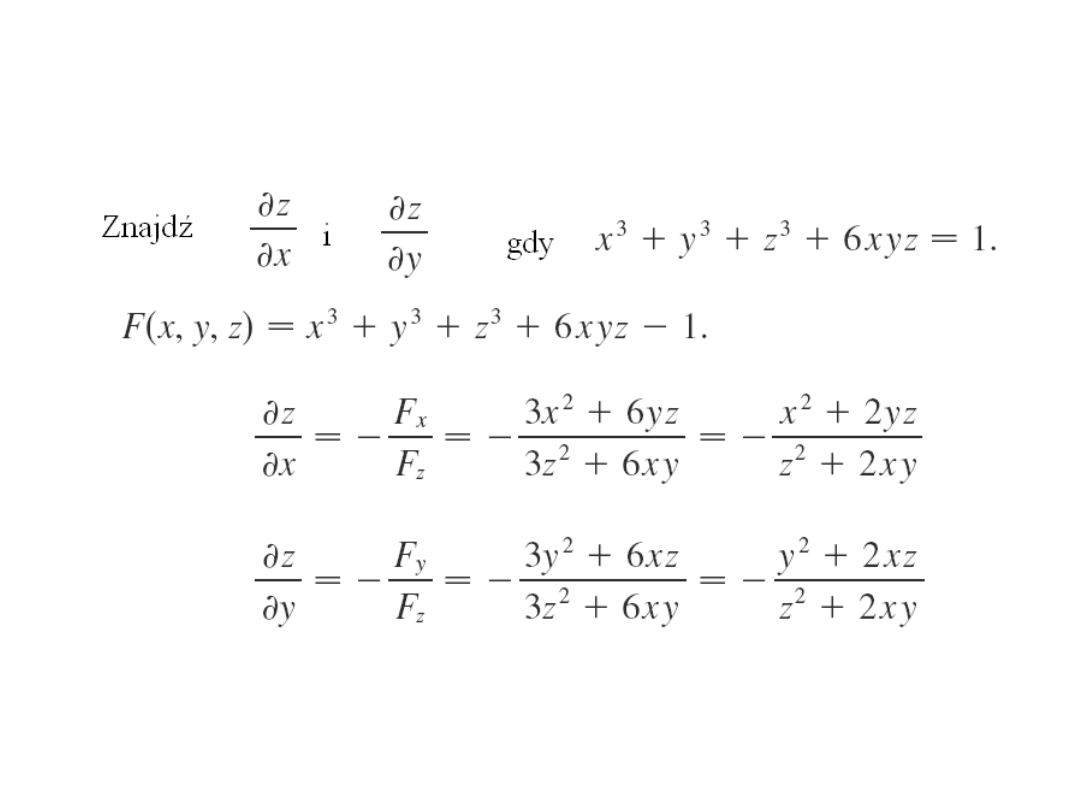
Przykład

Przykład

Ciśnienie (w kPa) objętość (w dcm

3

) i temperatura ( w

stopniach Kelvina) mola gazu idealnego związane są
zależnością PV = 8,31 T . Znajdź szybkość z jaką zmienia
się ciśnienie gdy temperatura w chwili początkowej równa
300

o

K rośnie z szybkością 0,1 K/s a objętość równa 100

dcm

3

rośnie z szybkością 0,2 dcm

3

/s.

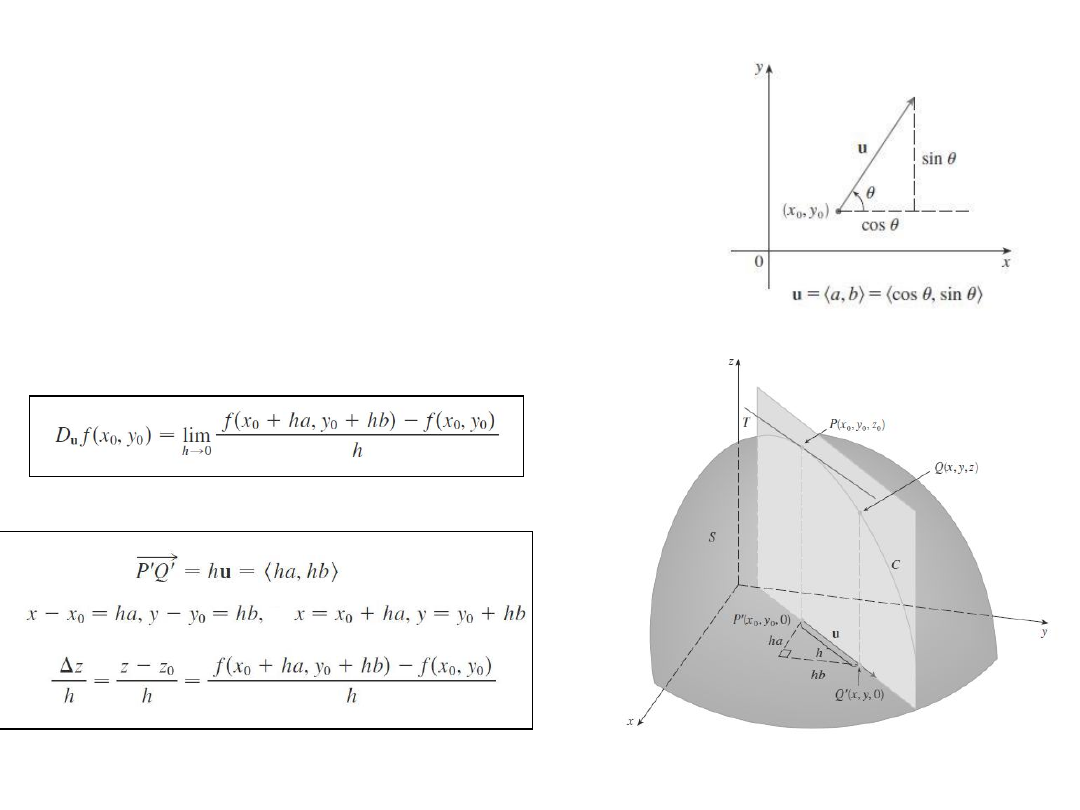
Pochodna

kierunkowa

Pochodna kierunkowa funkcji f w
punkcie (x

0

,y

0

) w kierunku wektora

jednostkowego u = (a,b)

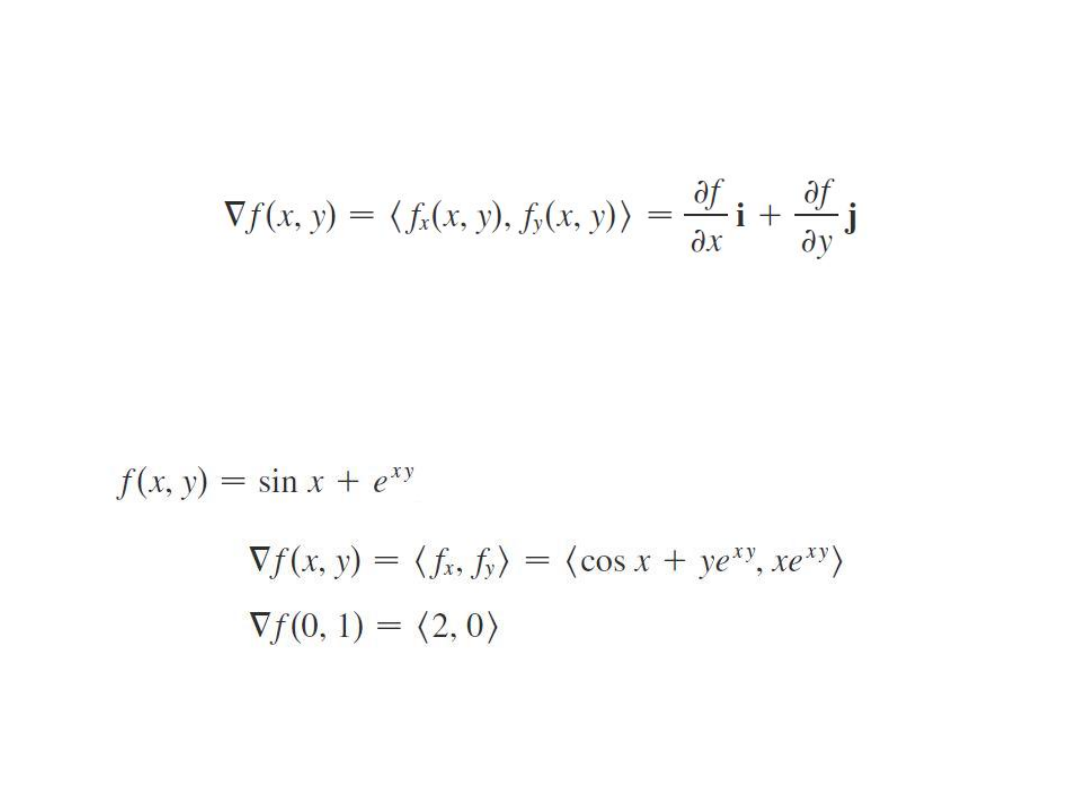
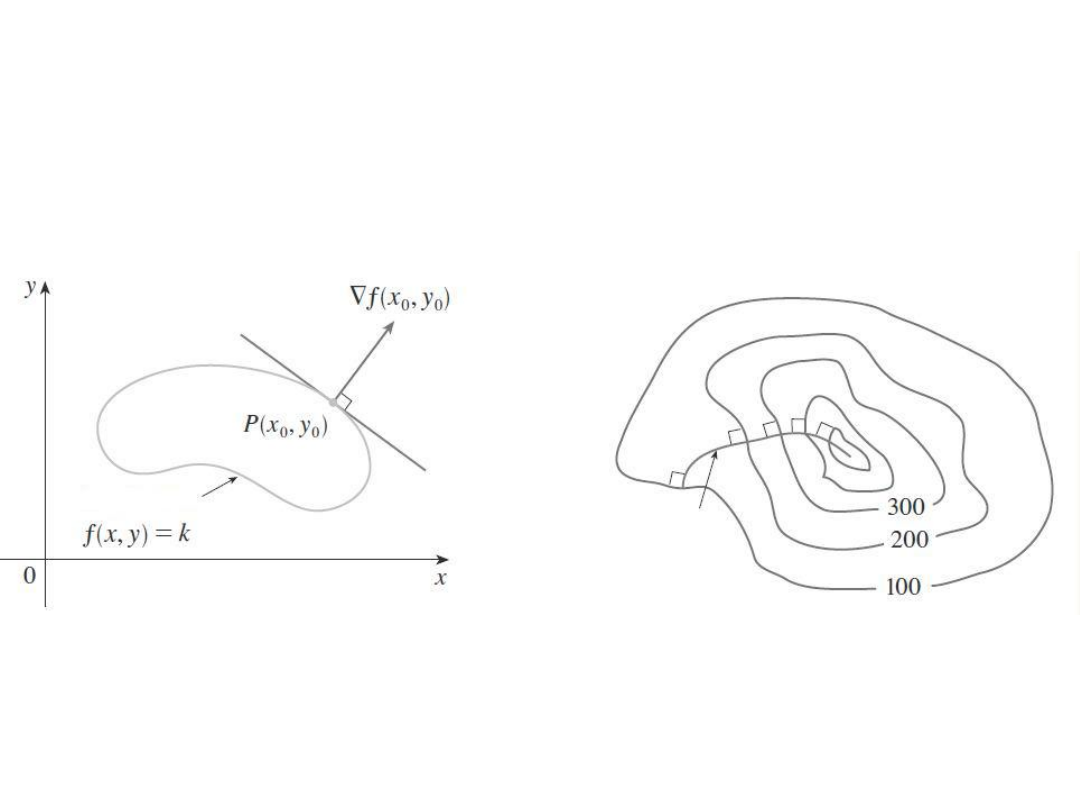
Wektor

gradientu.

Definicja

Przykład

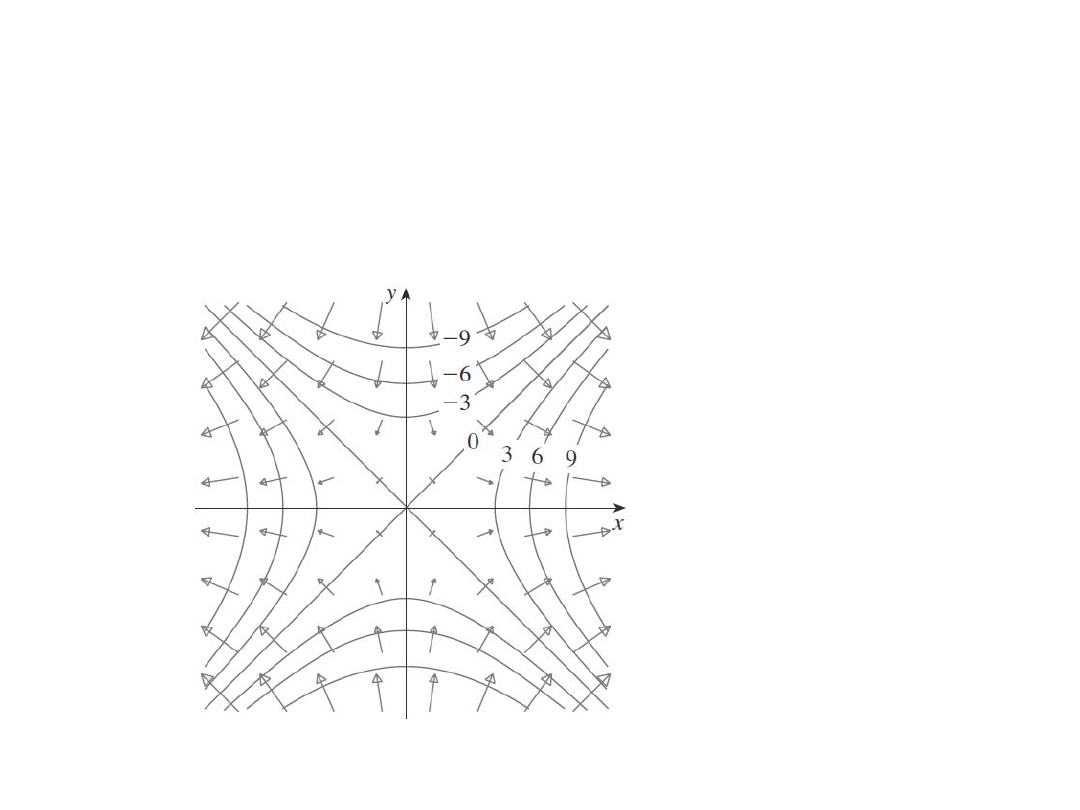
Przykład

2

2

)

,

(

funkcji

Gradient

y

x

y

x

f





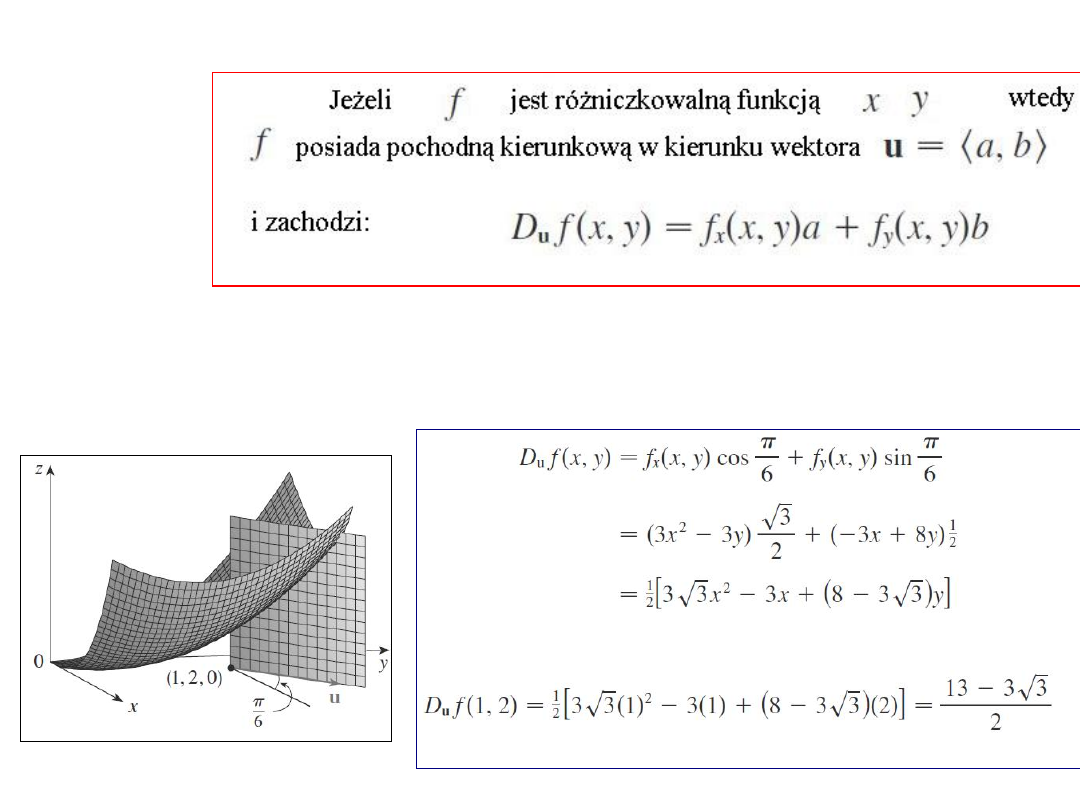
Twierdzeni

e

Przykła
d

Oblicz pochodną kierunkową D

u

f(x,y) funkcji f(x,y) = x3 -

3xy + 4y2 gdzie u jest wektorem jednostkowym, który tworzy
z osią ox kąt п/6. Jaka jest wartość w punkcie (1,2).

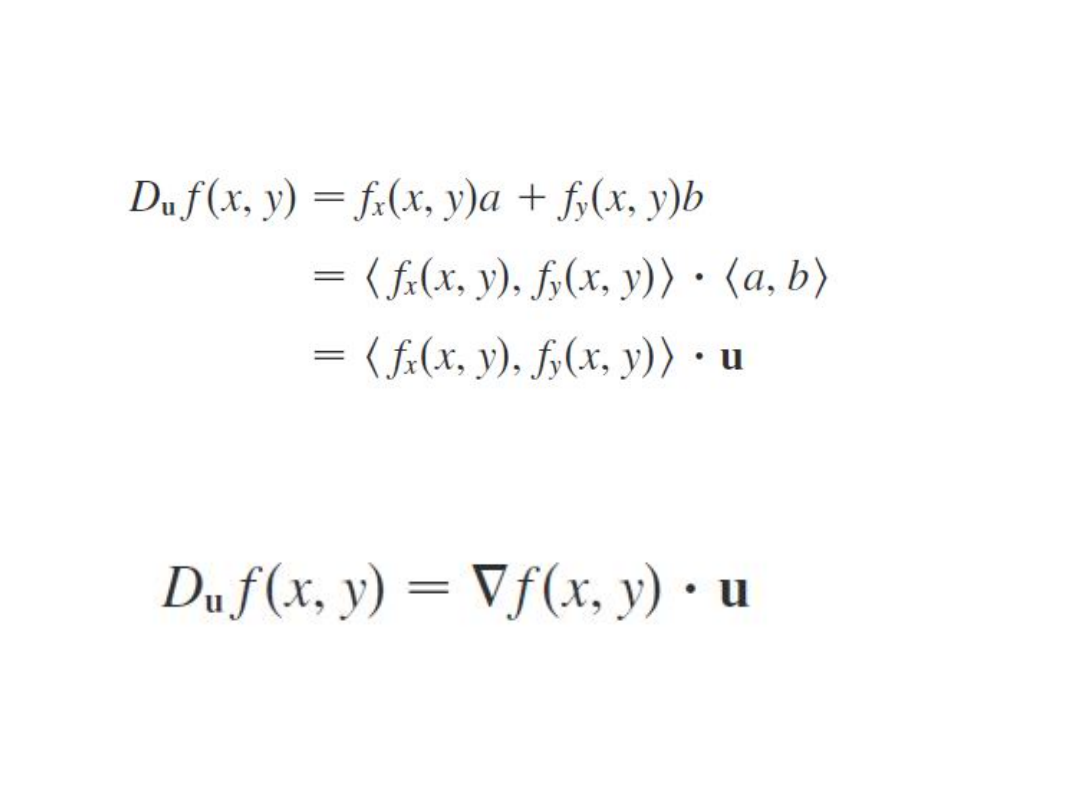
Z użyciem operatora gradientu można to zapisać:

Pochodna kierunkowa:

Funkcje trzech

zmiennych