7. POŁĄCZENIA SPRĘŻYSTE
Połączeniem sprężystym nazywamy złącze
umożliwiające przesuwanie części łączonych
względem siebie w zakresie zależnym od własności
sprężystych materiału łącznika.
Łączniki wykonujemy z materiałów:
- dużej podatności (np. guma, tworzywa sztuczne,
układy
płynowe);
- dużym module sprężystości (sprężyny metalowe).
Rys. 7.1. Sprężyna naciskowa (wg PN-85/ 'M-
80701). Wymiary sprężyn naciskowych na
rysunkach wykonawczych podaje się wg PN-
81/M-01148 — z uwzględnieniem wymagań
technologicznych
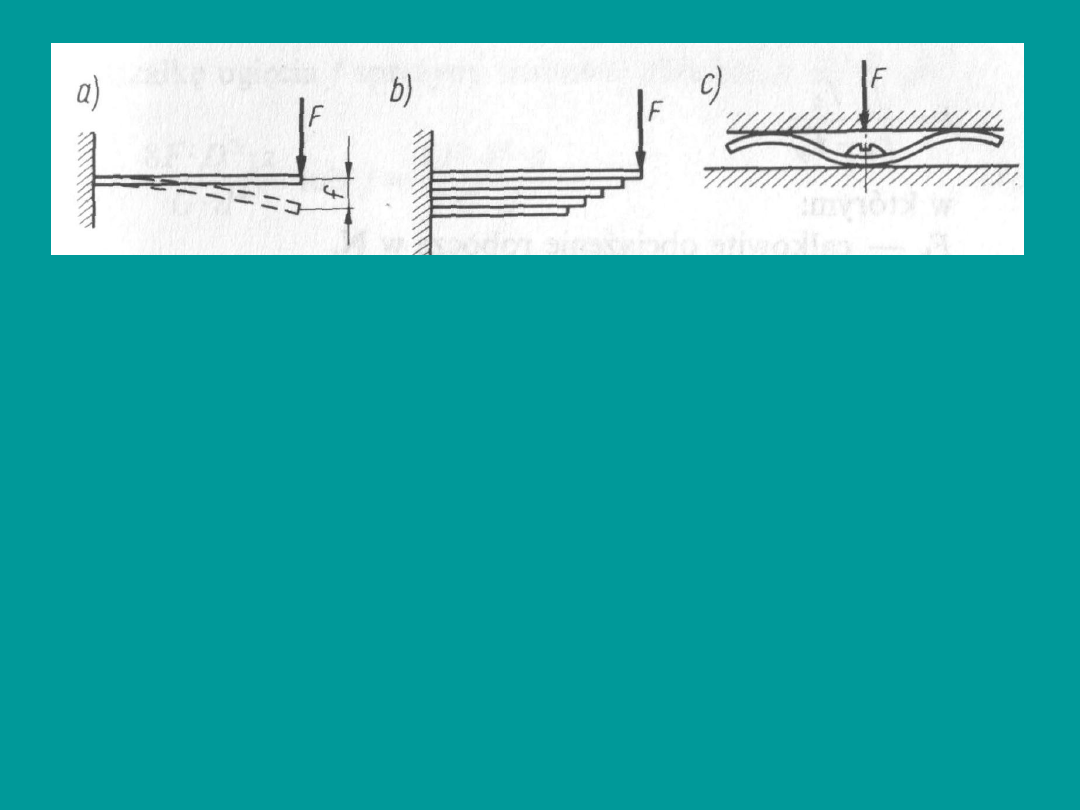
Rys. 7.2. Rodzaje sprężyn prętowych
płaskich
Do podstawowych rodzajów sprężyn
metalowych zaliczamy: sprężyny walcowe
śrubowe (rys. 7.1) oraz sprężyny prętowe
płaskie (rys. 7.2). Sprężyny metalowe
wykonuje się głównie ze stali sprężynowych.
Własności tych stali podano w tablicy 35.
Podstawową cechą użytkową sprężyn jest ich
sztywność. Dla sprężyn o charakterystyce liniowej
sztywność C (stałą sprężyny, wskaźnik sztywności
sprężyny) określa zależność
lub
(7.1)
w której:
F - obciążenie (napięcie) sprężyny,
f - strzałka ugięcia sprężyny,
M - moment skręcający,
φ- kąt skręcenia w radianach. Dla sprężyn o
charakterystyce liniowej C = const.
Sprężyny śrubowe obliczamy z warunku
wytrzymałościowego na skręcanie, a sprężyny
prętowe - na zginanie.
f
F
C
M
C
Przy obliczaniu sprężyn śrubowych korzystamy z
następujących wzorów:
gdzie:
f - całkowita strzałka ugięcia sprężyny przy
działaniu siły F,
f
1
- strzałka ugięcia jednego czynnego zwoju przy
działaniu siły
F,
z - liczba czynnych zwojów.
Dla sprężyn montowanych z napięciem
wstępnym F
p
= (0,l÷0,6)F
k
całkowitą strzałkę
ugięcia f określamy wg wzoru
(7.3)
1
f
z
f
p
k
k
r
F
F
F
f
f
w którym:
F
k
— całkowite obciążenie robocze w N,
F
p
- napięcie (obciążenie) wstępne w N,
f
r
— ugięcie robocze sprężyny w mm.
Współczynnik kształtu sprężyny δ wynosi
(7.4)
gdzie:
D - średnia średnica zwojów sprężyny,
d - średnica drutu (pręta).
Zalecane wartości współczynnika kształtu δ są
podane w podręczniku.
d
D
Warunek wytrzymałościowy na skręcanie
(7.5)
stąd
(7.6)
lub po podstawieniu
(7.7)
gdzie:
K - współczynnik poprawkowy, uwzględniający
wpływ innych czynników (oprócz skręcania) na
wytrzymałość sprężyn.
S
S
S
k
d
K
D
F
W
K
M
3
0
2
,
0
2
K
D
d
k
F
S
3
4
,
0
d
D
K
d
k
F
S
2
4
,
0
Strzałkę ugięcia f sprężyny śrubowej obliczamy wg
wzoru
lub
Na podstawie wzoru 7.9 określamy również ugięcie
jednego czynnego zwoju (korzystając z zależności f
= f
1
- z) lub obliczamy liczbę czynnych zwojów przy
określonej strzałce ugięcia sprężyny.
Wymiary sprężyny wyznaczamy z następujących
zależności:
Całkowita liczba zwojów
(7.10)
615
,
0
4
4
1
4
K
4
3
8
d
G
D
F
f
d
G
z
F
f
3
8
2
5
,
1
z
z
c
Luz osiowy między zwojami przy maksymalnym
obciążeniu
(7.11)
Długość sprężyny w stanie swobodnym
(7.12)
gdzie a - prześwit między zwojami (rys. 7.1);
a =f
1
+ e.
Skok zwoju w stanie swobodnym
s = a + d
(7.13)
d
e
2
,
0
1
,
0
d
d
a
z
L
c
0
Wznios linii śrubowej zwoju w stanie swobodnym
(7.14)
Całkowita długość drutu sprężyny
(7.15)
Do obliczeń przybliżonych w praktyce często są
stosowane tablice, na których podstawie dobieramy
wymiary sprężyn śrubowych. W tablicy 36 podano
wyniki obliczeń dla sprężyn ze stali, dla której
przyjęto k
s
= 400 MPa i G = 83 000 MPa.
D
s
tg
0
0
cos
c
c
z
D
l
Sprężyny płaskie (prętowe) obliczamy na zginanie
(7.16)
Strzałkę ugięcia f sprężyn płaskich wyznaczamy wg
podanych w tabl. 7.3 podręcznika lub w tabl. 19.
Przykładowo dla sprężyn z rys. 1.2a
(7.17)
Korzystając z wzorów 7.17 i 7.16 otrzymujemy po
przekształceniach
- grubość sprężyny
(7.18)
g
x
g
g
k
W
M
max
x
J
E
l
F
f
3
3
E
f
k
l
h
g
2
2
2
-szerokość sprężyny
(7.19)
Przy obliczaniu resorów przyjmuje się, że
b= n·b
l
(7.20)
gdzie:
b
1
- szerokość jednego pióra,
n - liczba piór resoru.
Uwaga:
Wzory 7.18 i 7.19 wyprowadzamy każdorazowo - w
zależności od wzoru na strzałkę ugięcia, podanego
w tablicy 7.3 podręcznika oraz w zależności od
M
gmax
.
g
k
h
l
F
b
2
6