Przekształcanie 

Przekształcanie 

wykresów funkcji

wykresów funkcji

 

 

Przesuwanie wzdłuż 

Przesuwanie wzdłuż 

osi

osi

 

y

y

Przesunięcie wykresu funkcji 

wzdłuż osi y powoduje zmianę 
wartości funkcji  bez zmiany 
wartości argumentu .

(zmienia się  y, ale wartość x zostaje taka 

sama)

 

 

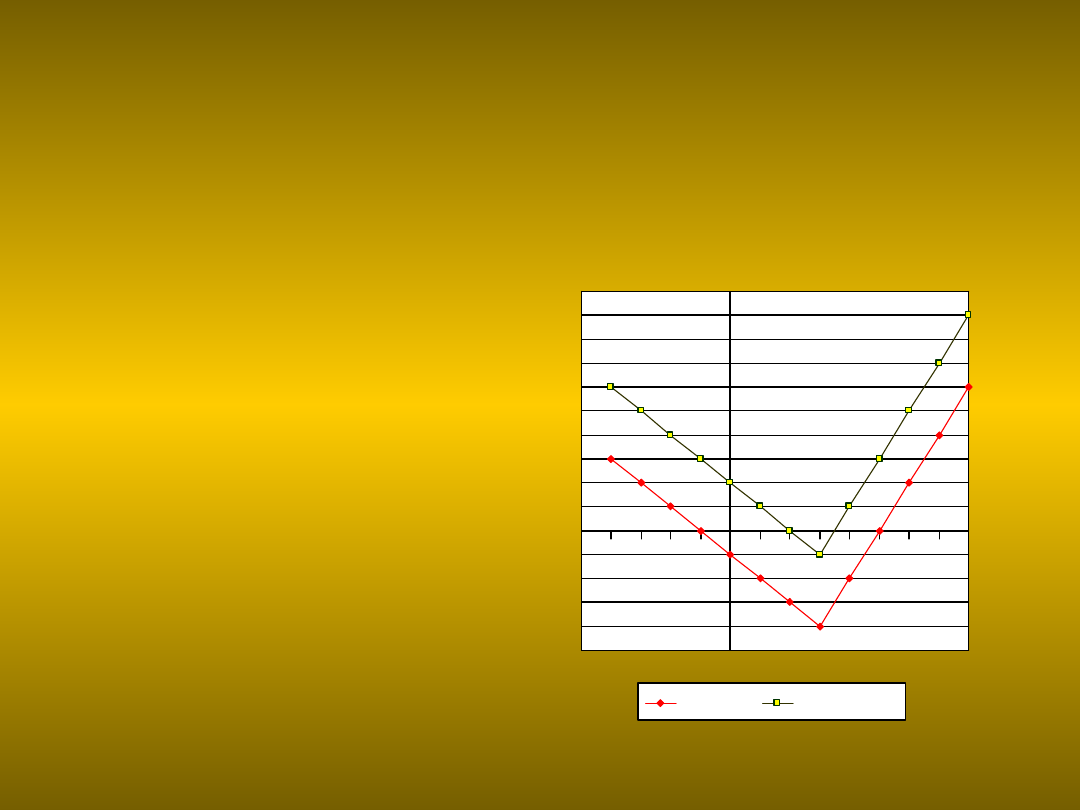
Przesunięcie w górę

Przesunięcie w górę

Przesuwając wykres funkcji 

w górę zwiększamy jej 
każdą wartość o długość 
wektora przesunięcia.

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

7

8

9

10

-4-3-2-1 0 1 2 3 4 5 6 7 8

y=f(x)

y=f(x)+3

Wykres funkcji y=f(x) 
przedstawionej obok 
został przesunięty w 
górę o wektor długości 
3 

 

 

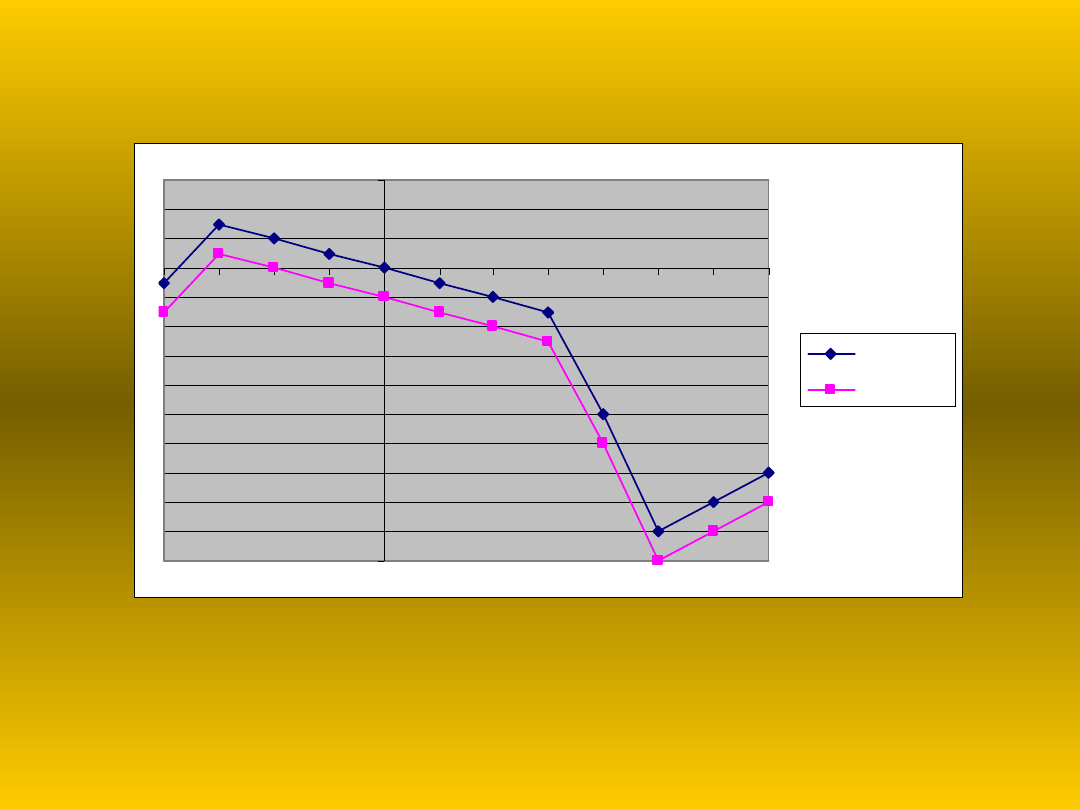
Przesunięcie w dół

Przesuwając wykres funkcji w dół zmniejszamy jej 

każdą wartość o długość wektora przesunięcia

 

(w powyższym przykładzie przesuwaliśmy o 2 jednostki w dół).

-20

-18

-16

-14

-12

-10

-8

-6

-4

-2

0

2

4

6

-4

-3

-2

-1

0

1

2

3

4

5

6

7

y=f(x)
y=f(x) - 2

 

 

Przesuwanie wzdłuż osi x

Przesunięcie wykresu funkcji wzdłuż osi x 

powoduje zmianę wartości argumentu x  

bez zmiany wartości funkcji .

 (zmienia się x, ale wartość y zostaje taka 

sama)

 

 

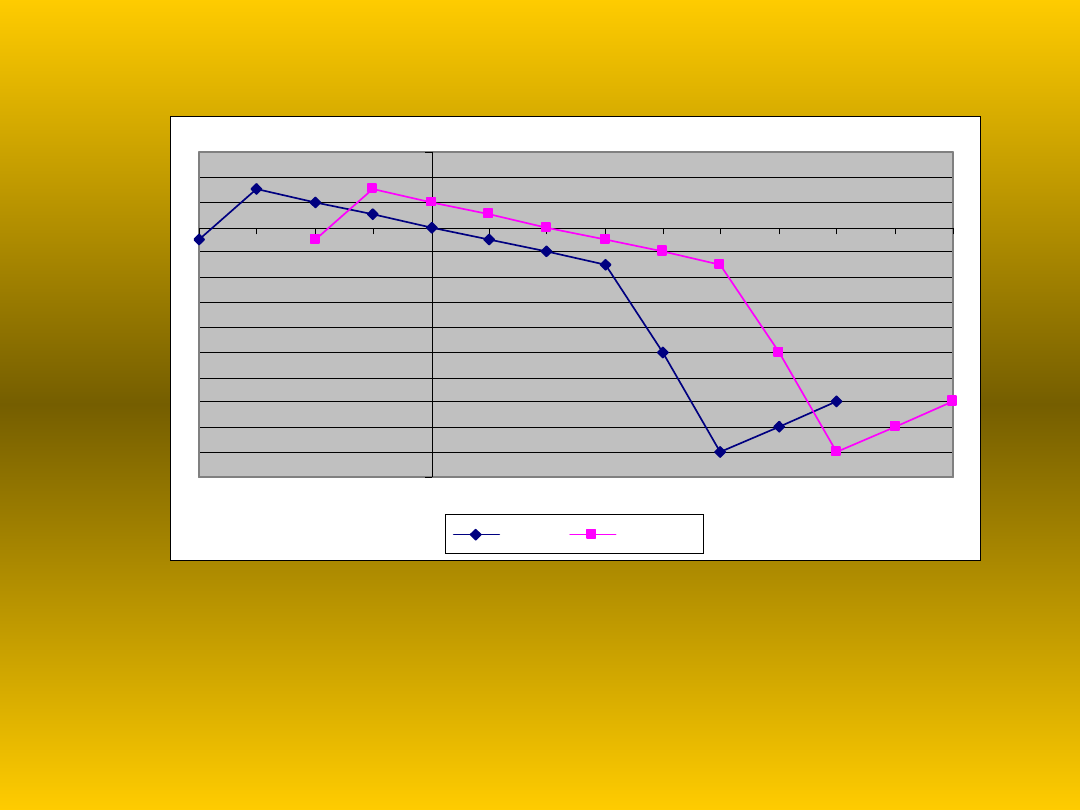
Przesunięcie w prawo

-20

-18

-16

-14

-12

-10

-8

-6

-4

-2

0

2

4

6

-4

-3

-2

-1

0

1

2

3

4

5

6

7

8

9

y=f(x)

y=f(x-2)

Wartość funkcji po przesunięciu dla argumentu x jest taka sama jak 

wartość funkcji przed przesunięciem dla argumentu x-a 

(a – ilość jednostek przesunięcia)

 

 

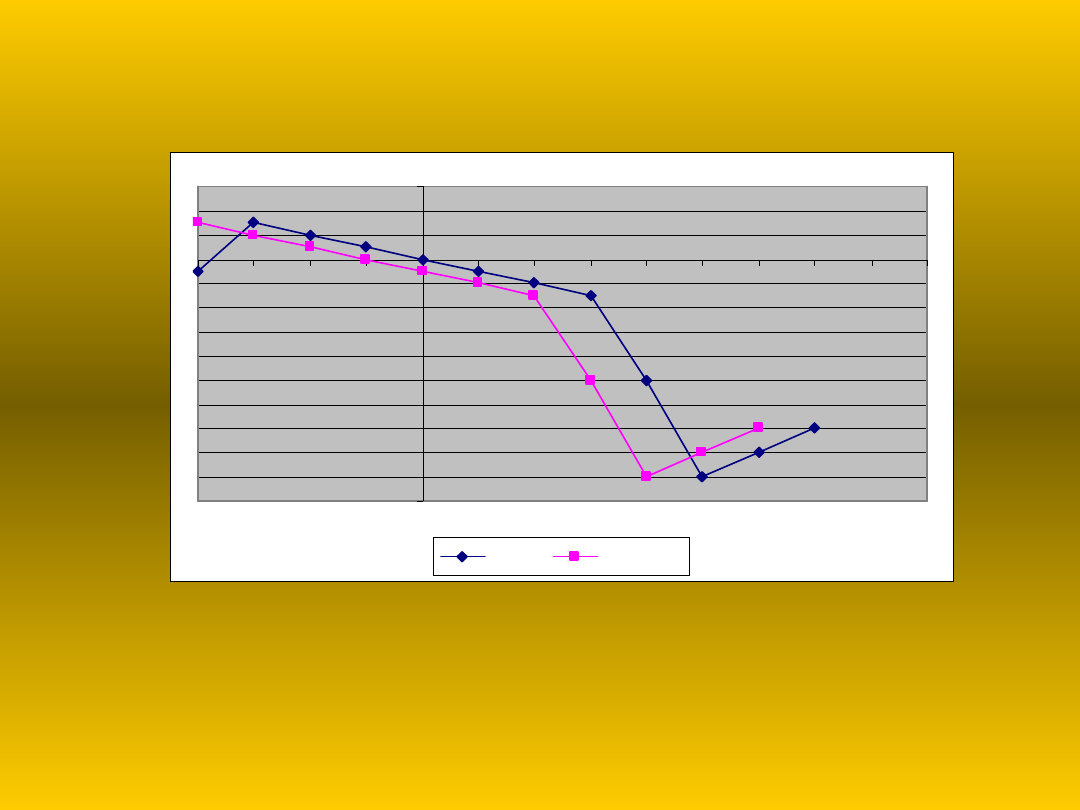
Przesunięcie w lewo

Wartość funkcji po przesunięciu dla argumentu x jest 

taka sama jak wartość funkcji przed przesunięciem 
dla argumentu x + a 

(a – ilość jednostek przesunięcia)

-20

-18

-16

-14

-12

-10

-8

-6

-4

-2

0

2

4

6

-4

-3

-2

-1

0

1

2

3

4

5

6

7

8

9

y=f(x)

y=f(x+1)

 

 

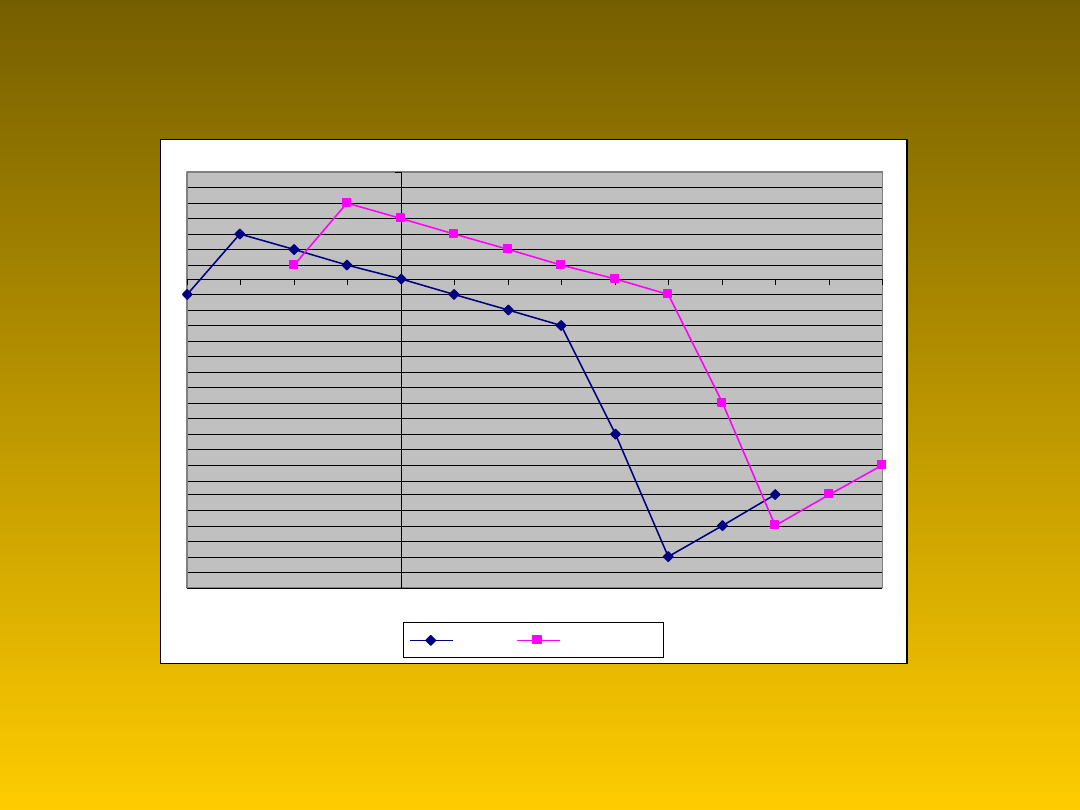
Przesunięcie wzdłuż osi x i 

Przesunięcie wzdłuż osi x i 

y

y

-20

-19

-18

-17

-16

-15

-14

-13

-12

-11

-10

-9

-8

-7

-6

-5

-4

-3

-2

-1

0

1

2

3

4

5

6

7

-4

-3

-2

-1

0

1

2

3

4

5

6

7

8

9

y=f(x)

y=f(x-2)+2

Przesunęliśmy wykres funkcji y = f(x) o 2 w 
prawo i 2 w górę

 

 

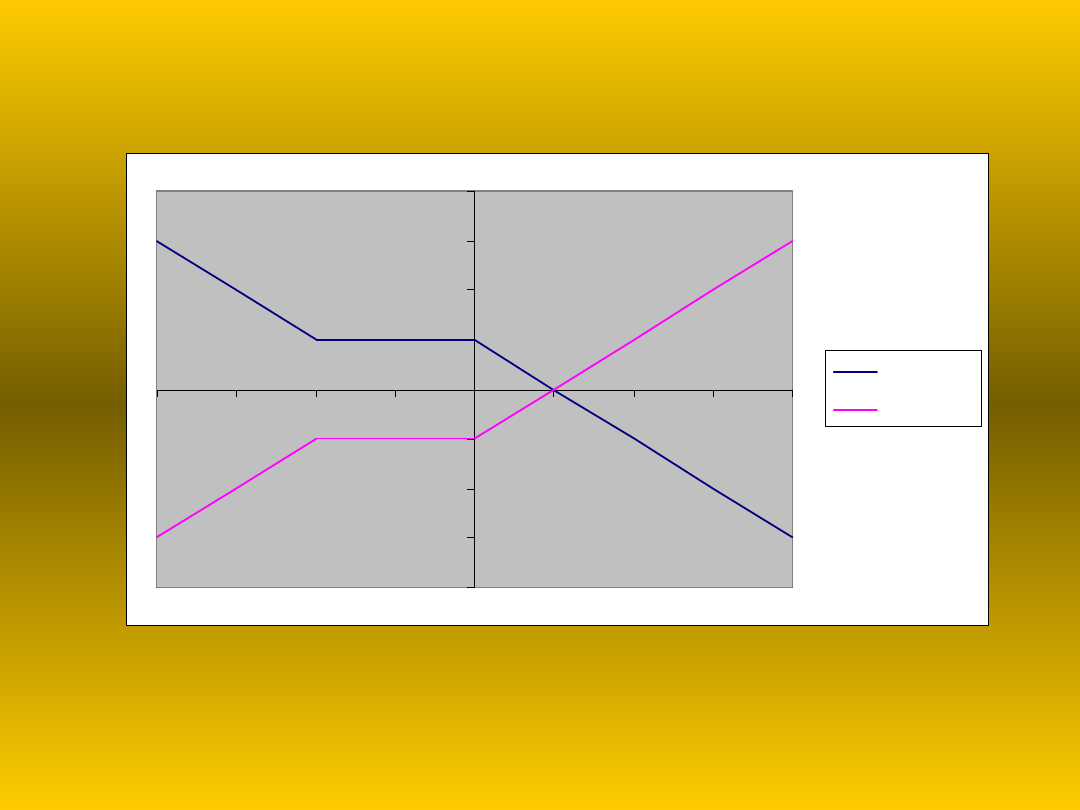
Odbicie symetryczne względem 

osi x

Wykres funkcji g powstał przez odbicie 

symetryczne wykresu funkcji f 
względem osi x. Dla każdego argumentu 
x wartości funkcji g i f są liczbami 
przeciwnymi.

g(x) = - f(x)

-4

-3

-2

-1

0

1

2

3

4

-4

-3

-2

-1

0

1

2

3

4

y=f(x)
g(x)=-f(x)

 

 

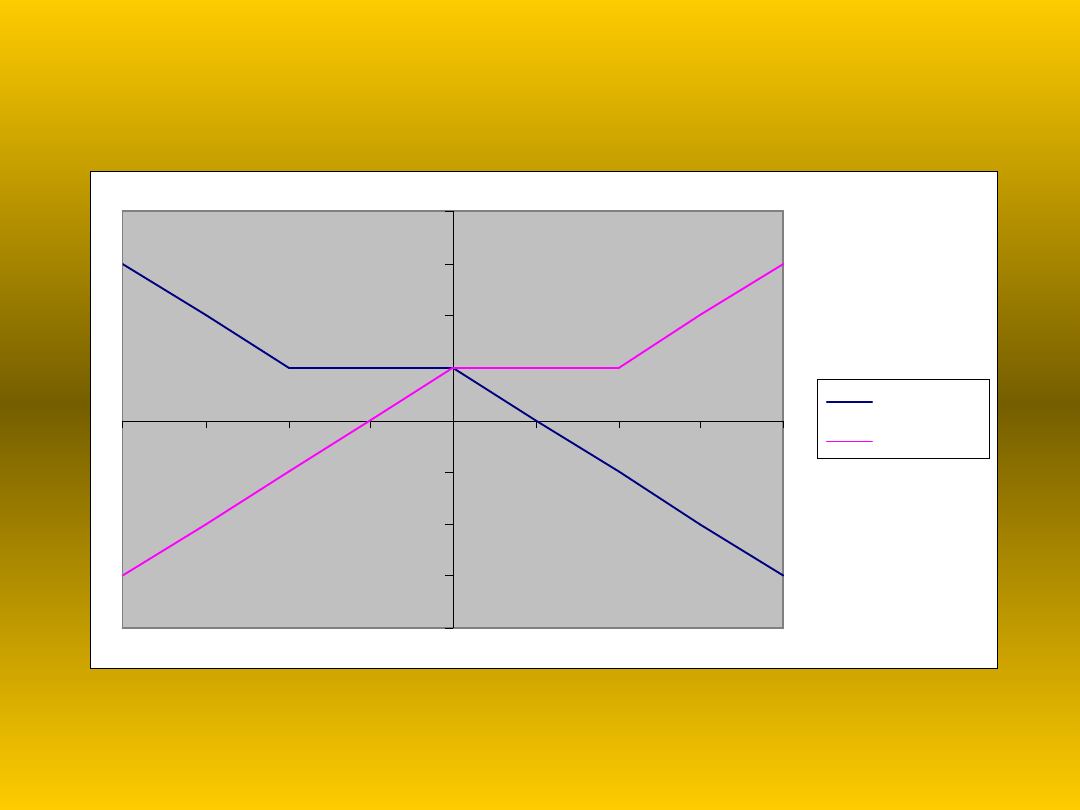
Odbicie symetryczne 
względem osi y

-4

-3

-2

-1

0

1

2

3

4

-4

-3

-2

-1

0

1

2

3

4

y=f(x)
g(x)=f(- x)

Wykres funkcji g powstał przez odbicie 
symetryczne wykresu funkcji f 
względem osi y. Dla każdego 
argumentu x wartości funkcji g jest 
taka sama jak wartość funkcji f dla 
argumentu –x.

g(x) = f(-x)