
Biostatystyka – Wykład 1
Biostatystyka – Wykład 1

2
Wybrane metody wnioskowania statystycznego
Wybrane metody wnioskowania statystycznego
1. Estymacja
• Punktowa
• Przedziałowa
2. Weryfikowanie hipotez

3
POPULACJA
P1 P2 P3
Pn
μ
б
x
s
We wnioskowaniu statystycznym interesuje nas
POPULACJA
Wykorzystujemy próbę do uzyskania informacji na temat
populacji

4
Estymacja
Estymacja
• Z prób reprezentatywnych obliczamy wielkości
statystyk
, które są
estymatorami
określonych
parametrów
populacji
• Przykładowo średnia arytmetyczna z próby jest
dobrym estymatorem wartości oczekiwanej
(wartości przeciętnej) populacji

5
• estymację punktową:
– czyli metodę szacunku, za pomocą której jako wartość
parametru zbiorowości generalnej przyjmuje się
konkretną wartość estymatora wyznaczonego na
podstawie n-elementowej próby (zakładamy, że wartość
statystki z próby leży blisko wartości parametru
populacji)
• estymację przedziałową:
– za pomocą której wyznacza się przedział liczbowy, który z
ustalonym prawdopodobieństwem zawiera nieznaną
wartość szacowanego parametru zbiorowości generalnej.
Wyróżnia się dwa rodzaje estymacji:
Wyróżnia się dwa rodzaje estymacji:

6
Statystki z próby jako estymatory parametrów populacji
Statystki z próby jako estymatory parametrów populacji
• Parametr populacji
, lub po prostu parametr,
to liczbowa charakterystyka populacji
• Statystyka z próby
, lub po prostu statystyka,
to liczbowa charakterystyka z próby

7
Estymatory punktowe
Estymatory punktowe
Estymator (statystyka
z próby)
Parametr
populacji
X
S
P
μ
σ
p

8
Przykład
Przykład
• zbiór: (1, 2, 3, ..., 8)
• prawdopodobieństwo wylosowania
każdej liczby = 1/8
• losujemy dwie liczby ze zwracaniem
(ważna kolejność) i obliczamy ich
średnią arytmetyczną
• jaki jest rozkład tych średnich?

9
Obliczymy średnią i odchylenie
standardowe z populacji X:
29
,
2
5
,
4
Natomiast wartość
oczekiwana
i odchylenie zmiennej losowej
X
śr
62
,
1
5
,
4
x
x
Zauważymy, że oczekiwana
wartość jest równa średniej z
populacji, natomiast
odchylenie standardowe
n
x
/
x = μ
10
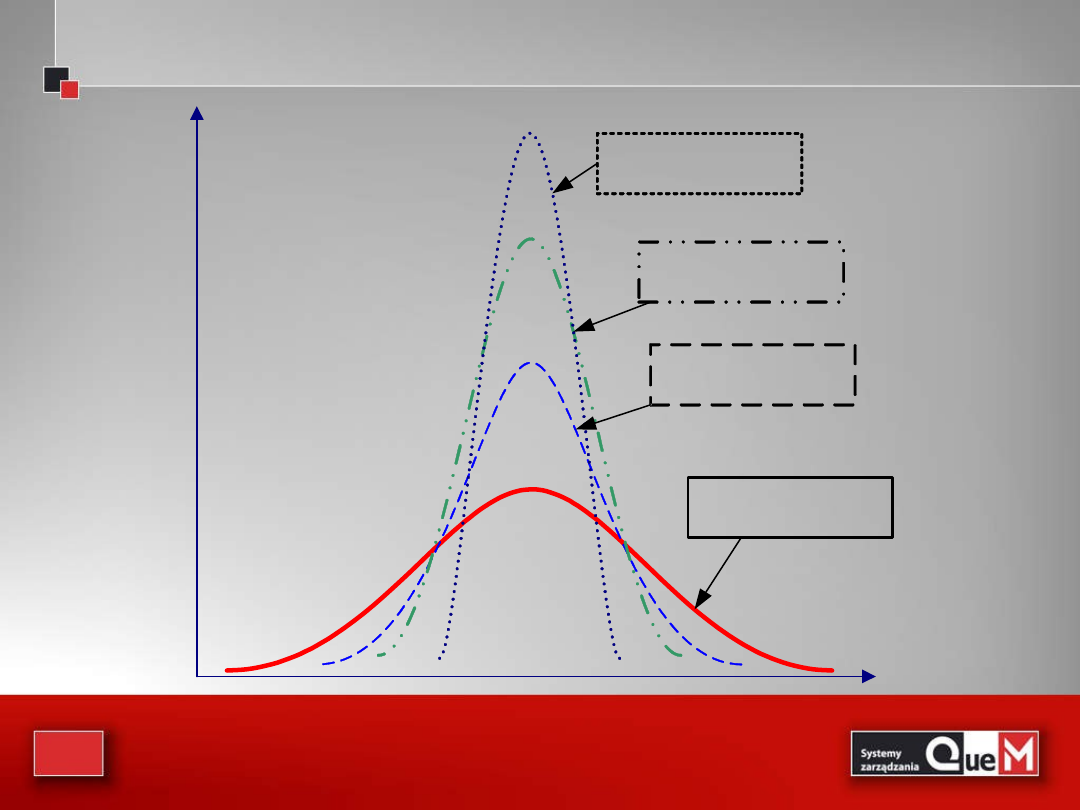
Poniżej na rysunku pokazano krzywą Gaussa dla populacji i krzywe normalne
dla zm.los. średniej , dla różnych liczebności prób.
Poniżej na rysunku pokazano krzywą Gaussa dla populacji i krzywe normalne
dla zm.los. średniej , dla różnych liczebności prób.
rozkład normalny
(w populacji)
rozkład zmiennej
Xśr przy n=2
rozkład zmiennej
Xśr przy n=4
rozkład zmiennej
Xśr przy n=16

11
Z rysunku widać, że jeśli liczebność próby wzrasta, to
odchylenie standardowe zmiennej maleje, dzięki czemu
zbliżenie się wartości średniej do staje się coraz bardziej
prawdopodobne. I tak doszliśmy do jednego z głównych
twierdzeń w teorii statystyki:
centralnego twierdzenia
granicznego
, które mówi:
Jeżeli pobieramy próbę z populacji o średniej μ i
skończonym odchyleniu standardowym σ , to rozkład
średniej z próby , dąży do rozkładu normalnego o
średniej μ i odchyleniu , gdy liczebność próby
wzrasta nieograniczenie, czyli dla „dostatecznie dużych n
X
n
/

12
Na rysunku poniżej pokazano kilka rozkładów w macierzystych
populacjach i wynikające stąd rozkłady , dla prób o różnej liczebności.
Rozkład
macierzystej
populacji
normalny
prawoskośny
jednostajny
Rozkład Xśr
n=2
n=10
n=30

13
W ogólnym przypadku próbę uważa się za
dostatecznie dużą, by stosowane były reguły
tw. granicznego, jeśli zawiera ona 30 i więcej
elementów
14
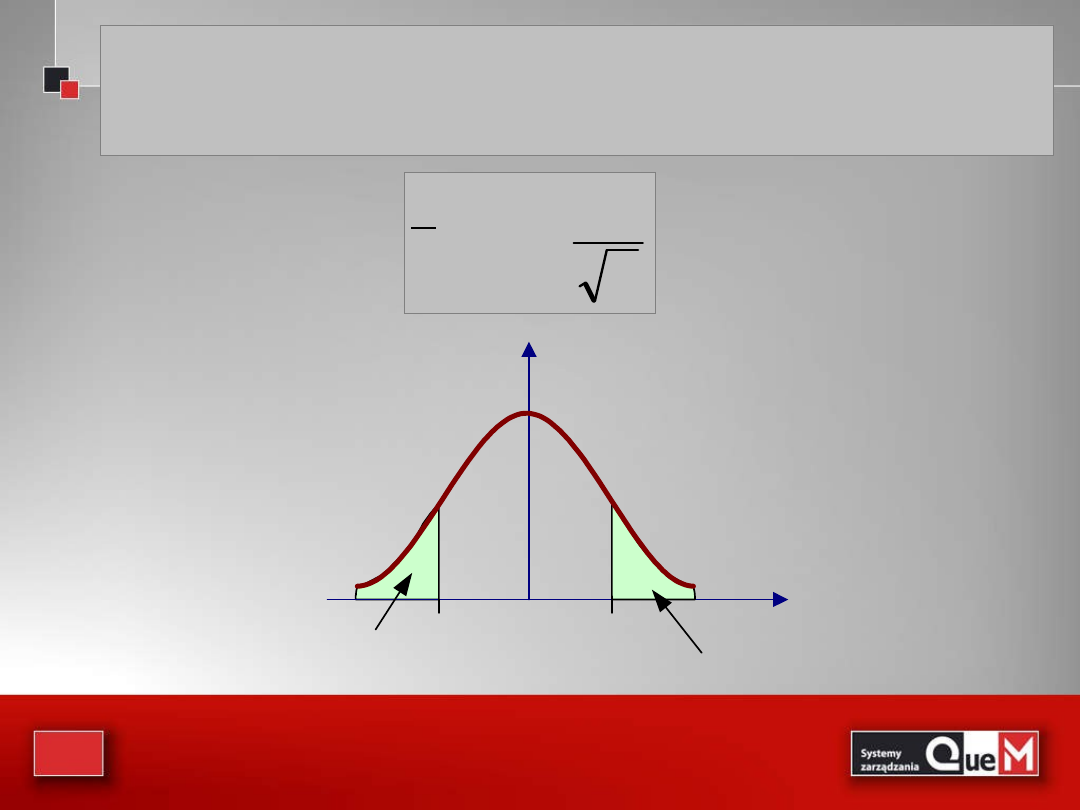
2
/
2
/
2
/
z
2
/
1
z
n
z
x
2
/
Przedział ufności dla μ przy (1-α) poziomie ufności,
gdy σ jest znane, a próba została pobrana z populacji
normalnej lub jest „dużą próbą”, wyznacza wzór:
15
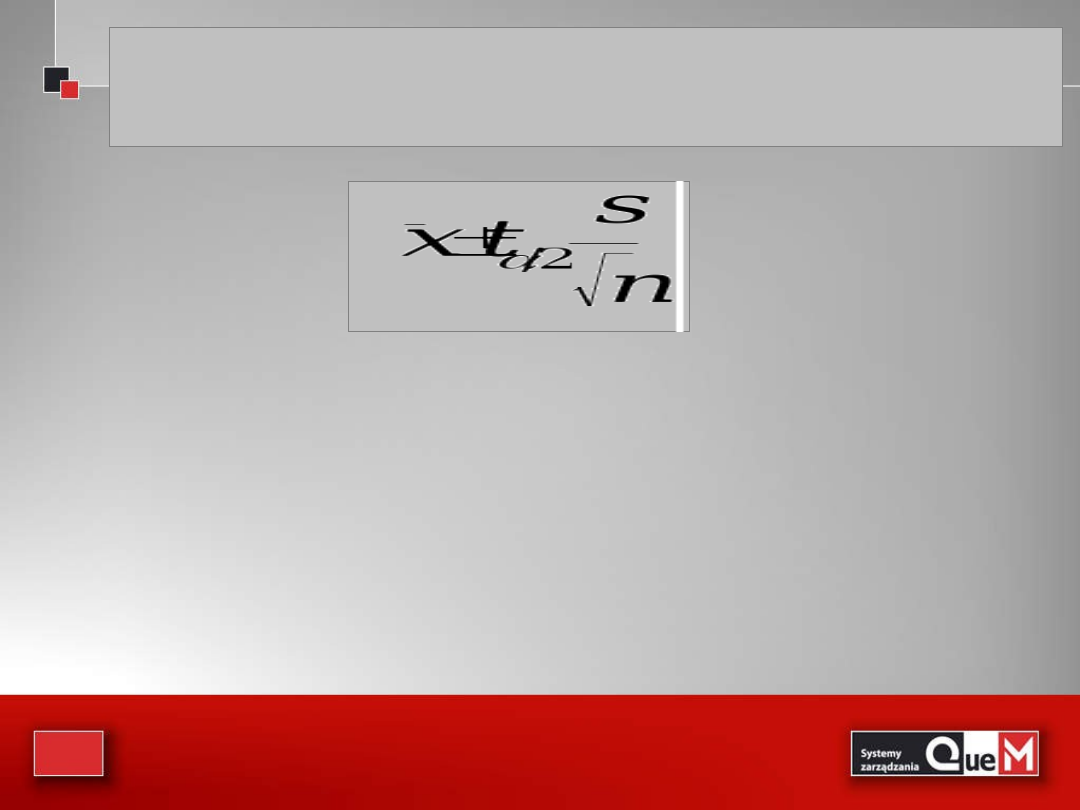
gdzie t
α/2
- jest wartością z rozkładu t-
Studenta
o n-1 stopniach swobody, która
odcina
pod krzywą gęstości pole o
mierze α/2 z prawej strony
Przedział ufności dla μ przy (1-α) poziomie ufności, gdy σ
nie jest znane, a próba została pobrana z populacji
normalnej lub jest „małą próbą”, wyznacza wzór:

16
• Przykład
• Chcemy oszacować średni wiek pielęgniarek
zatrudnionych w wiejskich ośrodkach
zdrowia. W tym celu ze zbiorowości tych
pielęgniarek wylosowano próbę liczącą 121
osób i otrzymano następujące wyniki: średnia
wieku pielęgniarek pracujących w wiejskich
ośrodkach zdrowia wynosi 45 lat oraz
odchylenie wynosi 13,5 lat. Oszacować średni
wiek pielęgniarek pracujących w wiejskich
ośrodkach zdrowia.

17
• Dane: n=121, M=45 lat, SD= 13,5 lat
Otrzymujemy następujący przedział ufności:
(45 – 1,96*13,5/121^0,5; 45 +
1,96*13,5/121^0,5)
po wyliczeniu mamy około:(42; 48 lat)

18
Przedziały ufności dla wariancji w populacji
Przedziały ufności dla wariancji w populacji
• W wielu sytuacjach interesuje nas wariancja lub odchylenie
standardowe w populacji. Tak jest np. w analizie procesu
produkcyjnego, w badaniach procesów masowej obsługi.
Jak już mówiliśmy nieobciążonym estymatorem wariancji w
populacji,
2
jest wariancja z próby S
2
• Do wyznaczenia przedziału ufności dla wariancji w
populacji musimy poznać nowy rozkład, tzw. rozkład
chi-
kwadrat
lub
2
19
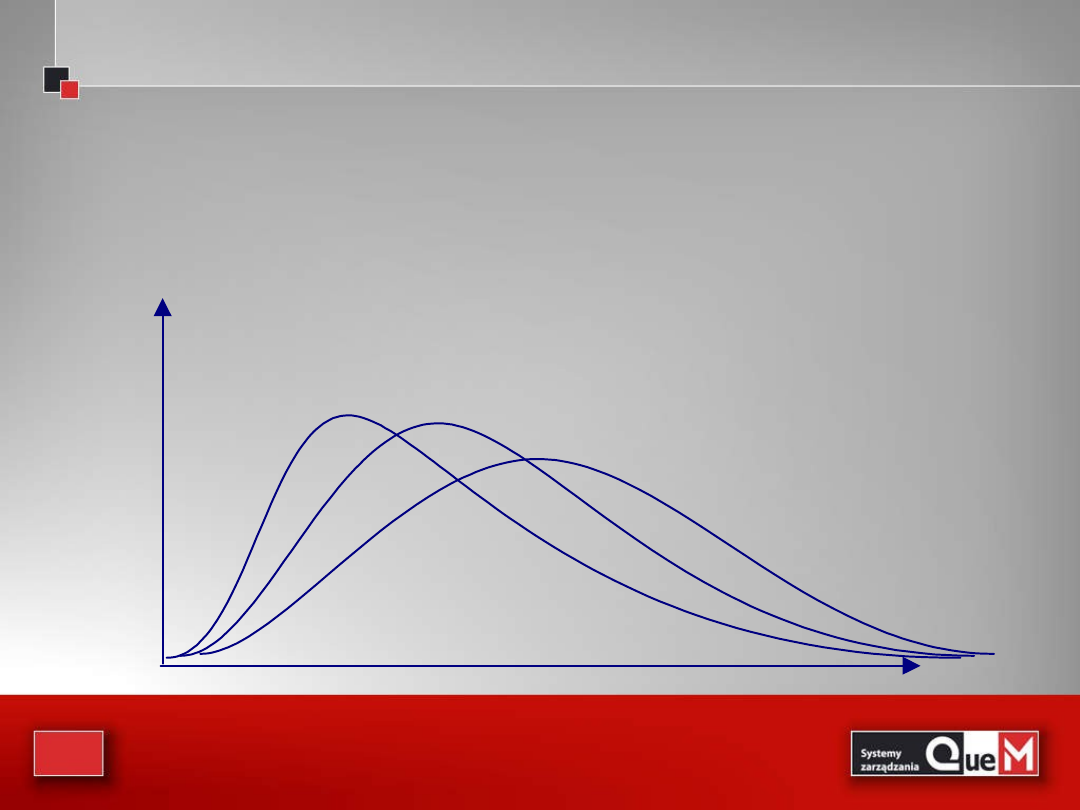
Rozkład chi-kwadrat
Rozkład chi-kwadrat
• Rozkład ten podobnie jak rozkład t, charakteryzuje się
liczba stopni swobody, df ( df=n-1 )
• W przeciwieństwie do rozkładu t, rozkład chi-kwadrat nie
jest symetryczny
df = 10
df = 30
df = 50

20
Rozkład chi-kwadrat
Rozkład chi-kwadrat
• Rozkład chi-kwadrat
jest rozkładem
prawdopodobieństwa sumy kwadratów niezależnych,
standaryzowanych, normalnych zmiennych losowych.
– Średnia rozkładu
jest równa liczbie stopni swobody df
– Wariancja
zaś jest równa liczbie stopni swobody
pomnożonej przez dwa.

21
Przedziały ufności dla wariancji w populacji
Przedziały ufności dla wariancji w populacji
(1-
)100% przedział ufności dla wariancji w populacji,
2
, gdy rozkład w
populacji jest normalny, wyznacza wzór:
2
2
/
1
2
2
2
/
2
)
1
(
;
)
1
(
S
n
S
n
gdzie:
2
2
/
jest wartością zmiennej w rozkładzie chi-kwadrat o n-1 stopniach
swobody, która odcina pole o mierze
2
/
z prawej strony;
2
2
/
1
jest wartością
zmiennej w rozkładzie chi-kwadrat, która odcina pole o mierze
2
/
lewej strony
(a tym samym 1-
2
/
z prawej strony).

Weryfikowanie hipotez
statystycznych
Weryfikowanie hipotez
statystycznych

23
• Podobnie jak testy w życiu codziennym, test
statystyczny też ma jednobitowy wynik:
„
jest OK albo nie jest OK”
– Wąchamy wczorajszą wędlinkę i kierujemy ją na stół
albo pod stół (do kosza;-)
– Nie ma trzeciej drogi, chyba że mamy psa, który nam
się opatrzył.

24
• Zwróćmy przy okazji uwagę na to, że przy
testowaniu możemy popełnić dwa rodzaje błędów:
– możemy wyrzucić dobrą szynkę
• jest to błąd pierwszego rodzaju
– albo zjeść zepsutą
• błąd drugiego rodzaju
• Kalkulacja ekonomiczna kosztu tych błędów jest bardzo
ważna przy projektowaniu testu, aczkolwiek może ona nie
być łatwa do przeprowadzenia

25
• W zarządzaniu jakością często stawiane jest pytanie
– czy wartość określonej statystyki uzyskana z próbki losowej
(szczególnie jeśli próbka ma małą liczność), pozwala sądzić, że
odpowiada ona wartości wymaganej (spodziewanej)
– lub też, czy uzyskana w wyniku działań doskonalących
poprawa jest tylko pozorna – wynika z małej liczby pomiarów
sprawdzających – czy rzeczywista
• Odpowiedzi na tak i podobnie postawione pytanie
uzyskuje się w tzw. testach statystycznych
Przykładowo:

26
Stosuje się dwie grupy testów:
Stosuje się dwie grupy testów:
• parametryczne i nieparametryczne
– stosowanie pierwszych wymaga przyjęcia założeń o
postaci rozkładu testowanej zmiennej losowej oraz
znajomości wybranych statystyk
– testy nieparametryczne
takich założeń nie wymagają,
ale nie są tak mocne jak parametryczne

27
Hipotezy statystyczne
Hipotezy statystyczne
• Hipoteza statystyczna to każde
przypuszczenie dotyczące rozkładu
zmiennej losowej weryfikowane na
podstawie n-krotnej realizacji tej
zmiennej
– Wyróżniamy:
• Hipotezy
– parametryczne i nieparametryczne
– proste i złożone

28
Weryfikowanie hipotez
Weryfikowanie hipotez
• Hipotezą zerową
, oznaczoną przez H
0
, jest hipoteza
w wartości jednego z parametrów populacji (lub
wielu)
–
Tę hipotezę traktujemy jako prawdziwą, dopóki nie uzyskamy
informacji statystycznych
dostatecznych do zmiany naszego
stanowiska
• Hipotezą alternatywną
, oznaczoną przez H
1
, jest
hipoteza przypisująca parametrowi (parametrom)
populacji wartość inną niż podaje to hipoteza zerowa

29
• Hipoteza zerowa:
– często opisuje sytuację, która istniała do tej pory
lub jest wyrazem naszego przekonania, które
chcemy sprawdzić
• Sprawdzenia dokonuje się
korzystając z informacji
zawartej w próbie losowej

30
• Sprawdzianem lub statystyką testu
– nazywamy statystkę z próby, której wartość obliczona
na podstawie wyników obserwacji jest wykorzystywana
do ustalenia czy możemy hipotezę zerową odrzucić czy
jej odrzucić nie możemy

31
Przykład 1:
Przykład 1:
Firma rozwożąca paczki zapewnia, że
średni czas dostarczenia przesyłki od drzwi
klienta do odbiorcy wynosi 28 minut. By
sprawdzić to stwierdzenie pobrano próbę
n=100 przesyłek i obliczono średni czas
dostawy 31,5 minut oraz odchylenie
standardowe 5 minut.

32
Test dla średniej
Test dla średniej
H
0
: µ = 28
H
1
: µ 28
zbudujmy 95% przedział ufności dla średniej:
]
48
,
32
;
52
,
30
[
100
5
96
,
1
5
,
31
n
u
x
2
/
Jeżeli mamy 95% ufności, że średni czas dostawy zawiera się
w przedziale [30.52; 32.48] minuty, to mamy 95% zaufania,
że czas ten nie znajdzie się poza tym przedziałem.
Wartość sprawdzana: 28 minut, leży poza tym przedziałem,
zatem odrzucamy hipotezę zerową.
1- = 0,95
= 5
33
Czego się nauczyliśmy z przykładu?
Czego się nauczyliśmy z przykładu?
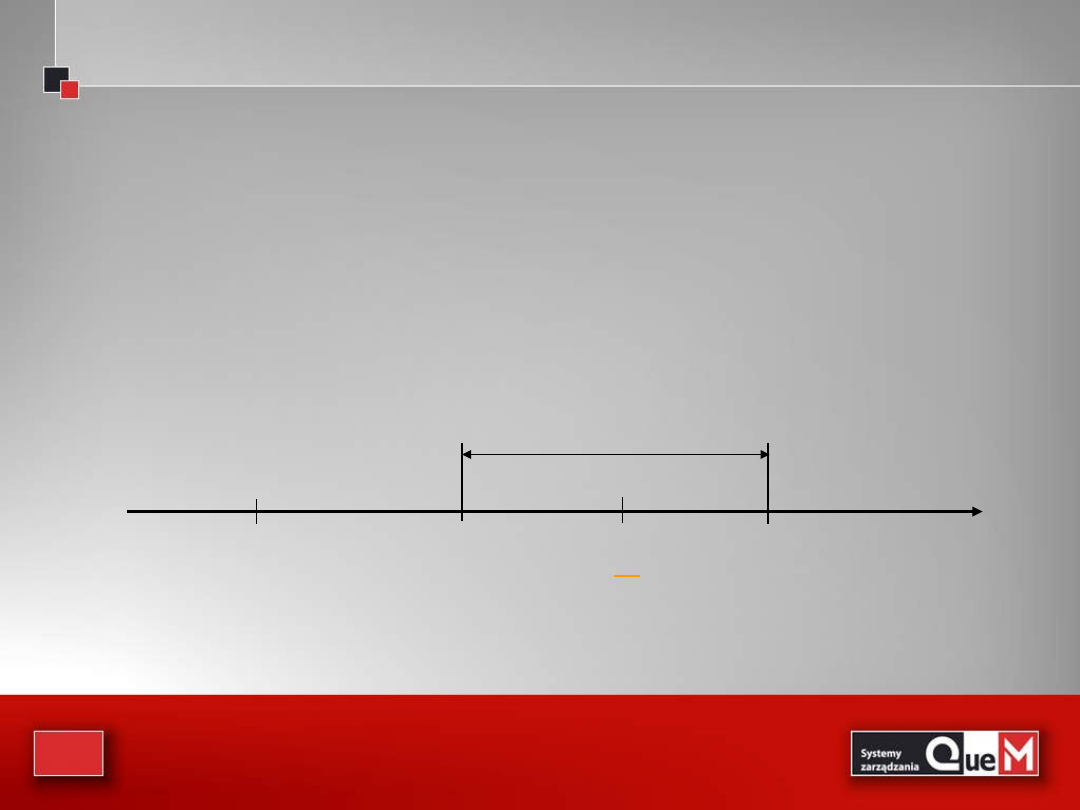
Po pierwsze:
przy weryfikowaniu testów można
budować przedział ufności wokół wartości
statystyki z próby i sprawdzać, czy weryfikowana
wartość parametru należy do przedziału
28
31,5
30,52
32,48
95% przedział ufności
0
x

34
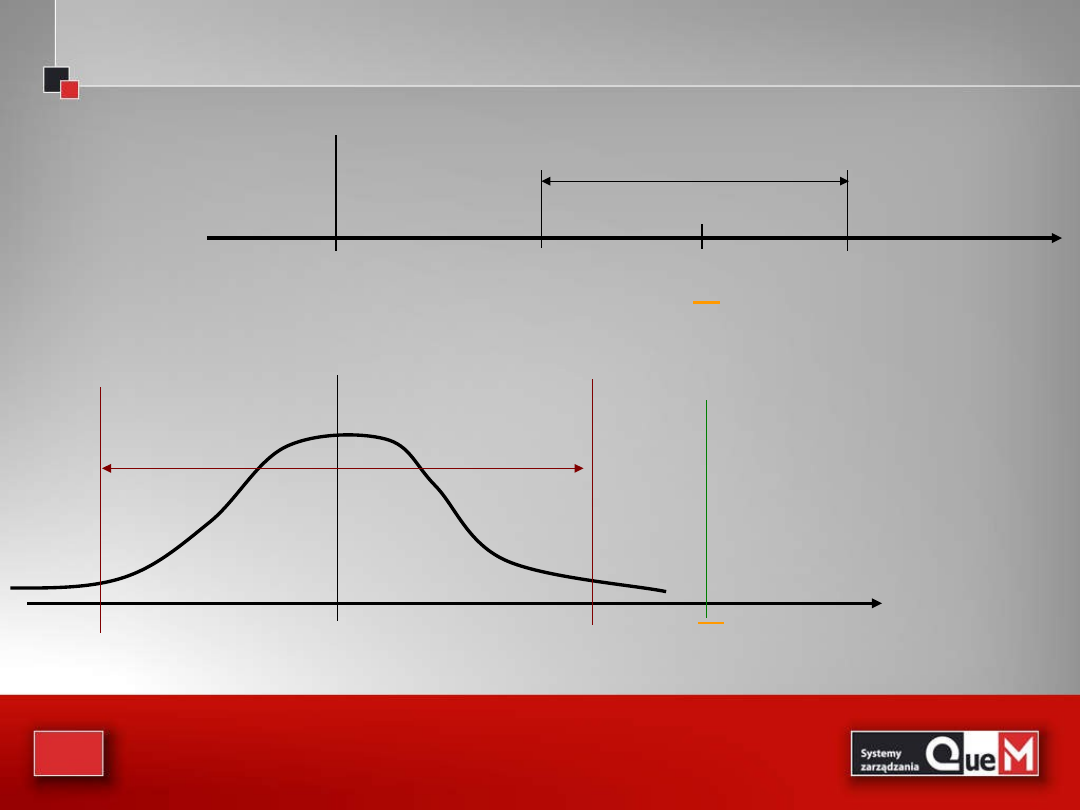
Z drugiej strony:
Z drugiej strony:
Można jako centrum traktować średnią populacji i
sprawdzać wartość statystyki z próby względem
przedziału ufności wokół parametru populacji
]
98
,
28
;
02
,
27
[
100
5
96
,
1
28
n
s
96
,
1
0
Wartość średnia z próby =31,5, zatem nie należy
do przedziału ufności. Hipotezę zerową odrzucamy.
35
28
31,5
30,52
32,48
95% przedział ufności
0
=2
8
x
28,98
27,02
95%
obszar
przyjęcia
Średnia z próby
znajduje się poza
obszarem
przyjęcia
x
36
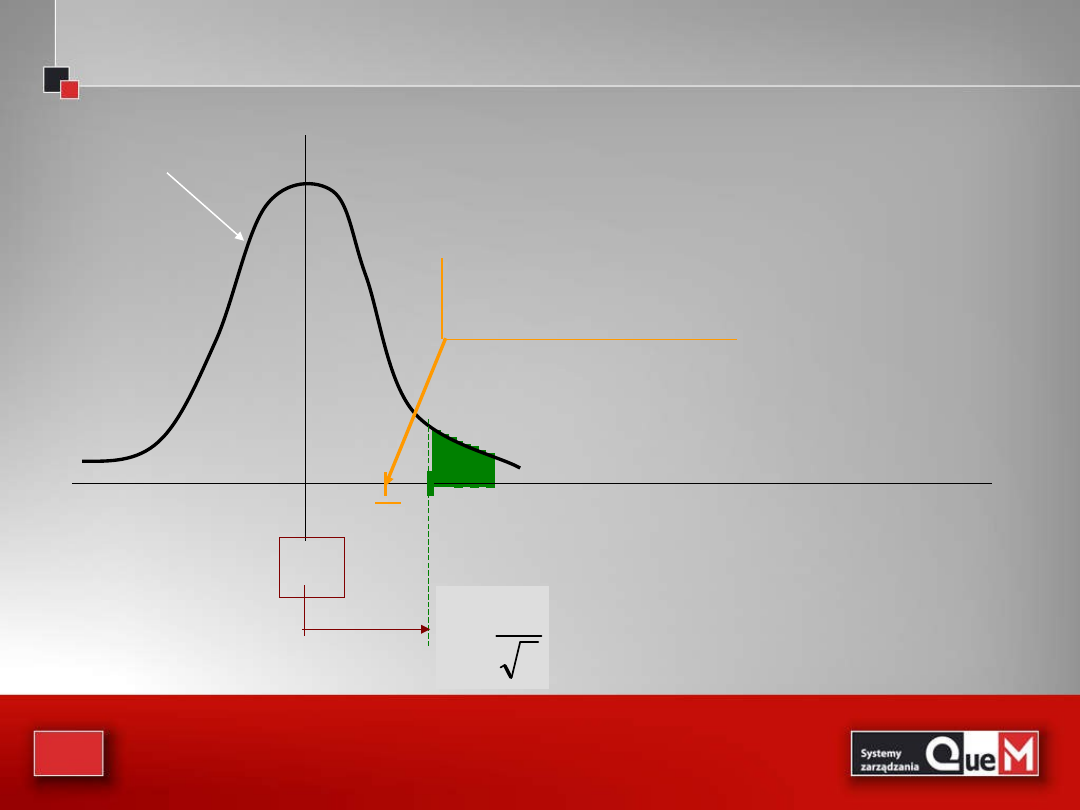
Interpretacja graficzna
Interpretacja graficzna
0
rozkład populacji
x
Pytanie: Czy ta średnia
może pochodzić z populacji
o średniej
0
i odchyleniu ?
n
σ
u
2
/
α
Jeśli średnia z próby
leży powyżej granicy, to
przypuszczenie że
populacja ma średnią
0
musi zostać odrzucone
37
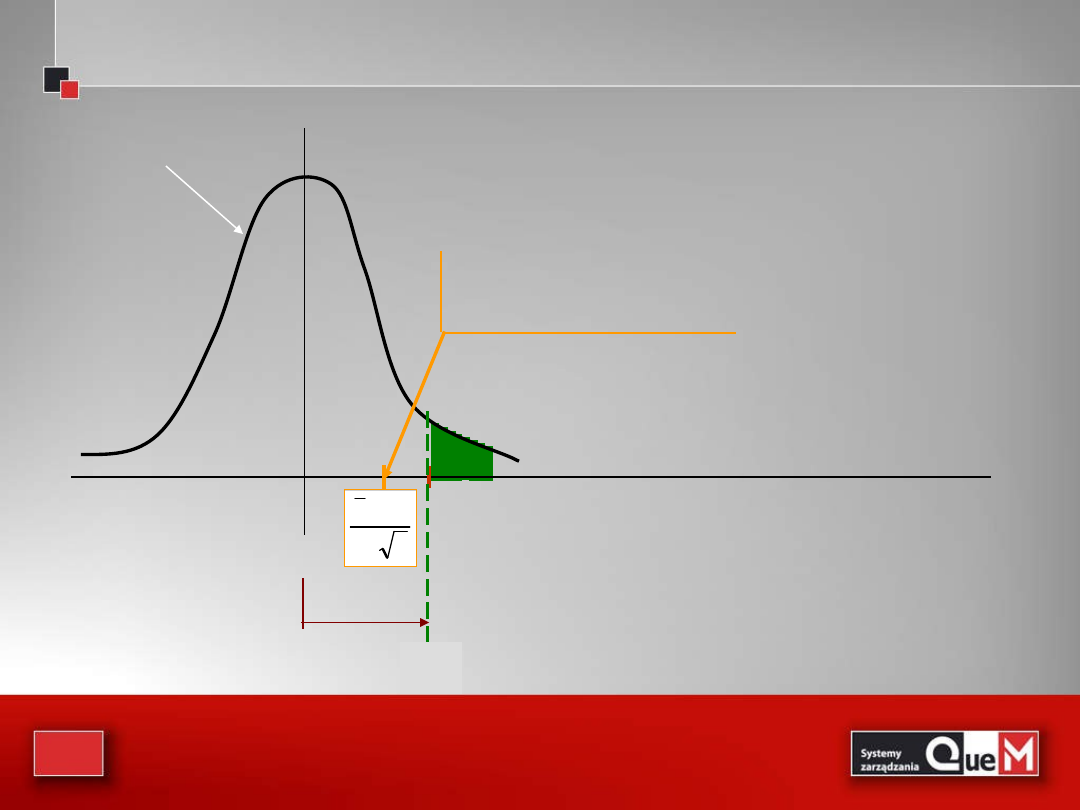
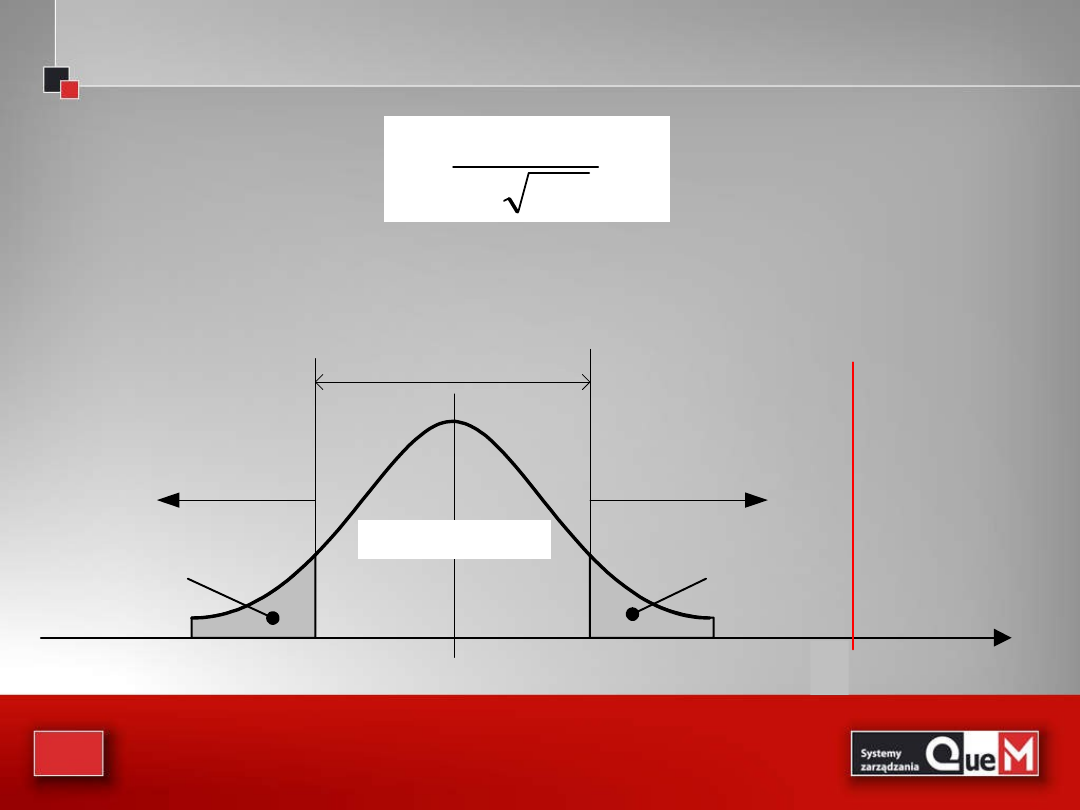
Standaryzowana forma testu statystycznego
Standaryzowana forma testu statystycznego
n
/
σ
μ
x
0
0
rozkład standaryzowany
Standaryzujemy średnią
z próby, czyli obliczamy
statystykę (sprawdzian)
Jeżeli obliczona wartość
statystyki leży poniżej
granicy u
/2
, to nie ma
podstaw do odrzucenia
hipotezy zerowej
2
/
α
u
38
obszar nieodrzucenia
obszar
odrzucenia
obszar
odrzucenia
0
-1,96
1,96
Miara pola = 0,025
Miara pola = 0,025
Miara pola = 0,95
z = 7,0
wartość
sprawdzianu
znajduje się w
polu odrzucenia
u
H
0
: µ = 28
H
1
: µ 28
7
100
/
5
28
5
,
31
u
Obszar krytyczny:
R = (-; -1,96)
(1,96; +)
Wracając do przykładu:

39
Prawdopodobieństwo odrzucenia/przyjęcia hipotezy
Prawdopodobieństwo odrzucenia/przyjęcia hipotezy
)
falszywa
H
/
na
nieodrzuco
H
(
P
)
prawdziwa
H
/
odrzucona
H
(
P
0
0
0
0
Hipoteza
Decyzja
Prawdziwa
Fałszywa
Przyjąć
Właściwe
postępowani
e
1-α
Błąd II-go
rodzaju
β
Odrzucić
Błąd I-go
rodzaju
α
Właściwe
postępowani
e
1-β

40
ponieważ założyliśmy, że hipoteza zerowa
odzwierciedla nasze przekonanie, to chcemy śledzić
pradwopodobieńswto I-go rodzaju
świadomość, że istnieje małe prawdopodobieństwo
popełnienia błędu I-go rodzaju, czyli odrzucenia
hipotezy zerowej, gdy nie powinna być ona
odrzucona,
czyni odrzucenie hipotezy zerowej
wnioskiem stanowczym

41
Nie można tego powiedzieć o akceptowaniu (czyli
nie odrzuceniu) hipotezy zerowej
Jeżeli akceptujemy hipotezę zerową (nie
odrzucamy jej) czujemy tylko, że
nie mamy
podstaw do jej odrzucenia

42
Przykład 2:
Przykład 2:
Przypuszcza się, że przeciętny czas jaki potrzebuje
komputer do wykonania pewnego zadania wynosi 3,24
sekundy.
Grupa naukowców z Bell Laboratories testowała
algorytmy, które mogłyby zmienić czas obliczeń.
Przeprowadzono badania: wybrano losowo próbę 200
cykli obliczeń komputera według nowych algorytmów i
otrzymano średni czas obliczeń 3,48 s przy odchyleniu 2,8
sekundy.
Jaki wniosek wyciągną naukowcy przy poziomie istotności
0,05?

43
H
0
: µ = 3,24
H
1
: µ 3,24
21
,
1
200
/
8
,
2
24
,
3
48
,
3
u
Obszar krytyczny:
R
0 05
= (-; -1,96) (1,96;
+)
Obszar krytyczny:
R
0 1
= (-; -1,65) (1,65;
+)
Otrzymana wartość u nie należy do obszaru krytycznego.
Zatem nie ma podstaw do odrzucenia hipotezy zerowej.
Oznacza to jedynie, że na przyjętym poziomie istotności
nie mamy dostatecznych powodów do odrzucenia H
0
.

44
Test dwustronny dla średniej w populacji dla dużej
próby
Test dwustronny dla średniej w populacji dla dużej
próby
H
0
: =
0
H
1
: ≠
0
Poziom istotności:
(zazwyczaj przyjmowany: 0,05; 0,01)
Statystyka testu:
n
σ
μ
x
u
0
Obszar krytyczny: R
= (-; -u
/2
) (u
/2
; +)
Reguła decyzyjna: hipotezę zerową odrzucić, jeśli
statystyka u należy do R

45
Test dwustronny dla średniej w populacji dla małej
próby
Test dwustronny dla średniej w populacji dla małej
próby
H
0
: =
0
H
1
: ≠
0
Poziom istotności:
(zazwyczaj przyjmowany: 0,05; 0,01)
Statystyka testu:
n
s
μ
x
t
0
Obszar krytyczny: R
= (-;
-t
/2
) (t
/2
; +)
Reguła decyzyjna: hipotezę zerową odrzucić, jeśli
statystyka u należy do R
ma rozkład t o n-1 stopniach swobody

46
Test dla porównania dwóch wartości oczekiwanych dwóch
populacji przy dużych próbach
Test dla porównania dwóch wartości oczekiwanych dwóch
populacji przy dużych próbach
H
0
:
1
=
2
H
1
:
≠
Poziom istotności:
(zazwyczaj przyjmowany: 0,05; 0,01)
Statystyka testu:
2
2
2
1
2
1
2
1
n
σ
n
σ
x
x
u
Obszar krytyczny: R
= (-; -u
/2
) (u
/2
; +)
Reguła decyzyjna: hipotezę zerową
odrzucić, jeśli
statystyka u należy do R
dwie badane populacje mają
rozkład normalny N(
1
,
1
) oraz
N(
2
,
2
)

47
Test dla porównania dwóch wartości oczekiwanych dwóch
populacji przy małych próbach
Test dla porównania dwóch wartości oczekiwanych dwóch
populacji przy małych próbach
H
0
:
=
H
1
:
≠
Poziom istotności:
(zazwyczaj przyjmowany: 0,05; 0,01)
Statystyka testu:
2
1
2
1
2
2
2
2
1
1
2
1
n
1
n
1
2
n
n
s
)
1
n
(
s
)
1
n
(
x
x
t
Obszar krytyczny: R
= (-; -u
/2
) (u
/2
; +)
Reguła decyzyjna: hipotezę zerową odrzucić,
jeśli
statystyka u należy do R
dwie badane populacje mają
rozkład normalny N(
1
,
1
) oraz
N(
2
,
2
), nieznane odchylenia

48
Test hipotezy o frakcji w populacji w przypadku dużej próby
Test hipotezy o frakcji w populacji w przypadku dużej próby
n
/
q
p
p
p
u
0
0
0
H
0
: p= p
0
H
1
: p ≠ p
0
jeśli próba jest duża, to rozkład
frakcji w próbie jest rozkładem
normalnym o średniej p i
odchyleniu pq/n
Poziom istotności:
(zazwyczaj przyjmowany: 0,05; 0,01)
Statystyka testu:
Obszar krytyczny: R
= (-; -u
/2
) (u
/2
; +)
Reguła decyzyjna: hipotezę zerową
odrzucić, jeśli
statystyka u należy do R

49
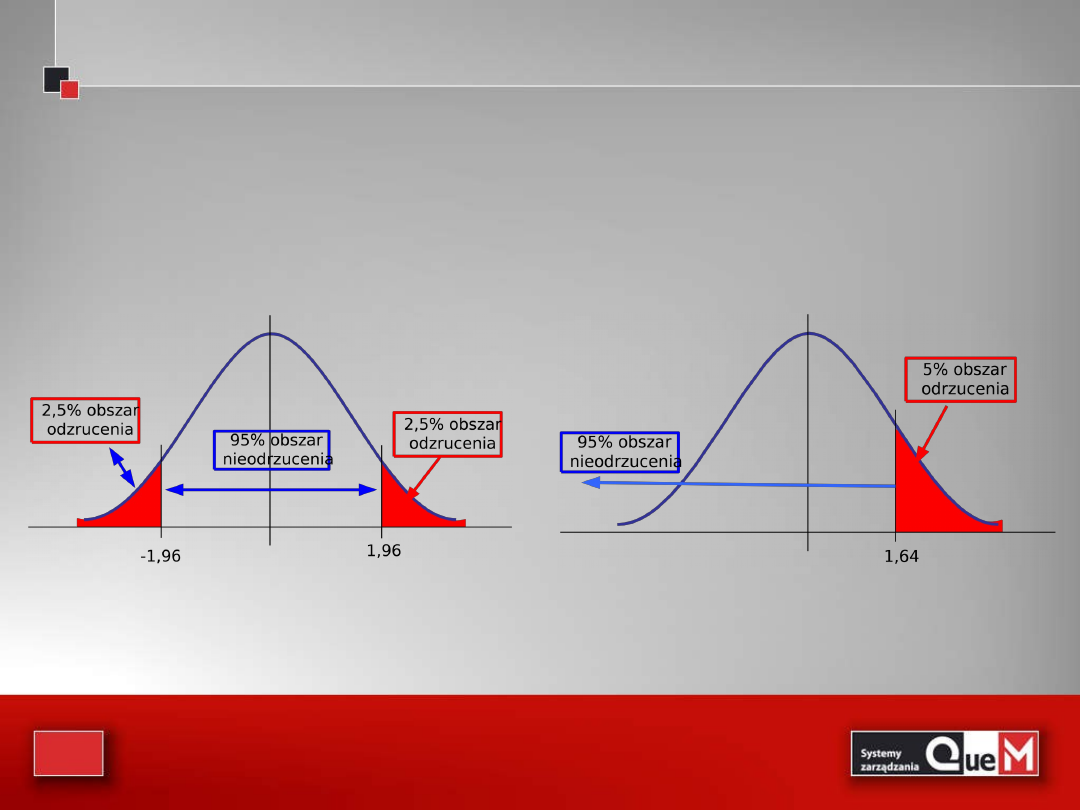
Testy jednostronne
Testy jednostronne
• Wybór rodzaju testu podyktowany jest potrzebą działania
• Jeżeli działanie (np. korygujące) będzie podjęte, gdy
parametr przekroczy pewną wartość a, to stosujemy test
prawostronny:
H
0
: μa
H
1
: μ>a
• Jeżeli działanie będzie podjęte, gdy parametr przyjmie
wartość mniejszą niż a, to stosujemy test lewostronny:
H
0
: μa
H
1
: μ<a
50
H
0
: μa
H
1
: μ>a
H
0
: μ=a
H
1
: μa

51
Test hipotezy o wariancji populacji
Test hipotezy o wariancji populacji
• bardzo często chcemy dowiedzieć się czegoś o wariancji
w populacji
2
:
• np. czy wariancja liczby sztuk wyrobu nie
przekroczyła pewnej granicy?
• np. o wariancji czasu obróbki na linii (powinna
być niewielka, aby nie tworzyły się przestoje)
• z reguły obawiamy się, że wariancja w populacji
przekroczy pewien poziom
• dlatego z reguły stosujemy test prawostronny

52
Test hipotezy o wariancji w populacji
Test hipotezy o wariancji w populacji
2
0
2
2
s
)
1
n
(
H
0
:
0
H
1
:
>
0
Poziom istotności:
(zazwyczaj przyjmowany: 0,05; 0,01)
Statystyka testu:
Obszar krytyczny: R
= (
; +)
Reguła decyzyjna: hipotezę zerową
odrzucić, jeśli
statystyka
2
należy do R
53
Prawdopodobieństwo błędu II-go rodzaju
Prawdopodobieństwo błędu II-go rodzaju
• w testach zakładamy błąd
• co z błędem ?
Stan rzeczy
Decyzje
H
0
H
1
H
0
H
1
słuszna
decyzja
słuszna
decyzja
bład I-go rodzaju jest poważniejszy
H
0
:
niewinna
H
1
: winna

54
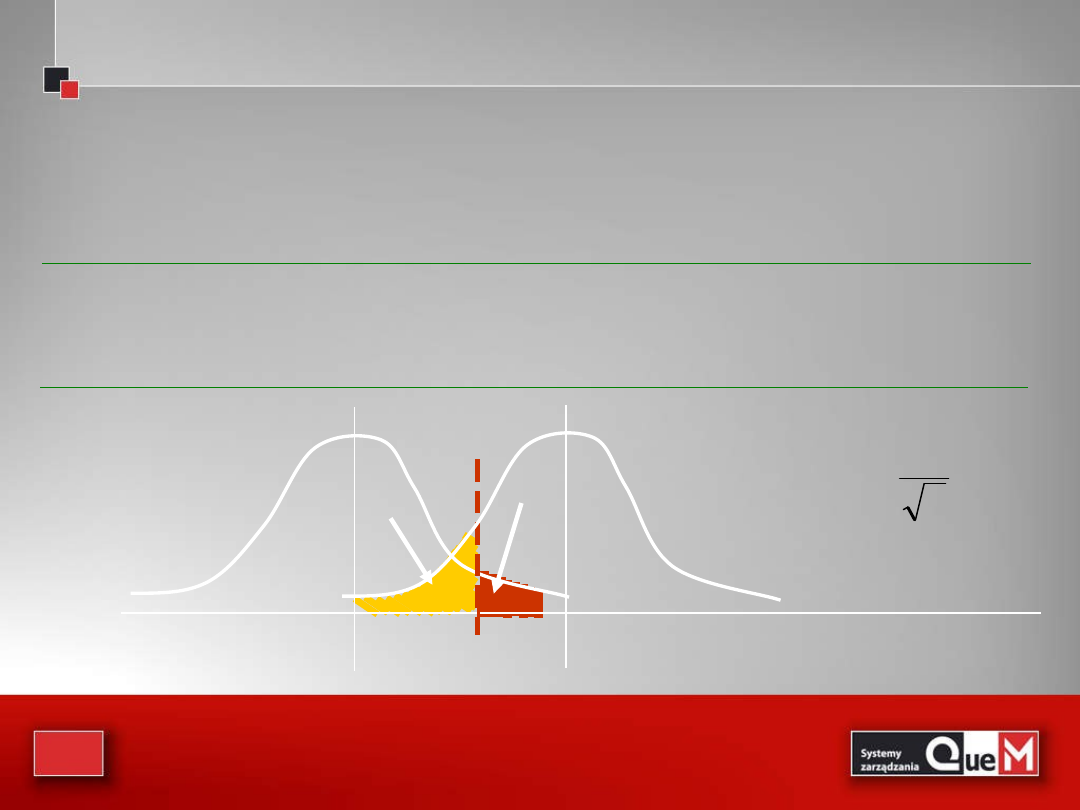
Prawdopodobieństwo błędu II-go rodzaju
Prawdopodobieństwo błędu II-go rodzaju
• niestety prawdopodobieństwo jest trudne do
wyznaczenia „a priori”
• zależy ono od tego, którą z możliwych wartości
przyjmie inetersujący nas parametr
• przykładowo dla testów dotyczących błąd
jest funkcją :
55
Przykład wyznaczania :
Przykład wyznaczania :
H
0
= 60
H
1
= 65
Mamy do czynienia z hipoteza prostą. Albo dojdziemy do
wniosku, że średnia populacji jest równa 60, albo że jest
równa 65.
W praktyce takie sytuacje zdarzają się rzadko.
n = 100
= 20
= 0,05
60
0
65
1
63,29
29
63
645
1
0
,
n
,
C

56
Jakie jest prawdopodobieństwo ?
Jakie jest prawdopodobieństwo ?
)
/
(
0
C
X
P
)
/
C
X
(
P
1
z góry ustalamy, zatem :
1963
,
0
)
855
,
0
U
(
P
)
n
/
C
n
/
X
(
P
)
/
C
X
(
P
1
1
1
Zatem prawdopodobieństwo przyjęcia błędnej hipotezy, że
średnia w populacji jest 60, podczas gdy w rzeczywistości wynosi
65, jest równe 0,1963.
Przeprowadzony test dopuszcza 5% ryzyko odrzucenia Ho gdy
jest ona prawdziwa i 19,63% ryzyko przyjęcia Ho gdy jest ona
fałszywa.

57
Moc testu
Moc testu
Mocą testu hipotezy statystycznej jest
prawdopodobieństwo odrzucenia hipotezy zerowej,
gdy jest ona fałszywa.
moc testu = 1-
W przykładzie: moc testu=1-0,1963=0,8037
Mamy 80,37% szans, że odrzucimy Ho gdy
średnia populacji jest równa 65, a nie 60.

58
Dla testów złożonych
Dla testów złożonych
przykładowo w przypadku testu jednostronnego
H
0
60
H
1
> 60
Jak zdefiniować moc testu w
takiej sytuacji?
Moc testu = P( odrzucenia Ho/ Ho jest fałszywa )
W przykładzie Ho może być fałszywa na
nieskończenie wiele sposobów: 61, 62, 67, 72.893
itd...

59
Moc testu dla wybranych wartości
1
Moc testu dla wybranych wartości
1
1
Moc=1-
61
62
63
64
65
66
67
68
69
0,8739
0,7405
0,5577
0,3613
0,1963
0,0877
0,0318
0,0092
0,0021
0,1262
0,2595
0,4423
0,6387
0,8037
0,9123
0,9682
0,9908
0,9979
załóżmy liczebność próby n=100, s=20, a=0.05

60
Własności mocy testu:
Własności mocy testu:
1.
Moc zależy od odległości między wartością
parametru zakładaną w hipotezie zerowej a
prawdziwą wartością parametru. Im większa
odległość tym większa moc.
2.
Moc zależy od wielkości odchylenia standardowego
w populacji. Im mniejsze odchylenie tym większa
moc.
3.
Moc zależy od liczebności próby. Im liczniejsza
próba, tym większa moc.
4.
Moc zależy od poziomu istotności testu. Im niższy
poziom istotności tym mniejsza moc testu.
nie możemy kontrolować punktu 1 i 2
kształtujemy jedynie pkt. 3 i 4

61
Podsumowując:
Podsumowując:
• w przypadku prowadzenia testu statystycznego dla
parametru populacji posługiwaliśmy się:
– przedziałem ufności (wokół
0
lub x
śr
)
– standaryzowanym przedziałem
• Istnieje 3 droga: wyznaczanie wartości
prawdopodobieństwa na prawo/lewo od wartości
sprawdzianu

62
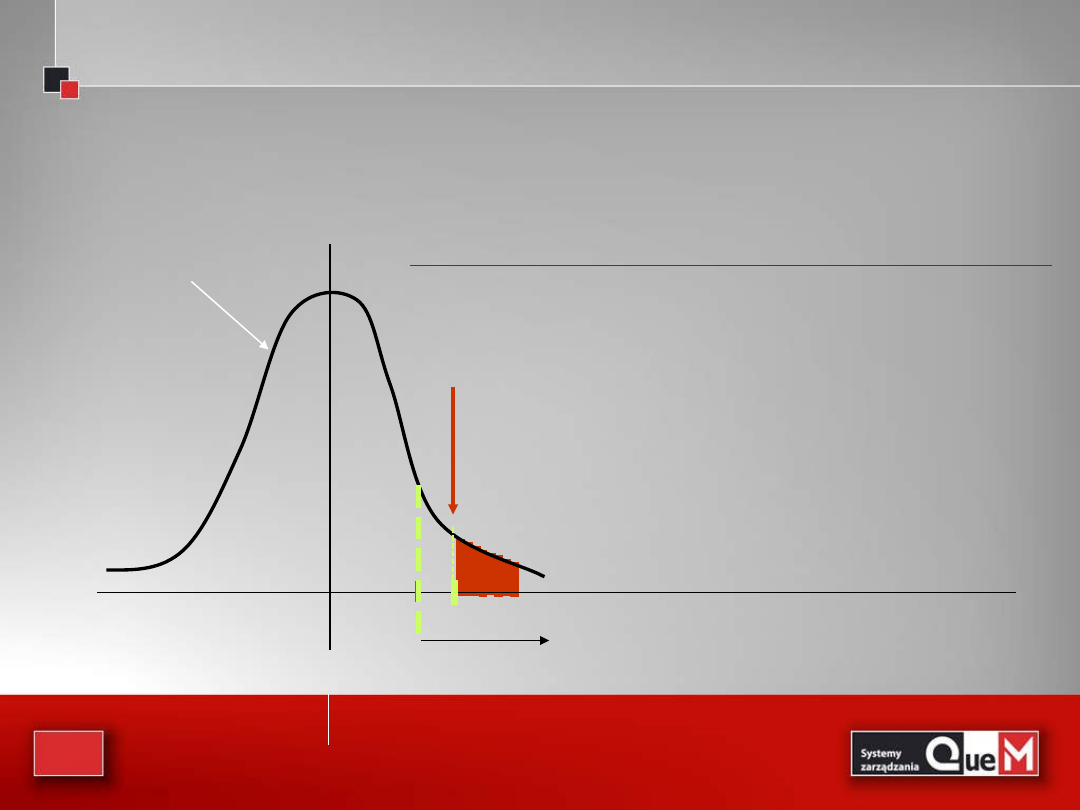
Wartość p – co to takiego?
Wartość p – co to takiego?
to najniższy poziom istotności, przy którym hipoteza
zerowa mogłaby być odrzucona przy otrzymanej
wartości sprawdzianu
to prawdopodobieństwo otrzymania takiej wartości
sprawdzianu, jaką otrzymaliśmy przy założeniu, że
hipoteza zerowa jest prawdziwa
63
Wartość p – co to takiego?
0
rozkład Z
Wartość sprawdzianu u=2,5
Wartość p = miara pola na prawo od u
p = 0.0062
H
0
:
60
H
1
:
>
60
= 0.01
stąd
u
kryt
=2,326
u=2,326

64
Interpretacja:
Interpretacja:
• jeśli otrzymana wartość sprawdzianu jest mało
prawdopodobna przy założeniu, że Ho jest
prawdziwa, to hipoteza Ho powinna być odrzucona
• jeśli otrzymana wartość sprawdzianu jest dosyć
prawdopodobna (większa od 0.05; 0.1) to
powinniśmy przyjąć hipotezę Ho
65
Wartość p
Wartość p
Jest czymś w rodzaju zindywidualizowanego
poziomu istotności
Załóżmy, że wartość p dla
wyznaczonego sprawdzianu
wynosi 0.0002
Informacja dla użytkownika
testu:
1)
Ho musiałaby być odrzucona
przy a=0.01
2)
Ho musiałaby być odrzucona
przy a=0.001 i przy wszystkich
poziomach aż do 0.0002!!
Informacja zawarta w p=0.0002 jest bogatsza niż w stwierdzeniu,
że Ho odrzucona na poziome =0.05

Regresja logistyczna
Regresja logistyczna
• W badaniach medycznych mamy często do
czynienia ze zmienną zależną typu
dychotomicznego, na przykład: 1 -
przeżycie, 0 - zgon; 1 - występuje dany
objaw (np. hiperglikemia, gorączka), 0 - nie
ma danego objawu; albo 1 - występuje
nowotwór, 0 - nie ma nowotworu. Wówczas
można postawić pytanie, która ze
zmiennych niezależnych wpływa istotnie na
przeżycie lub wystąpienie objawu.
66

Regresja logistyczna
Regresja logistyczna
• Szukamy oczywiście podobnego do funkcji
regresji powiązania prawdopodobieństwa
wystąpienia danego objawu z grupą
zmiennych niezależnych, takich jak wiek,
płeć, stężenie cholesterolu itd.
W takich sytuacjach nie możemy
wykorzystać regresji wielokrotnej. Wartości
estymatora takiej funkcji regresji mogą
bowiem przyjmować wartości mniejsze od
zera lub większe od jedności, które w naszym
przypadku nie mają interpretacyjnego sensu.
67

Regresja logistyczna
Regresja logistyczna
• Doskonałym narzędziem do tego typu zagadnień
jest właśnie regresja logistyczna. Dodatkową
zaletą regresji logistycznej jest to, że analiza i
interpretacja wyników są podobne jak w
poznanych wcześniej metodach klasycznej
regresji.
•
Ogólnie mówiąc, regresja logistyczna jest
pewnym matematycznym modelem, którego
możemy użyć w celu opisania wpływu kilku
zmiennych x1, x2,...xk (zarówno ilościowych, jak
i jakościowych) na dychotomiczną zmienną y.
68

Regresja logistyczna
Regresja logistyczna
• Regresję logistyczną, cieszącą się dużym
uznaniem w psychologii i medycynie,
wprowadzono już w XIX wieku. Pionierami byli
Verhulst i Pearl, którzy opracowali postać
krzywej logistycznej i zastosowali ją w
praktyce; jednakże pełny model w postaci
stosowanej dzisiaj po raz pierwszy podał i
zastosował w 1972 roku Finney.
Co leży u podstaw tej popularności? Przede
wszystkim funkcja logistyczna, której wykres
widoczny jest na rysunku 1.
69
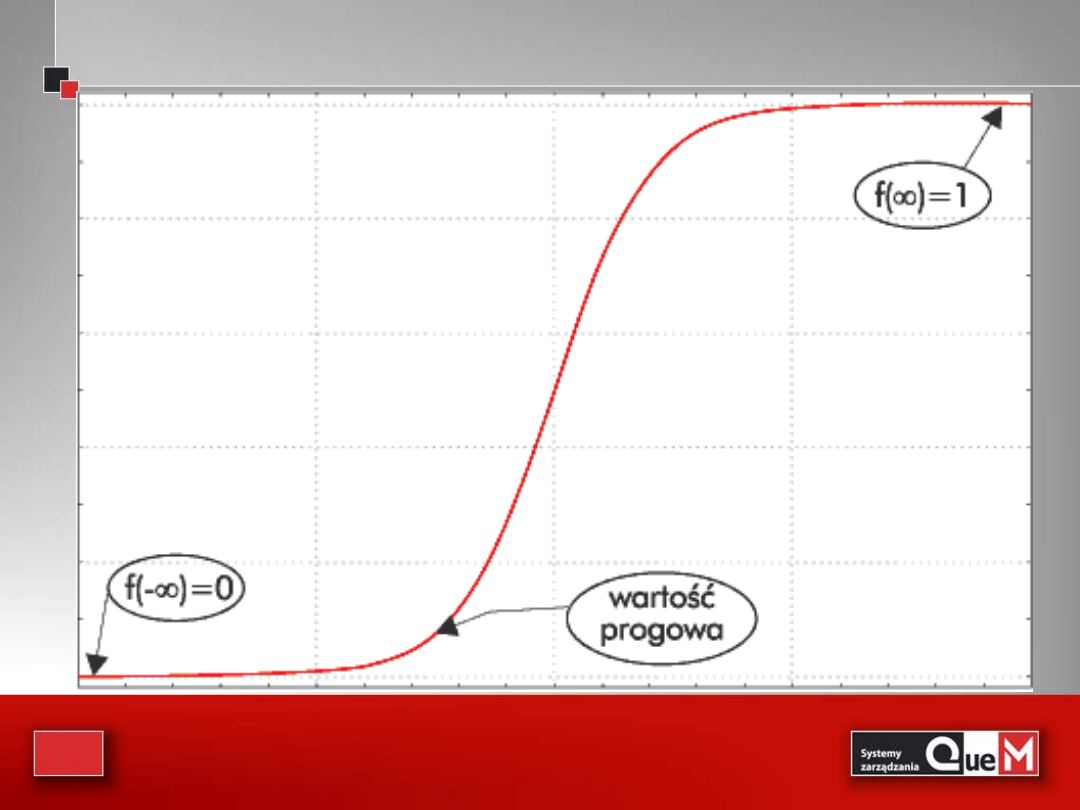
Rysunek 1
Rysunek 1
70

Regresja logistyczna
Regresja logistyczna
• Jak widać, przyjmuje ona wartości między 0 a 1.
Zakłada się ponadto, że jej wartość w -
jest równa 0, a dla z =+ f(z) jest równa
1.
• Jak zmienia się wartość funkcji logistycznej?
Wyróżniamy 3 etapy:
• 1) na początku przez pewien czas jest bliska 0;
2) potem od pewnego momentu (wartości
progowej) następuje nagły wzrost;
3) na końcu zbliża się do 1.
71

Model logistyczny zawdzięcza popularność
następującym właściwościom:
Model logistyczny zawdzięcza popularność
następującym właściwościom:
• 1. Funkcja logistyczna przyjmuje wartości od 0 do
1.
• 2. Model może opisywać wartości
prawdopodobieństwa, które, jak wiemy, są zawsze
zawarte między 0 a 1. Prawdopodobieństwa te
określają najczęściej ryzyko zachorowania lub
szanse wyzdrowienia. Dlatego model logistyczny
jest często jedynym, jaki możemy wybrać,
rozważając prawdopodobieństwa.
72

3. Kształt funkcji przypomina rozciągniętą
literę S.
3. Kształt funkcji przypomina rozciągniętą
literę S.
• Pokazuje on, że zmiany funkcji są
minimalne, jeśli wartości zmiennych są
mniejsze od pewnej wartości progowej.
Gdy ją przekroczą, wówczas wartość
funkcji zaczyna gwałtownie rosnąć do 1;
prawdopodobieństwo utrzymuje się na
wyjątkowo wysokim poziomie - blisko 1.
Pojęcie wartości progowej jest często
używane w badaniach medycznych i
epidemiologicznych.
73

Zdefiniujemy teraz pojęcie "model
logistyczny".
Zdefiniujemy teraz pojęcie "model
logistyczny".
• Oznaczmy w tym celu przez Y zmienną
dychotomiczną o wartościach:
1 - najczęściej dla zdarzeń pożądanych, na
przykład: przeżycie, wyzdrowienie,
niezakażenie, powodzenie leczenia;
0 - w przeciwnym wypadku, na przykład:
zgon, choroba, zakażenie, niepowodzenie
leczenia.
74

• Wówczas model regresji logistycznej wiążący
prawdopodobieństwo
jednego z dwóch możliwych wyników zmiennej Y ze zmiennymi
wyjaśniającymi jest określony równaniem
• gdzie
ai i = 0,...,k - to współczynniki regresji
x1, x2,...,xk - to zmienne niezależne, które mogą być mierzalne lub
jakościowe
75
Regresja logistyczna
Regresja logistyczna

Regresja logistyczna
Regresja logistyczna
• Prawa strona równania to warunkowe
prawdopodobieństwo, że zmienna Y
przyjmie wartość 1 dla wartości
zmiennych niezależnych x1, x2,...,xk.
• Jak w każdym modelu regresji, tak i tu
staramy się oszacować współczynniki
regresji a
o
, a
1
,...,a
k
. Chcemy w ten sposób
dopasować jak najlepszy model w oparciu
o wartości pewnej grupy danych.
76

Oczywiście liczebność grupy n musi być
dostatecznie duża, co oznacza, że n >10(k + 1),
gdzie k jest liczbą parametrów.
Oczywiście liczebność grupy n musi być
dostatecznie duża, co oznacza, że n >10(k + 1),
gdzie k jest liczbą parametrów.
• W celu znalezienia estymatorów a0, a1,...,ak
nie możemy stosować omówionej wcześniej
metody najmniejszych kwadratów.
•
Wymaga ona bowiem założenia o stałości
wariancji, które w przypadku zmiennej
dychotomicznej Y nie jest spełnione. W
przypadku regresji logistycznej stosujemy
metodę największej wiarygodności. Metoda
ta, której podstawy teoretyczne opracował
twórca analizy wariancji Fisher w 1929 roku,
jest jedną z najważniejszych metod estymacji.
77

Najogólniej mówiąc, metoda największej
wiarygodności maksymalizuje funkcję
wiarygodności, czyli iloczyn
Najogólniej mówiąc, metoda największej
wiarygodności maksymalizuje funkcję
wiarygodności, czyli iloczyn
• prawdopodobieństw pojawienia się
poszczególnych obserwacji z próby przy danych
parametrach modelu. Nie będziemy wchodzić w
szczegółowe matematyczne rozważania; zwrócę
tylko uwagę na istotę metody. Chodzi o to, aby
jako ocenę szacowanych parametrów brać te
wartości, dla których wiarygodność jest
największa. Intuicyjne uzasadnienie takiego
postępowania jest oczywiste - im większa
wiarygodność (prawdopodobieństwo)
zdarzenia, tym większa częstość względna
(realizacja) w długim ciągu doświadczeń.
78

W przypadku pojedynczego doświadczenia
możemy i powinniśmy się liczyć z jego
realizacją.
W przypadku pojedynczego doświadczenia
możemy i powinniśmy się liczyć z jego
realizacją.
• Dla małej wiarygodności częstość względna
jego wystąpienia jest bliska 0, i w
przypadku pojedynczej próby możemy w
ogóle nie brać pod uwagę możliwości jego
realizacji. W przypadku konkretnego
modelu im większa jest jego wiarygodność,
tym większe prawdopodobieństwo, że
wartości zmiennej zależnej pojawią się w
próbie. Innymi słowy - im większa
wiarygodność, tym lepsze dopasowanie
modelu do danych.
79

Estymatory wyznaczone metodą największej
wiarygodności
Estymatory wyznaczone metodą największej
wiarygodności
• dzięki swoim własnościom gwarantują
największe prawdopodobieństwo
otrzymania zaobserwowanych wartości
zmiennej zależnej. W statystycznych
pakietach komputerowych estymatorów
metody największej wiarygodności
poszukuje się, maksymalizując funkcję
wiarygodności L lub jej logarytm. Z
przyczyn obliczeniowych łatwiej jest
bowiem znaleźć ekstremum funkcji log L
niż samej funkcji L.
80

Dziękuję za uwagę
Dziękuję za uwagę
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
- Slide 75
- Slide 76
- Slide 77
- Slide 78
- Slide 79
- Slide 80
- Slide 81
Wyszukiwarka
Podobne podstrony:
06 Testowanie hipotez statystycznychid 6412 ppt
ESTYMACJA STATYSTYCZNA duża próba i analiza struktury, Semestr II, Statystyka matematyczna
ESTYMACJA STATYSTYCZNA2 duża próba i analiza struktury(2), Semestr II, Statystyka matematyczna
ESTYMACJA STATYSTYCZNA wskaźnika struktury, ESTYMACJA STATYSTYCZNA
ESTYMACJA STATYSTYCZNA duża próba i analiza struktury, ESTYMACJA STATYSTYCZNA
koło Struktura ESTYMACJA STATYSTYCZNA2 duża próba i analiza struktury, ESTYMACJA STATYSTYCZNA
Zadania-estymacja, Statystyka
ESTYMACJA STATYSTYCZNA duża próba, Semestr II, Statystyka matematyczna
ESTYMACJA STATYSTYCZNA2 duża próba i analiza struktury, Semestr II, Statystyka matematyczna
1 1 Statystykaid 8854 ppt
ESTYMACJA STATYSTYCZNA(2), Semestr II, Statystyka matematyczna
Statystyka matematyczna 2010 (duża próba), ESTYMACJA STATYSTYCZNA
Estymacja1, Statystyka
więcej podobnych podstron