Wpływ smukłości na nośność
słupów

Przykłady obliczeniowe

Słup w ustroju usztywnionym (o węzłach nieprzesuwnych):

• sprawdzenie kryterium smukłości słupa wydzielonego

• uwzględnienie efektów II rzędu metodą nominalnej
sztywności

• uwzględnienie efektów II rzędu metodą nominalnej
krzywizny

Słup w ustroju nieusztywnionym (o węźle lub węzłach
przesuwnych):

• sprawdzenie kryterium smukłości słupa wydzielonego

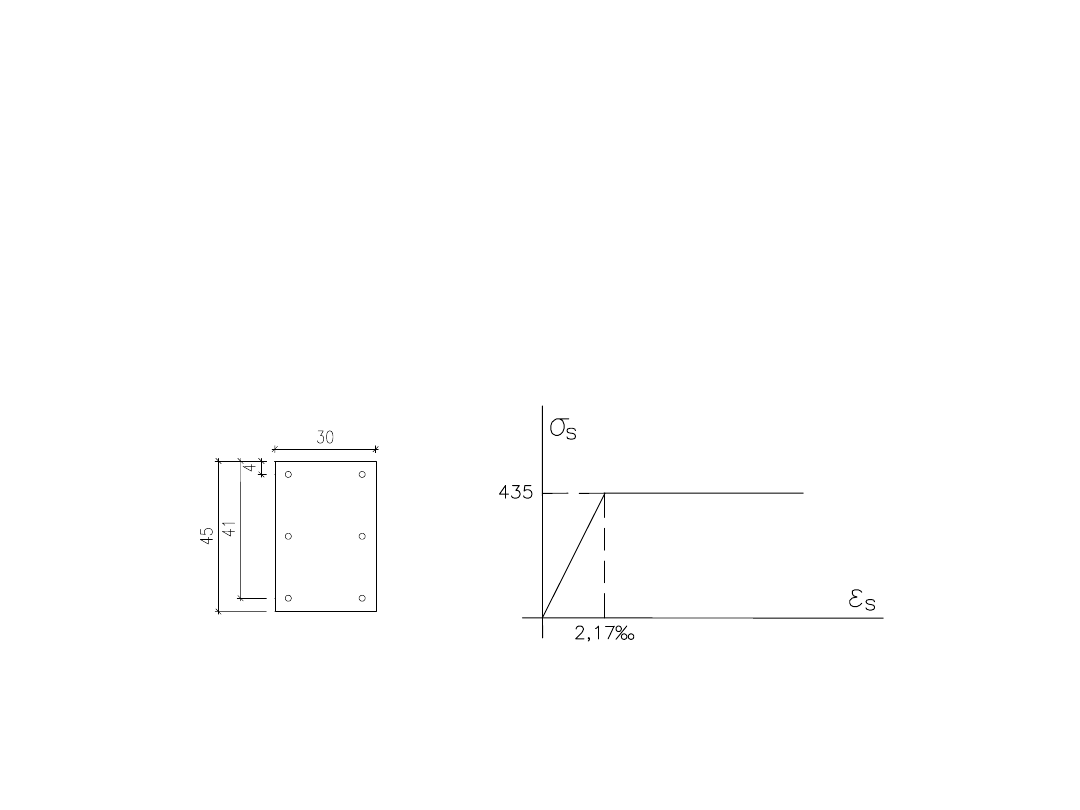
Założenia:

Beton C30/37 f

cd

= 30/1,4 = 21,43MPa

E

cm

= 32GPa

Stal B500 f

yd

= 500/1,15 = 435MPa

E

s

= 200GPa

ε

yd

= 2,17‰

Zbrojenie – 6 prętów o średnicy 18mm;
A

s1

= 2,54cm

2

(pojedynczy pręt)

Wysokość słupal=9,3m
Obliczeniowa siła podłużna

N

Ed

=1550kN

c

85

,

0

3

,

9

12

45

,

0

3

,

0

10

32

120

0130

,

0

3

6

1



















l

EJ

M

k



































2

2

1

1

0

k

45

,

0

k

1

k

45

,

0

k

1

l

5

,

0

l

m

50

,

6

1

,

0

45

,

0

1

,

0

1

85

,

0

45

,

0

85

,

0

1

3

,

9

5

,

0

l

0









































m

13

,

0

12

45

,

0

12

h

i







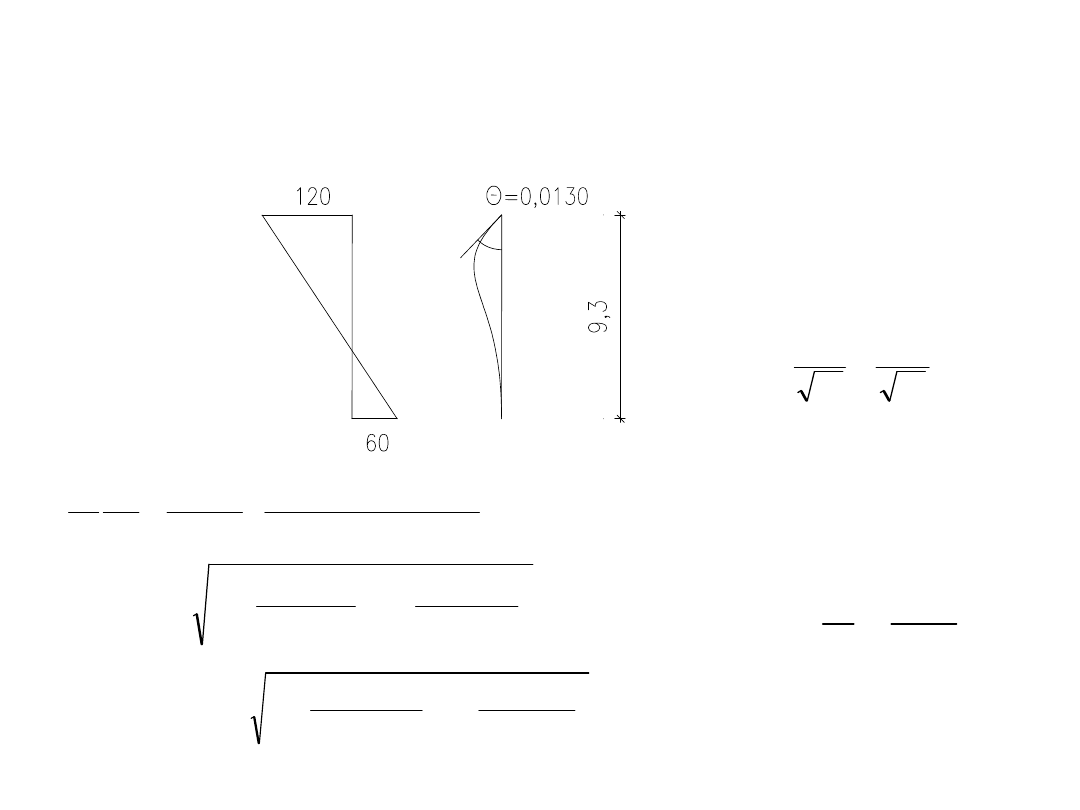
Efektywna długość słupa l

o

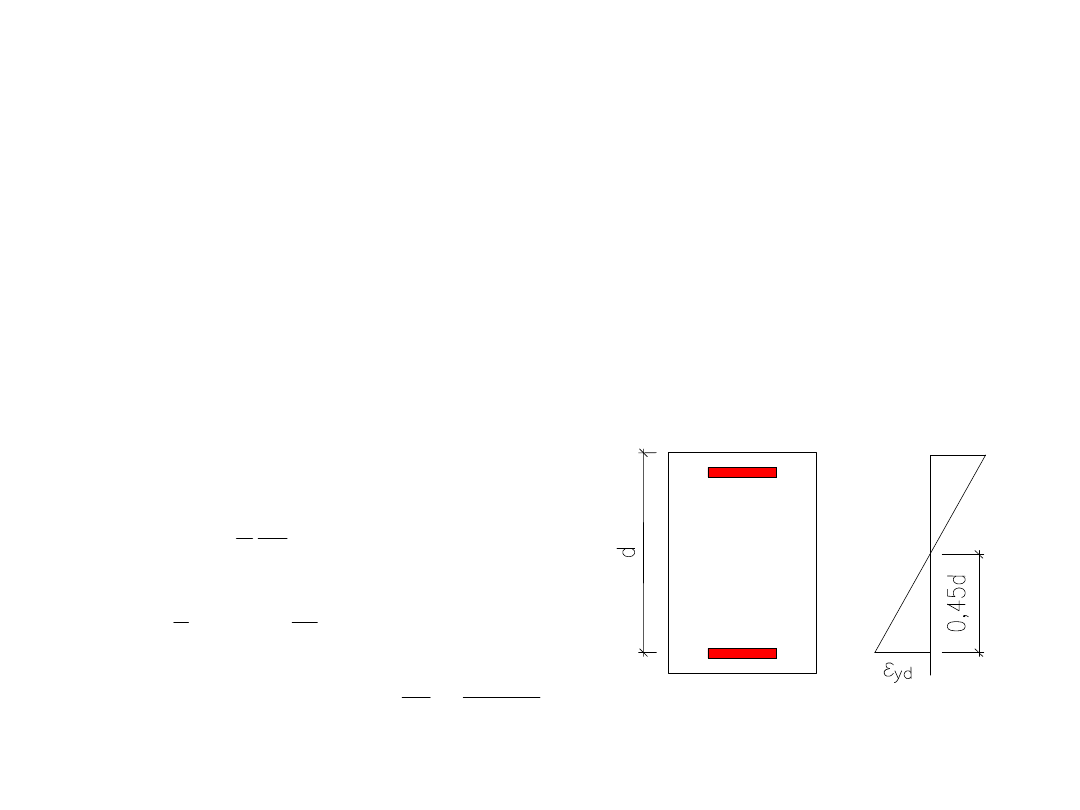
Z obliczeń statycznych otrzymano wykres momentów I rzędu i odkształcenie
w płaszczyźnie osi Y przekroju jak niżej

k

2

=

0,1

50

13

,

0

50

,

6

i

l

0









Słup w ustroju usztywnionym

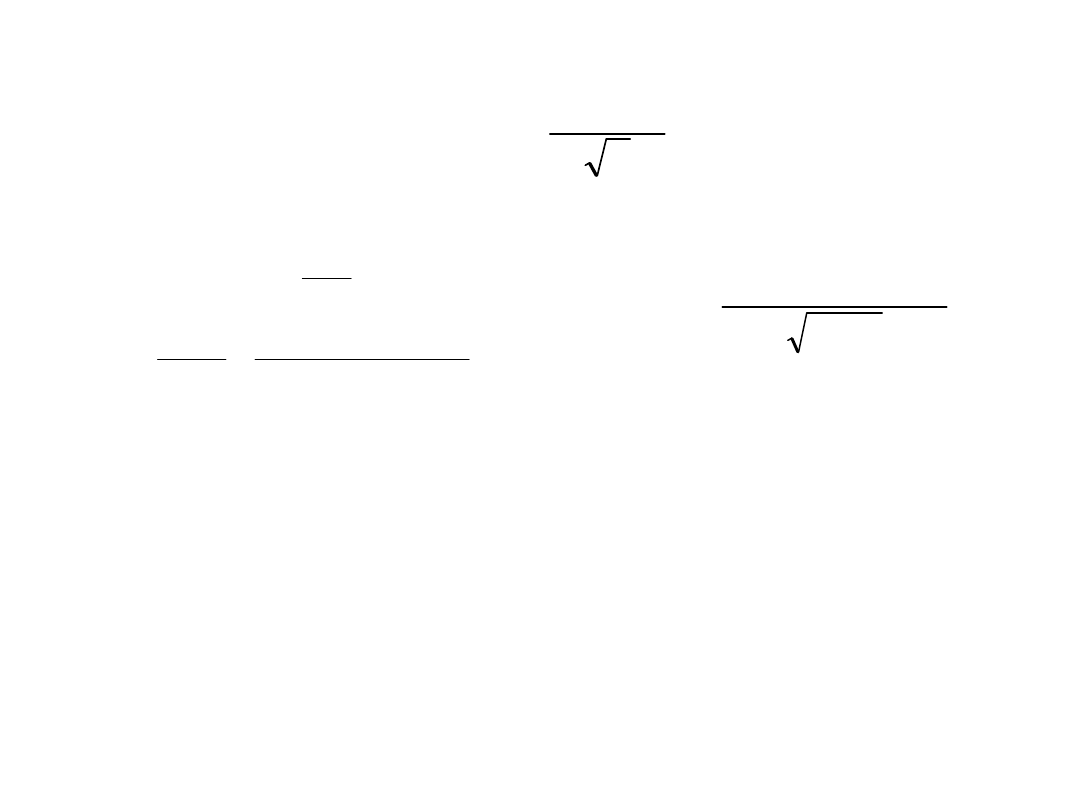
n

ABC

20

lim





536

,

0

21430

45

,

0

30

,

0

1550

f

A

N

n

cd

c

Ed











3

,

46

536

,

0

2

,

2

1

,

1

7

,

0

20

lim













Kryterium smukłości elementów wydzielonych

Ponieważ

 > 

lim

, należy uwzględnić wpływ smukłości na

nośność słupa.

Ekwiwalentny moment I rzędu wynosi

M

0e

= 0,6M

02

+ 0,4M

01

 0,4M

02

| M

02

|  | M

01

|

M

02

= 120kNm

M

01

= -60kNm

M

0e

= 0,6  120 + 0,4  (-60)

=48kNm
M

0e

= 0,4  120 = 48kNm

Przyjęto M

0e

= 48kNm

2

,

2

120

60

7

,

1

r

7

,

1

C

m













A = 0,7 B =
1,1

m

016

,

0

400

50

,

6

400

l

e

0

i







kNm

8

,

24

016

,

0

1550

e

N

M

i

Ed

Ed











Wpływ imperfekcji

Przyrost momentu na skutek imperfekcji

Momenty I rzędu
na podporze: M

0Ed

= 120 + 24,8 = 144,8kNm

ekwiwalentny:

M

0Ed

= 48 + 24,8 = 72,8kNm

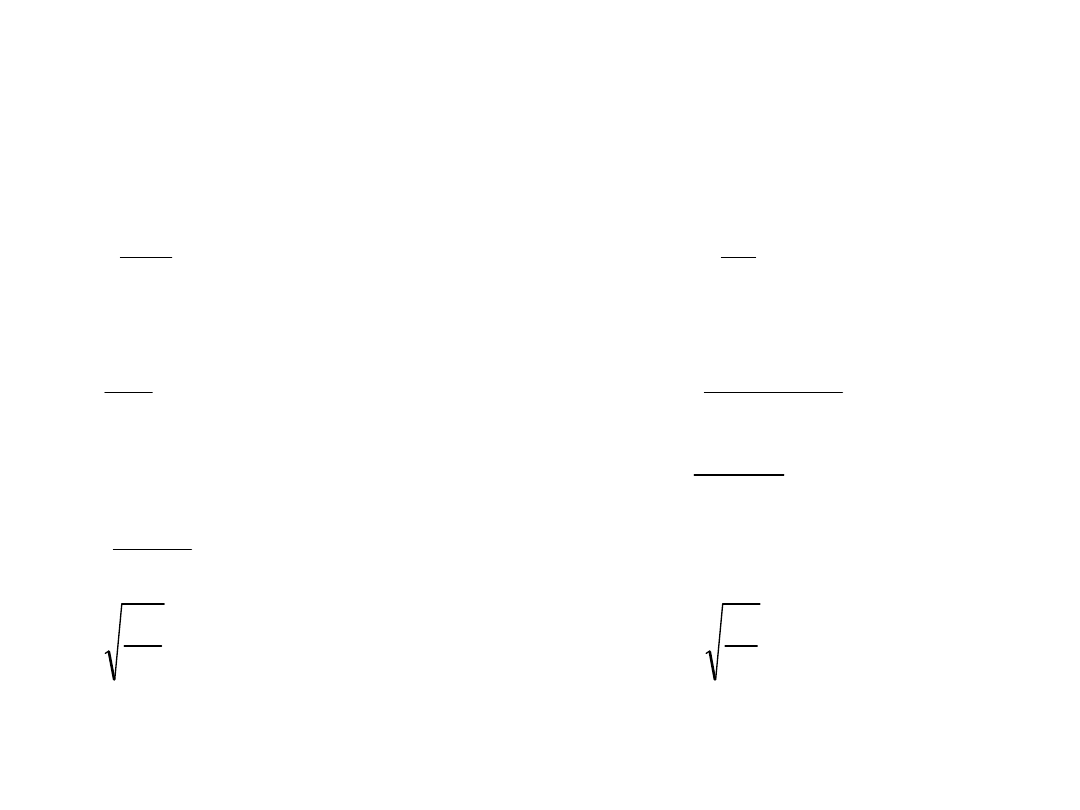
Metoda nominalnej sztywności

s

s

s

c

cd

c

J

E

K

J

E

K

EJ





cE

cm

cd

E

E





GPa

67

,

26

2

,

1

32

E

cd







cE

= 1,2 (zalecane)

12

bh

J

3

c



4

3

3

c

m

10

278

,

2

12

45

,

0

30

,

0

J











Jeżeli   0,002

K

s

= 1,0

ef

2

1

c

1

k

k

K







0113

,

0

45

30

54

,

2

6











K

s

= 1,0

20

f

k

ck

1



22

,

1

20

30

k

1





Wzory

Obliczenia

cd

c

Ed

f

A

N

n

536

,

0

21430

45

,

0

30

,

0

1550

n









20

,

0

170

n

k

2







20

,

0

16

,

0

170

50

536

,

0

2









k

Przyjęto k

2

= 0,16

Ed

0

0

ef

M

M









Przyjęto
(,t

0

) = 2,0

M

0Eqp

– moment zginający I rzędu wywołany

prawie stałą kombinacją obciążeń

M

0Ed

– moment zginający I rzędu wywołany

obliczeniową kombinacją obciążeń

7

,

0

M

M

Ed

0

Eqp

0





ef

= 2,0  0,7 = 1,4

Wpływ pełzania można pominąć, jeżeli

h

N

M

75

2

)

t

,

(

Ed

Ed

0

0













081

,

0

4

,

1

1

16

,

0

22

,

1









c

K

Trzeci warunek nie jest spełniony, pełzanie trzeba

uwzględnić.

Eqp

E

s

– obliczeniowy moduł sprężystości

zbrojenia

J

s

– moment bezwładności pola przekroju

zbrojenia względem środka ciężkości

powierzchni betonu

GPa

200

E

s







4

4

2

4

s

m

10

3477

,

0

04

,

0

225

,

0

10

54

,

2

2

2

J























Całkowity moment obliczeniowy, zawierający

moment II rzędu

2

3

4

3

3

875

,

11

10

10

3477

,

0

200

0

,

1

10

10

278

,

2

67

,

26

081

,

0

MNm

EJ





























































1

N

N

1

M

M

Ed

B

Ed

0

Ed

M

0Ed

– moment I rzędu

Ed

Ed

Ed

M

M

M

0

0

558

,

2

1

1550

2774

23

,

1

1































Momenty obliczeniowe
wynoszą

w górnym przekroju słupa
ekwiwalentny

Jeżeli przyjmie się β = 1,0

więc moment
ekwiwalentny

Sprawdzamy nośność ze
względu na moment
ekwiwalentny

M

Ed

= 72,8  2,558 =

186,2kNm

M

Ed

= M

0Ed

 2,266

M

Ed

= 72,8  2,266 =

165,0kNm

M

Ed

= 144,8kNm

2

Ed

0

Ed

M

M

M





M

0Ed

–

moment I rzędu zawierający wpływ

imperfekcji

M

2

– nominalny moment II rzędu

2

Ed

2

e

N

M 

c

l

r

1

e

2

0

2



0

r

r

1

K

K

r

1





d

45

,

0

r

1

yd

0





Metoda nominalnej krzywizny

Jeżeli zbrojenie nie jest zgrupowane przy

przeciwnych stronach przekroju, to

s

i

h

5

,

0

d





s

s

s

A

J

i 

m

151

,

0

6

185

,

0

2

2

i

2

s









m

376

,

0

151

,

0

45

,

0

5

,

0

d









m

1

0128

,

0

376

,

0

45

,

0

00217

,

0

r

1

0







0

,

1

1

K

ef











150

200

f

35

,

0

ck











167

,

0

150

50

200

30

35

,

0











4

,

1

ef





(jak w metodzie nominalnej sztywności)

23

,

1

4

,

1

167

,

0

1

K











0

,

1

n

n

n

n

K

bal

u

u

r









cd

c

Ed

f

A

N

n 

536

,

0

21430

45

,

0

30

,

0

1550

n









n

bal

= 0,4

n

bal

= 0,4

cd

c

yd

s

f

A

f

A





229

,

0

43

,

21

45

,

0

30

,

0

435

10

54

,

2

6

4



















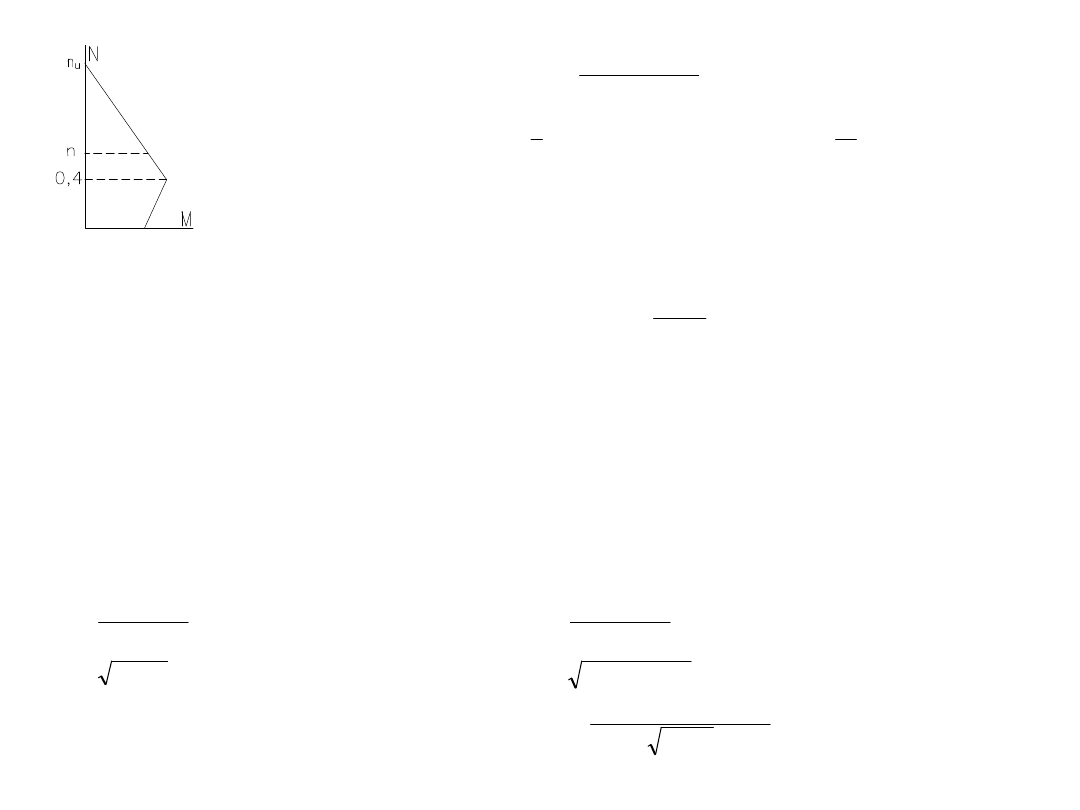
n

u

= 1+ 

n

u

= 1+ 0,229 = 1,229

836

,

0

4

,

0

229

,

1

536

,

0

229

,

1

K

r









m

1

0132

,

0

0128

,

0

23

,

1

836

,

0

r

1









c = 10 (~

2

)

c = 10

m

0558

,

0

10

50

,

6

0132

,

0

e

2

2







kNm

M

5

,

86

0558

,

0

1550

2







Momenty obliczeniowe

w przekroju górnym: M

Ed

= M

0Ed

M

Ed

= 144,8kNm

ekwiwalentny: M

Ed

= M

0Ed

+ M

2

M

Ed

= 72,8 + 86,5 = 159,3kNm

Sprawdzamy nośność ze względu na moment

ekwiwalentny

Uściślenie 

lim

ef

2

,

0

1

1

A







78

,

0

4

,

1

2

,

0

1

1

A









(było A = 0,70)







2

1

B

21

,

1

229

,

0

2

1

B









(było B = 1,10)

7

,

56

536

,

0

2

,

2

21

,

1

78

,

0

20

lim













W tym przypadku uwzględnienie efektów II rzędu nie jest wymagane!

- korekta wpływu pełzania i uwzględnienie rzeczywistego stopnia zbrojenia

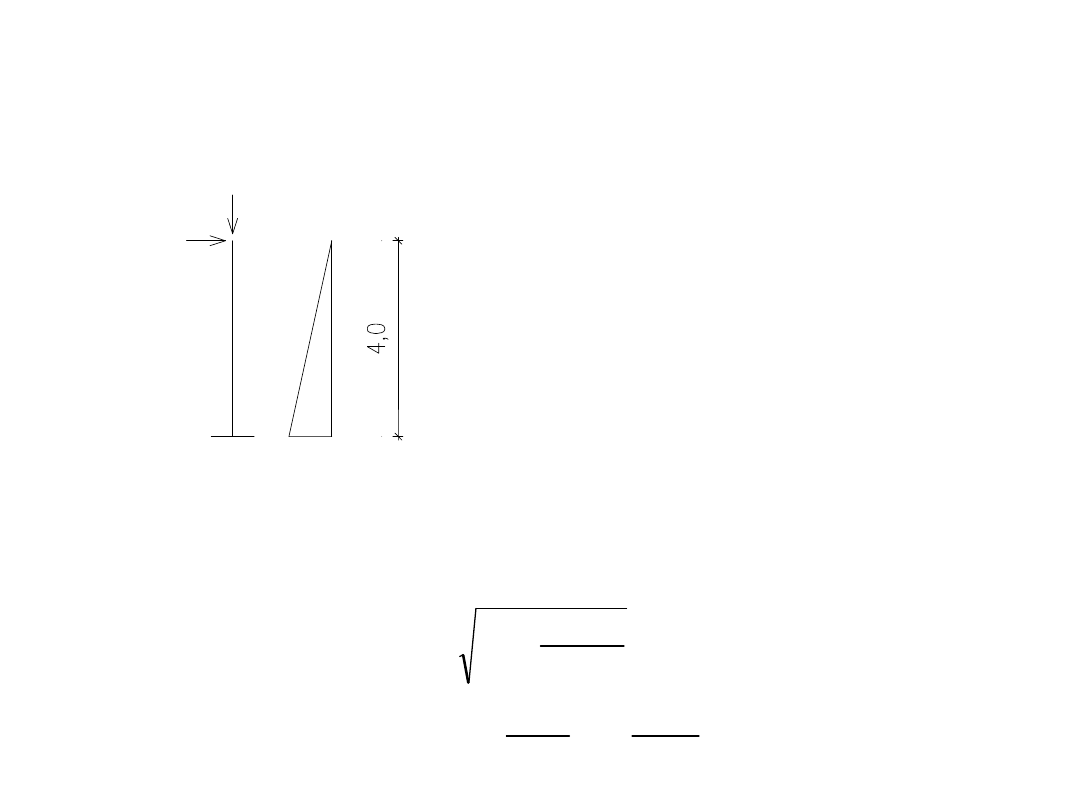
Słup wspornikowy (np. estakady)

Dane materiałowe i dotyczące przekroju jak
poprzednio





















































2

2

1

1

2

1

2

1

0

k

1

k

1

k

1

k

1

k

k

k

k

10

1

max

l

l

Długość efektywna

N

Ed

= 110kN

M

Ed

= 80kNm

Przyjęto

k

1

= 10 (k =  oznacza pełny

przegub)
k

2

= 0,1

Słup w ustroju nieusztywnionym

i

l

0





400

l

e

0

i



Imperfekcja

Moment obliczeniowy

m

32

,

8

08

,

2

41

,

1

max

0

,

4

l

0













64

13

,

0

32

,

8







038

,

0

21430

45

,

0

30

,

0

110

n









6

,

164

038

,

0

7

,

1

21

,

1

78

,

0

20

lim













m

021

,

0

400

32

,

8

e

i





M

Ed

= 80 + 110  0,021 =82,3kNm

> 64

Jeżeli przyjmiemy C = 0,7
(słup nieusztywniony) λ

lim

= 67,8 > 64