Liniowe obwody 

elementarne przy 

wymuszeniach 

sinusoidalnych.

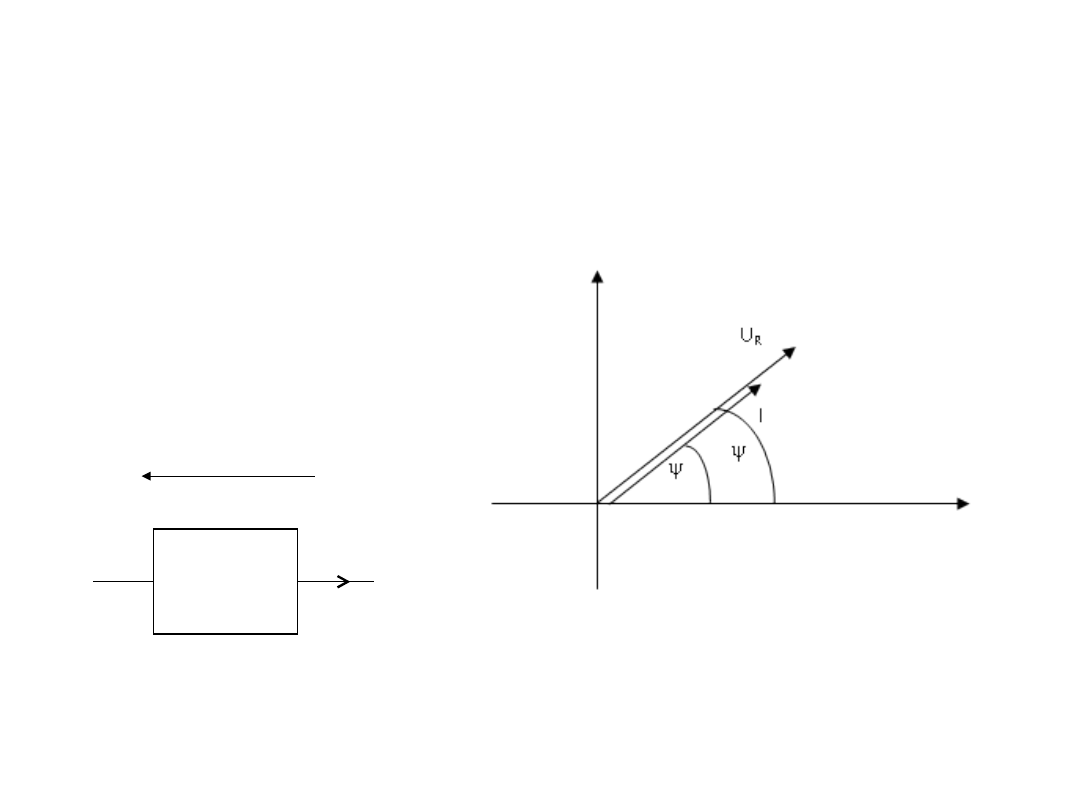
Zauważ, że przesunięcie fazowe pomiędzy prądem i napięciem na 
idealnym rezystorze jest równe =0, oraz że moc chwilowa 
pobierana przez rezystor zawsze jest równa zero.

U

R

I

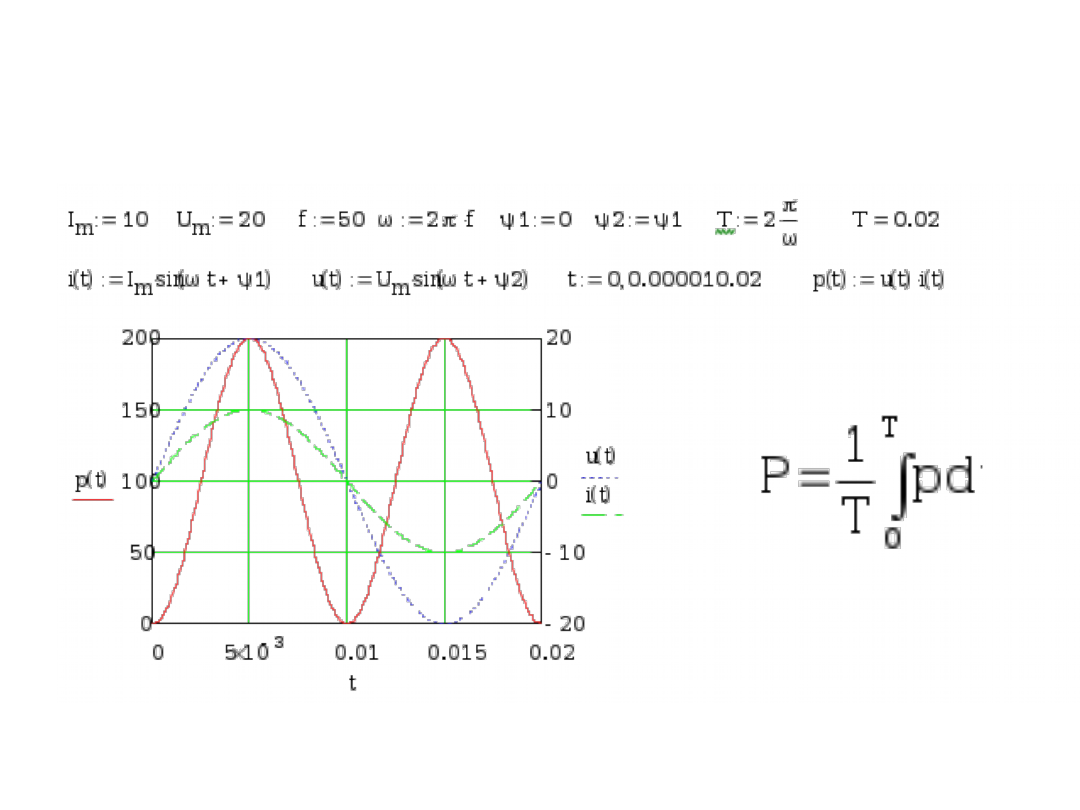
Moc czynna: całka za okres 

z mocy chwilowej

Na ekranie przedstawiono symulację w programie Mathcad  
przebiegów prądu i napięcia na rezystorze oraz mocy 
chwilowej. Przypomnij sobie, że interpretacją energii pobranej 
przez rezystor przy przepływie prądu stałego jest pole 
prostokąta (ekran 258). Stąd energia pobrana przy przepływie 
prądu zmiennego może być określona jako całka za okres z 
funkcji mocy chwilowej. Ponieważ w każdym okresie ilość 
pobranej energii jest jednakowa stąd można sformułować 
pojęcie średniej mocy dzieląc obliczoną energię przez okres. 
Tak sformułowaną moc średnią nazywamy mocą czynną dla 
dowolnych przebiegów okresowych napięcia i prądu.

Moc czynna: całka za okres 

z mocy chwilowej

Moc czynna przy przepływie 

prądu sinusoidalnego przez 

rezystor:

I

U

R

U

I

R

T

I

R

T

1

dt

I

R

T

1

2

2

t

2

sin

1

[

I

R

T

1

pdt

T

1

P

R

2
R

2

2

T

0

2

T

0

2

T

0

























































Zauważ, że wzory na moc pobieraną przez rezystor nie różnią się 
od stosowanych w obwodach prądu stałego. W tym, przypadku 
jednak prąd I oraz napięcie U

R

 są skutecznymi wartościami 

sygnałów sinusoidalnych. 
W dalszym ciągu pamiętajmy, że dużymi literami I,U oznacza 
będziemy wartości skuteczne. Literami z indeksem m (U

m

,I

m

) 

będziemy oznaczali amplitudy. Z kolei małymi literami u,i 
wielkości chwilowe (funkcje od czasu t).

Moc czynna przy przepływie 

prądu sinusoidalnego przez 

rezystor:

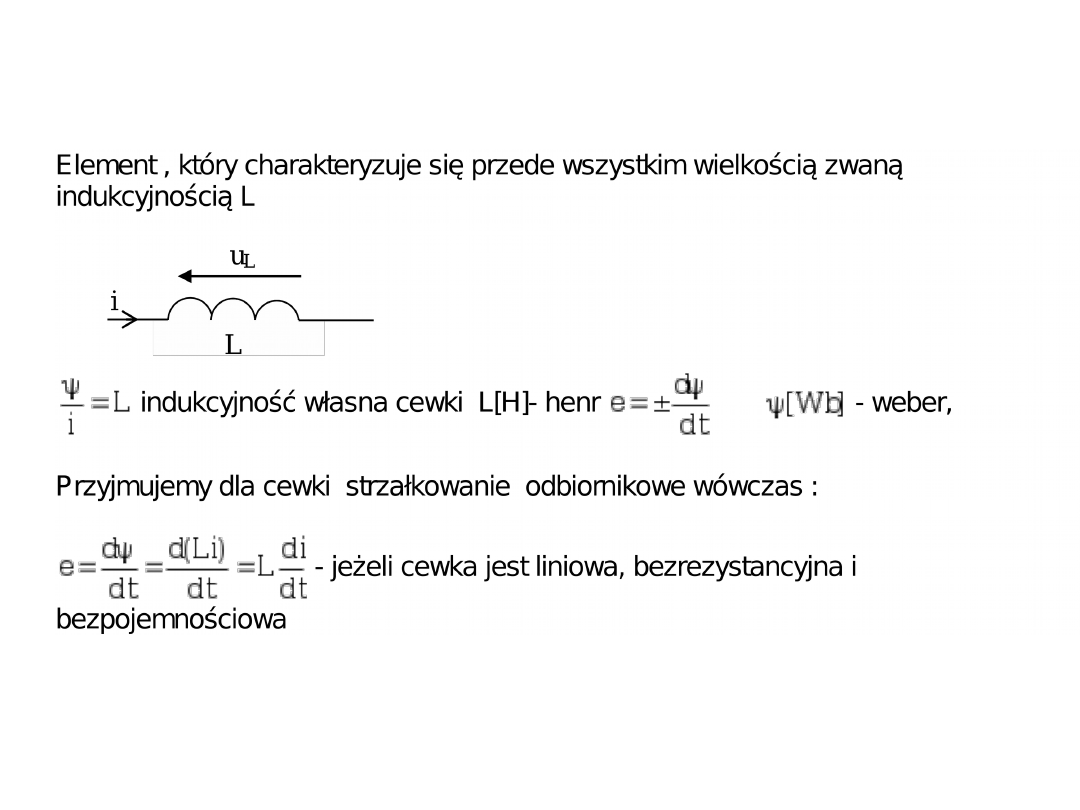
Cewka

Cewka

      Jeżeli  cewka  jest  liniowa  to  charakteryzuje  się  stałą 
wielkością (indukcyjność własna cewki) będącą stosunkiem 
strumienia  sprzężonego  z  nią  wytwarzanego  przez 
przepływający  przez  jej  uzwojenie  prąd  do  wartości  tego 
prądu.
Należy  pamiętać,  że  w  ogólnym  przypadku  rzeczywista 
cewka  może  być  elementem  nieliniowym    i  posiadać 
rezystancję,  Wówczas  napięcie  na  niej  nie  może  być 
wyrażone wzorem 

dt

di

L

e

oraz 
L=variab.

Porównując wzór na prawo Ohma w przypadku rezystancji z 
otrzymanym prawem Ohma dla indukcyjności, wielkość zwaną 
reaktancją możemy zinterpretować jako opór jaki cewka stawia 
napięciu. Im większa reaktancja tym mniejszy prąd przy danym 
napięciu.

Moc czynna pobierana 

przez cewkę:

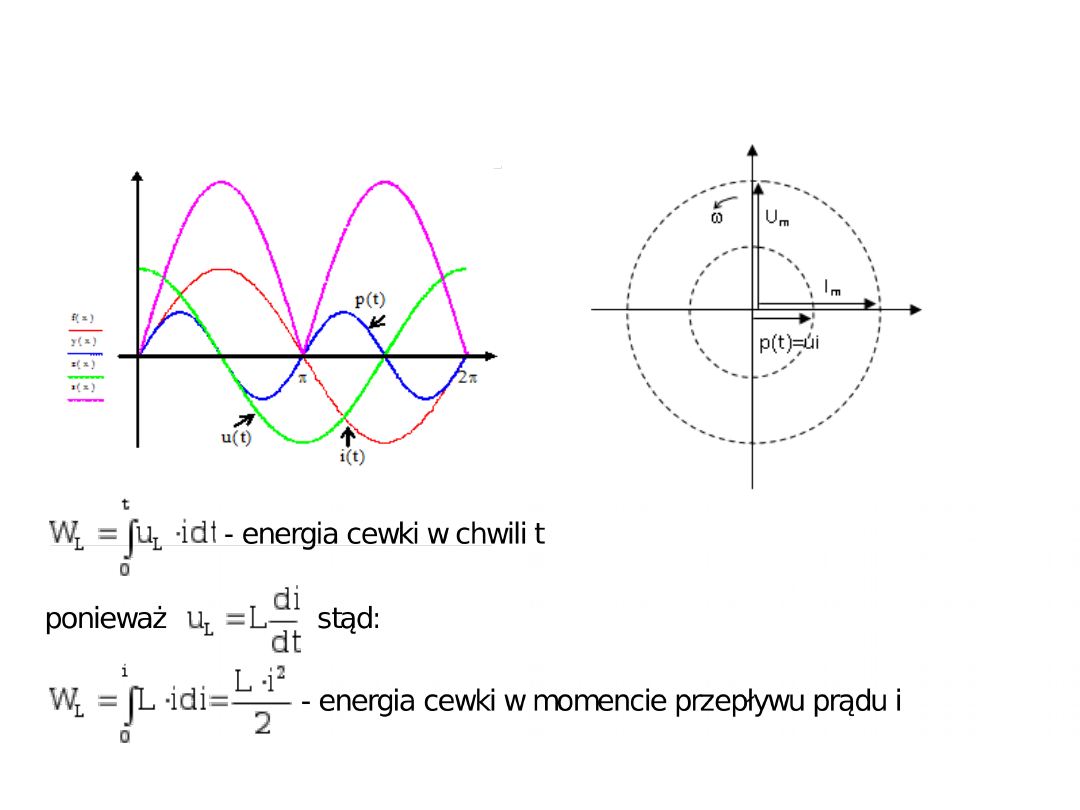
Energia cewki

Energia cewki

Kondensator

W ogólnym przypadku kondensator  (podobnie jak rezystor czy cewka) 
może charakteryzować się innymi wielkościami (jak indukcyjność czy 
rezystywność). Wówczas na model takiego kondensatora będą składały się 
dodatkowe idealne elementy:

Wzory określające zależność pomiędzy prądem a napięciem na 
kondensatorze dla dowolnych przebiegów sformułowano dla 
zastrzałkowania odbiornikowego. Zauważ, że zachowana jest 
zasada odbiornikowego strzałkowania  wszystkich dotychczas 
poznanych elementów tj. rezystancji, indukcyjności i pojemności. 

Analogicznie jak dla cewki, reaktancję kondensatora można 
interpretować jako opór jaki stawia kondensator napięciu 
zmiennemu.

UWAGA:

 wzory na reaktancje zarówno cewki jak i kondensatora 

mają sens tylko dla sygnałów sinusoidalnych. Dlaczego?

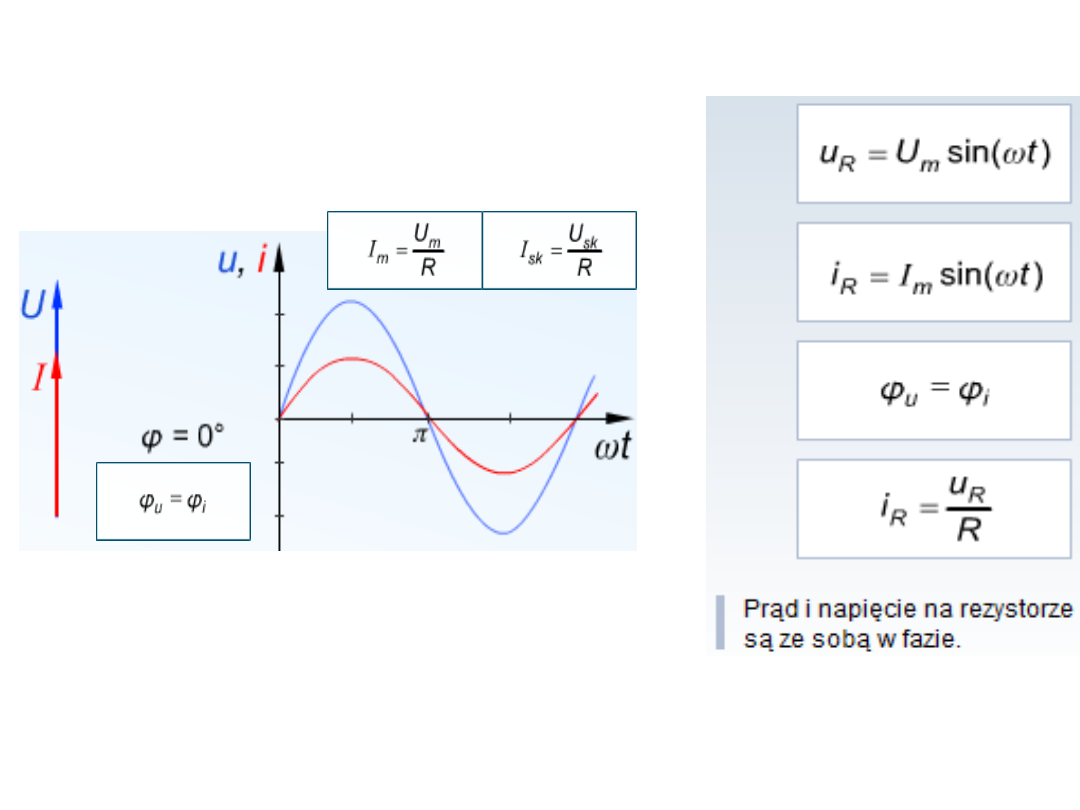
Obwody sinusoidalne z elementami R, 

L, C

Dla idealnego rezystora spełnione jest prawo 
Ohma, które dotyczy amplitud, oraz wartości 
skutecznych napięcia i prądu. Prąd i napięcie 
są ze sobą w fazie, przesunięcie miedzy 
prądem i napięciem wynosi 0°. Widać to na 
wykresie wektorowym, wektory prądu 
i napięcia pokrywają się.

Idealny rezystor o rezystancji R to 
taki, w którym zachodzi jedynie 
proces energetyczny, polegający 
na zamianie energii elektrycznej 
na ciepło.

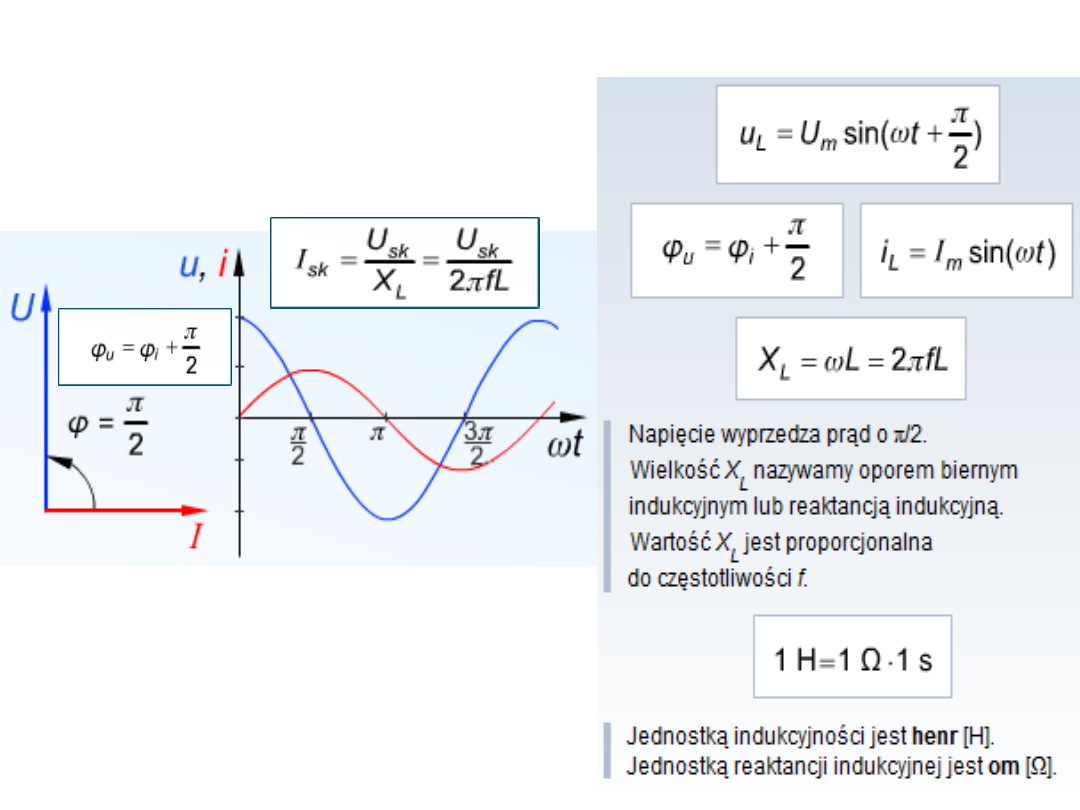
Obwody sinusoidalne z elementami R, 

L, C

Idealna cewka o 
indukcyjności L to taka, w 
której zachodzi jedynie 
proces energetyczny 
polegający na akumulacji 
energii w polu 
magnetycznym.

Dla idealnej cewki indukcyjnej spełnione 
jest prawo Ohma, które dotyczy wartości 
skutecznych napięcia i prądu.
Napięcie wyprzedza prąd o π/2 , 
przesunięcie między prądem i napięciem 
wynosi wynosi 90°, widać to na wykresie 
wektorowym, wektor napięcia jest 
prostopadły do wektora prądu.

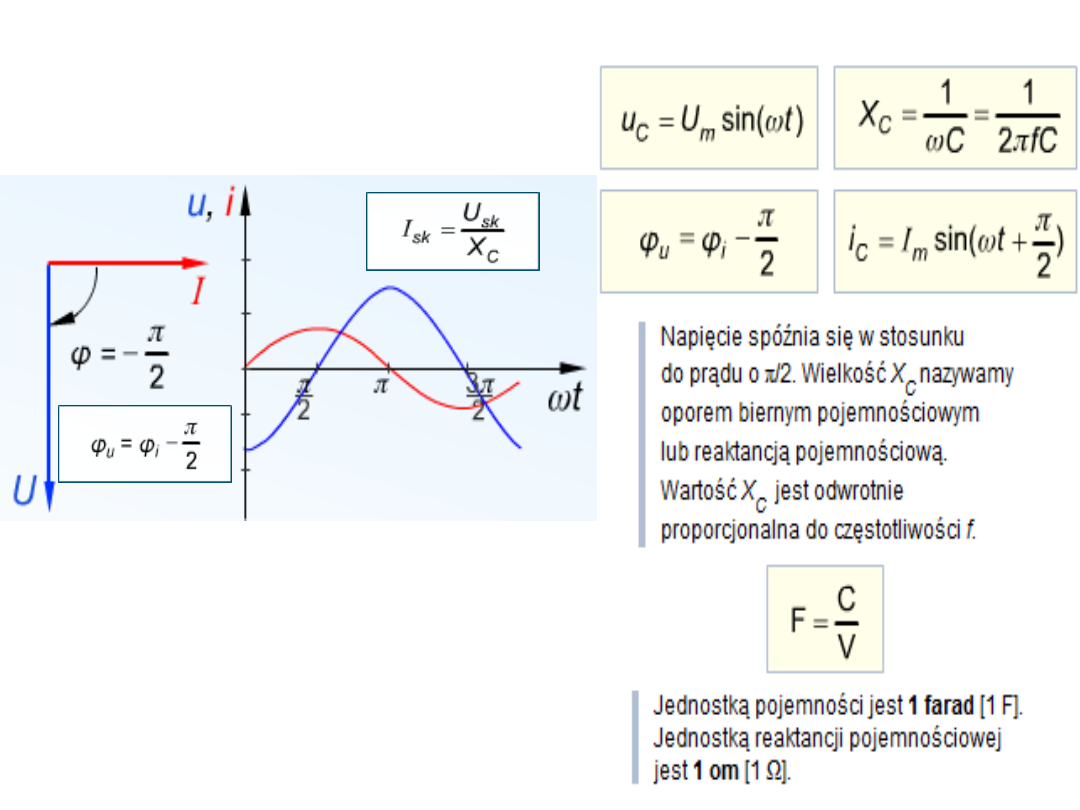
Obwody sinusoidalne z elementami R, 

L, C

Idealny kondensator o pojemności C 
to taki, w którym zachodzi jedynie 
proces 
gromadzenia energii w polu 
elektrycznym.

Dla idealnego kondensatora, spełnione 
jest prawo Ohma, które dotyczy wartości 
skutecznych napięcia i prądu. Napięcie 
spóźnia się w stosunku do prądu o  π/2, 
przesunięcie między prądem i napięciem 
wynosi -90°, widać to na wykresie 
wektorowym, wektor napięcia jest 
prostopadły do wektora prądu.

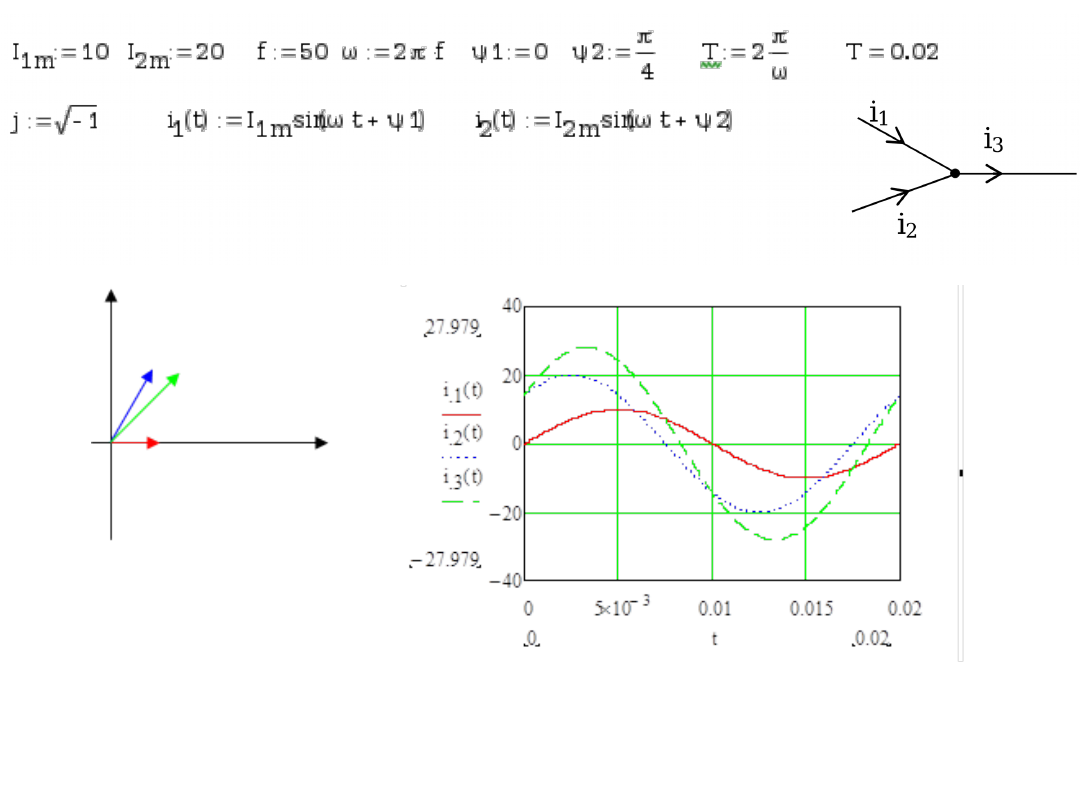
Ekran przedstawia symulacje w programie Mathcad I prawa Kirchhoffa. Obok wykresów po lewej 
stronie narysowano 3 wskazy odpowiadające (kolorystycznie) poszczególnym sinusoidom. Z 
rysunków tych wynika, że aby otrzymać wystarczające informację o prądzie i

3

(t) wystarczy dodać 

wskazy odpowiadające prądom i

1

(t) oraz i

2

(t). W elektrotechnice dla dodawania wektorowego 

wskazów wykorzystuje się metodę liczb zespolonych zwana metodą symboliczną.

METODA SYMBOLICZNA 

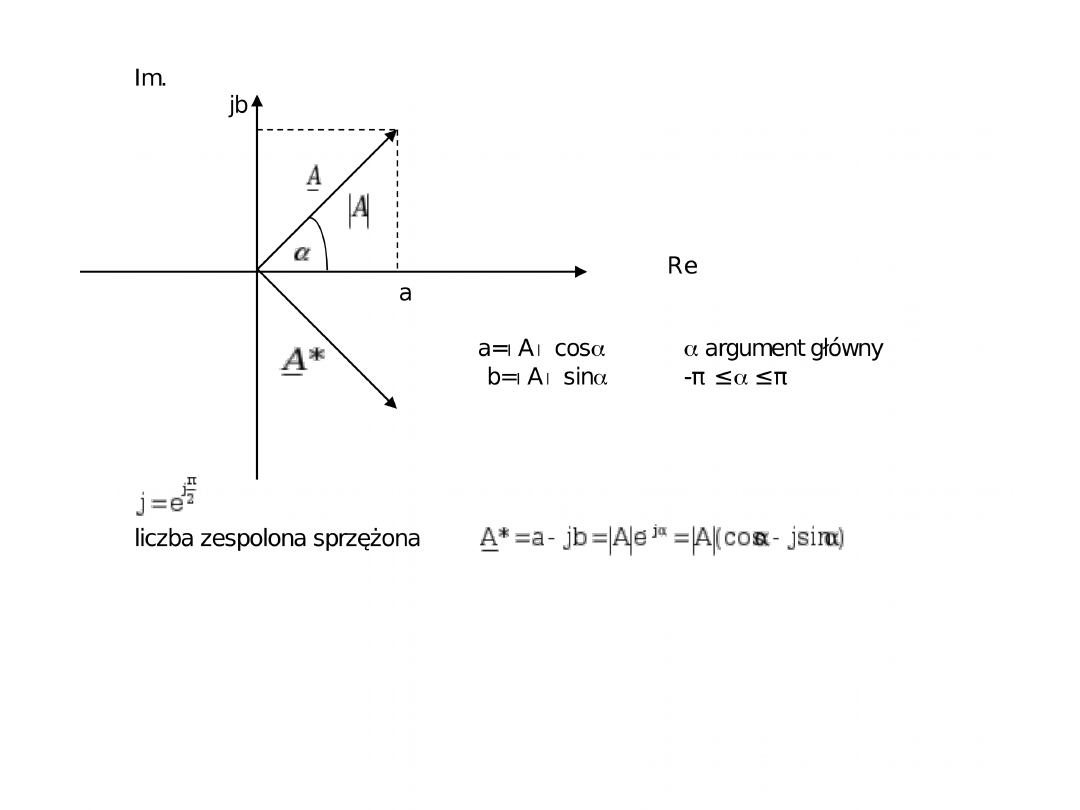
Układ współrzędnych dla liczb zespolonych składa się z dwóch osi: oś 
urojona  (oś rzędnych) oraz oś rzeczywista (oś odciętych). 

Działania na liczbach 

zespolonych:

W celu zastosowania metody symbolicznej do wyznaczenie sumy 
prądów ( lub napięć sinusoidalnych) przyjmujemy następującą 
zasadę zamiany funkcji sinusoidalnej na odpowiednik zespolony: 

















j

m

m

e

2

I

I

)

t

sin(

I

i(t)

Jak widać w wyrażeniu na prąd zespolony I znika wielkość t co 
odpowiada zatrzymaniu wskazu wirującego. W przyjętej zasadzie 
prąd zespolony I oparty jest na wartości skutecznej tzn. jego 
moduł będzie wartością skuteczną.

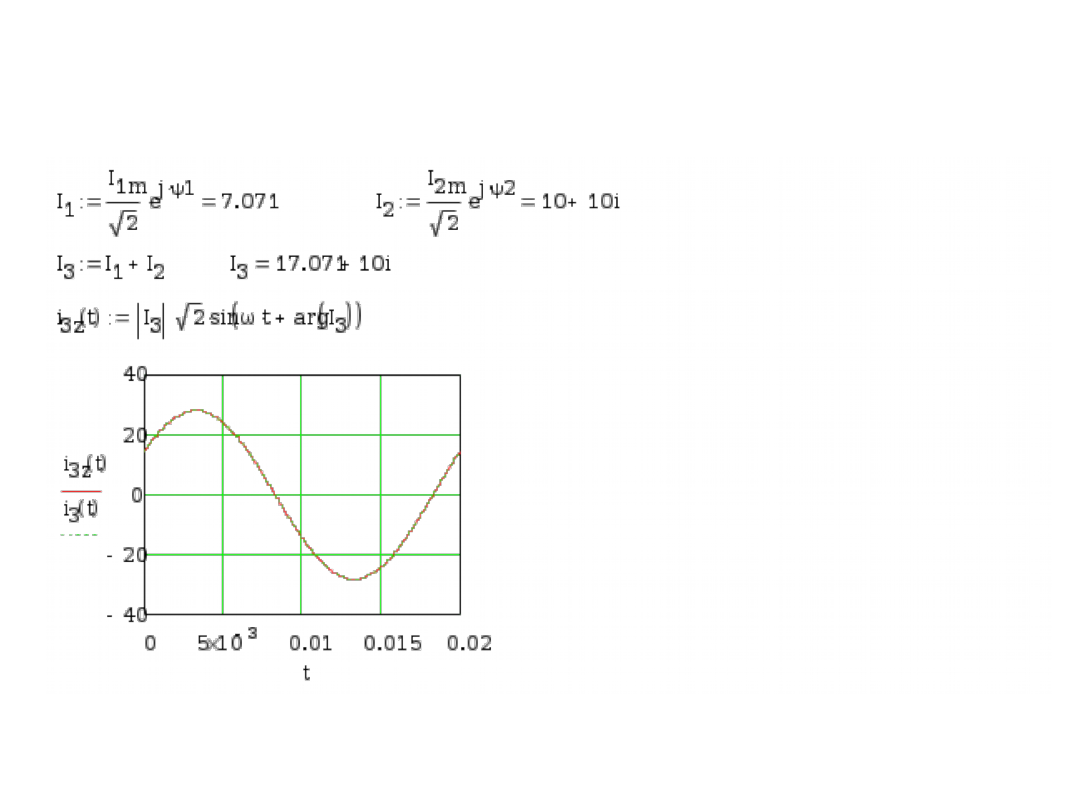
Kontynuacja przykładu z 

ekranu 273

Sposób wyznaczenia prądu 
sinusoidalnego będącego 
sumą dwóch składowych 
przedstawiono w programie 
Mathcad. Na podstawie 
otrzymanej liczby zespolonej 
I

3

 zdefiniowano funkcję 

sinusoidalną, którą nazwano 
i

3z

(t). Funkcję tą porównano z 

przebiegiem otrzymanym 
jako suma graficzna 
składowych sinusoid w 
ekranie 273. Jak widać 
otrzymano idealną zgodność 
co potwierdza poprawność 
metody symbolicznej.

Reaktancje zespolone

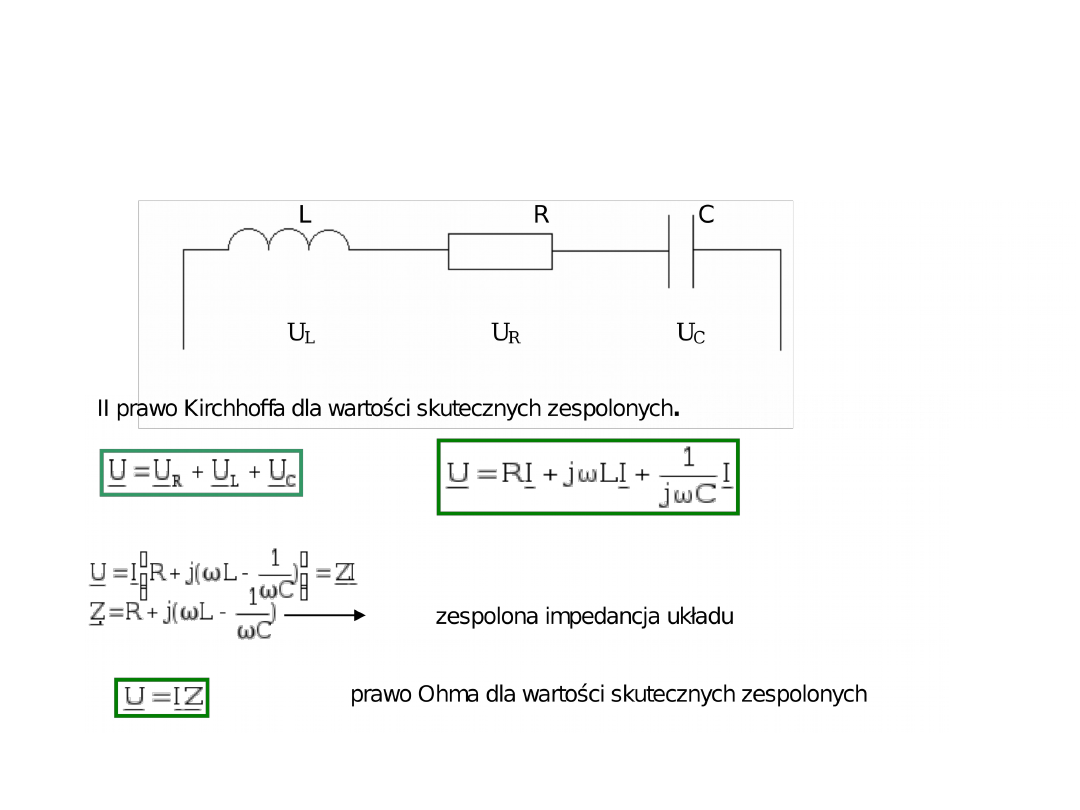
Zastosowanie metody 

symbolicznej na przykładzie 

obwodu szeregowego RLC

UWAGA: Wzór na połączenie szeregowe jest analogiczny jak w 
obwodach prądu stałego, ale może być zastosowany tylko w postaci 
zespolonej !!!

Sprawdź, że dla dowolnych liczb zespolonych mamy 

Z3

Z2

Z1

Z







Dzięki metodzie symbolicznej możemy prawa Kirchhoffa formułować  w 
postaci zespolonej. Dwójnik, który składa się z dowolnej kombinacji 
elementów R,L,C nazywamy ogólnie impedancją Z. Zwróć uwagę, że w 
powyższym przypadku mamy połączenie szeregowe trzech elementów co 
można zapisać:

C

j

1

L

j

R

X

X

R

3

Z

2

Z

1

Z

Z

c

L



























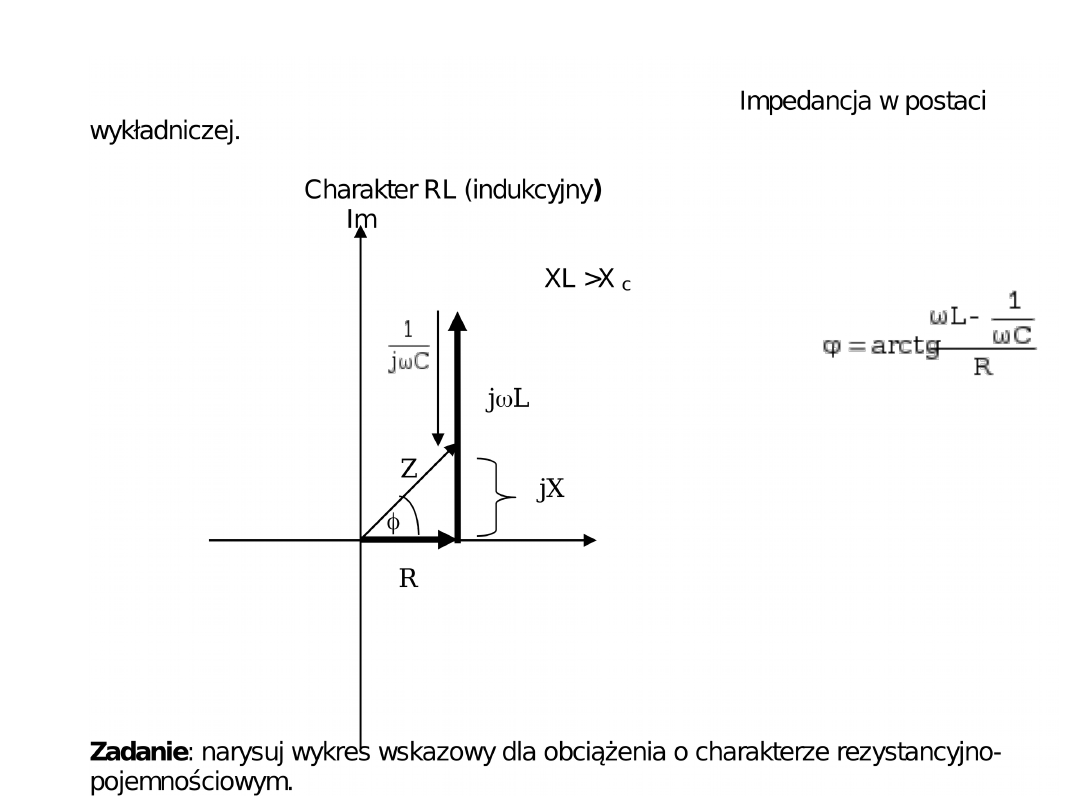
Charakter obciążenia 

Dowolne połączenie  elementów typu R,L,C zawsze daje impedancje 
zespoloną mającą część rzeczywistą i urojoną. Jeżeli część urojona jest 
dodatnia to mówimy, że odbiornik ma charakter rezystancyjno 
indukcyjny. Oznacza to, iż można dobrać takie parametry R,L, które dla  
danej pulsacji stanowiłyby dwójnik równoważny.
Odpowiedź:

     

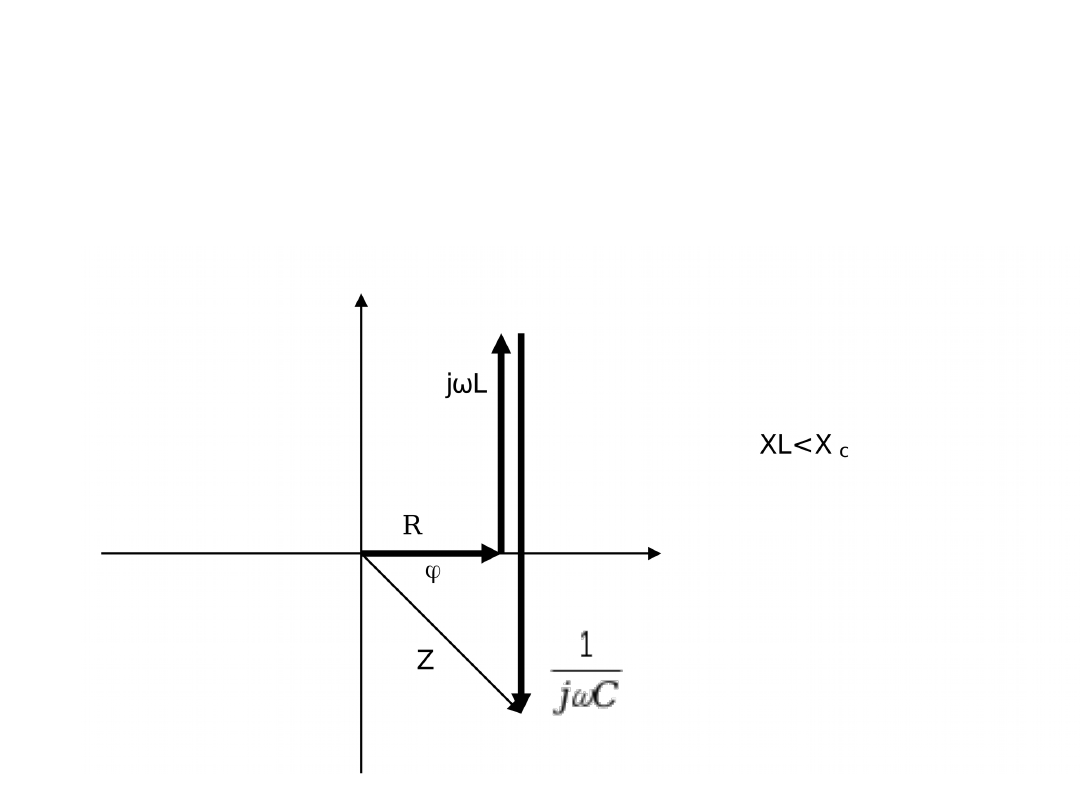
Charakter RC  (pojemnościowy)

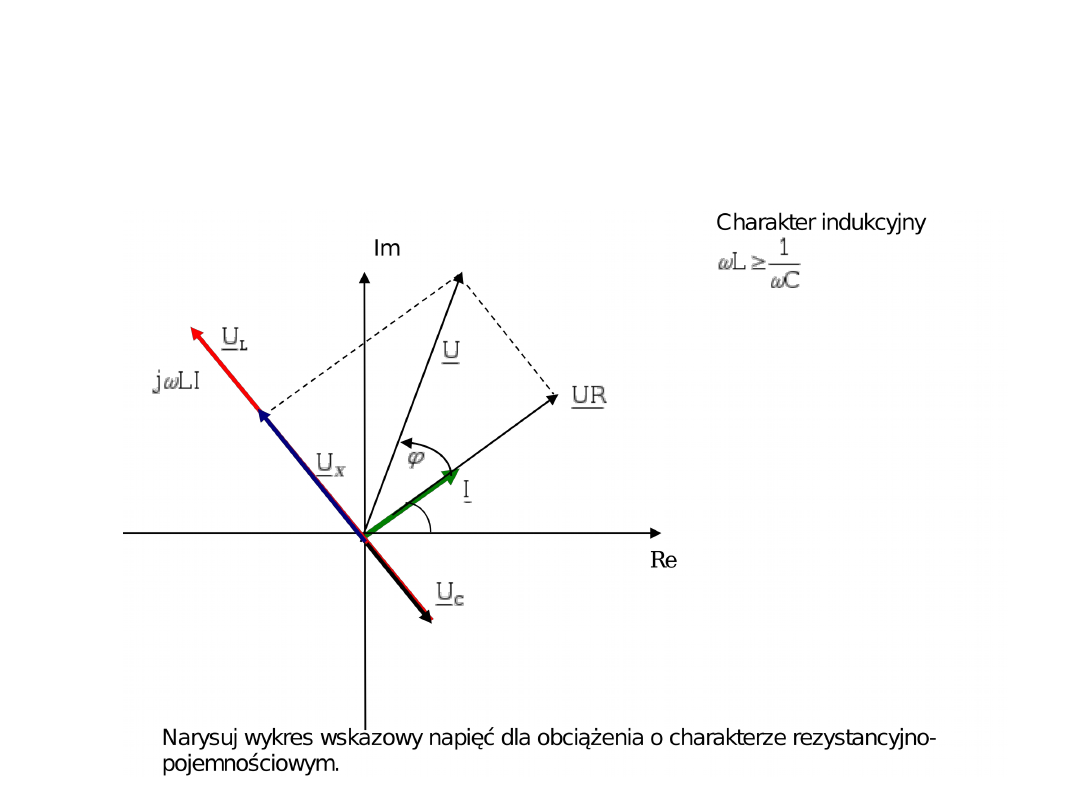
Wykres wskazowy napięć 

dla szeregowego 

połączenia RLC

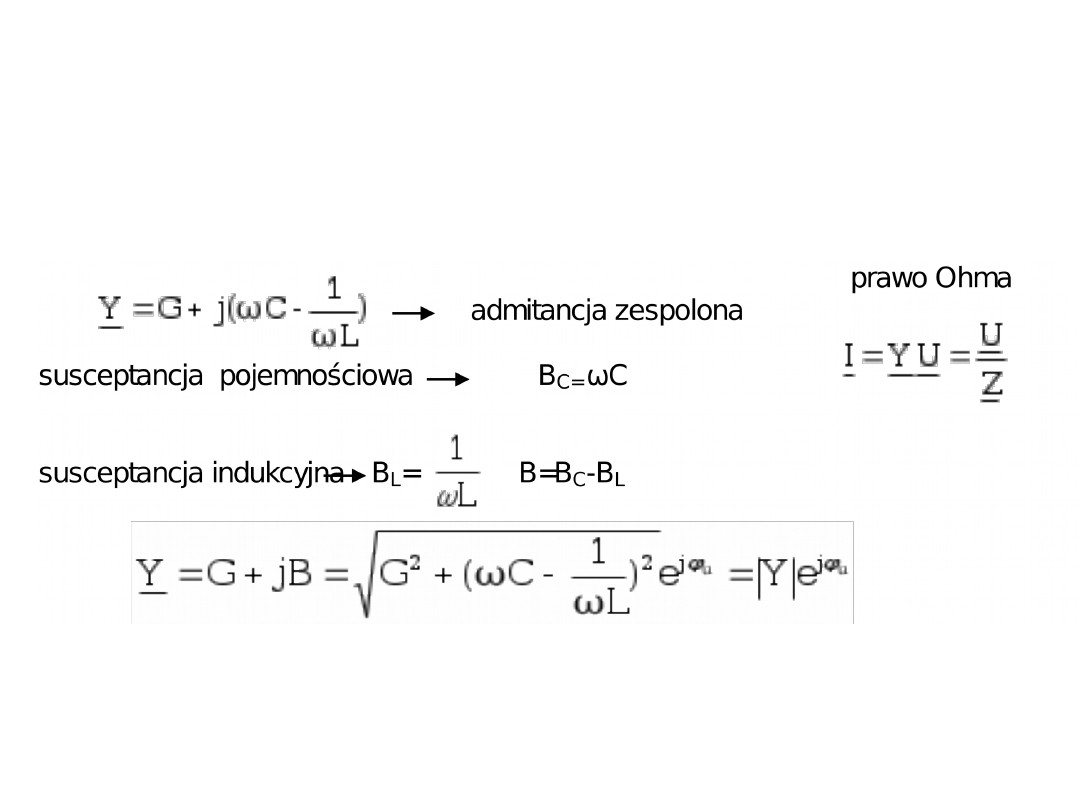
Powyższy wykres wskazowy warto zacząć rysować od prądu przy czym nie 
jest istotne pod jakim kątem go narysujemy w stosunku do osi realis 
(wskazy i tak wirują a my rysujemy ich układ dla dowolnie wybranej 
chwili). Natomiast napięcia musimy narysować zachowując zasadę 
odpowiednich przesunięć fazowych dla rezystancji indukcyjności i 
pojemności. 
 
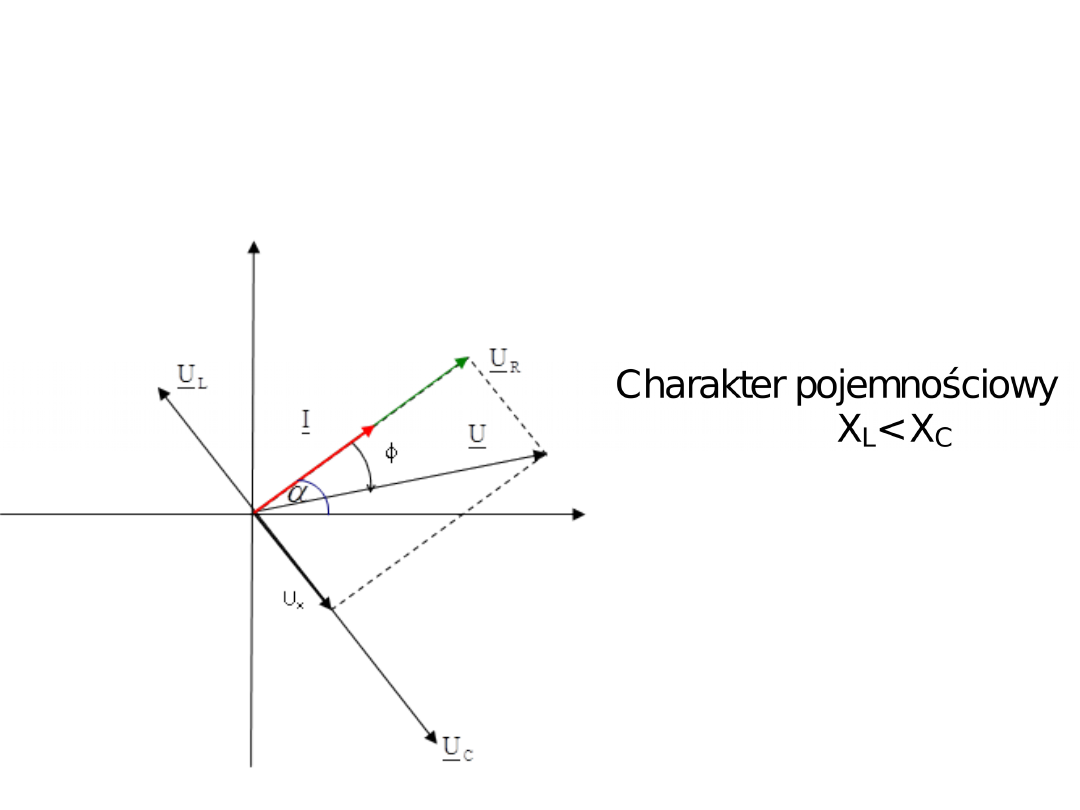
Odpowiedź: Wykres wskazowy dla charakteru pojemnościowego wygląda 
następująco:

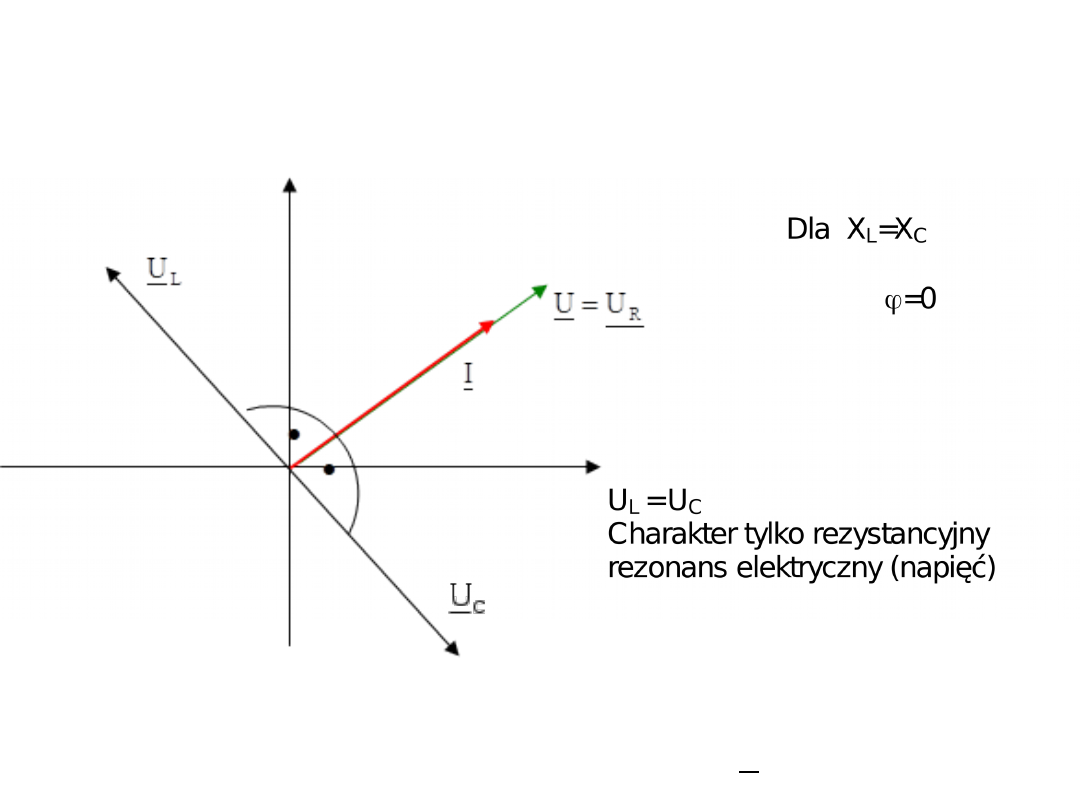
Przypadek szczególny- 

Rezonans napięć

Możliwa jest sytuacja kiedy obie reaktancje będą miały identyczne 
wartości co oznacza, że w sumie zespolonej zredukują się. Impedancja 
będzie miała wówczas tylko część rzeczywistą (Im{Z}=0).. Taki stan 
nazwiemy rezonansem szeregowym lub rezonansem napięć.

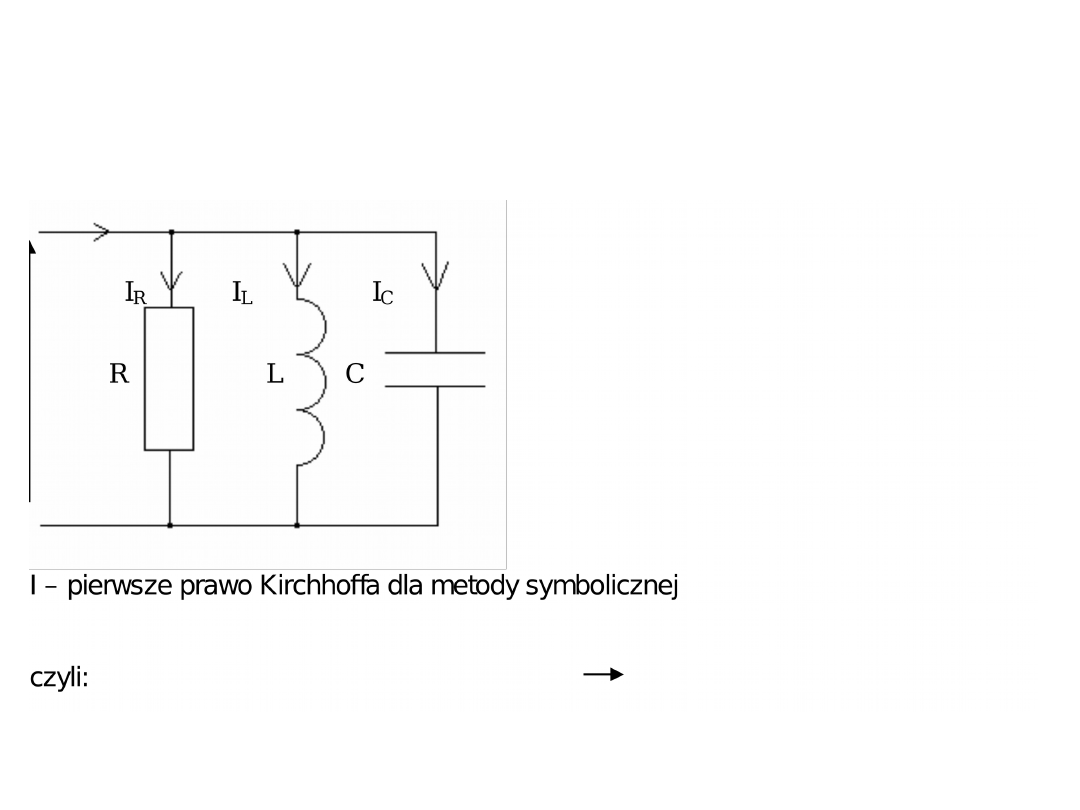
Zastosowanie metody 

symbolicznej: układ 

równoległy RLC

I

Zastosowanie metody 

symbolicznej: układ 

równoległy RLC

Zastosowanie metody 

symbolicznej: układ 

równoległy RLC

W teorii obwodów prądów zmiennych przez analogie do konduktancji 
definiuję się odwrotność reaktancji zwaną susceptancją oraz odwrotność 
impedancji zwaną admitancją.

Z

1

Y 

Zauważ że połączenie równoległe ma postać analogiczną jak w obwodach 
prądu stałego:

Y3

Y2

Y1

3

Z

1

2

Z

1

1

Z

1

Z

1

Y















UWAGA: Wzór na połączenie równoległe jest analogiczny jak w 
obwodzie prądu stałego, ale może być zastosowany tylko w 
postaci zespolonej !!!

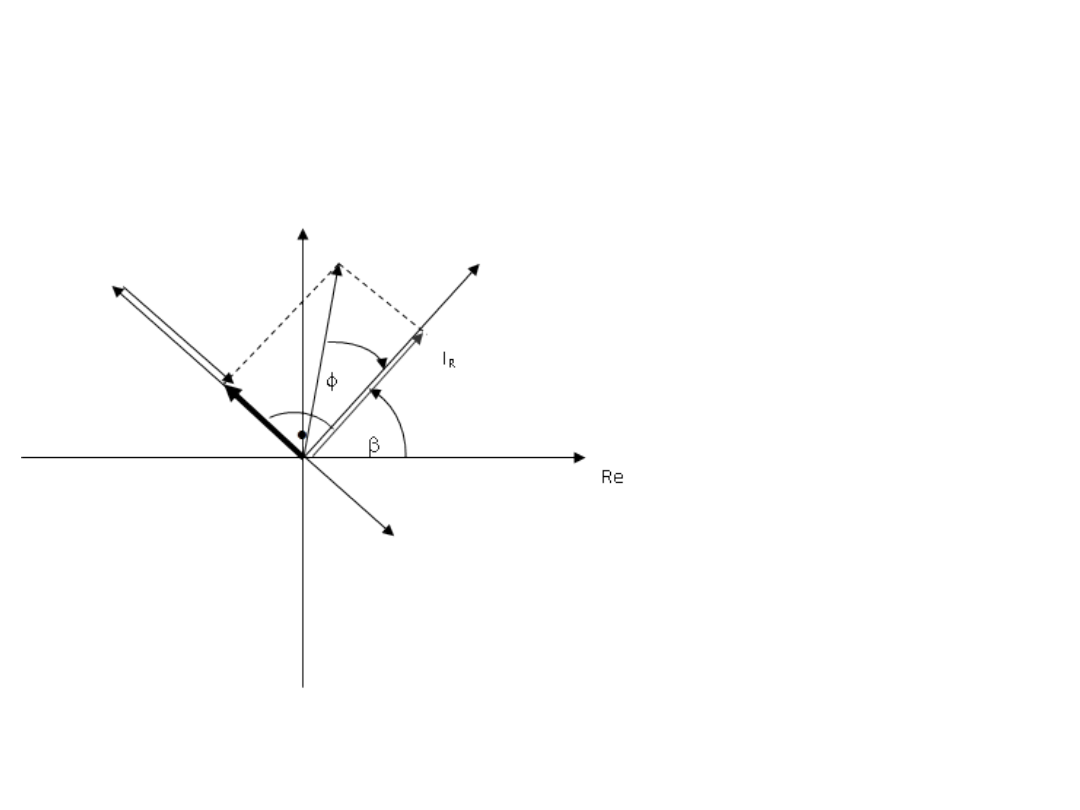
Wykres wskazowy dla 

układu równoległego RLC

0





 
Pytanie- jaki charakter miała impedancja wypadkowa dla powyższego 
przypadku?

Wykres wskazowy dla 

układu równoległego RLC

Tym razem powyższy wykres wskazowy warto zacząć rysować od 
napięcia przy czym nie jest istotne pod jakim kątem go narysujemy w 
stosunku do osi realis (wskazy i tak wirują a my rysujemy ich układ 
dla dowolnie wybranej chwili). Natomiast prądy musimy narysować 
zachowując zasadę odpowiednich przesunięć fazowych dla rezystancji 
indukcyjności i pojemności. 

Opowiedź: Ponieważ wykres wskazowy pokazuje, że prąd główny I 
wyprzedza ( o jakiś kąt ) napięcie zasilania oznacza to, że impedancja 
miała charakter rezystancyjno-pojemnościowy. 

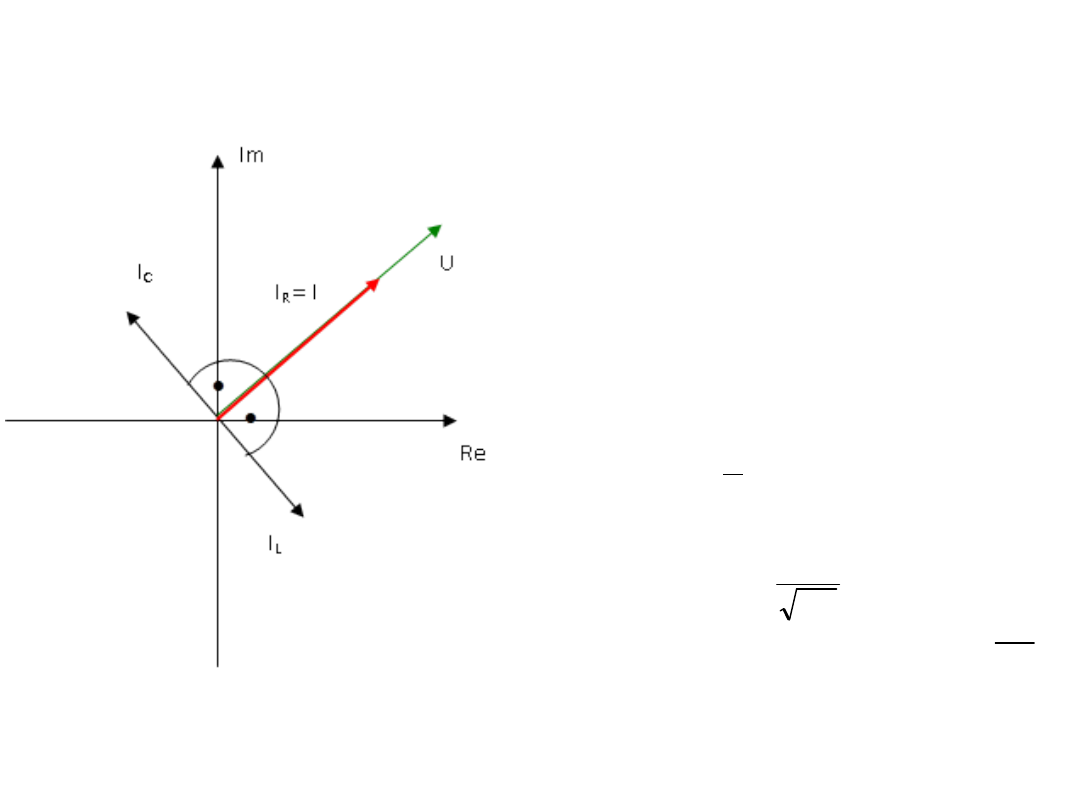
Rezonans równoległy 

(prądów)  I

x 

=0

Pytanie: Dla jakiej pulsacji w 
rozpatrywanym obwodzie nastąpi 
rezonans dla dwóch dowolnych 
wartości L,C?

Podobnie jak dla połączenia 
szeregowego w układzie 
równoległym może wystąpić 
sytuacja, w której wypadkowa 
admitancja nie będzie miała części 
urojonej (Im{Y}=0). W 
rozpatrywanym układzie sytuacja 
taka zajdzie również przy równych 
reaktancjach (X

c

=X

L

).

LC

1





C

1

L







Opowiedź: dla

. 

Wnika to z rozwiązania równania 

Uwaga: 

należy pamiętać, że pulsacja rezonansowa może mieć inny wzór dla 

różnych obwodów.