
„Mogę zapomnieć,
o czym usłyszałem,
albo zachować w
pamięci to,
co zobaczyłem.
To, co zrobiłem,
mogę zrozumieć.”
przysłowie chińskie

BRYŁY
OBROTOW
E
LEKCJA POWTÓRZENIOWA
Z MATEMATYKI
W KLASIE III GIMNAZJUM
opracowała mgr Grażyna
Brzeżańska
Gimnazjum nr 5 – Ruda Śląska
– 2004
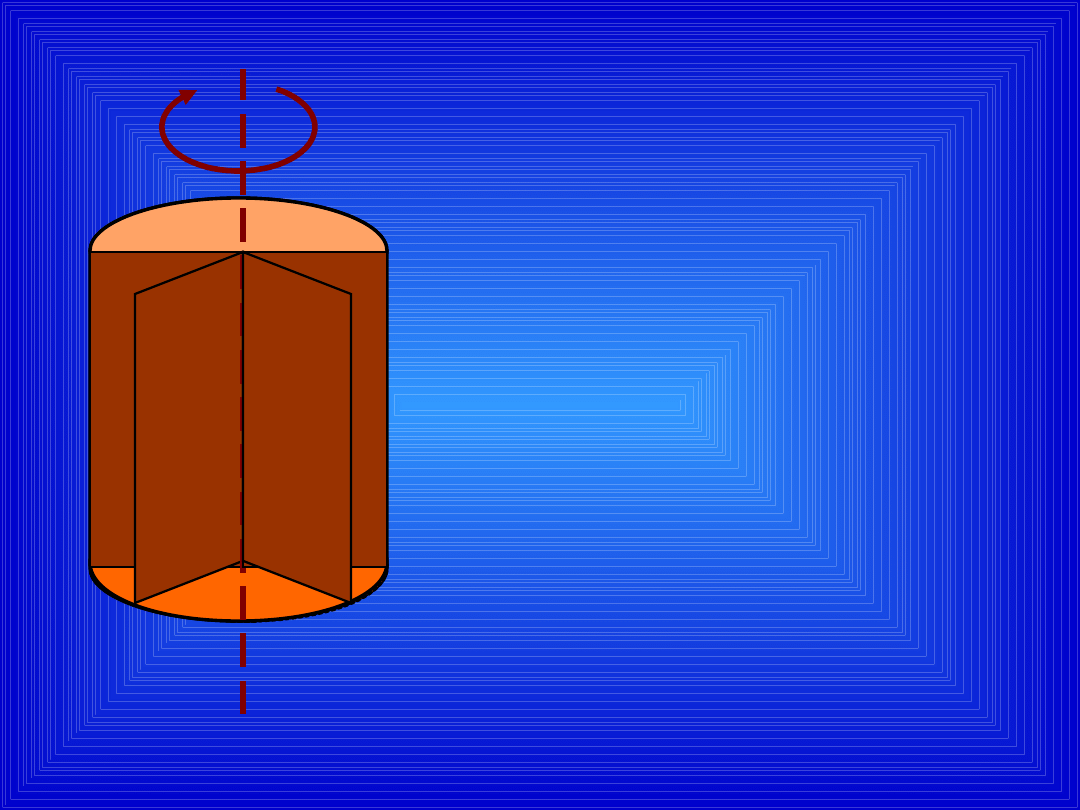
WALEC
powstaje
w wyniku
obrotu
prostokąta
wokół jednego
z boków
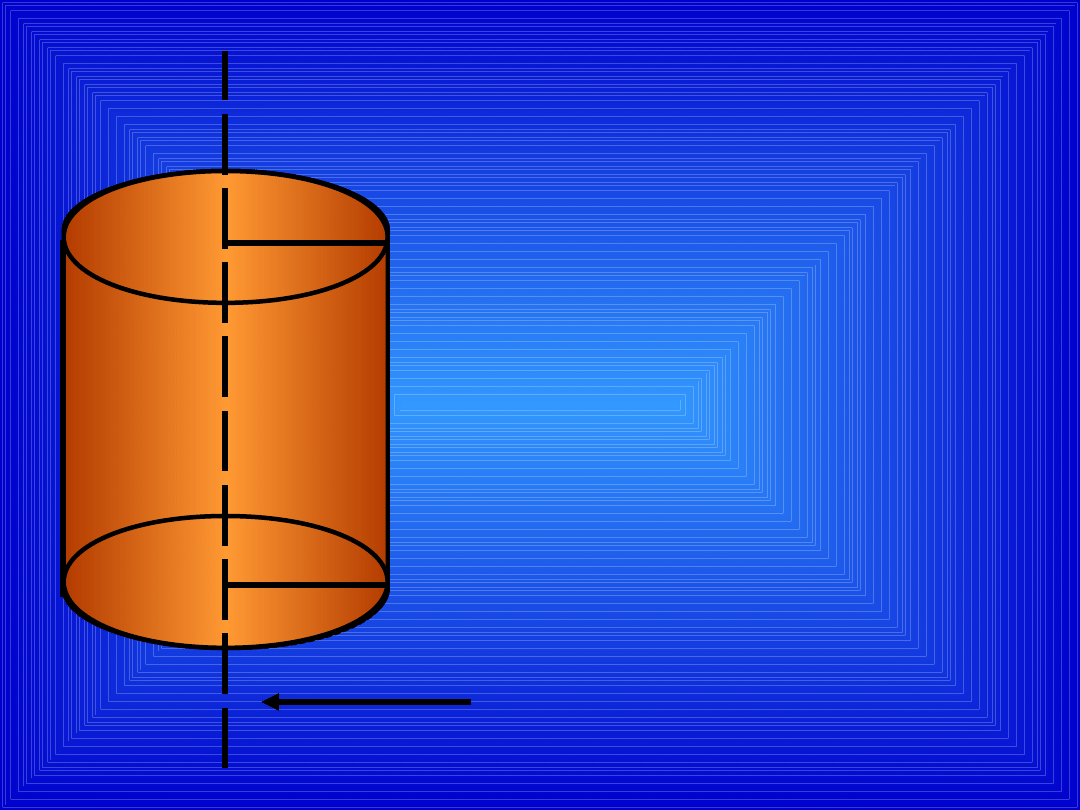
r
H
r
H
- promień
podstawy
- wysokość
walca
oś
obrotu
OPIS
WALCA
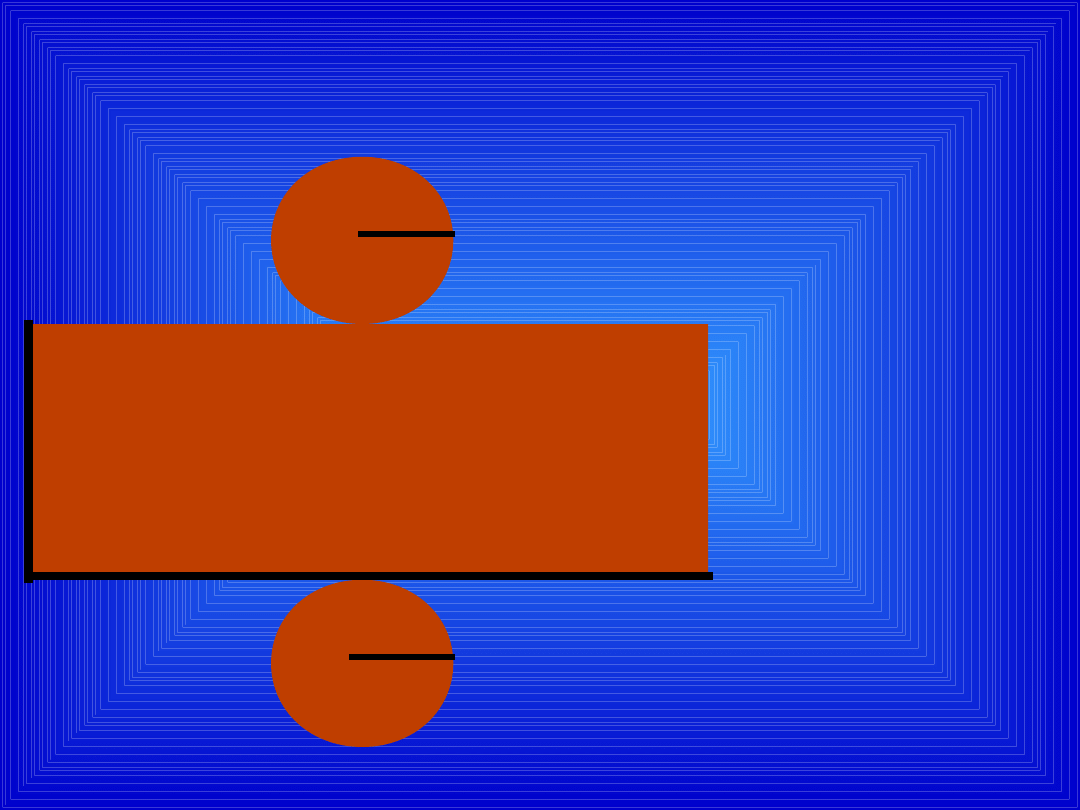
SIATKA
WALCA
r
H
2
r
P
b
= 2 r
H
P
p
= r
2
P
c
= 2 r
2
+
2 r H
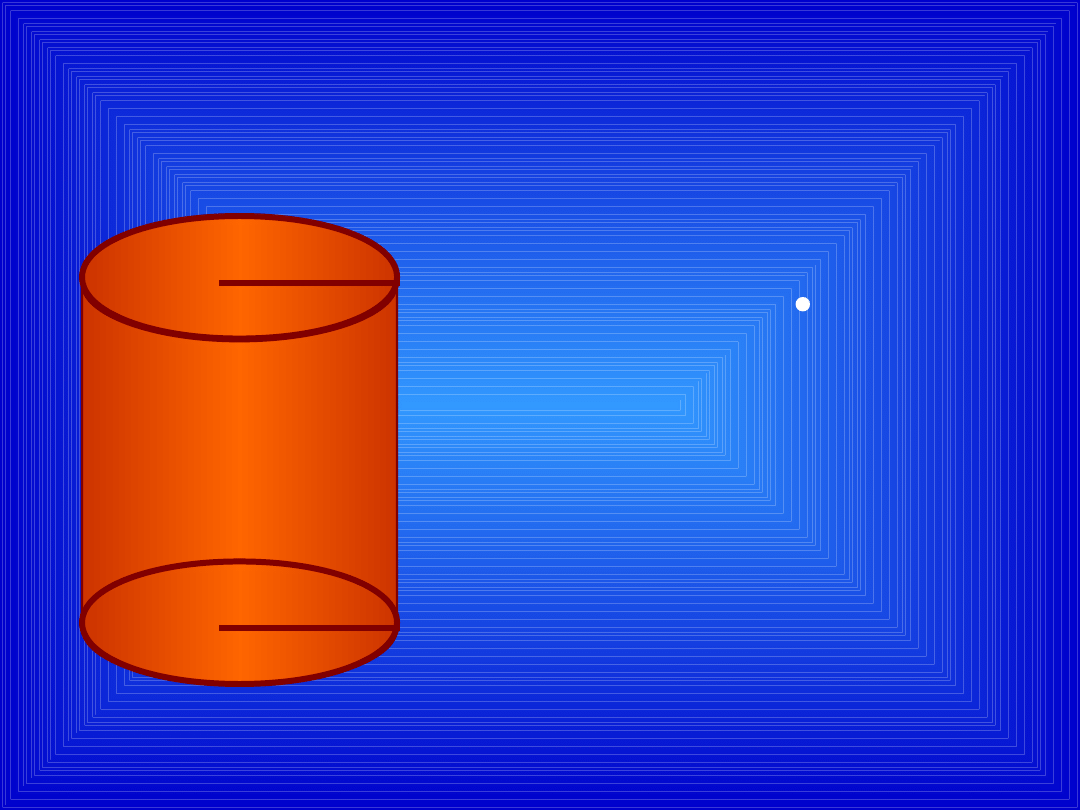
V
V
=
=
r
r
2
2
H
H
OBJĘTOŚĆ
WALCA
H
r
V
V
= P
= P
p
p
H
H
czyli
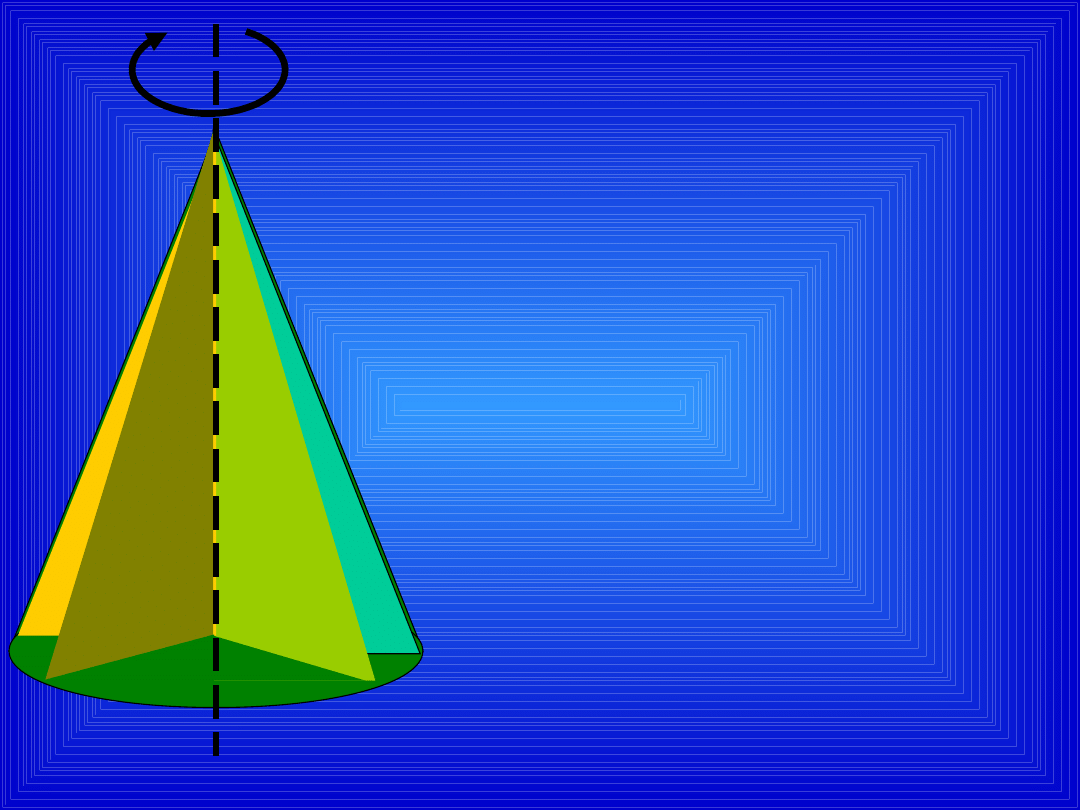
STOŻEK
powstaje w
wyniku obrotu
trójkąta
prostokątnego
wokół jednej
z
przyprostokątny
ch

H
r
H
r
l
l
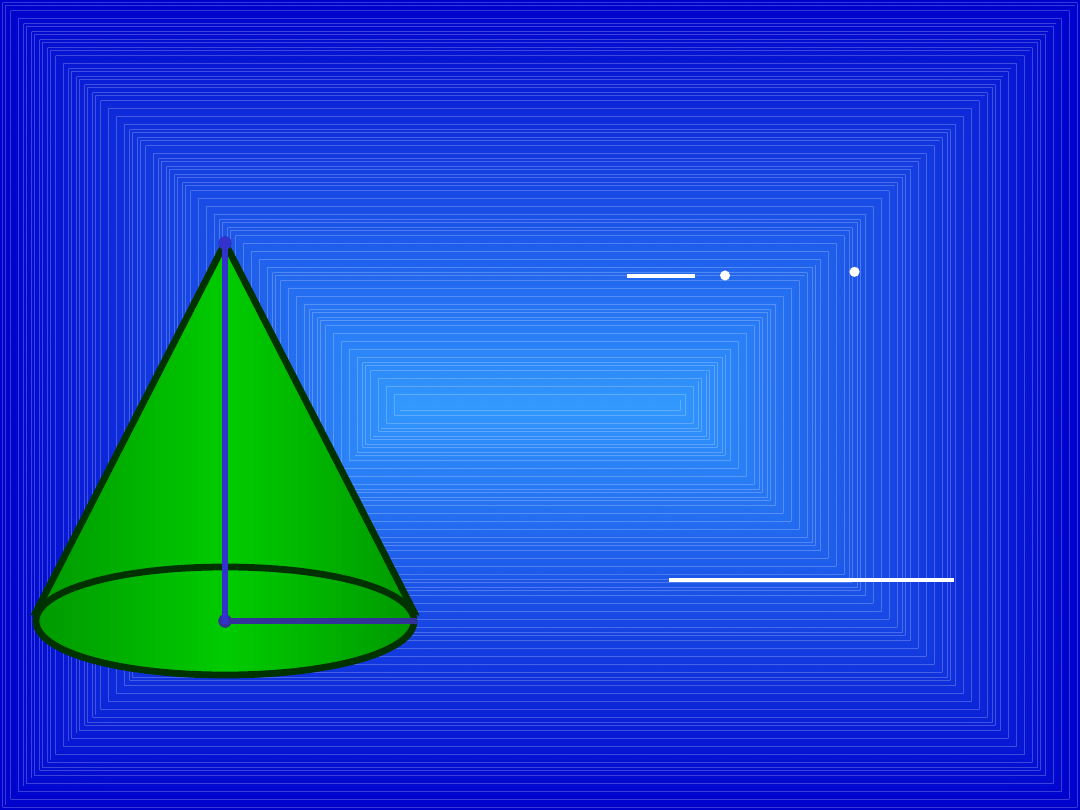
OPIS
STOŻKA
- promień
podstawy
- wysokość
stożka
- tworząca stożka
O
S
- spodek
wysokości
O
S - wierzchołek
stożka
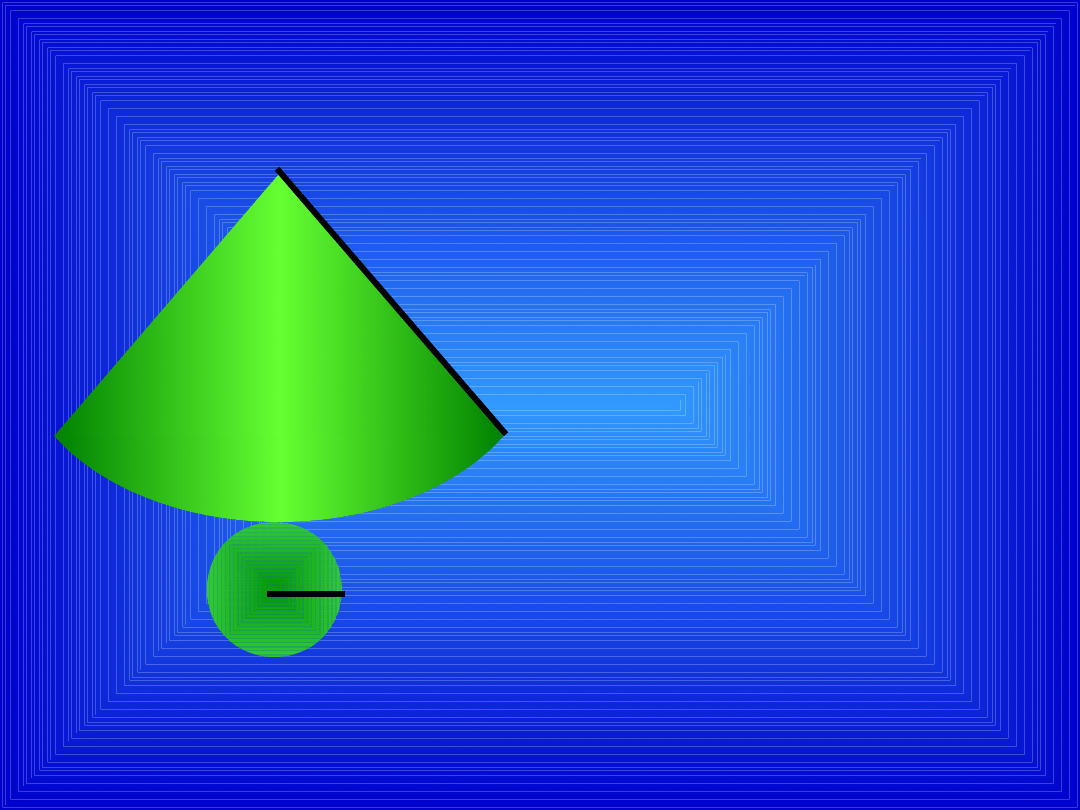
SIATKA
STOŻKA
r
l
P
p
=
r
2
P
c
=
r
2
+
r l
P
b
=
r l
OBJĘTOŚĆ
STOŻKA
V
V
=
=
r
r
2
2
H
H
3
H
r
V
V
=
=
P
P
p
p
H
H
1
3
czyli

KULA
powstaje
w wyniku
obrotu półkola
wokół średnicy
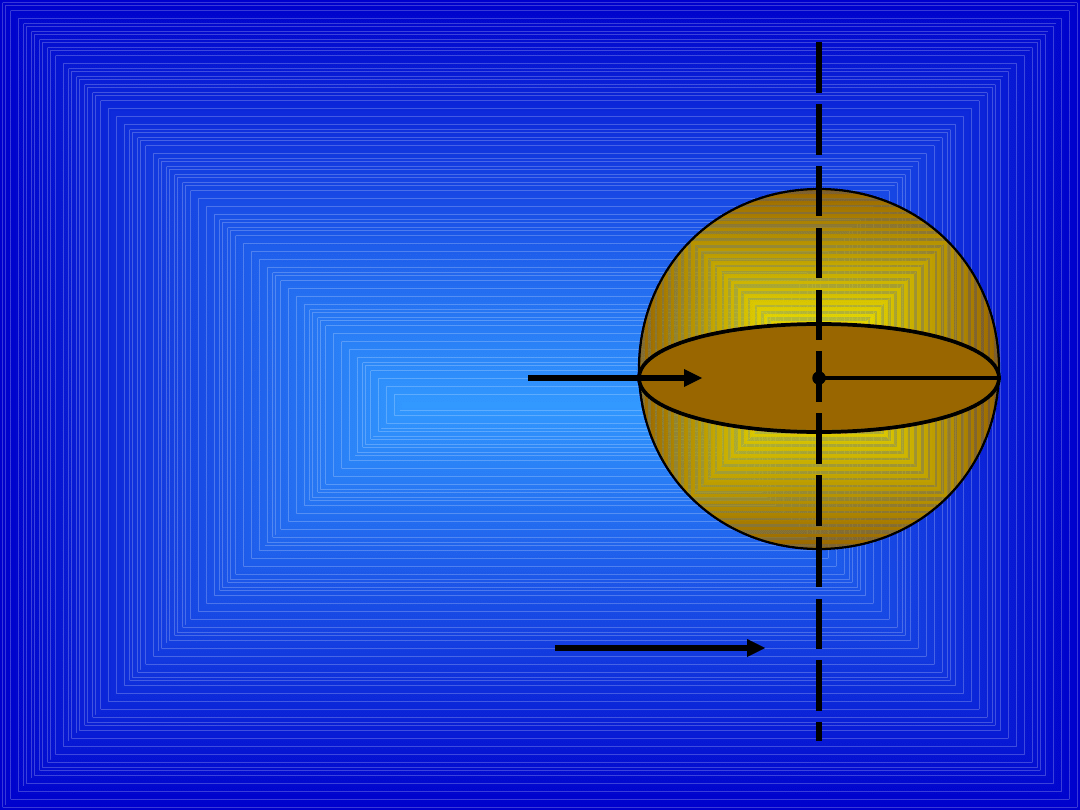
OPIS KULI
oś
obrotu
r
r
- promień
kuli
koło wielkie
kuli
S
S
- środek
kuli

POWIERZCHNIA
KULI
Powierzchnią kuli jest
sfera.
Według Archimedesa pole
powierzchni
kuli jest
4 razy
większe od pola
powierzchni
koła wielkiego kuli.
P
= 4
r
2

OBJĘTOŚĆ
KULI
Według Archimedesa
Według Archimedesa
objętość kuli jest
objętość kuli jest
4 razy
4 razy
większa
większa
od objętości
od objętości
stożka
stożka
,
,
którego
którego
podstawą jest
podstawą jest
koło wielkie kuli,
koło wielkie kuli,
a wysokością – promień
a wysokością – promień
kuli.
kuli.
r
r
V
V
= 4
= 4
•
•
r
r
2
2
•
•
r
r
3
czyli
V
=
4
3
•
r
3
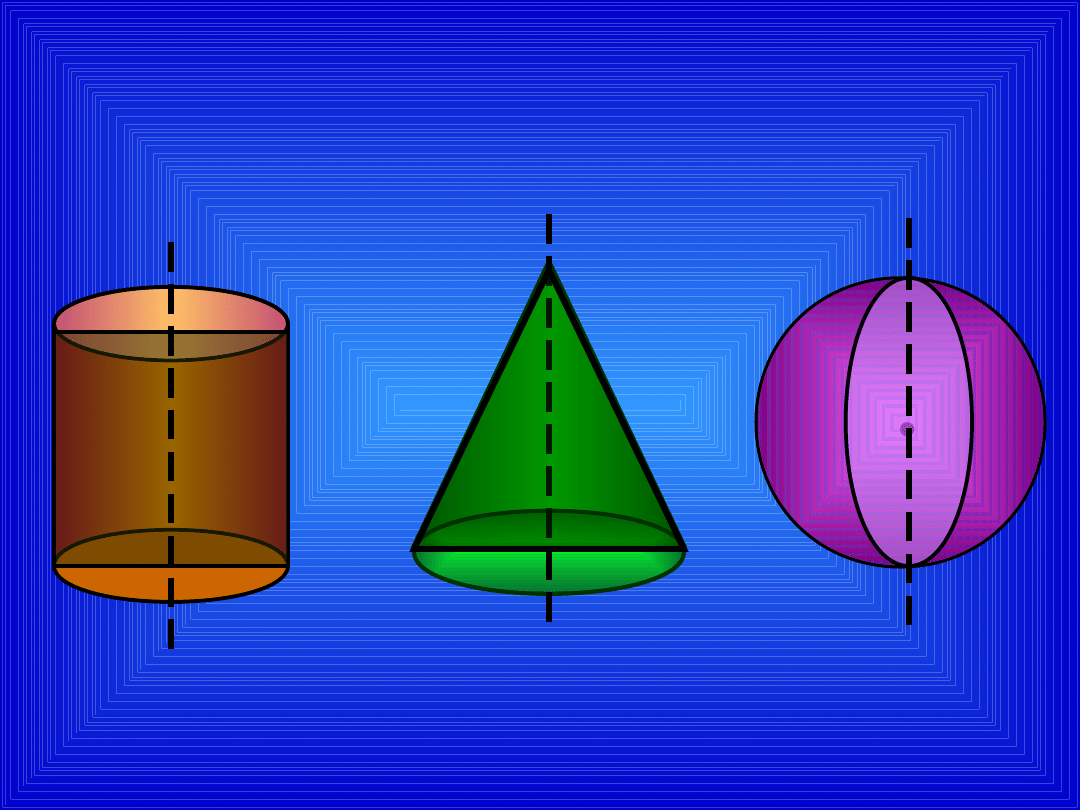
PRZEKROJE OSIOWE
prosto
kąt
koło
wielkie
trójkąt
równoramie
nny
kul
a
stoże
k
wale
c

SPRAWDŹ SWOJĄ WIEDZĘ
O BRYŁACH OBROTOWYCH
ZADANIE 1
ZADANIE 2
ZADANIE 3
ZADANIE 4
ZADANIE 5

ZADANIE 1
Uzupełnij zdania:
1) Walec powstaje w wyniku obrotu .....................
dookoła .............................................................
2) Odcinek łączący wierzchołek stożka z dowolnym
punktem na obwodzie koła to ............................
3) Przekrojem osiowym kuli jest ...........................
4) Wycinek koła jest powierzchnią boczną ...........
5) Powierzchnią kuli jest .......................................
KLIKNIJ
ZADANIE 2
Wykonaj proste obliczenia:
2) Pole powierzchni bocznej stożka
wynosi 10
cm
2
, a jego tworząca
ma długość 5 cm. Jaka jest długość
średnicy podstawy tego stożka?
3) Sfera kuli ma powierzchnię 36
cm
2
.
Jaka jest objętość tej kuli?
H
r
H
r
l
r
K
L
I
K
N
I
J
1)
Przekrój osiowy walca jest
kwadratem
o boku długości 10 cm.
Wyznacz pole
powierzchni bocznej tego
walca.
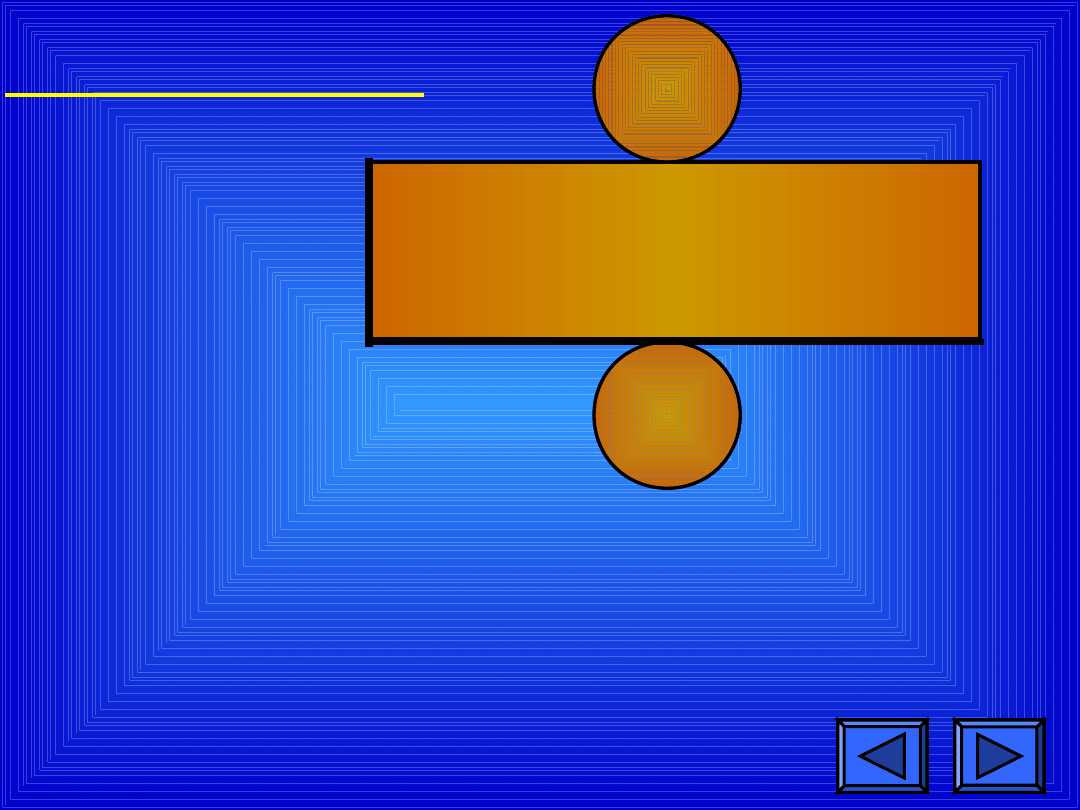
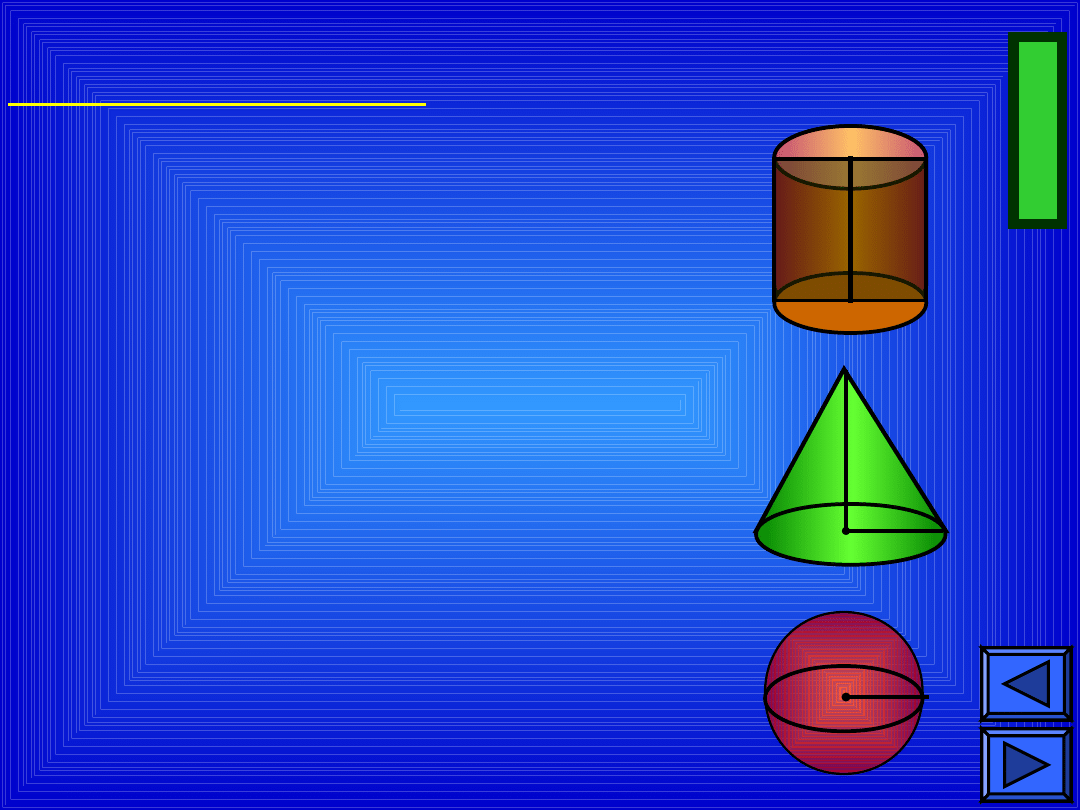
ZADANIE 3
0,5 dm
8
cm
Rysunek przedstawia siatkę pewnej bryły
obrotowej.
Jaką figurę przestrzenną otrzymasz po
sklejeniu tej
siatki? Oblicz jej objętość.
Odpowiednie dane odczytaj z rysunku.
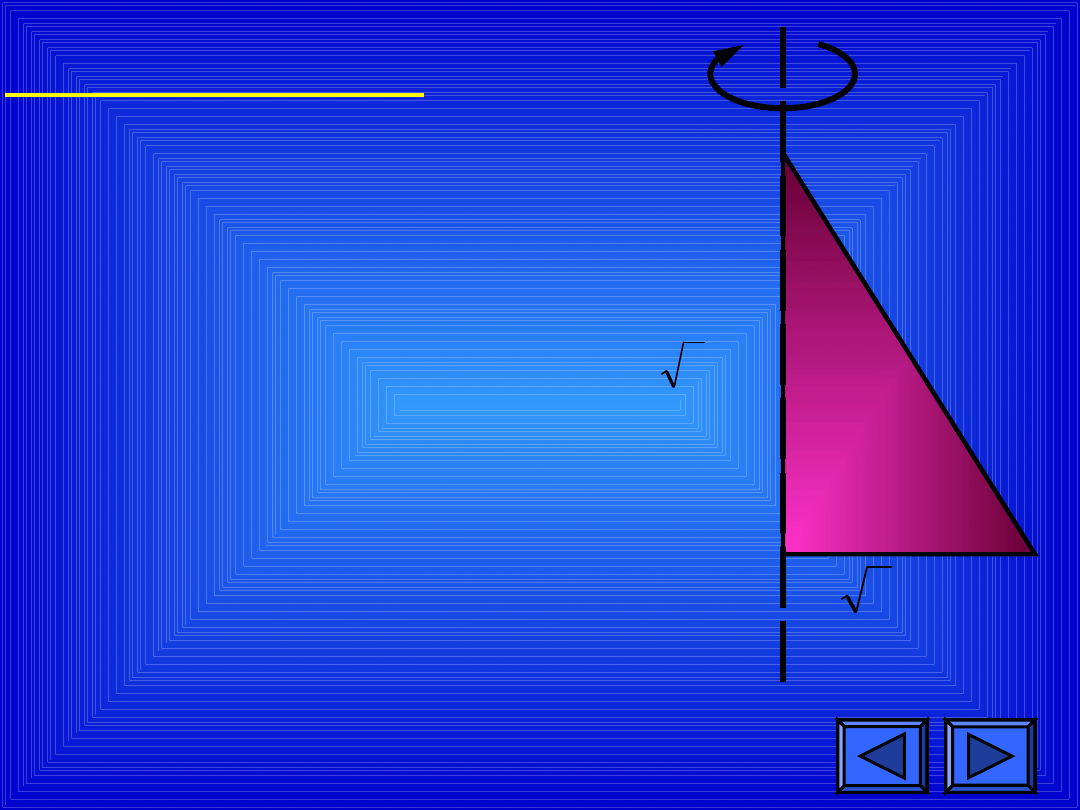
ZADANIE 4
Trójkąt prostokątny
obraca się wokół jednej
z przyprostokątnych.
2
cm
5
5
cm
Jaka bryła powstanie
w wyniku tego obrotu?
Oblicz pole jej powierzchni
bocznej.
Potrzebne dane odczytaj
z rysunku.
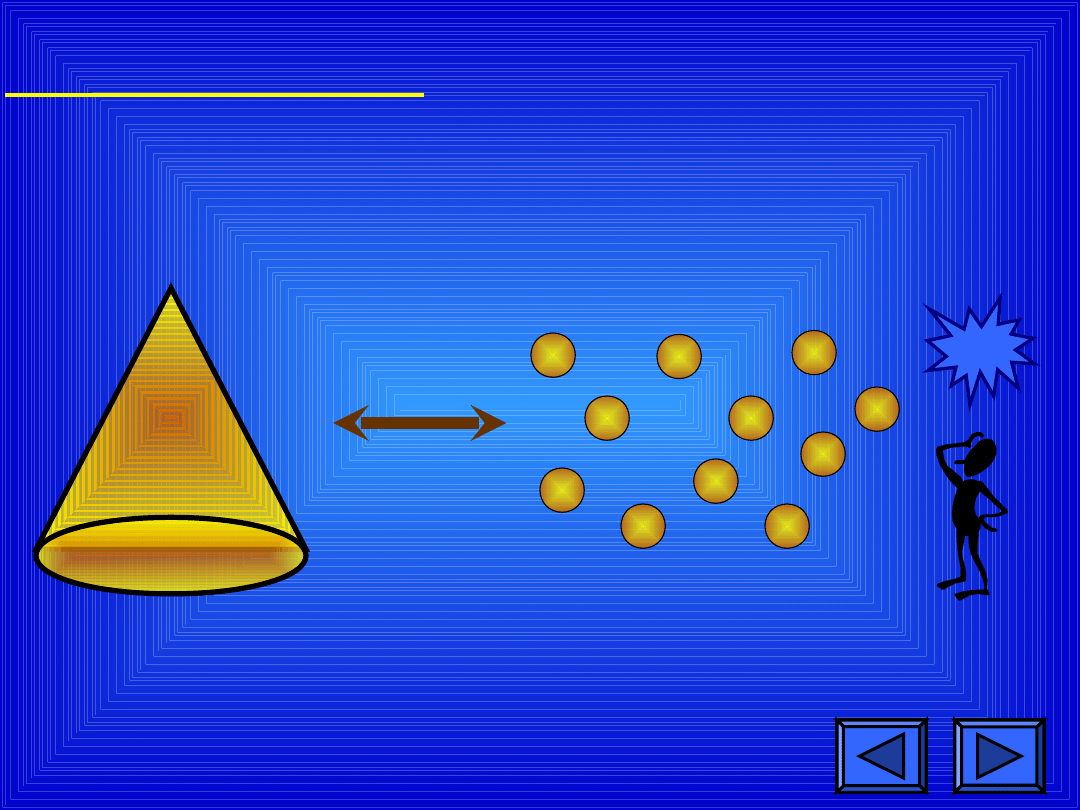
Mosiężny stożek o objętości
3,6
dm
3
przetopiono na kulki o
promieniu
3cm.
Ile takich kulek otrzymano?
wskazówka:
1dm = 10cm
1dm
3
= (10cm)
3
=
1000cm
3
?
WYNIKI
ZADANIE 5
MOŻESZ SPRAWDZIĆ WYNIKI
ZADAŃ RACHUNKOWYCH
ZADANIE 5
liczba kulek
= 100
ZADANIE 4
P =
cm
2
ZADANIE 3
V = 80 cm
3
ZADANIE 2
1) P
b
= 100 cm
2
2) r = 4 cm
3) V = 36
cm
3
5
5
KONIEC
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
Wyszukiwarka
Podobne podstrony:
Radioterapia VI rok (nowa wersja2)
bryły obrotowe powtorzenie - lekcja otwarta w III g, Matematyka dla Szkoły Podstawowej, Gimnazjum
Nowa wersja przykazań kościelnych, Gimnazjum i szkoła średnia
Bryły obrotowe cz II
Pytania na sprawdzian z komunikacji społecznej (nowa wersja)
BRYŁY OBROTOWE
Dyżury Szyman nowa wersja
Techniki badań politycznych - projekt nowa wersja, POLITOLOGIA
SBM nowa wersja
BRYŁY OBROTOWE rozwiązania
bryly obrotowe klasa3
BRYŁY OBROTOWE
PRZEWLEKŁA NIEWYDOLNOŚĆ NEREK NOWA WERSJA !!!
Wytyczne 2005 Resuscytacji Krążeniowo Oddechowej nowa wersja
Projekt IPP nowa wersja
więcej podobnych podstron