Prawdopodobieństwo

(Likelihood) rodowodów

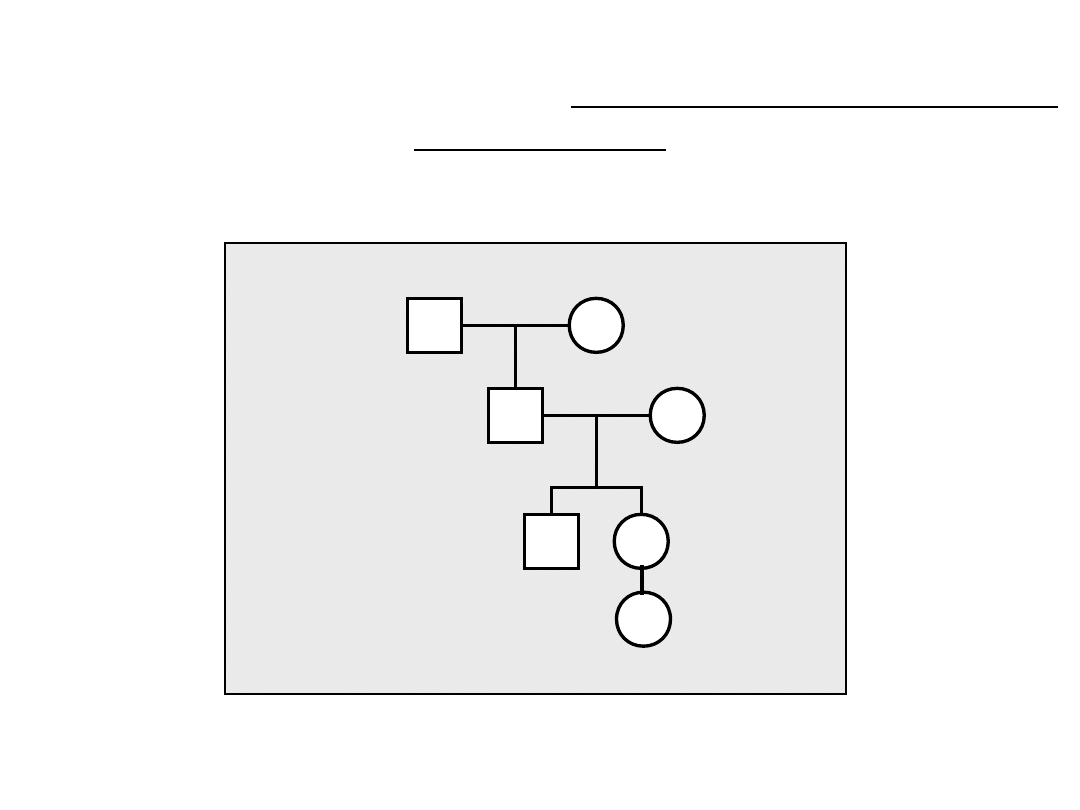
Prawdopodobieństwo (L) uzyskanych danych przy

założeniu określonego sposobu dziedziczenia i

określonego pokrewieństwa - dziedziczenie autosomalne

kodominujące

Oblicz prawdopodobieństwo poniższego rodowodu zakładając następujące

częstości markera: 1 –0,1; 2-0,2; 3-0,3.

3 4

1 2

1 3

1 1

1 1

1 3

2 x 0.1 x 0.2

2 x 0.3 x 0.4

0.1

2

0.5 x 0.5

0.5 x1

0.5 x 1

L= 2x0.1x0.2 x 2x0.3x0.4 x 0.5x0.5 x 0.1

2

x 0.5x1 x 0.5x1 x0.5x0.2

1 2

0.5 x

0.2

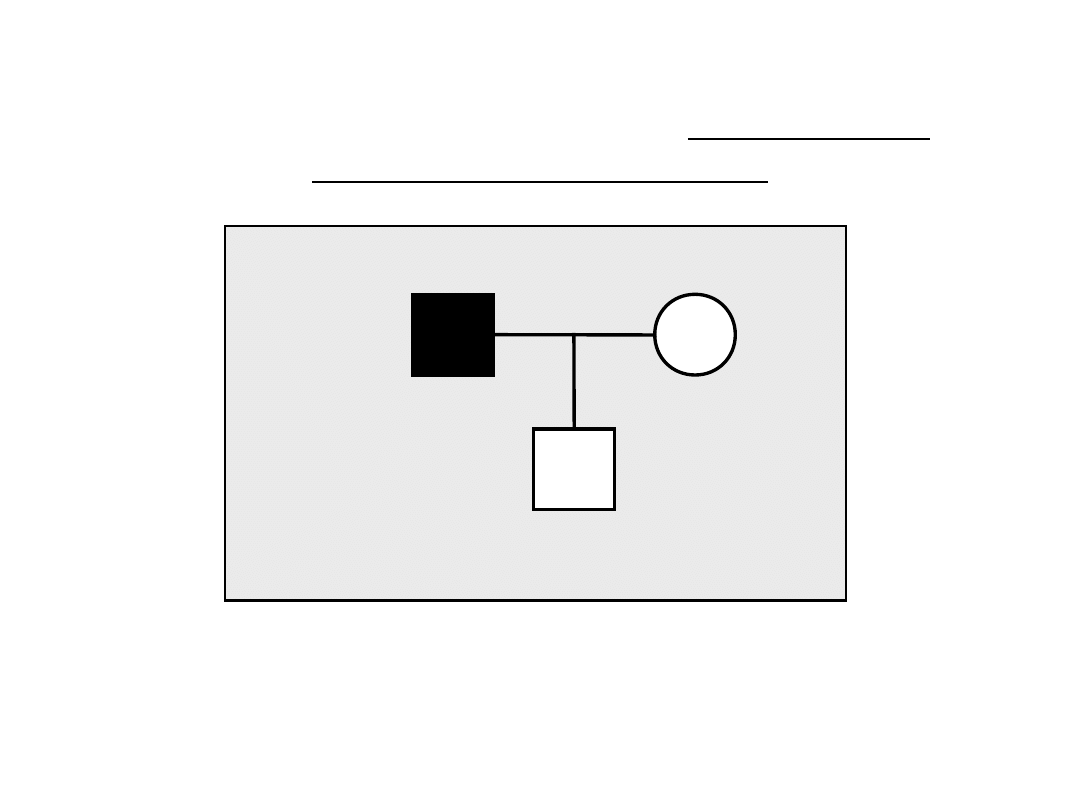
Prawdopodobieństwo (L) uzyskanych danych przy

założeniu określonego sposobu dziedziczenia i

określonego pokrewieństwa - dziedziczenie

autosomalne dominujące

d

2

2x D x d

0.5

1

L = 2Dd x d

2

x 0.5 x 1

Dd

dd

dd

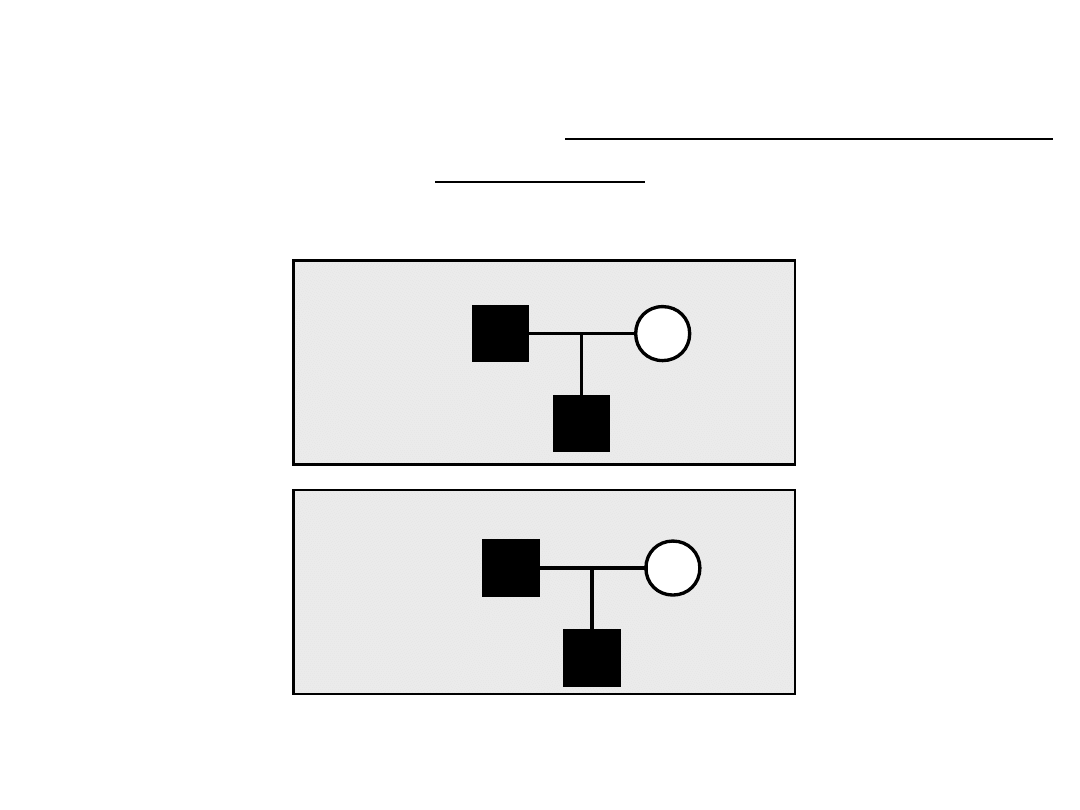
dD

dd

dD

DD

dd

dD

Prawdopodobieństwo (L) uzyskanych danych przy

założeniu określonego sposobu dziedziczenia i

określonego pokrewieństwa - dziedziczenie autosomalne

dominujące

Oblicz L przyjmując dziedziczenie autosomalne dominujące, 100%

penetrację i częstość zmutowanego genu w populacji = D

d

2

2x D x d

0.5

1

d

2

D

2

1

1

L = 2Dd x d

2

x 0,5 + D

2

x d

2

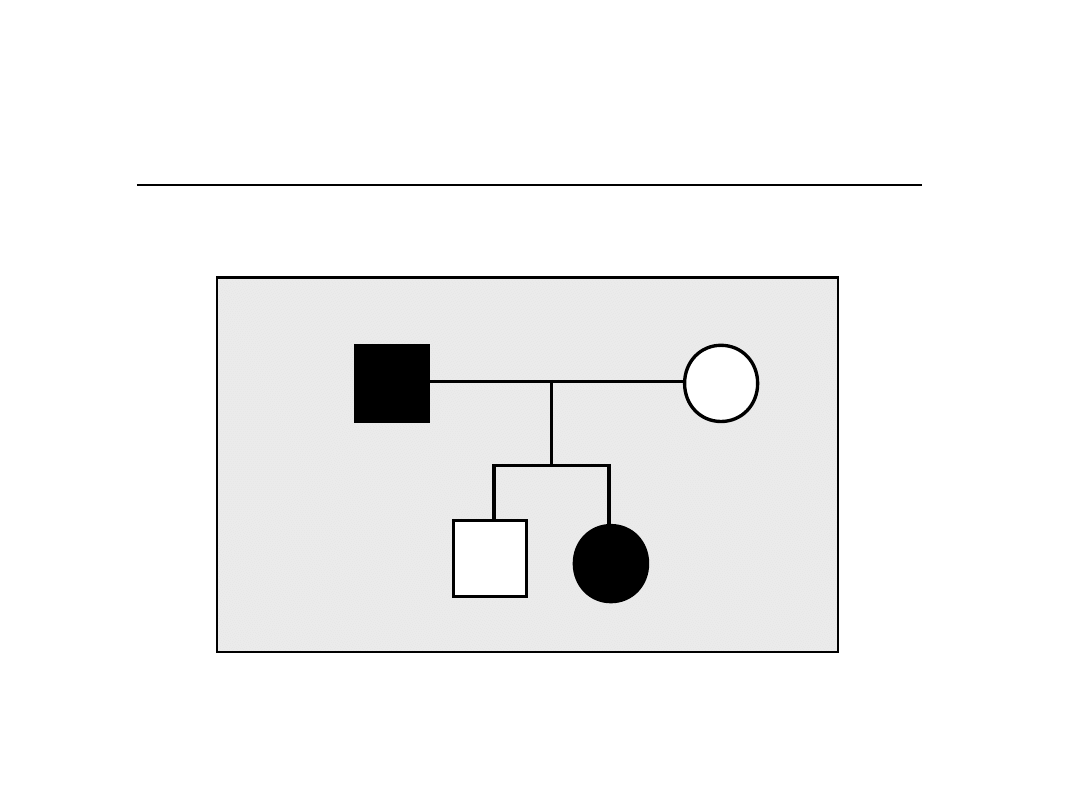
Prawdopodobieństwo (L) uzyskanych danych przy

założeniu określonego sposobu dziedziczenia i określonego

pokrewieństwa -

dziedziczenie dominujące sprzężone z płcią

Oblicz L przyjmując dziedziczenie dominujące sprzężone z płcią, 100%

penetrację

i częstość zmutowanego genu w populacji – D

d

2

D x 1

1

1

1

L = D x d

2

x 1 x 1

DY

dd

Yd

Dd

L (Likelihood) jest zazwyczaj

bardzo małą liczbą

Małe liczby wygodniej jest zapisywać
w formie logarytmu

np..:

0.000 000 001=10

-9

Log

10

10

-9

= -9

Prawdopodobieństwo

policzone j.w. samo w

sobie nie jest przydatne !

Ale gdy jest policzone dla

różnych hipotez, pozwala

na ich względne

porównanie.

Porównanie wykonuje się

obliczając iloraz

prawdopodobieństw dwóch

porównywanych hipotez.

Iloraz ten zwyczajowo nazywa

się parametrem LR – likelihood

ratio

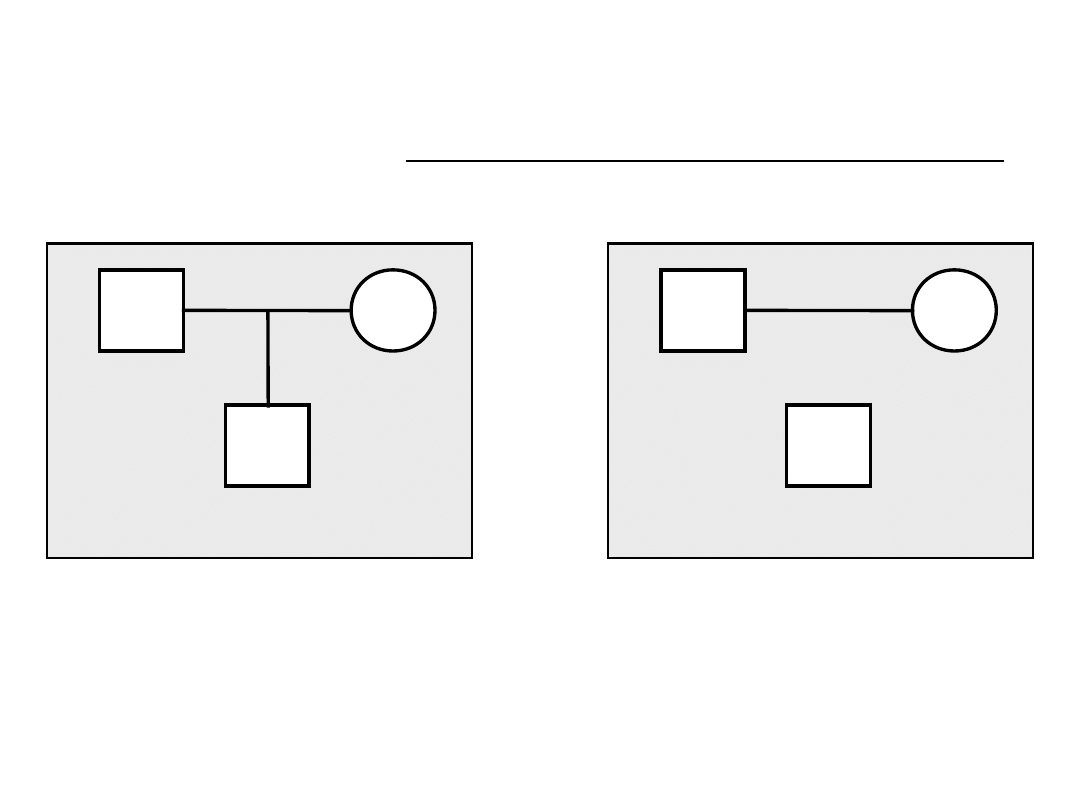
Iloraz prawdopodobieństw (LR) uzyskanych danych

przy założeniu dziedziczenie autosomalne

kodominującego i dwóch wariantów pokrewieństwa

Częstości markera: 1 –0,1; 2-0,2; 3-0,3.

3 4

1 2

1 3

3 4

1 2

1 3

L1 = 2x0,1x0,2 x 2x0,3x0,4 x 0,5x0,5

L2 = 2x0,1x0,2 x 2x0,3x0,4 x

2x0,1x0,3

LR=L1/L2 = 0,5x0,5

/

2x0,1x0,3 = 6,25

Wniosek:

Jest 6,25 razy bardziej prawdopodobne, że II1 jest dzieckiem I1 i I2

niż, że jest osobą niespokrewnioną z I1 i I2

I

I

II

II

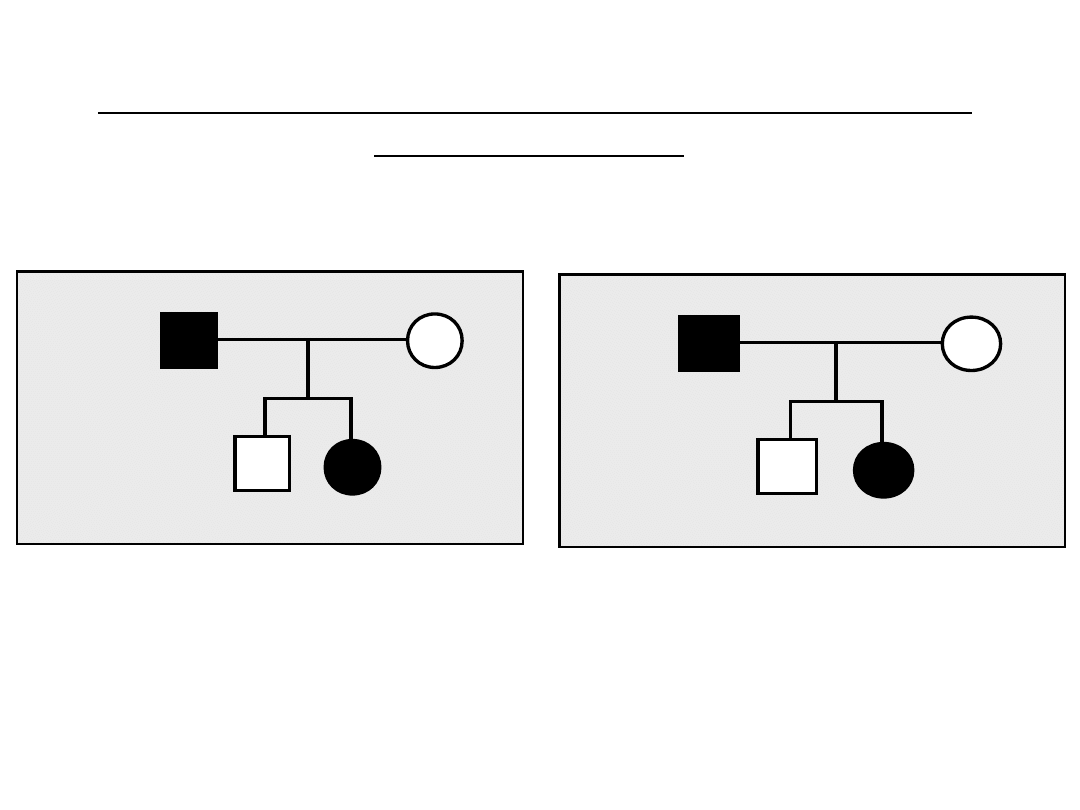
Iloraz prawdopodobieństw uzyskanych danych (LR)

przy założeniu dziedziczenia

autosomalnego dominującego vs. dominującego

sprzężone z płcią

L2 = D x d

2

L1 / L2 = 0,5 d ~ 0,5

Dominujące

sprzężone z płcią

d

2

D x 1

1

1

DY

dd

1

d

2

2x D x d

0,5

1

Dd

dd

0,5

L1 = 2x D x d x d

2

x 0,5 x 0,5

Autosomalne

dominujące

dd

Dd

dY

Dd

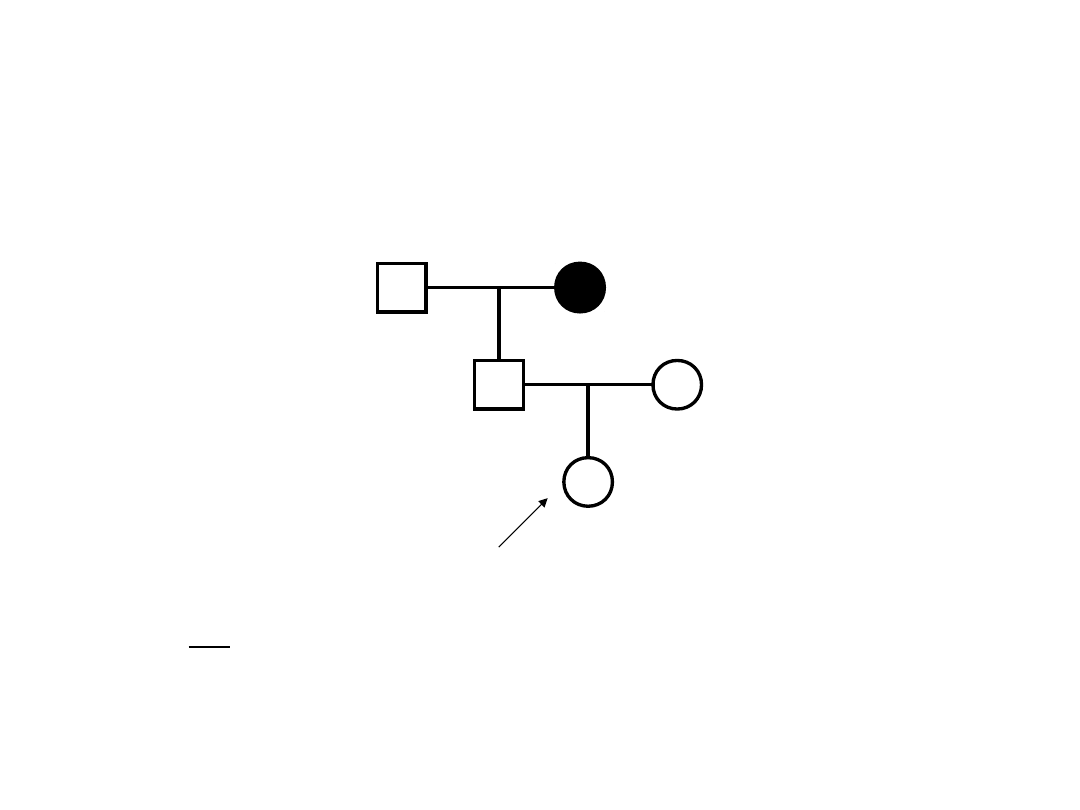
Ch. Huntingtona jest AD o późnym wieku ujawnienia. Pierwsze objawy pojawiają się
pomiędzy 30 a 60 r.ż. Zakładając, że 50% heterozygot ma objawy przed 50 r.ż. Oblicz
ryzyko dziedziczenia genu przez wskazaną osobę.

Obliczanie ryzyka przez analizę

ilorazu prawdopodobieństw (LR)

rodowodów I

L1(jest nosicielem)=0.5 x 0.5 x0.5 =1/8

L2(nie jest nosicielem)= 0.5 + 0.5x0.5x0.5 =4/8+1/8 = 5/8

L1/L2=LR=1/5

P

nosicielstwa

= 1/(1+5)=1/6

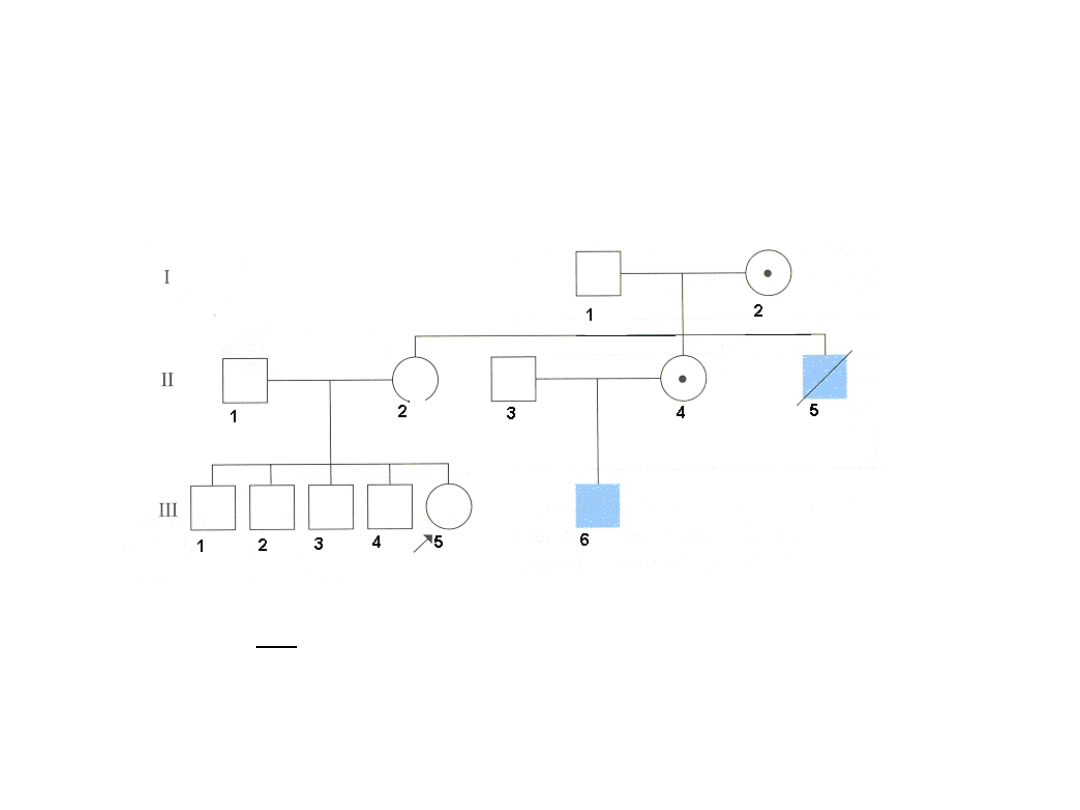
Obliczanie ryzyka przez analizę ilorazu

prawdopodobieństw (LR) rodowodów II

Określ ryzyko nosicielstwa choroby recesywnej sprzężonej z X dla
osoby III5

L1(III5 jest nosicielem)=0.5 x 0.5

5

=1/64

L2(III5 nie jest nosicielem)= 0.5 x 1

5

+ 0.5 x 0.5

5

=32/64+1/64=33/64

LR =L1/L2=1/33

P

nosicielstwa

=1/(1+33)=1/34

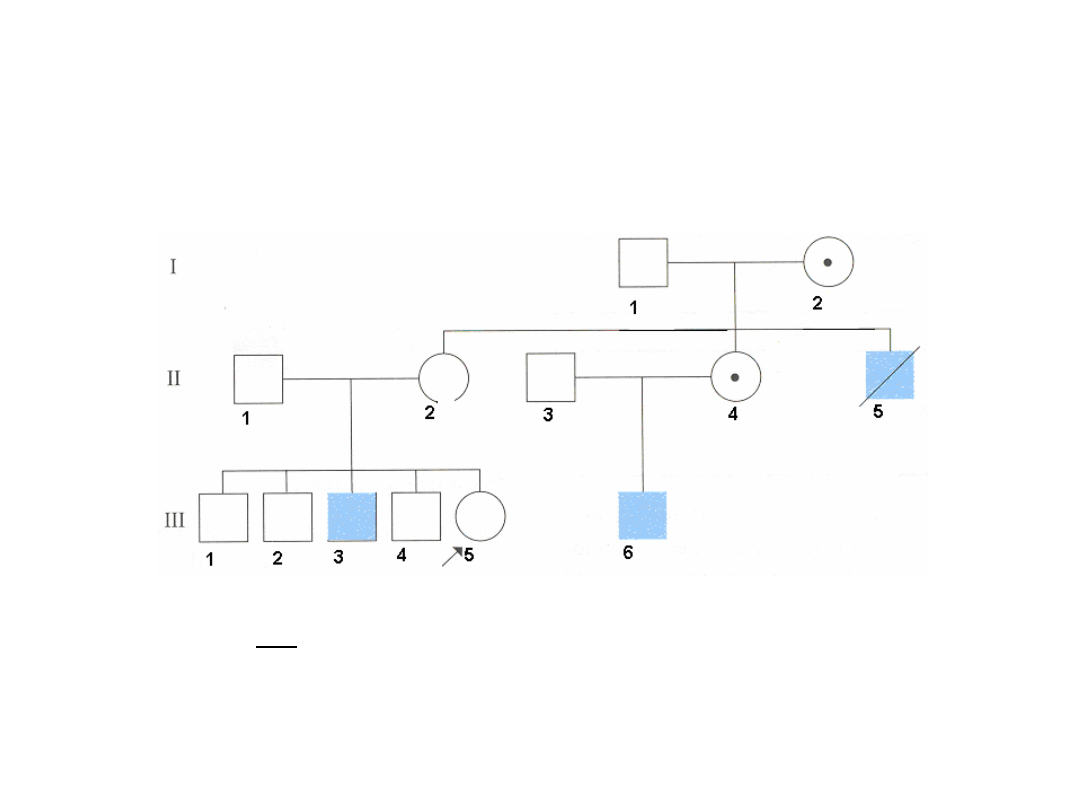
Obliczanie ryzyka przez analizę ilorazu

prawdopodobieństw (LR) rodowodów III

Określ ryzyko nosicielstwa choroby recesywnej sprzężonej z X dla
osoby III5

L1(III5 jest nosicielem)=0.5 x 0.5

5

=1/64

L2(III5 nie jest nosicielem)= 0.5 x 1 x 1 x 0 x 1 x 1 + 0.5 x 0.5

5

=1/64

LR =L1/L21=1

P

nosicielstwa

=1/(1+1)=1/2

LR

całościowe

= LR

1

x LR

2

x...x

LR

n

Ponieważ:

L1

całościowe

= L1

1

x L1

2

x...x L1

n

L2

całościowe

= L2

1

x L2

2

x...x L2

n

Czyli:

L1/L2

całościowe

=

(L1

1

x L1

2

x...x L1

n

)

(L2

1

x L2

2

x...x L2

n

)

=

LR

1

x LR

2

x...x LR

n