5.

5.

ZASADY STATYSTYCZNEJ

ZASADY STATYSTYCZNEJ

ANALIZY WYNIKÓW BADAŃ

ANALIZY WYNIKÓW BADAŃ

5.1.Wstęp

Jak już wspomniano na początku podręcznika, analizę statystyczną można oprzeć o funkcję

gęstości lub o dystrybuantę. W pierwszym przypadku posługiwać się trzeba histogramem

wymagającym podziału na klasy i wyboru liczności klas co prowadzi często do

niejednoznaczności uzyskiwanych wyników. W procesach inżynierskich bardziej jednoznaczne

wyniki daje metoda dystrybuanty empirycznej. W metodzie tej uzyskaną z badań dystrybuantę

empiryczną należy aproksymować dystrybuantą jednego z teoretycznych rozkładów.

Można tego dokonać jedną z trzech metod: metodą graficzną, metodą momentów i metodą

największej wiarygodności.

5.1.Oszacowanie punktowe

Metoda ta polega na zastosowaniu gotowych wzorów służących do oszacowania parametrów

określonego rozkładu. Pomijając całą teorię uzyskiwania odpowiednich wzorów matematycznych

służących do oszacowania (estymacji) odpowiednich parametrów, należy tylko wspomnieć, że

wzory te zwykle uzyskuje się z wykorzystaniem momentów poszczególnych zmiennych

losowych o odpowiednich rozkładach statystycznych (stąd nazwa metoda momentów). Poniżej

zestawiono wybrane sposoby estymacji punktowej dla wybranych rozkładów statystycznych.

5.1.1. Rozkład normalny

Wartość oczekiwana będąca podstawowym parametrem rozkładu normalnego

szacowana jest ze średniej:









n

i

i

x

n

X

1

1

gdzie: n - liczność próbki, x

i

- zaobserwowane realizacje zmiennej losowej.

Odchylenie średnie standardowe wykorzystywane jest jako estymator odchylenia

średniego :

1

)

(

2









n

X

x

S

i

Te dwa estymatory definiują poszukiwaną dystrybuantę rozkładu normalnego.

5.1.1. Rozkład Weibulla

Jedna z metod szacowania parametrów rozkładu Weibulla oparta jest o trzeci moment

centralny, którego nieobciążonym estymatorem jest:



















n

i

i

X

x

n

n

n

n

M

1

3

2

3

)

(

)

2

(

)

1

(

Wykorzystując oszacowanie M

3

oblicza się współczynnik skośności  z wyrażenia:

3

3

S

M





Dla znanego  odczytuje się z tabeli 5.1 parametry k, A, B, D rozkładu Weibulla

(zdefiniowane w tabeli 4.1) oraz oblicza się pozostałe parametry rozkładu z zależności:

A

B

D

gdzie

S

D

X

X

S

A

X

X

m

















0

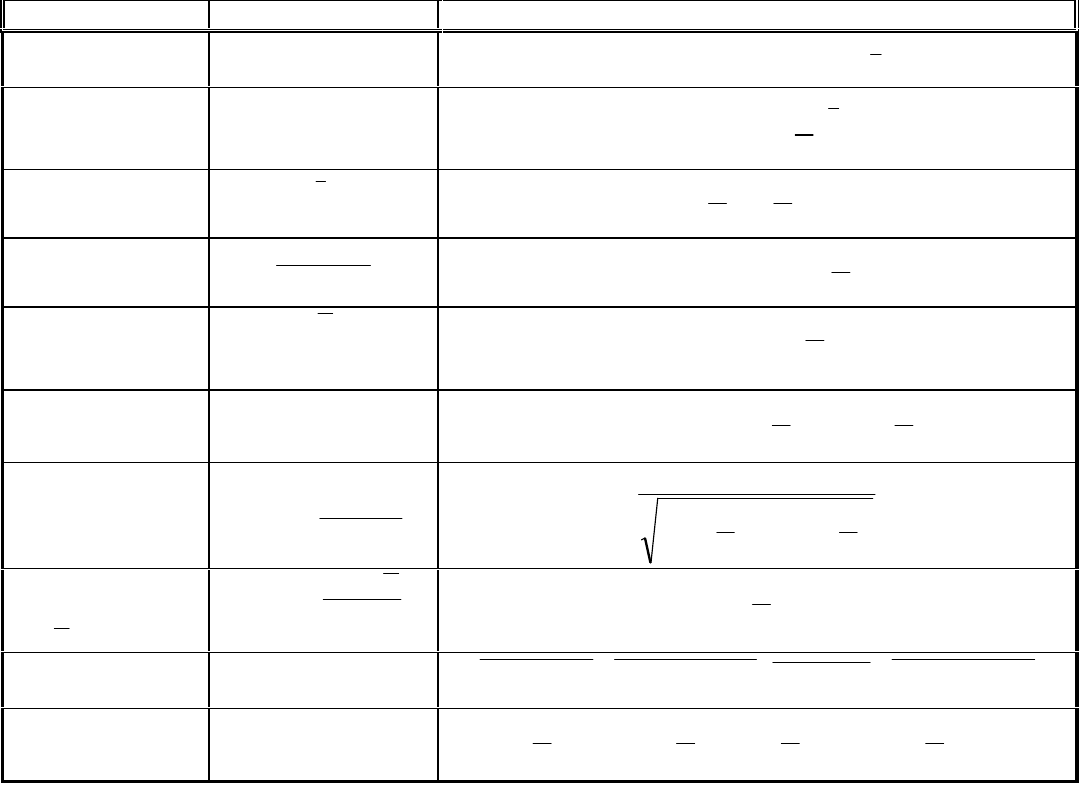
P a r a m e t r

S y m b o l

W z ó r

M e d i a n a



X

X

X

X

m

k

0

0

1

2







(

) ( l n

)

M o d a

~

X

1

1

1

)

(

1

0

0













 







k

dla

k

X

X

X

k

m

Z r e d u k o w a n y

m o m e n t r z ę d u l

z

l















k

l

k

l

M o m e n t r z ę d u l

(

)

x

X

l



0











 





k

l

X

X

l

m

1

)

(

0

P i e r w s z y

m o m e n t

( ś r e d n i a )

X

1

1

)

(

0

0













 







l

dla

k

l

X

X

X

m

W a r i a n c j a



2























 















 







k

k

X

X

m

1

1

2

1

)

(

2

2

0

S t a n d a r y z o w a n a

r ó ż n i c a o d X

m

d o X

0

B k

X

X

m

( ) 



0













 















 



k

k

1

1

2

1

1

2

S t a n d a r y z o w a n a

r ó ż n i c a o d X

m

d o

X

A k

X

X

m

( ) 





)

(

1

1

1

k

B

k

























 





T r z e c i m o m e n t

c e n t r a l n y



3

3

0

0

2

0

3

0

)

(

2

)

(

)

(

3

)

(

X

x

X

x

X

x

X

x



















W s p ó ł c z y n n i k

a s y m e t r i i



)

(

1

1

2

1

1

2

1

3

3

1

3

3

2

k

B

k

k

k

k

























 















 













 















 



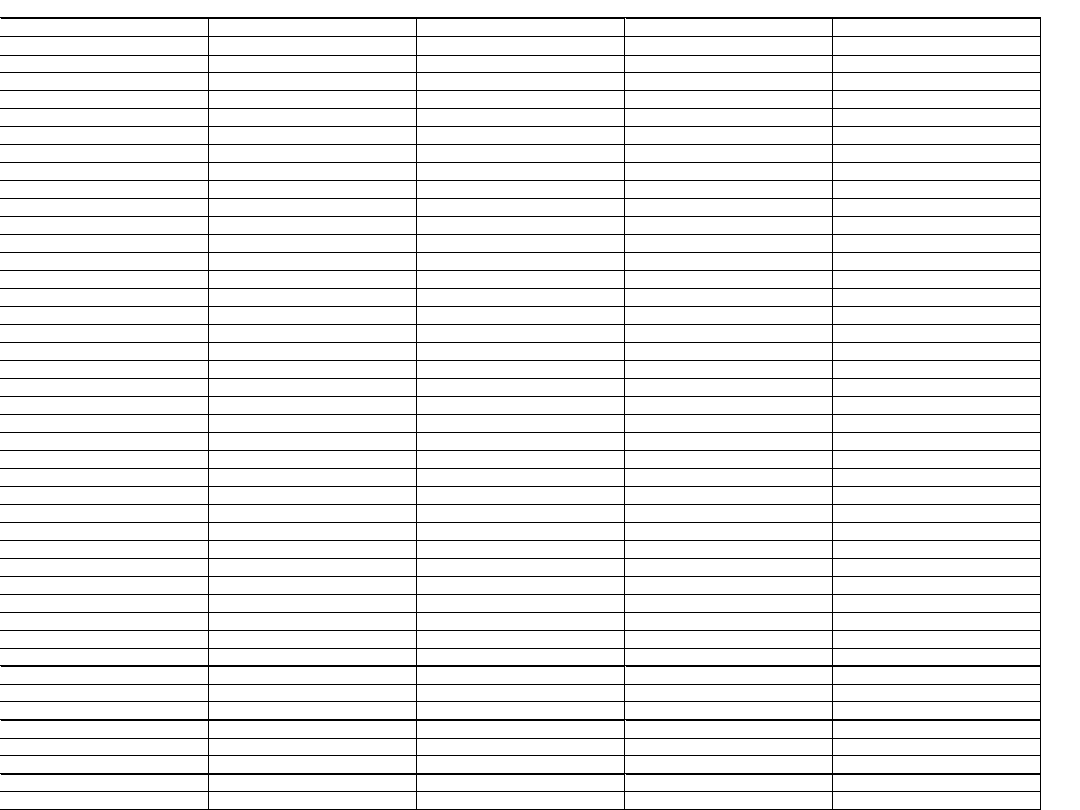
Tabela 5.1. Dane liczbowe do szacowania estymatorów rozkładu Weibulla wg [7]

k

A

B

D



0.5

-0.223607

0.224

0.447113

6.619

1.0

0.000000

1.000

1.000000

2.000

1.5

0.158669

1.631

1.472827

1.072

2.0

0.245598

2.159

1.913046

0.631

2.5

0.296936

2.634

2.336956

0.359

3.0

0.329748

3.081

2.751448

0.168

3.5

0.352096

3.512

3.160028

0.025

4.0

0.368084

3.933

3.564587

-0.087

4.5

0.379976

4.346

3.966282

-0.178

5.0

0.389102

4.755

4.365828

-0.254

5.5

0.395287

5.160

4.763762

-0.319

6.0

0.402069

5.563

5.160494

-0.374

6.5

0.406805

5.963

5.556206

-0.423

7.0

0.410749

6.362

5.951200

-0.465

7.5

0.414075

6.760

6.345521

-0.502

8.0

0.416915

7.156

6.739368

-0.535

8.5

0.419367

7.552

7.132896

-0.566

9.0

0.421497

7.947

7.525930

-0.592

9.5

0.423368

8.342

7.918742

-0.617

10.0

0.425026

8.736

8.311375

-0.638

10.5

0.428495

9.130

8.703660

-0.658

11.0

0.427812

9.524

9.095818

-0.676

11.5

0.429006

9.917

9.488068

-0.692

12.0

0.430073

10.310

9.879791

-0.708

12.5

0.431046

10.703

10.271504

-0.723

13.0

0.431947

11.096

10.663568

-0.733

13.5

0.432751

11.488

11.054852

-0.747

14.0

0.433501

11.880

11.446406

-0.758

14.5

0.434202

12.272

11.838192

-0.769

15.0

0.434827

12.664

12.229133

-0.781

15.5

0.435420

13.056

12.620502

-0.787

16.0

0.435971

13.448

13.011774

-0.796

16.5

0.436486

13.840

13.403097

-0.801

17.0

0.436978

14.232

13.794868

-0.814

17.5

0.437431

14.624

14.186113

-0.817

18.0

0.437830

15.014

14.576417

-0.824

18.5

0.438248

15.407

14.968422

-0.826

19.0

0.438598

15.797

15.358540

-0.842

19.5

0.438952

16.189

15.749647

-0.848

20.0

0.439309

16.581

16.141785

-0.850

20.5

0.439597

16.971

16.531586

-0.853

21.0

0.439899

17.363

16.922745

-0.859

21.5

0.440205

17.755

17.314880

-0.864

Cytat ze STATISTIKI
http://www.statsoft.pl/textbook/stathome.html

Ocena parametru położenia w trójparametrowym

rozkładzie Weibulla stwarza pewne problemy, których
dyskusję znaleźć można u Lawlessa (1982). W
szczególności, jeśli parametr kształtu jest mniejszy od 1,
to

nie

istnieje

rozwiązanie

metodą

największej

wiarygodności. W innych przypadkach natomiast może
się okazać, że funkcja wiarygodności posiada więcej niż
jedno maksimum (tzn. wiele maksimów lokalnych). W tym
ostatnim przypadku Lawless zaleca użycie najmniejszego
czasu awarii (lub wielkości odrobinę mniejszej) jako
wartości parametru położenia.

5.1.1. Rozkład Gumbela

(dwuwykładniczy)

P

a

r

a

m

e

t

r

y

r

o

z

kł

a

d

u

d

w

u

w

y

k

ł

a

d

n

i

c

z

e

g

o

m

o

ż

n

a

o

s

z

a

c

o

w

a

ć

z

z

a

l

e

ż

n

o

ś

c

i

:







ˆ

ˆ

ˆ

n

m

n

y

X

X

S







(

5

.

6

)

g

d

z

i

e

:



i

X

m

t

o

p

a

r

a

m

e

t

r

y

r

o

z

kł

a

d

u

;



n

i

n

y

t

o

o

d

p

o

w

i

e

d

n

i

o

p

o

p

u

l

a

c

y

j

n

e

o

d

c

h

y

l

e

n

i

e

s

t

a

n

d

a

r

d

o

w

e

i

p

o

p

u

l

a

c

y

j

n

a

ś

r

e

d

n

i

a

(

w

a

r

t

o

ś

c

i

t

e

p

o

d

a

j

e

t

a

b

e

l

a

5

.

2

.

)

.

Tabela 5.2. Dane liczbowe do oszacowania parametrów rozkładu dwuwykładniczego wg [7]

n

n

y



n

n

n

y



n

8

0.484

0.904

49

0.548

1.159

9

0.490

0.929

50

0.549

1.161

10

0.495

0.950

51

0.549

1.162

11

0.500

0.968

52

0.549

1.164

12

0.503

0.983

53

0.550

1.165

13

0.507

0.997

54

0.550

1.167

14

0.510

1.010

55

0.550

1.168

15

0.513

1.021

56

0.551

1.170

16

0.516

1.032

57

0.551

1.171

17

0.518

1.041

58

0.551

1.172

18

0.520

1.049

59

0.552

1.173

19

0.522

1.057

60

0.552

1.175

20

0.524

1.063

62

0.553

1.177

21

0.525

1.070

64

0.553

1.179

22

0.527

1.075

66

0.554

1.181

23

0.528

1.081

68

0.554

1.183

24

0.529

1.086

70

0.555

1.185

25

0.531

1.091

72

0.555

1.187

26

0.532

1.096

74

0.556

1.189

27

0.533

1.100

76

0.556

1.191

28

0.534

1.105

78

0.556

1.192

29

0.535

1.109

80

0.557

1.194

30

0.536

1.112

82

0.557

1.195

31

0.537

1.116

84

0.558

1.197

32

0.538

1.119

86

0.558

1.198

33

0.539

1.123

88

0.558

1.199

34

0.540

1.125

90

0.559

1.201

35

0.540

1.128

92

0.559

1.202

36

0.541

1.131

94

0.559

1.203

37

0.542

1.134

96

0.560

1.204

38

0.542

1.136

98

0.560

1.206

39

0.543

1.139

100

0.560

1.206

40

0.544

1.141

150

0.565

1.225

41

0.544

1.144

200

0.567

1.236

42

0.545

1.146

250

0.569

1.243

43

0.545

1.148

300

0.570

1.248

44

0.546

1.150

400

0.571

1.254

45

0.546

1.152

500

0.572

1.259

46

0.547

1.154

750

0.574

1.265

47

0.547

1.156

1000

0.575

1.269

48

0.548

1.157



0.577

1.283

5.1.Metoda graficzna

Każdy rozkład statystyczny zmiennej losowej X o dystrybuancie F(x) posiada sobie tylko

właściwą siatkę funkcyjną o odciętej

)

(

1

X







(5.7a)

i rzędnej

)]

(

[

2

x

F







(5.7b)

w której to siatce dystrybuanta F(x) jest linią prostą o równaniu











b

a

(5.8)

Współrzędne siatek funkcyjnych i równania prostych dla wybranych rozkładów

statystycznych zestawiono w tabeli 5.3.

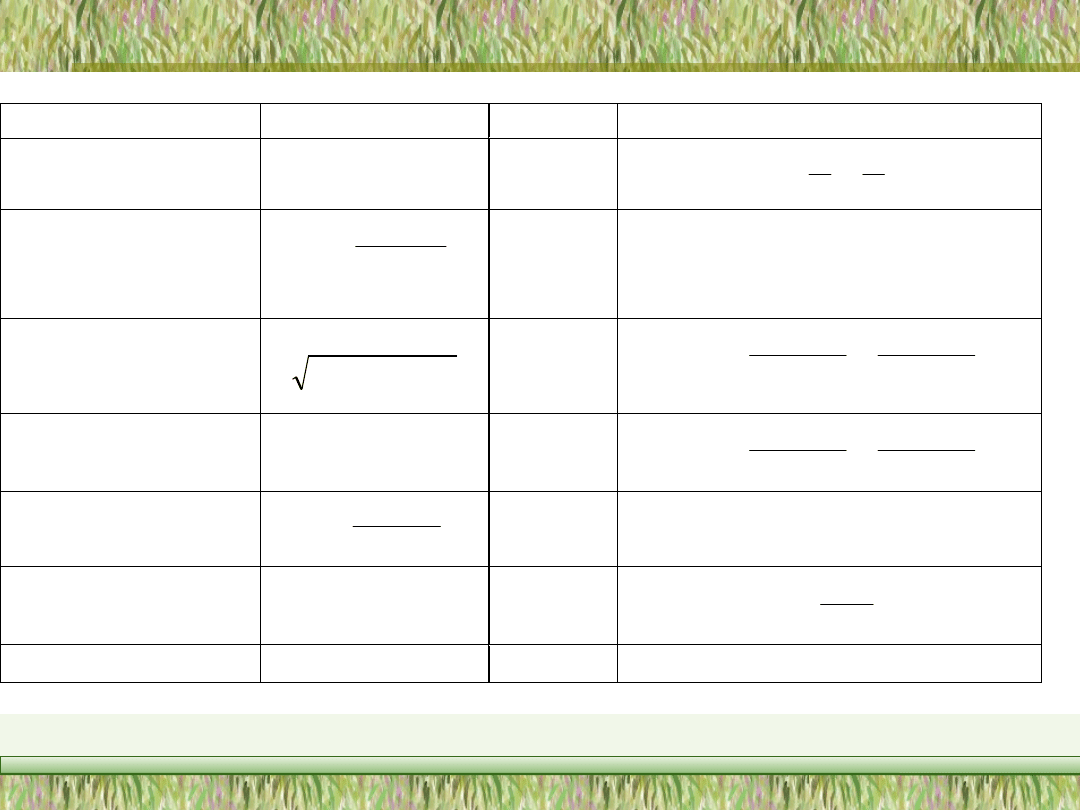
T a b e l a 5 . 3 . W s p ół r z ę d n e l i n i o w e w y b r a n y c h r o z k ł a d ó w s t a t y s t y c z n y c h

R o z kł a d / w s p ó ł r z ę d n e





R ó w n a n i e p r o s t e j

n o r m a l n y

)]

(

[

x

F

Y

x

x

y















1

W e i b u l l a

d l a s i a t k i u n i w e r s a l n e j

}

{

]

[

)

(

1

1

ln

ln

x

F



l n ( x - X

o

)

)

ln(

)

ln(

0

0

X

x

k

X

X

k

y

m















W e i b u l l a d l a s i a t k i o

u s t a l o n y m p a r a m e t r z e

k

k

x

F

)]

(

1

ln[





x

0

0

0

X

X

x

X

X

X

y

m

m











w y kł a d n i c z y

)]

(

1

ln[

x

F





x

0

0

0

X

X

x

X

X

X

y

m

m











d w u w y kł a d n i c z y

}

{

]

[

)

(

1

1

ln

ln

x

F



x

x

X

y

m















r ó w n o m i e r n y

F ( x )

x

c

d

c

x

y







p o tę g o w y

l g [ F ( x ) ]

l g ( x )

)

lg(

)

lg(

c

x

y













W

y

k

o

r

z

y

s

t

u

ją

c

w

s

p

ó

ł

r

z

ę

d

n

e



i



,

k

t

ó

r

e

p

o

w

y

k

o

r

z

y

s

t

a

n

i

u

t

r

a

n

s

f

o

r

m

a

c

j

i

o

k

r

eś

l

o

n

y

c

h

w

z

o

r

a

m

i

z

t

a

b

e

l

i

5

.

3

,

są

w

s

p

ó

ł

r

z

ę

d

n

y

m

i

l

i

n

i

o

w

y

m

i

d

l

a

d

a

n

e

g

o

r

o

z

k

ł

a

d

u

,

m

o

ż

n

a

z

a

s

t

o

s

o

w

a

ć

m

e

t

o

dę

n

a

j

m

n

i

e

j

s

z

y

c

h

k

w

a

d

r

a

t

ó

w

d

l

a

o

k

r

e

ś

l

e

n

i

a

p

a

r

a

m

e

t

r

ó

w

p

r

o

s

t

e

j

(

5

.

8

)

:































n

i

n

i

i

i

n

i

n

i

n

i

n

i

i

i

i

i

i

x

x

n

y

x

x

y

x

a

1

1

2

1

1

1

1

2

2

)

(

ˆ

(

5

.

9

a

)



 

























n

i

n

i

i

i

n

i

n

i

n

i

i

i

i

i

x

x

n

y

x

y

x

n

b

1

1

2

1

1

1

2

)

(

ˆ

(

5

.

9

b

)

g

d

z

i

e

z

a

x

i

i

y

i

p

o

d

s

t

a

w

i

a

s

ię

w

a

r

t

o

ś

c

i

o

b

l

i

c

z

o

n

e

z

t

a

b

e

l

i

5

.

3

p

r

z

y

p

o

d

s

t

a

w

i

e

n

i

u

z

a

F

(

x

)

i

x

o

d

p

o

w

i

e

d

n

i

c

h

p

r

a

w

d

o

p

o

d

o

b

i

eń

s

t

w

z

p

r

ó

b

y

i

w

a

r

t

o

ś

c

i

z

m

i

e

n

n

e

j

l

o

s

o

w

e

j

u

z

y

s

k

a

n

y

c

h

z

b

a

d

a

ń

.

O

s

z

a

c

o

w

a

n

e

w

s

p

ół

c

z

y

n

n

i

k

i

a

ˆ

i

b

ˆ

p

r

o

s

t

e

j

p

o

z

w

a

l

a

ją

w

y

k

r

e

ś

l

i

ć

d

y

s

t

r

y

b

u

a

n

t

ę

r

o

z

k

ł

a

d

u

w

j

e

g

o

s

i

a

t

c

e

f

u

n

k

c

y

j

n

e

j

o

r

a

z

w

y

z

n

a

c

z

yć

p

a

r

a

m

e

t

r

y

r

o

z

k

ł

a

d

u

w

e

d

ł

u

g

w

z

o

r

ó

w

p

o

d

a

n

y

c

h

w

t

a

b

e

l

i

5

.

4

.

T a b e l a 5 . 4 . O k r e ś l e n i e p a r a m e t r ó w w y b r a n y c h r o z k ł a d ó w n a p o d s t a w i e z n a j o m o ś c i

w s p ó ł c z y n n i k ó w r ó w n a n i a p r o s t e j w s i a t c e f u n k c y j n e j

R o z k ł a d

P a r a m e t r y

n o r m a l n y

b

b

a

ˆ

1

ˆ

ˆ

ˆ

ˆ











W e i b u l l a

d l a s i a t k i

u n i w e r s a l n e j











 







b

a

X

X

b

k

m

ˆ

ˆ

exp

ˆ

ˆ

ˆ

ˆ

0

W e i b u l l a d l a s i a t k i o

u s t a l o n y m

p a r a m e t r z e k

b

a

X

b

X

X

m

ˆ

ˆ

ˆ

ˆ

1

ˆ

ˆ

0

0









w y k ł a d n i c z y

b

a

X

b

X

X

m

ˆ

ˆ

ˆ

ˆ

1

ˆ

ˆ

0

0









d w u w y k ł a d n i c z y

b

a

X

b

m

ˆ

ˆ

ˆ

ˆ

ˆ









r ó w n o m i e r n y

b

a

d

b

a

c

ˆ

ˆ

1

ˆ

ˆ

ˆ

ˆ









p o t ę g o w y

)

ˆ

ˆ

(

10

ˆ

ˆ

ˆ

b

a

c

b









P

r

z

y

kł

a

d

5

.

1

.

D

a

n

e

są

w

y

n

i

k

i

b

a

d

a

ń

z

m

i

e

n

n

e

j

l

o

s

o

w

e

j

j

a

k

w

p

i

e

r

w

s

z

y

c

h

t

r

z

e

c

h

k

o

l

u

m

n

a

c

h

t

a

b

e

l

k

i

5

.

5

.

D

a

n

e

t

e

o

p

r

a

c

o

w

a

n

o

m

e

t

o

dą

g

r

a

fi

c

z

n

ą

d

l

a

t

r

ó

j

p

a

r

a

m

e

t

r

o

w

e

g

o

r

o

z

k

ł

a

d

u

W

e

i

b

u

l

l

a

,

k

t

ó

r

y

m

a

d

w

a

r

o

d

z

a

j

e

s

i

a

t

e

k

f

u

n

k

c

y

j

n

y

c

h

.

S

i

a

t

k

a

u

n

i

w

e

r

s

a

l

n

a

w

y

m

a

g

a

u

p

r

z

e

d

n

i

e

g

o

o

k

r

eś

l

e

n

i

a

p

a

r

a

m

e

t

r

u

p

r

z

e

s

u

n

i

ę

c

i

a

X

o

,

a

s

i

a

t

k

a

o

u

s

t

a

l

o

n

y

m

p

a

r

a

m

e

t

r

z

e

k

s

z

t

ał

t

u

k

w

y

m

a

g

a

u

p

r

z

e

d

n

i

e

g

o

o

k

r

eś

l

e

n

i

a

t

e

g

o

p

a

r

a

m

e

t

r

u

.

W

o

b

y

d

w

u

p

r

z

y

p

a

d

k

a

c

h

d

l

a

o

k

r

eś

l

e

n

i

a

t

y

c

h

p

a

r

a

m

e

t

r

ó

w

w

y

k

o

r

z

y

s

t

a

n

o

o

s

z

a

c

o

w

a

n

i

a

p

u

n

k

t

o

w

e

(

r

o

z

d

z

.

5

.

2

.

1

)

u

z

y

s

k

u

ją

c

o

d

p

o

w

i

e

d

n

i

o

893

.

88

ˆ

0



X

o

r

a

z

612

.

3

ˆ



k

.

W

y

k

o

r

z

y

s

t

u

ją

c

t

e

d

a

n

e

-

w

o

p

a

r

c

i

u

o

w

z

o

r

y

z

t

a

b

e

l

i

5

.

3

-

o

b

l

i

c

z

o

n

o

w

a

r

t

oś

c

i

i

x

ˆ

o

r

a

z

i

y

ˆ

z

e

s

t

a

w

i

o

n

e

w

k

o

l

u

m

n

a

c

h

4

i

5

d

l

a

s

i

a

t

k

i

u

n

i

w

e

r

s

a

l

n

e

j

i

w

k

o

l

u

m

n

a

c

h

6

i

7

d

l

a

s

i

a

t

k

i

o

u

s

t

a

l

o

n

y

m

p

a

r

a

m

e

t

r

z

e

k

s

z

t

ał

t

u

(

t

a

b

e

l

a

5

.

5

)

.

P

o

d

s

t

a

w

i

a

ją

c

t

e

w

a

r

t

o

ś

c

i

d

o

w

z

o

r

ó

w

5

.

9

o

s

z

a

c

o

w

a

n

o

p

a

r

a

m

e

t

r

y

a

ˆ

i

b

ˆ

p

r

o

s

t

e

j

5

.

8

.

Z

n

a

ją

c

p

a

r

a

m

e

t

r

y

a

ˆ

i

b

ˆ

-

w

y

k

o

r

z

y

s

t

u

ją

c

w

z

o

r

y

z

t

a

b

e

l

i

5

.

4

-

o

s

z

a

c

o

w

a

n

o

p

o

s

z

u

k

i

w

a

n

e

p

a

r

a

m

e

t

r

y

t

e

o

r

e

t

y

c

z

n

e

g

o

r

o

z

kł

a

d

u

W

e

i

b

u

l

l

a

.

W

y

n

i

k

i

o

b

l

i

c

z

e

ń

z

i

l

u

s

t

r

o

w

a

n

o

r

y

s

u

n

k

a

m

i

5

.

1

i

5

.

2

o

d

p

o

w

i

e

d

n

i

o

d

l

a

s

i

a

t

k

i

u

n

i

w

e

r

s

a

l

n

e

j

i

d

l

a

s

i

a

t

k

i

o

u

s

t

a

l

o

n

y

m

p

a

r

a

m

e

t

r

z

e

k

s

z

t

ał

t

u

.

J

a

k

w

i

d

a

ć

w

o

b

u

p

r

z

y

p

a

d

k

a

c

h

u

z

y

s

k

a

n

o

w

y

n

i

k

i

n

i

e

c

o

r

óż

n

e

,

c

o

j

e

s

t

w

p

r

z

y

p

a

d

k

u

o

s

z

a

c

o

w

a

ń

s

t

a

t

y

s

t

y

c

z

n

y

c

h

z

r

o

z

u

m

i

ał

e

i

o

c

z

e

k

i

w

a

n

e

-

o

b

a

s

p

o

s

o

b

y

w

y

k

o

r

z

y

s

t

a

n

i

a

m

e

t

o

d

y

g

r

a

fi

c

z

n

e

j

d

l

a

r

o

z

k

ł

a

d

u

W

e

i

b

u

l

l

a

w

y

c

h

o

d

zą

z

o

d

r

ę

b

n

y

c

h

z

a

ł

o

ż

e

ń

.

R

a

z

z

a

k

ł

a

d

a

s

i

ę

z

n

a

j

o

m

o

ś

ć

p

a

r

a

m

e

t

r

u

p

r

z

e

s

u

n

i

ę

c

i

a

a

d

r

u

g

i

r

a

z

z

a

kł

a

d

a

s

i

ę

z

n

a

j

o

m

o

ś

ć

p

a

r

a

m

e

t

r

u

k

s

z

t

a

ł

t

u

.

T

a

b

e

la

5

.

5

.

D

a

n

e

d

o

p

r

z

y

kła

d

u

S

z

e

r

e

g

k

u

m

u

la

c

y

jn

y

S

ia

t

k

a

f

u

n

k

c

y

jn

a

u

n

iw

e

r

s

a

ln

a

S

ia

t

k

a

f

u

n

k

c

y

jn

a

o

u

s

t

a

lo

n

y

m

p

a

r

a

m

e

t

r

z

e

k

s

z

t

ałt

u

k

x

i



i

i

n

)

(

ˆ

i

x

F

i

y

ˆ

i

x

ˆ

i

y

ˆ

i

x

ˆ

1

2

0

1

0

.

0

4

8

-3

.

0

2

0

3

.4

3

7

0

.

4

3

3

1

2

0

1

2

5

2

0

.

0

9

5

-2

.

3

0

2

3

.5

8

6

0

.

5

2

9

1

2

5

1

3

0

2

0

.

0

9

5

-2

.

3

0

2

3

.7

1

6

0

.

5

2

9

1

3

0

1

3

5

4

0

.

1

9

0

-1

.

5

5

4

3

.8

3

1

0

.

6

5

1

3

5

1

4

0

6

0

.

2

8

6

-1

.

0

8

9

3

.9

3

4

0

.

7

4

1

4

0

1

4

5

9

0

.

4

2

9

-0

.

5

8

1

4

.0

2

7

0

.

8

5

2

1

4

5

1

5

0

1

2

0

.

5

7

1

-0

.

1

6

6

4

.1

1

3

0

.

9

5

5

1

5

0

1

5

5

1

4

0

.

6

6

7

0

.

0

9

4

4

.1

9

1

1

.

0

2

6

1

5

5

1

6

0

1

7

0

.

8

1

0

0

.

5

0

6

4

.2

6

4

1

.

1

5

1

6

0

1

6

5

1

8

0

.

8

5

7

0

.

6

6

6

4

.3

3

2

1

.

2

0

2

1

6

5

1

7

0

1

9

0

.

9

0

5

0

.

8

5

5

4

.3

9

6

1

.

2

6

7

1

7

0

1

7

5

2

0

0

.

9

5

2

1

.

1

1

3

4

.4

5

6

1

.

3

6

1

1

7

5

0.1

1

10

100

1 10

3

6

4

2

0

y i

y i

pr (

)

x

,

,

xu

i u i x

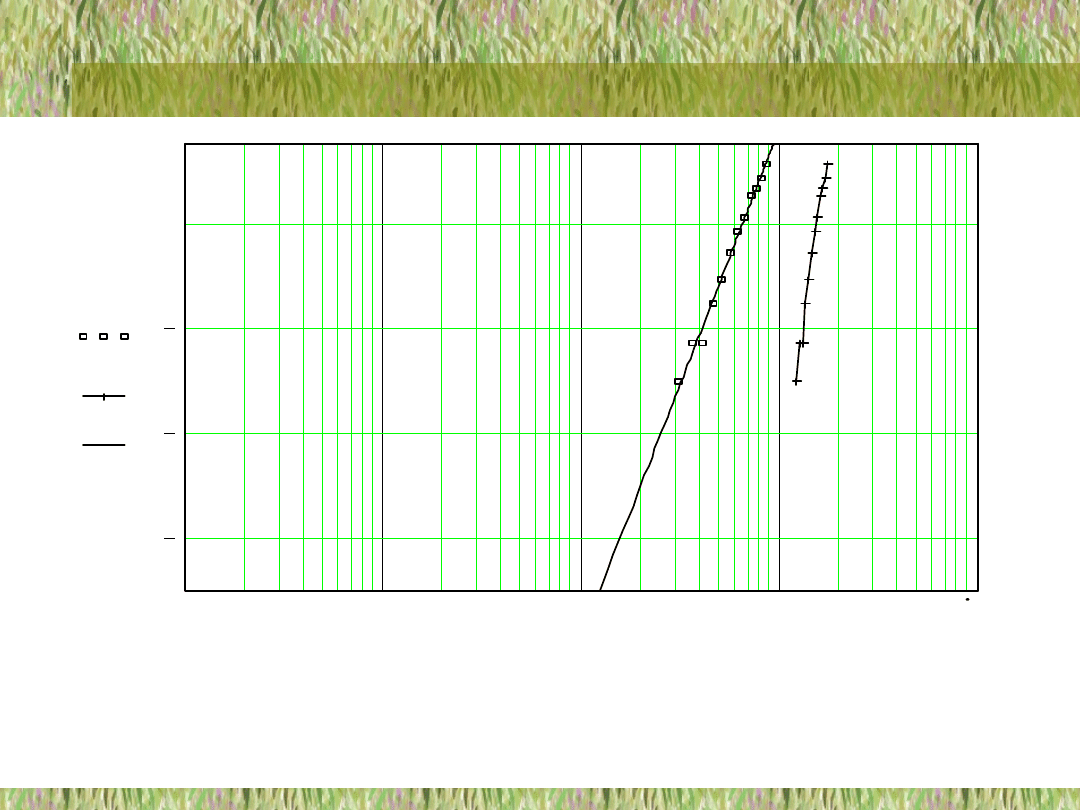
R y s . 5 . 1 . W y k r e s d y s t r y b u a n t y e m p i r y c z n e j ( p u n k t y ) i t e o r e t y c z n e j ( l i n i a c ią g ł a ) w

u n i w e r s a l n e j s i a t c e f u n k c y j n e j r o z kł a d u W e i b u l l a ( X

o

= 8 8 . 8 9 3 ) :

212.

4

ˆ

;

099.

154

ˆ

;

893.

88

ˆ

;

212.

4

ˆ;

598.

17

ˆ

0













k

X

X

b

a

m

50

75

100

125

150

175

200

225

250

0

0.4

0.8

1.2

1.6

2

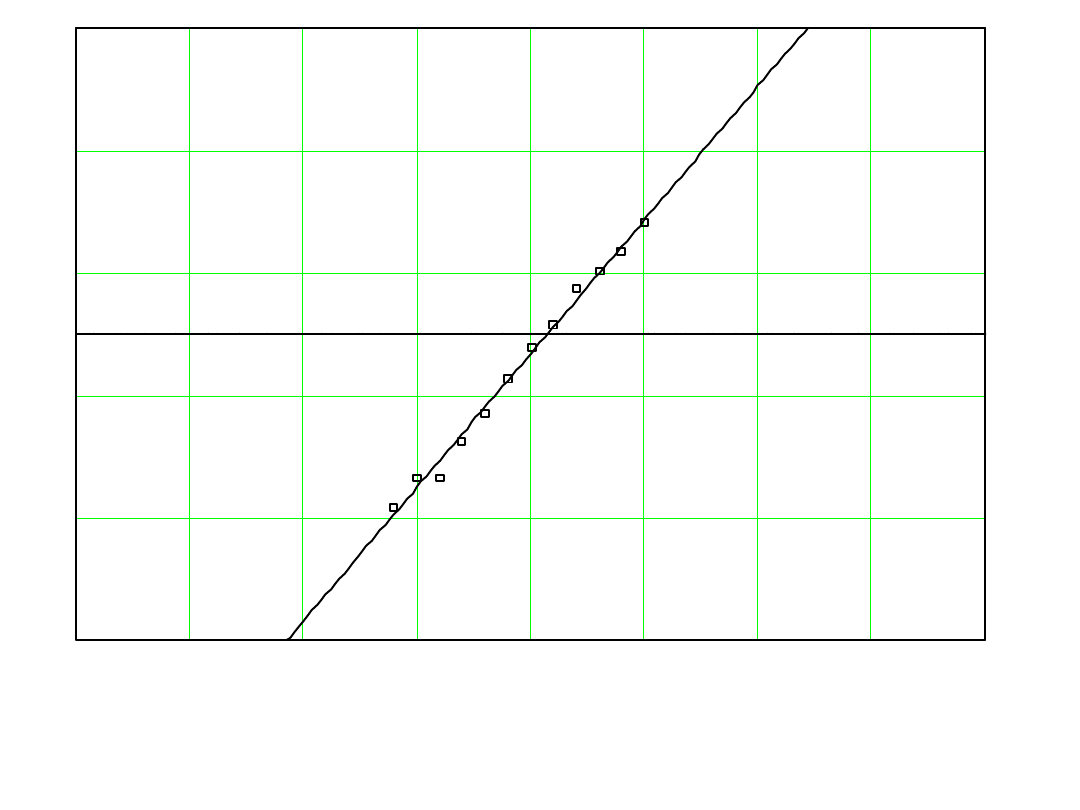
R y s . 5 . 2 . W y k r e s d y s t r y b u a n t y e m p i r y c z n e j ( p u n k t y ) i t e o r e t y c z n e j ( l i n i a c ią g ł a ) w s i a t c e

f u n k c y j n e j r o z kł a d u W e i b u l l a o u s t a l o n y m p a r a m e t r z e k s z t ał t u k ( k = 3 . 6 1 2 ) :

612.

3

ˆ

;

715.

153

ˆ

;

576.

96

ˆ

;

018.

0

ˆ

;

690.

1

ˆ

0













k

X

X

b

a

m