2. DYSTRYBUANTA, FUNKCJA

2. DYSTRYBUANTA, FUNKCJA

GĘSTOŚCI, FUNKCJA

GĘSTOŚCI, FUNKCJA

PRAWDOPODOBIEŃSTWA

PRAWDOPODOBIEŃSTWA

Rozw

ażm

y zdarzenie

X <

x polegające na tym

, że w

artość zm

iennej losow

ej X jest

m

niejsza od danej w

artości x. Funkcję Fx PX x

( )

(

)



 określającą zależność

praw

dopodobieństw

a PX x

(

)

 od w

artości

x, nazyw

a się dystrybuantą

danej zm

iennej losow

e

X. D

ystrybuanta F(x) jest funkcją niem

alejącą argum

entu x, przynajm

niej lew

ostronnie ciągłą i

zaw

sze spełnia w

arunek

0

1





F x

( )

przy czym F(-



) = 0 oraz F(



) = 1. Dystrybuanta F(x) może być zdefiniowana wzorem

F(x)=P(X



x) i wówczas jest przynajmniej prawostronnie ciągła. Dla zmiennej losowej ciągłej

P(X < x) = P(X



x). Jeżeli dziedziną dystrybuanty jest przedział [a, b] to F(x) = 0 dla x



a oraz

F(x) = 1 dla x > b. Jeżeli jest znana dystrybuanta F(x) to prawdopodobieństwo zdarzenia X



x

wynosi

)

(

1

)

(

x

F

x

X

P







natomiast prawdopodobieństwo zdarzenia, iż X jest w przedziale a  X < b wyznacza się z

wzoru:

)

(

)

(

)

(

a

F

b

F

b

X

a

P









Zmienne losowe mogą być dwojakiego rodzaju:

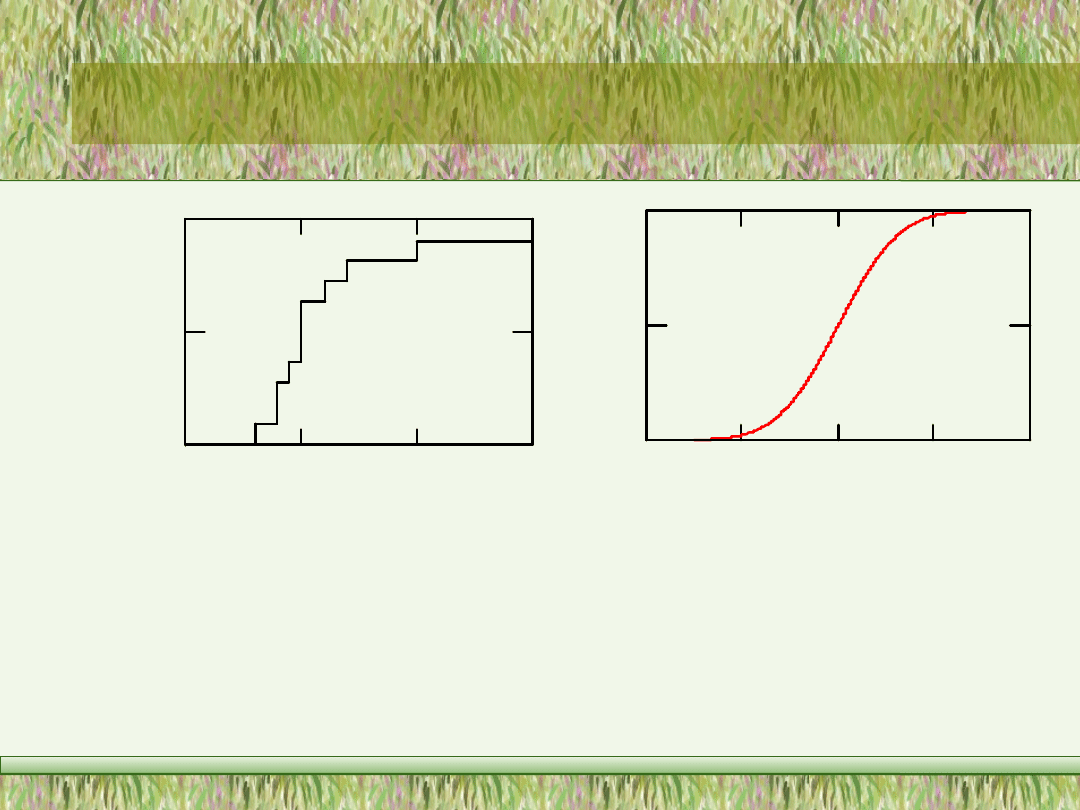
 zmienna losowa skokowa (dyskretna) o skończonej lub przeliczalnej liczbie możliwych

wartości (realizacji) - dystrybuanta takiej zmiennej losowej jest funkcją skokową (rys.

2.1);

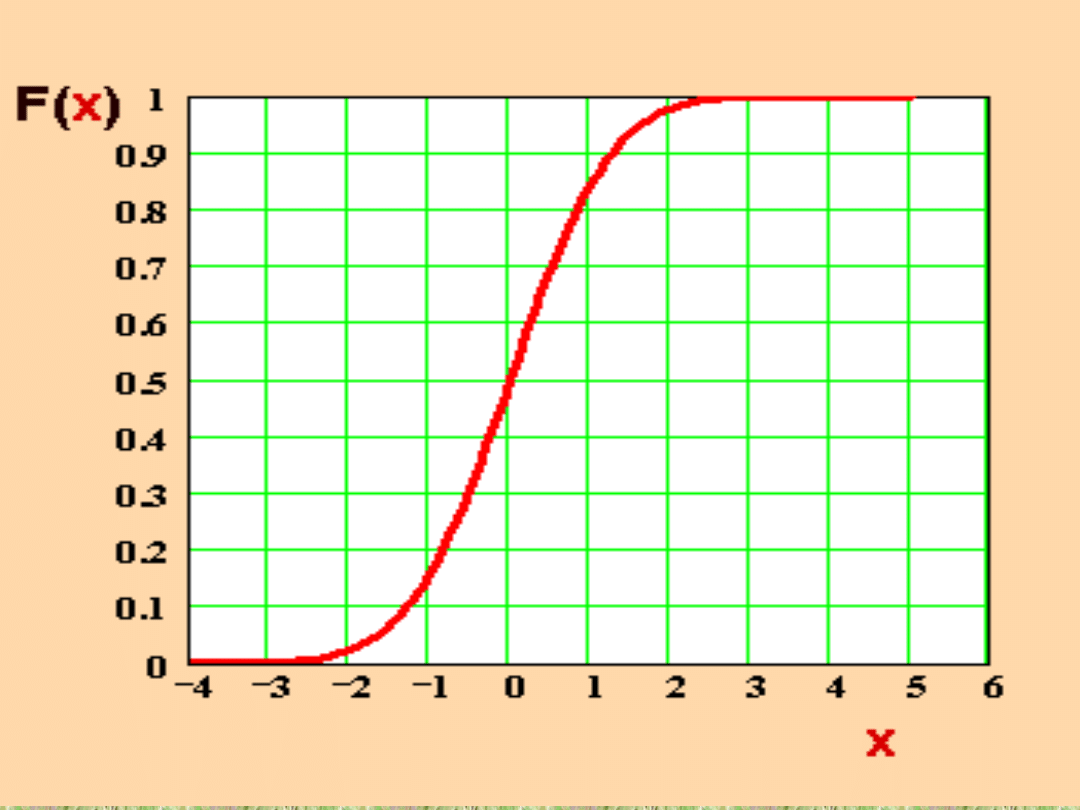
 zmienna losowa ciągła mogąca przyjmować dowolne wartości z określonego

przedziału liczb rzeczywistych - dystrybuanta takiej zmiennej losowej jest funkcją

ciągłą (rys. 2.2).

0

0.5

1

Rys. 2.1 Przykład dystrybuanty zmiennej losowej

skokowej

Rys. 2.2 Przykład dystrybuanty zmiennej losowej

ciągłej

p x

P X x

i

i

( )

(

)





Jeżeli stosuje się klasyfikację alternatywną np. wyrobów na sztuki dobre i złe lub

klasyfikację wielowartościową (np. napięcie i temperatura powyżej jakiejś wartości to źle a

odwrotnie to dobrze) to wynik badania wylosowanej sztuki jest zmienną losową skokową. W celu

określenia rozkładu zmiennej losowej skokowej X podaje się zbiór możliwych jej wartości oraz

funkcję

określającą prawdopodobieństwo zdarzenia X = x

i

dla każdej możliwej wartości x

i

(i = 1,2,..., n)

danej zmiennej losowej X. Funkcja ta nosi nazwę funkcji prawdopodobieństwa zmiennej losowej

X. Znając funkcję prawdopodobieństwa p(x

i

) zmiennej losowej skokowej X, można wyznaczyć

dystrybuantę F(x) tej zmiennej losowej dla dowolnej wartości rzeczywistej x, korzystając z

wzoru:











x

x

x

p

x

X

P

x

F

i

i

)

(

)

(

)

(

czyli poprzez sumowanie wartości funkcji prawdopodobieństwa p(x

i

) dla wszystkich realizacji

zmiennej losowej X mniejszych niż dana wartość x.

Dla zmiennej losowej ciągłej X zakłada się, że jej dystrybuanta F(x) jest różniczkowalna

w całym obszarze możliwych wartości tej zmiennej losowej. Istnieje wówczas nieujemna funkcja

0

)

(

)

(





dx

x

dF

x

f

nazywana funkcją gęstości prawdopodobieństwa albo funkcją gęstości danej zmiennej losowej X.

Wartość f(x)dx określa prawdopodobieństwo zdarzenia, iż zmienna losowa znajdzie się w
przedziale x



X < x+dx i jest nazywana elementem prawdopodobieństwa. Zatem gęstość

prawdopodobieństwa jest pochodną dystrybuanty, a dystrybuanta jest całką z gęstości

prawdopodobieństwa. Dla zmiennej losowej ciągłej zachodzi równość:

0

)

(

0

lim

)

(



















x

x

X

x

P

x

x

X

P

i stąd

)

(

)

(

)

(

)

(

)

(

)

(

a

F

b

F

b

X

a

P

b

X

a

P

b

X

a

P

b

X

a

P

























