WYKŁAD 3

WYKŁAD 3

I. DYNAMIKA PUNKTU 

I. DYNAMIKA PUNKTU 

MATERIALNEGO

MATERIALNEGO

1.  Zasady Dynamiki Newtona (I, II i 

1.  Zasady Dynamiki Newtona (I, II i 

III).

III).

2.  Dynamika ruchu punktu 

2.  Dynamika ruchu punktu 

materialnego po okręgu.

materialnego po okręgu.

3.

3.

Praca. 

Praca. 

  

  

4.

4.

Moc.

Moc.

5.

5.

Energia.

Energia.

II. DYNAMIKA BRYŁY SZTYWNEJ

II. DYNAMIKA BRYŁY SZTYWNEJ

1.

1.

Pojęcie bryły sztywnej. Rodzaje ruchów 

Pojęcie bryły sztywnej. Rodzaje ruchów 

bryły sztywnej.

bryły sztywnej.

2.

2.

Moment siły. Moment bezwładności. 

Moment siły. Moment bezwładności. 

Twierdzenie Steinera.

Twierdzenie Steinera.

3.

3.

Druga zasada dynamiki ruchu obrotowego.

Druga zasada dynamiki ruchu obrotowego.

4.

4.

Moment pędu.

Moment pędu.

5.

5.

Pierwsza zasada dynamiki ruchu 

Pierwsza zasada dynamiki ruchu 

obrotowego.

obrotowego.

6.

6.

Trzecia zasada dynamiki ruchu obrotowego.

Trzecia zasada dynamiki ruchu obrotowego.

7.

7.

Energia kinetyczna ruchu obrotowego.

Energia kinetyczna ruchu obrotowego.

8.

8.

Analogie pomiędzy ruchem prostoliniowym i 

Analogie pomiędzy ruchem prostoliniowym i 

obrotowym.

obrotowym.

III. ZASADY ZACHOWANIA W 

III. ZASADY ZACHOWANIA W 

MECHANICE 

MECHANICE 

1.

1.

Zasada zachowania pędu.

Zasada zachowania pędu.

2.

2.

Zasada zachowania momentu pędu.

Zasada zachowania momentu pędu.

3.

3.

Zasada zachowania energii.

Zasada zachowania energii.

IV. Druga młodość nadprzewodników 

IV. Druga młodość nadprzewodników 

–  nadprzewodniki 

–  nadprzewodniki 

wysokotemperaturowe

wysokotemperaturowe

I. DYNAMIKA PUNKTU 

I. DYNAMIKA PUNKTU 

MATERIALNEGO

MATERIALNEGO

Dynamika

Dynamika

Zajmuje się warunkami i przyczynami ruchu ciał. 

Zajmuje się warunkami i przyczynami ruchu ciał. 

Podstawę dynamiki stanowią trzy zasady podane przez 

Podstawę dynamiki stanowią trzy zasady podane przez 

Izaaka Newtona w 1687 r. 

Izaaka Newtona w 1687 r. 

Pierwsza zasada dynamiki (zasada 

Pierwsza zasada dynamiki (zasada 

bezwładności)

bezwładności)

Istnieje taki układ odniesienia, w którym jeżeli na ciało 

Istnieje taki układ odniesienia, w którym jeżeli na ciało 

nie działa żadna siła, lub siły działające na to ciało 

nie działa żadna siła, lub siły działające na to ciało 

równoważą się, to ciało zachowuje stan spoczynku lub 

równoważą się, to ciało zachowuje stan spoczynku lub 

porusza się ruchem jednostajnym po linii prostej.

porusza się ruchem jednostajnym po linii prostej.

Taki układ nazywamy 

Taki układ nazywamy 

inercyjnym

inercyjnym

.

.

Prawo to orzeka, że ciało nie przyspiesza samo z 

Prawo to orzeka, że ciało nie przyspiesza samo z 

siebie; przyspieszenie musi być narzucone z zewnątrz. 

siebie; przyspieszenie musi być narzucone z zewnątrz. 

Ciała spoczywające dążą do przebywania w stanie 

Ciała spoczywające dążą do przebywania w stanie 

spoczynku, ciała poruszające się dążą do utrzymania 

spoczynku, ciała poruszające się dążą do utrzymania 

tego ruchu bez zmiany prędkości. Ten opór ciał wobec 

tego ruchu bez zmiany prędkości. Ten opór ciał wobec 

zmian stanu ruchu nazywa się 

zmian stanu ruchu nazywa się 

bezwładnością (inercją)

bezwładnością (inercją)

.

.

 

0

.

0

F

 

i















const

v

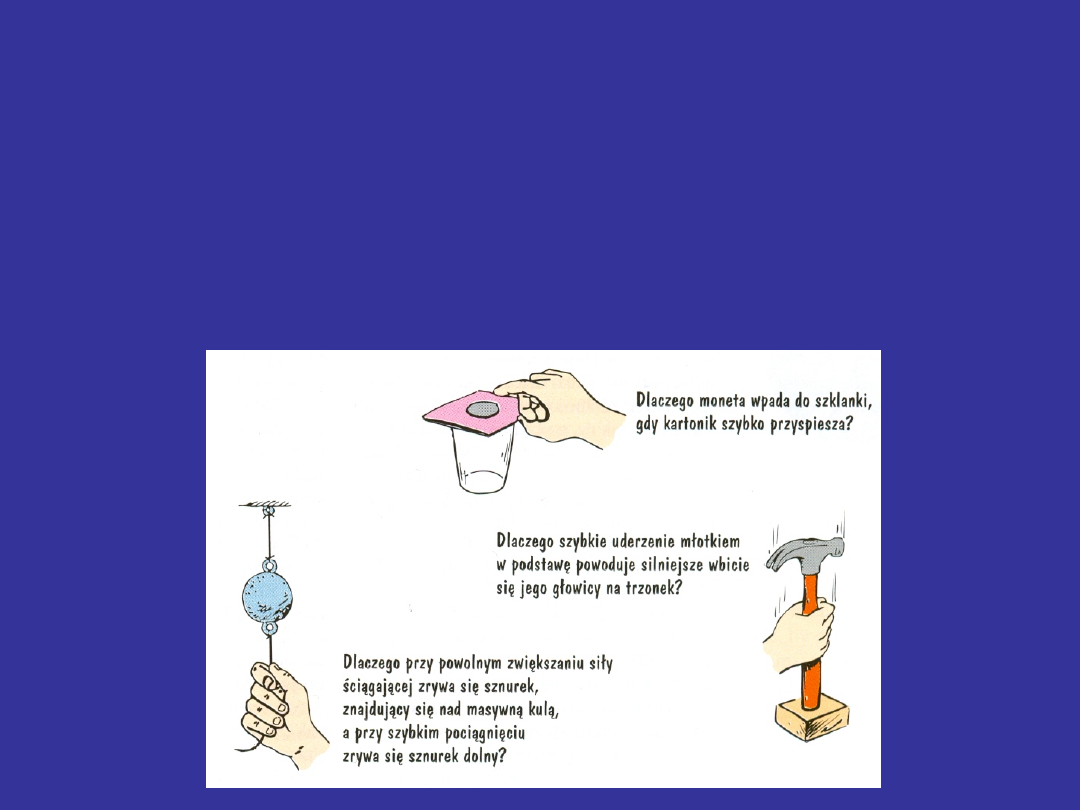
I zasada jest przełamaniem dogmatu 
Arystotelowskiego, że wszystkie ciała muszą się 
zatrzymać gdy nie ma sił zewnętrznych.
I zasadę dynamiki nazywa się też 

zasadą 

bezwładności

. 

Bezwładnością

 nazywamy 

własność ciała objawiającą się tym, że ciało nie 
zmienia ani kierunku, ani wartości swej 
prędkości, gdy nic na nie nie oddziałuje.

 

Przykłady
bezwładn

ośc

i

Druga zasada dynamiki

Druga zasada dynamiki

Jeżeli na ciało o masie m działają siły 

Jeżeli na ciało o masie m działają siły 

niezrównoważone o wypadkowej F, to ciało porusza 

niezrównoważone o wypadkowej F, to ciało porusza 

się ruchem przyspieszonym z przyspieszeniem a, 

się ruchem przyspieszonym z przyspieszeniem a, 

takim że a = F/m.

takim że a = F/m.

Korzystając z pojęcia pędu (p = mv) równanie 

Korzystając z pojęcia pędu (p = mv) równanie 

drugiej zasady dynamiki Newtona można zapisać w 

drugiej zasady dynamiki Newtona można zapisać w 

postaci:

postaci:

Czyli siła działająca na ciało jest równa pochodnej 

Czyli siła działająca na ciało jest równa pochodnej 

pędu względem czasu. Jest to bardziej ogólna 

pędu względem czasu. Jest to bardziej ogólna 

postać II zasady dynamiki. Istnieją bowiem zjawiska 

postać II zasady dynamiki. Istnieją bowiem zjawiska 

fizyczne w których masa zmienia się podczas ruchu 

fizyczne w których masa zmienia się podczas ruchu 

(np. masa rakiety maleje w miarę ubywania 

(np. masa rakiety maleje w miarę ubywania 

paliwa).

paliwa).

m

F

a

F



















0

F

 

i

 

dt

dp

dt

mv

d

dt

dv

m

ma









F

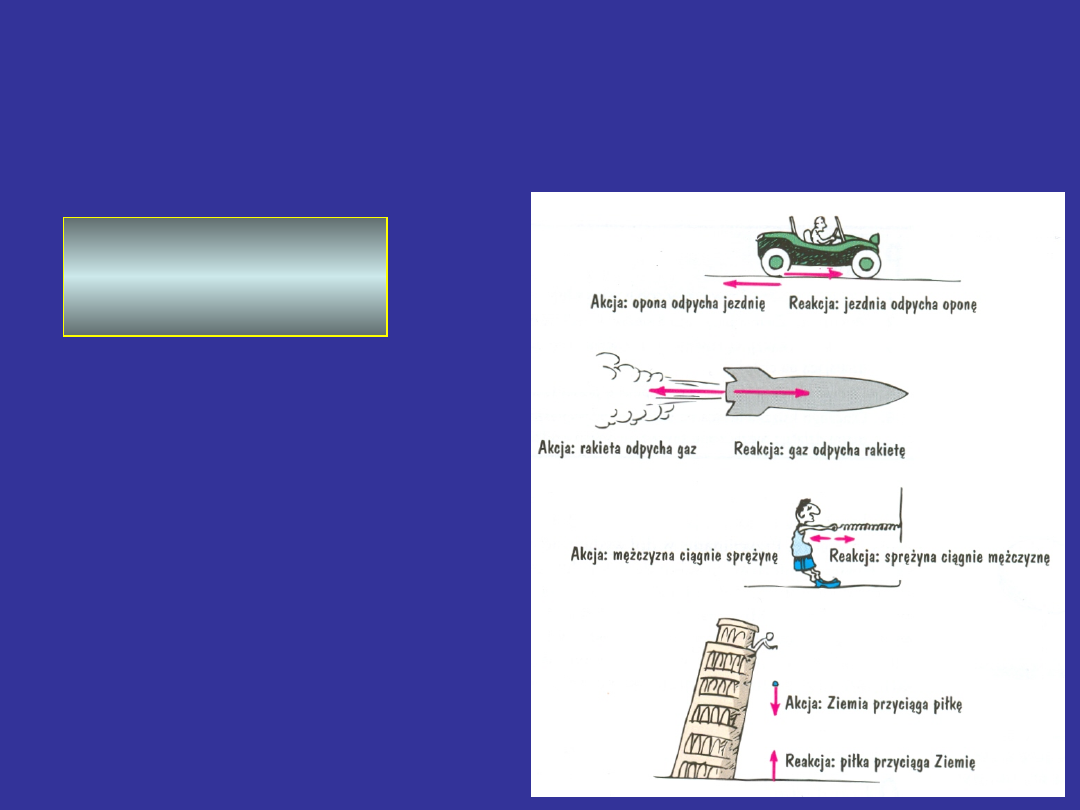
Trzecia zasada dynamiki

Trzecia zasada dynamiki

Jeżeli ciało A działa na ciało B pewną siłą F

Jeżeli ciało A działa na ciało B pewną siłą F

AB

AB

, to 

, to 

ciało B działa na ciało A siłą F

ciało B działa na ciało A siłą F

BA

BA

 równą co do 

 równą co do 

wartości bezwzględnej, lecz przeciwnie skierowaną, 

wartości bezwzględnej, lecz przeciwnie skierowaną, 

co wyrażamy wzorem:

co wyrażamy wzorem:

Siły te są jednakowe co do 

Siły te są jednakowe co do 

wielkości i skierowane 

wielkości i skierowane 

przeciwnie, lecz nie znoszą

przeciwnie, lecz nie znoszą

się ani nie równoważą, 

się ani nie równoważą, 

gdyż przyłożone są do 

gdyż przyłożone są do 

różnych ciał.

różnych ciał.

Siły akcji i reakcji

Siły akcji i reakcji

BA

AB

F

F









Dynamika ruchu punktu materialnego po okręgu

Dynamika ruchu punktu materialnego po okręgu

Zgodnie z 

I zasadą dynamiki

 tylko ruch jednostajny 

prostoliniowy może zachodzić bez działania sił, zatem 

ruch po okręgu wymaga istnienia siły (także ruch 

jednostajny po okręgu). 

W ruchu po okręgu musi wystąpić niezrównoważona 

siła skierowana do środka toru ruchu (do środka 

okręgu).

W ruchu ciała po okręgu występuje przyspieszenie 

normalne (dośrodkowe):

Zgodnie zatem z II zasadą dynamik na ciało 

poruszające się jednostajnie po okręgu musi działać 

siła:

Siła ta skierowana do środka okręgu, nazywa się siłą 

dośrodkową.

r

v

r

n

2

2







a

r

v

m

r

m

ma

F

n

n

2

2









Dynamika ruchu punktu materialnego po 

Dynamika ruchu punktu materialnego po 

okręgu

okręgu

We wszystkich przypadkach ruchu po okręgu 

stwierdza się istnienie siły dośrodkowej.

Inne przykłady:

• gdy pociąg porusza się po zakrzywionym torze, to siłę 

dośrodkową stanowi sprężyste oddziaływanie  

zewnętrznej szyny;

• w ruchu Księżyca wokół Ziemi siłą dośrodkową jest 

przyciąganie grawitacyjne Ziemi.

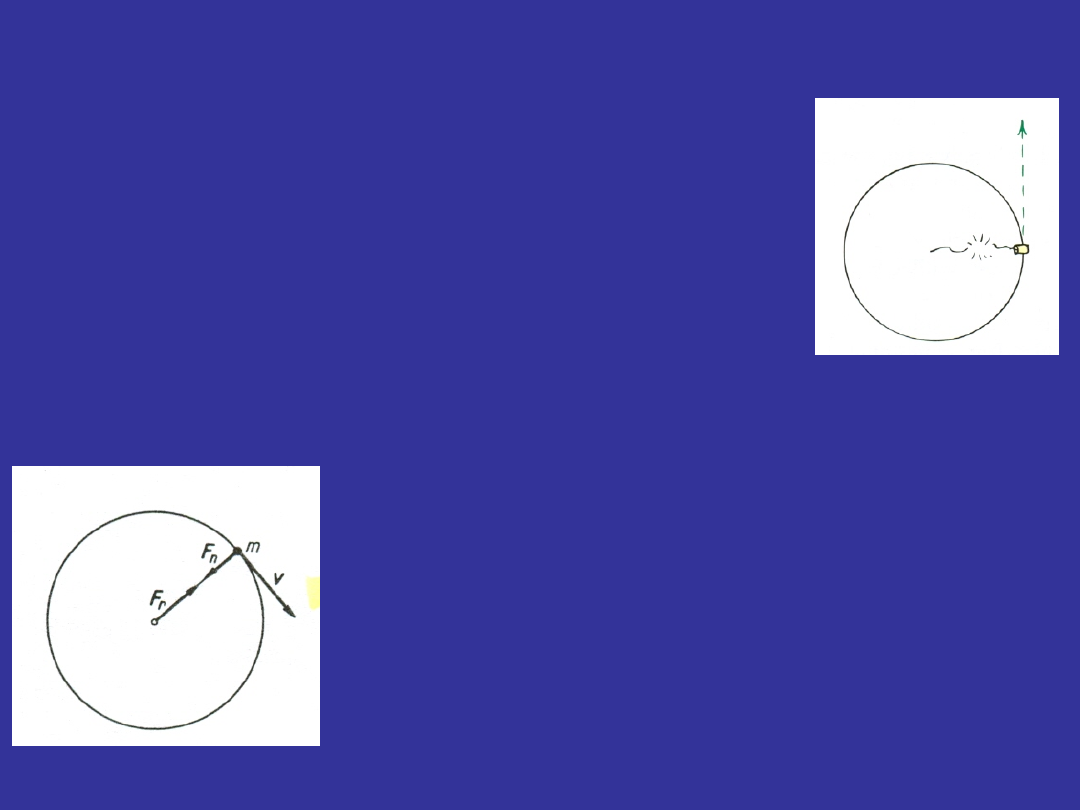
Na odważnik przymocowany do sznurka i 

wprawiony w ruch po okręgu działa siła 

dośrodkowa za pośrednictwem napiętego 

sznurka.

Siła dośrodkowa jest podstawą działania 

wszystkich wirówek. Np. na bieliznę 

działa siła dośrodkowa, a na wodę nie.

Siła dośrodkowa jest za mała, by 

utrzymać błoto na oponie i dlatego 

odrywa się ono wzdłuż linii prostych.

Dynamika ruchu punktu materialnego po 

Dynamika ruchu punktu materialnego po 

okręgu

okręgu

 Gdy na ciało poruszające się po 

okręgu w pewnej chwili przestaje 

działać siła dośrodkowa, to zgodnie z I 

zasadą dynamiki ruch ciała nie ustaje, 

lecz trwa dalej jako ruch jednostajny i 

prostoliniowy wzdłuż stycznej do toru 

kołowego; np. grudki błota odlatują od 

koła rowerowego po stycznej, 

podobnie jak iskry z tarczy 

szlifierskiej. 

Zgodnie z III zasadą dynamik działaniu 

siły dośrodkowej na ciało poruszające 

się po okręgu musi towarzyszyć 

działanie siły o tej samej wartości na 

więzy. Przez więzy rozumiemy te ciała, 

które wymuszają ruch ciała po okręgu 

(ręka, szyna kolejowa, Ziemia). Siłę 

działającą na więzy nazywamy siłą 

odśrodkową reakcji F

r

. Siła ta jest 

przyczyną zużywania się łożysk .

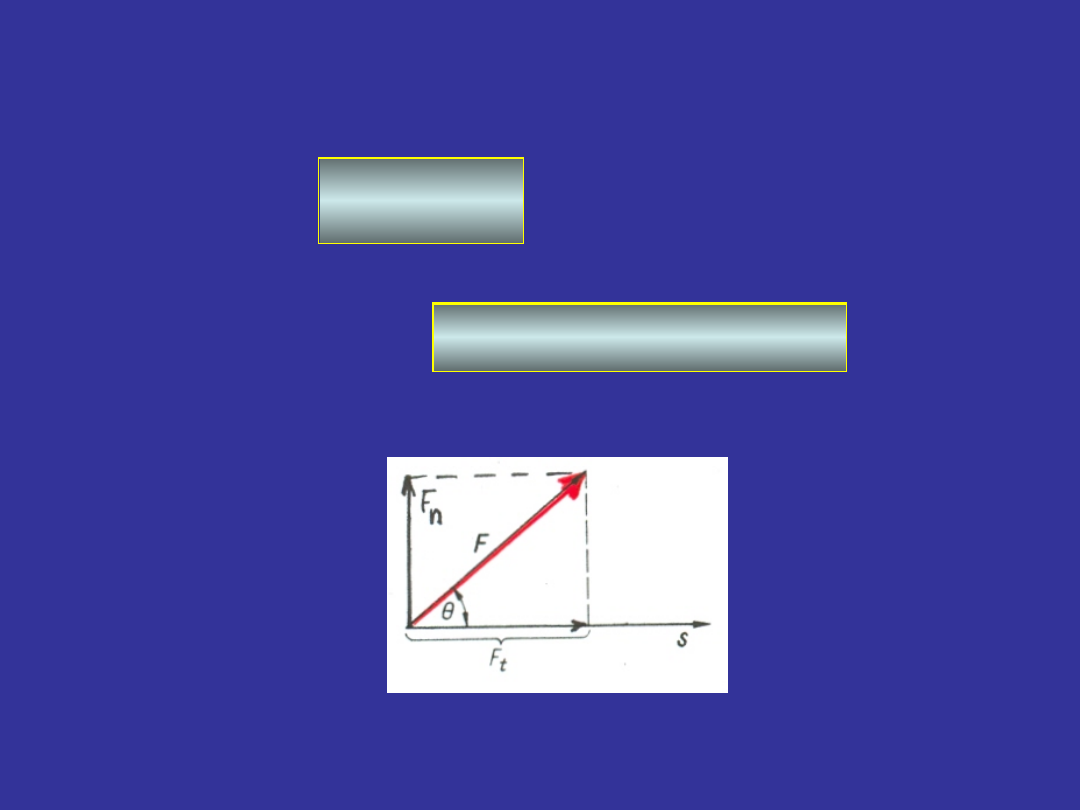
Praca

Praca

Praca W stałej siły F wyraża się iloczynem skalarnym 

Praca W stałej siły F wyraża się iloczynem skalarnym 

siły F i wektora przesunięcia s czyli:

siły F i wektora przesunięcia s czyli:

Jest więc wielkością skalarną

Jest więc wielkością skalarną

Zgodnie z definicją iloczynu skalarnego: 

Zgodnie z definicją iloczynu skalarnego: 

gdzie 

gdzie 





 kąt między kierunkami siły i przesunięcia 

 kąt między kierunkami siły i przesunięcia 

Pracę wykonuje tylko składowa F

Pracę wykonuje tylko składowa F

t

t

 

 

styczna do przesunięcia s

styczna do przesunięcia s







 s

F

 W

s

F

s

F

t











cos

 W

Praca może przyjmować zarówno wartości dodatnie, 

jak i ujemne.
Praca jest dodatnia, gdy  < 90

o

, a ujemna – gdy  > 

90

o

.  Praca jest równa 0, gdy kierunek siły jest 

prostopadły do kierunku przesunięcia ( = 90

o

).

Np. praca wykonana przez siłę ciężkości jest 

dodatnia przy spadku ciała, ujemna – przy 

podnoszeniu do góry, a równa zeru – przy 

przesuwaniu ciała po torze poziomym.
Jeżeli wartość F

t

 nie jest stała, lecz zależy od 

położenia ciała, wówczas należy rozpatrywać 

różniczkę pracy dW, będącą iloczynem siły F

t

 i 

różniczki przesunięcia ds:

W przypadku najogólniejszym, gdy tor, po którym się 

przesuwa ciało, jest krzywoliniowy, pracę definiuje 

się za pomocą całki krzywoliniowej jako:

 

gdzie A i B – punkty początkowy i końcowy toru.

ds

F

t





dW

 

ds

F

B

A







 W

Praca

Praca

Jednostką pracy w układzie SI jest dżul J:

Jednostką pracy w układzie SI jest dżul J:

Dżul jest to praca wykonana podczas przesunięcia 

Dżul jest to praca wykonana podczas przesunięcia 

punktu materialnego pod wpływem działania siły 

punktu materialnego pod wpływem działania siły 

1 N na odległość 

1 N na odległość 

1 m w kierunku działania siły.

1 m w kierunku działania siły.

Jednostki pracy stosowane w innych układach:

Jednostki pracy stosowane w innych układach:

1 kGm = 9,80665 J

1 kGm = 9,80665 J

1 erg = 1 dyna x 1 cm = 10

1 erg = 1 dyna x 1 cm = 10

-7

-7

 J

 J

Gdyby sztangista był wyższy, 

Gdyby sztangista był wyższy, 

musiałby

musiałby

wykonać większą pracę, aby 

wykonać większą pracę, aby 

podnieść

podnieść

sztangę.

sztangę.

2

2

1

1

1J

 

s

m

kg

m

N









Moc

Moc

Jest to wielkość wskazująca jaka pracę może 

Jest to wielkość wskazująca jaka pracę może 

wykonać dany układ w jednostce czasu.

wykonać dany układ w jednostce czasu.

Moc średnia:

Moc średnia:

Moc chwilowa:

Moc chwilowa:

Jednostką mocy w układzie SI jest wat [W]: moc 

Jednostką mocy w układzie SI jest wat [W]: moc 

jest równa jednemu watowi, jeżeli stała siła 

jest równa jednemu watowi, jeżeli stała siła 

wykonuje pracę jednego dżula w czasie 1 sekundy: 

wykonuje pracę jednego dżula w czasie 1 sekundy: 

1 W = 1 J/1 s = 1 J/s

1 W = 1 J/1 s = 1 J/s

Inne jednostki spoza układu SI:

Inne jednostki spoza układu SI:

1 kGm/s = 9,80655 W

1 kGm/s = 9,80655 W

1 KM = 75 kGm/s = 736 W

1 KM = 75 kGm/s = 736 W

t

W







P

 

v

F

dt

ds

F

dt

dW

t

W

t

t

t

















0

lim

P

 

Energia

Energia

Energia kinetyczna

Rozważmy  ruch prostoliniowy punktu materialnego, 
zachodzący pod wpływem działania siły F. Ruch ten 
jest jednostajnie przyspieszony, z prędkością 
początkową v

1

 i po przebyciu drogi s prędkością 

końcową v

2

. Praca siły F:

Energię kinetyczną punktu materialnego o masie m  
poruszającego się z prędkością v określamy wzorem:

Praca siły powodującej ruch punktu jest równa 
przyrostowi jego energii kinetycznej:   

W = E

k2

 – E

k1

2

2

2

2

1

2

2

2

1

2

2

mv

mv

a

v

v

ma

mas

s

F

W

t













2

2

mv

E

k



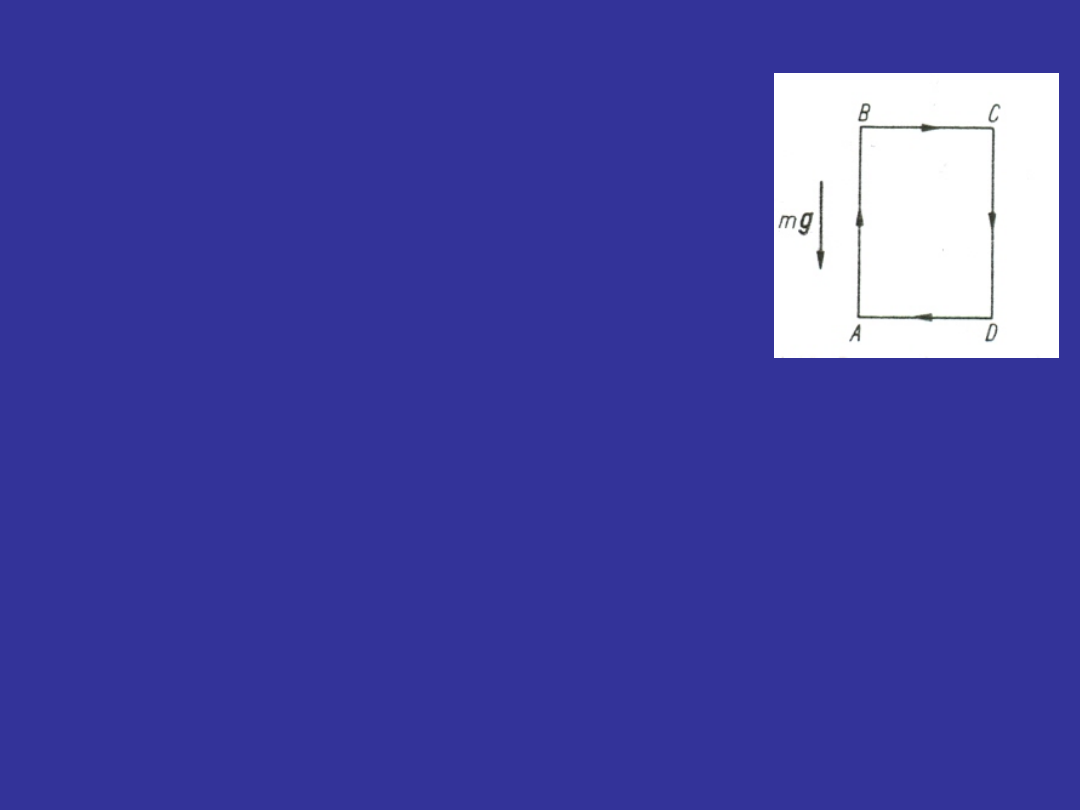
Siły zachowawcze

W polu siły ciężkości (skierowanym 

pionowo w dół) przesuwa się punkt 

materialny po torze zamkniętym 

ABCDA. Chcemy obliczyć pracę tej 

siły po torze zamkniętym ABCDA: 

W

AB

 = -mgh;

W

BC

 = 0;

W

CD

 = mgh;

W

DA

 = 0.

Zatem:            

W

ABCDA

 = 0.

Siłę nazywamy zachowawczą albo potencjalną, 

jeżeli jej praca po dowolnym torze zamkniętym jest 

równa zeru. 

Siła ciężkości jest siłą zachowawczą. Zachowawczą 

jest też siła sprężystości. Nie jest siłą 

zachowawczą siła tarcia, siła oporu powietrza, siła 

oporu (lepkość) cieczy.
Z faktu, że praca siły zachowawczej po drodze 

zamkniętej równa się zeru, wynika ważny wniosek:

Praca siły zachowawczej nie zależy od kształtu 

drogi, a tylko od wyboru punktu początkowego i 

końcowego.

Energia potencjalna

Energia potencjalna

Energią potencjalną ciała w punkcie P względem 

punktu O nazywamy pracę, jaką wykonuje siła 

zachowawcza przy przesunięciu tego ciała od 

punktu P do punktu O.

Wartość energii potencjalnej zależy od wyboru 

punktu odniesienia O.
Grawitacyjną energię potencjalną określamy jako 

pracę siły ciężkości mg na pionowym torze o 

wysokości h, zatem:

Energia potencjalna sprężystości jest równa:

gdzie x oznacza dowolne odkształcenie ciała 

(wydłużenie, skrócenie itp.).

mgh

E

p



2

2

1

kx

E

p



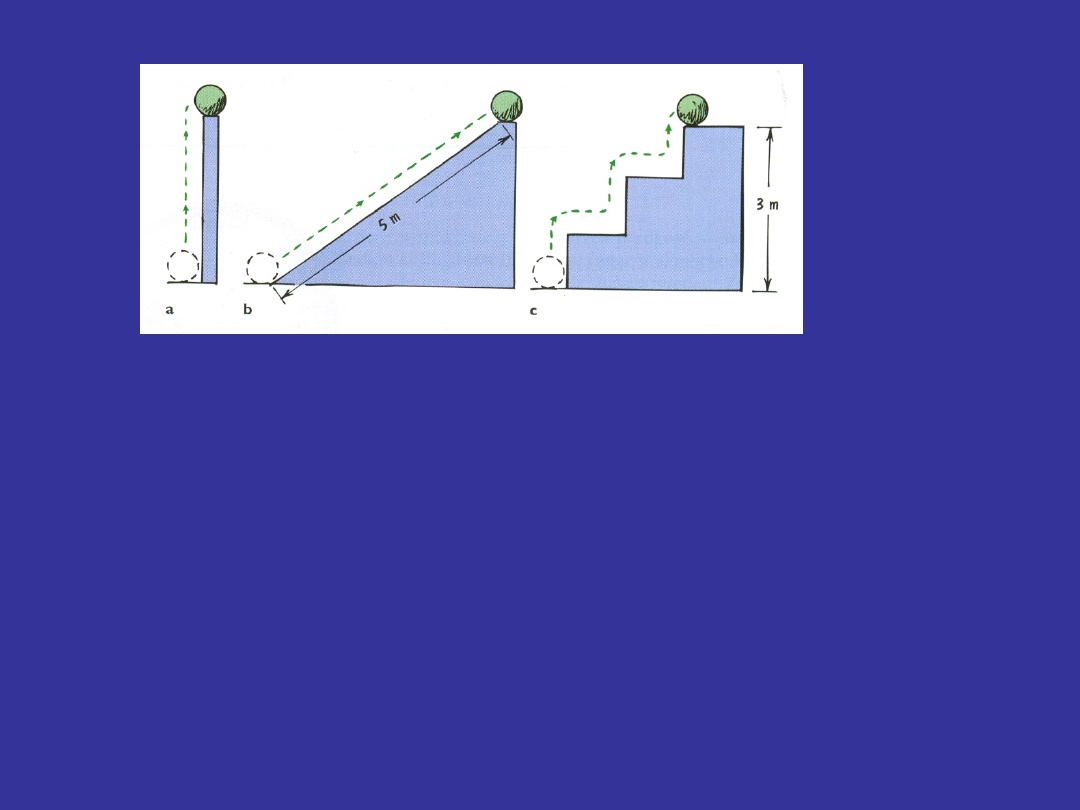
Energia potencjalna

Energia potencjalna

Energia potencjalna kuli o ciężarze 10 N jest taka 

sama 
(i równa 30 J) we wszystkich trzech przypadkach, 

gdyż praca podniesienia jej na wysokość 3 m jest 

niezależna od tego, czy:
(a) została podniesiona siłą 10 N;
(b) została wtoczona siłą 6 N po równi pochyłej o 

długości 5 m;
(c) została wniesiona siłą 10 N  po trzech schodach o 
     wysokości  1 m każdy. 
W ruchu poziomym (przy braku tarcia) nie jest 

wykonywana żadna praca.

II. DYNAMIKA BRYŁY SZTYWNEJ

II. DYNAMIKA BRYŁY SZTYWNEJ

Pojęcie bryły sztywnej

Pojęcie bryły sztywnej

Bryła sztywna to ciało, które pod działaniem sił nie 

Bryła sztywna to ciało, które pod działaniem sił nie 

ulega odkształceniom, tzn. odległości dwóch 

ulega odkształceniom, tzn. odległości dwóch 

dowolnych punktów takiego ciała pozostają stałe. 

dowolnych punktów takiego ciała pozostają stałe. 

Dla bryły sztywnej obowiązują wszystkie wnioski i 

Dla bryły sztywnej obowiązują wszystkie wnioski i 

zależności słuszne dla układu punktów 

zależności słuszne dla układu punktów 

materialnych.

materialnych.

Rodzaje ruchów bryły sztywnej

Rodzaje ruchów bryły sztywnej

Bryła sztywna może wykonywać dwa rodzaje 

Bryła sztywna może wykonywać dwa rodzaje 

ruchów prostych: 

ruchów prostych: 

postępowy i obrotowy

postępowy i obrotowy

.

.

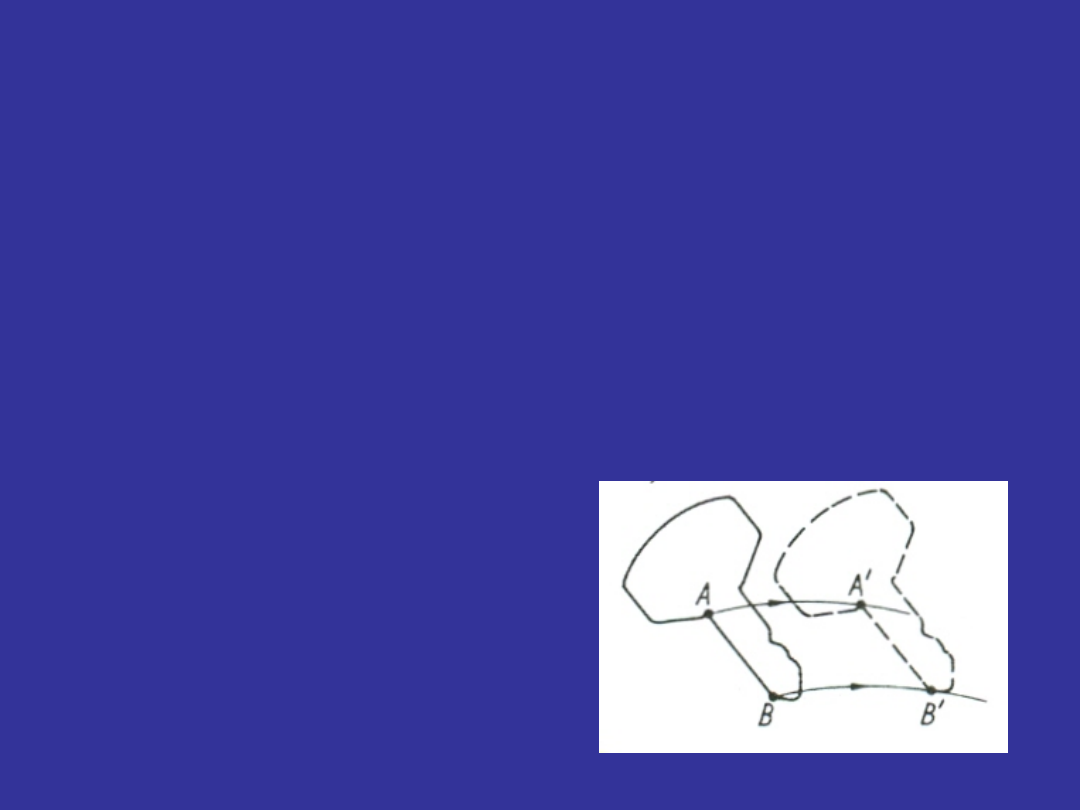
Ruchem postępowym

Ruchem postępowym

 bryły sztywnej nazywamy 

 bryły sztywnej nazywamy 

ruch, w którym dowolny odcinek łączący dwa 

ruch, w którym dowolny odcinek łączący dwa 

punkty bryły , np. A i B, zachowuje stale położenie 

punkty bryły , np. A i B, zachowuje stale położenie 

do siebie równoległe. Wszystkie punkty bryły

do siebie równoległe. Wszystkie punkty bryły

zakreślają takie same

zakreślają takie same

tory, mają jednakowe

tory, mają jednakowe

prędkości i przyspieszenia.

prędkości i przyspieszenia.

Ruch bryły sztywnej

Ruch bryły sztywnej

sprowadza się do 

sprowadza się do 

ruchu punktu

ruchu punktu

materialnego (najczęściej

materialnego (najczęściej

jest to środek masy).

jest to środek masy).

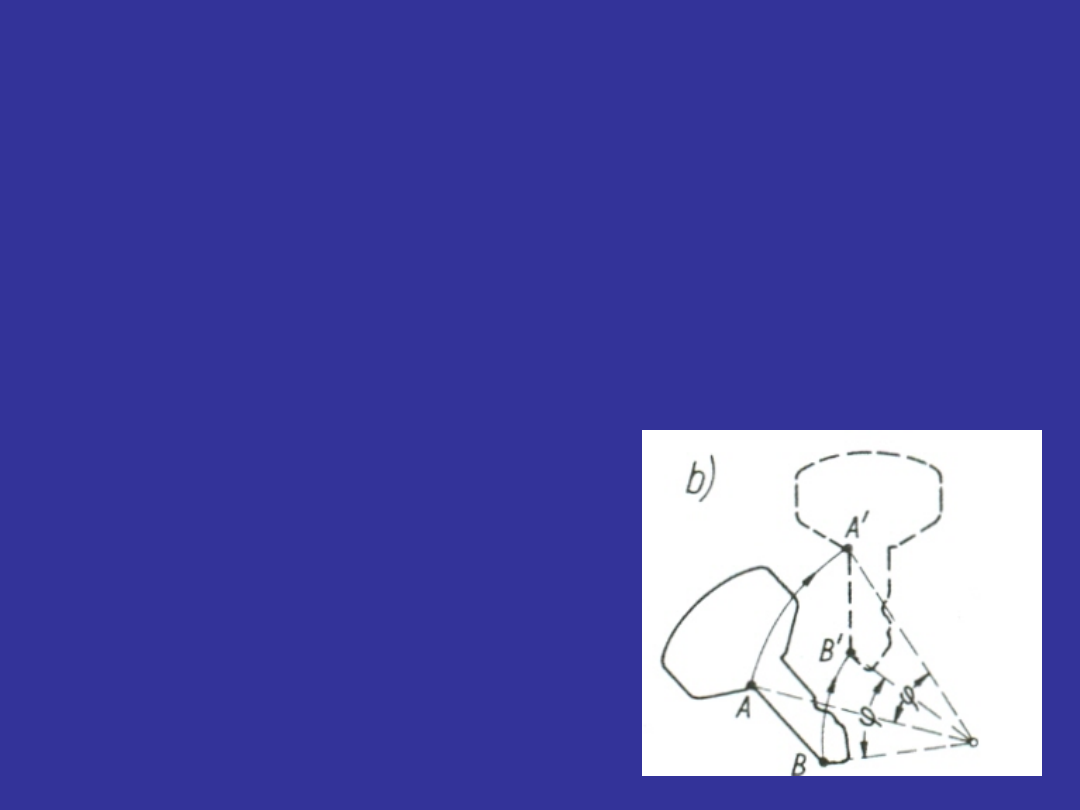
Ruch obrotowy

Ruch obrotowy

 bryły charakteryzuje się tym, że 

 bryły charakteryzuje się tym, że 

wszystkie punkty bryły poruszają się po 

wszystkie punkty bryły poruszają się po 

okręgach, których środki leżą na jednej prostej.

okręgach, których środki leżą na jednej prostej.

Prostą tą nazywamy osią obrotu. Punkty 

Prostą tą nazywamy osią obrotu. Punkty 

znajdujące się na osi obrotu są nieruchome, a 

znajdujące się na osi obrotu są nieruchome, a 

pozostałe punkty poruszają się po łukach 

pozostałe punkty poruszają się po łukach 

okręgów. 

okręgów. 

Poszczególne punkty bryły charakteryzuje ta 

Poszczególne punkty bryły charakteryzuje ta 

sama prędkość kątowa i przyspieszenie kątowe.

sama prędkość kątowa i przyspieszenie kątowe.

Natomiast prędkości liniowe punktów bryły 

Natomiast prędkości liniowe punktów bryły 

sztywnej są proporcjonalne do odległości punktu 

sztywnej są proporcjonalne do odległości punktu 

od osi obrotu (v = 

od osi obrotu (v = 





r).

r).

W życiu codziennym najczęściej 

W życiu codziennym najczęściej 

mamy do czynienia z ruchami

mamy do czynienia z ruchami

złożonymi. Możemy je rozłożyć

złożonymi. Możemy je rozłożyć

na ruch postępowy i obrotowy,

na ruch postępowy i obrotowy,

względem odpowiednio

względem odpowiednio

wybranego układu odniesienia.

wybranego układu odniesienia.

Przykładem takiego ruchu

Przykładem takiego ruchu

może być ruch toczącej się

może być ruch toczącej się

po podłodze piłki.

po podłodze piłki.

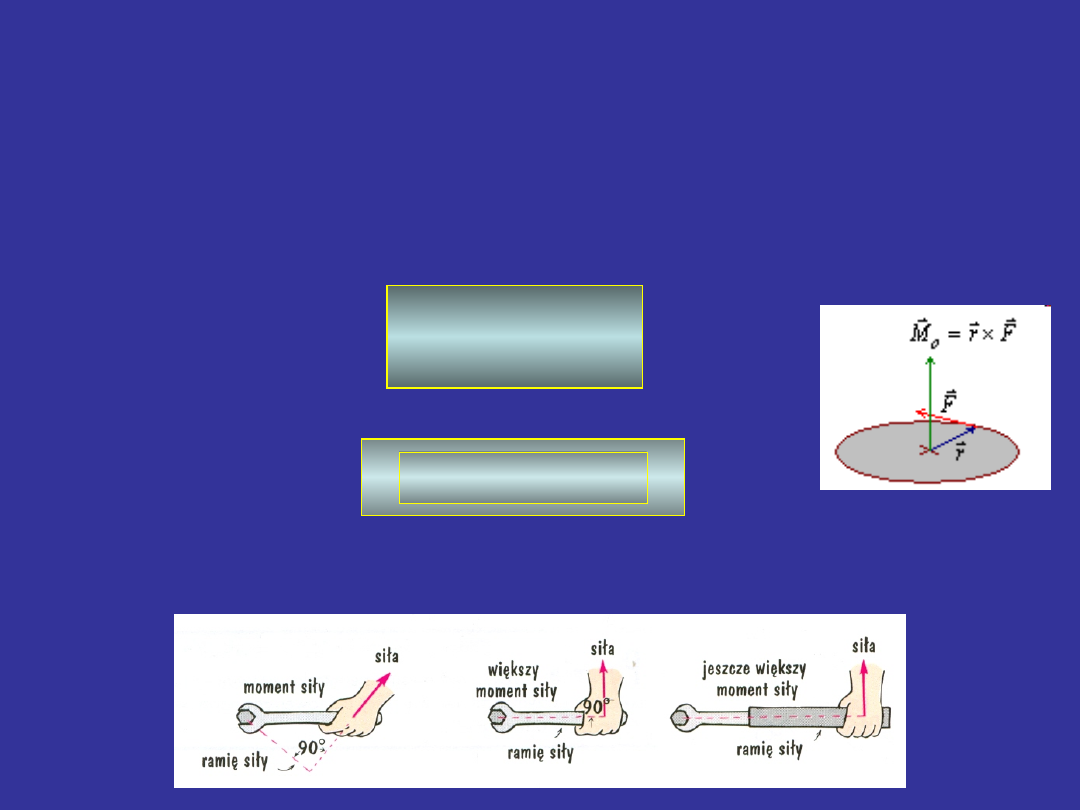
W ruchu obrotowym ważna jest nie tylko wartość 

siły, ale także jej kierunek i punkt przyłożenia.
Wielkość wywołującą ruch obrotowy nazywamy 

momentem siły

, który definiujemy następująco:

Momentem siły

 F względem punktu O osi obrotu 

nazywamy iloczyn wektorowy wektora wodzącego 

r punktu przyłożenia siły F i tej siły (początek r 

leży w punkcie O).

Wartość bezwzględna momentu siły wynosi:

Moment siły bywa też nazywany momentem 

obrotowym.
Jednostką momentu siły jest niutonometr (Nm).

 











F

r

M

 



sin

M

 

rF



Moment bezwładności

Moment bezwładności

W ruchu obrotowym bryły sztywnej ważną rolę 

W ruchu obrotowym bryły sztywnej ważną rolę 

odgrywa sposób rozmieszczenia masy bryły wokół 

odgrywa sposób rozmieszczenia masy bryły wokół 

osi obrotu. Wielkością charakteryzującą tę 

osi obrotu. Wielkością charakteryzującą tę 

własność bryły jest moment bezwładności.

własność bryły jest moment bezwładności.

Momentem bezwładności I bryły względem danej 

Momentem bezwładności I bryły względem danej 

osi nazywamy sumę iloczynów mas 

osi nazywamy sumę iloczynów mas 

poszczególnych punktów bryły i kwadratów ich 

poszczególnych punktów bryły i kwadratów ich 

odległości od danej osi, a więc:

odległości od danej osi, a więc:

Jednostką momentu bezwładności jest 1 kg m

Jednostką momentu bezwładności jest 1 kg m

2

2

. 

. 

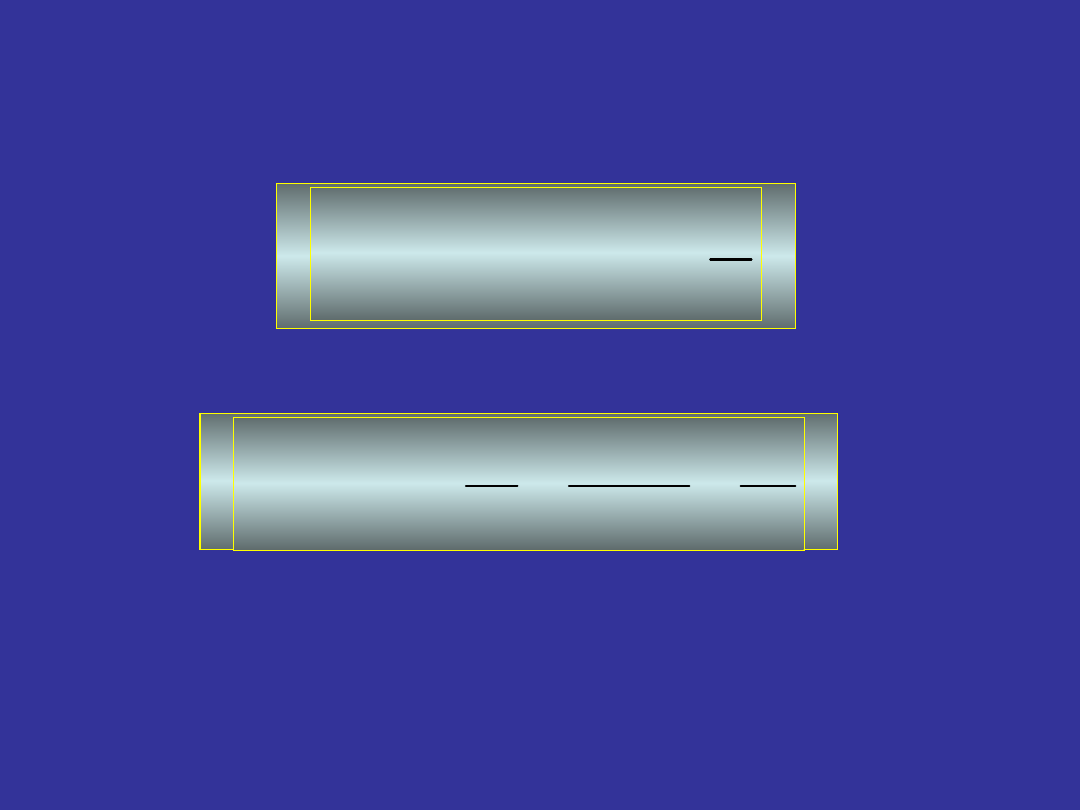
Moment bezwładności ciał o tej samej masie i tym 

Moment bezwładności ciał o tej samej masie i tym 

samym promieniu zależy od ich kształtu.

samym promieniu zależy od ich kształtu.

2

1

I

 

i

n

i

i

r

m







Moment bezwładności

Moment bezwładności

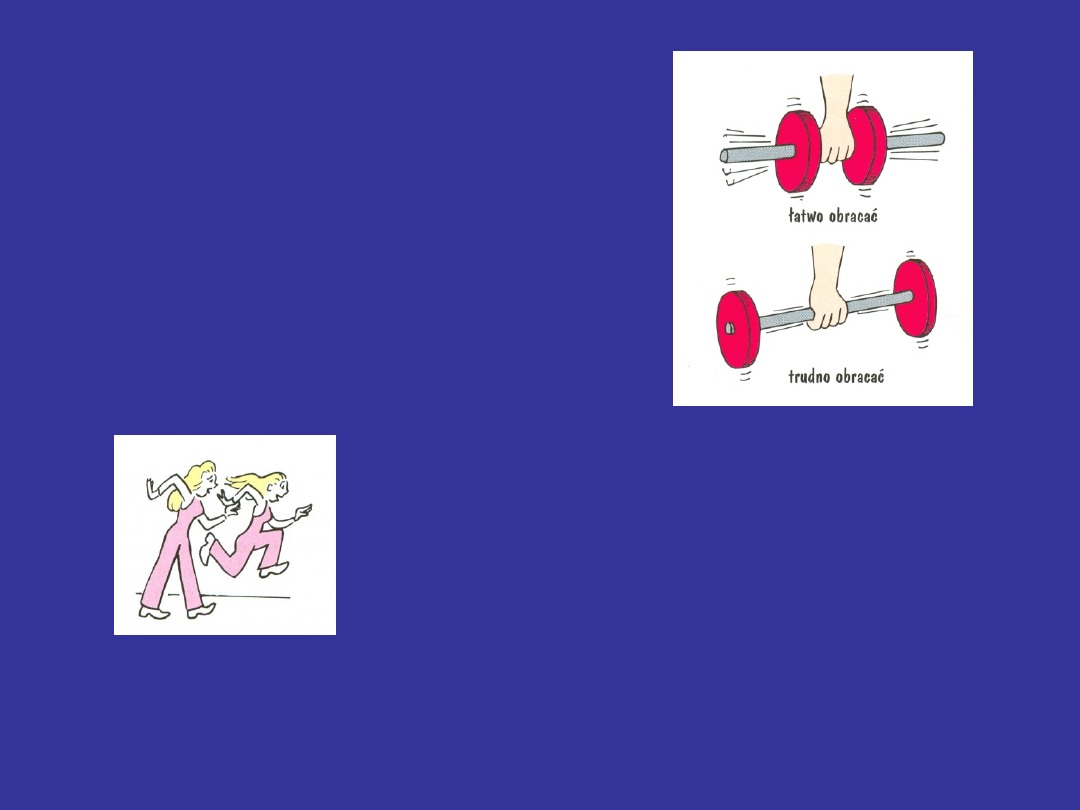
Im większy moment bezwładności, 

Im większy moment bezwładności, 

tym trudniej zmienić stan ruchu

tym trudniej zmienić stan ruchu

obrotowego, zatrzymać obrót

obrotowego, zatrzymać obrót

lub wprawić w ruch obrotowy.

lub wprawić w ruch obrotowy.

Fakt ten jest np. wykorzystywany

Fakt ten jest np. wykorzystywany

przez cyrkowych linoskoczków,

przez cyrkowych linoskoczków,

którzy dla utrzymania równowagi

którzy dla utrzymania równowagi

posługują się długimi drążkami.

posługują się długimi drążkami.

Podczas biegu mocno zginamy 

Podczas biegu mocno zginamy 

nogi w kolanach, zmniejszając 

nogi w kolanach, zmniejszając 

tym samym ich moment 

tym samym ich moment 

bezwładności.

bezwładności.

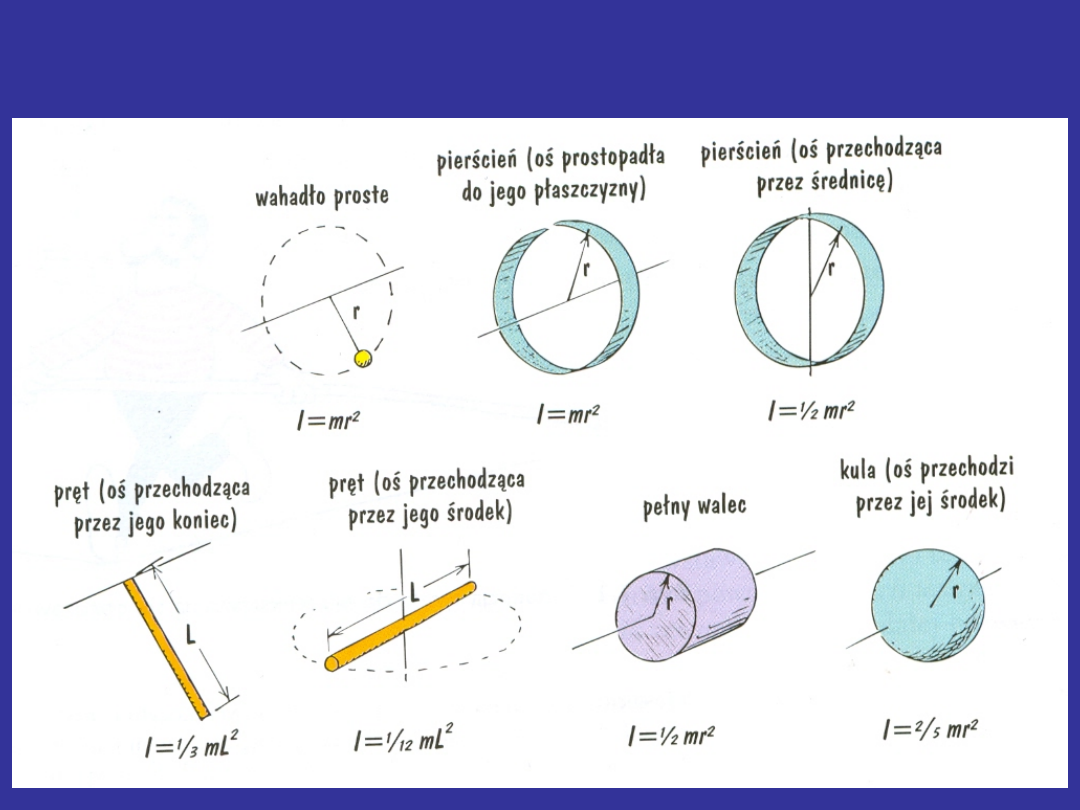
Moment bezwładności

Moment bezwładności

Momenty bezwładności niektórych brył

Momenty bezwładności niektórych brył

 

 

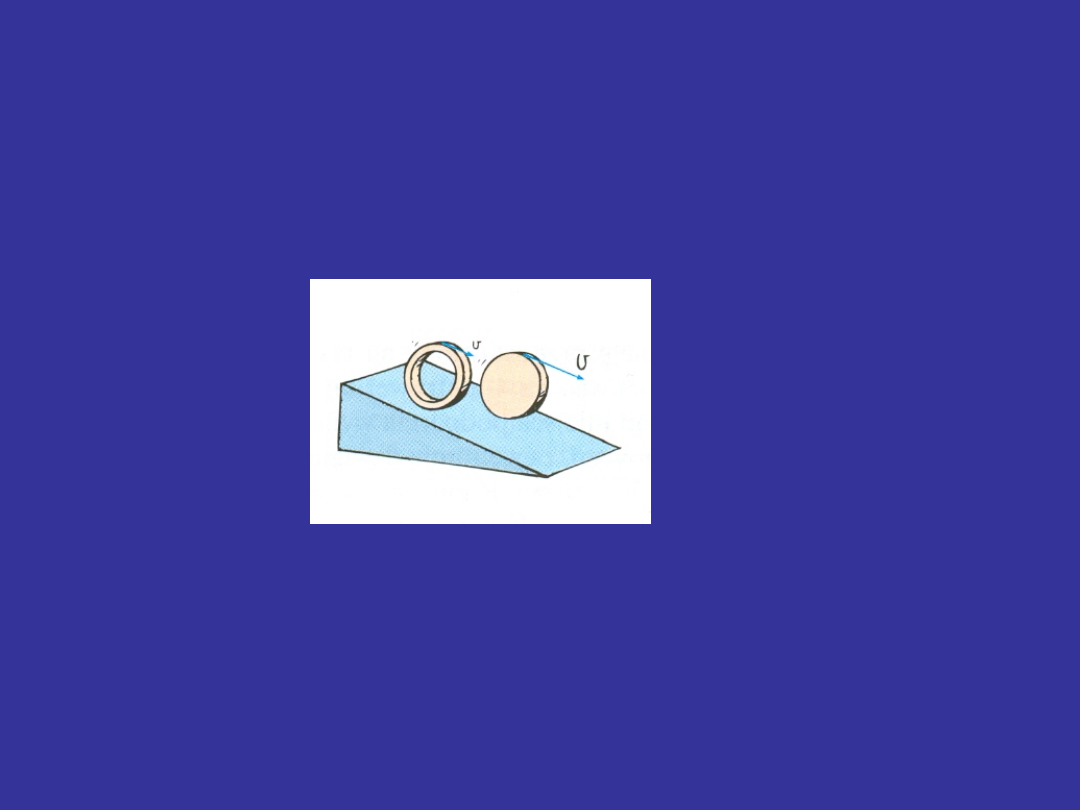
Moment bezwładności

Moment bezwładności

Ciała mające większe momenty bezwładności (przy 

Ciała mające większe momenty bezwładności (przy 

tej samej masie) silniej przeciwstawiają się ruchowi 

tej samej masie) silniej przeciwstawiają się ruchowi 

obrotowemu.

obrotowemu.

Które ciało stoczy się szybciej po równi pochyłej: 

Które ciało stoczy się szybciej po równi pochyłej: 

pełny walec czy pierścień o tej samej masie i tej 

pełny walec czy pierścień o tej samej masie i tej 

samej średnicy zewnętrznej?

samej średnicy zewnętrznej?

Pełny walec stacza się po równi pochyłej szybciej 

Pełny walec stacza się po równi pochyłej szybciej 

niż pierścień o tej samej masie i tej samej średnicy 

niż pierścień o tej samej masie i tej samej średnicy 

zewnętrznej, ponieważ pierścień ma większy 

zewnętrznej, ponieważ pierścień ma większy 

moment bezwładności (masa pierścienia skupiona 

moment bezwładności (masa pierścienia skupiona 

na jego obwodzie, daleko od osi obrotu) i jego 

na jego obwodzie, daleko od osi obrotu) i jego 

przyspieszenie jest mniejsze.

przyspieszenie jest mniejsze.

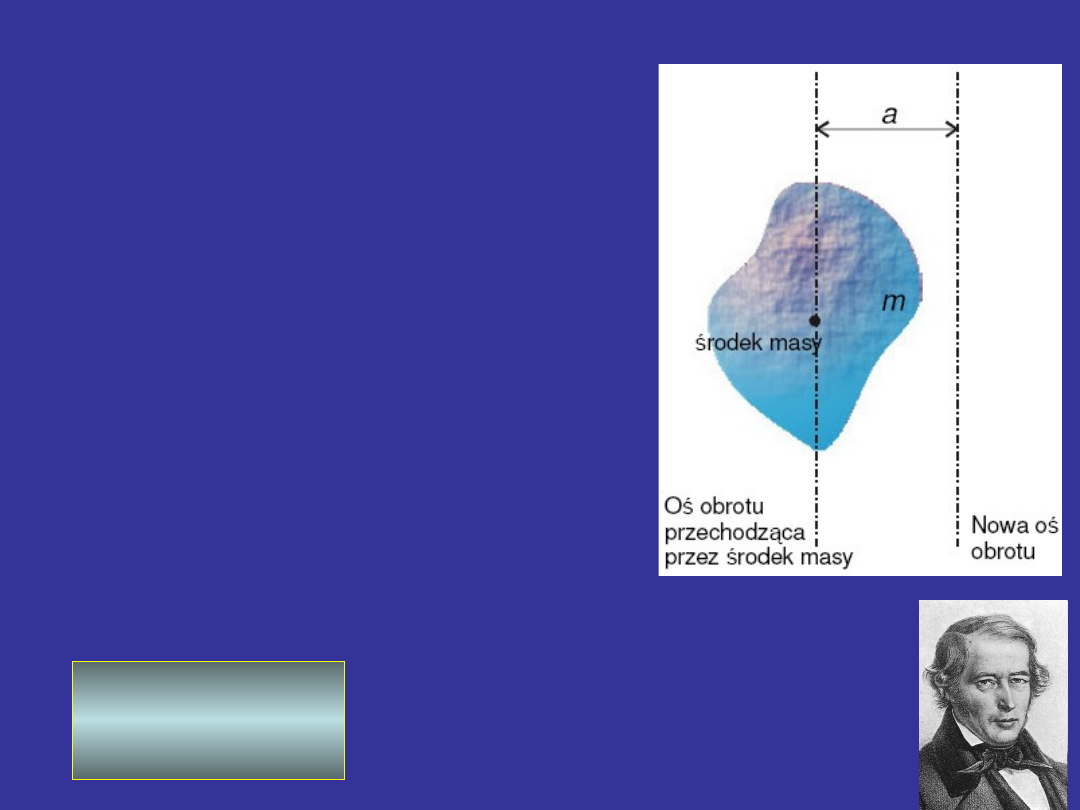
Twierdzenie Steinera

Twierdzenie Steinera

Aby obliczyć moment bezwładności

Aby obliczyć moment bezwładności

względem dowolnej osi, nie przecho-

względem dowolnej osi, nie przecho-

dzącej przez środek masy bryły,

dzącej przez środek masy bryły,

posługujemy się

posługujemy się

twierdzeniem Steinera

twierdzeniem Steinera

:

:

Moment bezwładności 

Moment bezwładności 

I

I

 bryły

 bryły

względem dowolnej osi jest równy

względem dowolnej osi jest równy

sumie momentu bezwładności 

sumie momentu bezwładności 

I

I

0

0

względem osi równoległej

względem osi równoległej

przechodzącej przez środek

przechodzącej przez środek

masy bryły oraz iloczynu

masy bryły oraz iloczynu

masy tej bryły 

masy tej bryły 

m

m

 i kwadratu 

 i kwadratu 

odległości 

odległości 

a 

a 

obu osi, czyli:

obu osi, czyli:

Jakob Steiner (1796-1863), 

Jakob Steiner (1796-1863), 

szwajcarski matematyk.

szwajcarski matematyk.

 

 

W 1834 na uniwersytecie w 

W 1834 na uniwersytecie w 

Berlinie 

Berlinie 

została utworzona  

została utworzona  

dla niego katedra 

dla niego katedra 

geometrii.

geometrii.

 

 

2

0

I

 

ma

I 



Druga zasada dynamiki ruchu obrotowego

Druga zasada dynamiki ruchu obrotowego 

Rozważmy obracającą się bryłę sztywną, składającą 

się z punktów materialnych m

1

, m

2

, ... , m

n

, na które 

działają siły F

1

, F

2

, ... , F

n

, a r

1

, r

2

, ... , r

n

 są 

promieniami punktów materialnych. Wypadkowy 

moment sił M działających na rozważaną bryłę 

wyniesie:

Słownie 

drugą zasadę dynamiki Newtona ruchu 

obrotowego

 można wyrazić następująco:

Jeśli na pewne ciało, które posiada pewien swój 

moment bezwładności I zadziałają zewnętrzne siły, 

które wywrą na to ciało pewien wypadkowy moment 

siły M, to w wyniku tego działania ciało będzie 

obracać się z przyspieszeniem kątowym  takim, że 































I

r

m

r

m

r

m

r

a

m

r

F

r

i

i

i

i

i

i

i

i

i

i

i

i

2

2

M



I



M











 

I

M

Moment pędu (kręt)

Moment pędu (kręt)

Moment pędu L punktu materialnego o masie m i 

wektorze wodzącym r, poruszającego się z 

prędkością v względem osi obrotu odległej o r od 

tego punktu definiujemy wzorem:

Moment pędu bryły jest sumą momentów pędu 

wszystkich jego punktów, czyli:

Moment pędu bryły równa się iloczynowi jej 

prędkości kątowej  i momentu bezwładności I.

Jednostką momentu pędu jest 1 kgm

2

/s.











I

r

m

r

m

i

i

i

i







2

2

L



I



L



2

mr

rmv

p

r

L









Moment pędu (kręt)

Moment pędu (kręt)

Posługując sie pojęciem momentu pędu można 

inaczej wyrazić 

drugą zasadę dynamiki Newtona

:

Pochodna momentu pędu L bryły względem czasu t 

jest równa momentowi siły M działającej na tę 

bryłę.

Mamy bowiem:

Dlaczego łatwiej zachować równowagę na rowerze 

jadącym niż stojącym?

Podczas ruchu koła roweru mają pewien moment 

pędu. Przewrócić rower znaczy: zmienić jego 

moment pędu, a to wymaga przyłożenia znacznie 

większego momentu sił niż w przypadku roweru 

nieruchomego.

 

dt

dL

dt

I

d

dt

Id

I

M















Pierwsza zasada dynamiki ruchu obrotowego

Pierwsza zasada dynamiki ruchu obrotowego

Rozważmy bryłę sztywną mogącą się obracać bez tarcia 

wokół stałej osi. Zgodnie z II zasadą dynamiki ruchu 

obrotowego (M=I), jeżeli na bryłę tę będzie działał 

moment siły M, to wywoła on ruch obrotowy bryły z 

określonym przyspieszeniem kątowym .

Przypuśćmy, że na obracającą się bryłę nie działa żaden 

moment siły, tzn. M=0. Wtedy, ponieważ bryła jest 

sztywna i jej moment bezwładności jest stały i różny od 

zera, przyspieszenie kątowe musi być równe zeru. 

Oznacza to, że prędkość kątowa obracającej się bryły, 

na którą nie działa moment siły, nie ulega zmianie.
Pierwsza zasada dynamiki ruchu obrotowego mówi, że:

Bryła sztywna nie poddana działaniu momentu siły 

pozostaje nieruchoma lub wykonuje ruch obrotowy 

jednostajny.

Słuszność tej zasady można sprawdzić obserwując koło 

o dużej masie, zamocowane na łożyskach. Koło takie 

wprawione w ruch obrotowy, zachowuje ten ruch bez 

zmiany tym dłużej, im lepsze są łożyska.

Trzecia zasada dynamiki ruchu obrotowego

Trzecia zasada dynamiki ruchu obrotowego

Istnienie momentu siły działającego na daną bryłę 

jest zawsze wynikiem oddziaływania na nią innej 

bryły.
Trzecia zasada dynamiki ruchu obrotowego mówi, 

że:

Jeżeli na bryłę A działa bryła B pewnym momentem 

siły M

AB

, to bryła B działa na A momentem M

BA

 

równym co do wartości, lecz przeciwnie 

skierowanym:

Słuszność tej zasady można sprawdzić obserwując 

działanie silników; np. w chwili uruchomienia 

silnika samochodu można zauważyć, że blok silnika 

ulega pewnemu skręceniu w kierunku przeciwnym 

do obrotu wału. Dzieje się tak dlatego, że 

wprawienie w ruch obrotowy wału silnika wymaga 

działania momentu siły, jednocześnie zaś działa 

przeciwnie skierowany moment na korpus silnika.

BA

AB

M

M





Energia kinetyczna ruchu obrotowego

Energia kinetyczna ruchu obrotowego

Bryła sztywna wprawiona w ruch obrotowy ma energię 

kinetyczną. Energie tę obliczamy, sumując energie 

kinetyczne poszczególnych punktów bryły. Energia 

dowolnego i-tego punktu bryły o masie m

i

 wynosi:

Energia kinetyczna całej bryły:

Energia kinetyczna ruchu obrotowego jest równa 

połowie iloczynu momentu bezwładności i kwadratu 

prędkości kątowej.
Analogia do wzoru na energię kinetyczną punktu 

materialn.













2

2

2

2

k

2

1

2

1

E

i

i

i

i

i

r

m

r

m

E





2

k

2

1

E



I



2

2

2

2

1

2

1



i

i

i

i

i

r

m

v

m

E





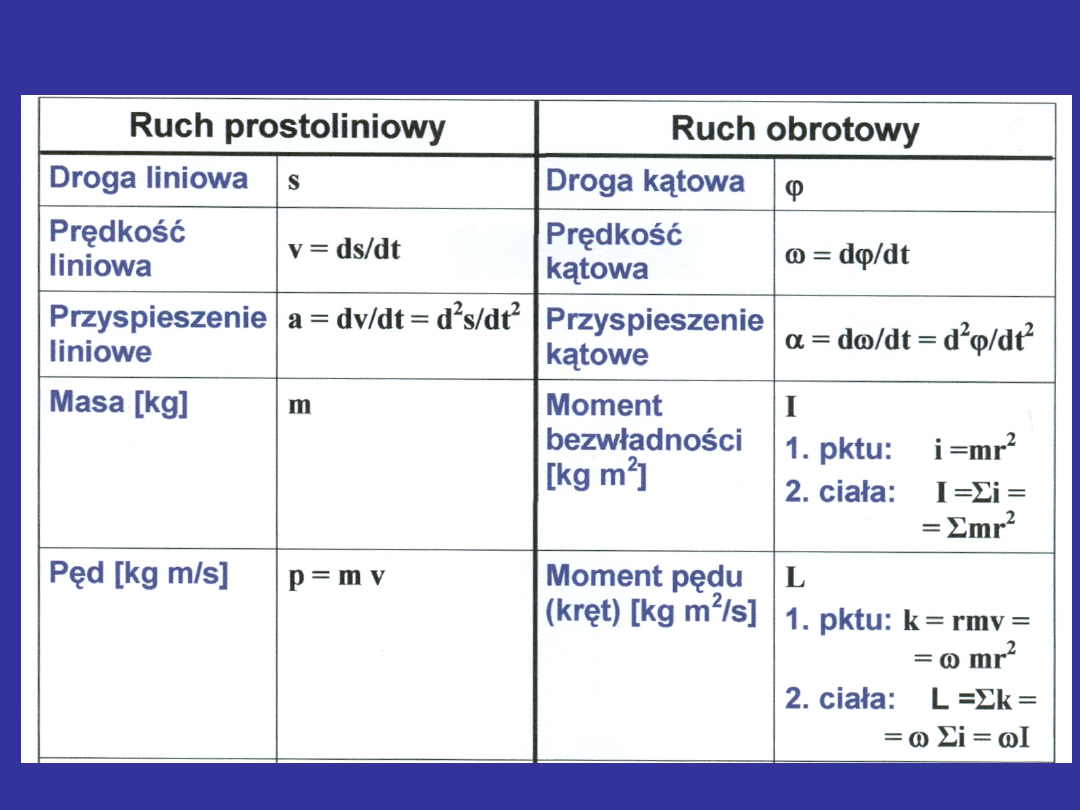
Analogia  między  ruchem  postępowym  i 

Analogia  między  ruchem  postępowym  i 

obrotowym

obrotowym

Analogia  między  ruchem  postępowym  i 

Analogia  między  ruchem  postępowym  i 

obrotowym

obrotowym

III. ZASADY ZACHOWANIA W 

III. ZASADY ZACHOWANIA W 

MECHANICE

MECHANICE

 

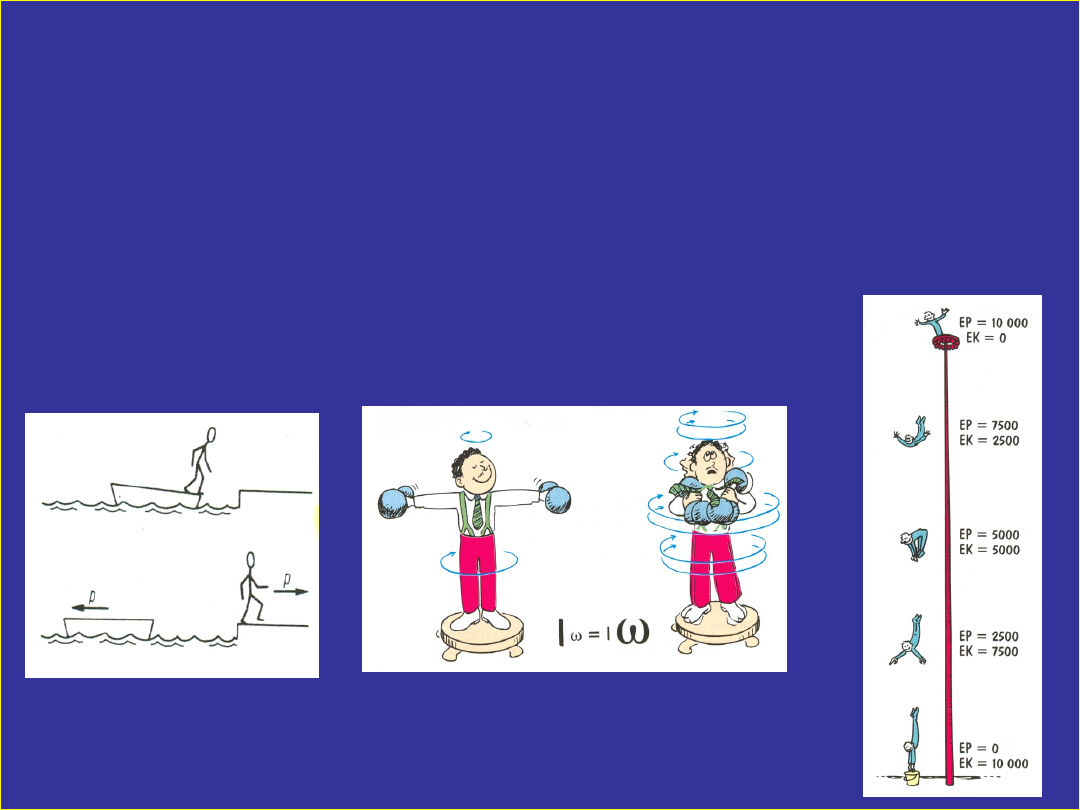
ZASADY ZACHOWANIA W MECHANICE

ZASADY ZACHOWANIA W MECHANICE

Zasadami 

zachowania 

nazywa 

się 

prawa 

stwierdzające, 

że 

jakaś 

wielkość 

fizyczna 

pozostaje stała w czasie.

              (iii) 

energii
W mechanice znamy trzy zasady zachowania:
       (i) pędu

   (ii) momentu pędu

  

Zasada zachowania pędu

Zasada zachowania pędu

Rozważmy układ punktów materialnych o masach 

Rozważmy układ punktów materialnych o masach 

m

m

1

1

, m

, m

2

2

, …, m

, …, m

n

n

, na które działają siły zewnętrzne F

, na które działają siły zewnętrzne F

1

1

, 

, 

F

F

2

2

, …, F

, …, F

n

n

. Według II zasady dynamiki Newtona dla 

. Według II zasady dynamiki Newtona dla 

dowolnego (i-tego) punktu zachodzi zależność:

dowolnego (i-tego) punktu zachodzi zależność:

                         

                         

,

,

która dla wszystkich punktów (sumowanie) 

która dla wszystkich punktów (sumowanie) 

przyjmuje postać:

przyjmuje postać:

,

,

tzn. suma wszystkich sił zewnętrznych działających 

tzn. suma wszystkich sił zewnętrznych działających 

na układ (suma sił wewnętrznych jest równa 0) jest 

na układ (suma sił wewnętrznych jest równa 0) jest 

równa sumie zmian w czasie pędów punktów 

równa sumie zmian w czasie pędów punktów 

materialnych (pędu całkowitego układu). Czyli:

materialnych (pędu całkowitego układu). Czyli:

dt

dp

a

m

F

i

i

i

i





















n

i

i

n

i

i

n

i

i

p

dt

d

dt

dp

F

1

1

1

dt

dp

F

z



Zasada zachowania pędu

Zasada zachowania pędu

Jest to twierdzenie o pędzie całkowitym:

Jest to twierdzenie o pędzie całkowitym:

Pochodna pędu całkowitego p układu względem 

Pochodna pędu całkowitego p układu względem 

czasu t jest równa wypadkowej sił zewnętrznych F

czasu t jest równa wypadkowej sił zewnętrznych F

z

z

 

 

działających na układ.

działających na układ.

Konsekwencją tego jest następująca relacja:

Konsekwencją tego jest następująca relacja:

gdy F

gdy F

z

z

 = 0,  to  p = const

 = 0,  to  p = const

Zależność ta wyraża 

Zależność ta wyraża 

zasadę zachowania pędu

zasadę zachowania pędu

, która 

, która 

mówi, że:

mówi, że:

Jeżeli wypadkowa sił zewnętrznych działających na 

Jeżeli wypadkowa sił zewnętrznych działających na 

układ punktów materialnych jest równa zeru, to pęd 

układ punktów materialnych jest równa zeru, to pęd 

całkowity tego układu jest stały.

całkowity tego układu jest stały.

Zgodnie z zasadą zachowania pędu:

Zgodnie z zasadą zachowania pędu:

Jeżeli wypadkowa sił wewnętrznych działających na 

Jeżeli wypadkowa sił wewnętrznych działających na 

układ jest równa zeru, to pęd układu w stanie 

układ jest równa zeru, to pęd układu w stanie 

początkowym jest równy pędowi układu w stanie 

początkowym jest równy pędowi układu w stanie 

końcowym.

końcowym.

 

 

Zasada zachowania pędu

Zasada zachowania pędu

PRZYKŁADY

PRZYKŁADY

Człowiek 

wyskakujący 

na  ląd  ze  stojącej  na 
wodzie 

łódki 

– 

pęd 

układu  (łódka-człowiek) 
pozostaje  stały  (równy 
zeru).

Działanie śruby okrętowej – 
nadanie 

wodzie 

pędu 

skierowanego 

w 

tył, 

wskutek 

czego 

statek 

uzyskuje  pęd  skierowany 
do przodu. Podobnie działa 
śmigło 

samolotu 

i 

śmigłowca;

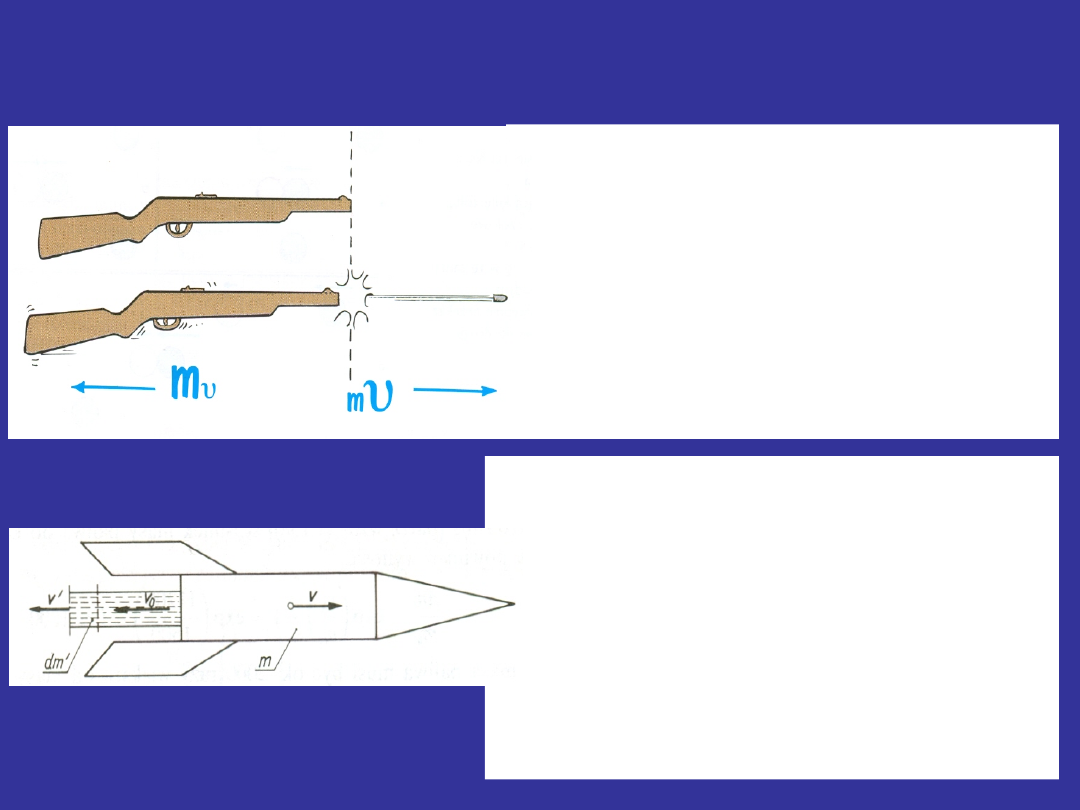
Zasada zachowania pędu

Zasada zachowania pędu

PRZYKŁADY

PRZYKŁADY

Zjawisko  odrzutu  przy 
użyciu 

broni 

palnej 

(pęd  uzyskany  przez 
karabin 

w 

chwili 

wystrzału  jest  równy 
co 

do 

wartości 

bezwzglę-dnej  pędowi 
pocisku);

Działanie 

silników 

odrzuto-wych 

i 

rakietowych 

(pęd 

unoszony  przez  gazy 
spalinowe jest równy co 
do 

wartości 

bezwzględnej 

pędowi 

uzyskanemu 

przez 

samolot lub rakietę).

Zasada zachowania momentu pędu (krętu)

Zasada zachowania momentu pędu (krętu)

Twierdzenie 

o 

momencie 

pędu 

(kręcie) 

Twierdzenie 

o 

momencie 

pędu 

(kręcie) 

całkowitym:

całkowitym:

Pochodna momentu pędu (krętu) całkowitego 

Pochodna momentu pędu (krętu) całkowitego 

układu względem czasu jest równa momentowi 

układu względem czasu jest równa momentowi 

wypadkowemu sił zewnętrznych: 

wypadkowemu sił zewnętrznych: 

Natomiast siły wewnętrzne układu nie mają 

Natomiast siły wewnętrzne układu nie mają 

wpływu na całkowity moment pędu układu 

wpływu na całkowity moment pędu układu 

(podobnie jak w zasadzie zachowania pędu).

(podobnie jak w zasadzie zachowania pędu).

Konsekwencją powyższego równania jest 

Konsekwencją powyższego równania jest 

następująca relacja:

następująca relacja:

gdy M

gdy M

z

z

 = 0,  to  L = const.

 = 0,  to  L = const.

dt

dL

M

z



Zasada zachowania momentu pędu (krętu)

Zasada zachowania momentu pędu (krętu)

Konsekwencją powyższego równania 

Konsekwencją powyższego równania 

 

 

jest następująca relacja:

jest następująca relacja:

gdy M

gdy M

z

z

 = 0,  to  L = const.

 = 0,  to  L = const.

Zależność ta wyraża zasadę zachowania 

Zależność ta wyraża zasadę zachowania 

momentu pędu (krętu), która mówi, że:

momentu pędu (krętu), która mówi, że:

Jeżeli moment wypadkowy sił zewnętrznych 

Jeżeli moment wypadkowy sił zewnętrznych 

działających na układ równa się zeru, to moment 

działających na układ równa się zeru, to moment 

pędu (kręt) całkowity tego układu jest stały.

pędu (kręt) całkowity tego układu jest stały.

Całkowity kręt układu wyraża się sumą:  

Całkowity kręt układu wyraża się sumą:  

    , 

    , 

a gdy prędkości kątowe poszczególnych brył są 

a gdy prędkości kątowe poszczególnych brył są 

równe, to: 

równe, to: 

dt

dL

M

z







i

i

I

L







I

I

L

i







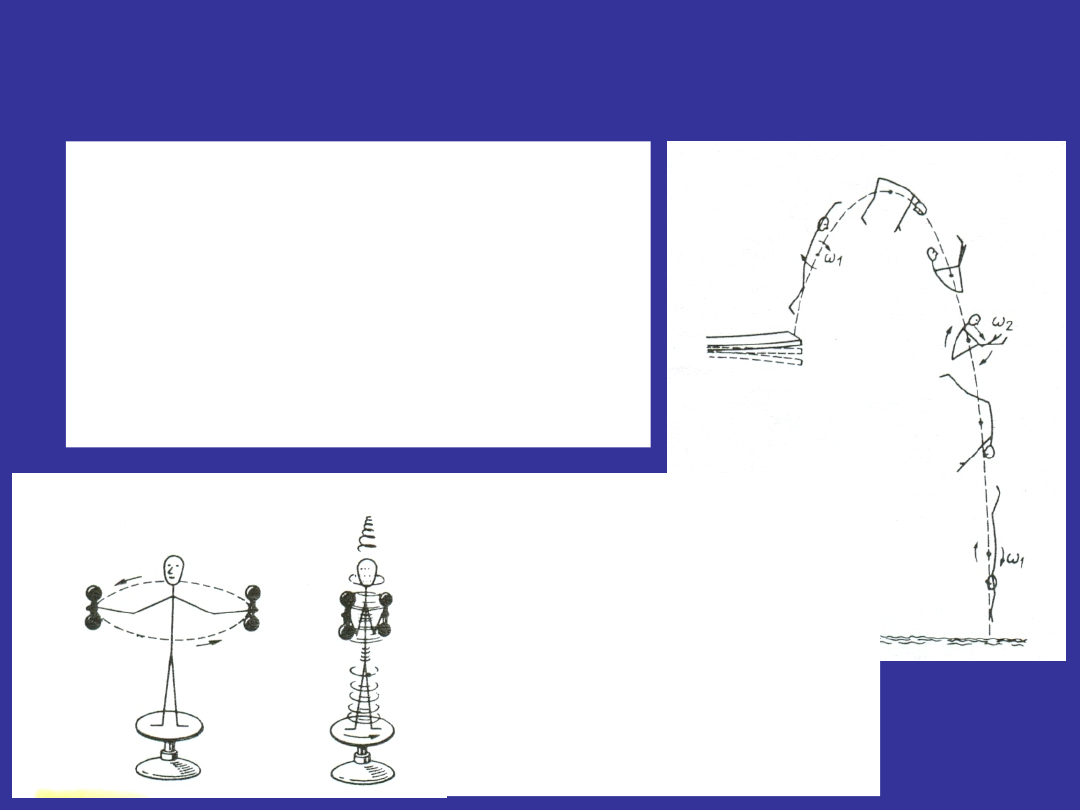
Zasada zachowania momentu pędu  

Zasada zachowania momentu pędu  

(krętu)

(krętu)

PRZYKŁADY

PRZYKŁADY

  

  

Zmiany  rozłożenia  masy 
ciała  wokół  osi  obrotu 
umożliwiają 

skoczkowi 

regulację 

prędko-ści 

obracania się jego ciała.
Podobne zjawisko 
obserwu-jemy w jeździe 
na lodzie przy 
wykonywaniu piruetów.

Obrotowy 

stołek: 

kręt 

układu 

(człowiek + hantle) 
pozostaje 

stały: 

zmniejszenie 
momentu 
bezwładności 
(I=mr

2

) 

wskutek 

zbliżenia 

han-tli 

przyspiesza obrót).

Zasada zachowania momentu pędu  

Zasada zachowania momentu pędu  

(krętu)

(krętu)

PRZYKŁADY

PRZYKŁADY

  

  

Kot  spadając 
wielokrotnie 
przemieszcza 
swoje 
kończyny 

i 

ogon,  tak  aby 
nastąpiła 
zmiana 
momentu 
bezwładności. 
Nastąpi  obrót 
ciała, 

ale 

prędkość 
kątowa 

nie 

ulegnie 
zmianie.

Gimnastyk 

może 

zmieniać 

prędkość 

obrotową 

przez 

odpowiednią 

zmianę 

momentu 
bezwładności 

ciała, 

gdyż  moment  pędu 
musi być zachowany.

Zasada zachowania energii

Zasada zachowania energii

Układ odosobniony

Układ odosobniony

 – układ na który nie dzia-

 – układ na który nie dzia-

łają żadne siły zewnętrzne; w układzie odoso-

łają żadne siły zewnętrzne; w układzie odoso-

bnionym działają więc tylko siły wewnętrzne. 

bnionym działają więc tylko siły wewnętrzne. 

Jeżeli założymy, że siły te są zachowawcze,

Jeżeli założymy, że siły te są zachowawcze,

 

 

to takie układy nazywamy 

to takie układy nazywamy 

zachowawczymi

zachowawczymi

.

.

Siła zachowawcza 

Siła zachowawcza 

– jeśli jej praca po

– jeśli jej praca po

dowolnym torze zamkniętym jest równa zeru.

dowolnym torze zamkniętym jest równa zeru.

Energia mechaniczna

Energia mechaniczna

 – suma energii

 – suma energii

kinetycznej i potencjalnej.

kinetycznej i potencjalnej.

Zasada zachowania energii:

Zasada zachowania energii:

Energia mechaniczna układu odosobnionego i 

Energia mechaniczna układu odosobnionego i 

zachowawczego jest stała, to znaczy:

zachowawczego jest stała, to znaczy:

      

      

E

E

k

k

 + E

 + E

p

p

 = const.

 = const.

Zasada zachowania energii

Zasada zachowania energii

W przypadku układów niezachowawczych, 

W przypadku układów niezachowawczych, 

energia mechaniczna tych układów nie jest stała.

energia mechaniczna tych układów nie jest stała.

Przykład:

Przykład:

metalowa kulka wrzucona z pewnej wysokości do 

metalowa kulka wrzucona z pewnej wysokości do 

zbiornika z gęsta smołą. Analiza makroskopowa i 

zbiornika z gęsta smołą. Analiza makroskopowa i 

mikroskopowa.

mikroskopowa.

Ogólna zasada zachowania energii mówi, że:

Ogólna zasada zachowania energii mówi, że:

Całkowita energia (mechaniczna, elektryczna, 

Całkowita energia (mechaniczna, elektryczna, 

magnetyczna chemiczna, jądrowa itp.) układu 

magnetyczna chemiczna, jądrowa itp.) układu 

odosobnionego jest wielkością stałą.

odosobnionego jest wielkością stałą.

W układzie odosobnionym zachodzą tylko 

W układzie odosobnionym zachodzą tylko 

przemiany jednych form energii w inne.

przemiany jednych form energii w inne.