Wnioskowanie

statystyczne c. d.

Wykład 8

Wnioskowanie statystyczne - polega na uogólnianiu
wyników otrzymanych na podstawie próby losowej
na całą populację generalną, z której próba została
pobrana

Wnioskowanie statystyczne dzieli się na:

1.  

Estymację

–

szacowanie

wartości

parametrów lub postaci rozkładu zmiennej na
podstawie próby – na podstawie wyników próby
formułujemy wnioski dla całej populacji

2. Weryfikację hipotez statystycznych –
sprawdzanie określonych założeń sformułowanych
dla

parametrów

populacji

generalnej

na

podstawie wyników z próby – najpierw wysuwamy
założenie, które weryfikujemy na podstawie
wyników próby

Estymator – wielkość (charakterystyka, miara),
obliczona na podstawie próby, służąca do oceny
wartości nieznanych parametrów populacji
generalnej.

Najlepszym z pośród wszystkich estymatorów
parametru w populacji generalnej jest ten, który
spełnia wszystkie właściwości estymatorów
(jest

równocześnie

nieobciążony,

zgodny,

efektywny, dostateczny).

Przedział ufności jest podstawowym
narzędziem

estymacji przedziałowej

.

Pojęcie to zostało wprowadzone do

statystyki

przez amerykańskiego

matematyka polskiego pochodzenia

Jerzego Spławę-Neymana

• Niech

cecha

X ma rozkład w

populacji

z nieznanym

parametrem θ. Z populacji wybieramy

próbę losową

(X1, X2, ..., Xn). Przedziałem ufności (θ - θ1, θ +
θ2) o współczynniku ufności 1 - α nazywamy taki
przedział (θ - θ1, θ + θ2), który spełnia warunek:

• P(θ1 < θ < θ2) = 1 − α
• gdzie θ1 i θ2 są funkcjami wyznaczonymi na

podstawie próby losowej.

Podobnie jak w przypadku

estymatorów

definicja pozwala

na dowolność wyboru funkcji z

próby, jednak tutaj kryterium

wyboru najlepszych funkcji

narzuca się automatycznie -

zazwyczaj będziemy

poszukiwać przedziałów

najkrótszych

Współczynnik ufności 1 - α jest

wielkością, którą można interpretować w
następujący sposób: jest to
prawdopodobieństwo, że rzeczywista wartość
parametru θ w populacji znajduje się w
wyznaczonym przez nas przedziale ufności.
Im większa wartość tego współczynnika, tym
szerszy przedział ufności, a więc mniejsza
dokładność estymacji parametru. Im
mniejsza wartość 1 - α, tym większa
dokładność estymacji, ale jednocześnie tym
większe prawdopodobieństwo popełnienia
błędu. Wybór odpowiedniego współczynnika
jest więc kompromisem pomiędzy
dokładnością estymacji a ryzykiem błędu. W
praktyce przyjmuje się zazwyczaj wartości:
0,99; 0,95 lub 0,90, zależnie od parametru.

Przykłady przedziałów

ufności

Ponieważ szukamy jak najkrótszych przedziałów

ufności, dlatego przy wyznaczaniu przedziału
staramy się wykorzystać jak najwięcej dostępnych
informacji o rozkładzie cechy w populacji. Jeśli np.
cecha ma rozkład normalny z odchyleniem
standardowym σ, to zastosowanie wzoru na przedział
ufności dla nieznanego σ również da poprawny
wynik, jednak przedział otrzymany tą metodą będzie
szerszy, czyli mniej dokładny. Z kolei wzory
ogólniejsze, np. dla nieznanego rozkładu, często
korzystają z rozkładów granicznych estymatorów i
dlatego wymagają dużej liczebności próby.

Estymacja przedziałowa

polega na budowie przedziału zwanego przedziałem
ufności, który z określonym prawdopodobieństwem
będzie zawierał nieznaną wartość szacowanego
parametru











1

)}

(

)

(

{

2

1

n

n

Z

g

Q

Z

g

P

gdzie:
Q – nieznany parametr populacji generalnej,

końce przedziałów (dolna i górna
granica przedziału), będące funkcją
wylosowanej próby

)

(

1

n

Z

g

)

(

2

n

Z

g

1–α współczynnik ufności – prawdopodobieństwo
tego, że wyznaczając na podstawie n-elementowych

prób wartość funkcji g

1

i g

2

(dolną i górną granicę

przedziału) średnio w (1-α)·100% przypadkach
otrzymamy przedziały pokrywające nieznaną
wartość parametru Q – z prawdopodobieństwem (1-
α) przedział ufności pokrywa nieznaną wartość
szacowanego parametru

Im krótszy przedział (różnica między górną i dolną

granicą przedziału),

tym bardziej precyzyjna jest estymacja

przedziałowa.

Im wyższa jest wartość współczynnika ufności,

tym większa jest długość przedziału.

Przedział ufności dla średniej w populacji o
rozkładzie normalnym ze znanym
odchyleniem standardowym

Estymatorem średniej w populacji jest średnia
arytmetyczna z próby , która ma rozkład
.

X

)

,

(

n

m

N



Przedział ufności dla średniej w populacji ma
postać:

























1

}

{

n

n

u

X

u

X

P

- wartość odczytana z tablic rozkładu
normalnego dla danego poziomu istotności
α

- odchylenie standardowe w populacji
generalnej



u



Względna miara precyzji oszacowania
jako miara dokładności dopasowania
określona jest wzorem:

%

100

)

(









n

X

u

X

B





Jeżeli:

- oszacowanie charakteryzuje się dużą

precyzją

- uogólnienia wyników na populację

generalną

należy dokonywać ostrożnie

- nie należy dokonywać żadnych uogólnień

na

populację generalną

%

5

)

(



X

B

%

10

)

(

%

5



 X

B

%

10

)

(



X

B

Przedział ufności dla średniej w populacji o
rozkładzie normalnym z nieznanym
odchyleniem standardowym

n < 30

Jeżeli próba jest mało liczna - stosujemy statystykę
t o rozkładzie t–Studenta dla n-1 stopni swobody



























1

}

{

1

1

,

1

1

,

n

S

n

n

S

n

t

X

m

t

X

P

gdzie:

- odchylenie standardowe z próby

- wartość odczytana z tablic rozkładu
Studenta dla
poziomu istotności α oraz n–1 stopni

swobody









n

i

i

n

x

x

S

1

2

1

)

(

1

, 

n

t



Gdy n > 30, wartość odczytaną z tablic

rozkładu Studenta możemy zastąpić wartością ,

odczytaną z tablic rozkładu normalnego oraz

.



















1

}

{

n

S

n

S

u

X

m

u

X

P

1

, 

n

t





u

S





- wartość odczytana z tablic rozkładu
normalnego dla danego poziomu istotności
α

- odchylenie standardowe w próbie



u

S

Względną precyzję oszacowania oceniamy
następująco:

dla n < 30

%

100

)

(

1

1

,













n

X

S

t

n

X

B



dla n > 30

%

100

)

(









n

X

S

u

X

B



1. W pewnej klasie wybrano losowo grupę 8 osobową,

która miała za zadanie rozwiązać zadanie z
matematyki. Zmierzono czas rozwiązania zadania
przez każdego z uczniów: 25, 16, 12, 10, 12, 21, 25,
20.

Oszacuj

metodą

przedziałową

dla

współczynnika ufności średni czas niezbędny do
rozwiązania zadania w całej zbiorowości uczniów.
Przyjmując poziom istotności  = 0,05.

2. W grupie losowo wybranych 625 pracowników w

dużym

koncernie

produkującym

samochody

osobowe, średnia liczba dni nieobecności w pracy
w badanym roku wynosiła 18, natomiast odchylenie
standardowe 3. Przyjmując poziom ufności na
poziomie

0,90

oszacować

średni

poziom

nieobecności

pracowników

w

całym

przedsiębiorstwie

oraz

ocenić

precyzję

oszacowania.

Problem minimalnej liczebność

próby

Minimalna liczebność próby - taka liczebność

próby, która zapewni wymaganą dokładność

(precyzję oszacowania) przy danym poziomie

wiarygodności (prawdopodobieństwa).

Przykład. Chcemy oszacować procent (frakcję)

mieszkańców

pewnego miasta, mających grupę „0”. Ilu należy

wylosować mieszkańców do próby, aby szacowanie

dokonać z błędem maksymalnym 5% przy

współczynniku 0,95.

Rozwiązanie

• Korzystamy ze wzoru: n=

u ^

2/4d^2

Z tablicy rozkładu normalnego N(0,1) dla

wsp. ufności 0,95 odczytujemy wartość
u=1,96.

Podstawiając do wzoru, mamy:
n= !,96^2/4*0,05^2= 384



u



u

Dla estymacji przedziałowej średniej m w
populacji przy znanym odchyleniu
standardowym σ w populacji

Poszukujemy takiej liczebność próby n, dla której
przy danym współczynniku ufności (1-α) połowa
długości przedziału ufności d – maksymalny błąd
szacunku – nie przekroczy ustalonej z góry
wartości.

2

2

2

d

u

n







2

2

2

d

u

n







stąd

Dla estymacji przedziałowej średniej m w
populacji przy nieznanym odchyleniu
standardowym σ w populacji

Losujemy próbę wstępną n

0

, obliczamy średnią i

wariancję z próby i na jej podstawie wyznaczamy
właściwą liczebność próby:

2

2

2

1

,

ˆ

0

d

S

t

n

n









t

α,n0-1

– wartość odczytana z tablic rozkładu Studenta

dla α i n

0

-1











n

i

i

n

X

X

S

1

1

1

2

)

(

ˆ

Jeżeli n ≤ n

0

to próbę wstępną traktujemy

jako właściwą. Jeżeli zaś n > n

0

to musimy

próbę powiększyć o n – n

0

.

1.

Firma

zajmująca

się

wyszukiwaniem

stanowisk

dla

personelu

kierowniczego

chce

oszacować średnią pensję, jaką może uzyskać
pracownik

pełniący

funkcję

kierowniczą,

z

dokładnością do 2000 $, przy poziomie ufności 95%.
Wiadomo, że rozkład pensji kierowniczych jest
rozkładem normalnym o wariancji 40 mln. Jak liczna
powinna być próba do oszacowania średniej pensji
kierowników?

2. W celu wyznaczenia przeciętnej długości

drogi

hamowania

samochodu

na

asfalcie,

przeprowadzono przy prędkości 40 km/h 12 prób i
otrzymano wyniki w metrach: 17,0; 19,0; 22,0; 20,5;
20,0; 21,0; 20,5; 20,0; 21,0; 18,0; 20,0; 21,0. Czy
liczba prób jest wystarczająca do wyznaczenia
przedziału ufności średniej o długości 0,5 m i dla 1- α
= 0,95. Ewentualnie, jaką liczbę prób należy jeszcze
przeprowadzić?

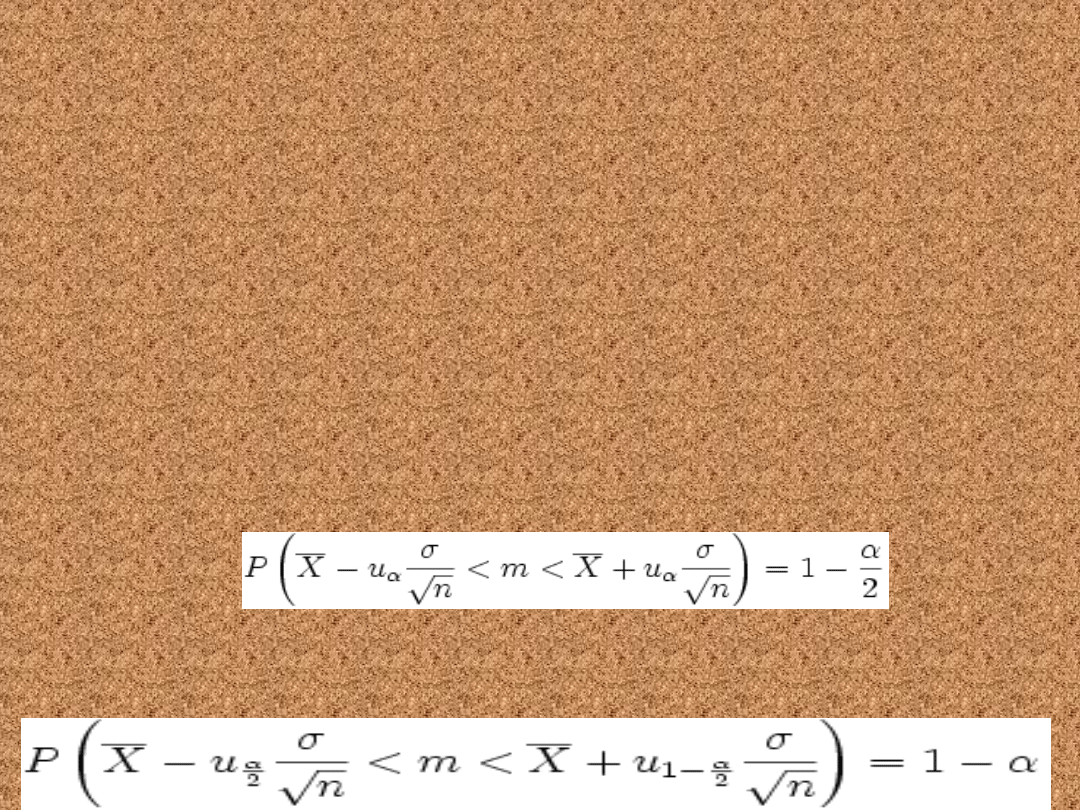
Przedział ufności dla

średniej.

Znane odchylenie

standardowe

• Cecha ma w populacji

rozkład normalny

N(m, σ), przy czym

odchylenie standardowe

σ jest znane.

Przedział ufności dla parametru m tego
rozkładu ma postać:

• lub równoznacznie:

lub
równoznacznie

gdzie:

n to liczebność próby losowej

oznacza średnią z próby
losowej

σ to odchylenie

standardowe populacji

u

α

jest statystyką,

spełniającą warunek:
P( − u

α

< U < u

α

) = 1 −

α, gdzie U jest zmienną

P( − uα < U < uα) = 1 − α, gdzie U
jest zmienną losową o rozkładzie
normalnym N(0,1).

ora
z

i

rozkładu N(0,1).

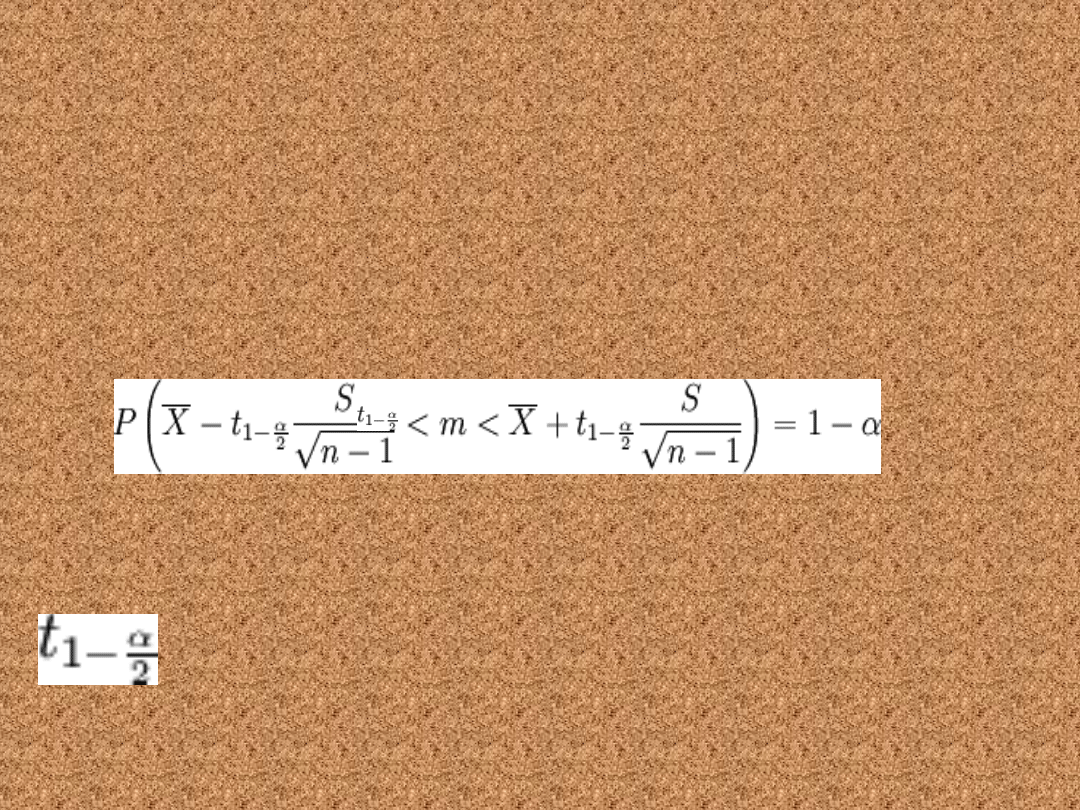
Nieznane odchylenie

standardowe

• Cecha ma w populacji rozkład normalny

N(m, σ), przy czym odchylenie standardowe

σ jest nieznane. Przedział ufności dla

parametru m tego rozkładu ma postać:

• gdzie:

• n to liczebność próby losowej

• oznacza średnią z próby losowej

• S to odchylenie standardowe z próby

ma

rozkład Studenta

z n - 1

stopniami swobody

Zwykle stosuje się ten wzór

dla małej próby (n<30). Tak
naprawdę działa on dla każdej
wielkości próby, jednak dla
dużych prób można przybliżyć
rozkład t Studenta rozkładem
normalnym, co jest łatwiejsze
do wyliczenia a dające niemal
takie same wartości (patrz
niżej

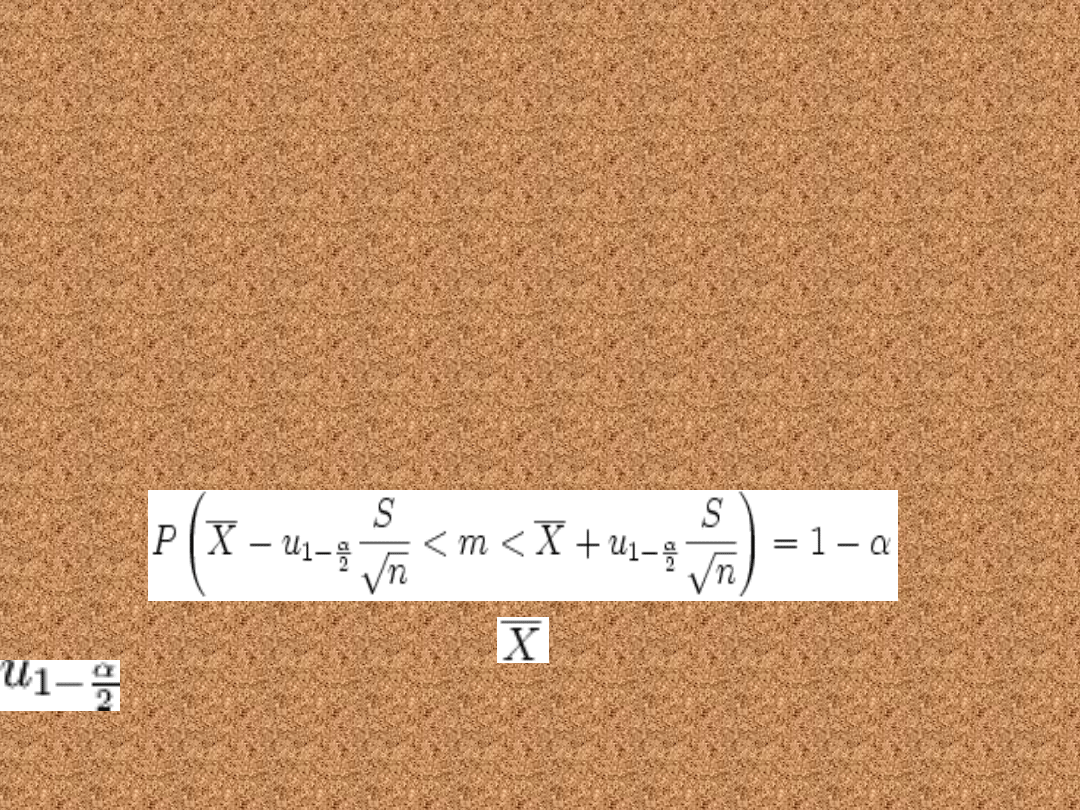
Nieznane odchylenie

standardowe – Duża próba

(n>30

• Cecha ma w populacji rozkład normalny N(m,

σ), przy czym odchylenie standardowe σ jest

nieznane, a próba jest duża (n>30). Granica

30 jest czysto umowna, im n jest większe, tym

wzór dokładniejszy. Przedział ufności dla

parametru m tego rozkładu ma postać:

gdzie:

n to liczebność próby losowej

oznacza średnią z próby losowej

S to odchylenie standardowe z próby

jest statystyką ze zmienną
losową o rozkładzie normalnym N(0, 1

).

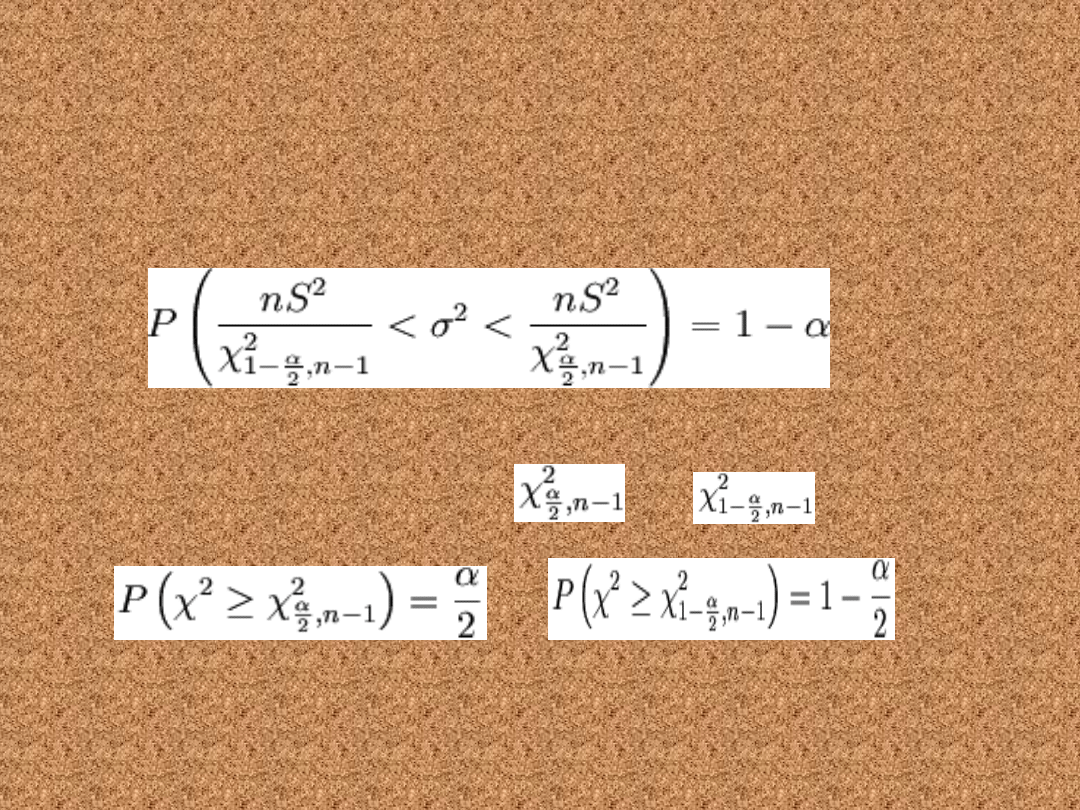
Przedział ufności dla

wariancji

• Poniższy wzór pozwala wyznaczyć

przedział ufności dla wariancji w
populacji o rozkładzie normalnym N(m,
σ)

gdzie: n to liczebność próby losowej, S to
odchylenie standardowe z próby,
i

i

to statystyki spełniające odpowiednio równości:

gdzie χ2 ma

rozkład chi-kwadrat

z n - 1

stopniami swobody

Podobnie jak poprzednio zwykle stosuje się ten wzór dla
małej próby (n<30), choć również działa on dla każdej
wielkości próby.

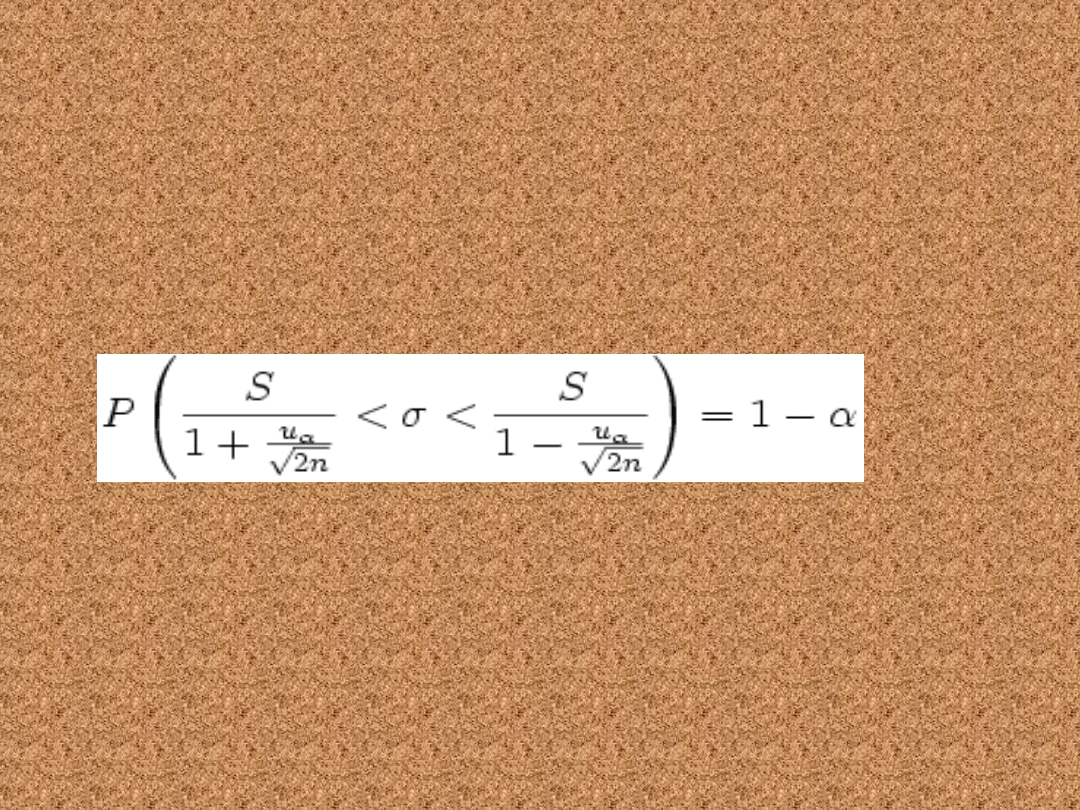
Duża próba (n>30)

• Poniższy wzór pozwala wyznaczyć

przedział ufności dla wariancji w
populacji o rozkładzie normalnym N(m,
σ) dla dużej próby, czyli umownie dla
n>30.

gdzie: n to liczebność próby losowej, S to odchylenie
standardowe z próby, uα jest statystyką, spełniającą
warunek:

gdzie U jest zmienną losową o rozkładzie normalnym N(0, 1).

P( − uα < U < uα) =
1 − α

Test dla proporcji

Test istotności dla wskaźnika

struktury

Testy dla proporcji to testy parametryczne służące do

weryfikacji hipotez dotyczących wartości proporcji w

populacji generalnej lub też do porównania wartości

proporcji w kilku populacjach – na podstawie

znajomości wartości tej proporcji w losowej próbie (czy

też dwóch lub kilku próbach) pobranych z populacji.

Proporcją w statystyce nazywamy liczbę (ułamek,

procent) wyrażający, jaka część elementów pewnego

zbioru spełnia określony warunek. Inne równoważnie

stosowane określenia to: frakcja, wskaźnik struktury.

Na przykład, jeśli w grupie \n osób jest \m palących, to

proporcja osób palących w tej grupie jest równa

Struktura i podział testów

Hipotezy dotyczące proporcji testuje się zgodnie z ogólnymi

zasadami testowania hipotez statystycznych: formułujemy

hipotezy, zakładamy poziom istotności α – dopuszczalną

wartość błędu pierwszego rodzaju, następnie na podstawie

danych z próby wyznaczamy wartość statystyki testowej,

po czym porównujemy ją z wartościami krytycznymi

odczytanymi z tablic odpowiedniego rozkładu

teoretycznego. Postać stosowanej statystyki testowej

zależy od następujących czynników:

• czy badamy hipotezę dotyczącą jednej, dwóch, czy wielu

proporcji

• jaka jest liczebność próby (prób) występujących w danym

zagadnieniu

• w przypadku dwu lub więcej prób – czy próby są

niezależne, czy zależne (powiązane).

• Poniżej przedstawiono w skrócie kilka testów najczęściej

wykorzystywanych w poszczególnych sytuacjach.

Testy dla jednej proporcji (test dla

prób dużych)

W próbie losowej o liczebności n jest m

elementów spełniających pewien
warunek. Wówczas proporcja w próbie
. Chcemy sprawdzić, czy taki wynik
losowania pozwala przyjąć, że w całej
populacji proporcja ta ma zadaną z góry
wartość po. Hipotezy mają postać:

H

o

:

H

1

: postać hipotezy alternatywnej zależy od

sformułowania zagadnienia: a) , b)
, c)

(b

)

(c

)

(b

)

(c

)

Założenia: próba musi być dostatecznie
duża, to znaczy jej liczebność musi spełniać
warunek n > 50, a otrzymana wartość
proporcji z próby powinna spełniać
warunek: 0,2 < p < 0,8. Można wtedy
zastosować statystykę o rozkładzie
normalnym. Obliczamy:

gdzie qo = 1 − po
Wartość tak obliczonej statystyki
porównujemy z wartością krytyczną (lub
dwiema wartościami krytycznymi)
wyznaczonymi na podstawie poziomu
istotności α dla zmiennej losowej o rozkładzie
normalnym

.

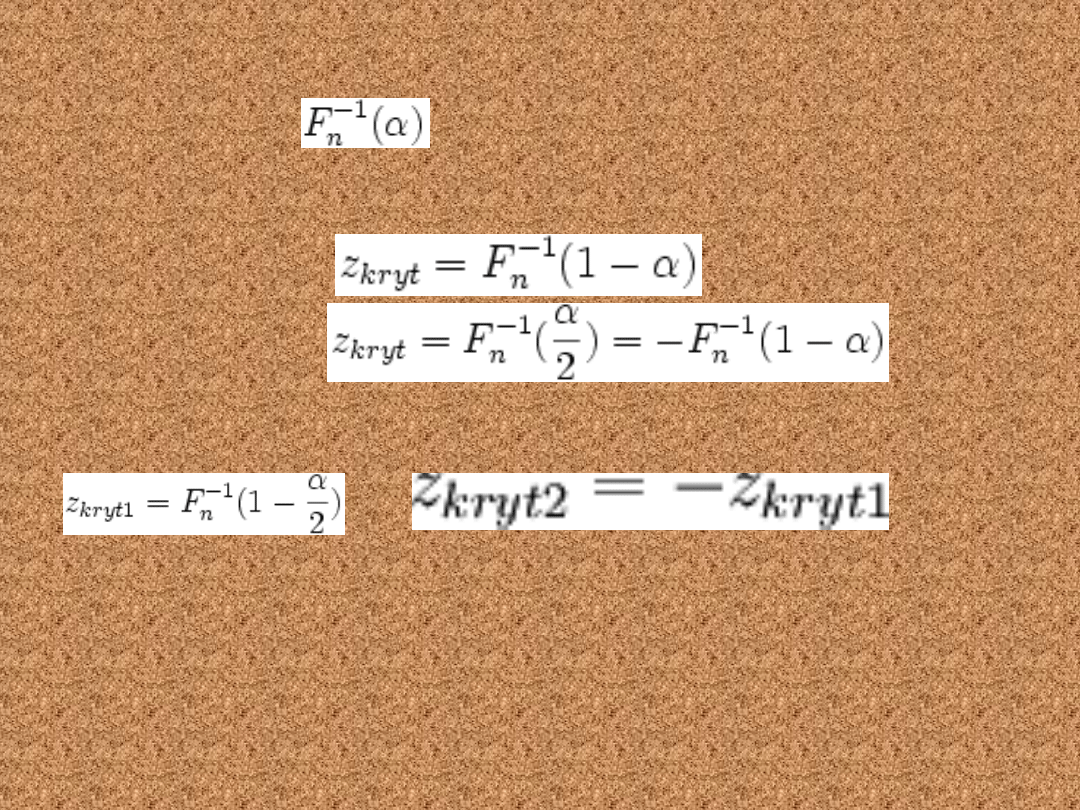
Wartości krytyczne znajdujemy z tablic dystrybuanty
rozkładu normalnego. Jeżeli F

n

(z) jest dystrybuantą

standardowego rozkładu normalnego, a

-

funkcją odwrotną do dystrybuanty, natomiast α -

założonym poziomem istotności – to odczytujemy:

dla przypadku (a):

w przypadku

(b):

zaś w przypadku (c) mamy 2 wartości
graniczne

Przedział krytyczny: w przypadku (a) jest prawostronny,
czyli gdy z > zkryt – odrzucamy H0, w przypadku
przeciwnym – nie ma podstaw do jej odrzucenia.w
przypadku (b) – przedział krytyczny jest lewostronny (dla
z < zkryt odrzucamy H

0

), w przypadku (c) – przedział

krytyczny jest obustronny.

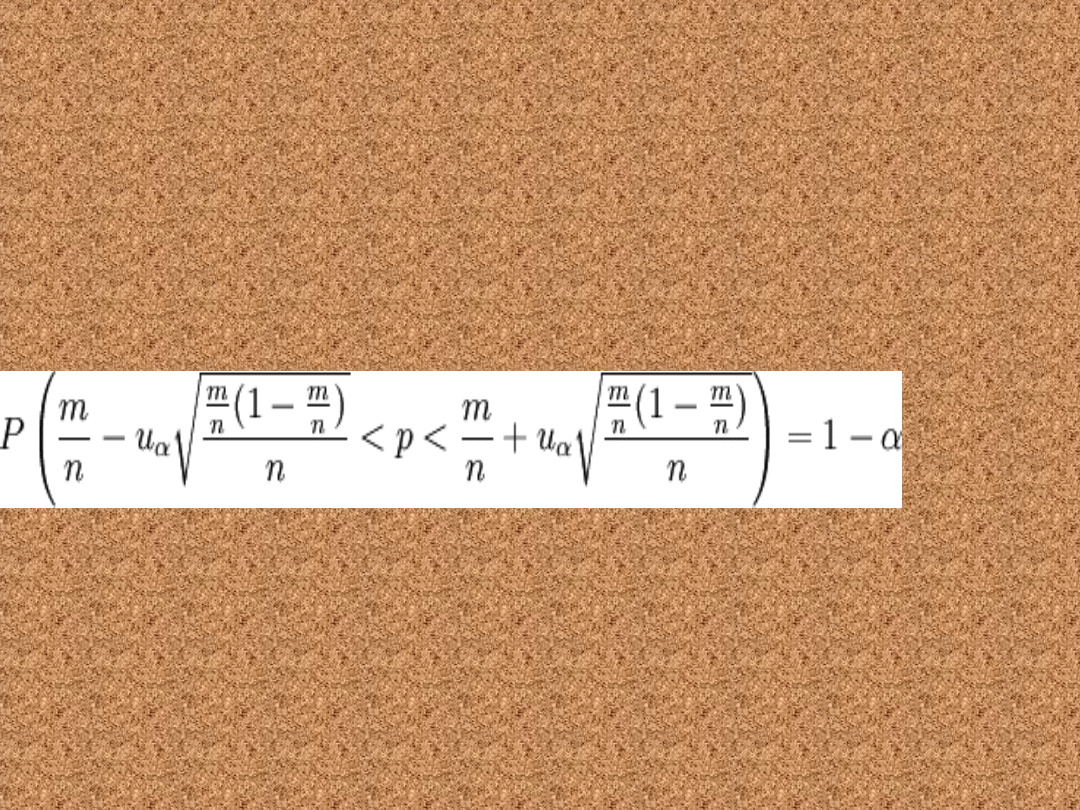
Przedział ufności dla odsetka

(wskaźnik struktury)

• Poniższy wzór pozwala wyznaczyć

przedział ufności dla odsetka w
populacji o rozkładzie normalnym N(m,
σ).

gdzie:
n to liczebność próby losowej
m to liczebność wybranej grupy z próby
uα jest statystyką, spełniającą warunek:
P( − uα < U < uα) = 1 − α gdzie U jest zmienną
losową o rozkładzie normalnym N(0, 1).

Testy dla dwóch proporcji

Dwie próby niezależne

Poniżej omówiono dwa testy –

jeden dla dużych liczebności
prób, oparty na statystyce z o
rozkładzie normalnym,
analogiczny do omówionego
powyżej dla jednej próby, drugi,
możliwy do zastosowania przy
nieco mniejszych liczebnościach
prób, oparty na statystyce o
rozkładzie chi-kwadrat

Test dla dwóch prób

dużych

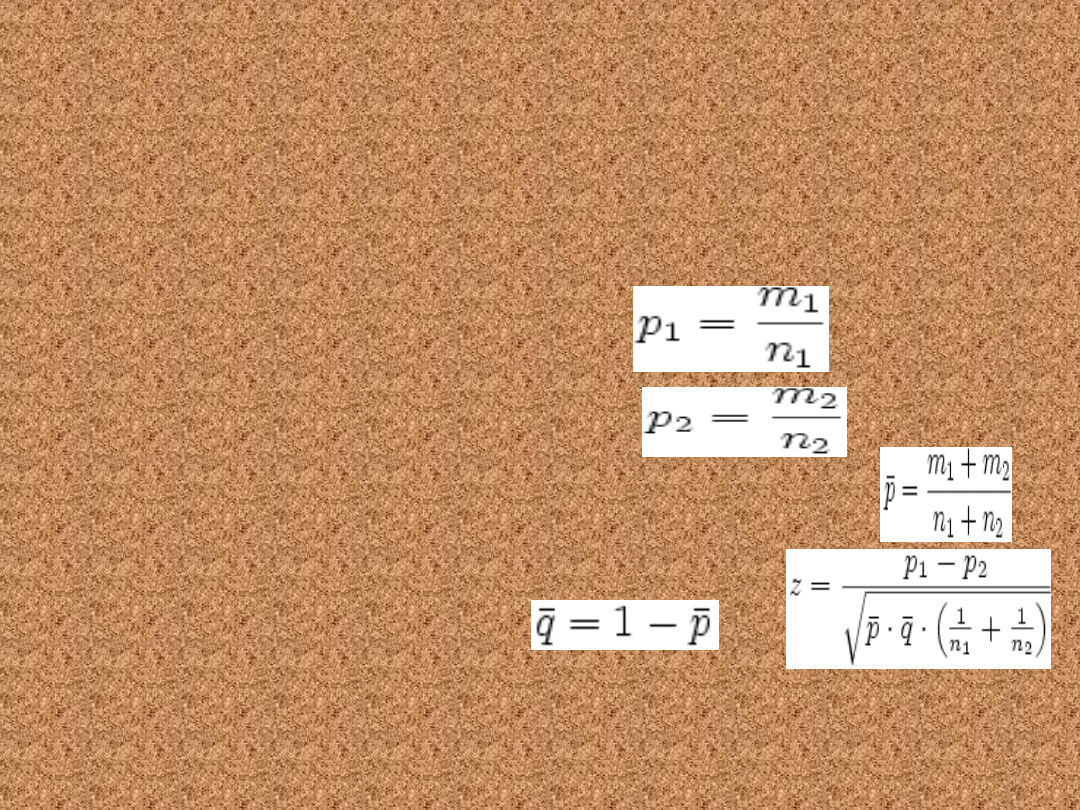
• Liczebności prób powinny spełniać

relacje: n1 > 50 i n2 > 50. Jeżeli
spośród n1 elementów pierwszej próby
m1 spełnia określony warunek, to
proporcja z próby jest równa

Analogicznie dla drugiej próby

Wyznaczamy proporcję dla „próby połączonej”

oraz

a następnie wyznaczamy
wartość statystyki z , gdzie :

Statystyka ta ma rozkład normalny i wartości

krytyczne oraz obszary krytyczne wyznaczamy dla tego
testu tak samo, jak to opisano wcześniej w teście dla
jednej proporcji

Test dla dwóch prób o mniejszych

liczebnościach (oparty na statystyce

chi-kwadrat

Tutaj liczebności muszą spełniać warunek: n

= n

1

+n

2

> 20

Liczby elementów spełniających lub

nie spełniających zadanego warunku w
poszczególnych populacjach można zapisać
w tabeli 2x2:

Liczba elementów:

Próba

1

Próba

2

Suma:

spełniających warunek

(TAK)

a

b

a + b

nie spełniających

warunku (NIE)

c

d

c + d

Suma:

n

1

=a+

b

n

2

=b+

d

n=a+b+c

+d

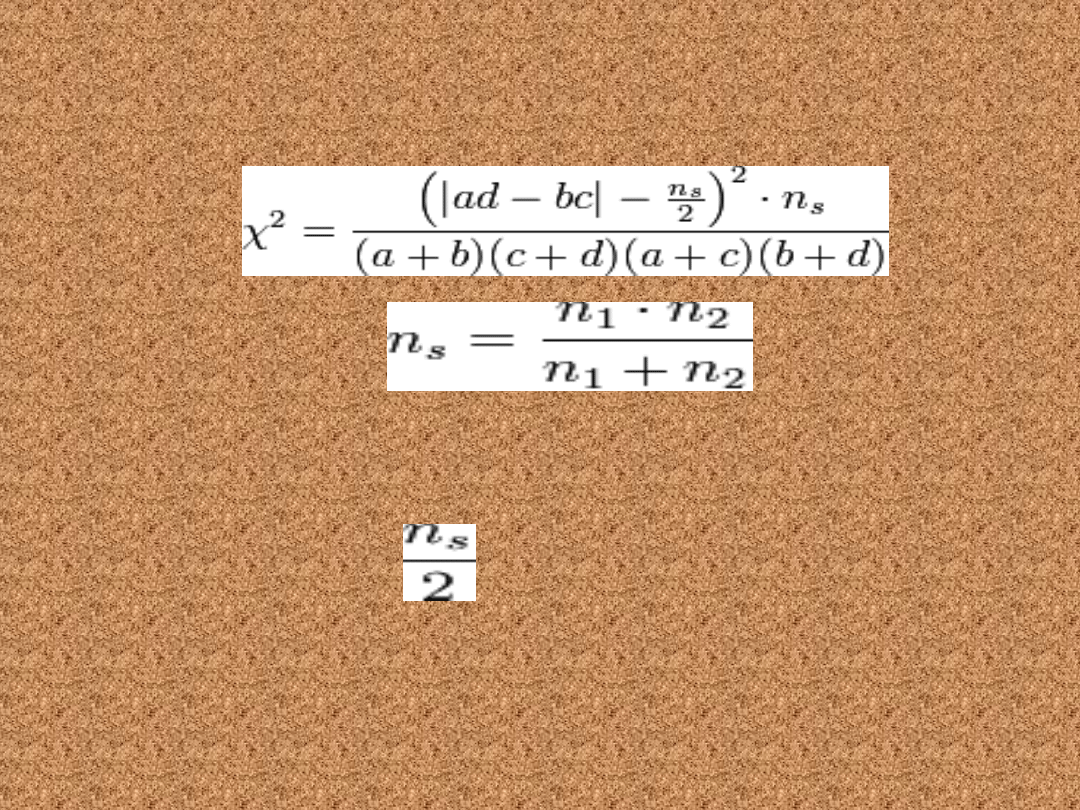
Na podstawie tabeli obliczamy

wartość statystyki

gdzie

Jeżeli liczebności prób są na tyle
duże,
że n

1

+ n

2

> 40 - można wówczas

pominąć w liczniku składnik

w nawiasie. Wartości krytyczne
wyznacza się z tablic rozkładu chi-
kwadrat o 1 stopniu swobody.

Dwie próby zależne

•

Ten przypadek występuje na przykład wtedy, gdy te
same obiekty czy osoby stanowiące próbę są badane
dwukrotnie w różnych warunkach. Wtedy zwykle
liczebności obu prób są jednakowe: n1 = n2 = n

Wynikiem takiego eksperymentu są 4 liczby,
stwierdzające, ile obiektów w każdej z prób
spełnia lub nie spełnia warunku. Wyniki takie
można zestawić w tabelce 2x2:

Liczebności

Próba 2: TAK Próba 2: NIE

Próba 1:TAK

a

b

Próba 1: NIE

c

d

Te same wyniki można też

zaprezentować w postaci tabelki proporcji
zamiast liczebności (gdzie np.

itd.)

Proporcj

e:

Próba 2:

TAK

Próba 2:

NIE

Próba
1:TAK

p

11

p

10

Próba 1:
NIE

p

01

p

00

W zależności od liczebności prób
możliwe są różne
odmiany testu

.

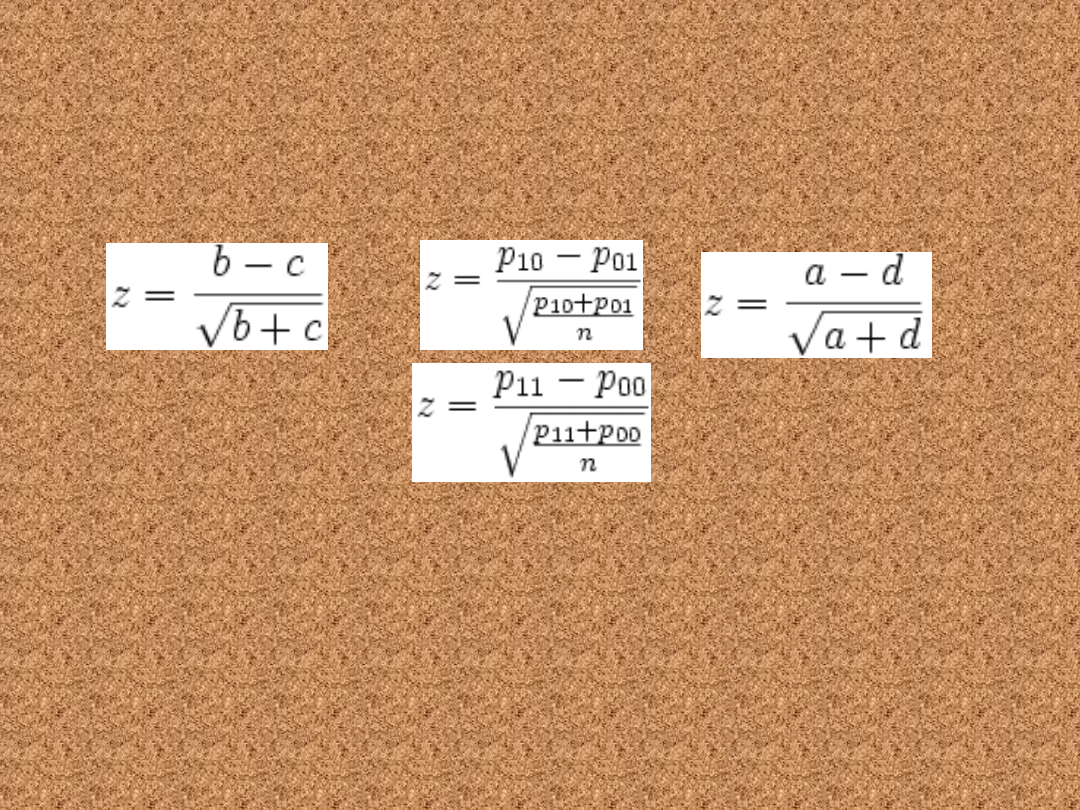
Liczebność duża

• Jeżeli , to wyznaczamy statystykę z o

rozkładzie normalnym z jednego ze wzorów

(

stosujemy dowolny z powyższych wzorów,

zależnie od dostępnych danych). Wartość
statystyki z porównujemy z wartością zkryt
wyznaczoną z tablic rozkładu normalnego,
przy czym postępowanie jest takie samo,
jak opisane powyżej dla testu dla jednej
proporcji

.

Przedział ufności dla

współczynnika korelacji

• Poniższy wzór pozwala wyznaczyć

przedział ufności dla

współczynnika korelacji

w populacji o

rozkładzie normalnym N(m, σ). Tak jak
poprzednio działa on dla dowolnej próby
choć jest zwykle stosowany tylko dla
prób małych, n<30.

gdzie: n to liczebność próby losowej, uα jest statystyką,
spełniającą warunek:

P( − uα < U < uα) = 1 − α gdzie U jest
zmienną losową o rozkładzie normalnym
N(0, 1).

r to wspólczynnik korelacji

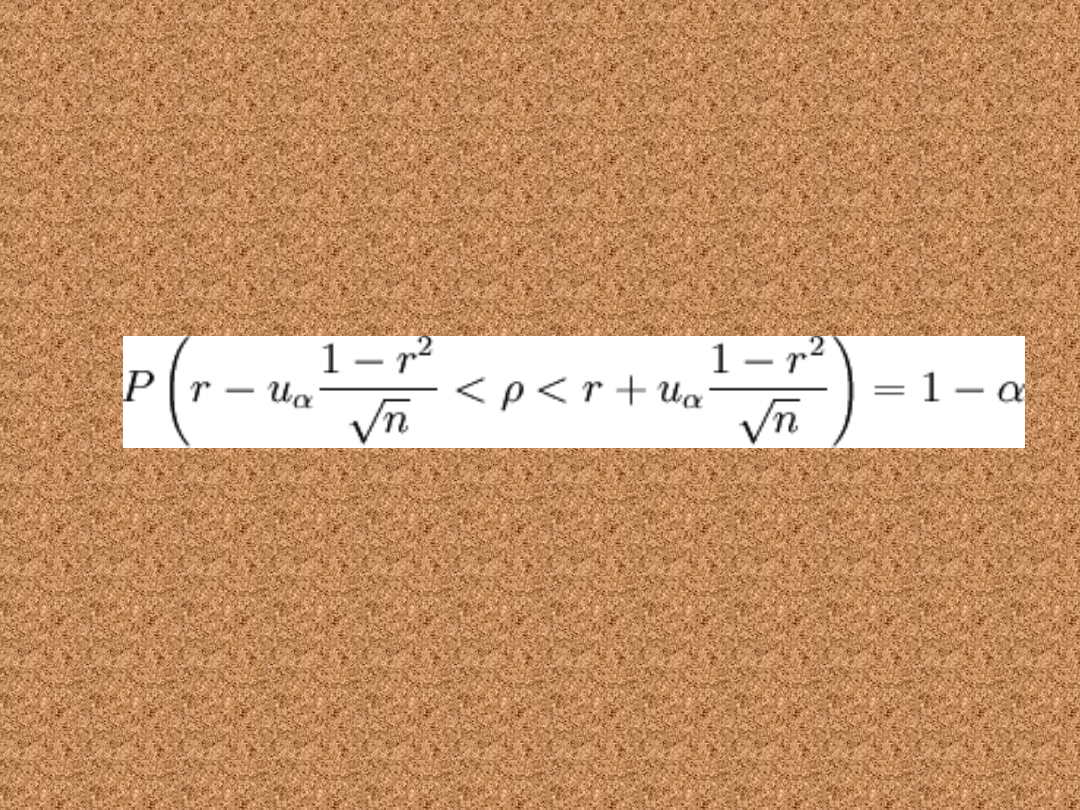
Duża próba (n>30)

• Poniższy wzór pozwala wyznaczyć

przedział ufności dla

współczynnika korelacji

w populacji o

rozkładzie normalnym N(m, σ)

gdzie: n to liczebność próby losowej, uα jest statystyką,
spełniającą warunek: P( − uα < U < uα) = 1 − α gdzie U
jest zmienną losową o rozkładzie normalnym N(0, 1),

r to wspólczynnik
korelacji

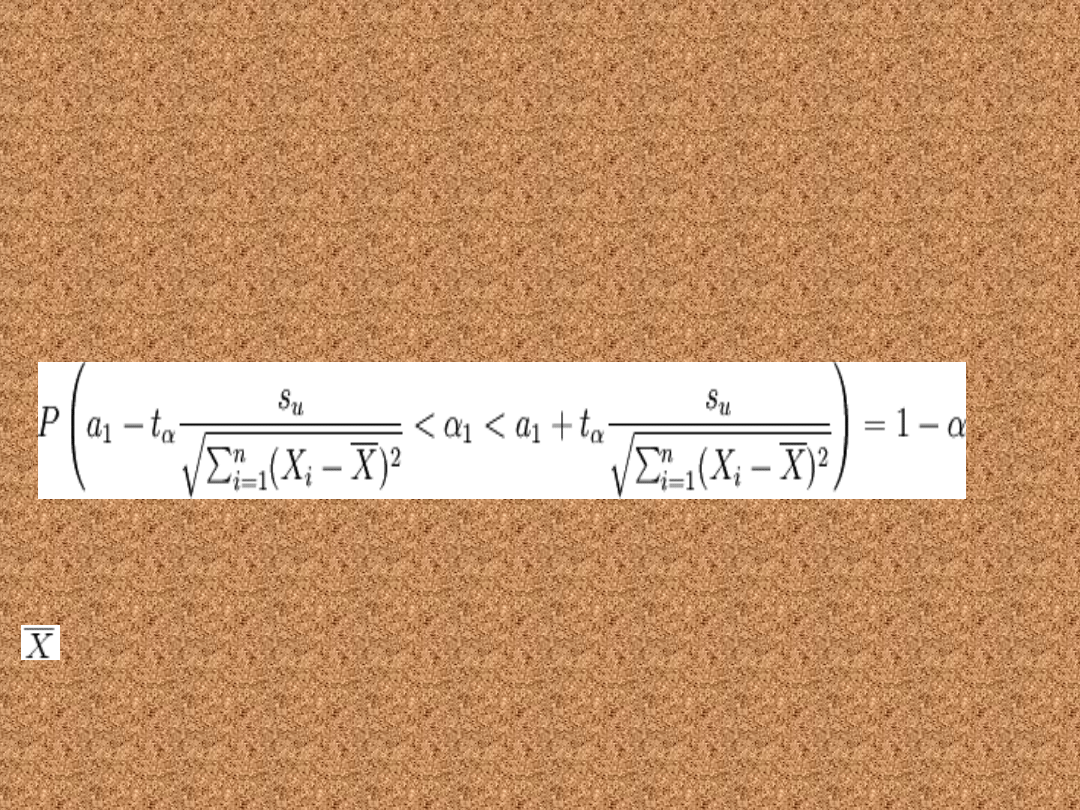
Przedział ufności dla

współczynnika α1

• Poniższy wzór pozwala wyznaczyć

przedział ufności dla współczynnika α1
w populacji o rozkładzie normalnym
N(m, σ)

gdzie: X to wartość z próby
losowej

oznacza średnią z próby losowej, t

α

ma

rozkład Studenta

z n - 2

stopniami swobody

Jeśli chcemy oszacować parametr z

określoną dokładnością d, możemy, po
odpowiednich przekształceniach wzorów
na przedziały ufności, wyznaczyć
liczebność próby losowej potrzebną do
osiągnięcia zakładanej dokładności.

Przykład: Wiemy, że wzrost

Wikipedystów ma rozkład normalny z
odchyleniem standardowym 25,28 cm
(dane chyba nieprawdziwe). Obliczmy ilu
Wikipedystów wystarczy zmierzyć, aby z
prawdopodobieństwem 95% wyznaczyć
średni wzrost Wikipedysty z
dokładnością do 5 cm.

Minimalna liczebność

próby]

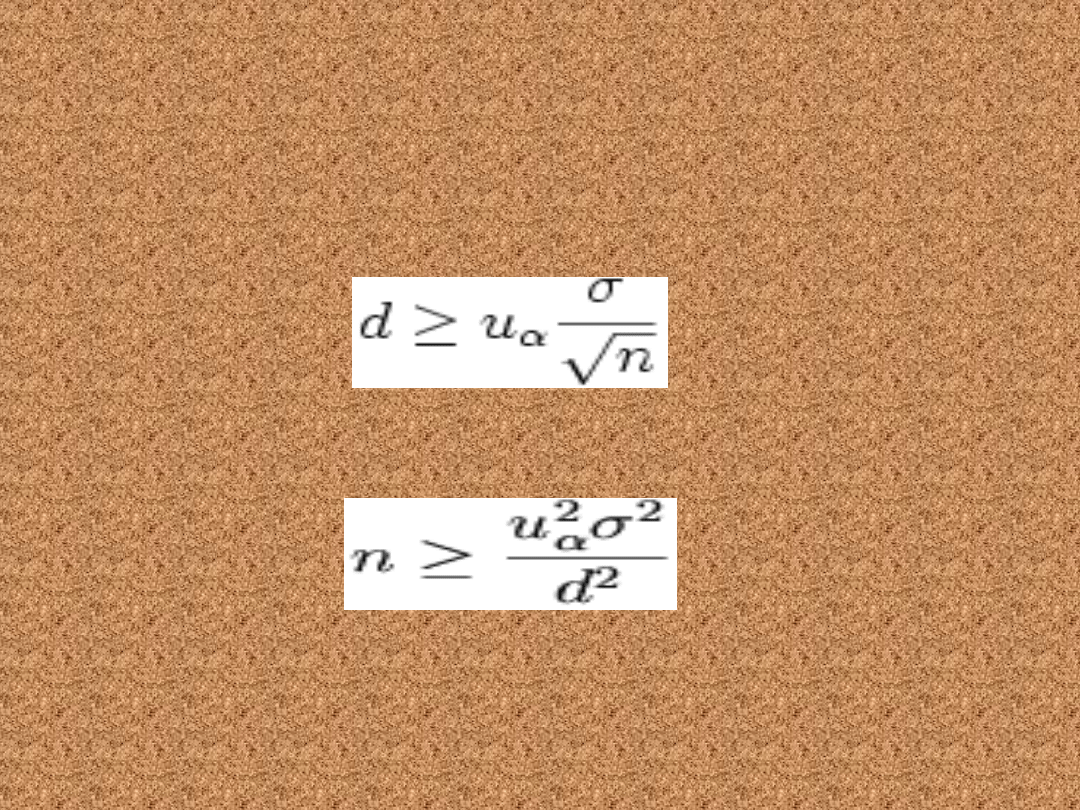
Jeśli chcemy uzyskać dokładność 5 cm, należy

zadbać o to, aby połowa długości przedziału ufności
była mniejsza lub równa niż 5 cm. Ze wzoru na
przedział ufności dla rozkładu normalnego o
znanym odchyleniu standardowym wynika, że
dokładność estymacji powinna spełniać zależność:

Przekształcamy podaną nierówność uzyskując

pożądany wzór na liczebność próby

Podstawiając do wzoru wartości σ = 25,28; d = 5 cm;
uα = 1,96 (wartość obliczona na podstawie tablic
rozkładu normalnego), uzyskujemy minimalną
wielkość próby na poziomie 99 Wikipedystów.

Test serii

• Test serii — zwany też testem serii Stevensa lub

testem serii Walda-Wolfowitza — jest jednym z

nieparametrycznych

testów

losowości

próby

. Stosujemy

go m. in., gdy chcemy sprawdzić, czy wyniki

eksperymentu

spełniają postulat

losowości

próby

.

• Hipotezę

zerową

i

alternatywną

formułujemy w sposób

następujący:

– H0: dobór jednostek do próby jest losowy;
– H1: dobór jednostek do próby nie jest losowy.

•

Jedną z metod

weryfikacji

wyżej zapisanej hipotezy jest

test serii.

Pod pojęciem

serii

rozumiemy każdy ciąg

identycznych elementów w zbiorze
uporządkowanym według przyjętego kryterium.

Na przykład, jeżeli odnotujemy płeć

studentów podchodzących kolejno do egzaminu,
możemy otrzymać ciąg:

M M Ż Ż M Ż Ż Ż M M Ż M Ż Ż Ż.

W tym przykładowym ciągu,

uporządkowanym według kolejności pojawiania
się elementów dwóch rodzajów (M i Ż), powstało
8 serii składających się z jednakowych
elementów występujących obok siebie.
Zakładając, że pojawienie się kolejnych
elementów jest losowe, ogólna liczba serii w
ciągu n-elementowym jest zmienną losową K o
znanym i ujętym w tablice rozkładzie. Jest ona

statystyką

w opisywanym teście losowości próby.

Sposób wyznaczania wartości

statystyki z próby:
Kolejno zapisane n obserwacji zmiennej
ciągłej tworzy ciąg podstawowy;
Obserwacje porządkujemy rosnąco i
wyznaczamy

medianę

;

W ciągu podstawowym oznaczamy
symbolami A i B wartości różniące się od
mediany:

xi<Me oznaczamy A;
xi>Me oznaczamy B;
xi=Me pomijamy.

Analizując ustawienie symboli A i B,
zliczamy utworzoną liczbę serii k, która
jest wartością statystyki otrzymaną z
próby;

Obszar krytyczny testu jest

dwustronny.
Jeżeli nA,nB ≤ 20, to wartości krytyczne
odczytujemy z tablic rozkładu liczby serii
(tablica H) jako:k1(α/2;nA;nB)     oraz    
k2(1-α/2;nA;nB),

gdzie nA i nB oznaczają
odpowiednio liczbę elementów
oznaczonych symbolami A i B.

Zliczoną w próbie liczbę serii k
porównujemy z wartościami krytycznymi
testu.
Jeżeli wystąpi k≤ k1 lub k≥ k2,
odrzucamy H0 na rzecz H1, co będzie
oznaczało, że próba nie ma charakteru
losowego.

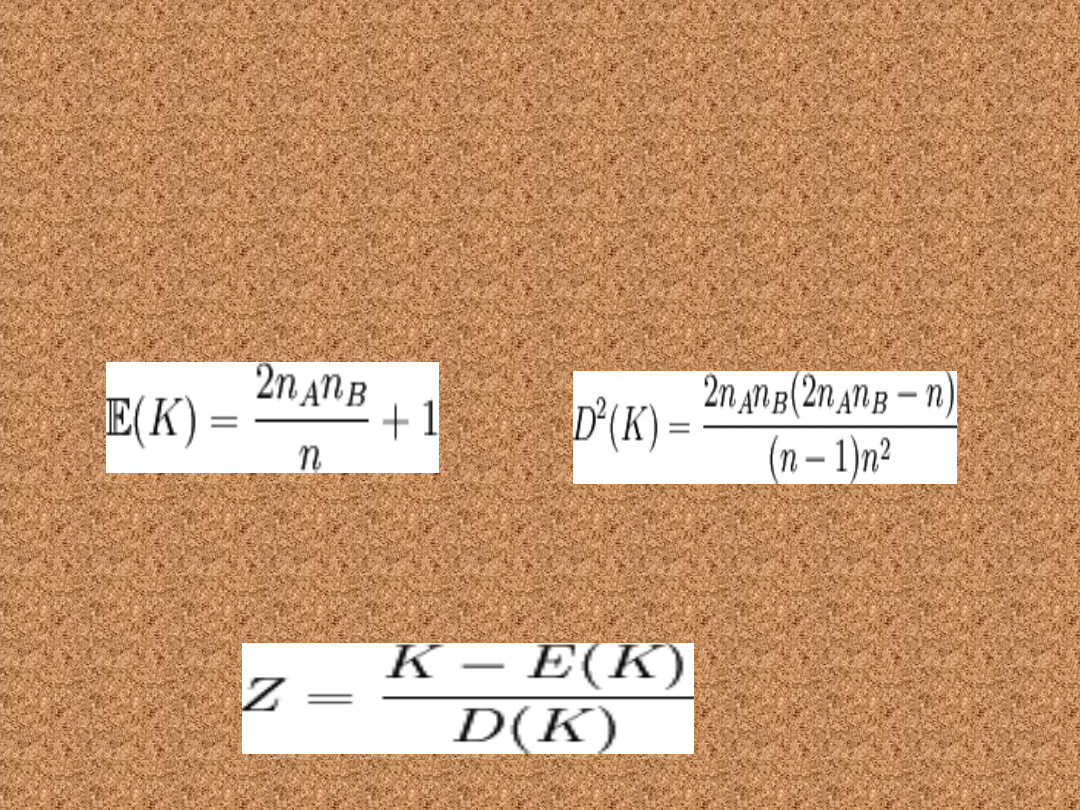
Jeżeli nA i nB ≥ 20, to zmienna losowa K

dąży asymptotycznie do rozkładu normalnego

N{E(K),D(K)}. Wartość średnia i wariancja

zmiennej są określone wzorami: eżeli nA i

nB ≥ 20, to zmienna losowa K dąży

asymptotycznie do rozkładu normalnego

N{E(K),D(K)}. Wartość średnia i wariancja

zmiennej są określone wzorami:

Wykorzystując te parametry, obliczamy

statystykę Z, która przy założeniu prawdziwości

H_{0} ma rozkład N(0,1).