FIZYKA

FIZYKA

Dr inż. Marek PROFASKA

[e-mail]

tel.[phone] kom.607-746-544

Kinematyka ciała

Kinematyka ciała

sztywnego

sztywnego

KINEMATYKA ciała

KINEMATYKA ciała

sztywnego

sztywnego

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Przypadki ruchu ciała sztywnego:

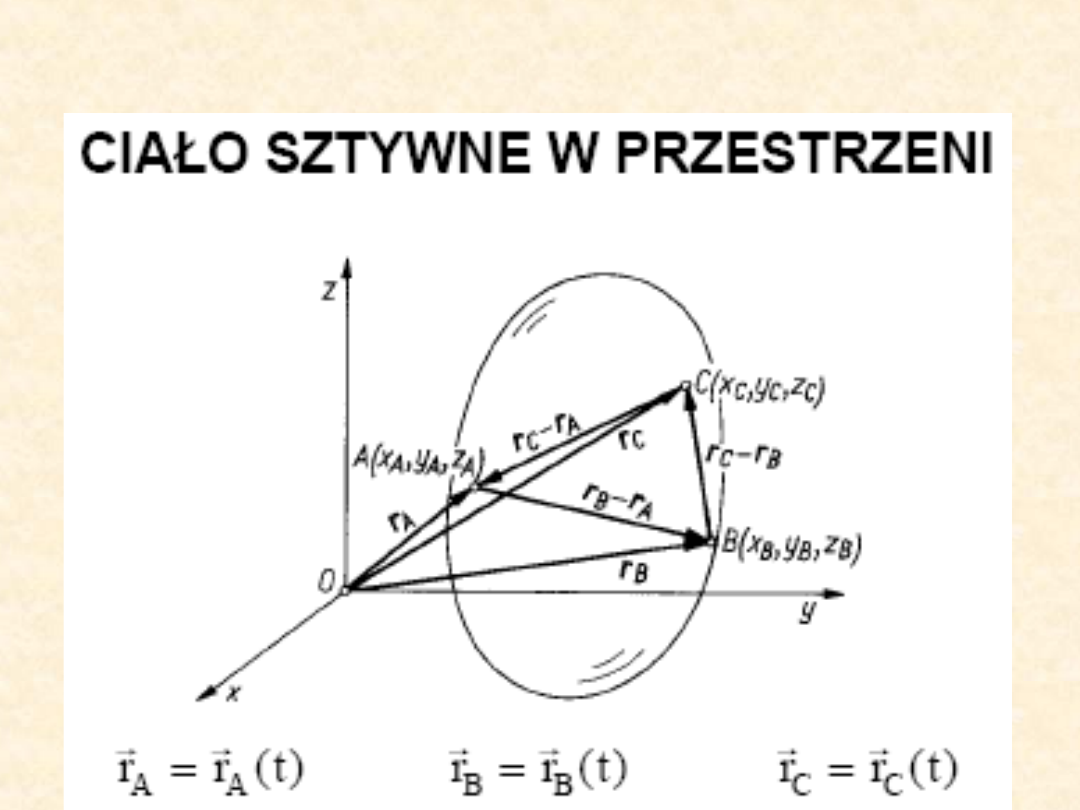
Ruch ciała sztywnego określany
jest przez ruch trzech punktów
tego ciała (jest to najmniejsza
liczba punktów związanych
ze sobą w sposób sztywny,
spełniających warunki
sztywności).
Tory tych punktów to tzw. kierownice ruchu.

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

W zależności od kierownic rozróżniamy:

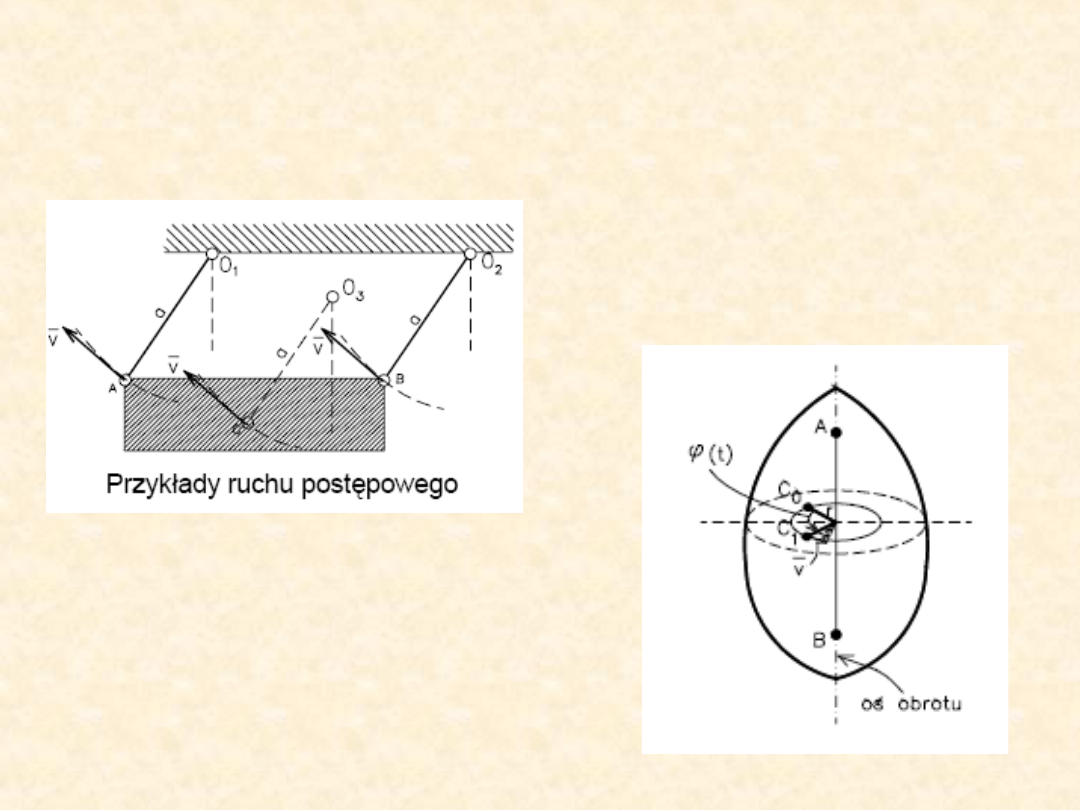
1)

przesunięcie

– kierownice proste

równoległe (ruch ten określany jest przez

ruch

jednego punktu ciała sztywnego).

2)

ruch postępowy

– kierownice krzywe do

siebie równoległe ( ruch określony jest

przez ruch jednego punktu ciała) – np. ruch

tłoka, klatka dźwigu.

3)

ruch obrotowy

– kierownice dwóch

punktów ciała redukują się do punktów i

wyznaczają oś obrotu.

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

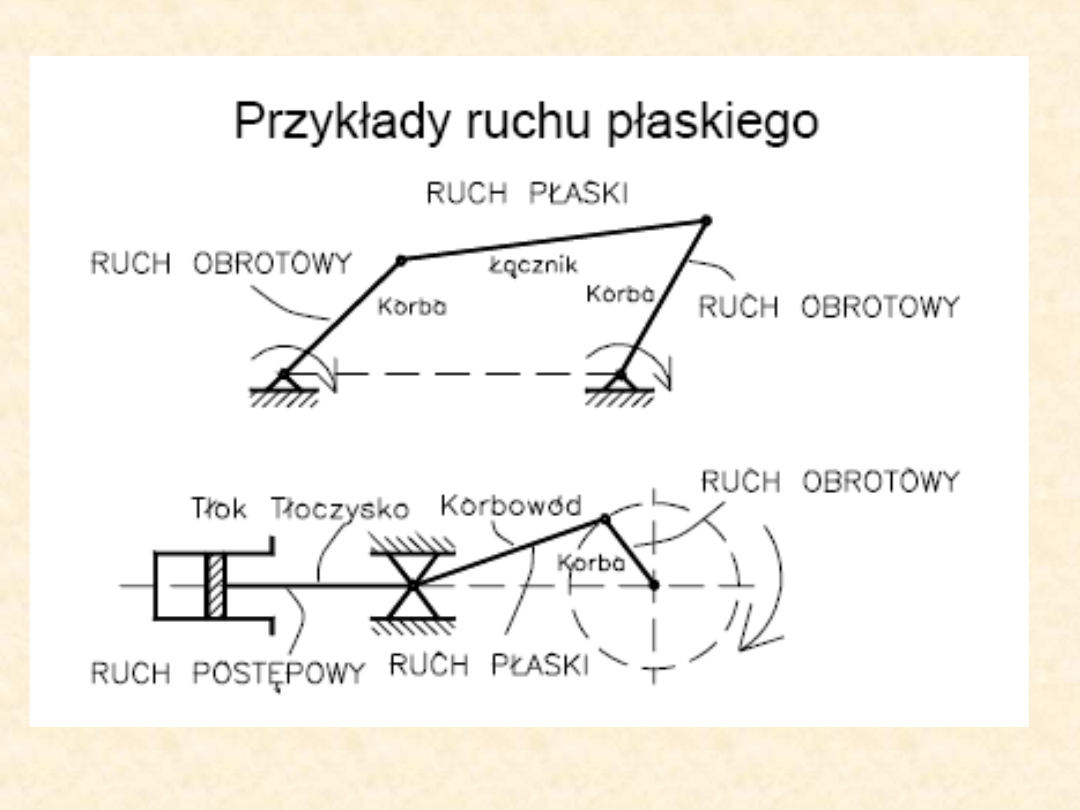
4)

ruch płaski

– kierownice leżą w

płaszczyznach do siebie równoległych.
Chwilowy ruch płaski można traktować
jako chwilowy obrót dookoła tzw. Osi
chwilowego obrotu. Suma ruchów
chwilowych oddaje nam zatem ruch płaski.

5)

ruch kulisty

– kierownice jednego z

punktów redukują się do punktu.

6)

ruch ogólny

– kierownice dowolnie

zorientowane w przestrzeni.

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Ruch obrotowy

Nieruchome punkty A i B określają

położenie przechodzącej przez nie

prostej zwanej osią obrotu. Tor

dowolnego punktu nie leżącego na osi

obrotu jest kołem. Równanie ruchu

obrotowego ciała sztywnego

zapisujemy w postaci zależności kąta

obrotu od czasu:

φ = φ (t).

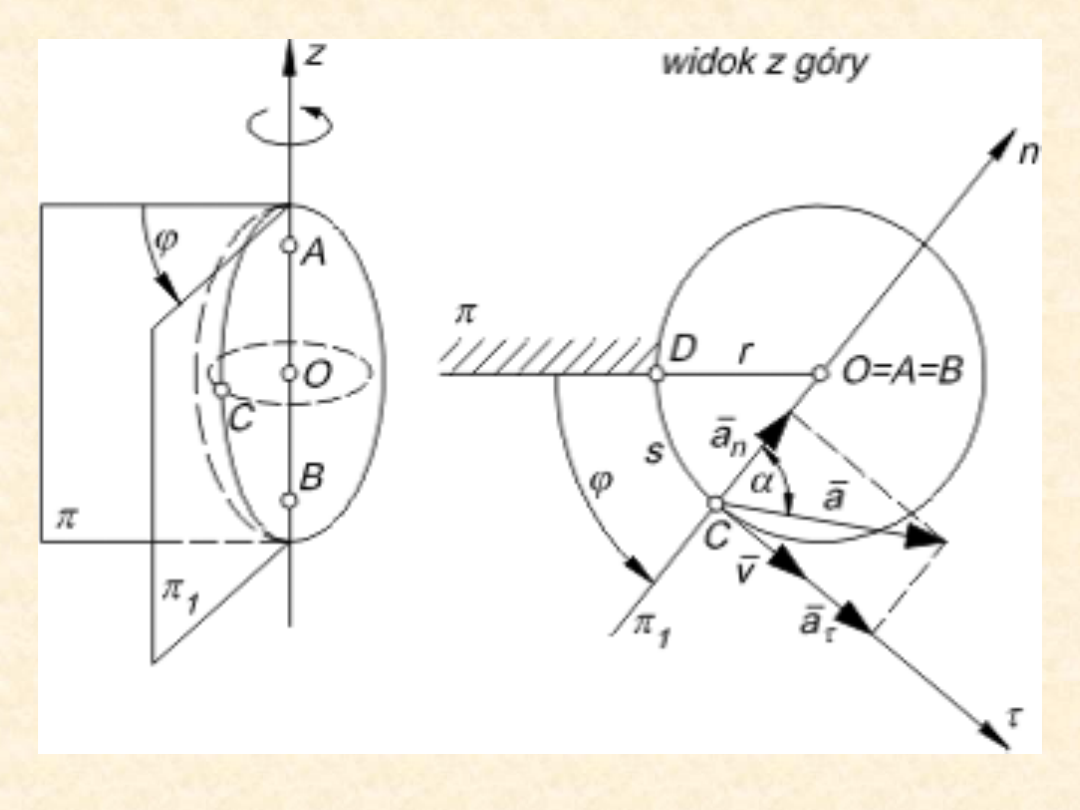
Ruch
obrotowy

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Średnią prędkość kątową

określamy jako iloraz różnicowy
przyrostu współrzędnej kątowej oraz
przyrostu czasu:

t

sr











KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Obliczając granicę ilorazu różnicowego

przy t dążącym do zera,
otrzymujemy

prędkość kątową

:

























dt

d

t

t

lim

0

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Jeśli prędkość kątowa ω = const ,

wówczas ruch obrotowy jest ruchem
jednostajnym.

C

t

dt

t



















KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

W zależności od warunków

początkowych możliwe są 4 warianty
równania współrzędnej kątowej
(podobnie jak w ruchu punktu).

Np. dla t = 0 i φ = φ

0

,

otrzymamy C = φ

0

, φ = φ

0

+ ω t

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

W zagadnieniach technicznych opisując

ruch obrotowy, często zamiast
prędkości kątowej używamy liczby
obrotów na minutę oznaczanej przez n.

gdzie n – liczba obrotów na minutę.
ω - prędkość kątowa [s

-1

] .

30

60

2

n

n

















KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Zmienność w czasie prędkości

kątowej nazywamy
przyspieszeniem kątowym.

Przyspieszenie kątowe średnie

:

t

sr











KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Przyspieszenie kątowe w danej chwili:













 















dt

d

t

t

lim

0

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Jeżeli

wektory ω i ε mają taki sam

zwrot

mamy do czynienia z ruchem

przyspieszonym, w przypadku zwrotów
przeciwnych z ruchem opóźnionym.

Jeżeli

przyspieszenie kątowe ε jest

stałe

mamy do czynienia z ruchem

jednostajnie zmiennym.

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

W zależności od warunków

początkowych możliwych jest 16
wariantów równania współrzędnej
kątowej (podobnie jak
w ruchu punktu).

KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Dla warunków początkowych t = 0 ,

φ=φ

0

,

ω = ω

0

otrzymujemy:

C

t

dt

t























t













0

2

2

0

0

t

t



















KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Zależność pomiędzy prędkością

kątowa i liniową.

r









KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Zależność pomiędzy

przyspieszeniem kątowym i
stycznym:

r

a









r

r

r

a

n









2

2

2





2

2

n

a

a

a







KINEMATYKA

KINEMATYKA

ciała sztywnego

ciała sztywnego

Ruch obrotowy zmienny występuje

gdy:

φ =φ(t) , ω = ω(t), ε = ε(t).

KINEMATYKA

KINEMATYKA

Dziękuję za uwagę

!