Układy RLC
Technika Cyfrowa i
Impulsowa
Ernest Jamro
C3-504, tel. 6172792
Katedra Elektroniki
Akademia Górniczo-Hutnicza
Układy RLC
Technika Cyfrowa i
Impulsowa
Ernest Jamro
C3-504, tel. 6172792
Katedra Elektroniki
Akademia Górniczo-Hutnicza
1
)
(
dt
t
s
1
0
1
0
0
)
(
1
t
t
t
)
(s
F
e
s
a
a
s
1
2
)
(
1
s
2
2
s
2
2
s
s
)
0
(
)
(
f
s
sF
dt
t
f
d
)
(
s
s
F )
(
t
dt
t
f
0
)
(
transformata
Laplace’a
F(s)
oryginalny przebieg
czasowy f(t)
opis
1
(t)
delta Diraca, impuls o
nieskończenie krótkim czasie
trwania (t=0) i nieskończenie
dużej amplitudzie
1(t)
Skok jednostkowy:
f(t-a)
przebieg opóźniony o czas a
e
-a
t
typowy przebieg w obwodach RC
F(s+)
e
-
t
f(t)
Przebieg tłumiony w czasie
t
e
-
t
Przebieg dla rezystancji
krytycznej (=0) dla obwodów
RLC
sin(
t)
Przebieg oscylacyjny
cos(
t)
Przebieg oscylacyjny
Pochodna względem czasu
Całkowanie względem czasu
Przekształcenie
Laplace’a
0
)
(
)
(
dt
e
t
f
s
F
st
Kondensator
U
Q
C
d
S
C
dt
dq
i
dt
i
q
dt
du
C
i
dt
i
C
u
1
różniczkowanie względem napięcia całkowanie
względem prądu
i= s
C
u (założenie: u(t=0)=0)
sC
i
u
sC
i
u
Z
1
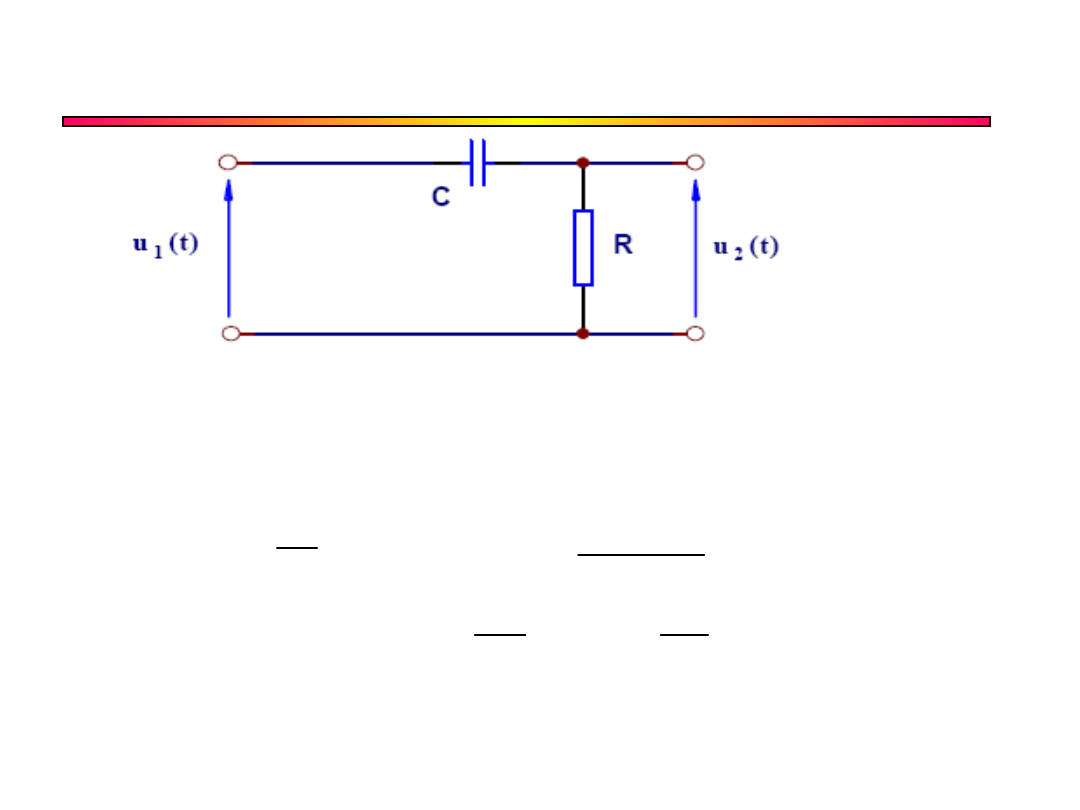
Układ różniczkujący RC
Dziedzina czasu
t
u
RC
u
t
u
RC
d
d
d
d
1
2
2
R
u
i
2
dt
u
u
d
C
i
)
(
2
1
czyli
= RC - stała czasowa
Obliczenia w dziedzinie
Laplace’a
Wymuszenie: skok napięcia
s
s
s
U
sC
R
R
s
U
s
U
1
1
1
1
2
Otrzymujemy:
- skok napięcia
at
e
a
s
1
t
e
U
t
u
t
M
1
2
s
U
s
E
t
U
t
u
M
g
M
1
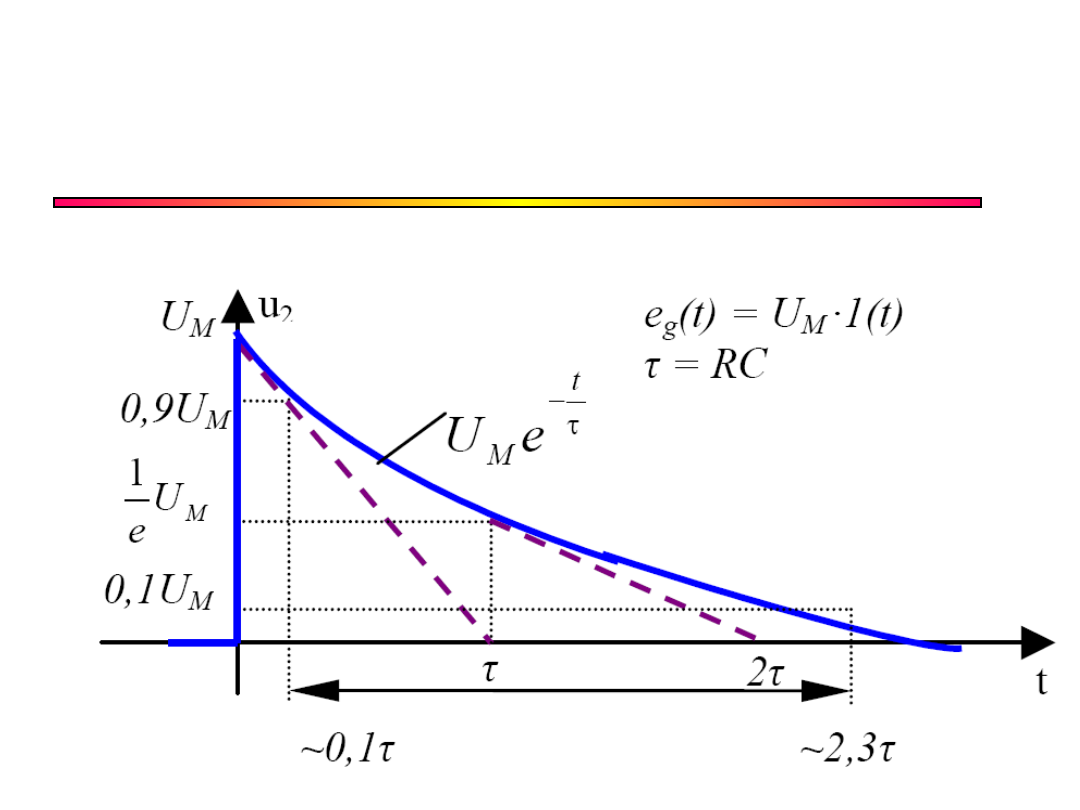
Przebieg czasowy (odpowiedz
układu różniczkującego RC na skok
jednostkowy)
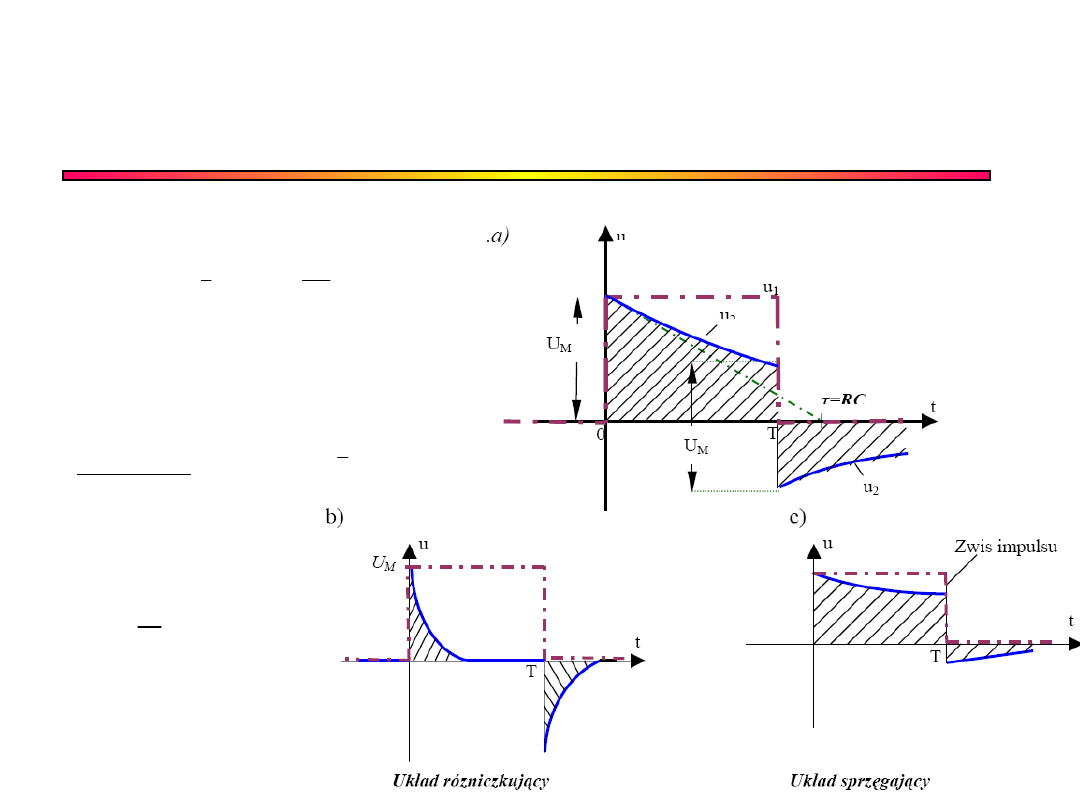
Układ różniczkujący RC -
odpowiedz na przebieg
prostokątny
T
t
e
t
e
U
t
u
T
t
t
M
1
1
2
T
T>>
T<<
%
100
1
%
100
2
T
M
M
e
U
T
u
U
z
Zwis:
Zwis dla T<<
[%]
100
T
z
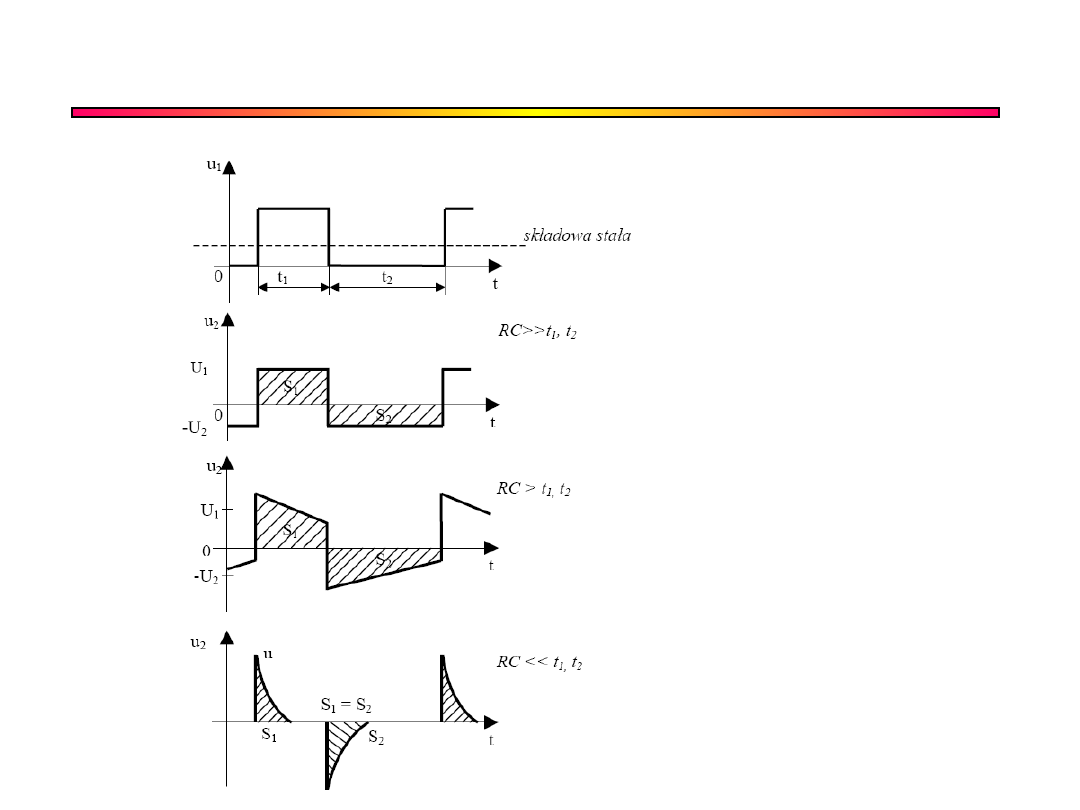
Układ różniczkujący RC a składowa
stała
Układ różniczkowy
nie przenosi
składowej stałej:
S
1
=S
2
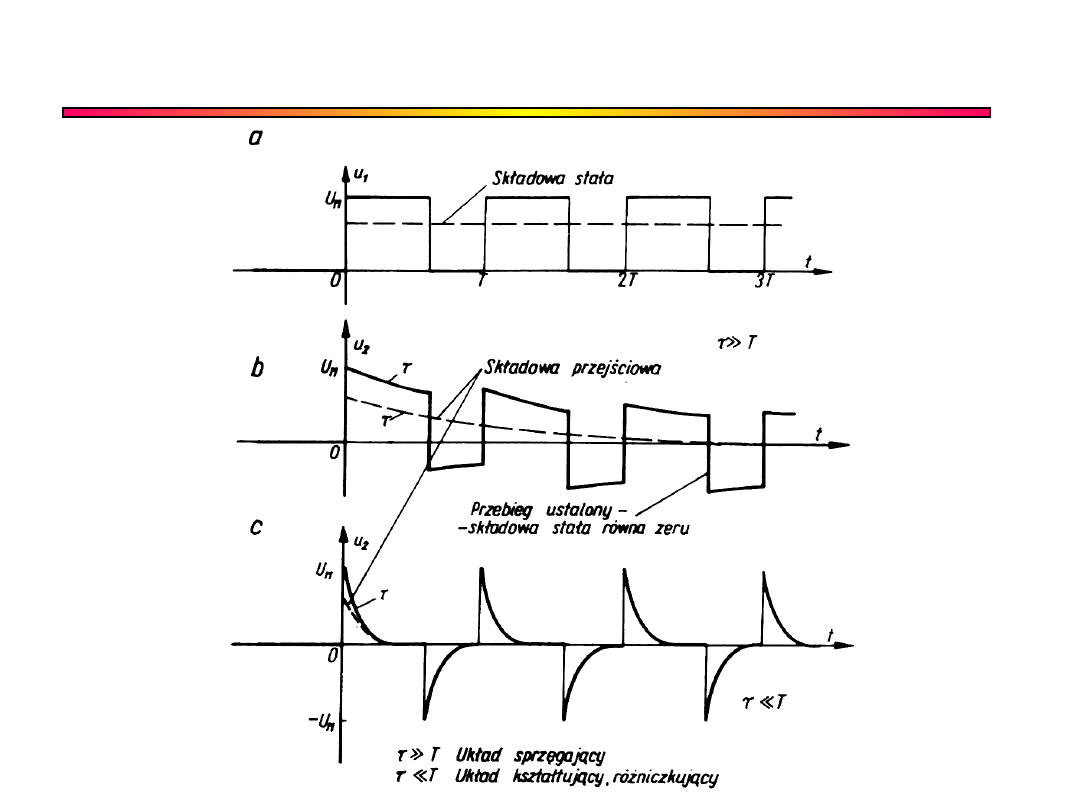
Składowa przejściowa
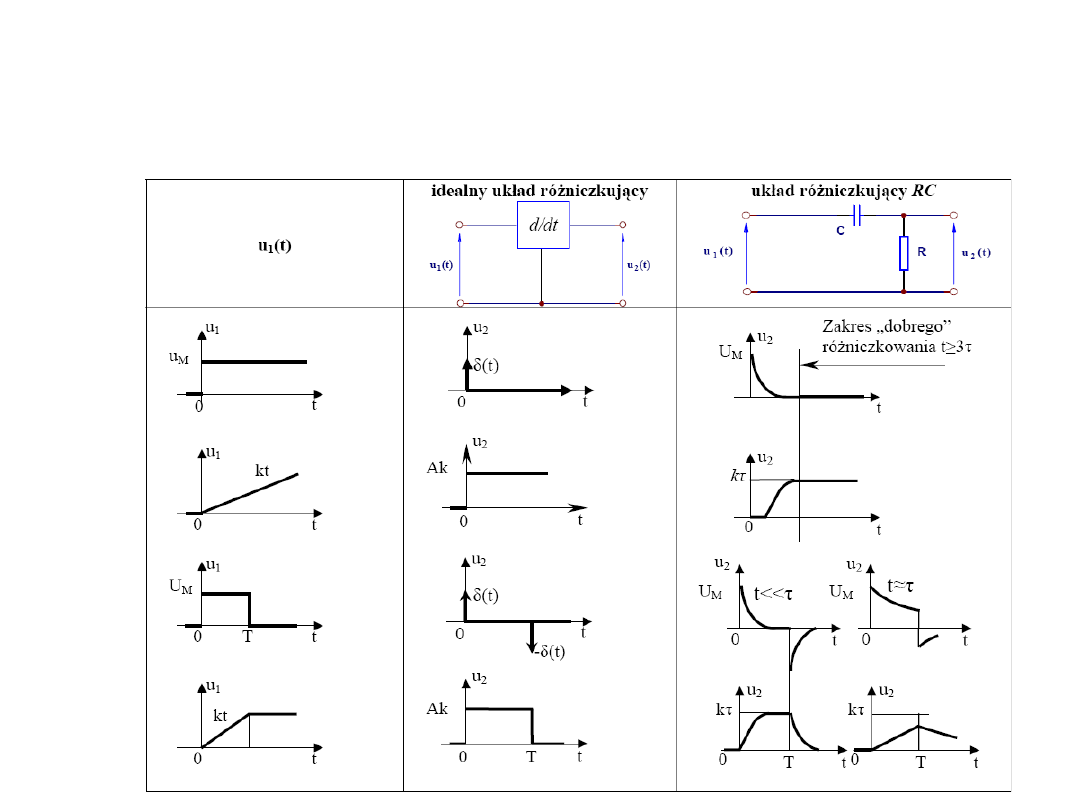
Układ różniczkujący i inne
wymuszenia
Układ całkujący RC
2
2
1
d
d
u
t
u
u
s
s
U
sC
R
sC
s
U
s
U
1
1
1
1
1
1
2
Filtr
dolnoprzepustowy
t
e
U
t
u
t
M
1
1
2
RC
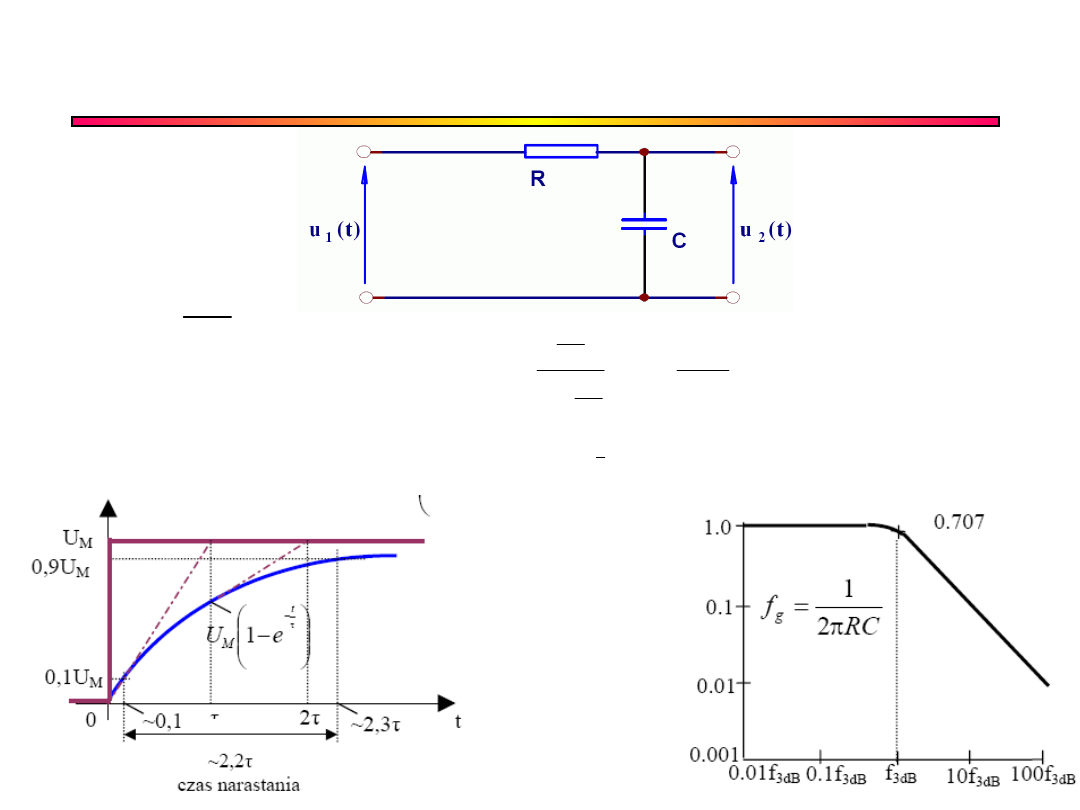
Czas narastania
Jako czas narastania przyjmuje się czas narastania
odpowiedzi na skok jednostkowy od 10% do 90%
wartości amplitudy impulsu skokowego:
t
10
można obliczyć ze wzoru:
t
90
można obliczyć ze wzoru:
t
n
= t
90
- t
10
2,2
.
Częstotliwość graniczna a czas narastania:
Wypadkowa czasów narastania:
t
M
M
e
U
U
1
1
.
0
1
.
0
)
9
.
0
ln(
10
t
t
M
M
e
U
U
1
9
.
0
3
.
2
)
1
.
0
ln(
90
t
g
g
n
f
f
RC
t
35
,
0
2
2
,
2
2
,
2
2
,
2
...
2
3
2
2
2
1
2
n
n
n
n
t
t
t
t
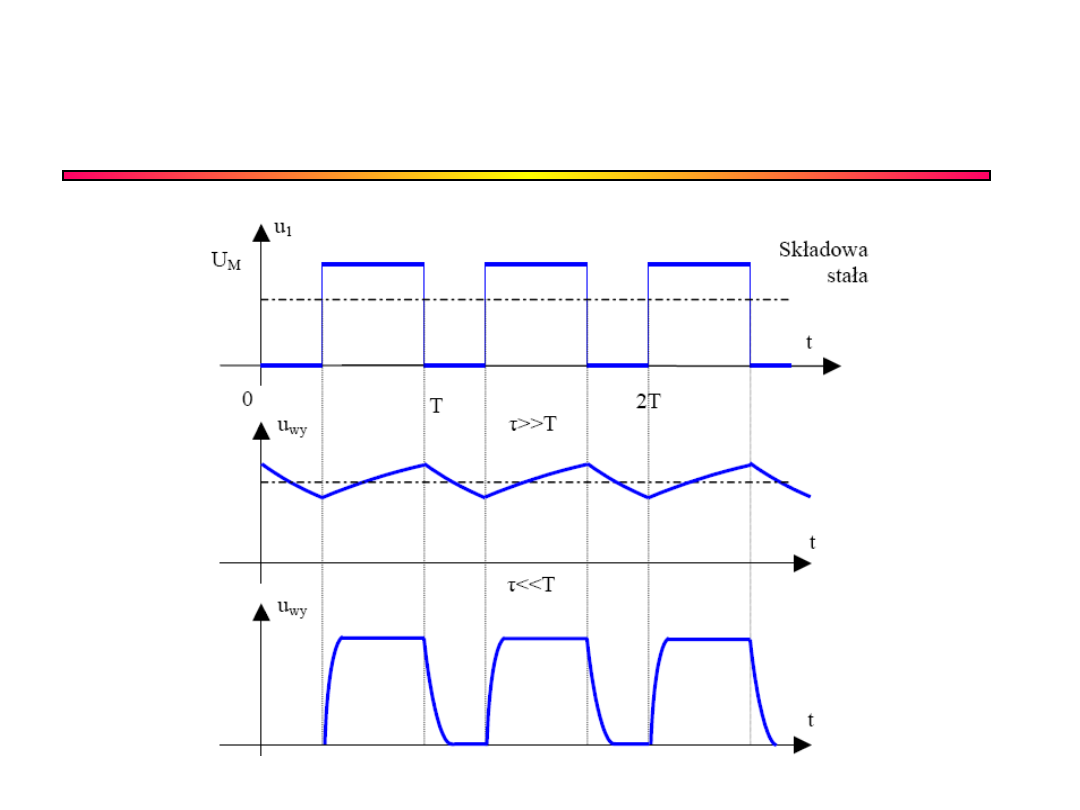
Odpowiedz układu
całkującego RC na falę
prostokątną
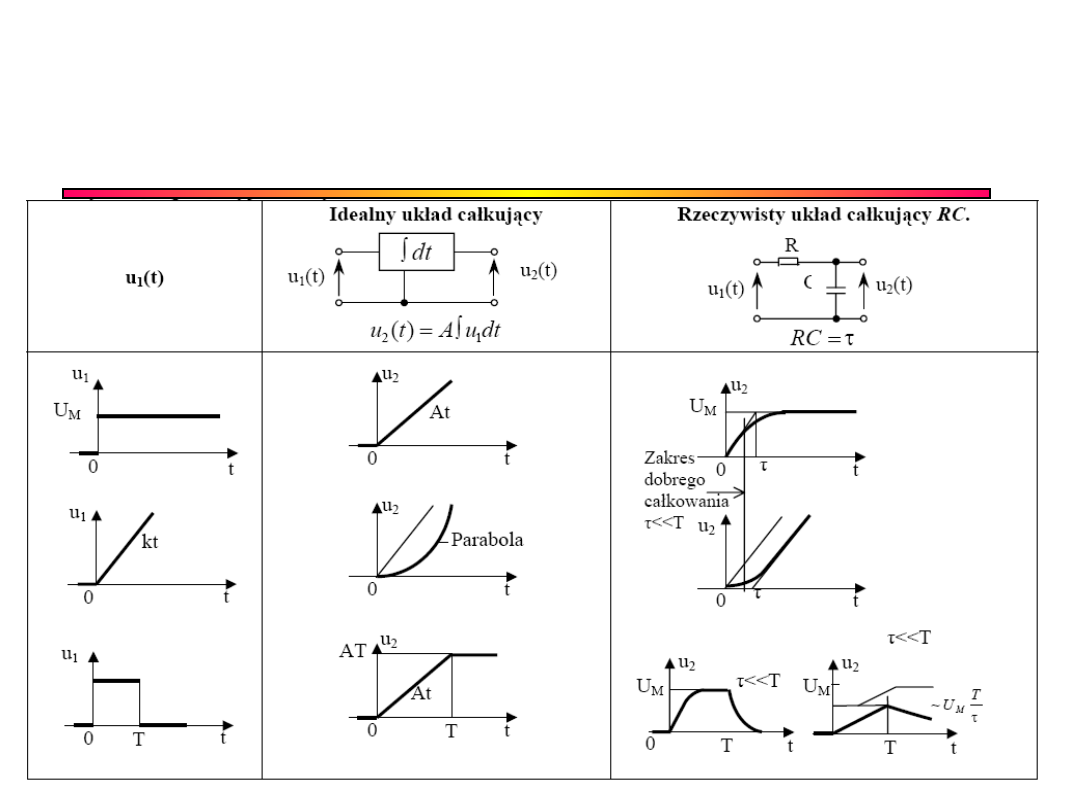
Układ całkujący i inne
wymuszenia
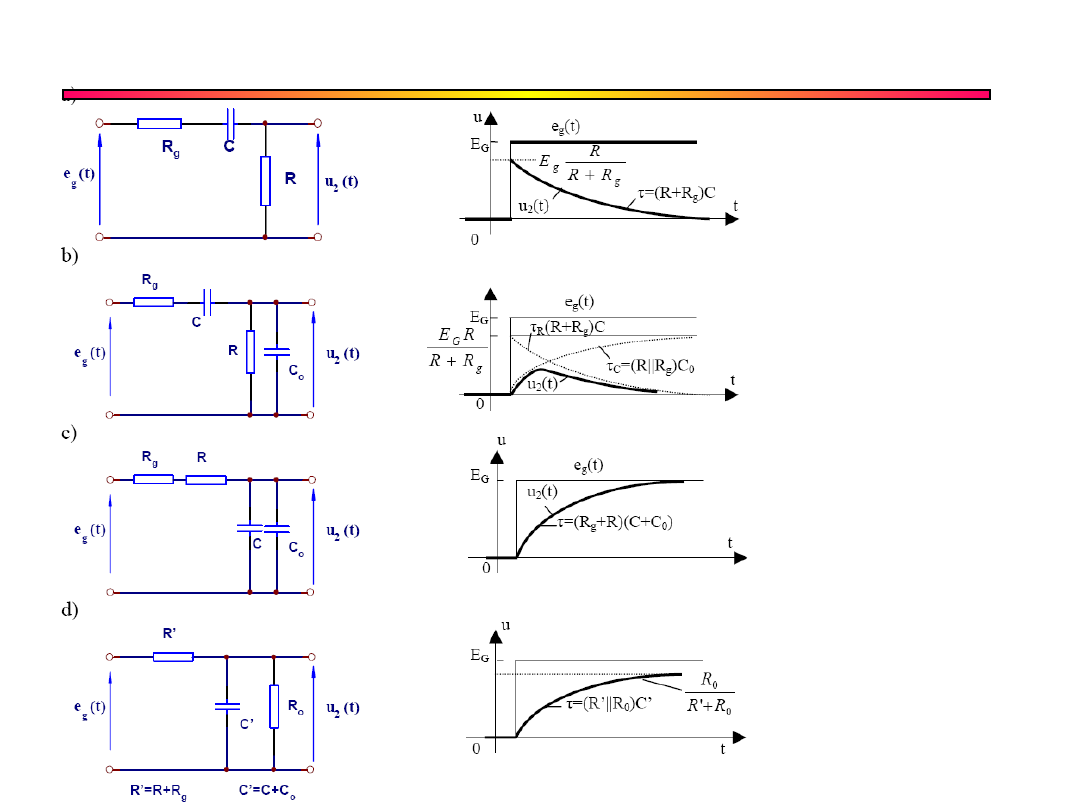
Wpływ rezystancji
generatora
Zobacz na
zasadę
Thevenina
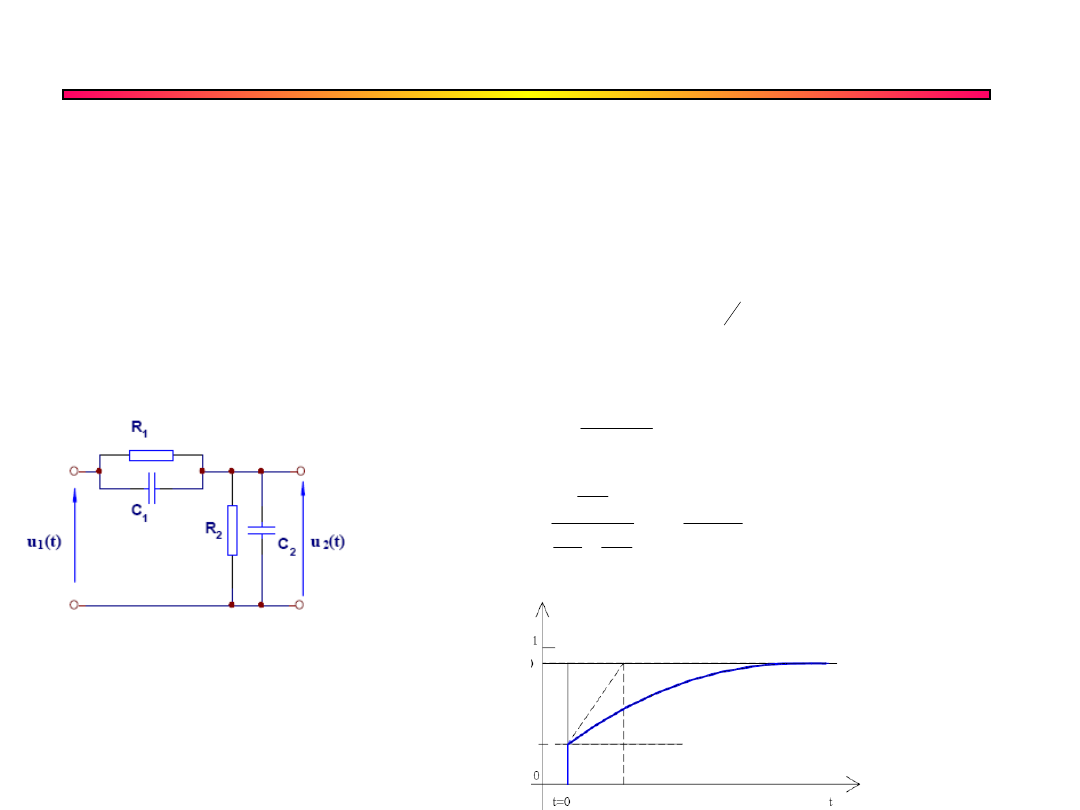
Metoda czoła i grzbietu
U(t=0) – napięcie przy założeniu że kondensatory są
zwarte
U(t=) – napięcie przy założeniu że kondensatory są
rozwarte
Stała czasowa obliczana dla R jako rezystancja
widziana z zacisków kondensatora C
Przykład:
t
e
t
U
t
U
t
U
t
u
)]
(
)
0
(
[
)
(
2
1
2
R
R
R
U
t
U
M
2
1
1
2
1
2
1
1
1
0
C
C
C
U
sC
sC
sC
U
t
U
M
M
C
w
= C
1
+C
2
R
w
= R
1
||R
2
=C
w
R
w
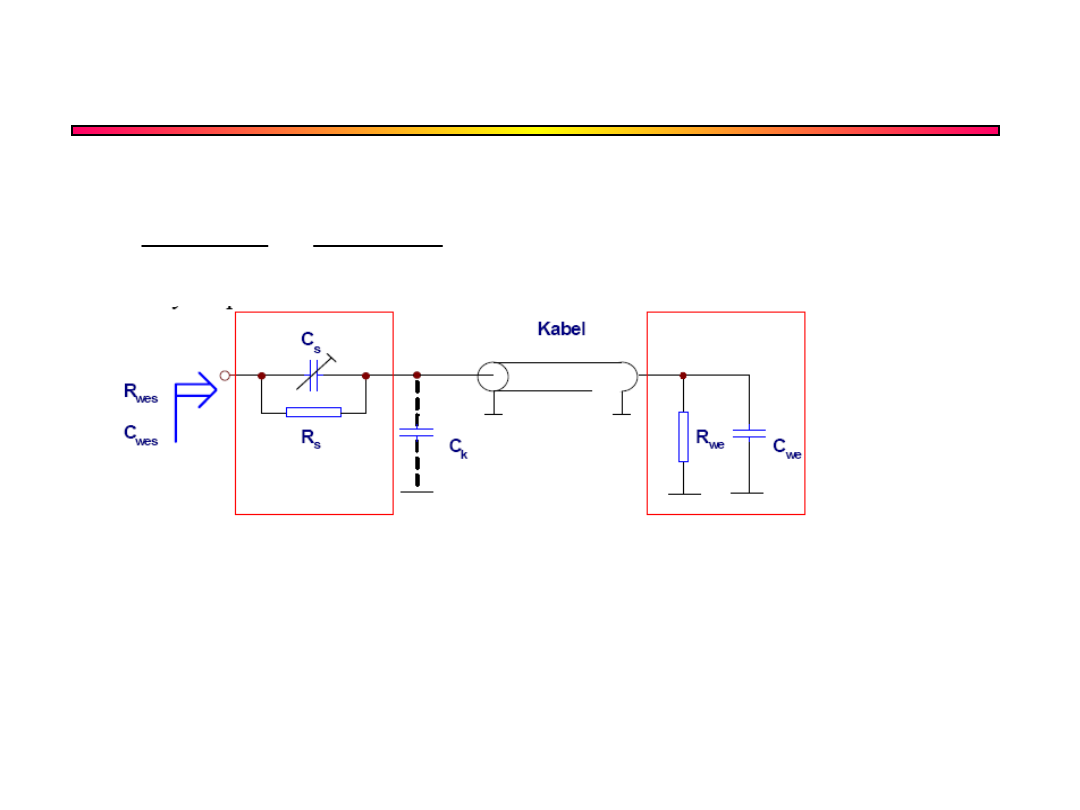
Dzielnik skompensowany – sonda
oscyloskopowa
2
1
1
2
1
2
C
C
C
R
R
R
U(t=0
+
)=U(t
) czyli
lub R
1
C
1
= R
2
C
2
W oscyloskopie R
we
=1M, C
we
10pF
R
S
=9M, C
s
1pF
Stosunek podziału napięcia k=10,
R
wes
=10M= k R
we
, C
wes
=C
we
/k
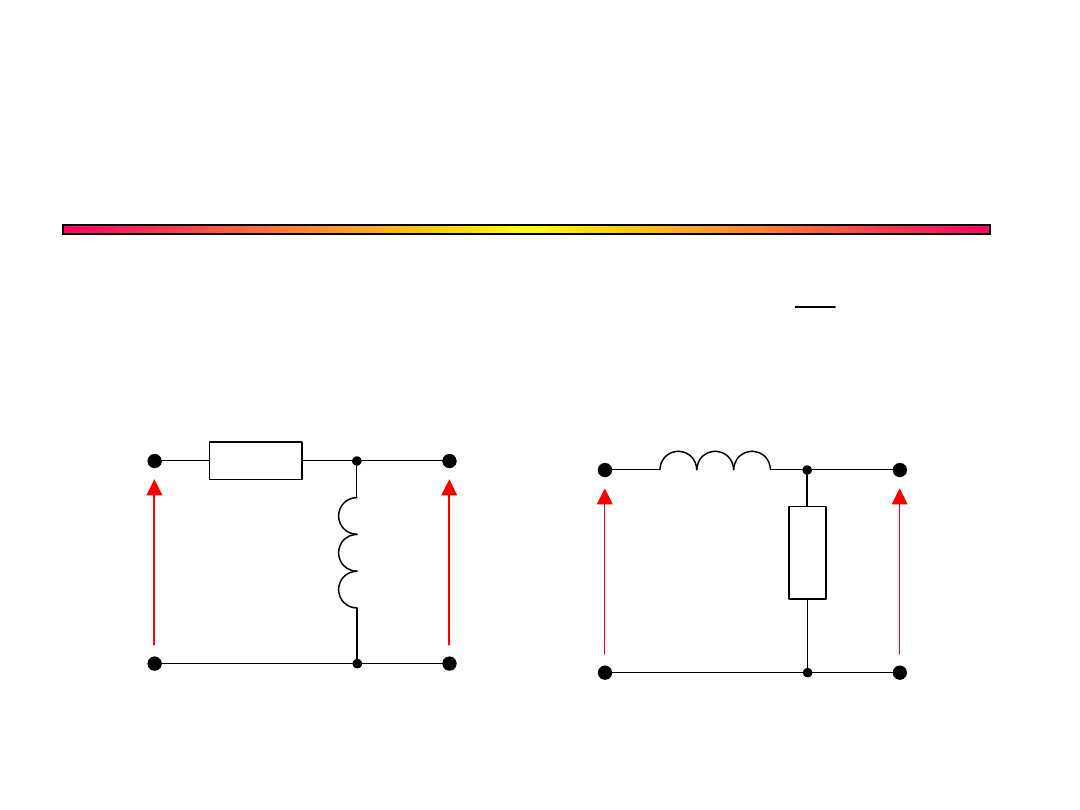
Układy całkujące i
różniczkujące RL
Działają podobnie jak układy RC
Stała czasowa =L/R
U
1
U
2
R
L
U
1
U
2
R
L
Różniczkujący
Całkujący
dt
di
L
u
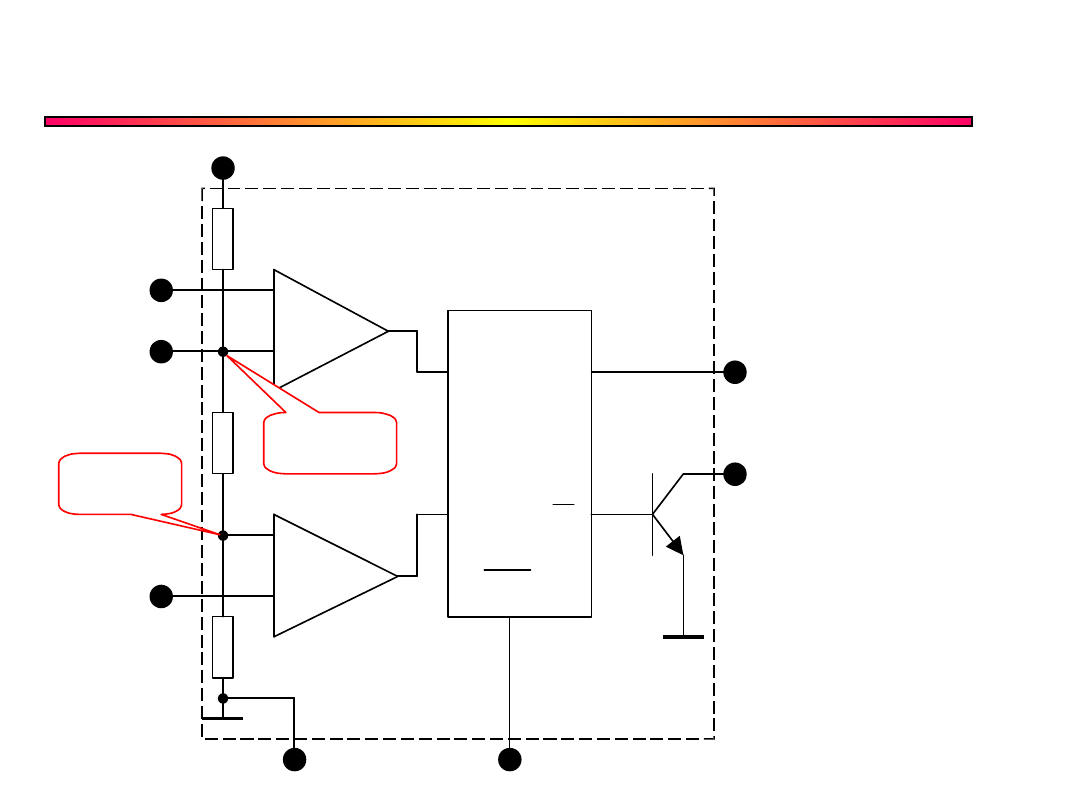
Timer 555
+
–
+
–
R Q
S Q
Reset
8 - Vcc
3 - Wyjście
7 - Rozładowanie
4 - Zerowanie
1- Masa
6 - Próg
przełączenia
5 - Modulacja
2- wyzwalanie
Vcc/3
2Vcc/3
R
R
R
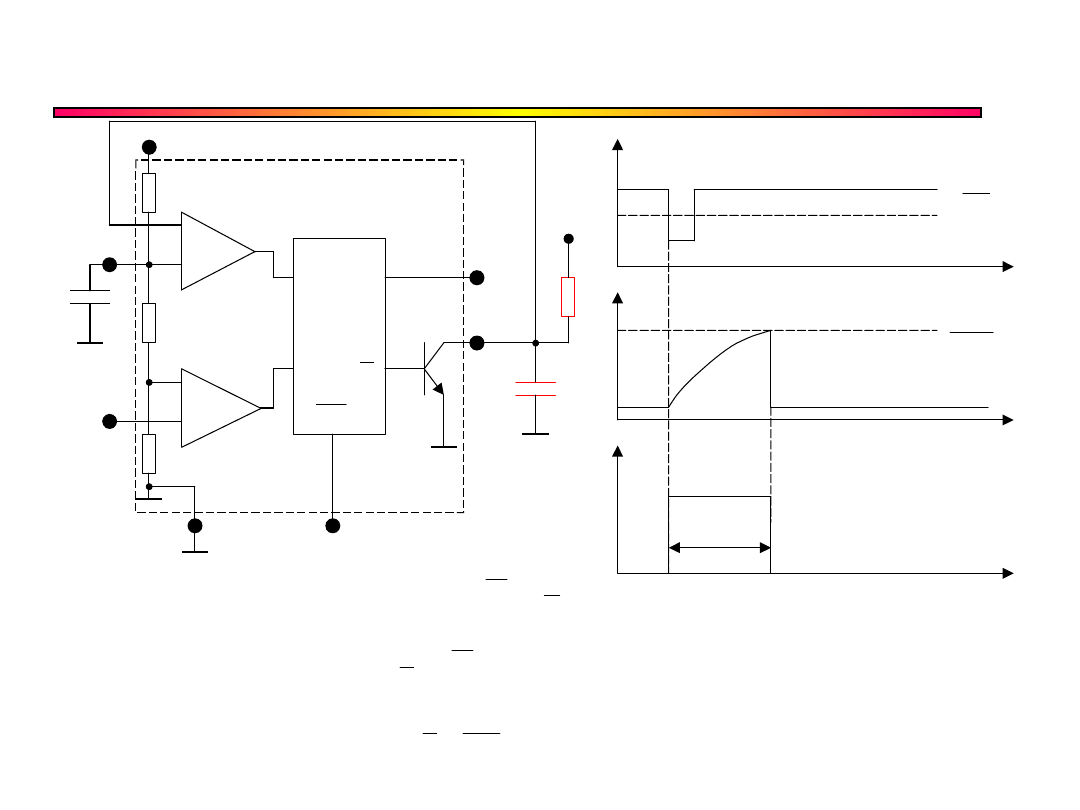
Monowibrator
+
–
+
–
R Q
S Q
Reset
Wyjście
Vcc
C
Vcc
R
Wyzwalanie
W yzwalanie
t
t
C
3
CC
V
t
W y
3
2
CC
V
t
1
RC
RC
t
RC
t
e
Vcc
e
Vcc
RC
t
RC
t
1
,
1
)
3
ln(
3
1
ln
3
1
3
2
)
1
(
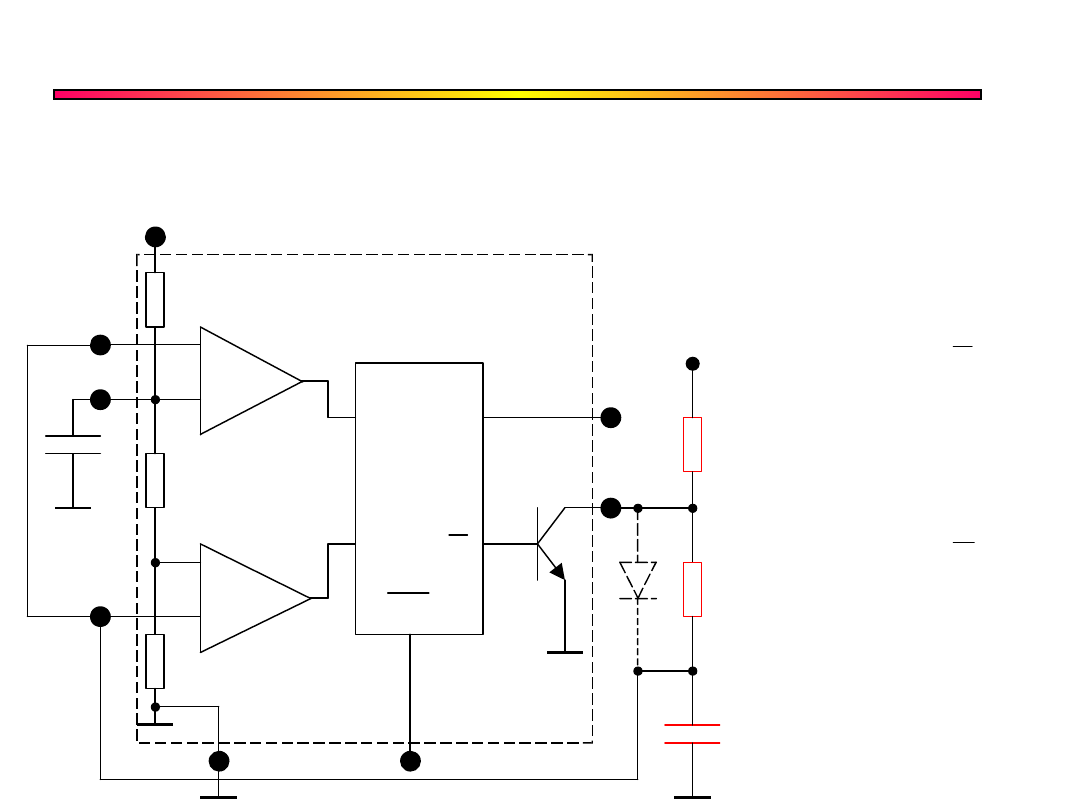
Multiwibrator
+
–
+
–
R Q
S Q
Reset
Wyjście
Vcc
C
Vcc
R
A
R
B
D
)
1
(
)
(
)
0
(
)
(
/
/
t
t
e
t
u
e
t
u
t
u
0
)
(
3
2
)
0
(
:
)
(
3
1
)
0
(
:
t
u
V
t
u
ie
Rozłozłado
V
t
u
V
t
u
Ładowanie
CC
CC
CC
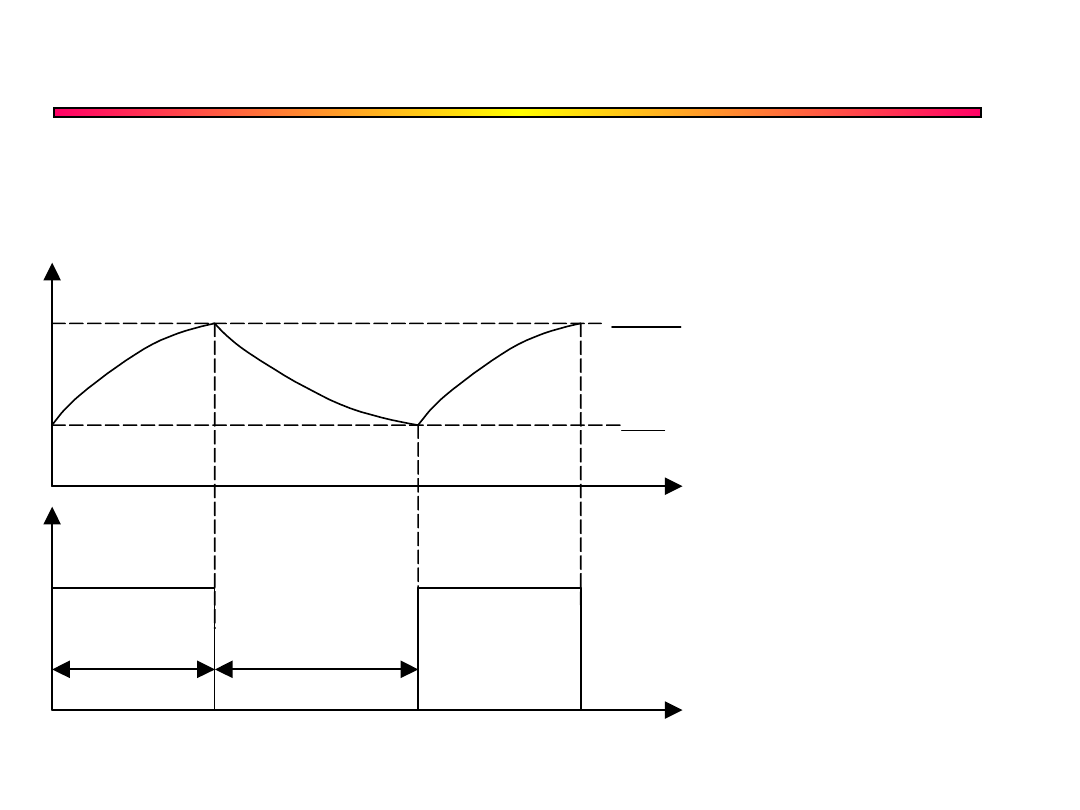
Multiwibrator - przebiegi
t
C
3
CC
V
t
Wy
3
2
CC
V
t
1
t
2
Bez Diody:
t
1
= 0,7(R
A
+ R
B
)C
t
2
= 0,7R
B
C
T=t
1
+t
2
=
0,7(R
A
+2R
B
)C
Z Diodą:
t
1
= 0,7R
A
C
t
2
= 0,7R
B
C
T=t
1
+t
2
=
0,7(R
A
+R
B
)C
Bez diody – brak wypełnienia 0.5
Z diodą – wypełnienie 0.5 ->
R
A
=R
B
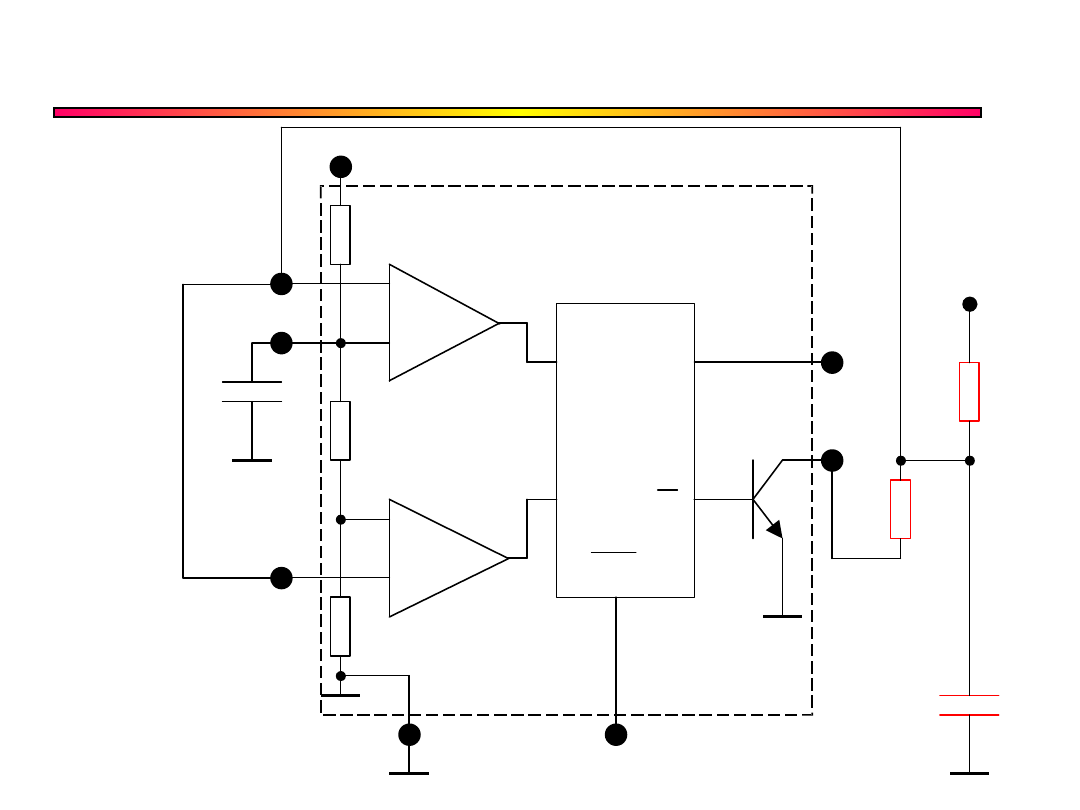
Multiwibrator – wypełnienie 0.5 bez
diody
+
–
+
–
R Q
S Q
Reset
Wyjście
Vcc
C
Vcc
R
A
R
B
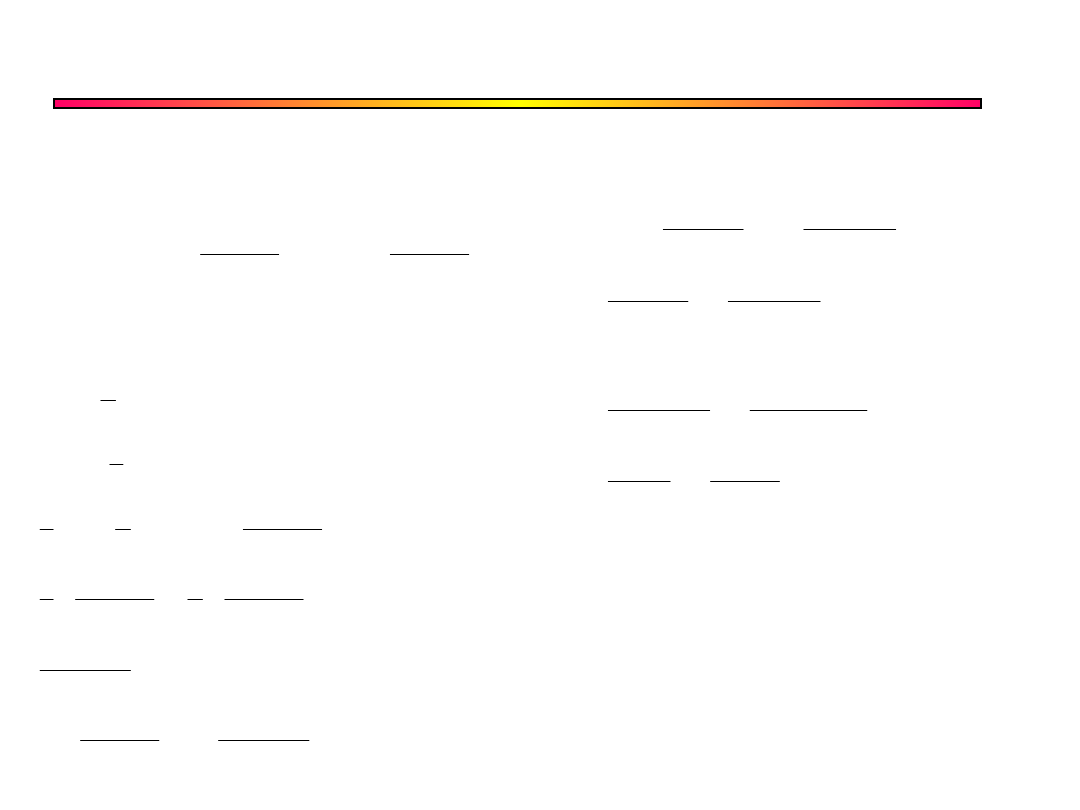
Multiwibrator – wypełnienie 0.5 bez
diody
)
2
2
ln(
2
2
)
3
2
(
3
1
)
1
(
3
2
3
1
?
3
1
)
(
)
1
(
3
2
)
(
)
1
(
)
(
)
0
(
)
(
:
:
:
7
.
0
)
2
ln(
:
2
/
/
/
/
2
2
/
/
/
/
1
B
A
B
A
B
A
B
A
t
B
A
B
A
t
A
B
B
A
B
B
t
CC
A
B
B
t
CC
CC
CC
t
T
t
CC
t
t
B
A
B
A
T
CC
A
B
B
T
A
A
R
R
R
R
C
R
R
R
R
t
e
R
R
R
R
e
R
R
R
R
R
R
e
V
R
R
R
e
V
V
t
V
t
u
e
V
e
V
t
u
e
t
u
e
t
u
t
u
rze
kondensato
na
Napiecie
R
R
R
R
R
V
R
R
R
V
Thevelin
e
Rozadowani
C
R
C
R
t
Ładowanie
423
.
0
:
)
2
1
2
ln(
)
1
(
)
2
ln(
)
2
2
ln(
)
1
(
)
2
ln(
)
2
2
ln(
)
2
ln(
)
2
2
ln(
)
2
ln(
:
5
.
0
ln
2
1
k
numeryczne
e
Rozwiazani
k
k
k
k
R
k
R
R
k
R
k
R
R
k
R
k
R
R
R
R
R
R
R
R
R
R
R
R
C
R
R
R
R
C
R
t
t
ienie
wype
Warunek
A
A
A
A
A
A
A
B
B
A
B
A
B
A
B
B
A
B
A
B
A
B
A
A
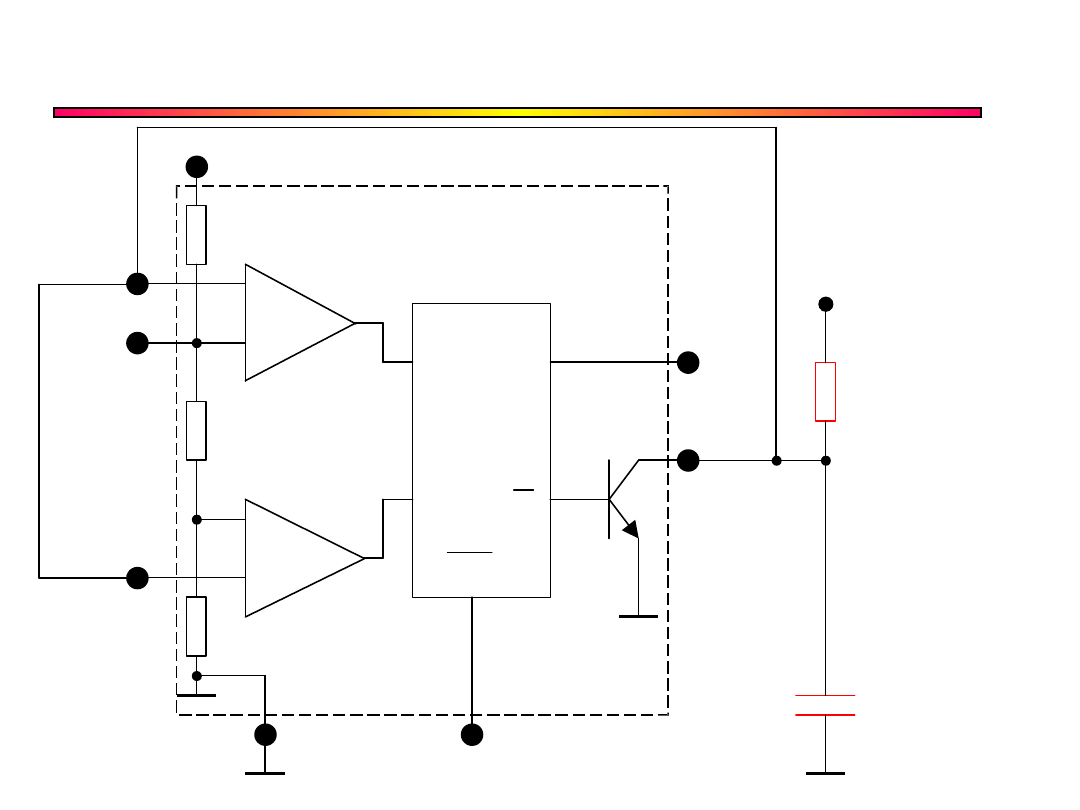
Przetwornik napięcie /
częstotliwość
+
–
+
–
R Q
S Q
Reset
Wyjście
Vcc
C
Vcc
R
A
Wejście
Przetwornik U/f
)
2
2
2
ln(
)
1
(
2
1
?)
(
)
(
2
1
)
0
(
)
1
(
)
(
)
0
(
)
(
/
/
/
/
k
k
RC
t
e
V
e
V
k
V
k
V
U
k
V
k
U
t
u
V
t
u
U
t
u
e
t
u
e
t
u
t
u
t
CC
t
CC
CC
CC
we
CC
we
CC
we
t
t
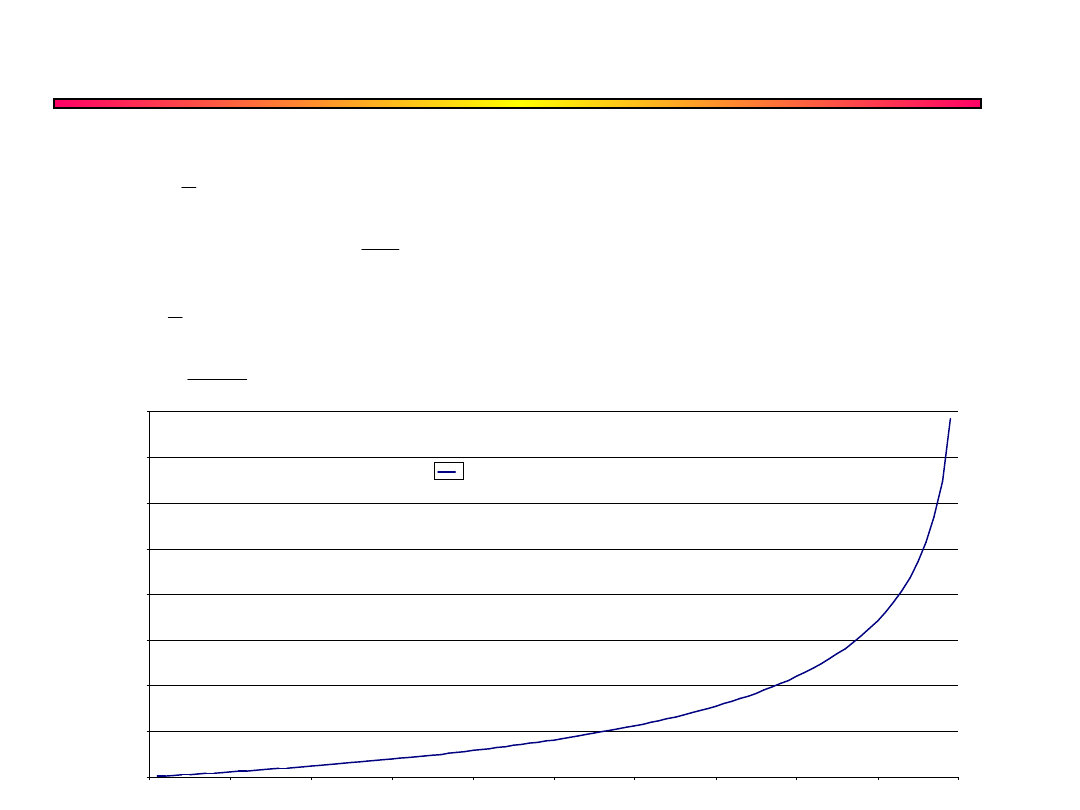
Wada – funkcja
silnie nieliniowa
szczególnie dla
U
we
V
CC
0
0,5
1
1,5
2
2,5
3
3,5
4
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
t
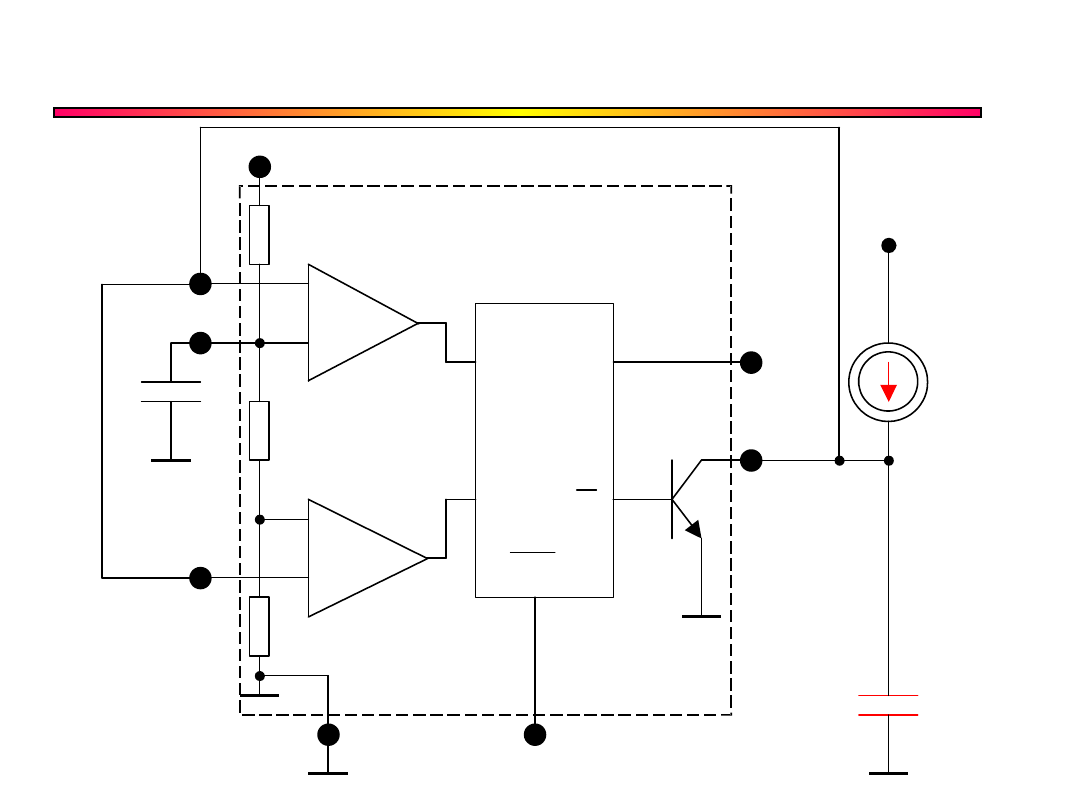
Ulepszony Przetwornik I/f
+
–
+
–
R Q
S Q
Reset
Wyjście
Vcc
C
Vcc
i(t)
Ulepszony przetwornik I/f
– c.d.
CC
CC
CC
V
C
I
t
f
I
V
C
t
V
U
I
U
C
t
C
t
I
dt
i
C
U
3
1
3
3
1
1
Częstotliwość
proporcjonalna do
prądu. W prosty sposób
można zbudować
przetwornik I/U i w ten
sposób otrzymamy
liniowy przetwornik U/f
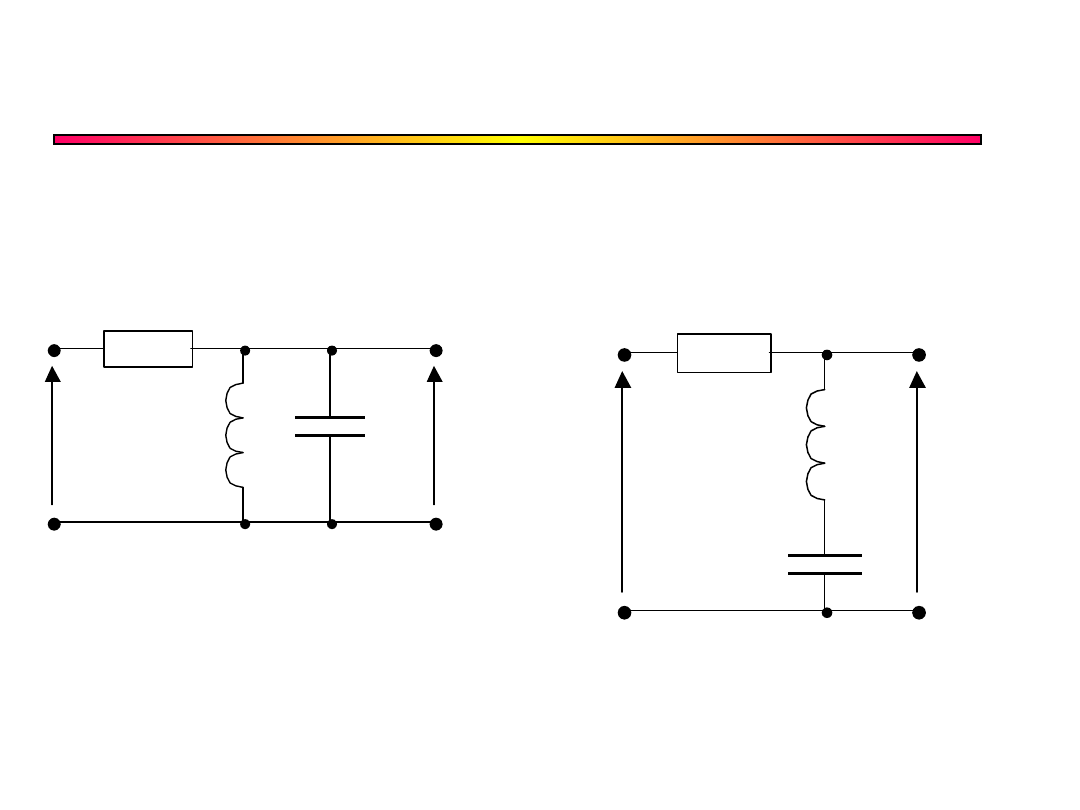
Obwody RLC
U
1
U
2
R
L
C
U
1
U
2
R
L
C
Równoległy
Szeregowy
Obwód równoległy
LC
s
RC
s
s
RC
R
Ls
RLC
s
Ls
C
L
sC
R
RsL
C
L
sC
sL
C
L
R
sC
sL
C
L
sC
sL
sC
sL
R
sC
sL
sC
sL
s
H
1
1
1
1
1
1
1
1
1
2
2
Można dokonać następującego podstawienia:
LC
1
RC
1
2
2
s
s
s
s
H
Dla wymuszenia skokiem jednostkowym (U
1
(s)=
1/s) otrzymujemy:
2
2
2
1
2
1
1
1
)
(
)
(
s
s
LC
s
RC
s
RC
s
U
s
H
s
U
Różne rozwiązania
równania
Analizując transformacje Laplace’a dla powyższego
modułu możemy otrzymać następujące przypadki:
f(t)= sin(
t) - drgania niegasnące
f(t)= e
-
t
sin(
t)
- drgania gasnące
f(t)= te
-t
–drgania krytyczne
f(t)= C
1
e
-a
t
+ C
2
e
-b
t
–
brak drgań
Najważniejsza jest równania kwadratowego
2
2
)
(
s
s
F
2
2
)
(
)
(
s
s
F
2
)
(
1
)
(
s
s
F
b
s
C
a
s
C
b
s
a
s
s
F
2
1
)
(
)
(
1
)
(
2
2
s
s
Przebiegi (obwód
równoległy)
2
2
s
s
s
s
H
<0 (drgania)
=0 – przebieg krytyczny (rezystancja
krytyczna)
2
2
0
0
2
2
2
0
)
2
(
s
s
s
s
U
4
2
2
2
0
RC
1
LC
1
C
L
R
2
1
C
L
R
2
1
)
sin(
)
(
0
2
/
0
2
t
e
t
u
t
2
/
2
)
(
t
e
t
t
u
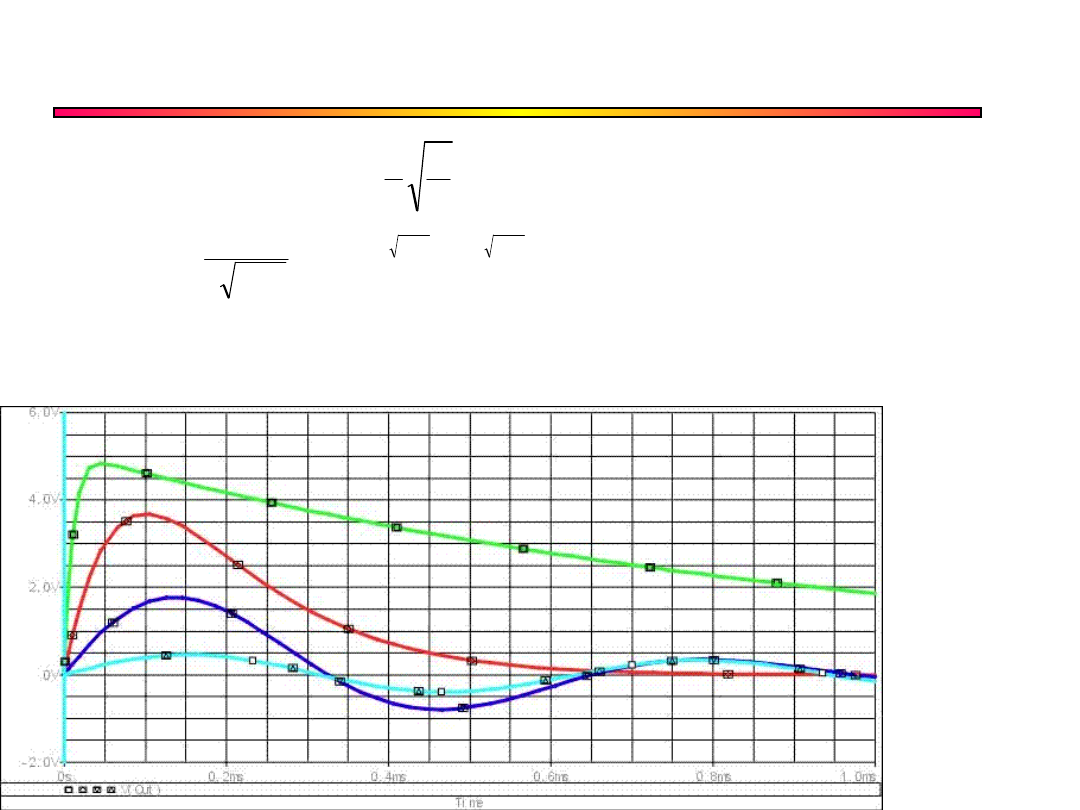
Przebiegi (obwód równoległy)
Brak drgań >0
)
(
2
)
(
2
0
2
0
2
/
2
0
2
t
t
t
e
e
e
t
u
C
L
R
2
1
Zielon
y
R<R
kr
Czerwony
R=R
kr
Niebieski
R>R
kr
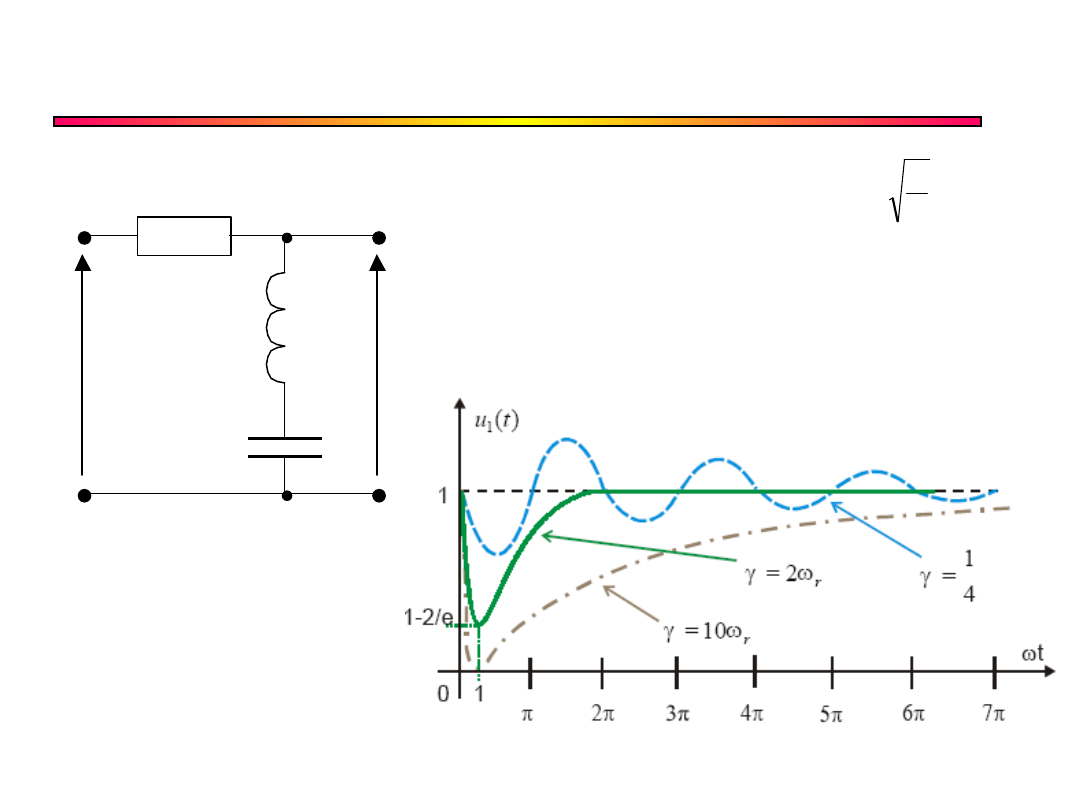
Obwód szeregowy
U
1
U
2
R
L
C
C
L
R 2
Rezystancja krytyczna
Drgania dla R<R
kr