Wymiary ciała

 

 

Punkt materialny

• Idealizacja rzeczywistych obiektów stosowana gdy 

rozmiary obiektów są nieistotne w porównaniu z 

przebywaną przez te obiekty drogą.

• Sprowadza się cały obiekt materialny do punktu i 

opisuje położenie obiektu za pomocą trzech 

współrzędnych przestrzennych i czasu.

• Taką idealizację stosuje się by uprościć obliczenia 

(często jest to jedyny sposób wykonania obliczeń)

• Nie można obiektu traktować jako 

punkt materialny gdy wykonuje ruchy 

obrotowe 

 

 

Środek ciężkości

• Środek ciężkości ciała, to taki punkt (czasami 

może on nawet nie zawierać się w obrębie 
ciała), że po podparciu w tym punkcie za 
pomocą siły przeciwnej do siły grawitacji 
(równoważącej tę grawitację), grawitacja nie 
spowoduje obrotu tego ciała. 

 

 

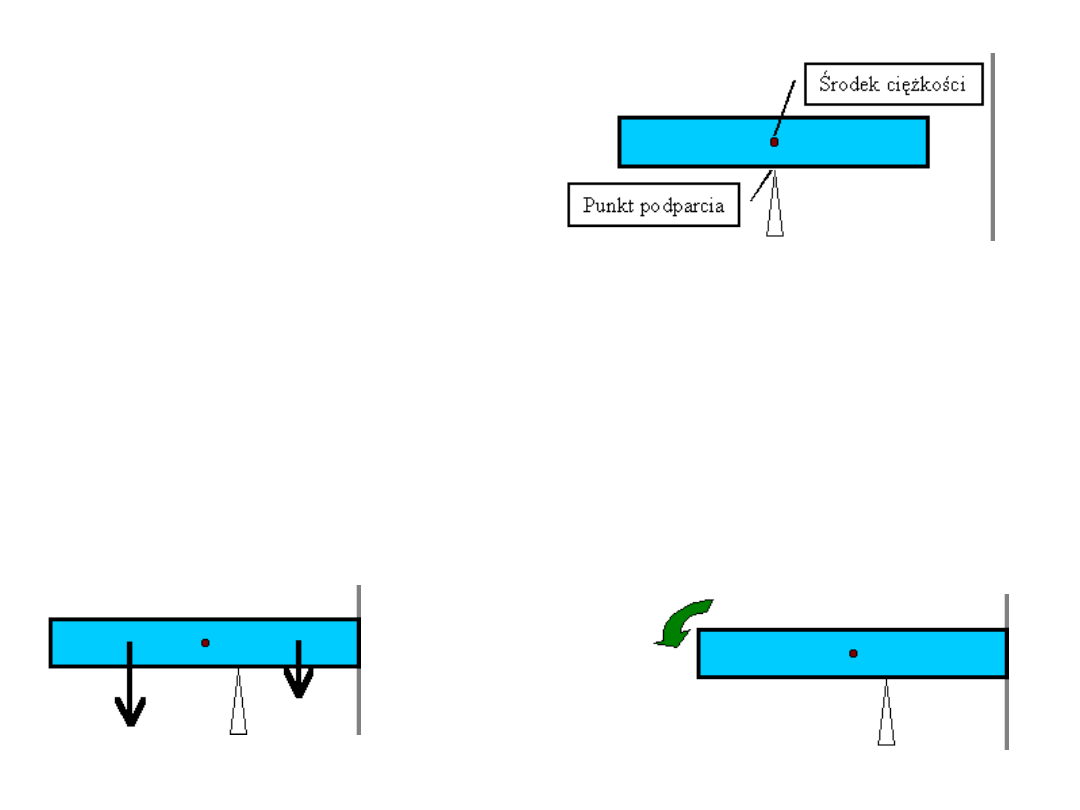
Środek ciężkości

• Punkt stabilnego podparcia spełniający warunek stabilności 

nie przewracania się, nie przekręcania pod wpływem działającej 

siły ciężkości utrzymywanego przedmiotu musi znajdować się 

dokładnie nad, lub pod środkiem ciężkości.

•  Jeśli ciało podeprzemy obok środka ciężkości, to w 

większości położeń będzie się ono przekręcało albo przewracało 

 

 

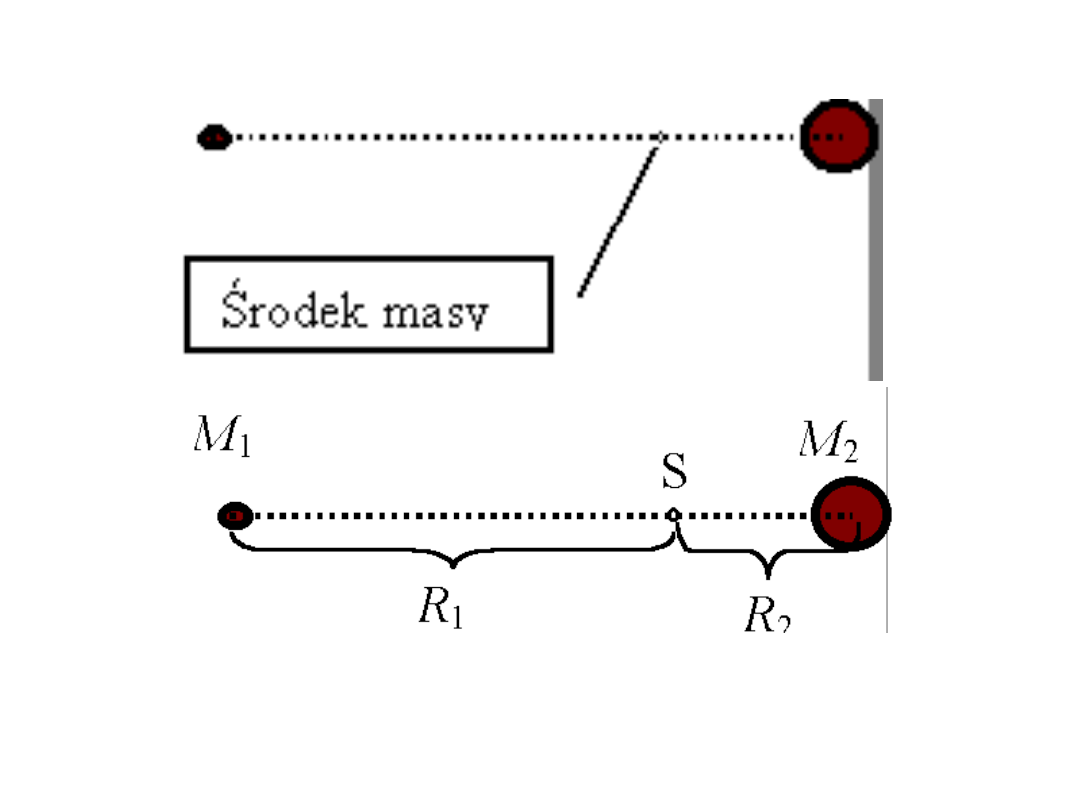
Środek masy układu dwóch 

punktów

• M

1

R

1

 = M

2

R

2

 

 

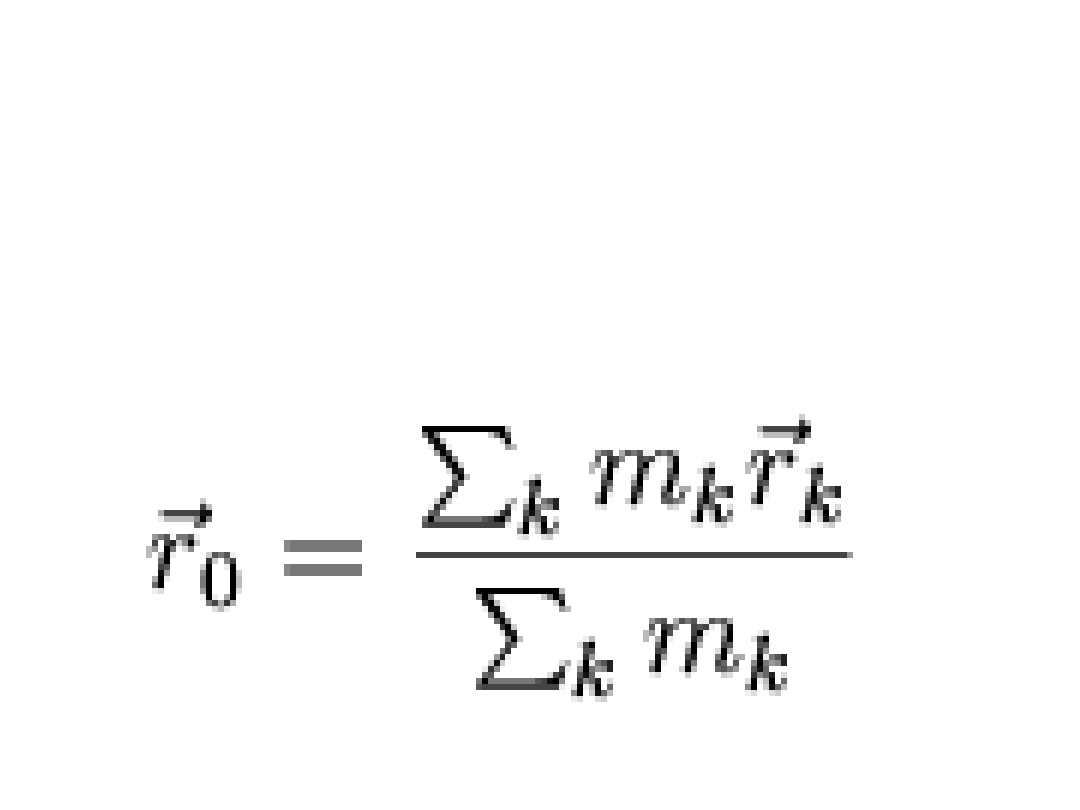
Środek masy

• Środek masy ciała lub układu ciał jest punktem, w 

którym skupiona jest cała masa w opisie układu 
jako masy punktowej.

 

• Wzór na wektor wodzący środka masy

 

 

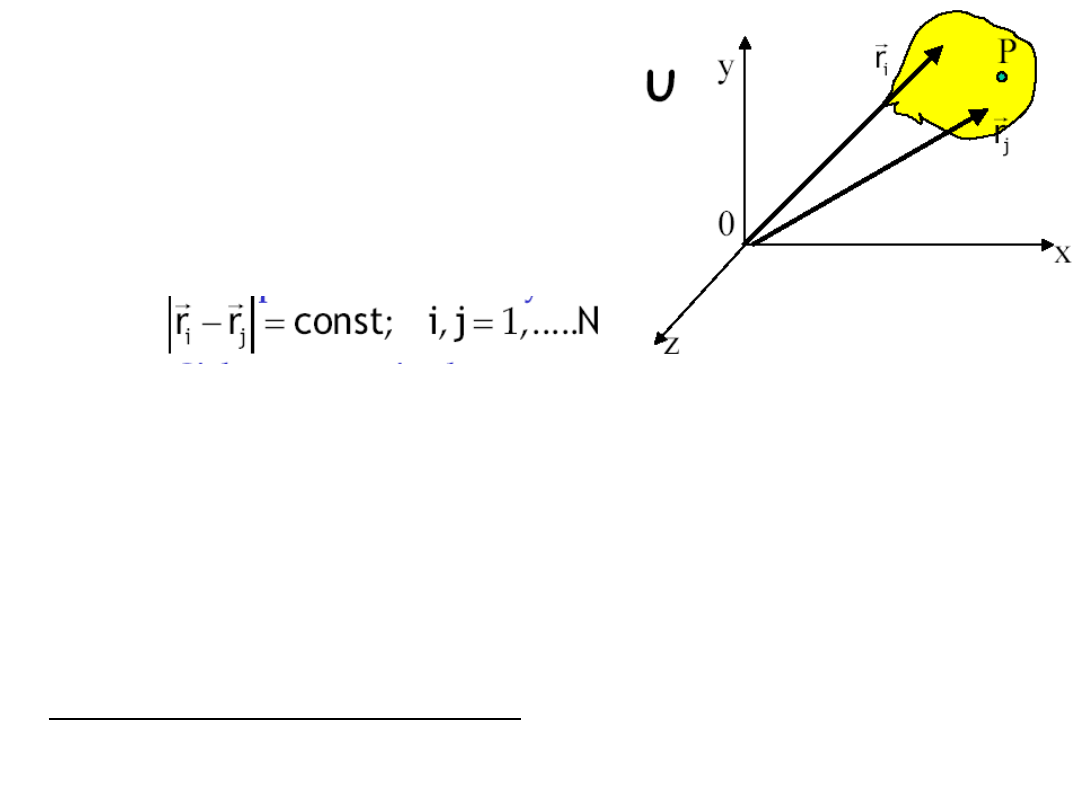
Model 

matematyczny 

ciała sztywnego

• Zbiór punktów materialnych takich, że

• Ciało sztywne nie ulega odkształceniom w wyniku 

działania sił.

• Swobodne ciało sztywne ma 6 stopni swobody:
• 3 translacyjne, opisujące ruch wybranego punktu P 

np. jego środka masy,

• 3 rotacyjne

• Ciało doskonale sztywne to takie ciało, w którym 

odległości między dwoma dowolnymi jego punktami 

materialnymi nie zmieniają się w trakcie ruchu 

 

 

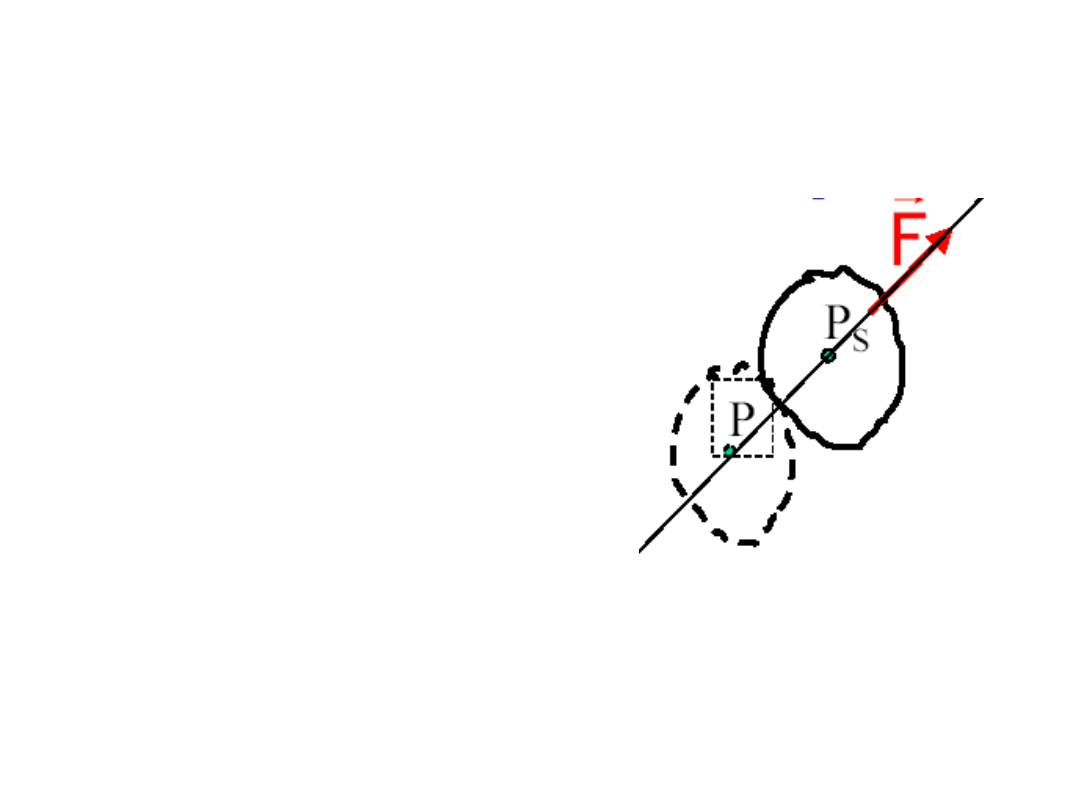
Ruchy ciała 

sztywnego

translacja

• Swobodne ciało 

sztywne ulega 
przesunięciu w 
kierunku działania siły 
zewnętrznej F gdy ten 
kierunek przechodzi 
przez środek masy 
ciała PS.

• W tej konfiguracji nie 

ma  momentu siły.

 

 

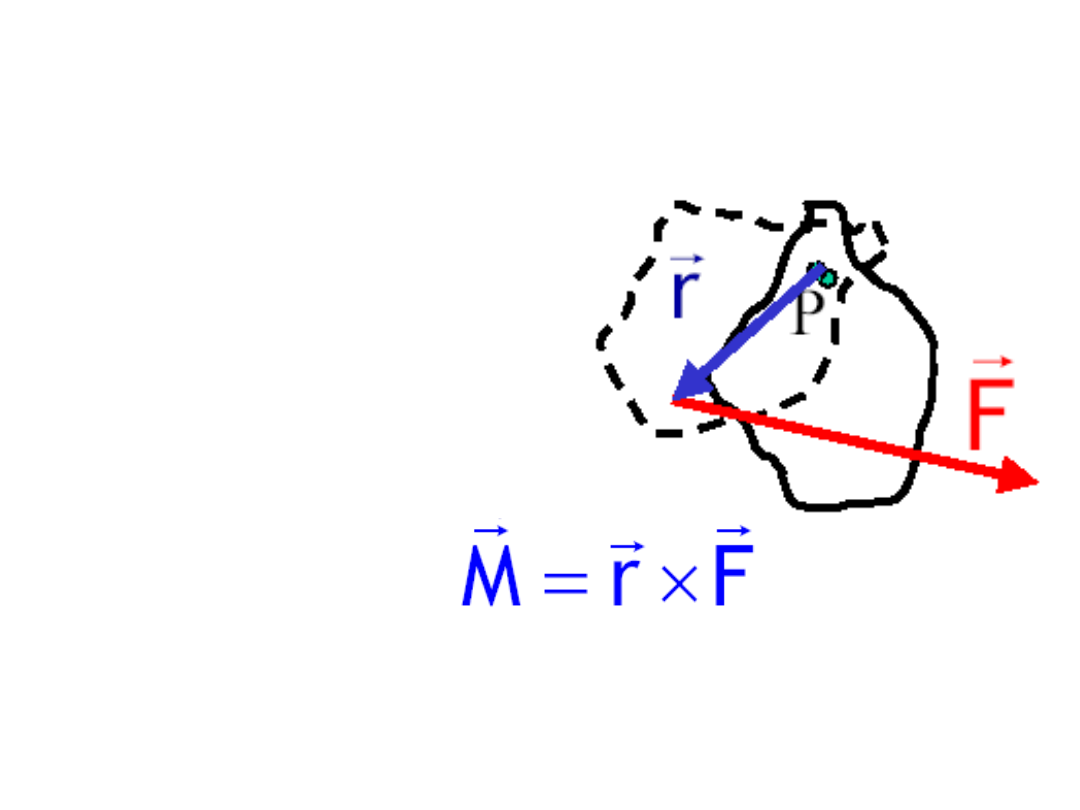
Ruchy ciała sztywnego

obrót

• Gdy dowolny punkt 

ciała P jest 
unieruchomiony ciało 
dokonuje obrotu 
dookoła niego.

• Obrót następuje 

wskutek działania 
momentu siły

• względem P:

 

 

Ruch 

rodzaje ruchu

• Prostolinijny ruch postępowy
• Występuje wtedy gdy tory ruchu wszystkich punktów 

obiektu są do siebie równoległe i pokonały te sama 

drogę w jednostce czasu.

• Opisuje go II zasada dynamiki, jest to taki ruch w 

którym wszystkie punkty ciała poruszają się po  torach  

wzajemnie równoległych w tych samych przedziałach 

czasu doznając jednakowych przemieszczeń.

•  II zasada dynamiki mówi: aby zmienić właściwości 

ruchu postępowego  musimy użyć siły.

 

 

Ruch wokół osi

Poszczególne punkty zakreślają okręgi, współśrodkowe , których 

środek nie bierze udziału w ruchu tworząc oś obrotu.

• Ruch odbywa się wokół osi obrotu, zatem punkty lezące na niej 

są nieruchome, pozostałe poruszają się z jednakowymi 

prędkościami kątowymi.

•  Miara drogi przebytej jest kąt zakreślony przez promień.
 
• Przyczyną wywołującą ruchy obrotowe są momenty siły 

(odpowiednik siły w ruchu postępowym) 

• Ruch opisuje II zasada dynamiki dla ruchu obrotowego 

odpowiednik II zasady dla ruchu postępowego.

 

 

Ruch złożony

Tworzą go wypadkowe ruchu postępowego i 

obrotowego

Każdy ruch można przedstawić jako kombinacje 

ruchu postępowego i obrotowego

 

 

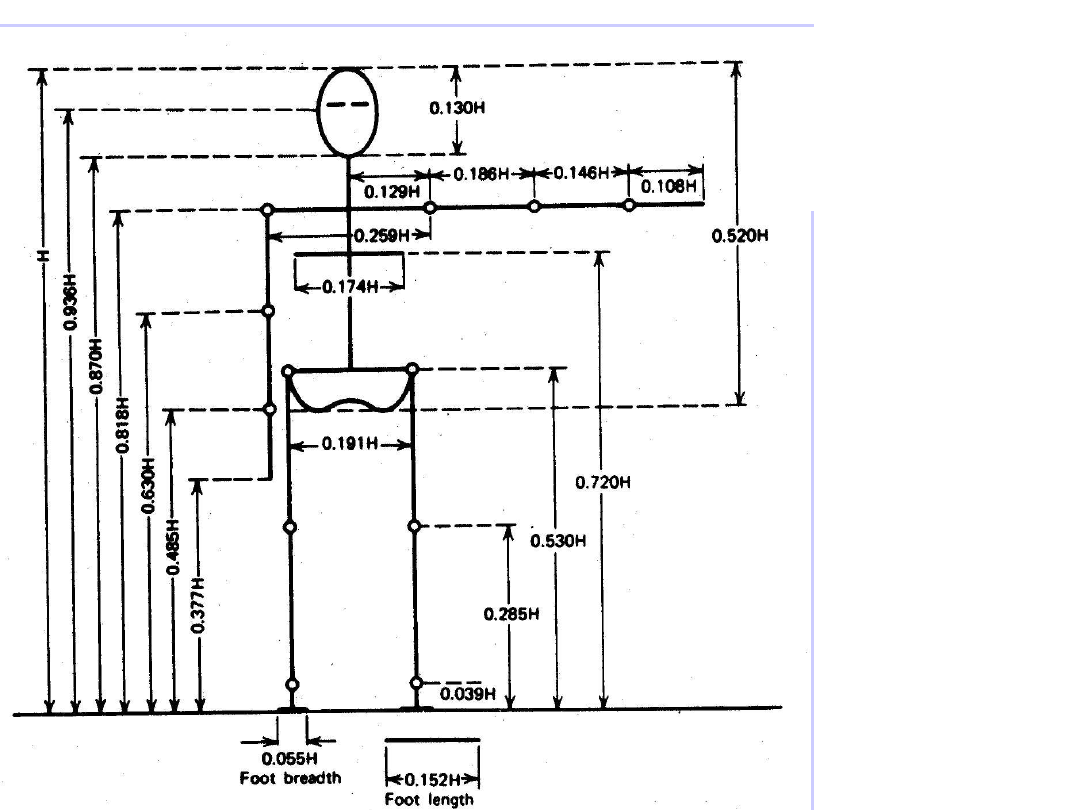
Długości 
segmentów ciała 
wyrażone w 
funkcji wzrostu 

 

 

• Analiza kinetyczna i kinematyczna wymaga 

znajomości rozkładu masy, gęstości, środków 
ciężkości poszczególnych części ciała

 

 

Gęstość, masa, 

bezwładność

• Ciężar całego ciała
• Gęstość różnych tkanek

– kości = 1.8 kg/dm

3

   

– mięśnie  1.0 /dm

3

 

– tłuszcz  0.7 /dm

3

 

– płuca < 1.0

 

 

Gęstości fragmentów ciała

– Każdy fragment ciała ma specyficzną 

gęstość

– Każdy fragment ma różny skład 

tkankowy (np. głowa i noga) 

– Gęstość poszczególnych fragmentów 

ciała wzrasta z gęstością całego ciała 

– Kończyny górne i dolne mają większą 

gęstość niż reszta

 

 

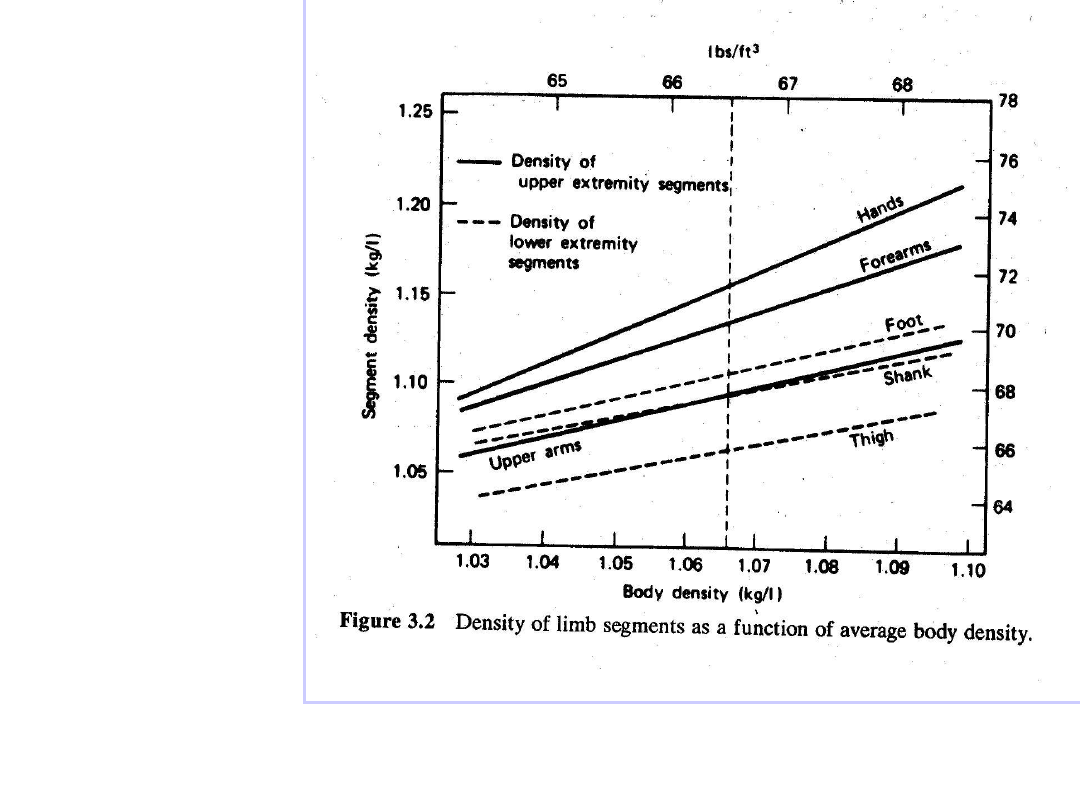
Gęstość 

różnych 

części 

ciała w 

zależności 

od 

gęstości 

całego 

ciała

 

 

Gęstość ciała, wzór 

empiryczny

d = 0.69 + 0.9c

m

                  d-kg/l

 c

m

 = (wysokość (m))/(masa (kg))

1/3

• Dla wyższych osobników o tej 

samej masie mamy większą 
gęstość

• DLACZEGO?

 

 

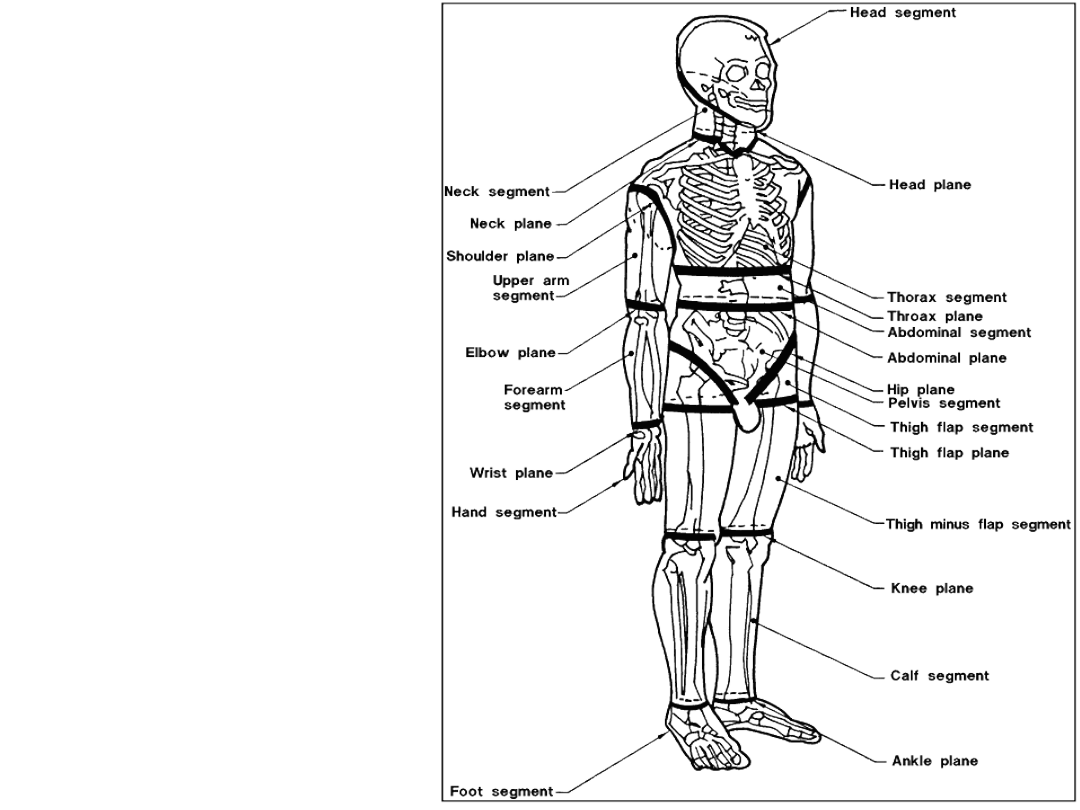
Podział ciała 

człowieka na 

segmenty

 

 

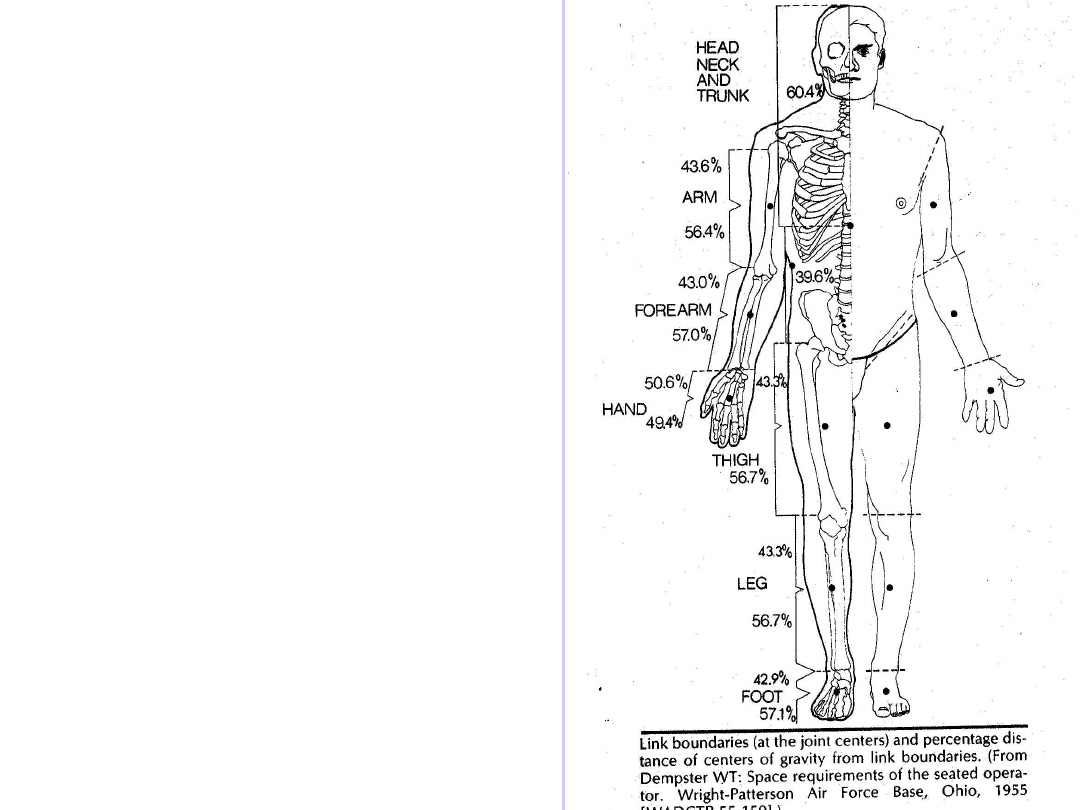
Podział ciała 

ludzkiego na 

segmenty

 

 

Zasady przy obliczaniu środków 

ciężkości segmentów ciała

•  

Wymiarem dominującym każdej części ciała jest jej długość

• Pod względem kształtu części ciała przypominają bryły 

obrotowe, mają oś symetrii

• Rozkład materii wewnątrz każdej z nich jest symetryczny 

względem geometrycznej osi symetrii

• Środki ciężkości segmentów ciała będą leżeć na ich osi 

symetrii

• Środek ciężkości dzieli długość danego segmentu na dwa 

odcinki, wymagane jest policzenie tylko jednej współrzędnej, 
odległości środka ciężkości od jednego końca segmentu

 

 

Przykładowe wzory na liczenie masy 

segmentów ciała

• X1=ciężar ciała; x2=długość ciała

Ramię 

Udo 

0,25 + 0,03012*x1- 
0,0027 * x2 =

-2,649 + 0,1463 * x1 
+ 0,0137 * x2 =

 
Przedramię 

 
Podudzie 

0,3185 + 0,01445 * 
x1 - 0,00114 * x2 =

-1,592 + 0,0362 * x1 
+ 0,0121 * x2 =

Ręka 

Stopa 

-0,1165 + 0,0036 * 
x1 + 0,00175* x2 =

-0,829 + 0,0077 * x1 
+ 0,0073 * x2 =

 

 

Przykładowe wzory na liczenie promieni 

wodzących segmentów ciała

 (odległości środka ciężkości od osi obrotu)

• X1=ciężar ciała; x2=długość ciała

Ramię 

Udo 

1,67 + 0,030 * x1- 
0,0054 * x2 =

-2,42 + 0,038 * x1 + 
0,135 * x2 =

 
Przedramię 

 
Podudzie 

0,192 + 0,028 * x1 - 
0,093 * x2 =

-6,05-0,039 * x1 + 
0,142 * x2 =

Ręka 

Stopa 

4,11 + 0,026 * x1 + 
0,033x2 =

3,767 + 0,065 * x1 + 
0,033 * x2 =

 

 

Promienie wodzące

przykłady

Ramię
• 1,67 + 0,03 x1 + 0,054 x2 =  
• 1,67 + 0,03 · 80 + 0,054 · 180 =  
• 1,67 + 2,4 + 9,72 = 13,79 cm
•  
• Przedramię
• 0,192 – 0,028 x1 + 0,093 x2 = 
• 0,192 – 0,028 · 80  + 0,093 · 180 =
• 0,192 – 2,24 + 16,74 = 14,69 cm
•  
• Ręka 
• 4,11 + 0,026 x1 + 0,033 x2 =
• 4,11 + 0,026 · 80 + 0,033 · 180 =
• 4,11 + 2,08 + 5,94 = 12,13 cm 

 

 

Promienie wodzące

przykłady

Udo 
• -2,42 + 0,038 x1 + 0,135 x2 =
• -2,42 + 0,038 · 80  + 0,135 · 180 =
• -2,42 + 3,04 + 24,3 =  24,92 cm
•  
• Podudzie
• -6,05 – 0,039 x1 + 0,142 x2 = 
• -6,05 – 0,039 · 80  + 0,142 · 180 = 
• -6,05 – 3,12 + 25,56 = 16,39 cm
•  
• Stopa 
• 3,767 + 0,065 x1 + 0,033 x2 =
• 3,767 + 0,065 · 80  + 0,033 · 180  =
• 3,767 + 5,2 + 5,94 = 14,9 cm

 

 

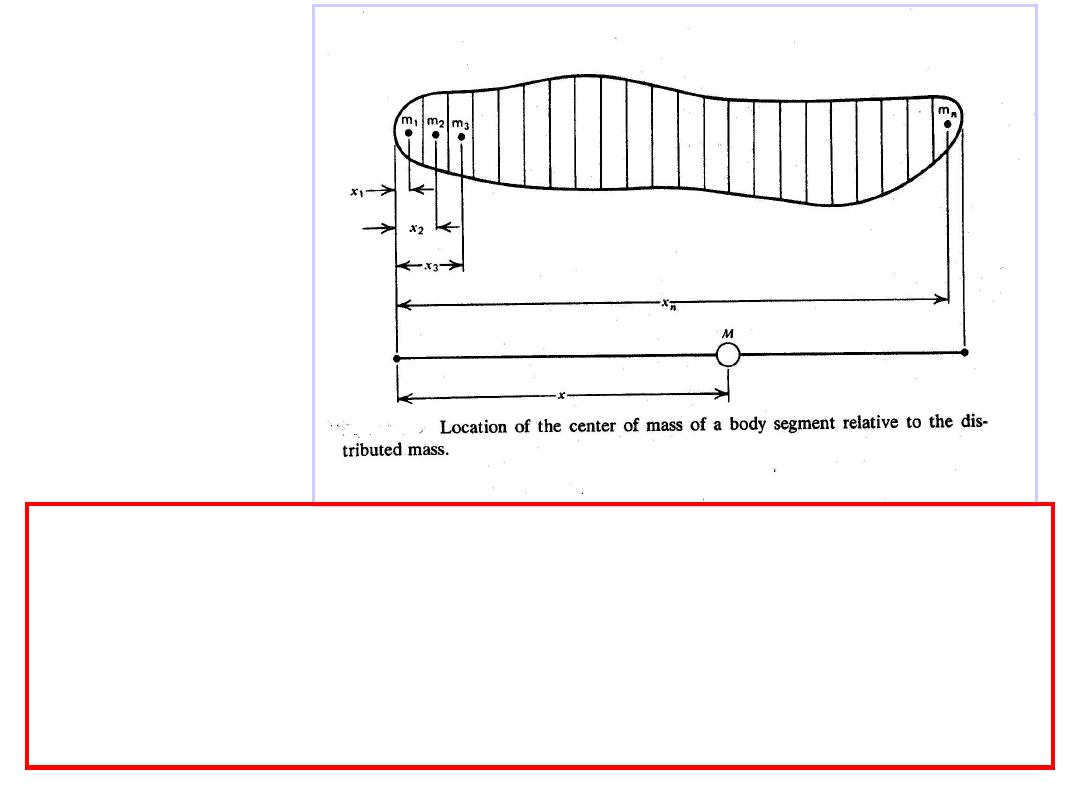
Całkowita 

masa 

segmentu

Masa = m

i

m

i

 = d

i

V

i

  

     gęstość = 

masa/objętoś

ć

M =  d

i

V

i

Jeśli segment jednorodny

M = d V

i

to

Mx =  m

i

x

i

 

 

Twierdzenia dotyczące środka 

ciężkości

• Środek ciężkości figur płaskich leży w środku 

geometrycznym

• Jeżeli bryła ma płaszczyznę symetrii, to środek 

ciężkości leży w tej płaszczyźnie.

• Gdy bryła ma dwie płaszczyzny symetrii, 

środek ciężkości leży na linii ich przecięcia.

• Gdy bryła ma trzy płaszczyzny symetrii, środek 

ciężkości leży w punkcie przecięcia się tych 
płaszczyzn.

 

 

Obliczanie środka ciężkości ciała lub 

fragmentu ciała

- określić  masy poszczególnych elementów systemu

- pomnożyć każdą masę segmentu przez 

współrzędną X środka masy segmentu

- Podzielić przez masę całego fragmentu

- To samo wykonać dla wsp. Y

x

0

 = m

1

x

1

 + m

2

x

2

 + m

3

x

3

 + + m

n

x

n

M

y

0

 = m

1

y

1

 + m

2

y

2

 + m

3

y

3

 + + m

n

y

n

M

 

 

Tabelka do obliczeń

Segment

Masa 

segmentu

x środka 

masy

x * masa

y środka 

masy

y * masa

Segment 1

m

1

x

1

m x

1

y

1

m y

1

Segment 2

m

2

x

2

mx

2

y

2

my

2

Segment 3

m

3

x

3

m x

3

y

3

m y

3





 



 







 



 







 



 



Segment n

m

n

x

n

mx

n

y

n

my

n

 

 = M

 

 /M= x 

środka 

masy

 

/M = y 

środka 

masy

  

 

 

zad01

• Jakie jest położenie środka masy 

dwóch kul połączonych bardzo 
lekkim prętem o masach i 
współrzędnych

• K1 2kg współrzędne (0,2; 0,4)
•  K1 6kg współrzędne (0,3; 0,7)

 

 

zad02

• Jakie jest położenie środka masy 

trzech kul połączonych bardzo 
lekkim prętem o masach i 
współrzędnych

• K1 5kg współrzędne (0,1; 0,3; 3,4)
•  K2 6kg współrzędne (0,4; 0,7; 2,6)
• K3 9kg współrzędne (0,3; 0,8; 1,4)