Stężenie procentowe i molowe

Stężenie procentowe – liczba gramów substancji rozpuszczonej w 100 gramach
roztworu.

masa substancji rozpuszczonej
Stężenie % = -------------------------------------------- · 100%
masa całego roztworu

Stężenie molowe – liczba moli danej substancji rozpuszczonej w 1dm

3

roztworu.

Liczba moli substancji
Stężenie molowe = ---------------------------------
Objętość roztworu

Zadanie 1. Rozpuszczono 10 g chlorku sodu w 100 g wody. Jakie jest stężenie
procentowe roztworu?

Masa roztworu 10 g + 100 g = 110 g
110 g - 100%
10 g NaCl - x%
x = 9,1%
Odpowiedź: stężenie procentowe roztworu wynosi 9,1%.

Zadanie 2. Ile moli i ile gramów nadmanganianu potasu znajduje się w 150 cm

3

2- molowego roztworu tego związku?
M

KMnO4

= 158 g/mol

1000 cm

3

- 2 mole KMnO

4

150 cm

3

- x moli

x = 0,3 mola

1 mol KMnO

4

- 158 g

0,3 mola KMnO

4

x g

x = 47,4 g KMnO

4

Odpowiedź:W 150 cm

3

2M roztworu KMnO

4

znajduje się 0,3 mola (47,4 g) KMnO

4

.

Zadanie 3. Sporządzono 15 cm

3

wodnego roztworu KOH o stężeniu procentowym

33%. Gęstość roztworu wynosi 1,32 g/cm

3

. Ile g KOH znajduje się w roztworze?

Obliczamy masę całego roztworu
1 cm

3

roztworu waży 1,32 g

15 cm

3

- x g

x = 19,8 g
19,8 g roztworu KOH - 100%
x g KOH 33%
x = 6,53 g
Odpowiedź: W roztworze znajduje się 6,53 g KOH.

Zadanie 4. Jakie jest stężenie molowe tego roztworu?
Obliczamy ile jest moli w 6,53 g KOH:
M

KOH

= 56 g/mol 56 gKOH - 1 mol

6,53 g - x moli
x = 0,12 mola
W 15 cm

3

znajduje się 0,12 mola. Obliczmy ile moli znajduje się w 1 dm

3

. Jest to

stężenie molowe.
15 cm

3

- 0,12 mola

1000 cm

3

- x mola

x = 8 moli
Odpowiedź: Stężenie molowe roztworu wynosi 8 moli/dm

3

.

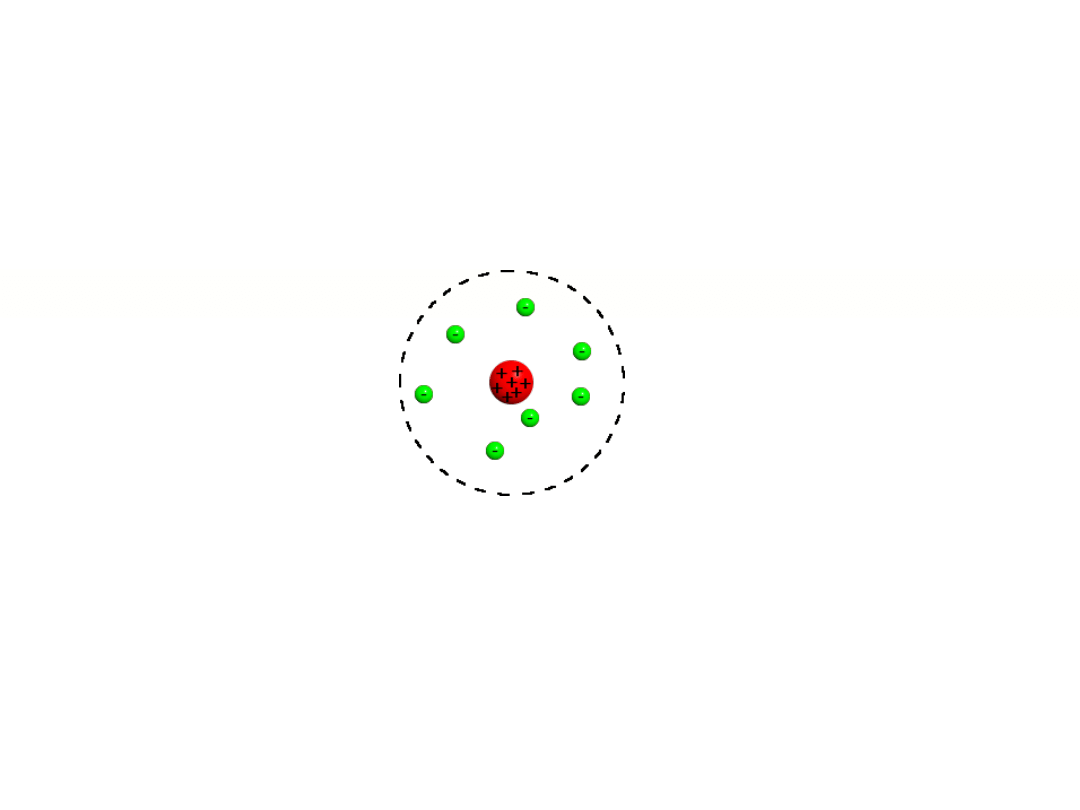
Budowa atomu

Atom = elektrony + jądro
Jądro = protony + neutrony = nukleony

Planetarny model atomu Rutherforda (1912 r)

Ładunek dodatni zgromadzony jest w niewielkim i bardzo gęstym jądrze gromadzącym większość
masy atomu.
Ujemnie naładowane elektrony okrążają jądro, podobnie jak planety okrążają słońce.

Ładunki: elektron(-), proton (+), neutron(0)

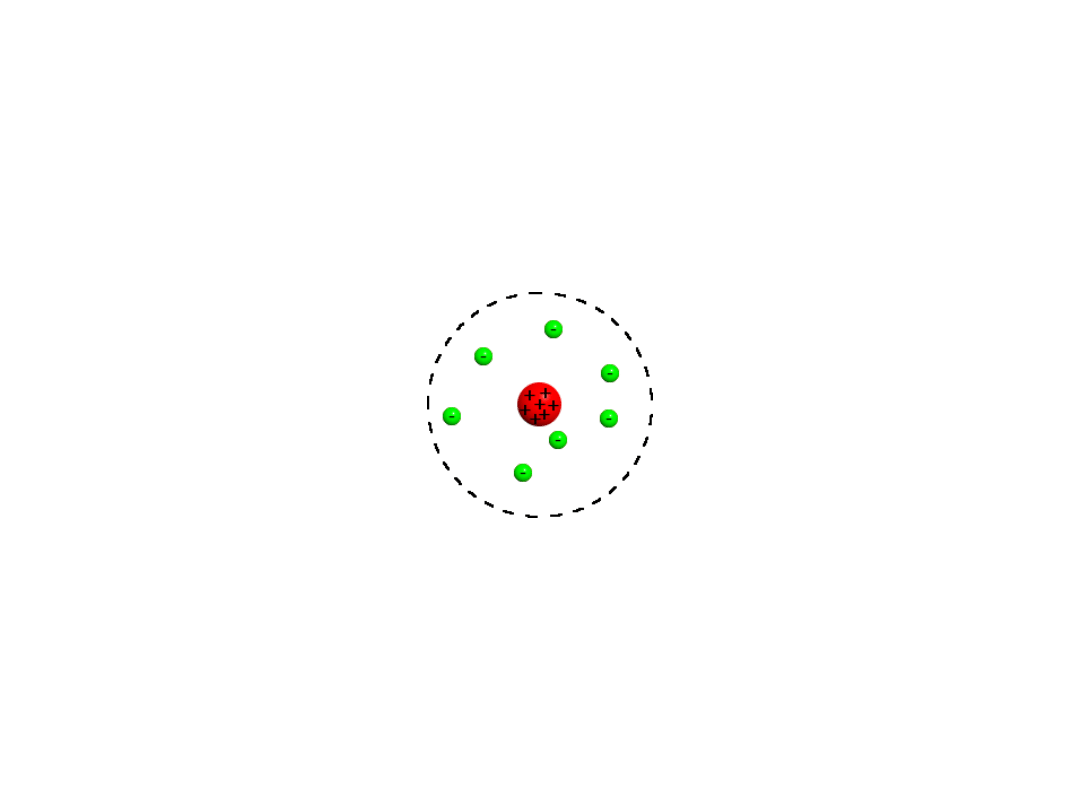
Budowa atomu

Atom = elektrony + jądro
Jądro = protony + neutrony = nukleony

Planetarny model atomu Rutherforda (1912 r)

Ładunek dodatni zgromadzony jest w niewielkim i bardzo gęstym jądrze gromadzącym większość
masy atomu.
Ujemnie naładowane elektrony okrążają jądro, podobnie jak planety okrążają słońce.

Ładunki: elektron(-), proton (+), neutron(0)

Model atomu Bohr’a (1913r) (modyfikacja modelu planetarnego)

Elektrony mogą krążyć tylko po ściśle określonych torach – orbitach stacjonarnych.
Każdej orbicie odpowiada określona energia elektronu.
Elektron w stanie stacjonarnym krąży tylko po jednej dozwolonej orbicie
nie tracąc energii.
Przeskok elektronu z jednej orbity na drugą daje zysk lub stratę ściśle określonej
porcji energii (kwantu), którego wartość określa równanie Plancka:

E = h•ν

h = stała Plancka = 6,625•10

-34

J·s podstawowa stała fizyczna

ν = częstotliwość absorbowanego lub emitowanego promieniowania

Moment pędu elektronu w jakimś określonym stanie jest wielkością skwantowaną

Pojęcie kwantowania energii elektronu jest aktualne do dziś.
Stan, w którym energia ma wartość najniższą z możliwych jest nazywany
stanem podstawowym.

Model atomu Bohra w pierwszej wersji zakładał, że elektron krąży wokół jądra
(protonu).
Potem wprowadzono modyfikacje: elektron i proton krążą wokół wspólnego
środka masy leżącego blisko protonu.

Średnica atomu wodoru: 1Å 1Å = 1•10

-10

m

Ograniczenia modelu atomu Bohra:
Model dobrze sprawdza się przy opisie atomu wodoru, natomiast trudno
opisać atomy większe od atomu wodoru.
Trudno opisać powstawanie wiązań chemicznych

Model planetarny nadal pozostaje użyteczną analogią zaczerpniętą
ze świata makroskopowego, jednak do poprawnego opisu atomów

niezbędna jest teoria kwantowa.

Zasady mechaniki kwantowej wykorzystane do opisu
atomów i wiązań między nimi

1. Dualizm falowo-korpuskularny

Fale i cząstki są dwoma przejawami jednej i tej samej rzeczywistości
fizycznej (Einstein).

Każdej poruszającej się cząstce lub obiektowi odpowiada fala
(Luis de Broglie, francuski fizyk, laureat nagrody Nobla 1929r)

h

λ = ----
p

równanie de Broglie’a, obliczenie długości fali λ odpowiadającej strumieniowi cząstek

o pędzie p

h = stała Plancka = 6,625•10

-34

J·s podstawowa stała fizyczna

Zasada nieoznaczoności Heisenberga (1927r)

Jest konsekwencją dualizmu falowo-korpuskularnego.
Zasada nieoznaczoności mówi, że dla ciał tak małych jak elektrony,
nie można z dowolną dokładnością wyznaczyć położenia i pędu cząstki.
Można mówić jedynie o prawdopodobieństwie.

Zasada ta jest uogólniana na inne pary wielkości fizycznych
np. czas i energię – nie można z dowolną dokładnością wyznaczyć jednocześnie
czasu życia nietrwałej cząstki i energii związanej z nią fali de Broglie’a.

W mechanice klasycznej wielkości fizyczne mogą zarówno przyjmować dowolną
wartość jak i zmieniać się o dowolną wartość.
W mikroukładach, takich jak elektron w atomie, niektóre wielkości mogą przyjmować
tylko określone wartości zwane kwantami.

2. Równanie Schroedingera

W mechanice klasycznej równanie ruchu Newtona przedstawia się następująco
(II zasada dynamiki Newtona):

F = m•a (F = wartość siły, m = masa bezwładna, a = przyśpieszenie)

Rozwiązanie tego równania daje liczby.

W mechanice falowej układowi atomowemu przypisuje się funkcję falową Ψ,
zmieniającą się w czasie i przestrzeni.
Dla stanów stacjonarnych, które zostają zachowane przez dłuższy czas,
funkcja falowa Ψ jest niezależna od czasu i zmienia się jedynie zależnie
od miejsca w przestrzeni.

HΨ = EΨ

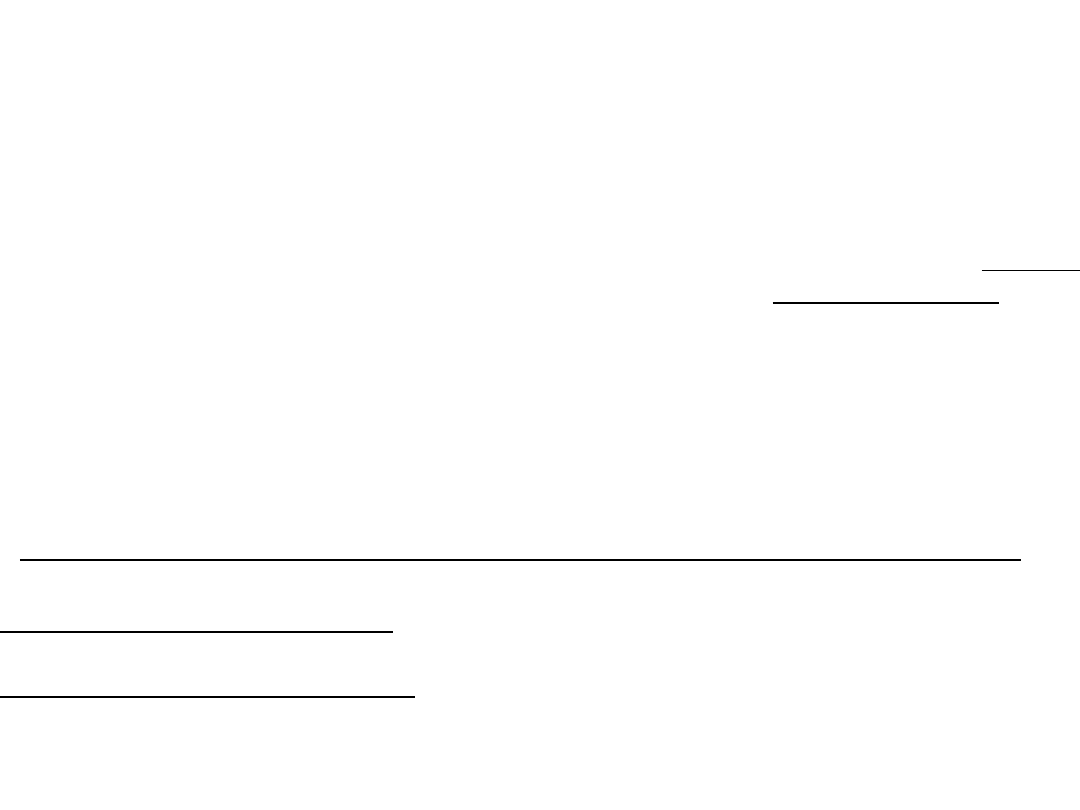
HΨ = EΨ

H – operator Hamiltona, czyli określony przepis matematyczny,
jak należy postępować z funkcją falową Ψ.

Rozwiązaniem równania Schroedingera nie są liczby lecz funkcje tzw. orbitale.
Funkcja Ψ stanowiąca rozwiązanie równania nazywa się funkcją własną.
E – wartości energii obliczone przy zastosowaniu funkcji własnej nazywa się
wartościami własnymi.

Dla układu atomowego istnieją różne funkcje falowe Ψ

1

, Ψ

2

,...... Ψ

n

odpowiadające

różnym stanom energetycznym układu i stanowiące rozwiązania równania falowego.

Ψ jest funkcją współrzędnych położenia rozważanej cząstki.

Znaczenie funkcji falowej Ψ:
sens fizyczny ma kwadrat modułu funkcji falowej [Ψ(r)]

2

. Oznacza on

gęstość prawdopodobieństwa znalezienia cząstki w punkcie r.

Elektron w atomie wodoru

Teoria Bohr’a zakładała kwantowanie tylko jednego parametru: energii.

W ramach mechaniki kwantowej pięć parametrów ruchu elektronu podlega
kwantowaniu.
Odpowiada im 5 liczb kwantowych:

1. Główna liczba kwantowa n

n = 1, 2, 3....
Zbiór stanów kwantowych o tej samej wartości głównej liczby kwantowej
nazywa się powłoką elektronową.
K, L, M, N, O, P, Q symbole literowe powłok

2n

2

liczba stanów kwantowych o tej samej wartości głównej liczby kwantowej

Np. dla n = 1 istnieją 2 stany kwantowe, co oznacza, że na powłoce K mogą
znajdować się maksymalnie 2 elektrony.
Dla n = 2 istnieje 8 stanów kwantowych, a więc na powłoce L może znajdować się
Maksymalnie 8 elektronów.

2. Poboczna (orbitalna) liczba kwantowa l

Liczba l kwantuje orbitalny moment pędu elektronu i określa kształt orbitalu.
l = 0, 1, 2, 3....

Najmniejsza wartość l = 0, największa l = n-1
W powłoce K (n = 1) liczba l przybiera tylko jedną wartość l = 0.
W powłoce L (n = 2) liczba l przybiera 2 wartości l = 0, l = 1.
W powłoce M (n = 3) liczba l przybiera 3 wartości l = 0, l = 1, l = 2.

Zbiór stanów kwantowych, w których każdy ma taką samą wartość n
i taką samą wartość l nazywa się podpowłoką elektronową.

l = 0 (podpowłoka s), orbital jest kulistą chmurą i nazywa się orbitalem s
l = 1 (podpowłoka p), orbitale są w kształcie przestrzennych ósemek
i nazywają się orbitalami p
l = 2 (podpowłoka d), kształt orbitali bardziej skomplikowany, orbitale d
l = 3 (podpowłoka f), kształt orbitali bardziej skomplikowany, orbitale f

3. Magnetyczna liczba kwantowa m

Liczba m kwantuje orientację przestrzenną orbitalnego momentu pędu elektronu.
Przyłożone pole magnetyczne wpływa na energię atomu, ponieważ krążący
elektron można rozpatrywać jako prąd. Zewnętrzne pole magnetyczne zmienia
wzajemne ustawienie się orbitali w przestrzeni.
Magnetyczna liczba kwantowa m opisuje zmianę wzajemnego ustawienia się
orbitali w przestrzeni.
Dopuszczalne wartości m: -l, -(l-1),...-1, 0, 1,...,(l-1), l

Dla wartości l = 0 (podpowłoka s) liczba magnetyczna m = 0 a orbital s ma ciągle
kształt kuli i nie zmienia swojego ukierunkowania pod wpływem
pola magnetycznego.

Dla l = 1 (podpowłoka p) liczba magnetyczna m uzyskuje 3 wartości m: -1,0, 1,
co oznacza, że istnieją 3 orbitale p w kształcie ósemek ale inaczej zorientowane
w układzie osi xyz. Stan p w polu magnetycznym ulega rozszczepieniu na
3 podpoziomy p (3 orbitale p).

Dla l = 2 (podpowłoka d) liczba m uzyskuje 5 wartości m: -2, -1, 0, 1, 2 co oznacza,
że podpowłoka d ulega rozszczepieniu na 5 podpoziomów (5 orbitali d).

 

                                                   

 

                                                                                                                                                        

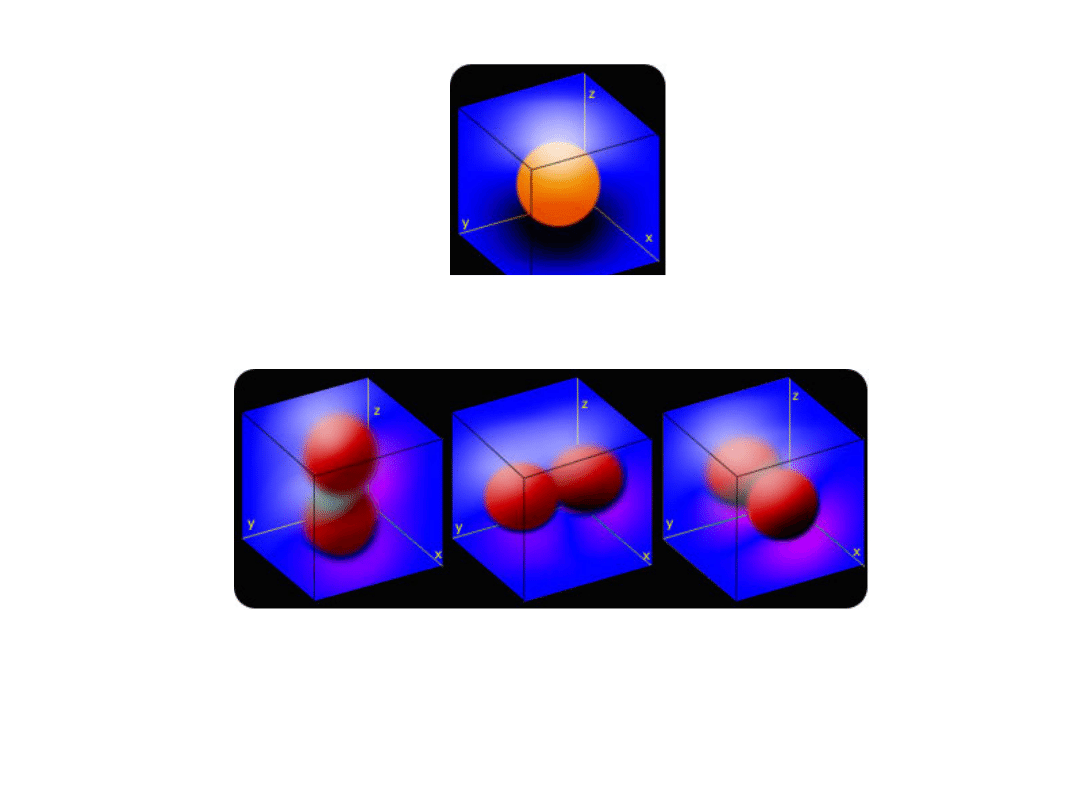
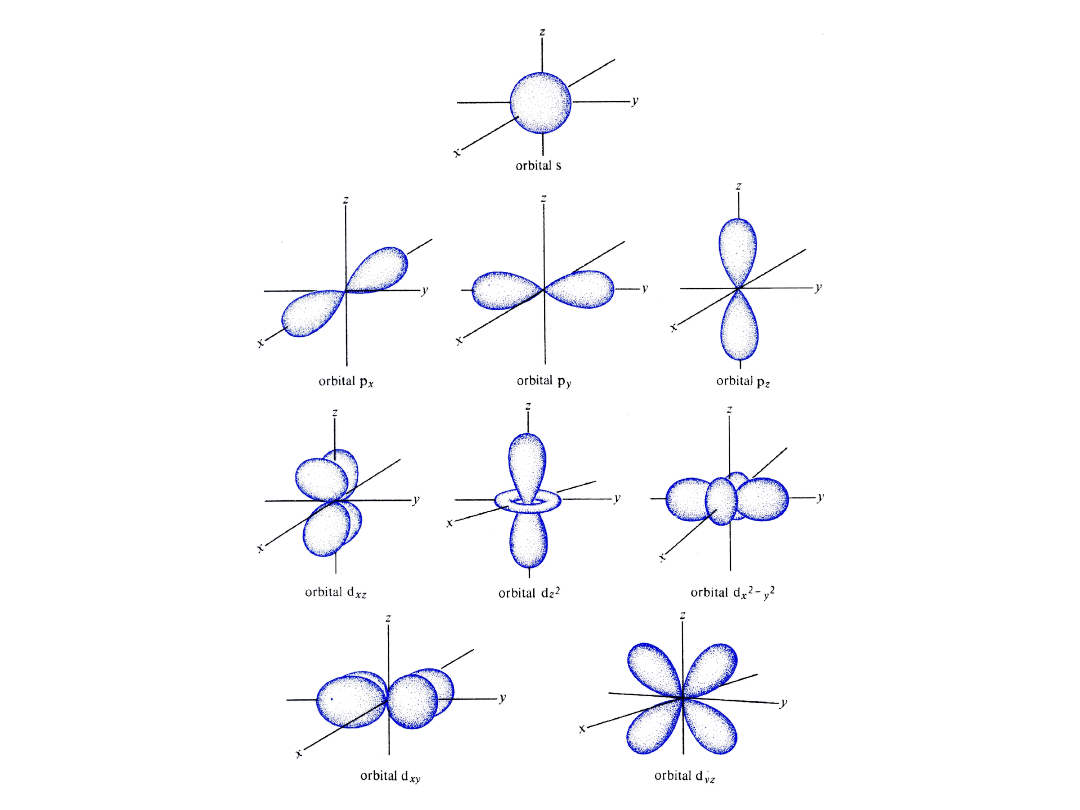
Powierzchnia graniczna orbitali s

Powierzchnia graniczna orbitali p

p

z

p

y

p

x

 

                                                                                                                                                        

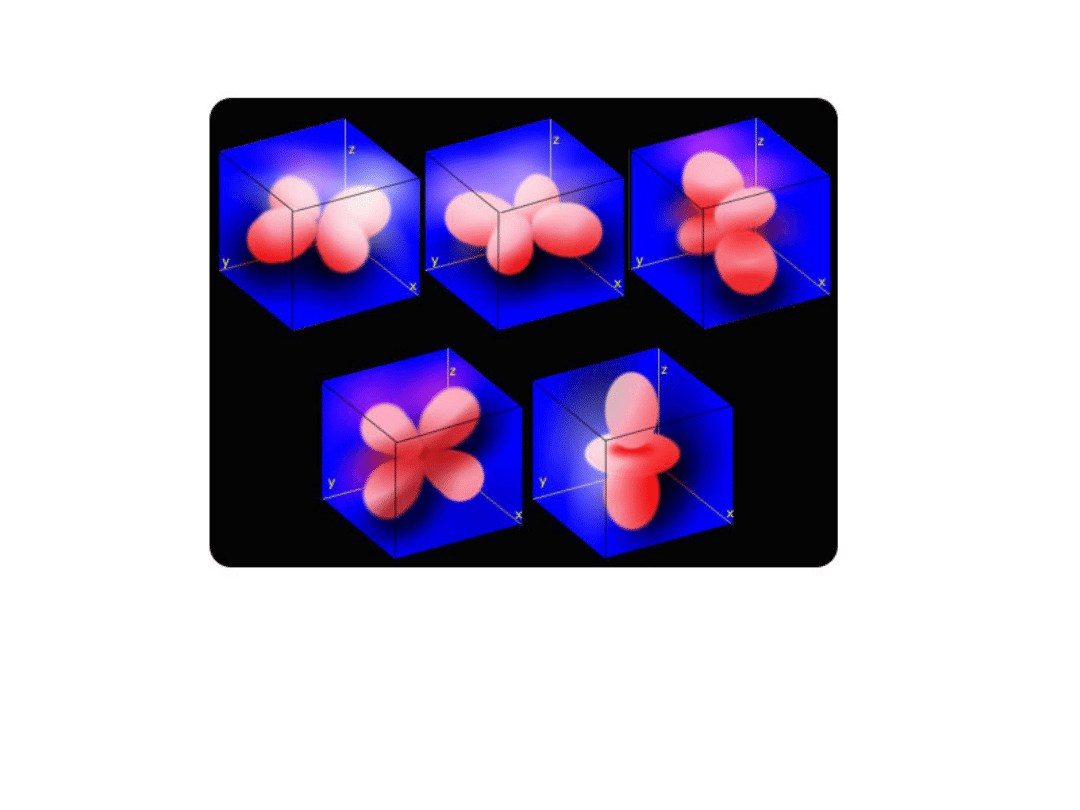
Powierzchnia graniczna orbitali d

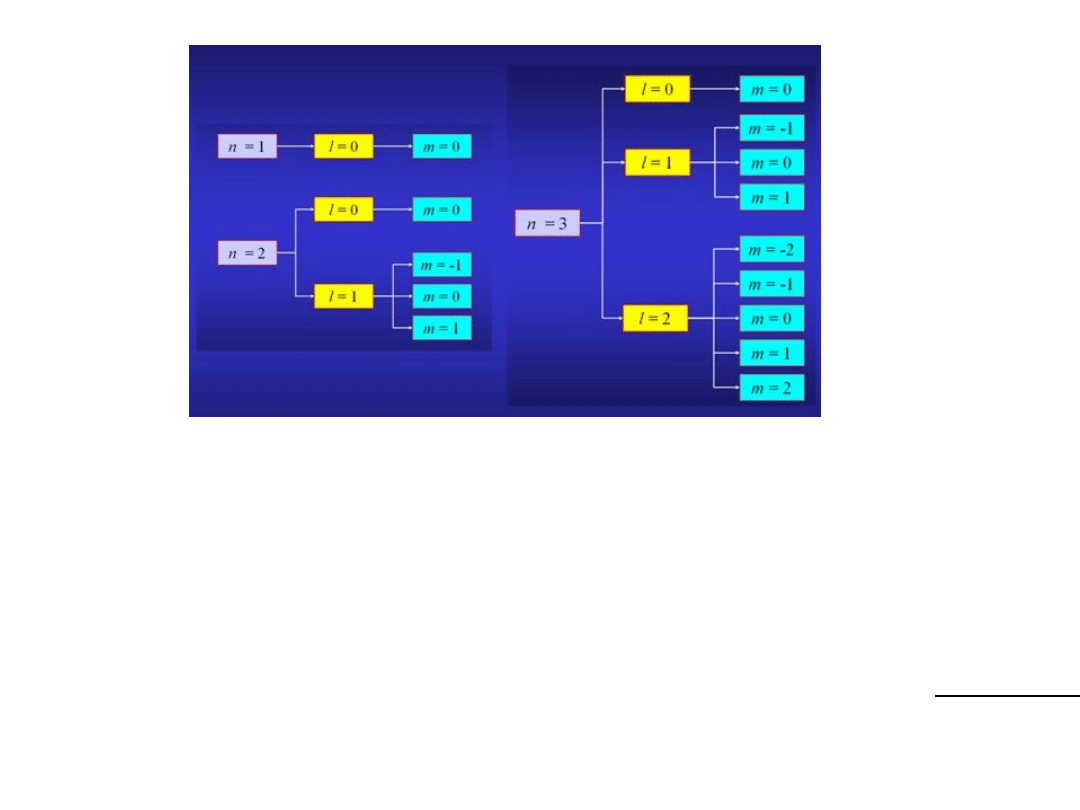
Maksymalna liczba orbitali na powłokach:

Powłoka K: 1 orbital (1s)
Powłoka L: 4 orbitale (2s i 3 orbitale 2p)
Powłoka M: 9 orbitali (3s, 3 orbitale 3p i 5 orbitali 3d)

Każdy orbital może być obsadzony przez maksymalnie 2 elektrony.

4. Spinowa liczba kwantowa s

–

kwantuje wewnętrzny moment pędu elektronu

Oprócz ruchu wokół jądra (ruchu orbitalnego) elektron w atomie wykonuje
dodatkowy ruch wewnętrzny.
Moment pędu tego ruchu wewnętrznego nazwano spinem.

s = ½

Wszystkie stany kwantowe mają identyczną wartość spinu.

5. Magnetyczna spinowa liczba kwantowa m

s

–

określa orientację

przestrzenną wektora spinu

m

s

= -

½

, +

½

Każdy orbital to dwa stany kwantowe różniące się tylko magnetyczną spinową
liczbą kwantową.

Zakaz Pauliego

W danym atomie nie mogą istnieć elektrony opisane tymi samymi wartościami
wszystkich liczb kwantowych. Poszczególne elektrony muszą różnić się wartością
przynajmniej jednej liczby kwantowej.

Reguła Hunda:

1. W danej podpowłoce powinna być możliwie największa liczba
niesparowanych elektronów;
2. Niesparowane elektrony, zajmujące poziomy orbitalne danej podpowłoki,
mają identyczną orientację spinu.
3. Pary elektronowe tworzą się dopiero po zajęciu wszystkich poziomów orbitalnych
danej podpowłoki przez niesparowane elektrony.

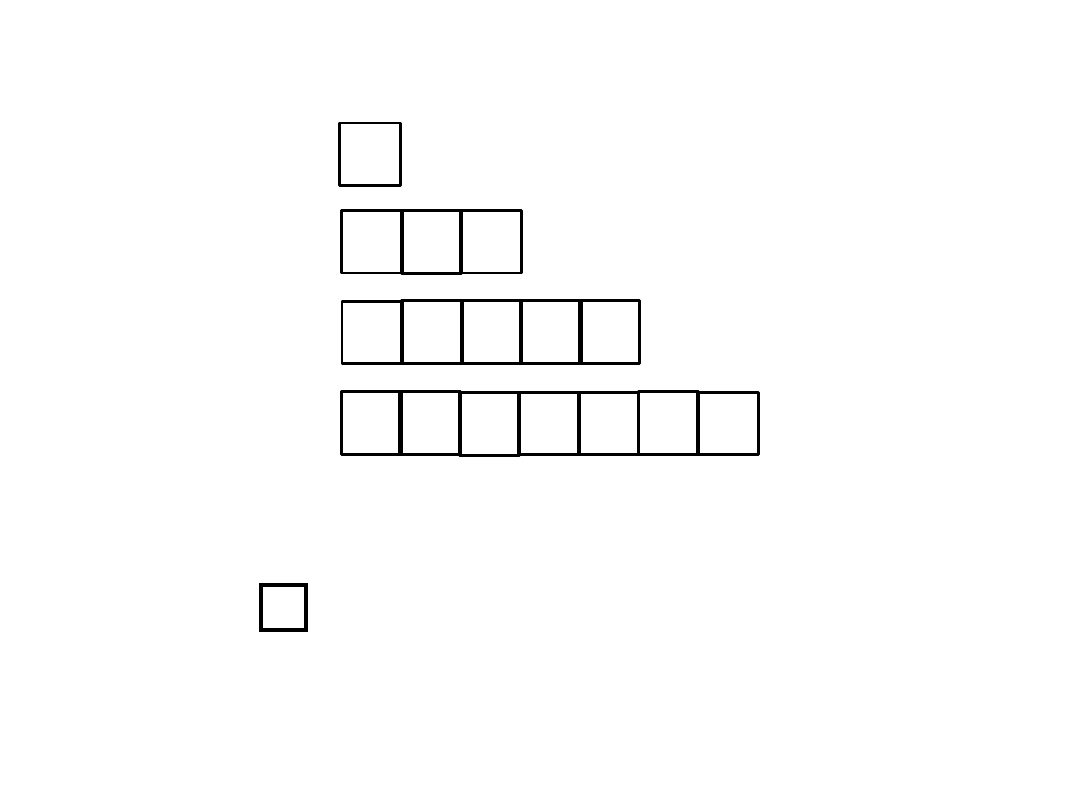
Podpowłoka s

Podpowłoka p

Podpowłoka f

Podpowłoka d

Ilość orbitali na podpowłokach

= orbital

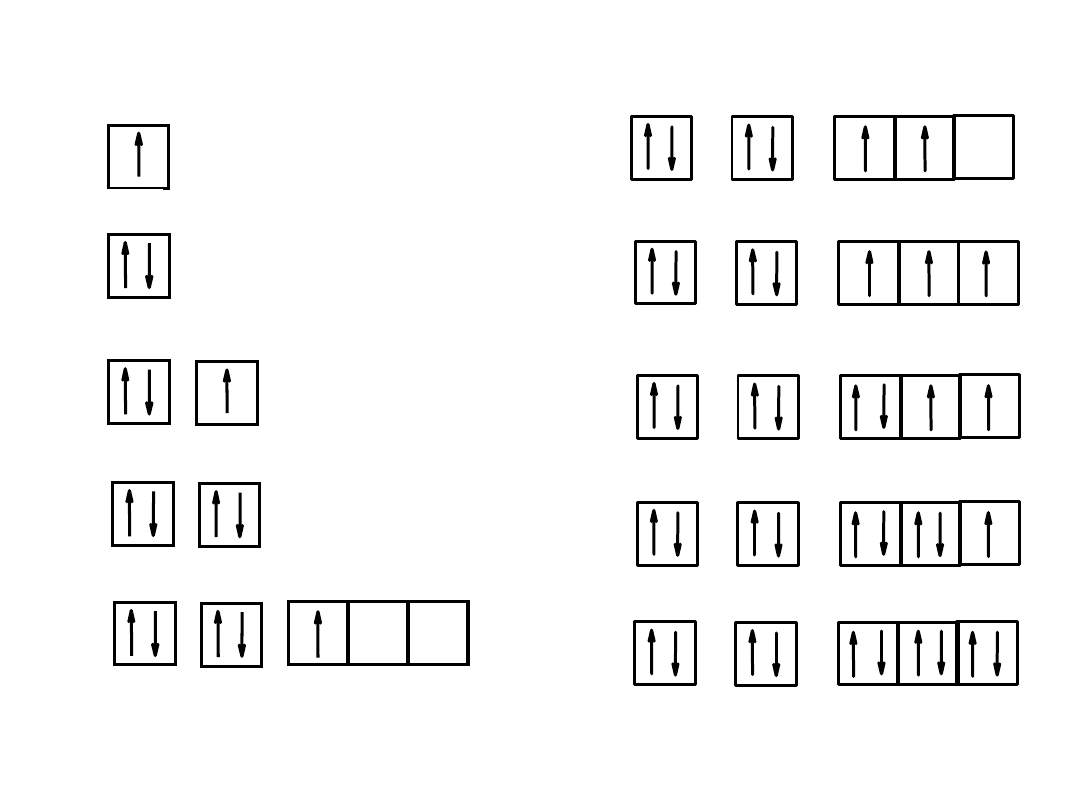
1

H 1s

1

2

He 1s

2

3

Li 1s

2

2s

1

4

Be 1s

2

2s

2

5

B 1s

2

2s

2

2p

1

Kolejność zajmowania stanów kwantowych w atomach pierwiastków

6

C 1s

2

2s

2

2p

2

7

N 1s

2

2s

2

2p

3

8

O 1s

2

2s

2

2p

4

7

F 1s

2

2s

2

2p

5

8

Ne 1s

2

2s

2

2p

6

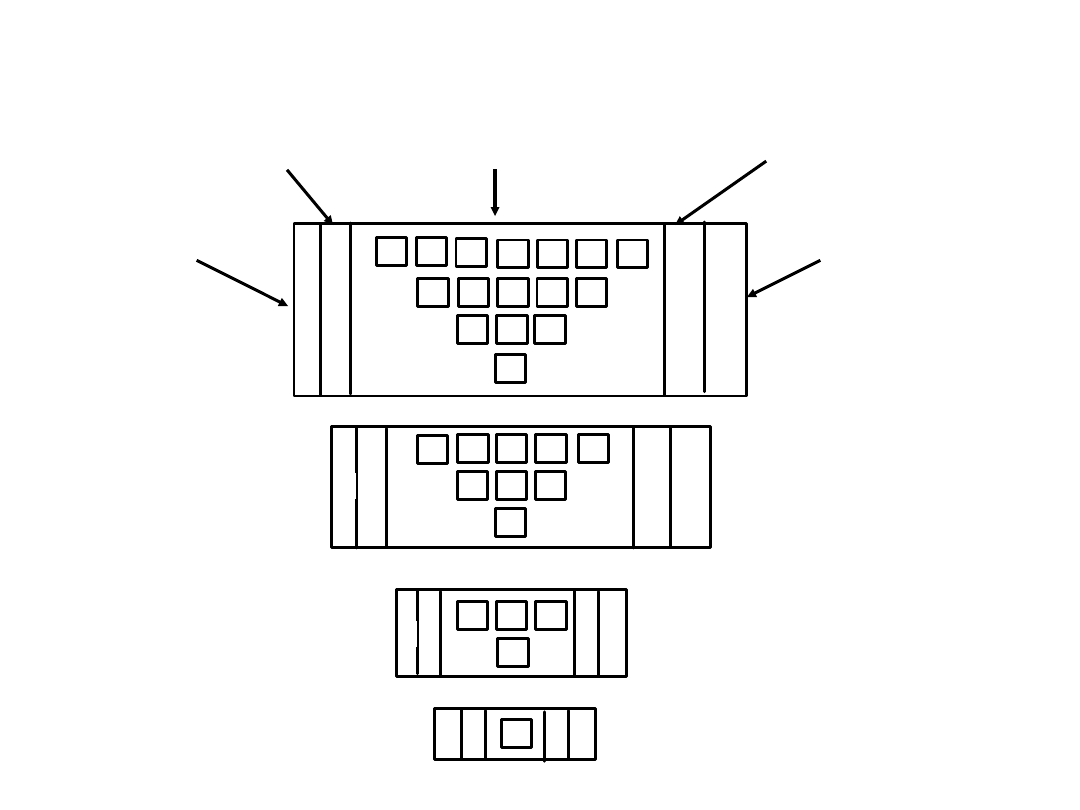
K s

2

2

M

s

p

2

6

8

L

s

p

d

2

6

10

18

N

s

p

d

f

2

6

10

14

32

Powłoki, podpowłoki i orbitale

powłoka

podpowłoki

orbitale

Maksymalna ilość
elektronów na podpowłokach

Maksymalna ilość
elektronów na powłoce

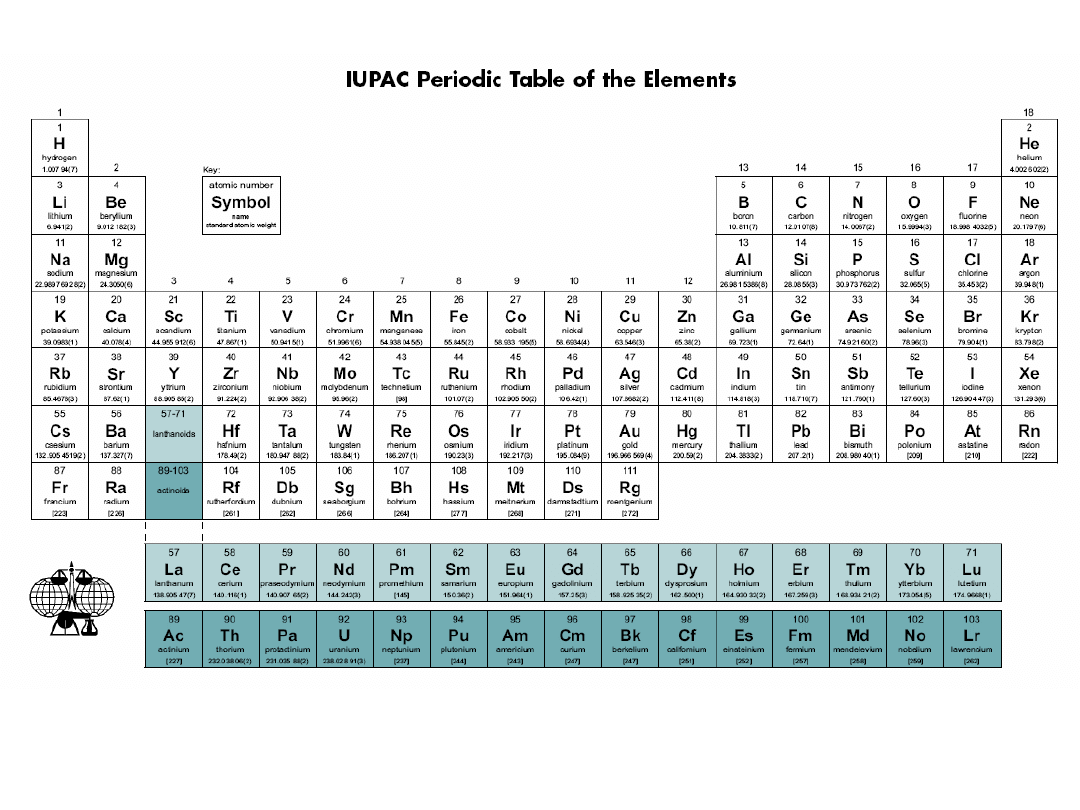
Konfiguracja elektronowa a prawo okresowości

Liczba atomowa = liczba elektronów w atomie = liczba protonów w jądrze atomu

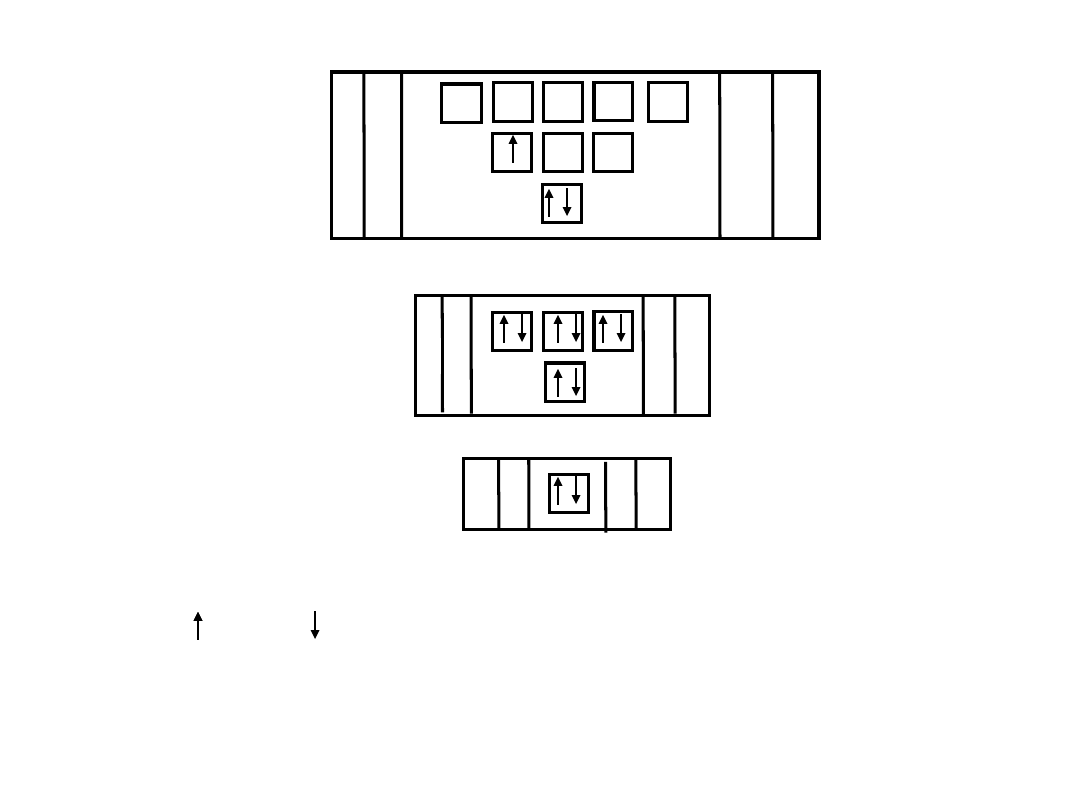
Konfiguracja elektronowa w atomie glinu

13

Al

K

s

2

2

M

s

p

2

6

8

L

s

p

d

2

6

10

18

13

Al - 13 elektronów rozmieszczonych na 3 powłokach

lub - Elektrony o różnych spinach

13

Al 1s

2

2s

2

2p

6

3s

2

sp

1

Na podstawie układu okresowego można odtworzyć konfigurację elektronową
atomów pierwiastków w stanie podstawowym.

Pierwiastki należące do danego okresu charakteryzują się taką samą liczbą powłok,
w których znajdują się elektrony. Numer okresu = liczba powłok elektronowych.

Podział układu okresowego na bloki:

Blok s – 1 i 2 grupa i hel,
Blok p – od 13 do 18 grupy (bez helu),
Blok d – od 3 do 12 grupy
Blok f – lantanowce i aktynowce

Taki podział pierwiastków jest związany z lokalizacją elektronów walencyjnych.
Elektrony walencyjne biorą udział w procesach chemicznych.

Jądro + elektrony niewalencyjne = rdzeń atomowy

Bloki s i p – atomy pierwiastków grup głównych, w których elektrony
walencyjne znajdują się tylko na zewnętrznej powłoce.

Bloki d i f - atomy pierwiastków grup pobocznych, w których elektrony walencyjne
mogą być zgrupowane na dwóch lub trzech podpowłokach.

Grupy główne

:

liczba elektronów walencyjnych = liczba elektronów w powłoce zewnętrznej =

s + p

Grupy poboczne

:

liczba elektronów walencyjnych = liczba elektronów w powłoce zewnętrznej s + liczba

elektronów podpowłoki d leżącej pod powłoką zewnętrzną =

s + d

Przykłady:

Zadania:

1. Sporządzono 300 g roztworu NaCl, w którym znajduje się 20% wag. soli.
Z roztworu następnie odparowano 50 g wody. Obliczyć stężenie % tak
otrzymanego roztworu.

2. Ile cm

3

0,01M roztworu NaOH należy użyć aby zobojętnić 10 cm

3

0,05 M roztworu HCl.

3. 50 cm

3

0,2 M roztworu NaOH zobojętniono 100 cm

3

roztworu HCl.

Jakie jest stężenie molowe HCl?

4. Jaka maksymalna ilość MgO przereaguje z 40 cm

3

0,5 M roztworu H

2

SO

4

?

5. Sporządzono 20 cm

3

wodnego roztworu HNO

3

o stężeniu procentowym

30%. Gęstość roztworu wynosi 1,18 g/cm

3

. Ile gramów i ile moli HNO

3

znajduje się w roztworze?

6.

Sporządzono 100 cm

3

wodnego roztworu KOH o stężeniu procentowym

11%. Gęstość roztworu wynosi 1,10 g/cm

3

. Ile gramów i ile moli KOH

znajduje się w roztworze?
7. Pewną ilość soli NaNO

3

rozpuszczono w wodzie i otrzymano 100 cm

3

roztworu o stężeniu 0,5 molowym. Ile gramów soli użyto do sporządzenia
tego roztworu?

H

1,01

1

He

2

4,00

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57-71

58

59

60

61

62

63

64

65

66

67

68

69

70

71

57

72

73

74

75

76

77

78

79

80

81

82

83

84

85

86

87

88

89-103

89

90

91

92

93

94

95

96

97

98

99

100

101 102

103

104

105

106

107

108

109

Na

Li

K

Rb

Cs

Fr

6,9

23,0

39,1

85,5

132,9

9,0

Be

Mg

Ca

24,3

40,1

Sr

Ba

Ra

87,6

137,3

B

C

N

O

F

Ne

10,8 12,0 14,0 16,0 18,0 20,2

Al

Si

P

S

Cl

Ar

27,0 28,1 31,0 32,1 35,5 40,0

Sc

Ti

V

Cr

Mn

Fe

Co

Ni

Cu

Zn

Ga

Ge

As

Se

Br

Kr

45,0

47,9 50,9

52,0 54,9

69,7 72,6 74,9

79,0 79,9

83,8

55,8

58,9 58,7 63,5 65,4

Y

Zr

Nb

Mo

Tc

Ru

Rh

Pd

Ag

Cd

In

Sn

Sb

Te

I

Xe

88,9 91,2

92,9 96,0

98

101,1 102,9 106,4 107,9 112,4 114,8 118,7 121,8 127,6 126,9 131,3

Hf

Ta

W

Re

Os

Ir

Pt

Au

Hg

Tl

Pb

Bi

Po

At

Rn

Rf

Db

La

Ac

178,5 180,9 183,8 186,2 190,2 192,2 195,1 197,0 200,6 204,4 207,2 209,0 209 210

222

Ce

Pr

Nd

Th

Pa

U

He

2

4,0

symbol

l. atomowa

masa atomowa

1

2

3

4

5

6

7

9 10

11

12

13 14 15

16 17

18

8

1

2

3

4

5

6

7