
1
Problematyka wykładu
•Podział rejestrów i liczników
•Metody syntezy liczników
•Przykłady realizacji scalonych liczników
•Układy realizacji równoległego wprowadzania informacji do
rejestrów
2
Podział rejestrów
Szeregowe
Ze względu na wprowadzanie i
wyprowadzanie danych
Równoległe
Szeregowo-równoległe
Równoległo-szeregowe
3
Podział liczników
Modulo S
Do S
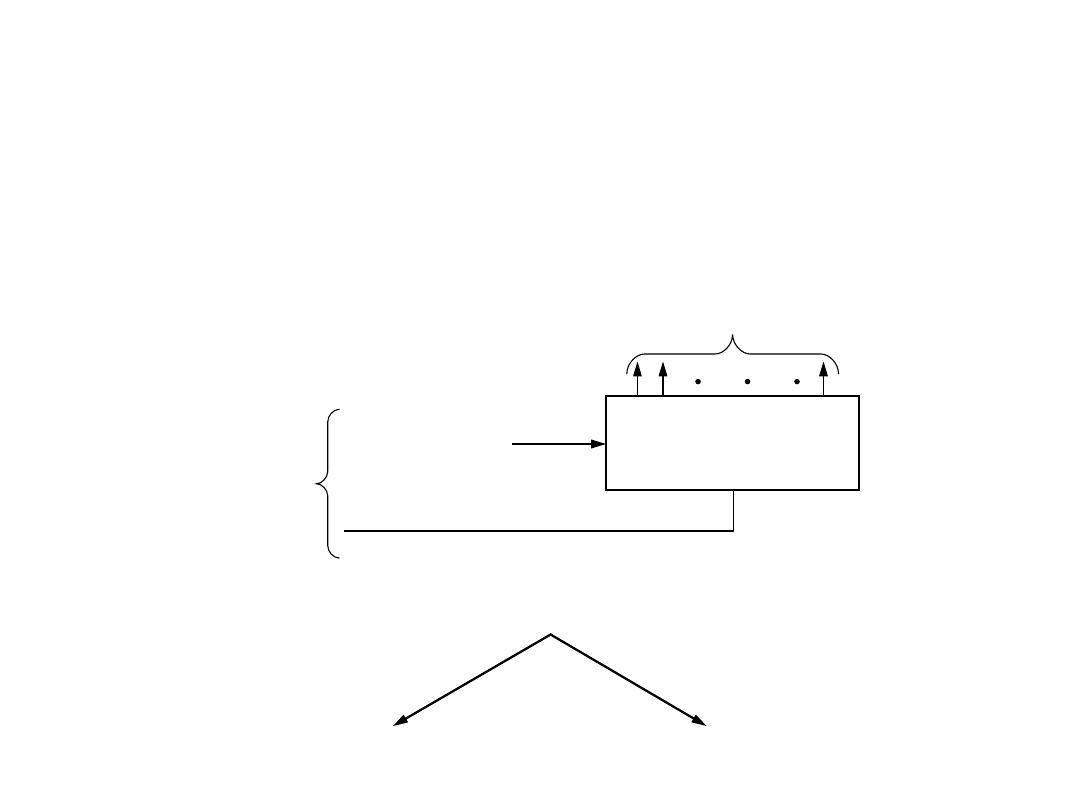
Licznikiem
nazywamy sekwencyjny układ cyfrowy służący do zliczania
i pamiętania liczby impulsów podawanych w określonym
przedziale czasu na jego wejście zliczające.
Symbol licznika
Pod względem powtarzania cyklu
Układ sekwencyjny
S - stanowy
Wyjścia
Impuls zerujący
(ustawiający)
Impulsy zliczane
Wejścia
4
Podział liczników
Jednokierunkowe
Pod względem kierunku zliczania
Dwukierunkowe
(rewersyjne)
Zliczające w przód
Zliczające wstecz
O stałej długości cyklu
Pod względem długości cyklu
O zmiennej długości cyklu
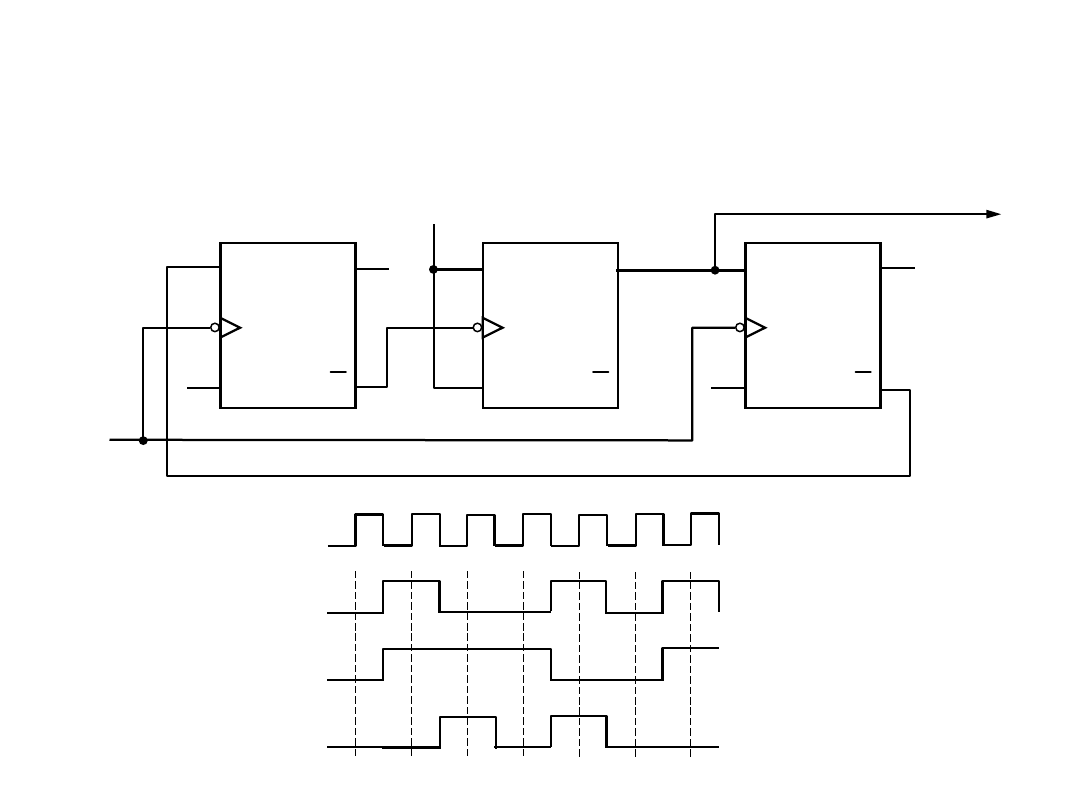
5
Pojemność
licznika dwójkowego można zmieniać za pomocą układu
odpowiednich sprzężeń logicznych.
Wejści
e
A
B
C
0
3
6
2
5
0
0
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
0
0
J
K
Q
Q
C
J
K
Q
Q
C
J
K
Q
Q
C
Wejści
e
”
1
”
A
”
1
”
B
C
Wyjści
e
”
1
”
Metody syntezy liczników
1
1
0
3
6
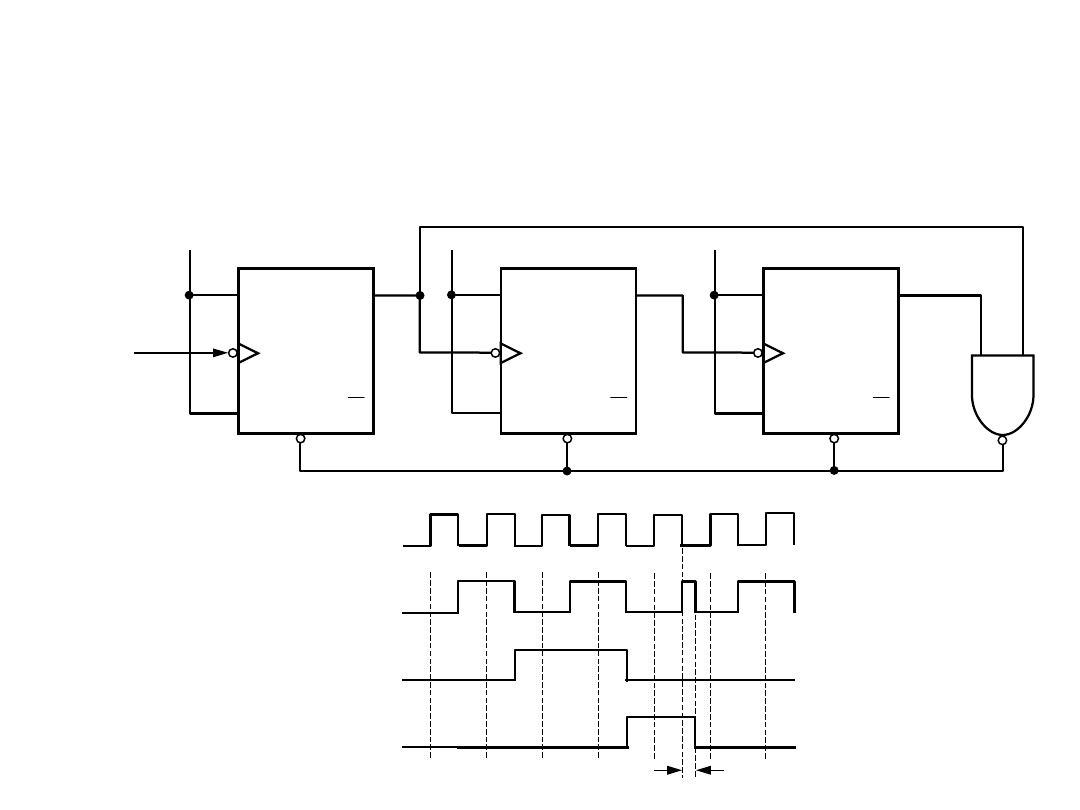
Metody syntezy liczników
Pojemność
licznika dwójkowego można zmieniać poprzez zdekodowanie
stanu licznika odpowiadającego współczynnikowi podziału i
wyzerowanie tym stanem licznika.
Wejści
e
A
B
C
1
J
K
Q
Q
C
J
K
Q
Q
C
J
K
Q
Q
C
Wejści
e
”
1
”
A
B
C
”
1
”
”
1
”
R
R
R
t
0
0
0
0
1
4
2
3
0
1
0
0
0
1
0
1
1
0
0
0
1
1
0
1
0
0
0
1
0
0
1
0
1
7
Metody syntezy liczników
J
K
Q
Q
C
J
K
Q
Q
C
J
K
Q
Q
C
Wejści
e
”
1
”
A
B
C
”
1
”
”
1
”
R
R
R
0
0
1
Wejści
e
A
B
C
0
1
4
2
3
0
1
S
1
1
1
R
1
0
1
0
0
0
0
0
1
0
1
1
0
0
8
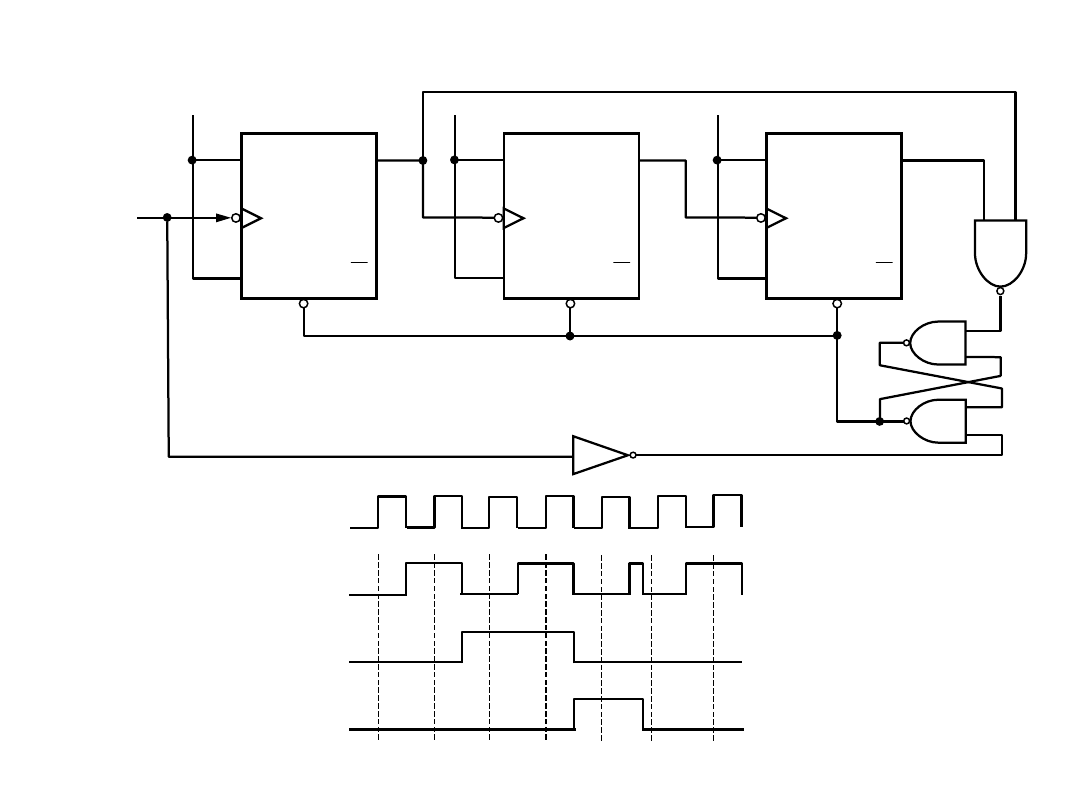
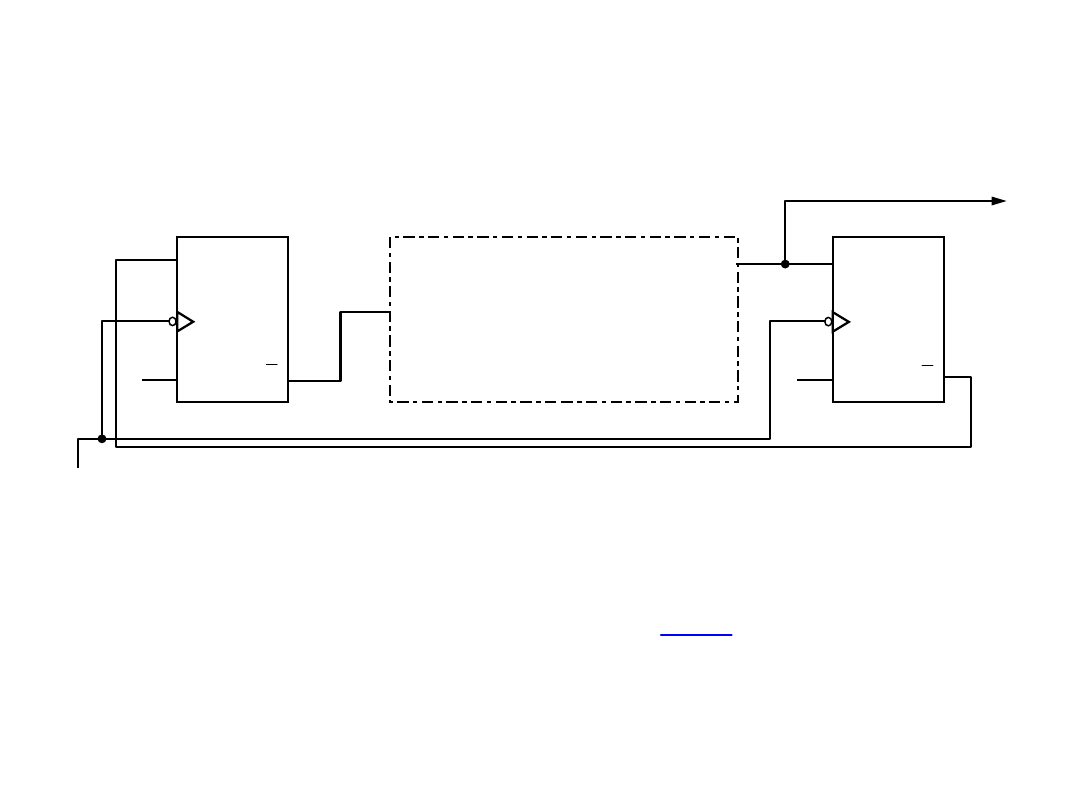
Metody syntezy liczników
Pojemność
licznika rozkładamy na czynniki i łączymy człony wynikające z
tego rozkładu.
J
K
Q
C
J
K
Q
C
1:n
”
1
”
”
1
”
Wejście
Wyjście
Podział pojemności licznika w
stosunku:
(2
1)
n+
Dzielnik
częstotliwości
1
2
1
wy
we
f
n
=
+
9
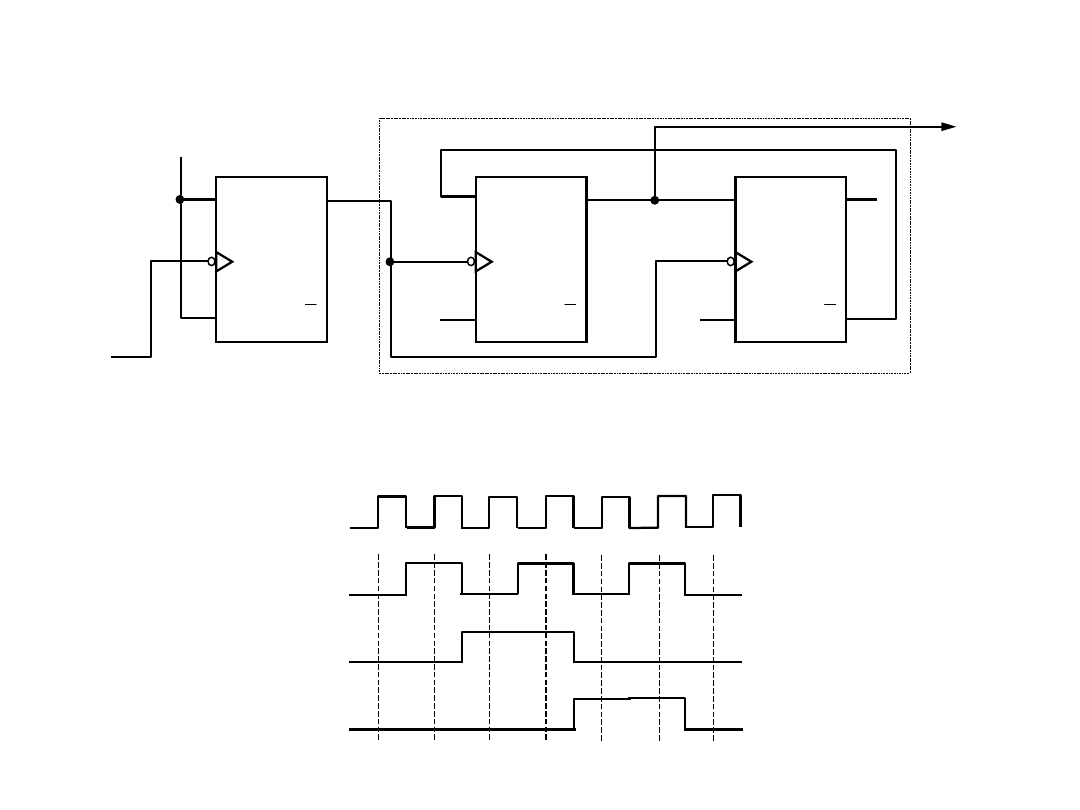
Metody syntezy liczników – licznik mod 6
A
B
C
0
0
0
Wejści
e
A
B
C
0
1
4
2
3
5
0
”
1
”
J
K
Q
C
Q
J
K
Q
C
”
1
”
Q
J
K
Q
C
”
1
”
Q
3:1
Wejści
e
1
0
0
0
1
0
1
1
0
0
0
1
1
0
1
0
0
0
10
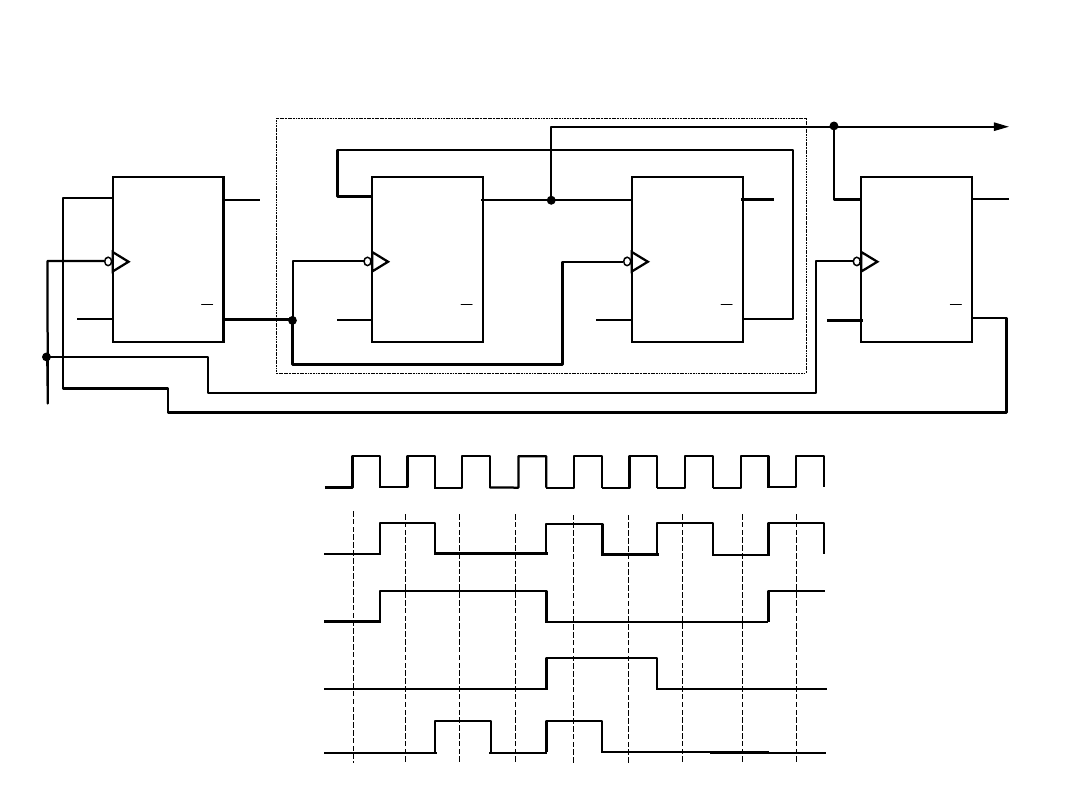
Metody syntezy liczników – licznik mod 7
0
3
13
10
2
4
1
0
3
Wejści
e
A
B
C
D
A
B
C
J
K
Q
C
Q
J
K
Q
C
”
1
”
Q
J
K
Q
C
”
1
”
Q
3:1
Wejści
e
D
J
K
Q
C
Q
”
1
”
”
1
”
Wyjści
e
0
0
0
0
1
1
0
0
0
1
0
1
0
1
0
0
1
0
1
1
0
0
1
0
1
0
0
0
0
0
0
0
1
1
0
0
11
5V
VCC
V1
10kHz 5V
U1A
1D
2
1Q
5
~1Q
6
~1CLR
1
3
~1PR
4
7474N
U1B
2D
12
2Q
9
~2Q
8
~2CLR
13
11
~2PR
10
7474N
U2B
2D
12
2Q
9
~2Q
8
~2CLR
13
11
~2PR
10
7474N
A
B
C
5V
VCC
V1
10kHz 5V
U1A
1D
2
1Q
5
~1Q
6
~1CLR
1
3
~1PR
4
7474N
U1B
2D
12
2Q
9
~2Q
8
~2CLR
13
11
~2PR
10
7474N
U2B
2D
12
2Q
9
~2Q
8
~2CLR
13
11
~2PR
10
7474N
A
B
C
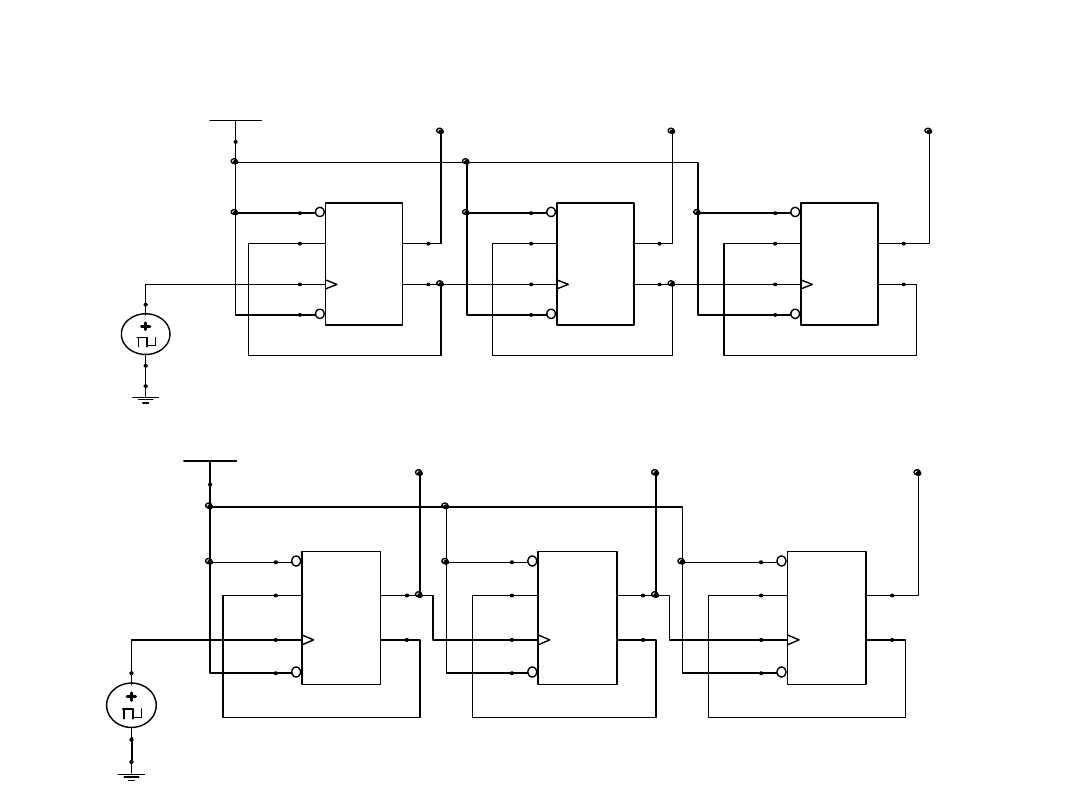
Przykłady liczników
Licznik zliczający w przód na D
Licznik zliczający wstecz na D
12
U1A
7473N
1J
14
1CLK
1
1Q
12
1K
3
~1CLR
2
~1Q
13
U1B
7473N
2J
7
2CLK
5
2Q
9
2K
10
~2CLR
6
~2Q
8
U2A
7473N
1J
14
1CLK
1
1Q
12
1K
3
~1CLR
2
~1Q
13
5V
VCC
V1
10kHz 5V
A
B
C
U1A
7473N
1J
14
1CLK
1
1Q
12
1K
3
~1CLR
2
~1Q
13
U1B
7473N
2J
7
2CLK
5
2Q
9
2K
10
~2CLR
6
~2Q
8
U2A
7473N
1J
14
1CLK
1
1Q
12
1K
3
~1CLR
2
~1Q
13
5V
VCC
V1
10kHz 5V
A
B
C
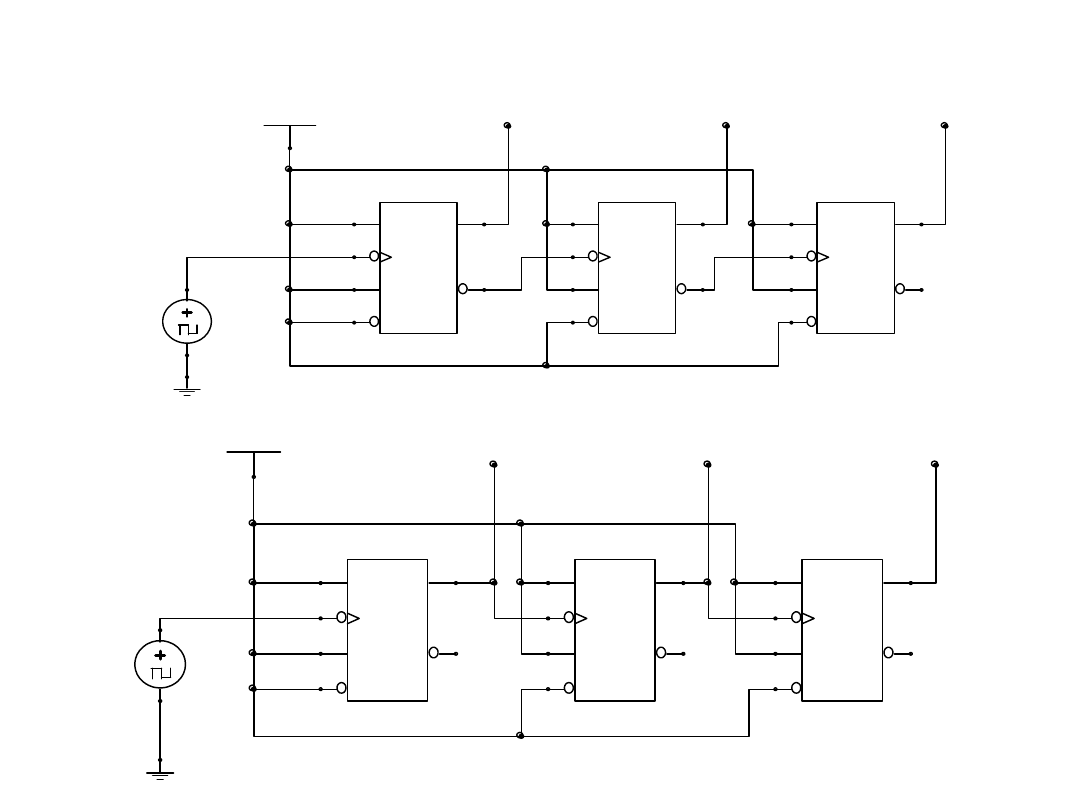
Przykłady liczników
Licznik zliczający w przód na JK
Licznik zliczający wstecz na JK
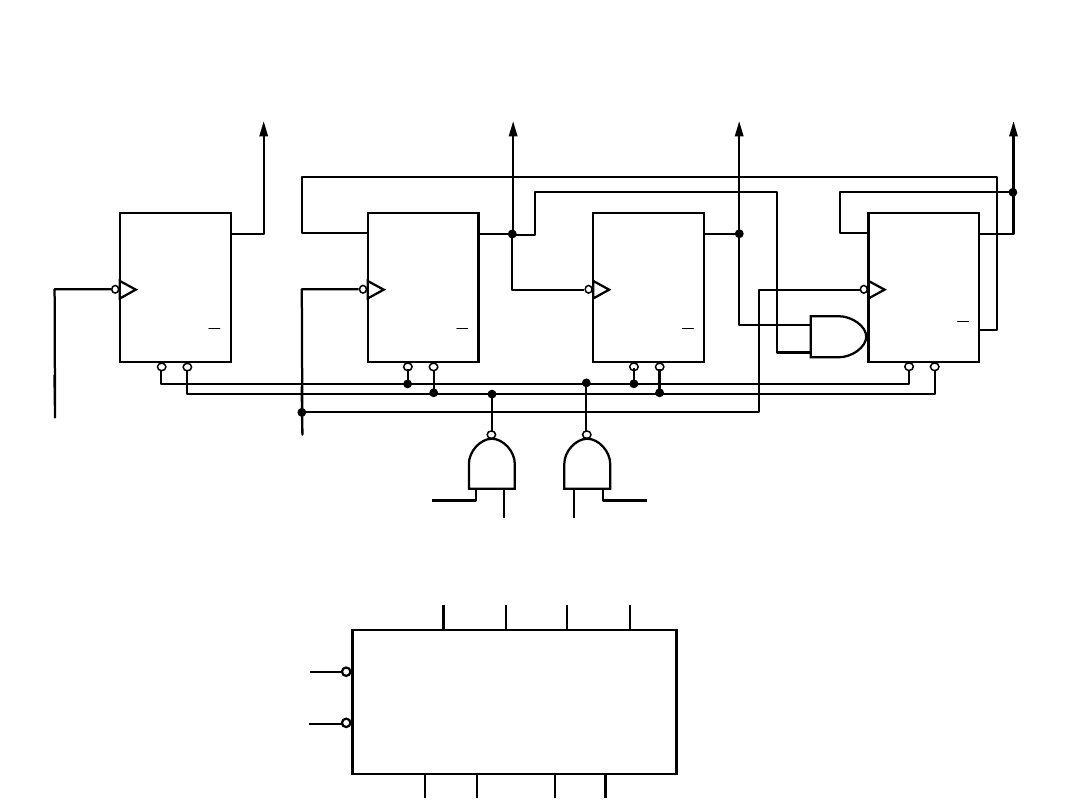
13
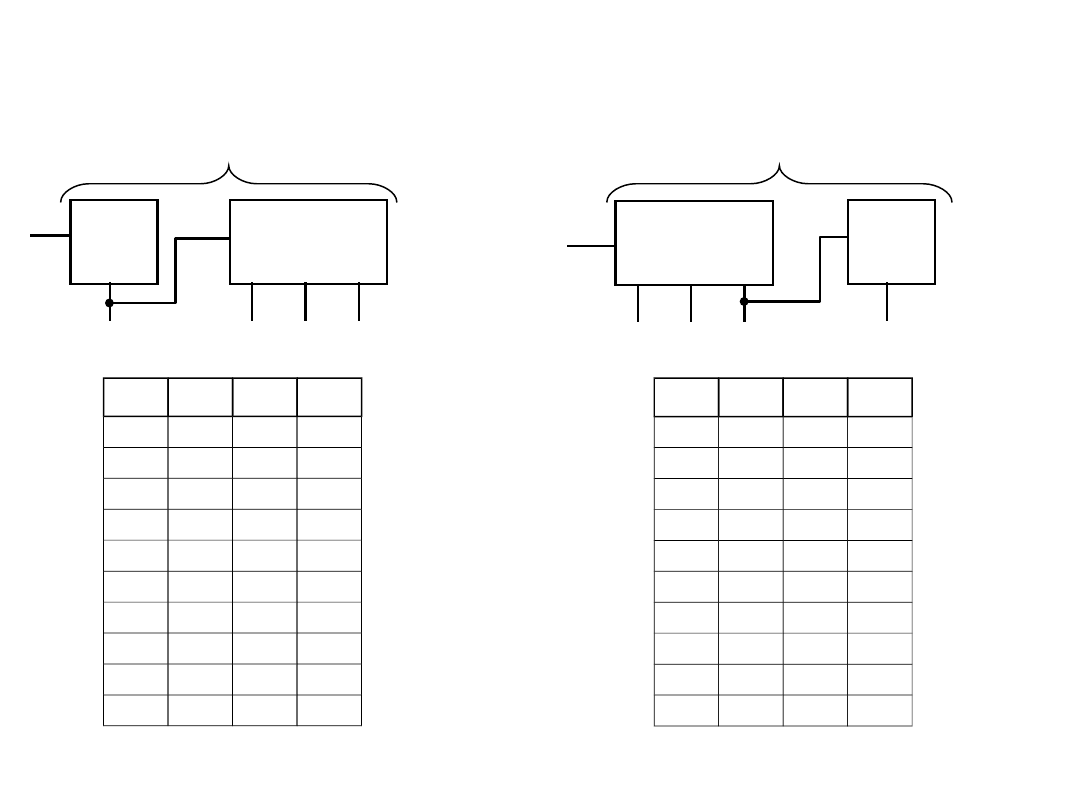
Realizacje scalone liczników
asynchronicznych
Licznik 7490 – dekada licząca
A
B
C
R0(
1)
A
we
D
R
S
Q
C
Q
J
K
Q
C
Q
J
K
Q
C
Q
J
K
Q
C
Q
R0(
2)
R9(
1)
R9(
2)
BD
we
Symbol
R0(1
)
R0(2
)
R9(1
)
R9(2
)
A
B
C
D
DB
we
A
we
7490
14
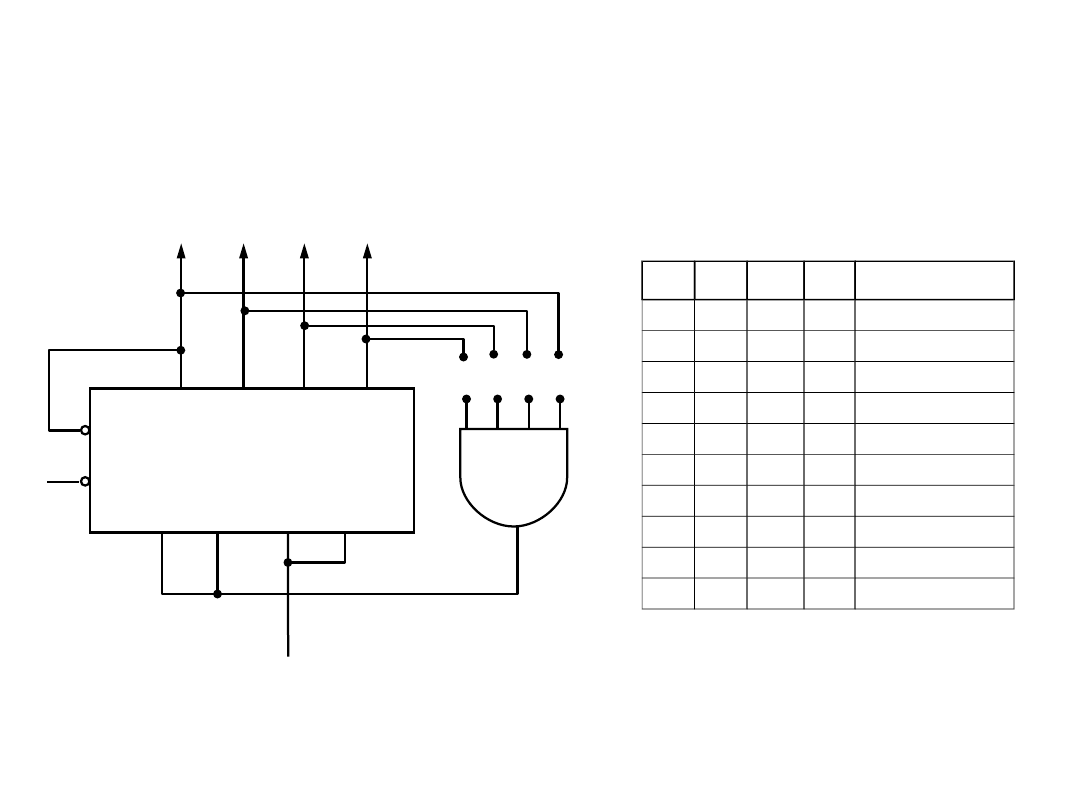
Realizacje scalone liczników
asynchronicznych
Możliwe tryby pracy
:2
:5
A
we
A
B
C
D
7490
:2
:5
A
we
A
B
C
D
7490
BD
we
A
B
C
D
0
0
0
0
1
0
0
0
0
1
0
0
1
1
0
0
0
0
1
0
1
0
1
0
0
1
1
0
1
1
1
0
0
0
0
1
1
0
0
1
B
C
D
A
0
0
0
0
1
0
0
0
0
1
0
0
1
1
0
0
0
0
1
0
0
0
0
1
1
0
0
1
0
1
0
1
1
1
0
1
0
0
1
1
15
Realizacje scalone liczników
asynchronicznych
Programowalny dzielnik
częstotliwości
R0(1
)
R0(2
)
R9(1
)
R9(2
)
A
B
C
D
BD
we
A
we
7490
”0
”
We
x
4
x
3
x
2
x
1
X
4
X
3
X
2
X
1
Podział przez
O
O
O
O
----
O
O
O
Z
1
O
O
Z
O
2
O
O
Z
Z
3
O
Z
O
O
4
O
Z
O
Z
5
O
Z
Z
O
6
O
Z
Z
Z
7
Z
O
O
O
8
Z
O
O
Z
9
O – otwarte; Z - zamknięte
Tablice programowania
Przykład: Licz_90.msm;
Dzielnik_czestotliwosci.msm
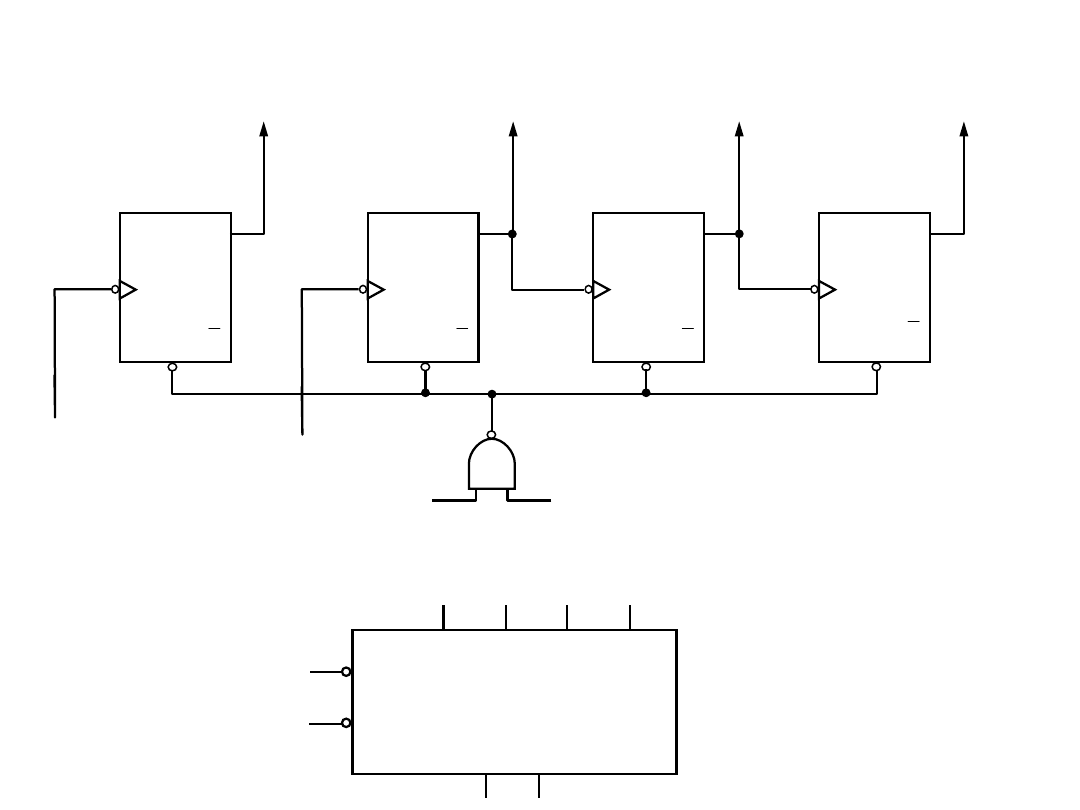
16
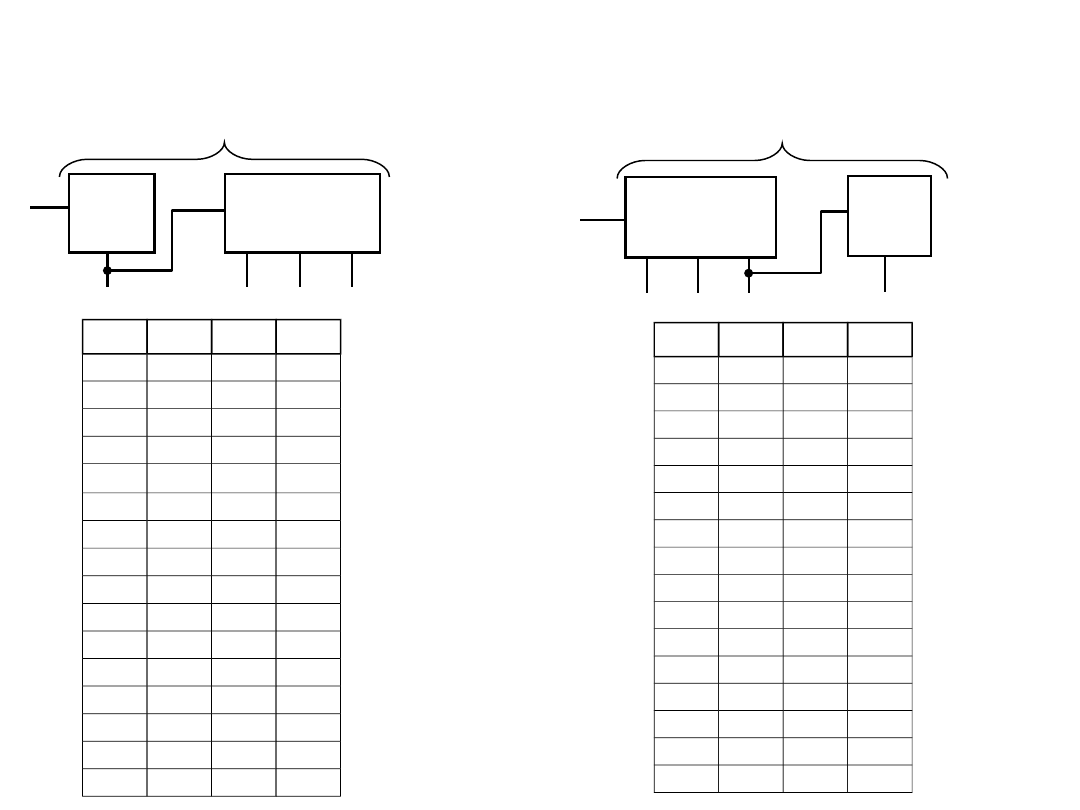
Realizacje scalone liczników
asynchronicznych
Licznik 7493
Symbol
R0(1
)
R0(2
)
A
B
C
D
B
we
A
we
7493
A
B
C
R0(
1)
A
we
D
J
K
Q
C
Q
J
K
Q
C
Q
J
K
Q
C
Q
J
K
Q
C
Q
R0(
2)
B
we
17
Realizacje scalone liczników
asynchronicznych
Możliwe tryby pracy
:2
:8
A
we
A
B
C
D
7493
:2
:8
A
we
A
B
C
D
7493
B
we
A
B
C
D
0
0
0
0
1
0
0
0
0
1
0
0
1
1
0
0
0
0
1
0
1
0
1
0
0
1
1
0
1
1
1
0
0
0
0
1
1
0
0
1
0
1
0
1
1
1
0
1
0
0
1
1
1
0
1
1
0
1
1
1
1
1
1
1
B
C
D
A
0
0
0
0
1
0
0
0
0
1
0
0
1
1
0
0
0
0
1
0
1
0
1
0
0
1
1
0
1
1
1
0
0
0
0
1
1
0
0
1
0
1
0
1
1
1
0
1
0
0
1
1
1
0
1
1
0
1
1
1
1
1
1
1
18
Realizacje scalone liczników
asynchronicznych
Programowalny dzielnik
częstotliwości
R0(1
)
R0(2
)
A
B
C
D
B
we
A
we
7493
We
x
4
x
3
x
2
x
1
X
4
X
3
X
2
X
1
Podział przez
O
O
O
O
----
O
O
O
Z
1
O
O
Z
O
2
O
O
Z
Z
3
O
Z
O
O
4
O
Z
O
Z
5
O
Z
Z
O
6
O
Z
Z
Z
7
Z
O
O
O
8
Z
O
O
Z
9
Z
O
Z
O
10
Z
O
Z
Z
11
Z
Z
O
O
12
Z
Z
O
Z
13
Z
Z
Z
O
14
Z
Z
Z
Z
15
O – otwarte; Z - zamknięte
Tablice programowania
Przykład:
Dzielnik_czestotliwosci_93.msm
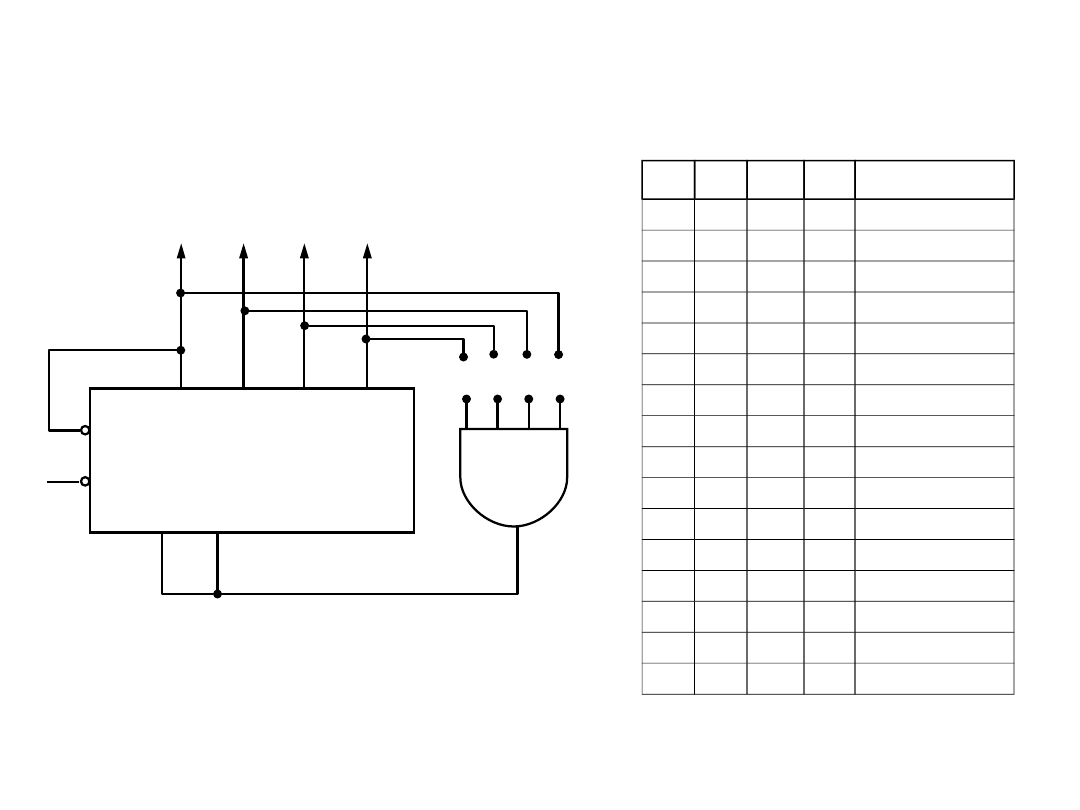
19
Licznik synchroniczny mod 5
A
B
C
Wejści
e
J
1
K
Q
C
Q
J
K
Q
C
Q
J
K
Q
C
Q
R
R
R
Zerowani
e
J
2
Wejści
e
A
B
C
0
0
0
0
1
2
3
4
0
1
0
0
0
1
0
1
1
0
0
0
1
0
0
0
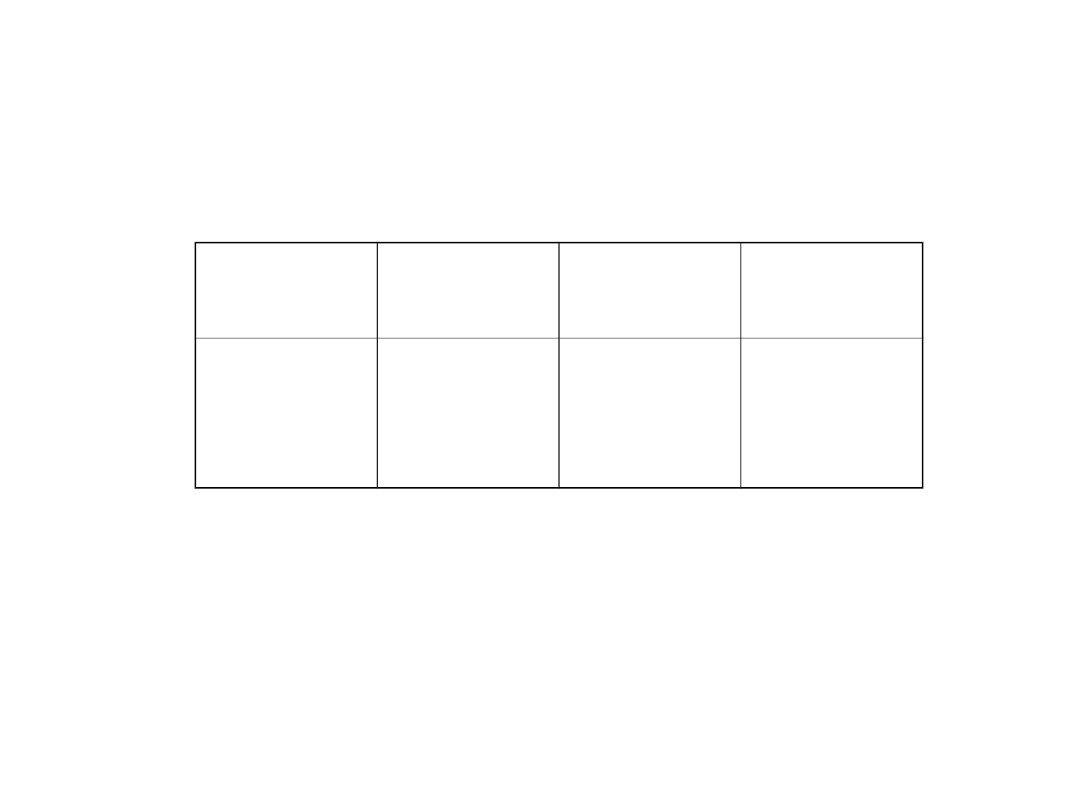
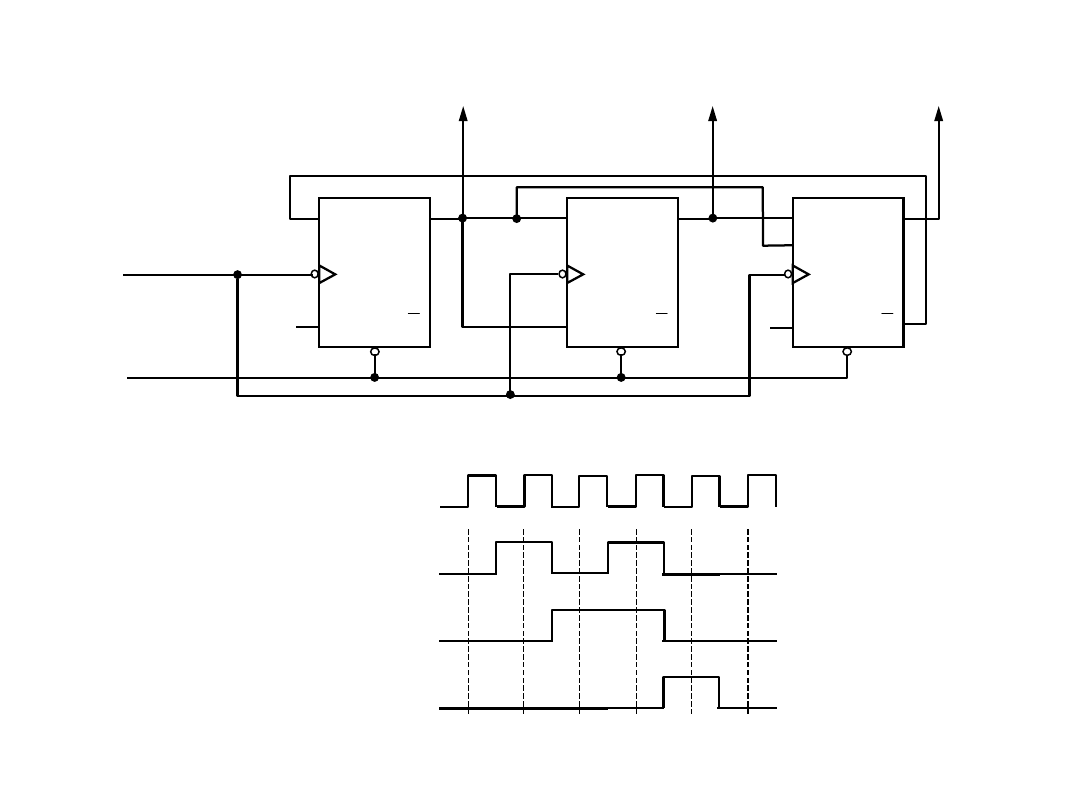
20
Synteza licznika synchronicznego
Q
n
Q
n+1
S R
J K
D
0 0
0 1
1 0
1 1
0 ---
1 0
0 1
--- 0
0 ---
1 ---
--- 1
--- 0
0
1
0
1
Zaprojektować licznik synchroniczny zliczający w kodzie Gray’a
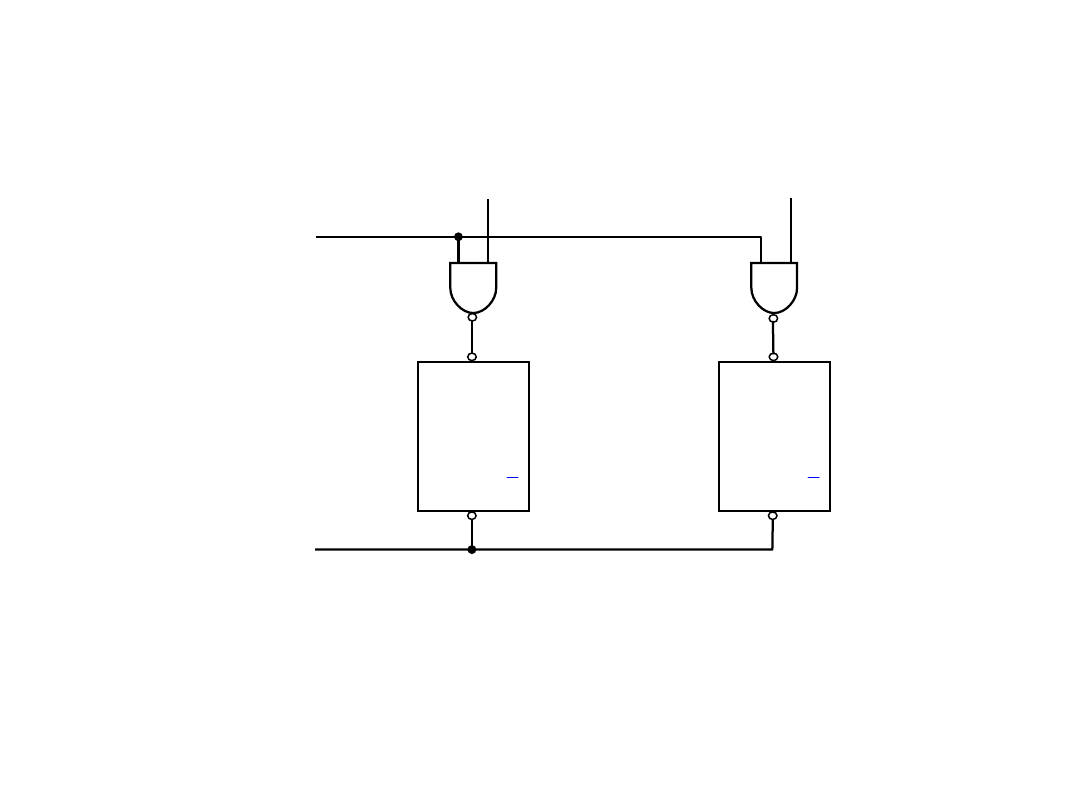
21
Układy równoległego wprowadzania informacji do
rejestrów
A
0
X
Zerowani
e
A
n
. . .
. . .
Q
Q
S
R
Q
Q
S
R
0
1
1
x
x
1
Wada:
Konieczność wyzerowania rejestru przed wprowadzeniem
informacji z wejść równoległych.
1
0
1
1
1
X
1
0
0
1
22
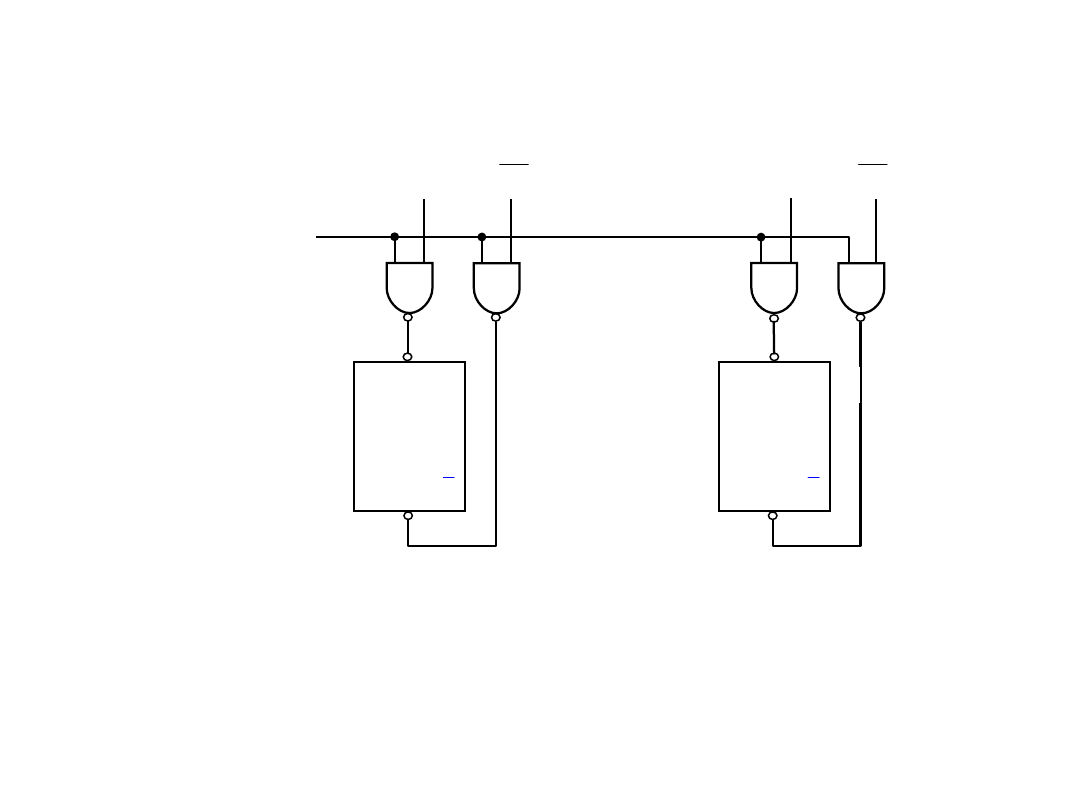
Układy równoległego wprowadzania informacji do
rejestrów
•Wyzerowanie rejestru realizowane poprzez równoległe wprowadzenie
wartości 0.
A
0
X
A
n
. . .
. . .
Q
Q
S
R
Q
Q
S
R
0
A
n
A
0
1
0
1
1
X
X
X
X
1
1
1
0
0
1
0
0
1
1
1
0
1
•Konieczność podawania wartości wprowadzanych równolegle w postaci
prostej i zanegowanej.
Wada:
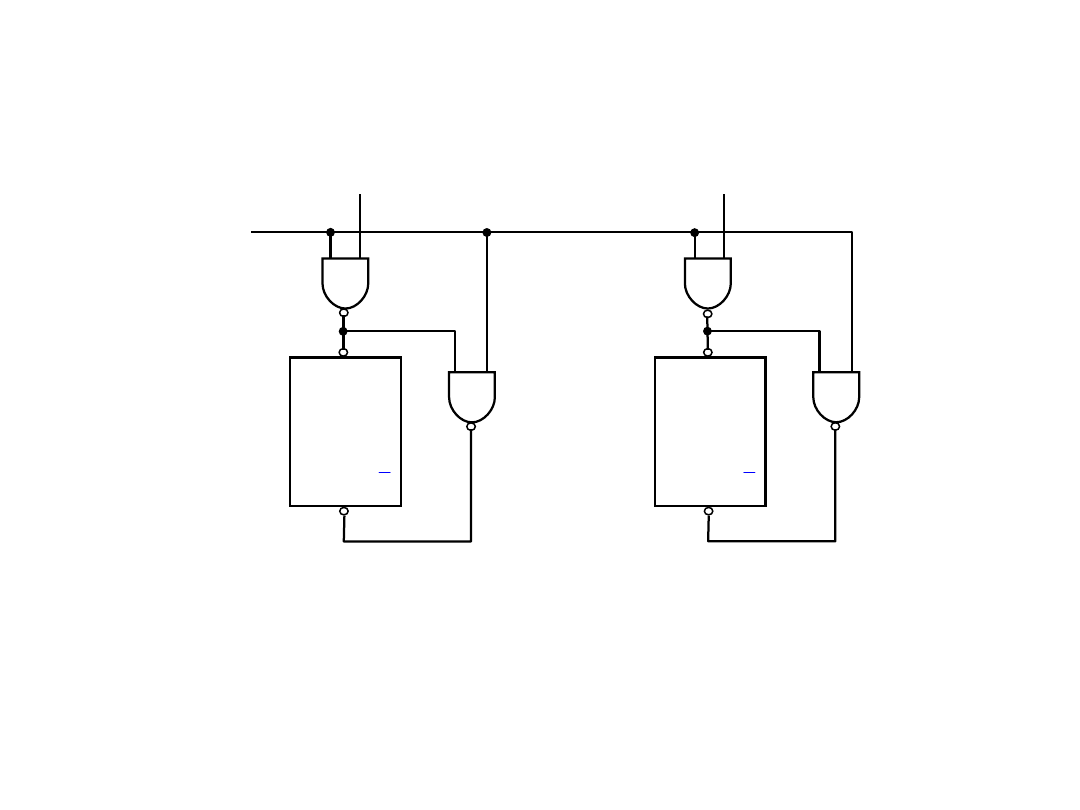
23
Układy równoległego wprowadzania informacji do
rejestrów
•Wyzerowanie rejestru realizowane poprzez równoległe wprowadzenie
wartości 0.
Wada:
A
0
X
A
n
. . .
. . .
Q
Q
S
R
Q
Q
S
R
0
1
1
X
X
1
1
1
0
0
0
1
1
1
1
0
0
1
24
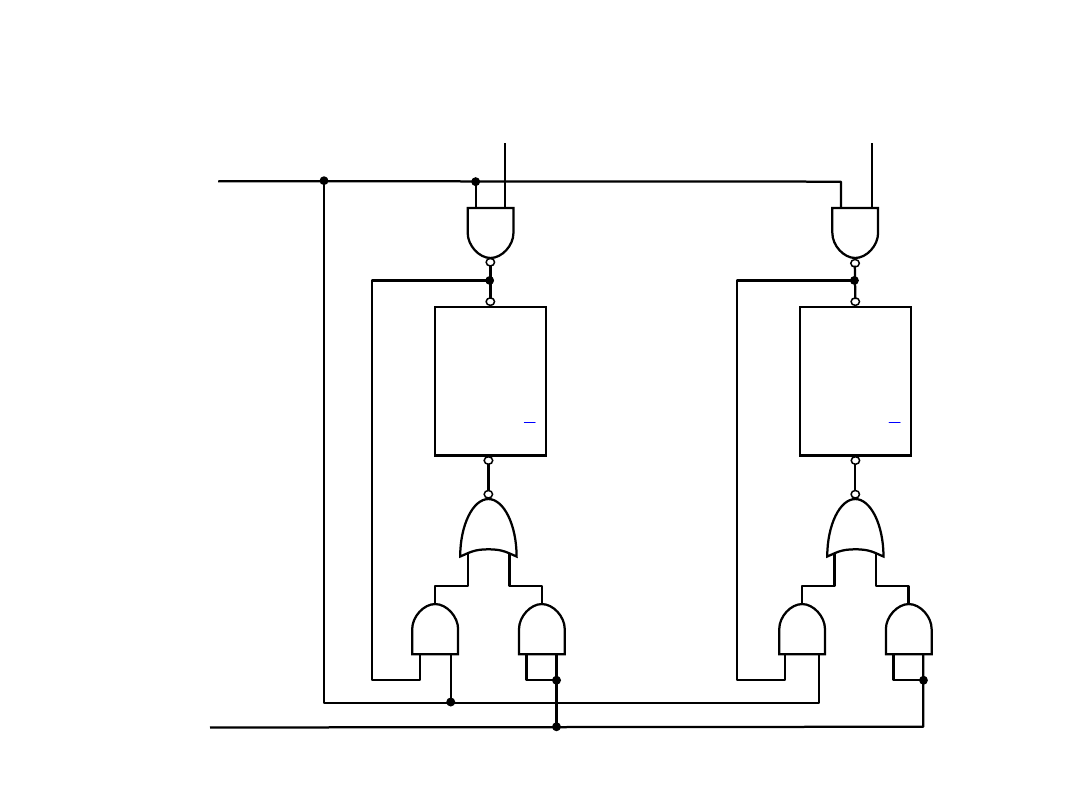
Układy równoległego wprowadzania informacji do
rejestrów
A
0
X
A
n
. . .
. . .
Q
Q
S
R
Q
Q
S
R
Zerowanie
0
0
1
1
1
0
X
X
0
1
0
0
1
1
1
1
1
0
0
0
0
0
0
0
1
1
1
1
0
0
1
1
0
0
0
0
1
0
1
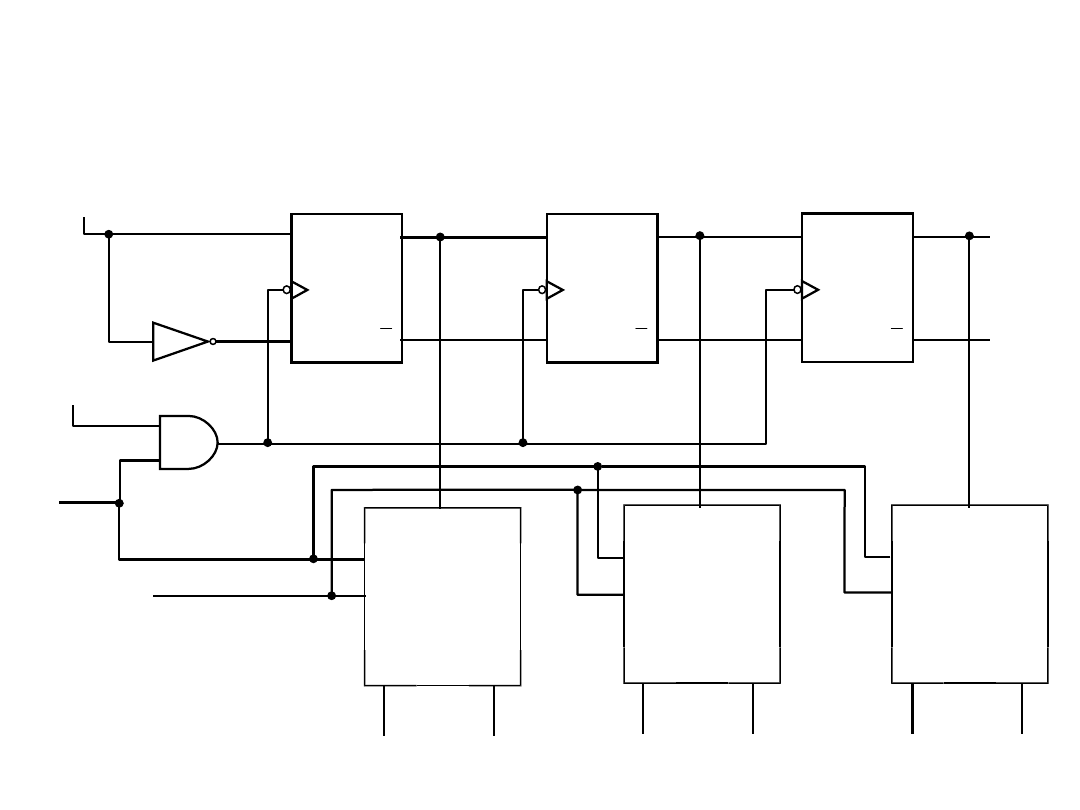
25
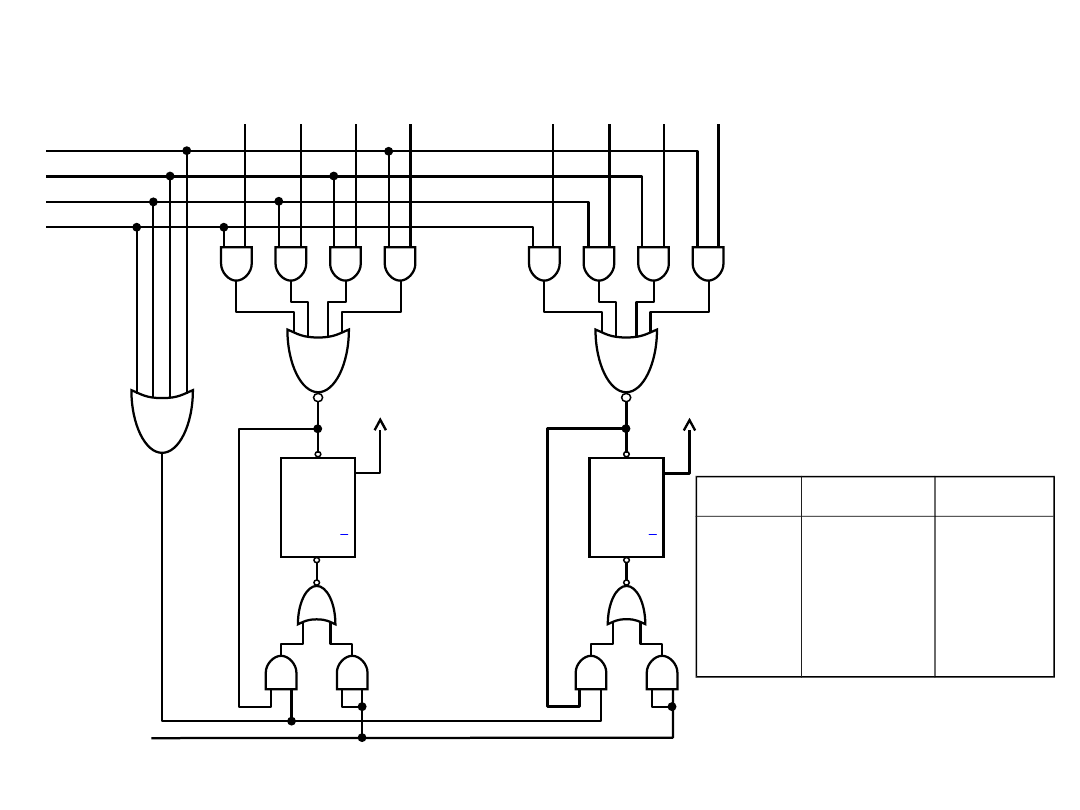
Układy równoległego wprowadzania informacji z
kilku źródeł
X
4
. . .
. . .
Q
Q
0
S
R
Q
Q
1
S
R
Zerowani
e
X
3
X
2
X
1
A
0
B
0
C
0
D
0
A
n
B
n
C
n
D
n
Wyj 0
Wyj n
Zer.
X
1
X
2
X
3
X
4
Q
0
… Q
n
0
0
0
0
1
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
0 0 0 0
A
0
… A
n
B
0
… B
n
C
0
… C
n
D
0
… D
n
0 … 0
26
Przykład
Zbudować, wykorzystując przerzutnik typu JK, 3-bitowy rejestr
szeregowo-równoległy z możliwością wyprowadzania informacji do
dwóch odbiorników.
J
K
Q
C
Q
J
K
Q
C
Q
J
K
Q
C
Q
Wej. danych
A
B
C
Wej. zegarowe
Tryb
DANE
TRYB
STER
WY1
WY2
Wyb.
wyjścia
DANE
TRYB
STER
WY1
WY2
DANE
TRYB
STER
WY1
WY2
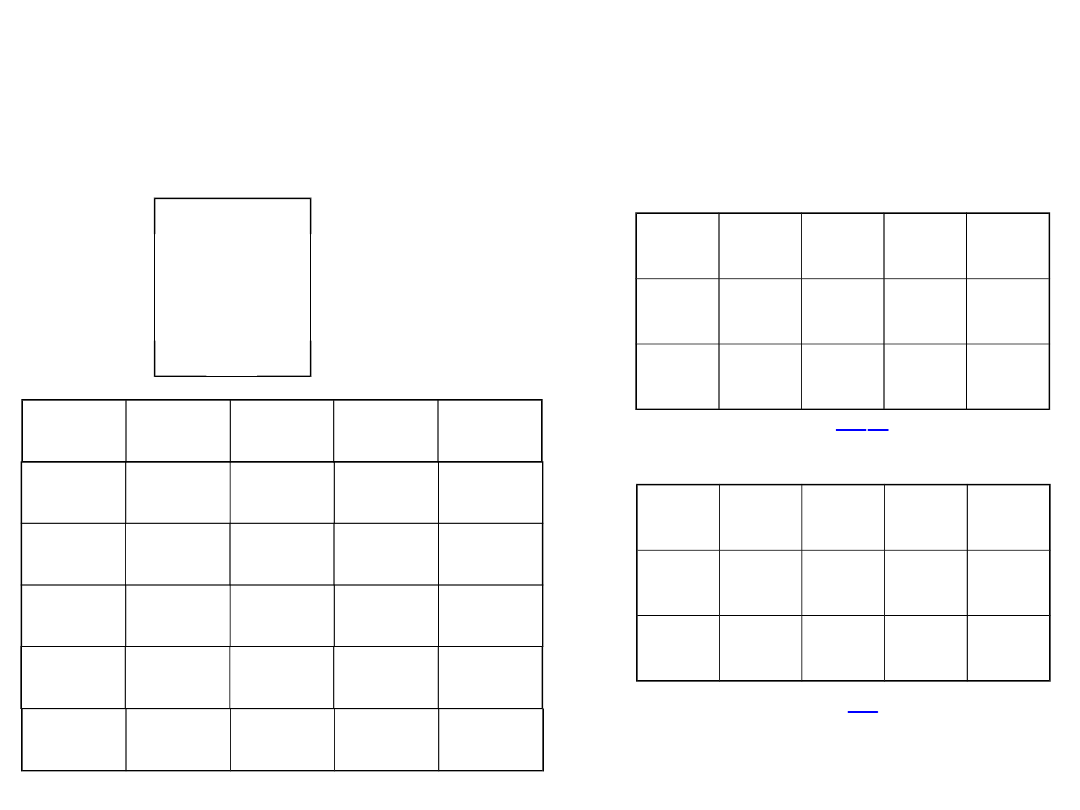
27
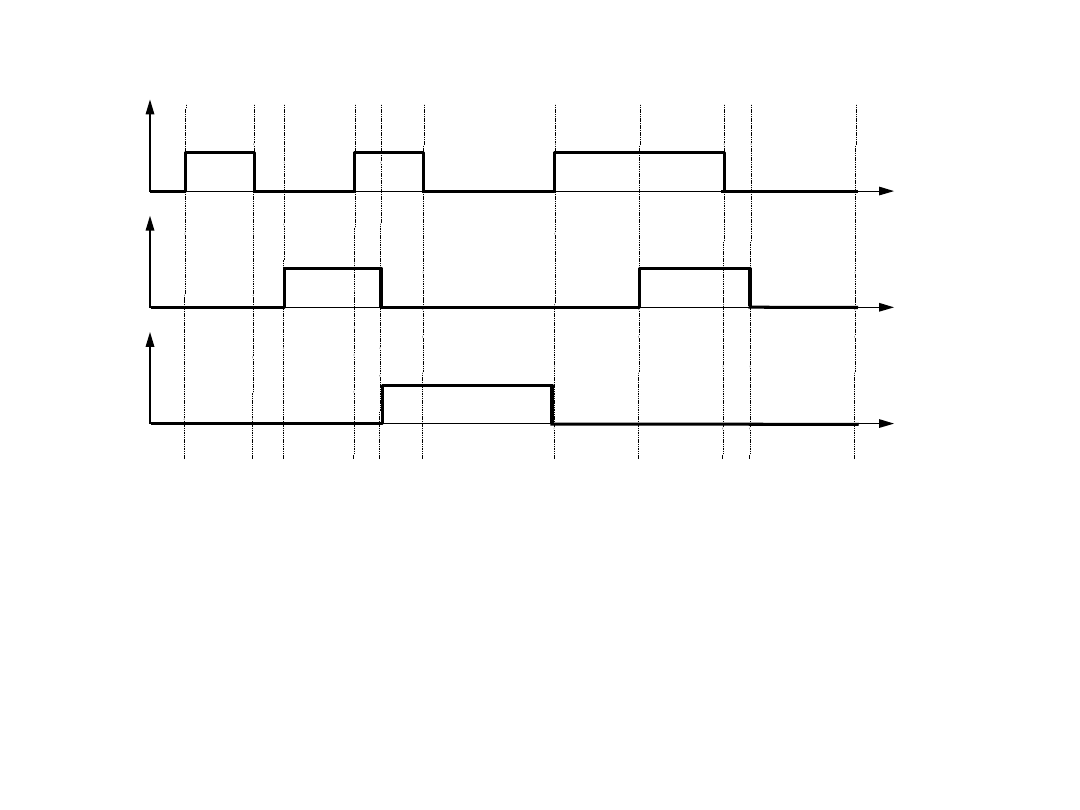
Przykład
Zbudować, wykorzystując przerzutnik typu JK, 3-bitowy rejestr
szeregowo-równoległy z możliwością wyprowadzania informacji do
dwóch odbiorników.
DANE
TRYB
STER
WY1
WY2
TRYB(T) STER(S) DANE(D
)
WY1
WY2
0
1
0
0
0
0
0
1
1
0
0
0
0
0
0
1
X
X
0
0
0
1
1
0
1
S D
T
00
01
11
10
1
0
0
0
0
0
0
1
0
0
S D
T
00
01
11
10
1
0
0
0
0
0
0
0
1
0
1
WY
T S D
= g g
2
WY
T S D
= g g
28
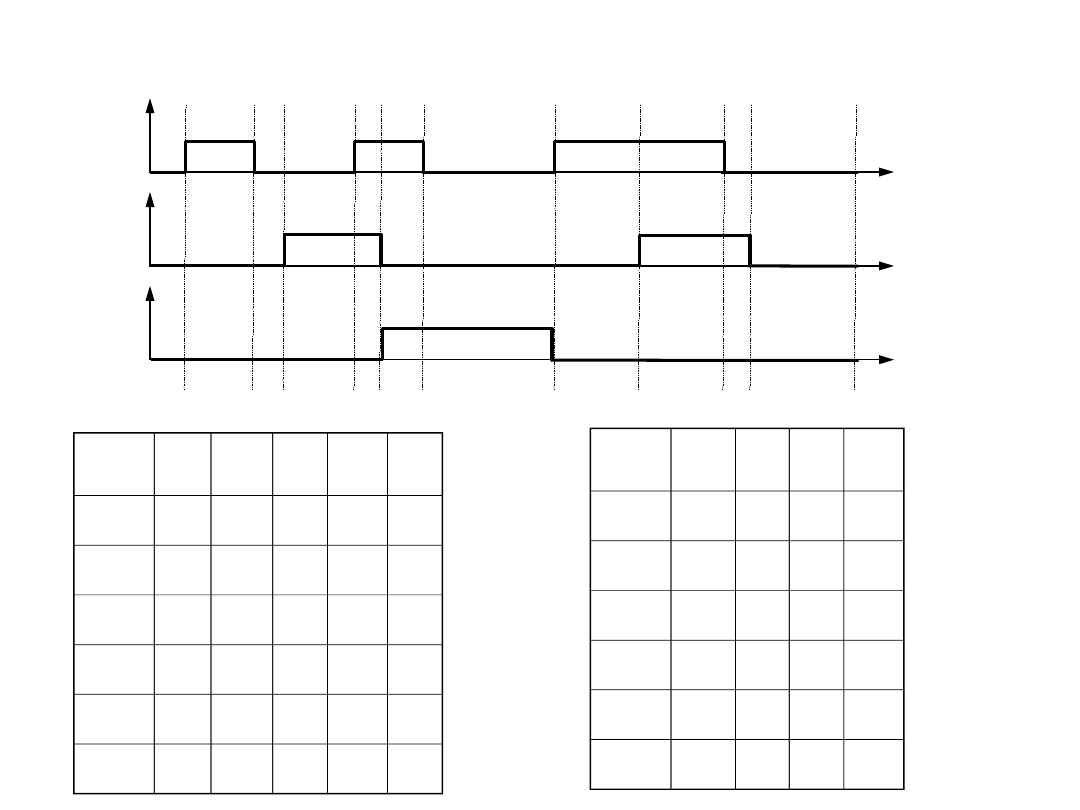
Realizacja przykładowego układu
sekwencyjnego
x
1
x
2
y
t
t
t
S
1
S
2
S
1
S
3
S
4
S
5
S
6
S
2
S
4
S
3
S
1
Równoważność
stanów
1
1
( ( )
( ))
(( ( , )
( , )) ( ( , )
( , )))
i
j
i
j
i
j
i
j
s
s
s
s
x
s x
s x
s x
s x
l
l
d
d
d
d
ں="�=��
Moore’a
2
2
( ( , )
( , )) (( ( , )
( , )) ( ( , )
( , )))
i
j
i
j
i
j
i
j
s
s
x
s x
s x
s x
s x
s x
s x
l
l
d
d
d
d
ں=�="��
Mealy’ego
29
Realizacja przykładowego układu
sekwencyjnego
x
1
x
2
y
t
t
t
S
1
S
2
S
1
S
3
S
4
S
5
S
6
S
2
S
4
S
3
S
1
X
1
X
2
S
00
01
10
11
Y
S
1
---
S
3
S
2
---
0
S
2
S
1
---
---
S
4
0
S
3
S
1
---
---
S
4
0
S
4
---
S
3
S
5
---
0
S
5
S
6
---
---
---
1
S
6
---
---
S
2
---
1
X
1
X
2
S
00
01
10
11
S
1
---
S
3
/0 S
2
/0
---
S
2
S
1
/0
---
---
S
4
/0
S
3
S
1
/0
---
---
S
4
/0
S
4
---
S
3
/0 S
5
/1
---
S
5
S
6
/1
---
---
---
S
6
---
--- S
2
/0
---
Automat Moore’a
Automat Mealy’ego
30
Realizacja przykładowego układu
sekwencyjnego
X
1
X
2
S
00
01
10
11
Y
S
1
---
S
3
S
2
---
0
S
2
S
1
---
---
S
4
0
S
3
S
1
---
---
S
4
0
S
4
---
S
3
S
5
---
0
S
5
S
6
---
---
---
1
S
6
---
---
S
2
---
1
Automat Moore’a
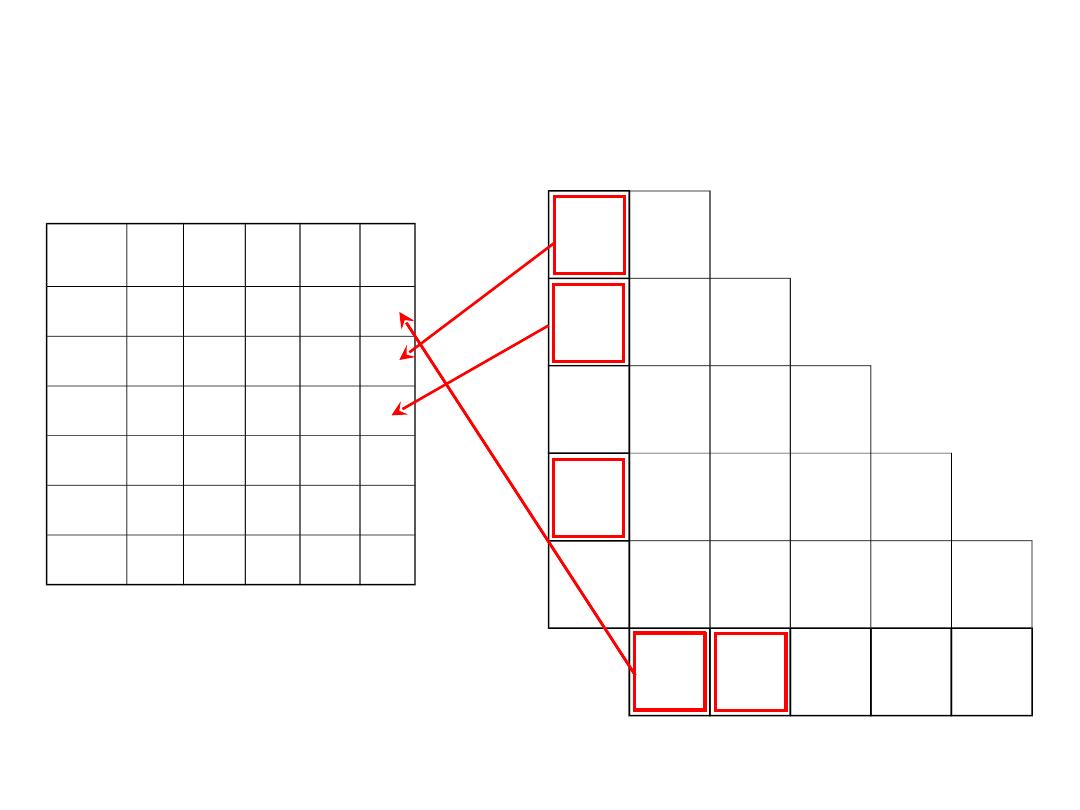
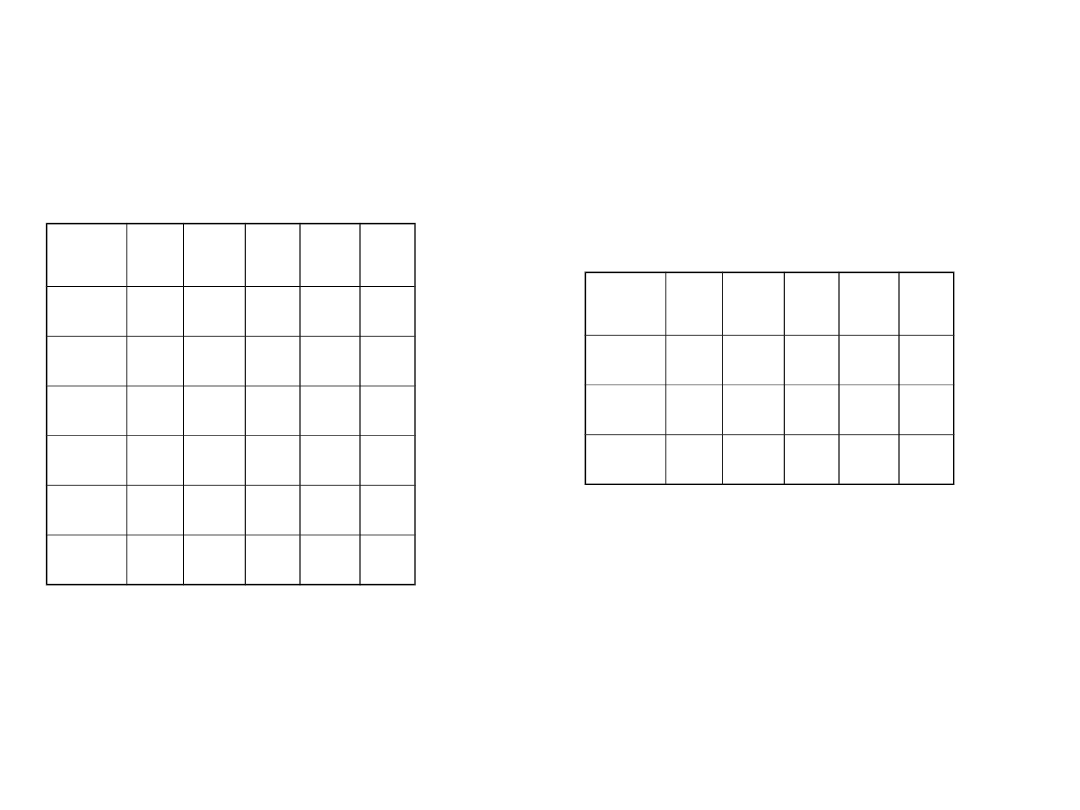
Minimalizacja liczby stanów
2
3
4
5
6
1
2
3
4
5
Tablica trójkątna
S
2
S
5
S
1
S
2
S
3
S
a
S
5
S
6
S
b
31
Realizacja przykładowego układu
sekwencyjnego
X
1
X
2
S
00
01
10
11
Y
S
1
---
S
3
S
2
---
0
S
2
S
1
---
---
S
4
0
S
3
S
1
---
---
S
4
0
S
4
---
S
3
S
5
---
0
S
5
S
6
---
---
---
1
S
6
---
---
S
2
---
1
Automat Moore’a
Automat zminimalizowany
S
1
S
2
S
3
S
a
S
5
S
6
S
b
X
1
X
2
S
00
01
10
11
Y
S
a
S
a
S
a
S
a
S
4
0
S
4
---
S
a
S
b
---
0
S
b
S
b
---
S
a
---
1
Tablica przejść i wyjść automatu
zminimalizowanego
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
Wyszukiwarka
Podobne podstrony:
Napęd Elektryczny wykład
wykład5
Psychologia wykład 1 Stres i radzenie sobie z nim zjazd B
Wykład 04
geriatria p pokarmowy wyklad materialy
ostre stany w alergologii wyklad 2003
WYKŁAD VII
Wykład 1, WPŁYW ŻYWIENIA NA ZDROWIE W RÓŻNYCH ETAPACH ŻYCIA CZŁOWIEKA
Zaburzenia nerwicowe wyklad
Szkol Wykład do Or
Strategie marketingowe prezentacje wykład
Wykład 6 2009 Użytkowanie obiektu
wyklad2
wykład 3
wyklad1 4
wyklad 5 PWSZ
więcej podobnych podstron