Optyka geometryczna i falowa

• Odbicie i załamanie
• Zasada Fermata
• Warunki stosowalności optyki geometrycznej
• Zasada Huygensa
• Interferencja, doświadczenie Younga

– A. Koherencja
– B. Natężenie w doświadczeniu Younga

• Interferencja w cienkich warstwach

1. Odbicie i załamanie

- współczynnik załamania;

bezwzględny

n = c/v

względny

n

2,1

= v

1

/v

2

- prawo odbicia i załamania:

promień odbity i załamany leżą w jednej płaszczyźnie utworzonej

przez promień padający i prostopadłą do powierzchni odbijającej w

punkcie padania (normalna padania)

tzn. w płaszczyźnie rysunku.

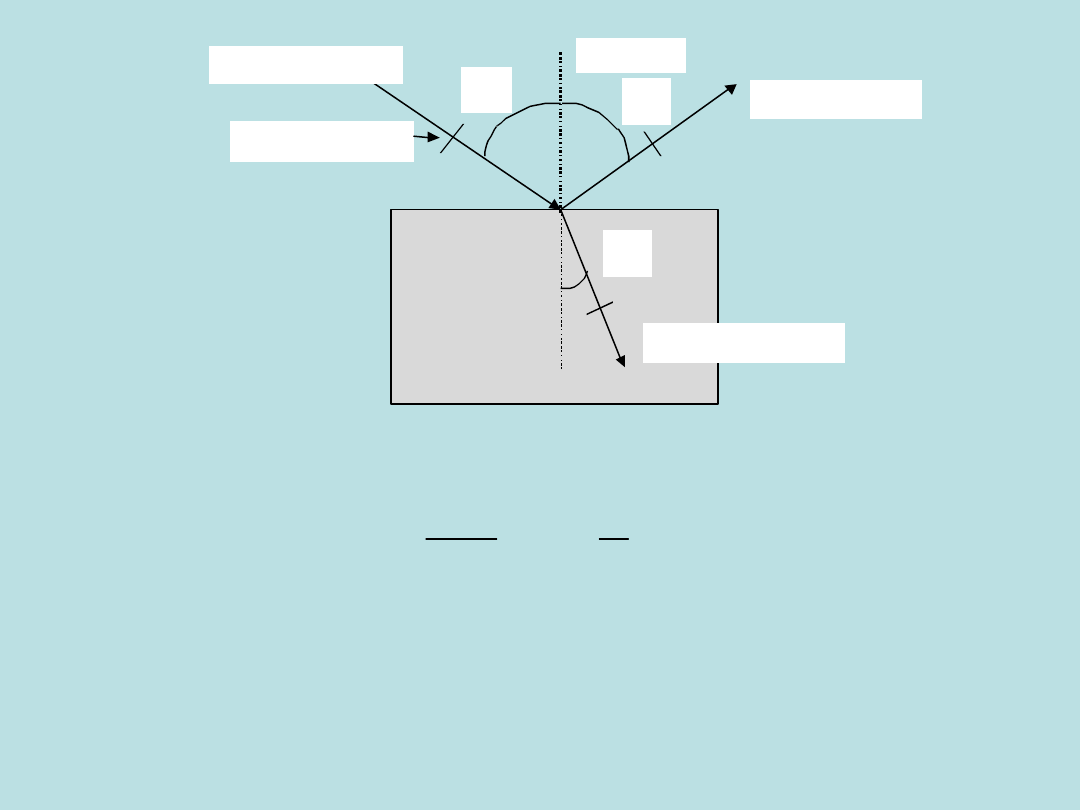
normalna

Promień odbity

Promień załamany

Promień padający



1



1

’



2

Czoło fali płaskiej

- prawo dla odbicia



1

=



1

’

- prawo dla załamania

2

1

1

,

2

2

1

sin

sin

v

v

n 







Prawa te można wyprowadzić z równań Maxwella, ale jest to

matematycznie zbyt trudne.

Można te prawa optyki wyprowadzić w oparciu o prostą (ale ważną)

zasadę odkrytą w 1650 r przez Pierre Fermata.

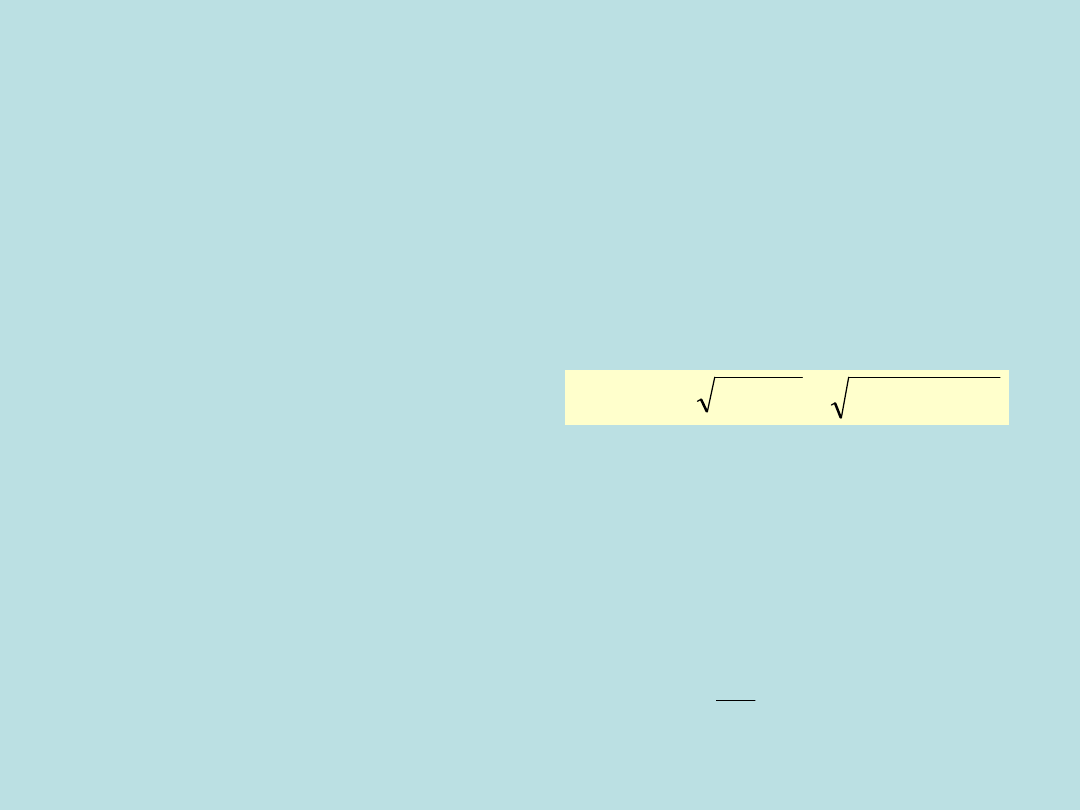
2. Zasada Fermata

Promień świetlny biegnący z jednego punktu do drugiego

przebywa drogę, na której przebycie trzeba zużyć w porównaniu
z innymi, sąsiednimi drogami, minimum (albo maksimum) czasu.

Całkowita długość drogi promienia wynosi

2

2

2

2

)

(

x

d

b

x

a

l

APB













gdzie x - zmienna zależna od
położenia punktu P (punkt odbicia
promienia).

0

d

d



x

l

0

)

1

)(

(

2

]

)

(

[

2

1

2

)

(

2

1

d

d

2

/

1

2

2

2

/

1

2

2





















x

d

x

d

b

x

x

a

x

l

czyli

lub przekształcając

2

2

2

2

)

(

x

d

b

x

d

x

a

x











Porównując z rysunkiem widzimy, że jest to równoważne zapisowi

sin

 = sin’

czyli

 = ’

co jest

prawem odbicia

.

W omawianych przypadku czas przebycia drogi czyli droga -
minimalna.

Podobnie postępujemy w celu wyprowadzenia prawa załamania.

3. Warunki stosowalności optyki geometrycznej

Omawiając

odbicie i załamanie

fal (płaskich) posługiwaliśmy się

pojęciem

promienia.

Wygodne i przydatne pojęcie do opisu tych zjawisk, nie jest pomocne
przy opisie

ugięcia światła (fal),

gdyż niemożliwe jest wydzielenie

pojedynczego promienia z padającej fali płaskiej.

3.

Warunki stosowalności optyki geometrycznej

• Omawiając odbicie i załamanie fal (płaskich) posługiwaliśmy

się pojęciem

promienia.

• Wygodne i przydatne pojęcie do opisu tych zjawisk, nie jest

pomocne przy opisie

ugięcia światła

(fal), gdyż niemożliwe

jest wydzielenie pojedynczego promienia z padającej fali

płaskiej.

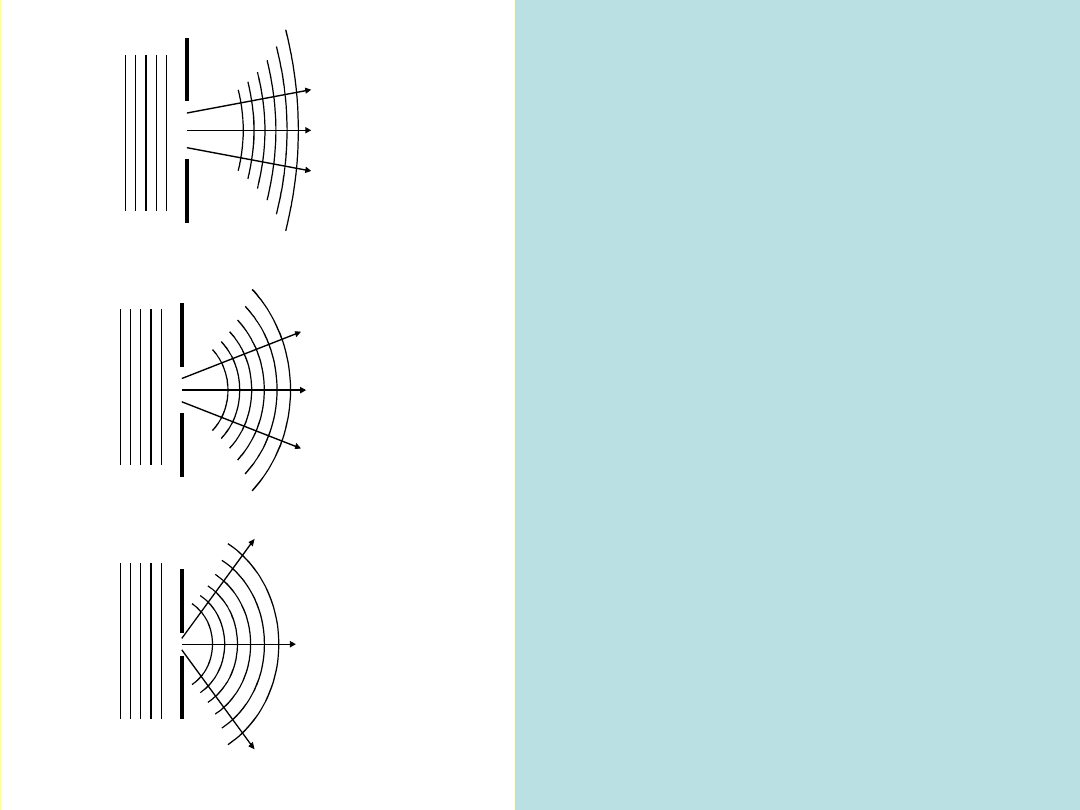
a=5

a=3

a=

Widzimy, że ugięcie staje się coraz
bardziej wyraźne gdy a/  0.

To

ugięcie

jest

charakterystyczne

dla

wszystkich rodzajów fal.

Ugięcie fal na szczelinie (albo
przeszkodzie) wynika z zasady
Huyghensa.

Szczeliny o szerokości a = 5

, a = 3 oraz a = 

Teoria:

-

nie

wspomina

o

elektromagnetycznym charakterze
światła;

- nie wyjaśnia, że światło jest falą
poprzeczną.

Teoria Huyghensa - oparta jest na
konstrukcji geometrycznej zwanej
zasadą

Huyghensa

-

pozwala

przewidzieć, gdzie znajdzie się
czoło fali w dowolnej chwili w
przyszłości, jeżeli znamy jej obecne
położenie.

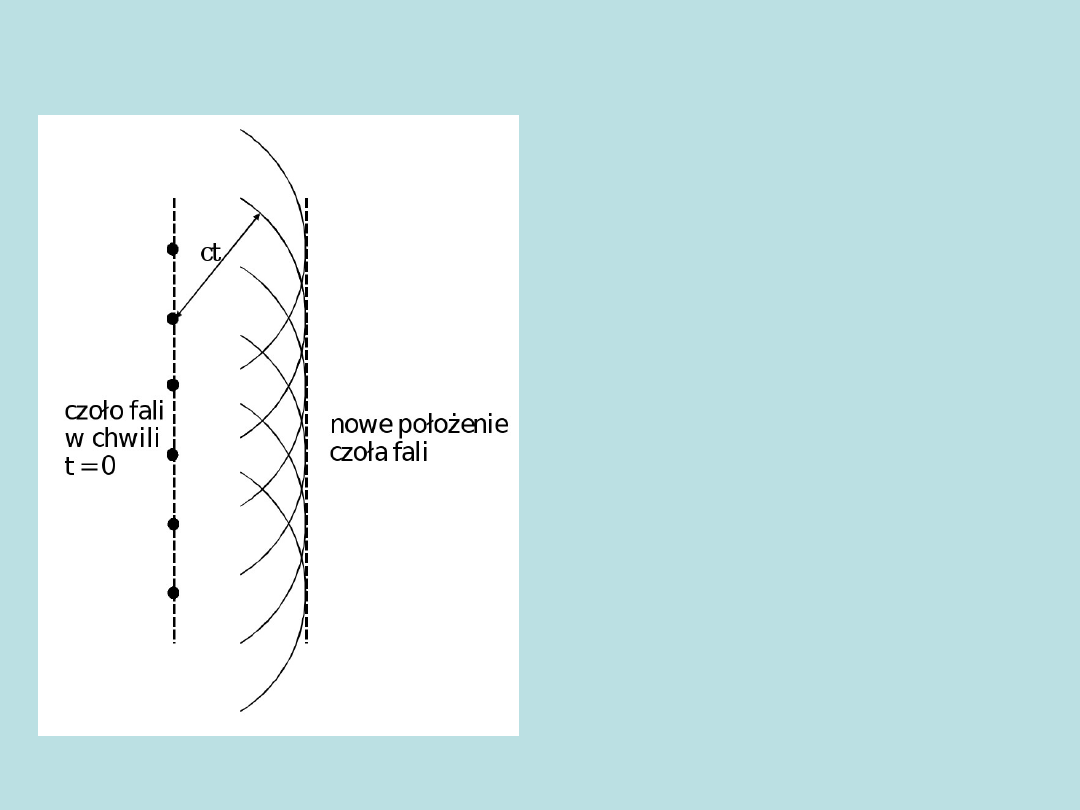
Wszystkie punkty czoła fali
można

uważać

za

źródła

nowych fal kulistych.
Położenie czoła fali po czasie t
będzie dane przez powierzchnię
styczną do tych fal kulistych.

4. Zasada Huyghensa

Teoria światła

zakłada, że światło jest falą (a nie strumieniem

cząstek)

(Christian Huyghens - 1678 r).

Dane jest czoło fali płaskiej w próżni.

Zgodnie z zasadą Huyghensa

-

wybrane punkty

na tej powierzchni

traktujemy jako

źródła fal kulistych

.

Po czasie t promienie tych fal będą równe ct, gdzie c jest prędkością
światła.

Powierzchnia styczna

do tych fal po czasie t jest nową

powierzchnią falową

.

Powierzchnia falowa fali płaskiej jest płaszczyzną rozchodzącą
się z prędkością c.

Uwaga: Można oczekiwać (w oparciu o tę zasadę), że wbrew obserwacji
fala Huyghensa może się rozchodzić zarówno do tyłu, jak i do przodu.
Zakłada się w modelu, że natężenie tych fal kulistych (Huyghensa)
zmienia się w sposób ciągły od maksimum dla kierunku „w przód”, do
zera dla kierunku „w tył”.

Zasada Huyghensa

daje się zastosować jakościowo do

wszelkich zjawisk

falowych

(np.

odbicia i załamania).

Ugięcia fal na szczelinie (przeszkodzie)

Czoło fali dochodzi do szczeliny, każdy jej punkt traktujemy jako źródło
fal kulistych Huyghensa. Przez szczelinę przechodzi tylko część fal,
reszta fale zostaje wyeliminowana i wiązka zagina się w obszar tzw.
cienia geometrycznego.

•Warunkiem stosowalności optyki geometrycznej jest więc,

aby wymiary liniowe wszystkich obiektów (soczewek,

pryzmatów, szczelin itp.) były o wiele większe od długości

fali (a >>  ).

•Jeżeli

a <<



przy opisie światła bierzemy pod uwagę

falowy

charakter światła

(ugięcie fali jest znaczące, gdy szczelina ma

rozmiar porównywalny z długością fali

a ≈



) – mówimy wtedy o

optyce falowej (a ≈

)

.

•Optyka geometryczna jest więc szczególnym (granicznym)
przypadkiem optyki falowej.

•Zajmiemy się teraz właśnie optyką falową.

•Gdy szerokość szczeliny staje się duża (w stosunku do długości fali)

a

>>



to ugięcie można zaniedbać - światło rozchodzi się po liniach

prostych (przedstawiamy je w postaci promieni podlegających prawom

odbicia i załamania) – mówimy o

optyce geometrycznej (a >>



).

5. Interferencja światła, doświadczenie

Younga

1.Wykazane, przez Thomasa Younga (w 1801 r.) istnienie

interferencji

fal świetlnych (nakładania się) było pierwszym

eksperymentem wskazującym na falowy charakter światła.

Doświadczenie Younga - oświetlił światłem słonecznym
ekran, w którym był zrobiony mały otwór S

0

.

Przechodzące światło padało następnie na drugi ekran z
dwoma otworami S

1

i S

2

.

Dalej rozchodziły się dwie, nakładające się fale kuliste tak
jak na rysunku.

S

0

S

2

S

1

Warunki stosowalności optyki
geometrycznej

nie

są

spełnione - na szczelinach
następuje

ugięcie

fal

-

optyka falowa

(szczeliny S

0

,

S

1

, S

2

≤ ).

Jeżeli umieścimy

ekran

w

jakimkolwiek miejscu, tak
aby przecinał on nakładające
się na siebie fale to możemy
oczekiwać

pojawienia się na

nim ciemnych i jasnych plam
następujących

po

sobie

kolejno.

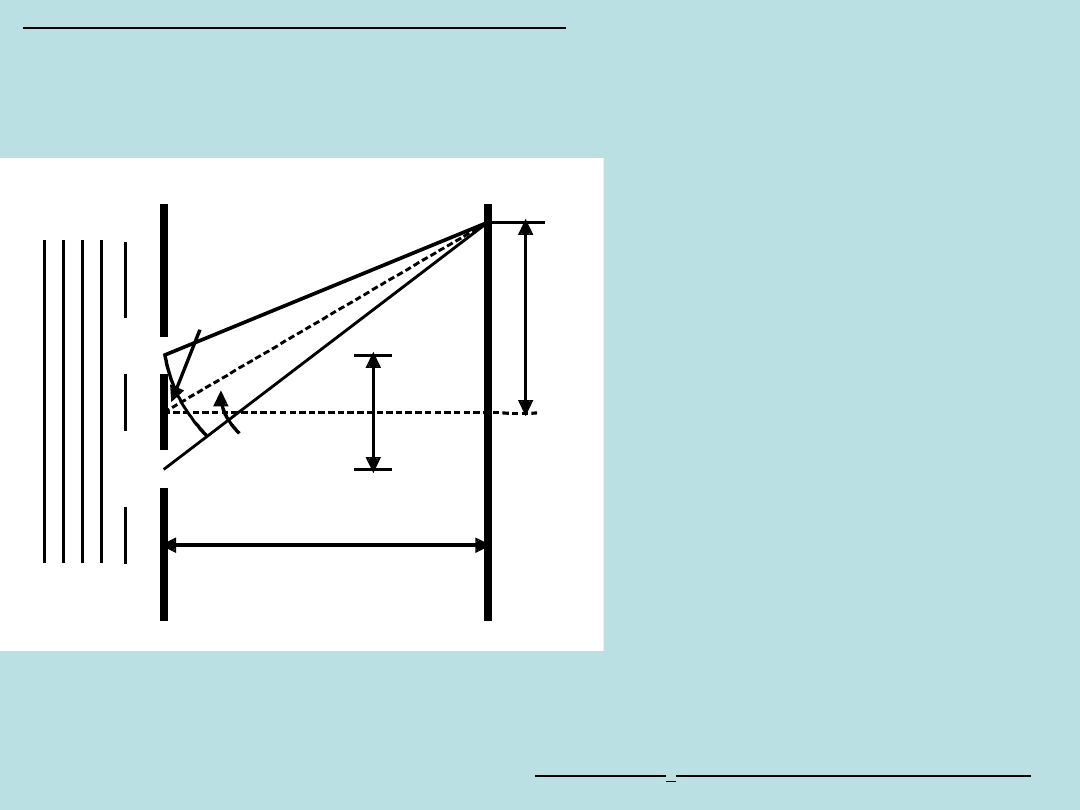
Analiza ilościowa doświadczenie Younga
Zakładamy, że:
(1)światło padające jest monochromatyczne (jedna długość fali);
(2)punkt P - dowolny punkt na ekranie, odległy o r

1

i r

2

od wąskich szczelin

S

1

i S

2

;

(3) PS

2

= Pb;

(4) d << D, wtedy kąt S

1

S

2

b

jest równy

 (z dużą

dokładnością);

S

1

S

2

d

D

y

P

r

1

r

2





O

b

(5) oba promienie (ze szczelin
S

1

i S

2

) są zgodne w fazie,

gdyż pochodzą z tego samego
czoła fali płaskiej.
Jednak ich drogi do punktu P
są różne, więc i ich fazy mogą
być różne.

Jeżeli odcinki Pb i PS

2

są identyczne (tak to skonstruowaliśmy) -

o

różnicy faz decyduje różnica dróg optycznych tj. odcinek S

1

b.

Aby w punkcie P było

maksimum

to odcinek S

1

b musi zawierać całkowitą

liczbę długości fal.

Po przebyciu odcinka równego

 - faza fali powtarza się,

więc dla drogi

m



fala ma fazę taką jak na początku tej drogi;

Odcinek S

1

b nie wpływa na różnicę faz a ponieważ

fale były zgodne w

źródle

(szczeliny S

1

i S

2

) więc

będą zgodne w fazie w punkcie P

.

Warunek ten możemy zapisać w postaci

S

1

b = m

,

m = 0, 1, 2, ......,

lub

dsin

 = m, m = 0, 1, 2, ......, (maksima)

Każdemu maksimum powyżej punktu O, odpowiada symetryczne
maksimum poniżej punktu O. Istnieje też

centralne maksimum

opisywane przez m = 0.

Dla uzyskania minimum w punkcie P, odcinek S

1

b musi zawierać

połówkową liczbę długości fal, to jest:

S

1

b = (m+1/2)

,

m = 0,1,2,....,

lub

dsin

 = (m+1/2) , m = 0, 1, 2, ......, (minima)

inaczej

dsin

 = (2m+1)/2, m = 0, 1, 2, ......, (minima)

Równanie opisujące położenie kątowe maksimów może posłużyć do

wyznaczenia długości fali

m

d





sin



Z

tej

relacji

Young

wyznaczył

długości

fal

światła widzialnego.

A. Koherentność

Podstawowym warunkiem powstania dobrze określonego obrazu

interferencyjnego jest, aby

fale świetlne które przybywają z

punktów S

1

i S

2

miały dokładnie określoną różnicę faz

 stałą

w czasie.

(faza - określony stan fali w danym miejscu i czasie,

równanie fali E = Emsin(kx-

t)).

Np. miejsce na ekranie, dla którego różnica faz wynosi

 - oznacza

fizycznie, że fale docierające tam wygaszają się (przy założeniu tej
samej amplitudy); mamy ciemny prążek.

Warunkiem stabilności obrazu jest więc

stałość w czasie różnicy

faz fal wychodzących ze źródeł S

1

i S

2

- źródła koherentne czyli

spójne.

Gdy w krótkim czasie są spełnione warunki dla maksimum, a za

chwile (b. krótką np. 10

-8

s) dla minimum, a jeszcze za chwilę

warunki pośrednie, a

natężenie (w danym punkcie na ekranie) jest

sumą natężeń od poszczególnych źródeł - źródła niespójne,
niekoherentne.

Jak wytworzyć światło spójne?
Zwykłe źródła światła takie jak żarówki (żarzące się włókno) dają

światło niespójne dlatego, że emitujące atomy działają zupełnie
niezależnie.

Natomiast lasery są współcześnie szeroko stosowane źródła

światła spójnego. Zasadę działania lasera poznamy na dalszych
wykładach.

B. Natężenie w doświadczeniu Younga

Załóżmy, że składowe pola elektrycznego obu fal w punkcie P
zmieniają się następująco

E

1

= E

0

sin

t

E

2

= E

0

sin(

t+)

 = 2v - częstość kołowa fal,  - różnica faz między nimi.

 - zależy od położenia punktu P, a tym samym od kąta .

Załóżmy, że E

0

nie zależy od 

(szczeliny są dostatecznie wąskie, tak

że światło ugięte na każdej ze szczelin oświetla środkową część ekranu
równomiernie)

Wynika stąd, że wypadkowe pole elektryczne w punkcie P jest równe

E = E

1

+ E

2

Uwaga: Mówimy o polu E, a nie polu B (fali EM) ponieważ działanie
pola B na detektory światła (w tym oko ludzkie) jest znikome.

Równanie dla E powinno być wektorowe, ale w tych przypadkach
wektory E są do siebie równoległe, więc wystarczy równanie
algebraiczne.

Podstawiając równania dla obu fal obliczamy pole wypadkowe

E = E

0

sin(

t+) + E

0

sin

t = 2E

0

cos(

/2) sin(t+/2)

lub

E = E



sin(

t+)

gdzie

 = /2

oraz

E



= 2E

0

cos



Uwaga: Mówimy o polu E, a nie polu B (fali EM) ponieważ działanie
pola B na detektory światła (w tym oko ludzkie) jest znikome.

Równanie dla E powinno być wektorowe, ale w tych przypadkach
wektory E są do siebie równoległe, więc wystarczy równanie
algebraiczne.

Podstawiając równania dla obu fal obliczamy pole wypadkowe

E = E

0

sin(t+) + E

0

sint = 2E

0

cos(/2) sin(t+/2)

Lub

E = E



sin(t+)

gdzie

 = /2

oraz

E



= 2E

0

cos

Obliczamy natężenie fali wypadkowej

I



 E



2

Stosunek natężeń dwu fal: fali wypadkowej i fali pojedynczej

2

0

0















E

E

I

I











2

2

0

cos

cos

4

m

I

I

I





czyl
i

czyli

Natężenie zmienia się:

- od zera (dla punktów, w których  = 2 = )

- do maksymalnego (dla punktów, w których  = 2 = 0).

Różnica faz wiąże się z różnicą dróg S

1

b poprzez prostą relację

różnica faz/2π = różnica dróg/λ









sin

2

d



)

sin

(

2









d











sin

d



Stąd

lub

Poprzez to równanie mamy

zależność natężenia fali wypadkowej I



od kąta

.

6. Interferencja w cienkich warstwach

Barwy cienkich błonek, baniek mydlanych, plam np. oleju na wodzie są
wynikiem interferencji.
Na rysunku pokazana jest warstwa o grubości d i współczynniku
załamania n.

Jeżeli światło pada prawie prostopadle - geometryczna różnica dróg
pomiędzy obu promieniami wynosi prawie 2d.
Można więc oczekiwać, że maksimum interferencyjne (punkt A jasny)
wystąpi gdy odległość 2d będzie całkowitą wielokrotnością długości fali.

W źródle (fale
monochromatyczne, spójne)
istnieje taki punkt S, że dwa
promienie wychodzące z tego
punktu mogą dotrzeć do oka po
przejściu przez punkt A.
Promienie przebiegają różne
drogi: (1) odbija się od górnej,
(2) odbija się od dolnej
powierzchni błonki.

Czy punkt A będzie jasny czy
ciemny - zależy od wyniku
interferencji fal w punkcie A.

1

2

Okazuje się, że tak nie jest z dwu powodów.
(1)długość fali odnosi się do długości fali w błonce



n

a nie do jej długości w

powietrzu

. Oznacza to, że musimy rozważać drogi optyczne, a nie

geometryczne (zasada Fermata).

Przypomnijmy, że prędkość fali jest związana z częstotliwością (barwą) i

długością fali

v =

v

oraz, że

przy przejściu do innego ośrodka zmienia się prędkość i długość fali, a

częstotliwość pozostaje bez zmiany.

Ponieważ przy przejściu z powietrza do materiału o współczynniku

załamania n prędkość maleje n razy

v = c/n

to długość fali też maleje n razy



n

=

/n

(2) fala odbijając się od ośrodka optycznie gęstszego (większe n)

zmienia swoją fazę o

 (gdy odbicie zachodzi od powierzchni ośrodka

rzadszego optycznie fala odbija się bez zmiany fazy).

Oznacza to, że

promień odbity od górnej powierzchni błonki zmienia

fazę, a promień odbity od dolnej granicy nie.

Uwzględniając oba czynniki tj.

różnice dróg optycznych oraz zmiany faz

przy odbiciu

.

Dla dwóch promieni pokazanych na rysunku warunek na maksimum ma
postać

2d = m



n

+



n

/2,m = 0, 1, 2, ....,

Gdzie:



n

/2 - opisuje zmianę fazy przy odbiciu (od górnej powierzchni) bo

zmiana fazy o 180 (

) jest równoważna różnicy dróg równej połowie

długości fali (różnica faz/2p = różnica dróg/l).

Ponieważ



n

= /n

otrzymujemy więc













 



2

1

2

m

dn

Analogiczny warunek na minimum ma postać



m

dn

2

Równania te są słuszne jeżeli współczynnik załamania błonki jest
większy lub mniejszy od współczynnika załamania ośrodków po obu
stronach błonki.

m = 0, 1, 2,....(minimum)

m = 0, 1, 2,..... (maksima)