Budowa i drgania sieci 

Budowa i drgania sieci 

krystalicznej 

krystalicznej 

 

 

http://www.wtc.wat.edu.pl/dydaktyka/fizyka-wykRogalski/Wyklad15.pdf
http://pl.wikipedia.org/wiki/Sie%C4%87_krystaliczna

Rysunki zaczerpnięto ze stron internetowych:

 

 

Budowa ciał stałych

Ciała stałe cechują się stabilnością kształtu. Ciała stałe mogą mieć strukturę 

krystaliczną

 lub 

amorficzną (ciała bezpostaciowe)

. Ciała amorficzne są na 

ogół anizotropowe. Z pewnego punktu widzenia mogą być traktowane jako 
przechłodzone ciecze.

Ciała krystaliczne mogą stanowić pojedynczy monokryształ lub mieć budowę 
polikrystaliczną. W obrębie krystalitu występuje 

uporządkowanie dalekiego 

zasięgu

, tzn. okresowe przestrzenne uporządkowanie atomów, które tworzą 

sieć 

krystaliczną

.

Miejsca w sieci punktowej, zwane węzłami, są obsadzone przez atomy lub grupy 
atomów. Najmniejszą, powtarzająca się okresowo grupę nazywamy 

bazą

.

 

 

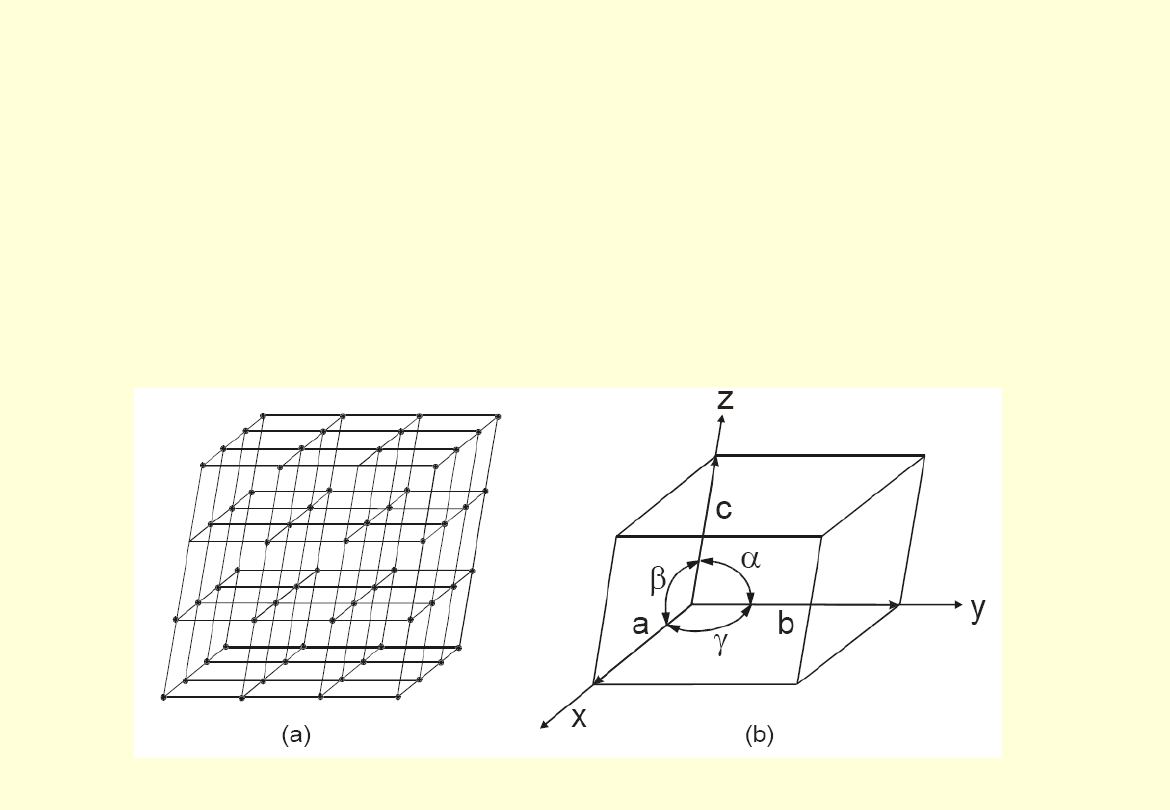
Budowa krystaliczna ciał stałych

• Sieć krystaliczna

 - sposób wypełnienia atomami przestrzeni tak, 

że pewna konfiguracja atomów zwana 

komórką elementarną

 jest 

wielokrotnie powtarzana. 

Elementarne wektory translacji: położenie dowolnego, powtarzającego 
się elementu sieci spełnia warunek: 

c

p

b

n

a

m

R















 

 

Komórkę elementarną charakteryzują: długości wektorów translacji (stałe sieci: a, 

b, c) oraz kąty między nimi. Położenia węzłów sieci przedstawia się w formie 
krotności stałych sieci.

Innymi ważnymi cechami sieci są:



właściwości symetrii



liczba atomów w pierwszej strefie koordynacyjnej i strefach dalszych



odległość między najbliższymi atomami 



liczba atomów w komórce elementarnej



współczynnik upakowania, tzn stosunek objętości atomów do objętości zajętej 
przez kryształ.

 

 

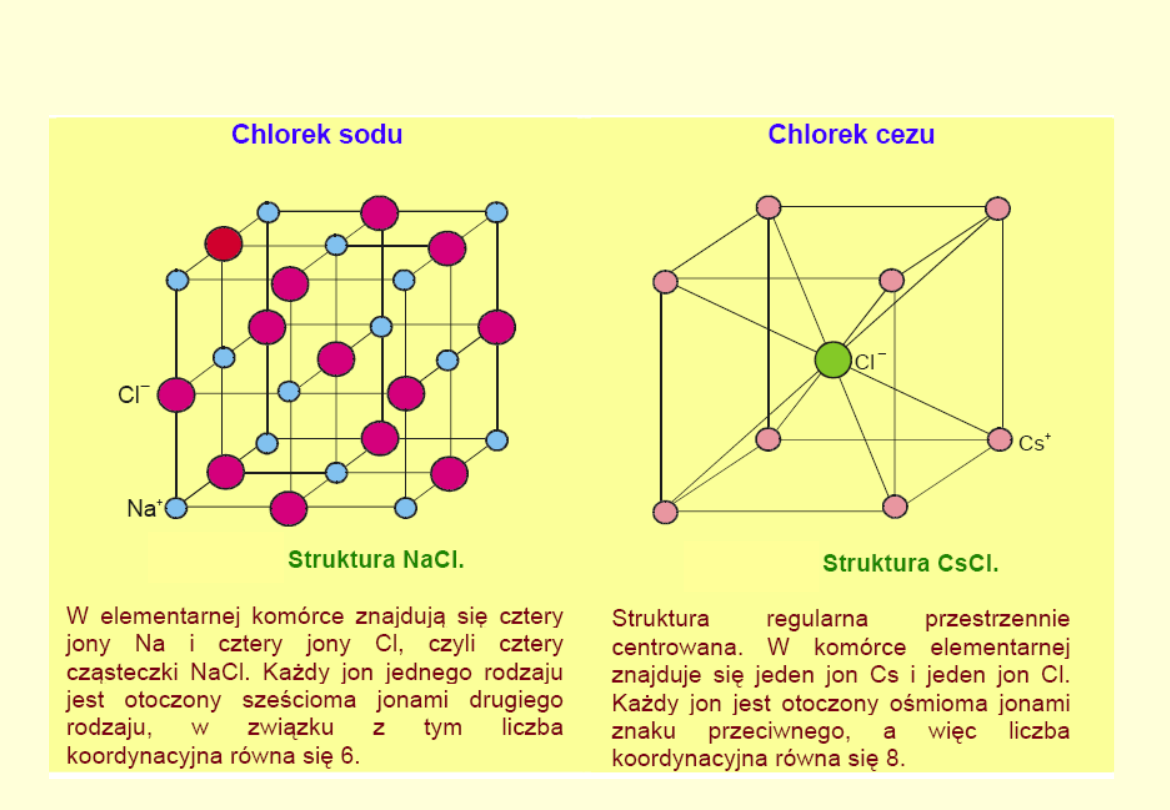
Przykłady sieci krystalicznych

 

 

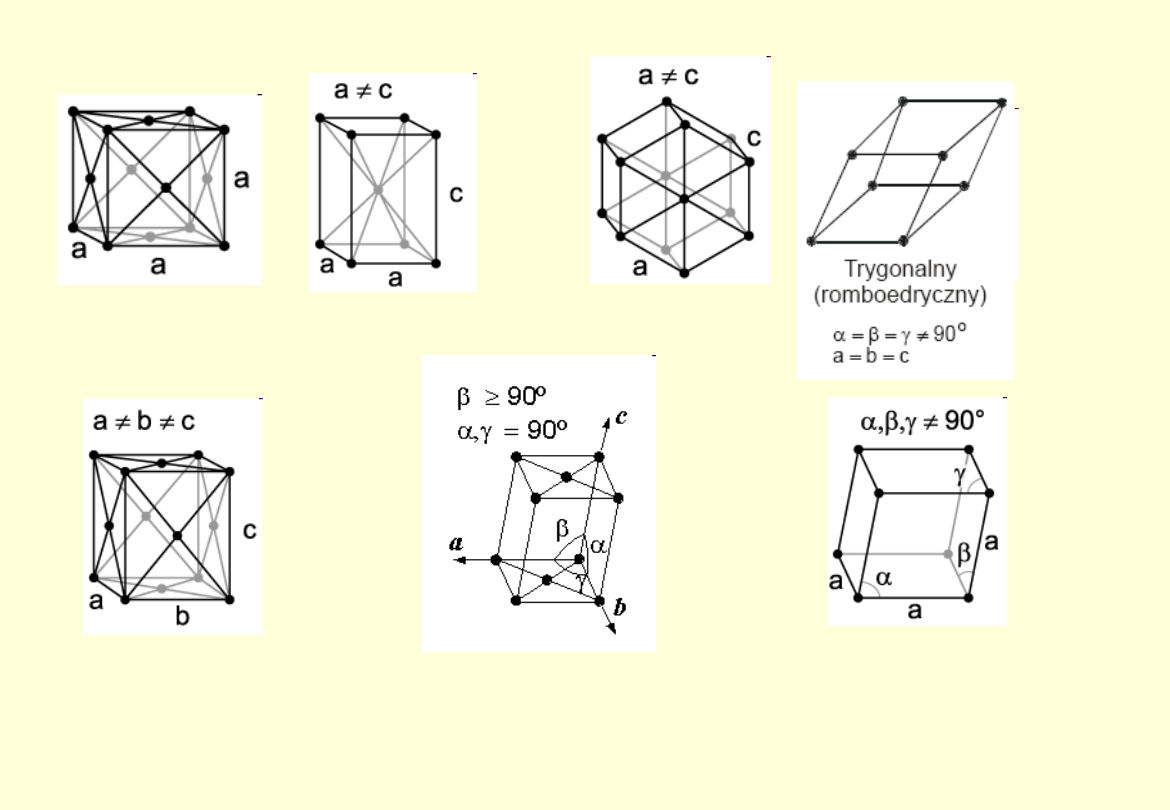
Komórki elementarne mogą być: P – prymitywne; C – centrowanie na 
podstawach; F – centrowanie na wszystkich ścianach; I – centrowanie 
przestrzenne. 

Sieć Bravais:

układ 
regularny

układ 
tetragonalny

układ 
heksagonalny

układ 
trygonalny
(romboedryczn
y)

a=b=c

układ rombowy

układ jednoskośny

układ trójskośny

Układy krystalograficzne (7 układów)

C

F

P

I

P,I,F

P,I

P,I,F, C

P,C

F

P

 

 

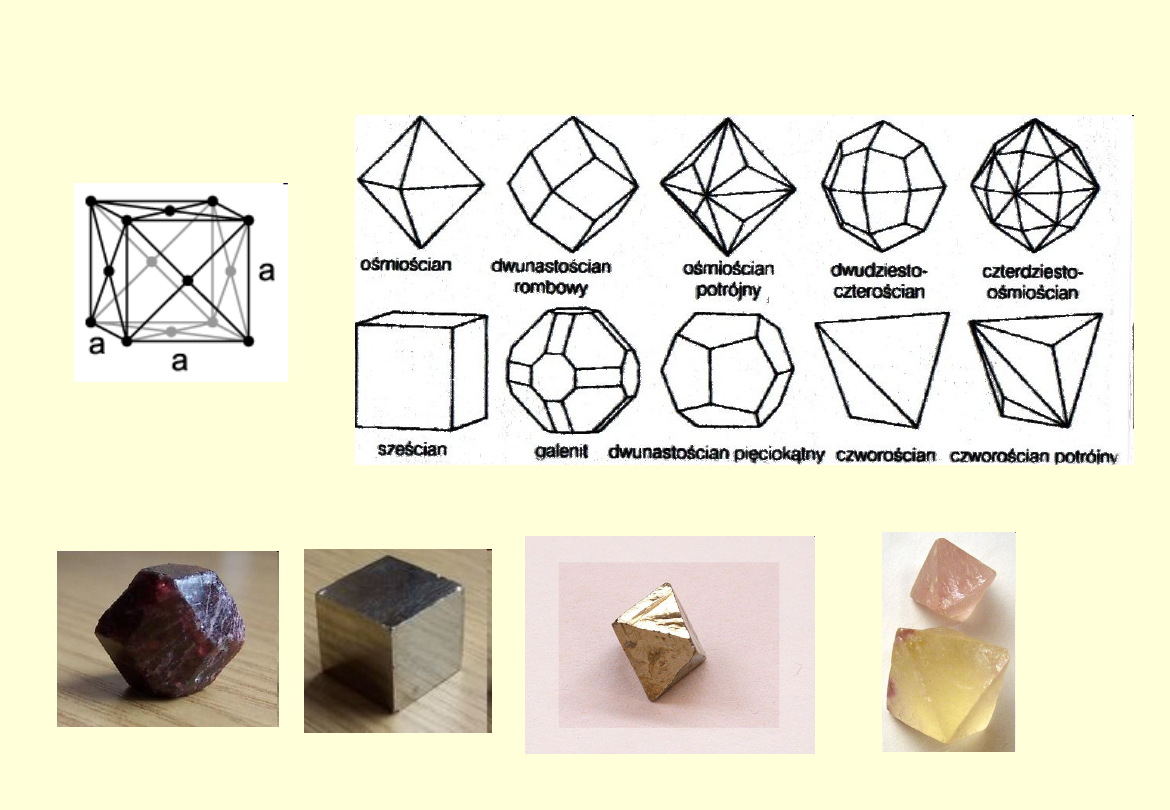
Układ regularny – przykłady 

komórek

 

 

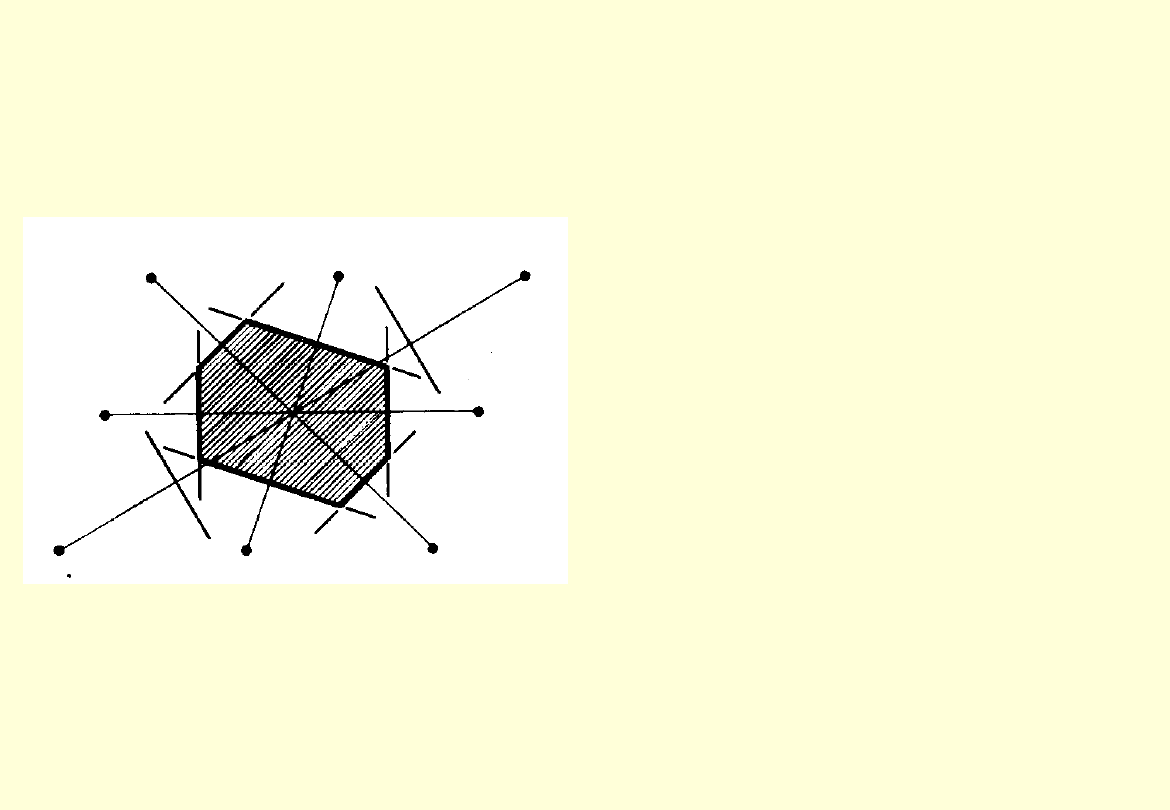
Komórka elementarna o najmniejszej objętości nazywana jest 

komórką 

Wignera-Seitza

. Konstruujemy ją następująco: 

Wybieramy dowolny węzeł sieci i łączymy go odcinkami z najbliższymi węzłami. 
Komórka Wignera- Seitza  jest to przestrzeń zawarta wewnątrz płaszczyzn 
normalnych wystawionych w punktach środkowych odcinków  łączących  
poszczególne węzły sieci.

Bardzo ważnymi cechami sieci są 

symetrie

: ze względu na 

obroty, 

odbicie względem płaszczyzny 

lub

 

inwersję punktową

.

Opis kierunków w sieci

Kierunek prostej identyfikuje się za pomocą trzech najmniejszych (co do 
wartości) liczb całkowitych, wyrażających proporcje między współrzędnymi 
(na osiach X, Y, Z) dowolnego wektora leżącego na prostej.

Wskaźniki kierunków zapisuje się w postaci: [h, k, l]

 

 

Płaszczyzny sieciowe, wskaźniki Millera

Płaszczyzną sieciową nazywamy każdą płaszczyznę w krysztale,  na której 
leżą co najmniej 3 węzły sieci nie leżące na jednej prostej.  Praktycznie na tak 
zdefiniowanej płaszczyźnie, w nieskończonym krysztale, leży  zawsze 
nieskończona ilość węzłów sieci. Płaszczyznę definiujemy przez podanie 
parametrów odpowiedniego równania płaszczyzny. Z elementarnej geometrii 
otrzymujemy następującą relację określającą położenia punktów sieci na 
płaszczyźnie.









 

z,

y

x

M

l

k

h

gdzie h, k, l są liczbami całkowitymi. Gdy M=1, otrzymujemy równanie 
płaszczyzny najbliższej początkowi układu współrzędnych. Łatwo sprawdzić, 
że: 

l

k

h

M

M

M

,

,

oznaczają współrzędne (w jednostkach stałych sieci) punktów przecięcia 
płaszczyzny z osiami X, Y, Z. 

 

 

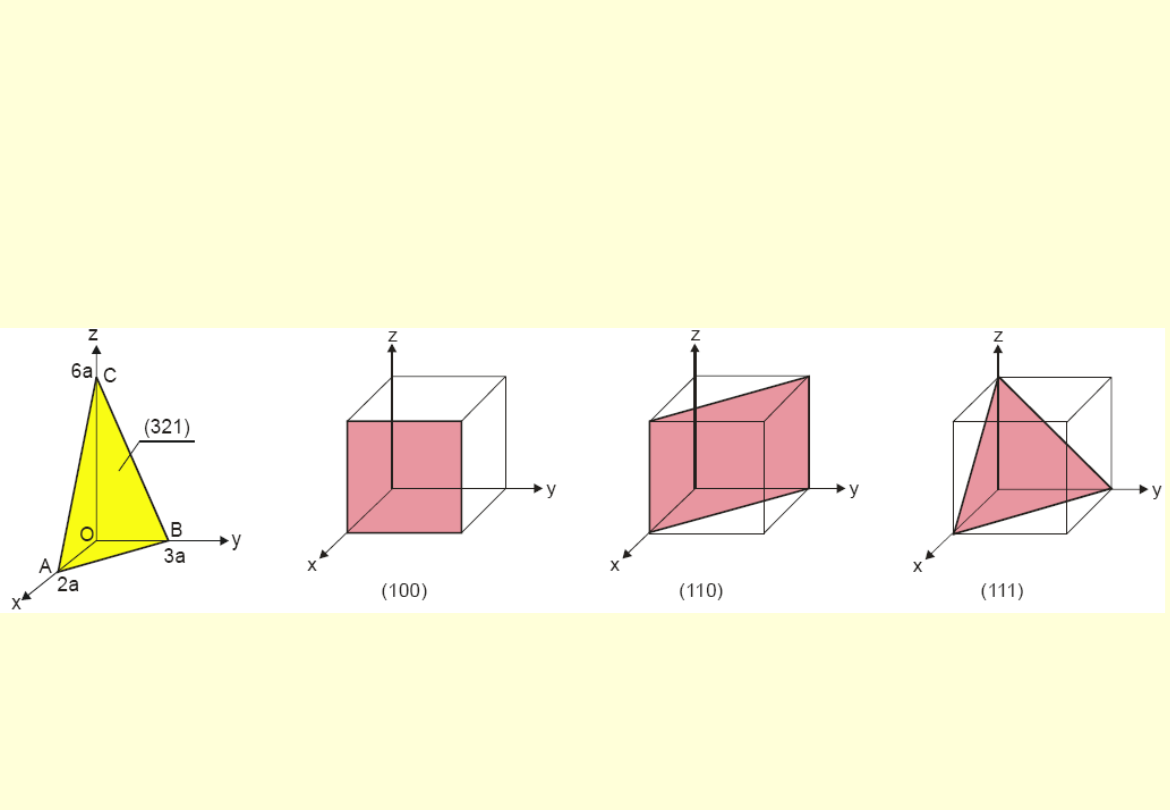
Skrótowo płaszczyznę oznacza się w postaci: (h, k, l). Tak np. (2, 1, 0) oznacza 
płaszczyznę równoległą do osi Z i przecinającą osie X, Y w punktach o 
współrzędnych ½, 1. Liczby h, k, l nazywa się wskaźnikami Millera.

 

 

Wektory sieci odwrotnej

Sieć odwrotna do sieci krystalicznej, cechującej się wektorami 
translacji                       jest to (wyobrażona) sieć, której 
wektory translacji mają postać: 

c

,

b

,

a







)

c

b

(

a

b

a

2π

C

)

c

b

(

a

a

c

2π

B

)

c

b

(

a

c

b

2π

A





























































,

,

Dowolny wektor sieci odwrotnej może być zapisany w postaci:

 

l,

2π

c

G

 

n,

2π

b

G

 

m,

2π

a

G

:

czym

przy

,

C

l

B

n

A

m

G

































Komórkę elementarną w sieci odwrotnej (komórkę Wignera-Seitza) nazywamy 
I strefą Brillouina. 

c

,

b

,

a







Przykład

  W sieci sześciennej prostej wektory              są wzajemnie 

prostopadłe i mają tę samą długość. Dlatego wektory sieci odwrotnej też są 
prostopadłe do siebie i ich długości są równe:

c

,

b

,

a







a

2π

a

a

2π

C

B

A

3

2









Wektory sieci odwrotnej mają więc w tym przypadku takie same kierunki, jak 
wektory 

c

,

b

,

a







 

 

Drgania sieci krystalicznej

Atomy sieci krystalicznej wykonują drgania wokół swych położeń równowagi. 

Amplituda drgań cieplnych zależy od temperatury i nie przekracza !0

-11

m. 

Drgania te wpływają na wiele zjawisk, np. 

• przewodnictwo cieplne, 
• przewodnictwo elektryczne, 
• rozszerzalność cieplną.

Przy małych amplitudach drgań można przyjąć, że oddziaływanie między 

atomami jest harmoniczne (tzn. siła jest proporcjonalna do wychylenia, a 
energia potencjalna proporcjonalna do kwadratu wychylenia. Układ 
drgających atomów możemy wówczas traktować jako układ oscylatorów 
harmonicznych.

Najniższa energia oscylatora kwantowego jest większa od zera, zatem nawet 

w temperaturze zera bezwzględnego występują drgania atomów (tzw. 

drgania zerowe

). 

Atomy są sprzężone ze sobą, zatem przemieszczenie jednego z nich 

wywołuje przemieszczenie atomów sąsiednich. Zaburzenie to rozchodzi się 
w krysztale w postaci 

fal sprężystych (lub inaczej sieciowych)

.

 

 

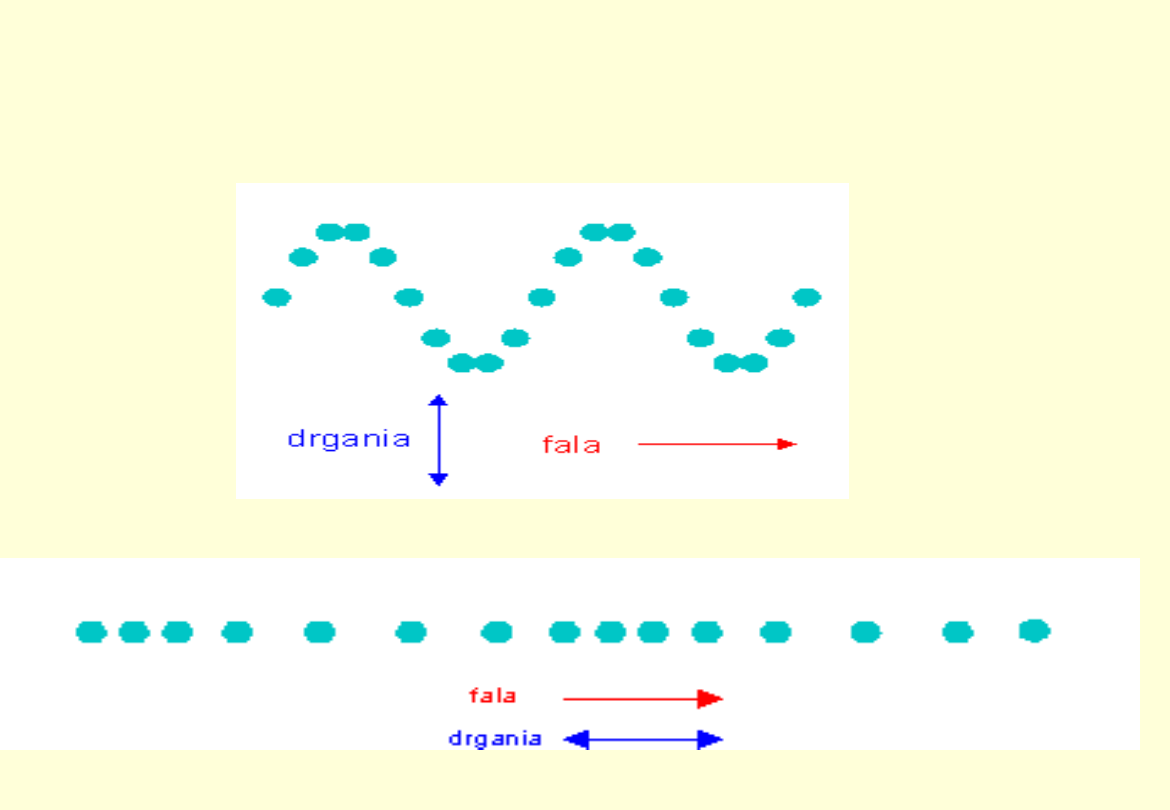
Wzdłuż jednego kierunku mogą rozchodzić się fale poprzeczne o dwóch 
niezależnych kierunkach drgań, a także fale podłużne.

 

 

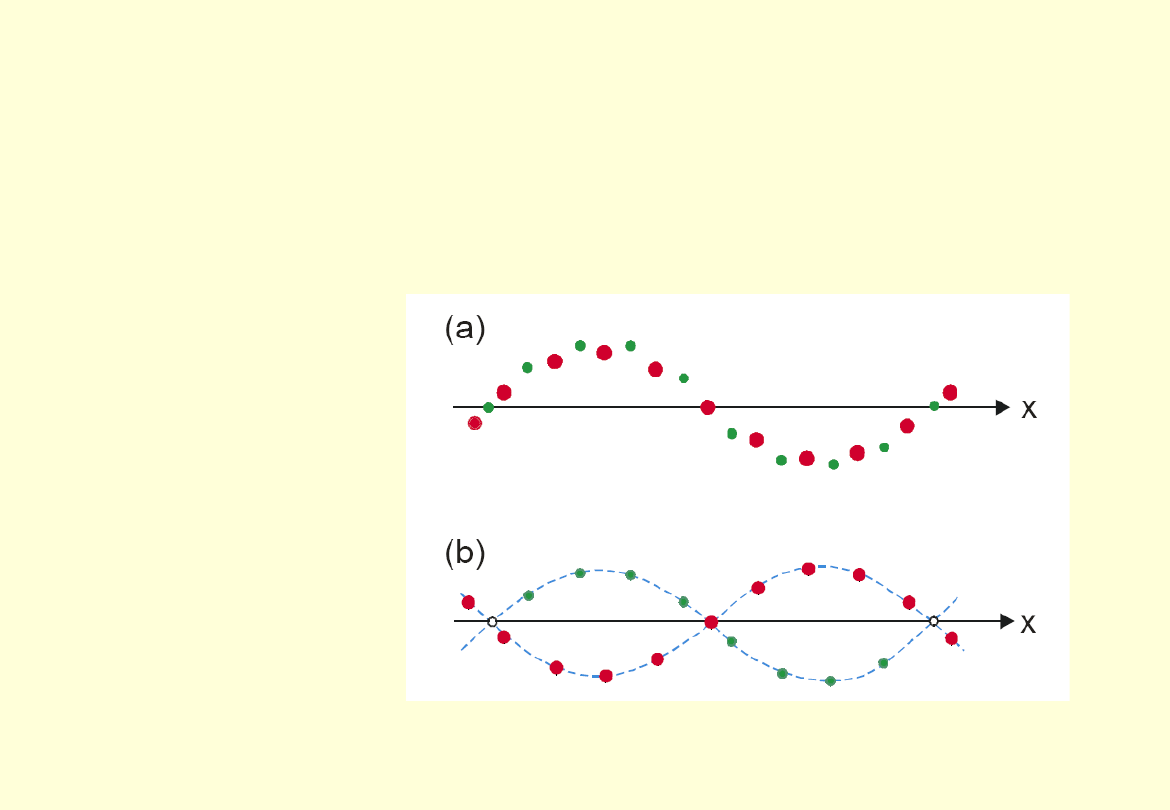
Jeżeli kryształ zbudowany jest z dwóch rodzajów atomów, to w łańcuchu 
atomów, ułożonych wzdłuż wybranego kierunku w sieci, mogą rozchodzić 
się fale w postaci:

• drgań akustycznych 

(mniejsze częstości)

• drgań optycznych 

(większe częstości)

 

 

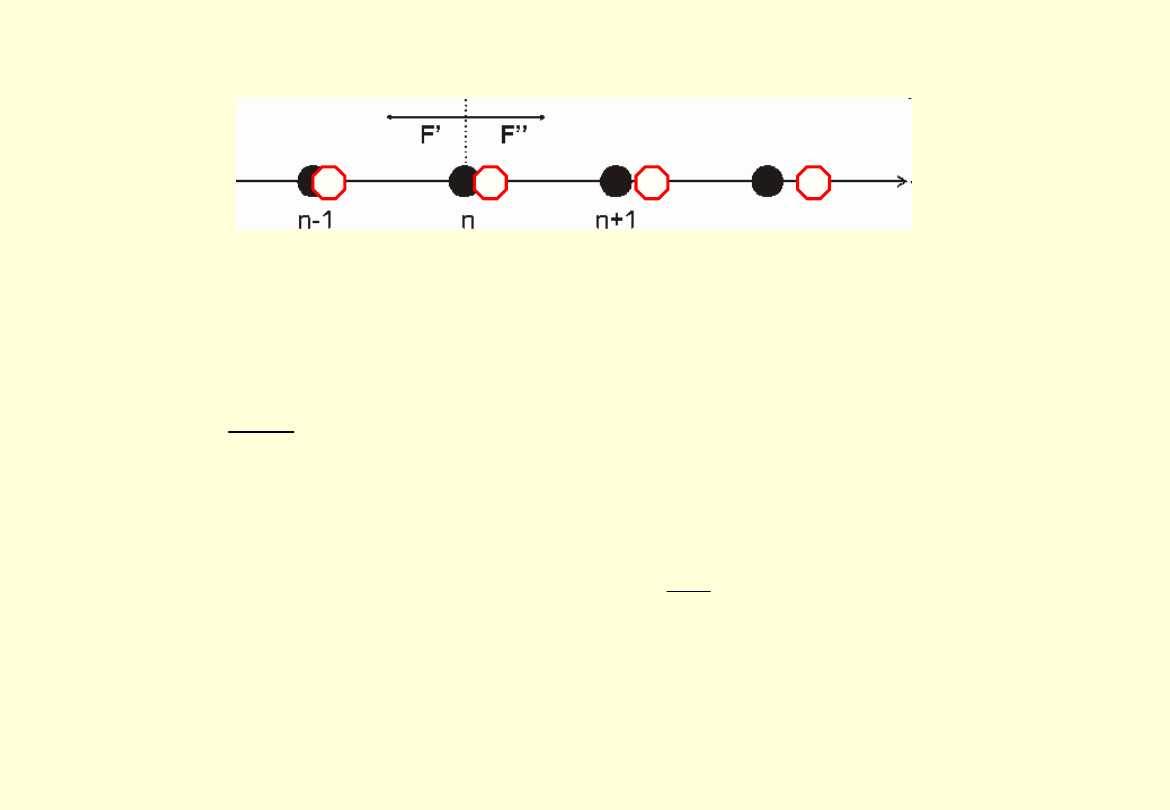
Podobne rozróżnienie można zrobić w przypadku drgań podłużnych. Rozważmy 
jednowymiarowy łańcuch jednakowych atomów znajdujących się (w stanie równowagi) 
w odległości a od siebie 

Zapiszmy równanie ruchu dla n-tego atomu. Jeśli siła jest proporcjonalna do 
względnego przemieszczenia atomów (w stosunku do położeń równowagi), to 
siła wypadkowa:

)

u

2u

b(u

dt

u

d

m

)

u

2u

b(u

)

u

(u

)

u

b(u

F'

F"

F

1

n

n

1

n

2

n

2

1

n

n

1

n

1

n

n

n

1

n





































Rozwiązanie ma postać:

ν

2π

ω

,

λ

2π

k

ωt)],

exp[i(nka

u

u

0

n









gdzie 

na

 oznacza odległość od początku łańcucha, k jest długością wektora 

falowego, a ω – częstością (in. pulsacją).

 

 

podstawiając to rozwiązanie do równania ruchu otrzymujemy:

2

ka

sin

m

b

2

ω

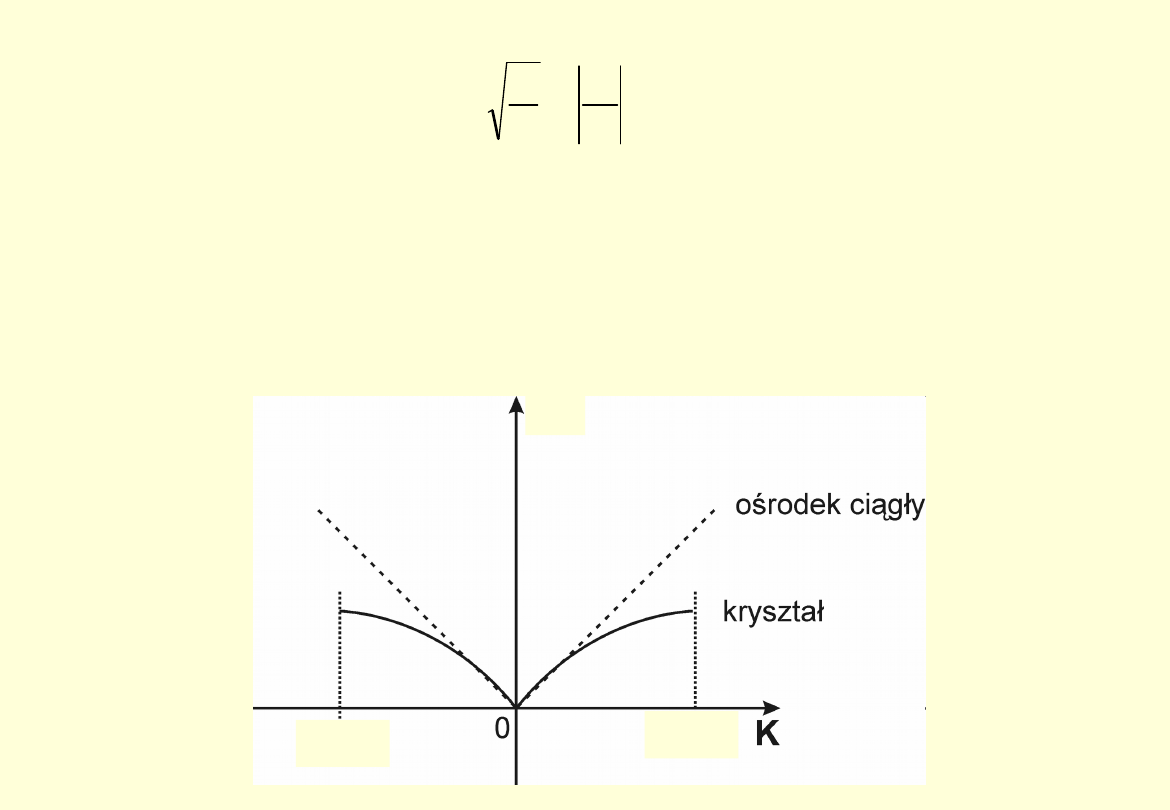
Jest to tzw. 

zależność dyspersyjna 

(zależność ω(k)). Przedstawia funkcję 

okresową o okresie 2π/a, który odpowiada komórce elementarnej w sieci 
odwrotnej. Można więc ograniczyć przedział zmienności argumentu do I strefy 
Brillouina, tzn przedziału (- π/a, π/a).

Wykres pokazuje, że w pobliżu granicy strefy Brillouina wykres zależności 
dyspersyjnej kryształu znacząco różni się od linii prostych, które cechowałyby 
ośrodek ciągły.

ω

-π/a

π/a

 

 

Prędkość fazowa drgań cieplnych zależy więc od długości fali

a

m

b

v

:

k

małych

dla

,

k

2

ka

sin

m

b

2

k

ω

v

f

f







W tym wypadku fale drgań cieplnych pokrywają się ze znanymi z fizyki ogólnej 
falami sprężystymi, a prędkość fazowa pokrywa się z prędkością dźwięku. 
Pomiar prędkości dźwięku w krysztale umożliwia określenie stałęj siłowej b.

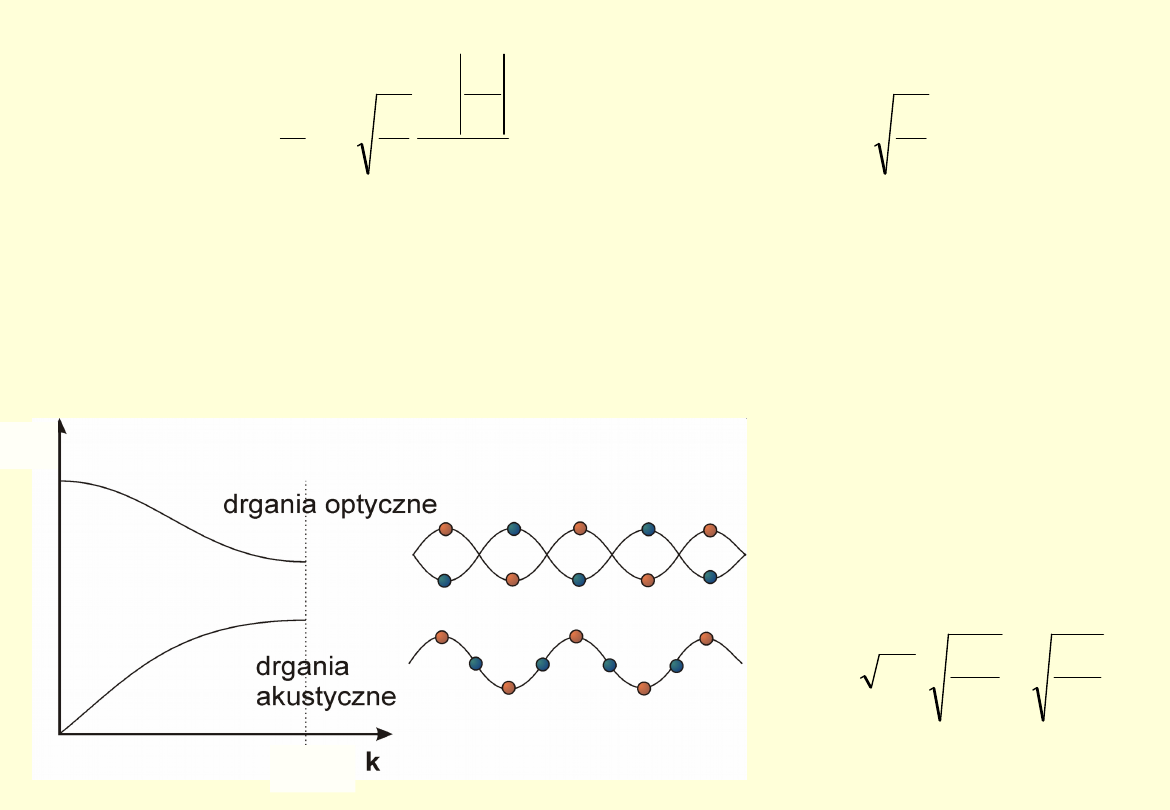
W przypadku sieci złożonej z dwóch rodzajów atomów dostajemy dwa rodzaje 
rozwiązań, odpowiadające falom akustycznym i optycznym.

π/a

ω

Zakresy częstości nie 
zachodzą na siebie. 
Istnieje przerwa, której 
nie da się wyjaśnić na 
gruncie teorii 
makroskopowej.

)

m

1

m

1

(

2b

Δω

B

A





 

 

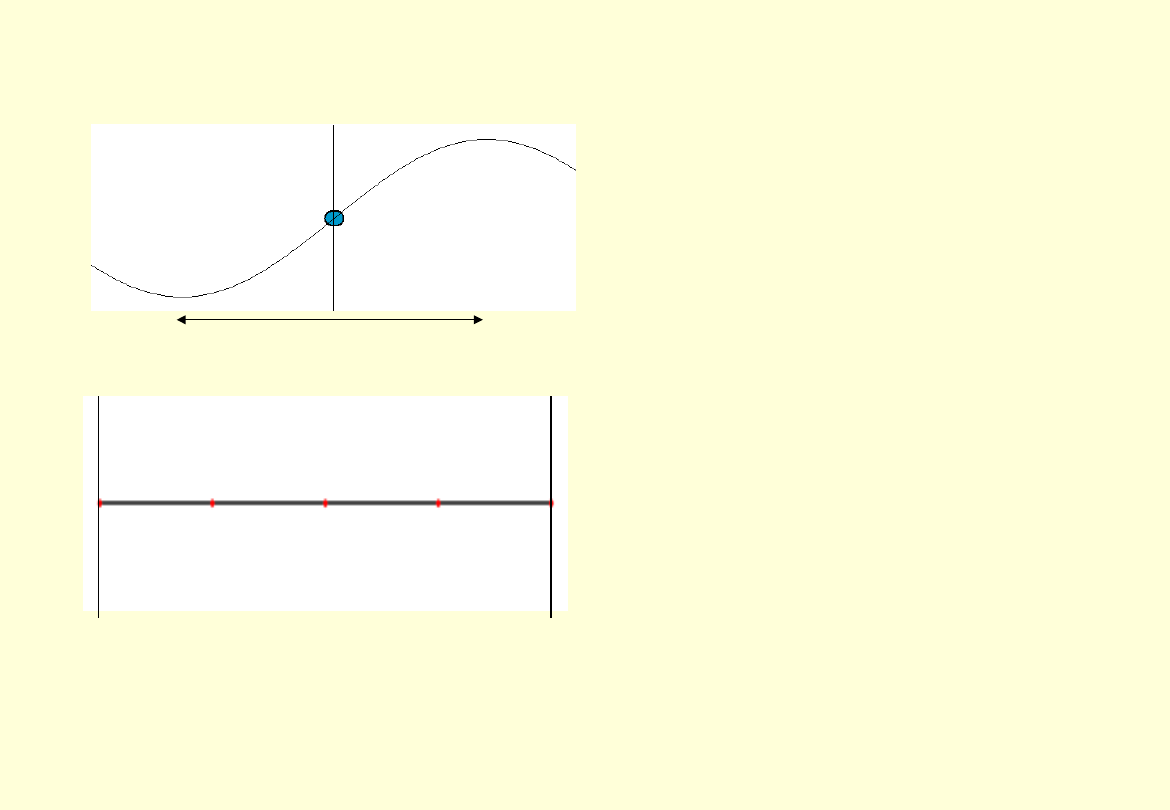
Fale biegnące i stojące

λ / 2

Fala stojąca — „fala”, której pozycja 
w przestrzeni pozostaje niezmienna 
(powstaje np. w ośrodku 
ograniczonym poprzez interferencję 
dwóch fal poruszających się w 
przeciwnych kierunkach.

Fala stojąca to w istocie drgania 
ośrodka nazywane też drganiami 
normalnymi. Miejsca gdzie amplituda 
fali osiąga maksima nazywane są 
strzałkami, zaś te, w których 
amplituda jest zawsze zerowa 
węzłami fali stojącej. 

W

W

S

S

W

Fala biegnąca może 

rozchodzić się w ośrodku 

nieskończonym

 

 

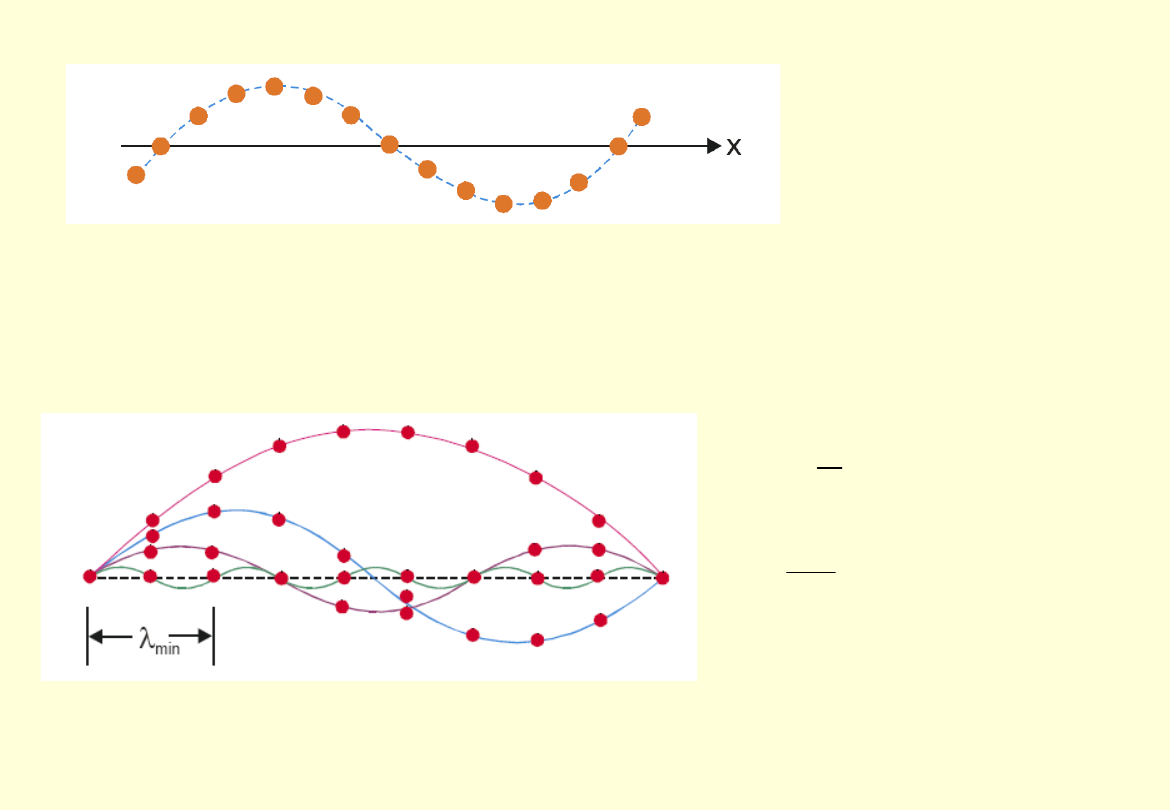
Rozważmy poprzeczną falę biegnącą w sieci złożonej z atomów jednego 
rodzaju.

W ośrodku ograniczonym fala odbija się od granicy ośrodka i interferuje z falą 
pierwotną – powstaje 

fala stojąca

 (są to tzw. drgania normalne, in. mody). 

Długość fali jest związana z rozmiarem dostępnej przestrzeni L (np. grubością 
warstwy materiału lub rozmiarem kryształu). Największa długość spełnia 
warunek: 

λ

max

=2L, 

w każdym innym przypadku: 

n

2L

λ

3...

2,

1,

n

,

2

λ

n

L







Najmniejsza długość fali spełnia warunek: 

λ

min

=2a (sąsiednie atomy 

stanowią węzły – lub strzałki - fali stojącej).