1

Algorytmy genetyczne

i ich zastosowanie

2

1.

Problem optymalizacji globalnej

2.

Algorytmy genetyczne

3.

Przykład zastosowanie AG w interpretacji danych
pomiarowych

4.

Podsumowanie i literatura o AG

3

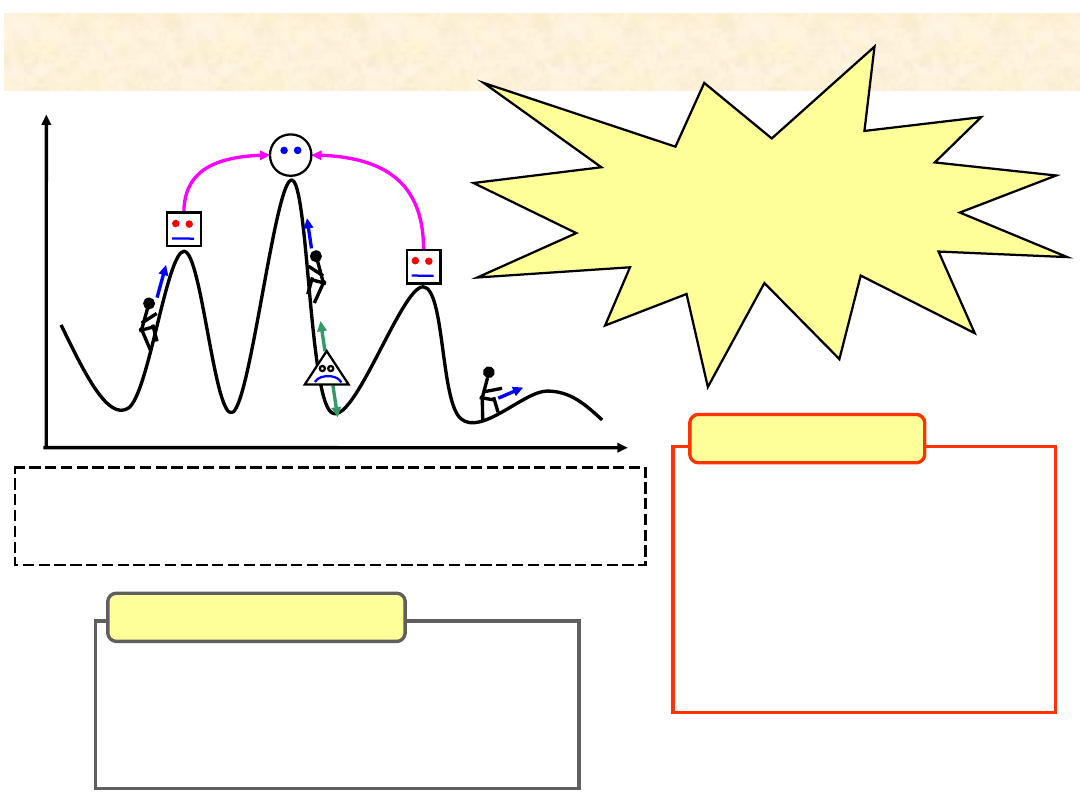
1. Problem optymalizacji globalnej

– analityczne

– numeryczne (np. gradientowe)

– enumeracyjne

Metody klasyczne

Jak znaleźć

globalne maksimum

(globalne minimum)

– błądzenie przypadkowe

– symulowane wyżarzanie

– sieci neuronowe

– logika rozmyta

– algorytmy genetyczne

Nowe metody

f(x)

x

maksimum globalne

maksimum
lokalne

?

Np.: wieloparametrowe dopasowanie
krzywych teoretycznych do
punktów eksperymentalnych  parametry modelu

4

2. Wiadomości podstawowe o AG

AG

=

Poszukiwanie maksymalnej wartości funkcji

przystosowania oparte na mechanizmach doboru

naturalnego oraz dziedziczności łączące ewolucyjną

zasadę przeżycia najlepiej przystosowanych

z systematyczną i po części losową wymianą

informacji

.

5

1957-62: Barricelli, Fraser, Martin, Cockerham

– modelowanie procesów genetycznych

1960: Holland (Uniw. Michigan) – systemy
adaptacyjne  AG
1967: Bagley – program gry w 6 pionków
1971: Hollstien; 1975: De Jong – optymalizacja
funkcji
1985: Goldberg – optymalizacja pracy gazociągu

Historia algorytmów genetycznych

6

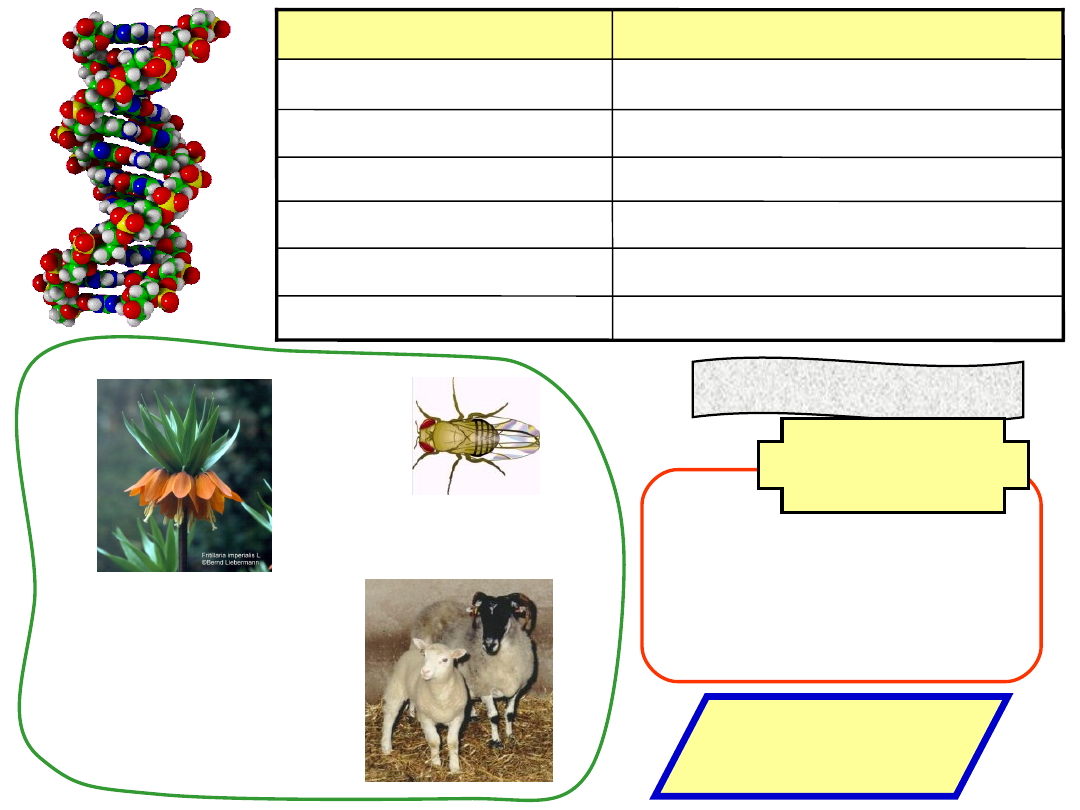
Podstawowe pojęcia w algorytmach genetycznych

W genetyce za pojedyncze cechy osobnika odpowiada gen,

mający wiele możliwych postaci zwanych allelami.

Gen identyfikujemy podając jego miejsce w chromosomie (locus)

oraz jego funkcję. Mówimy przykładowo, ze gen określający kolor

oczu, ma pozycję 10 i allel odpowiadajacy kolorowi niebieskiemu.

W algorytmach genetycznych interesujące nas cechy

badanego układu są zakodowane w ciągi kodowe.Cechy mogą być

umiejscowione na różnych pozycjach ciągu kodowego.

W genetyce genotyp – postać genów, fenotyp – zespól cech

osobnika o danym genotypie.

W algorytmach genetycznych genotypowi odpowiada

struktura kodu, a fenotypowi zbiór parametrów, rozwiązanie albo

punkt w przestrzeni rozwiązań.

7

wymiana ciągów bitów

krzyżowanie

negacja bitów

mutacja

zbiór punktów

populacja

punkt w przestrzeni rozwiązań

osobnik

ciąg bitów

chromosom

bit

gen

komputer (AG)

biologia (genetyka)

DNA

00101010101011100

liczby
tekst

(ASCII, tex, doc)

grafika

(bmp, gif, jpeg)

dźwięk

(wav, midi, mp3)

wideo

(avi, mpeg)

kod binarny

Operowanie

na kodzie!

8

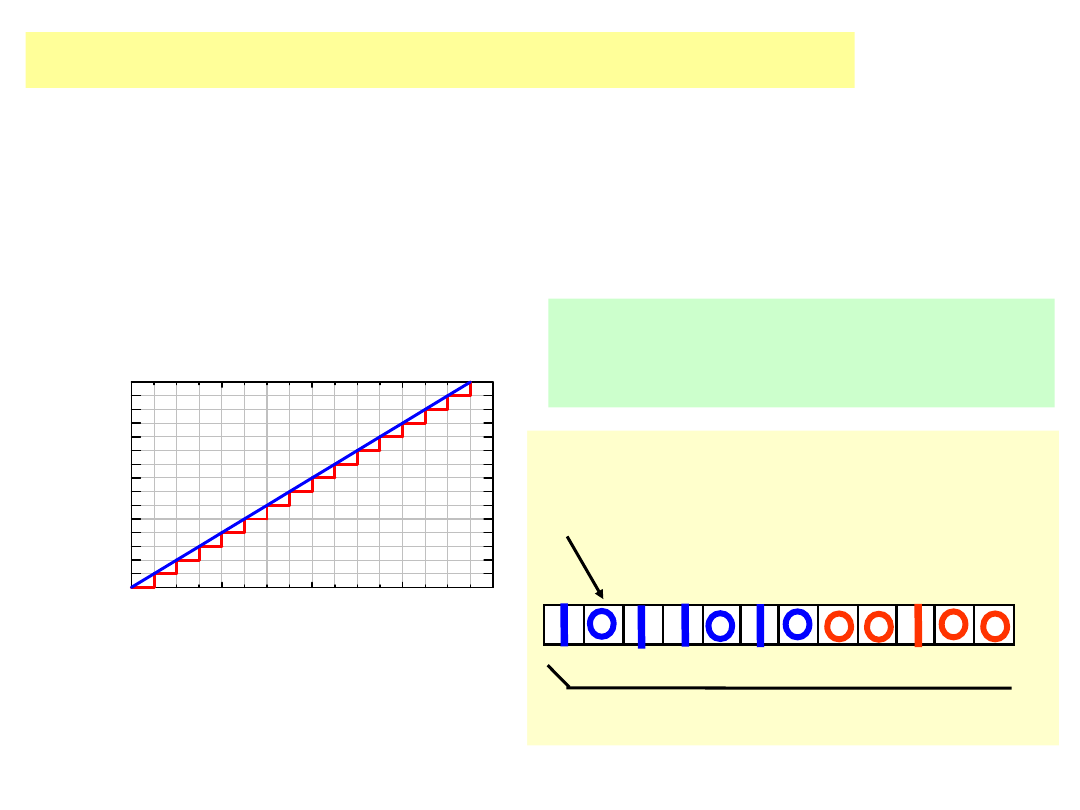
Kodowanie liniowe za pomocą

n

bitów x



[a, b]:



podział [a, b] na

2

n

podprzedziałów



wartości z

k

-tego podprzedziału 

k-1

w postaci binarnej

Kodowanie logarytmiczne x
= kodowanie liniowe log|x|

gen

chromosom

Kodowanie wielu zmiennych

 sklejanie łańcuchów

zmienna 1

zmienna 2

zmienna rzeczywista x

0,00

0,25

0,50

0,75

1,00

k

o

d

b

in

a

rn

y

0

1

10

11

100

101

110

111

1000

1001

1010

1011

1100

1101

1110

1111

Kodowanie binarne liczb rzeczywistych

9

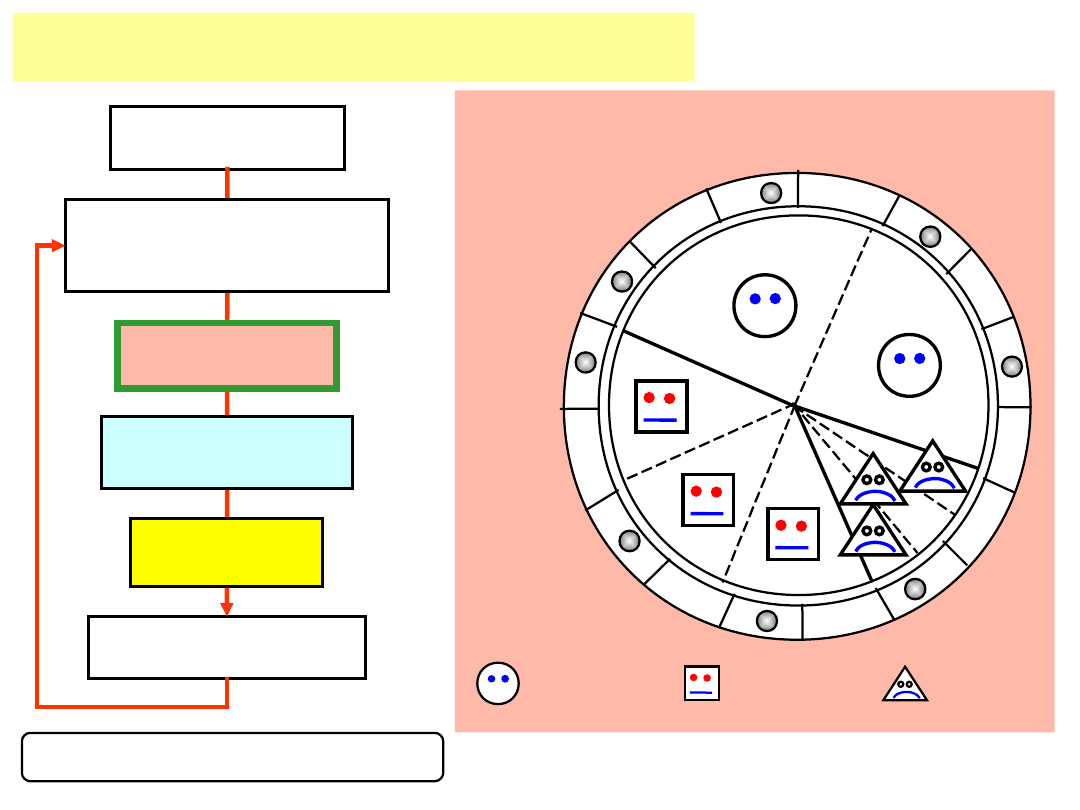
Metoda ruletki – prawdopodobieństwo
wyboru osobnika proporcjonalne do
wartości

FP

1. pokolenie

nowe pokolenie

obliczenie

FP

dla

każdego osobnika

mutacja

krzyżowanie

selekcja

FP

= funkcja przystosowania

2  4

3  3

3  1

Operatory genetyczne: selekcja

10

1. pokolenie

nowe pokolenie

obliczenie

FP

dla

każdego osobnika

mutacja

krzyżowanie

selekcja

FP

= funkcja przystosowania

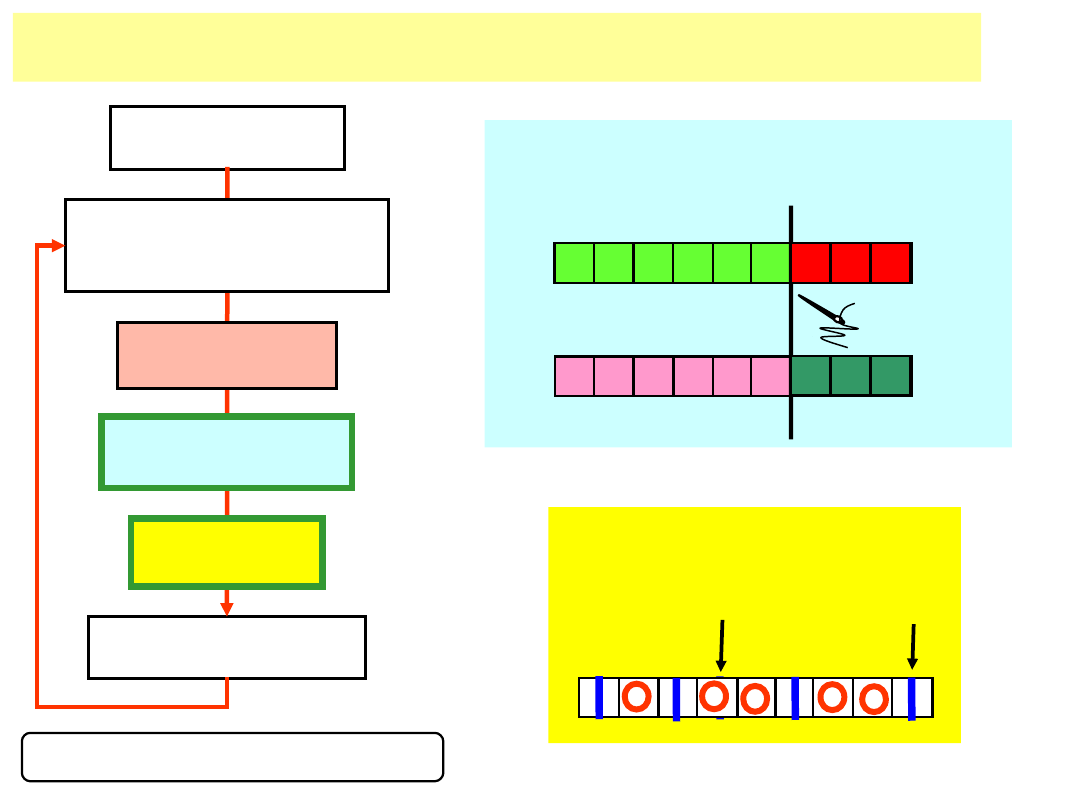
mutacja

negacja bitów z małym

prawdopodobieństwem

krzyżowanie jednopunktowe

wymiana fragmentów chromosomów

rodzice



dzieci

Operatory genetyczne: krzyżowanie i mutacja

11

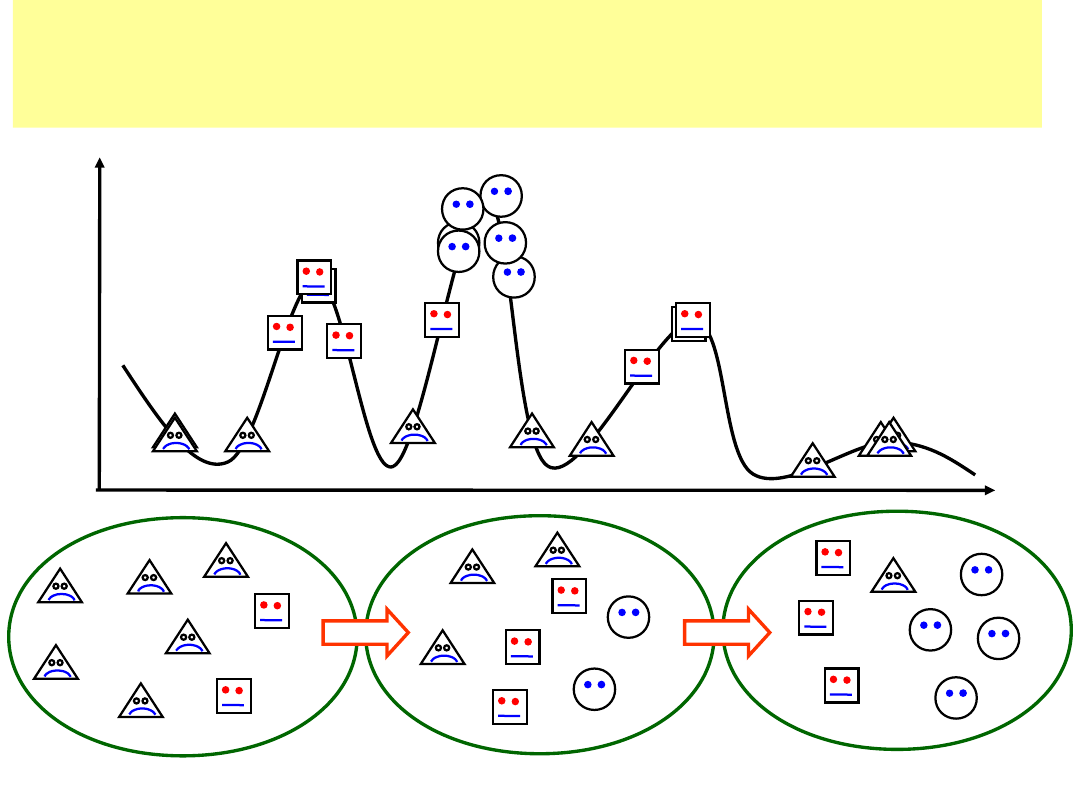
FP

maksimum globalne

1. pokolenie

2. pokolenie

itd.

Ewolucja – dążenie do optymalnego rozwiązania

12

Schematy w algorytmach genetycznych

Schematem S nazywamy zbiór chromosomów jednoznacznie

zdefiniowany przez wzorzec podobieństwa , określający cechy

wspólne tego zbioru. W przypadku kodowania binarnego wzorzec

podobieństwa określa się przy pomocy trzech symboli { 0,1, #}, przy

czym symbol # oznacza dowolną z dwóch wartości 0 lub 1.

Do schematu S należą chromosomy o wartościach

identycznych jak we wzorcu na pozycjach na których nie występuje

symbol #. Przykładowo wzorcowi 01##10 odpowiadają chromosomy

010010, 010110, 011010, 011110.

P

S

13

Schematy w algorytmach genetycznych

Rzędem schematu o(S) jest liczba symboli

różnych od #

we wzorcu .

Przykładowo dla schematu 0#101100# o(S)=7.

Długością definiującą schematu

( rozpiętością schematu)

dS)jest odległość pomiedzy skrajnymi pozycjami

schematu różnymi od #.

Przykładowo dla schematu 0#101100# S)= 8-

1=7.

W niektórych publikacjach rozpiętość jest

definiowana jako odle-

głosć skrajnych określonych pozycji +1, co

odpowiada liczeniu lewej skrajnej pozycji od 0 a nie

od 1.

P

S

14

Schematy w algorytmach genetycznych

Funkcją przystosowania (x) nazywamy odwzorowanie

kodu x osobnika w wartość mówiąca o jego przystosowaniu do

środowiska.

Jeżeli szukamy wartości maksymalnej funkcji wielu

zmiennych to funkcja przystosowania jest tożsama z funkcją,

której ekstremum poszukujemy.

Wartością przystosowania schematu (S) jest średnia

wartość funkcji przystosowania wszystkich chromosomów

należących do danego schematu.

(S) = (x)

1

n 

x∈S

15

Twierdzenie o schematach

Założenia:

1. osobniki nalezą do nieskończenie dużej populacji.

2. w populacji tej znajdują się osobniki o chromosomach

należących do wszystkich schematów.

3. selekcja jest proporcjonalna do wartości funkcji

przystosowania.

4. kodowanie binarne, krzyżowanie jednopunktowe, mutacja

bitowa o bardzo małym prawdopodobieństwie.

16

Twierdzenie o schematach

Teza:

Wartość oczekiwana liczby chromosomów należących do

danego schematu w kolejnej genaracji jest

szacowana zgodnie ze wzorem:

gdzie: liczebnosć osobników nalezących do schematu S w

populacji t+1, prawdopodobieństwo krzyżowania, długość

chromosomu.

E

∣

S

∣



P

t1

≥

∣

S

P

t

∣

S



S

1−p

c

dS

n−1

−oS p

m



E

∣

S

∣



P

t1

p

c

∣S∣

17

Metody selekcji

Selekcja następuje

1. na etapie reprodukcji czyli wyboru rodziców z populacji bazowej

P do operacji genetycznych ,w wyniku których powstaje

populacja tymczasowa T, dająca w rezultacie kolejnych operacji

genetycznych populację potomną O.

2. na etapie sukcesji czyli tworzenia nowej populacji w oparciu

o starą populację P i populację potomną O.

Jeżeli do nowej populacji wchodzą tylko osobniki z O to nie

zawsze przejdą do następnej populacji najlepsze osobniki ze starej

populacji bazowej. Wady tej nie ma selekcja elitarna , w której do

następnego populacji bazowej przechodzą najlepsze osobniki ze

starej populacji bazowej oraz z polulacji O.

18

Reprodukcja proporcjonalna (metoda ruletki)

Prawdopodobieństwo wylosowania osobnika do reprodukcji jest

wprost proporcjonalne do wartości jego funkcji przystosowania.

Przykład. Mamy 4 osobniki odpowiednio o wartościach funkcji

przystosowania f1=15 , f2=45 , f3=6, f4=55.

Sumujemy wartości funkcji przystosowania fs=15+45+6+55=121.

Do reprodukcji losujemy osobniki odpowiednio z

prawdopodobieństwem p1=15/121, p2=45/121, p3=6/121,

p4=55/121.

19

Reprodukcja rangowa

Każdemu osobnikowi w populacji bazowej nadaje się numer

rangę równą jego miejscu w uporządkowanej względem malejącej

wartości funkcji przystosowania populacji.( osobnik najlepszy ma

rangę 1).

Następnie definiuje się zmienną losową przypisując każdemu

osobnikowi prawdopodobieństworeprodukcji na podstawie

jego rangi. Funkcja ta musi byc nierosnąca wzgledem rangi.

Przykładowa funkcja:

gdzie:

a oraz k wybieramy aby

p

r

 X =ak1−

r X 

r

max



r

max

= max

X ∈P

t

rX



i=1



p

r

X=1,

0≤ p

r

X ≤1,

20

Reprodukcja turniejowa

Wybieramy z jednakowym prawdopodobieństwem q

osobników z populacji bazowej. Nastepnie z tak utworzonej

populacji Q wybieramy najlepszego osobnika do populacji

tymaczasowej T. Proces powtarzamy aż do zapełnienia populacji T.

Losowanie do populacji Q mozemy prowadzić ze

zwracaniem oraz bez zwracania.

21

Sukcesja z całkowitym zastępowaniem

Jest to najczęściej stosowanym sposobem tworzenia kolejnej

populacji bazowej. Staje się nią cała populacja potomna.

Sukcesja tan nie wprowadza mechanizmu nacisku

selektywnego.

22

Sukcesja z częściowym zastępowaniem

W najprostszym wariancie przyjmuje się współczynnik

wymiany owa populacja bazowa składa się z  osobników

z populacji potomnej oraz z (1- osobników ze starej populacji

bazowej. Część osobników ze starej populacji bazowej usuwamy

korzystając z jednej z poniższych metod;

- usuwamy najgprzej przystosowane osobniki,

- usuwamy osobniki najbardziej podobne do potomnych, należy

wprowadzić miarę podobieństwa osobników.

- usuwamy losowo wybrane osobniki.

23

Sukcesja elitarna

Polega na tym, że częsć osobników ze starej populacji

bazowej przechodzi do nawej populacji, w taki sposób, aby

zagwarantować przeżycie co najmniej najlepszego osobnika.

Najpierw sortuje się populację bazową i wybiera 

najlepszych osobników tworząc populację . W drugim kroku

tworzy się nastepną populację bazową wybierając  najlepszych

osobników z sumy populacji potomnej i populacji .

P



t

T

t

P

t

P

t1

P



t

24

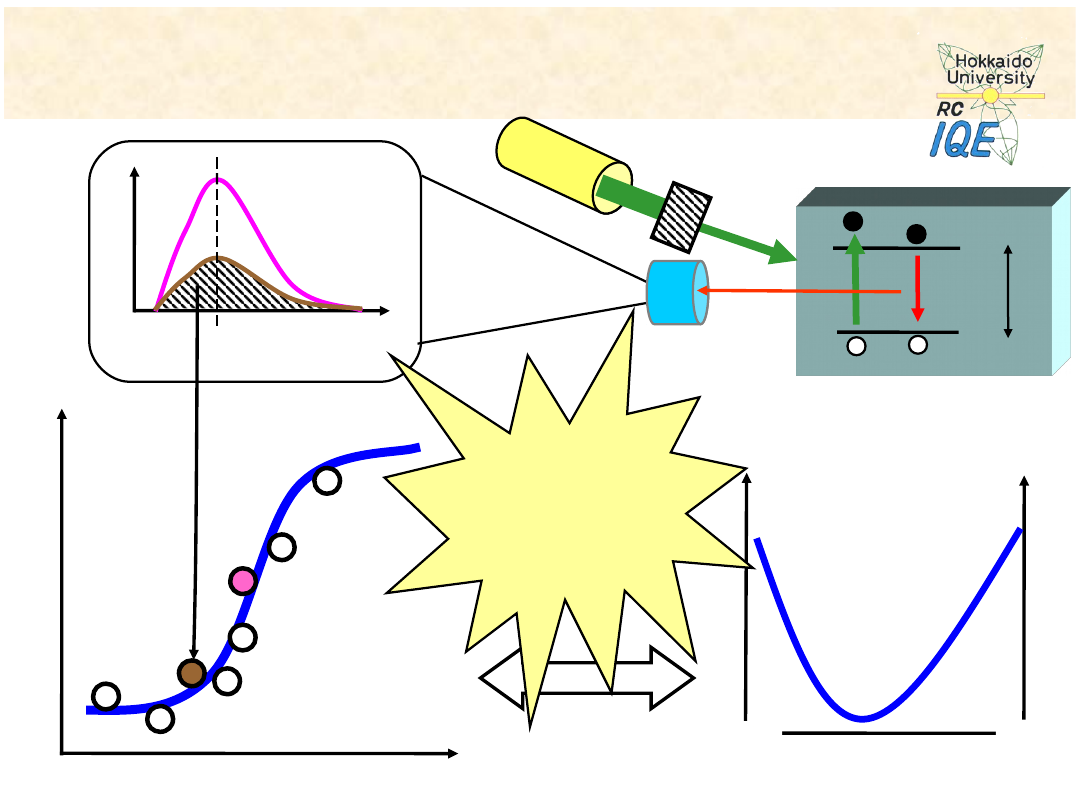
3. Zastosowanie AG w dopasowaniu…

na przykładzie metody PLS

3

próbka
temp. pokojowa

E

C

E

V

E

g

fotodetektor



laser

filtr

Y

PL

=

I

PL

/



natężenie światła wzbudzającego



w

y

d

a

jn

o

ś

ć

k

w

a

n

to

w

a

P

L

N

SS

(E)

eV

-1

cm

-2

E

C

E

V

energia, eV

Analiza

ilościowa

!

E

PL

E

g



1

>



2

25

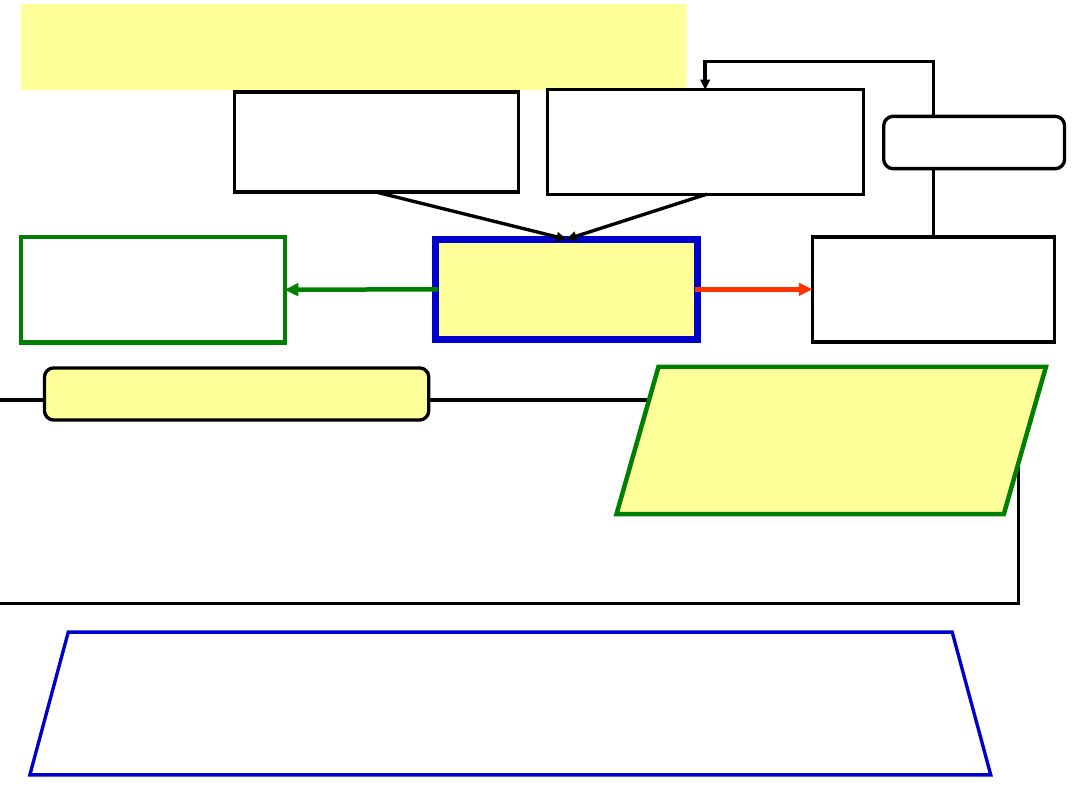
Schemat analizy danych w PLS

3

Procedura

dopasowująca

Dane

eksperymentalne

Zależność

teoretyczna Y

PL

()

5 parametrów

N

SS

(E)

Wyznaczenie

N

SS

(E)

dobrze

źle

1. dobór

procedury dopasowującej

2. definicja

błędu dopasowania

:

 pomiary w jednostkach względnych

 jednoczesna analiza wielu zależności eksperymentalnych

2 kluczowe problemy

Ad 1. Wybór algorytmu genetycznego:

 metoda bezgradientowa (szybkość obliczeń)

 brak wstępnych danych o N

SS

(E)

Symulator

Dopasowanie

=

= minimalizacja

błędu dopasowania

26

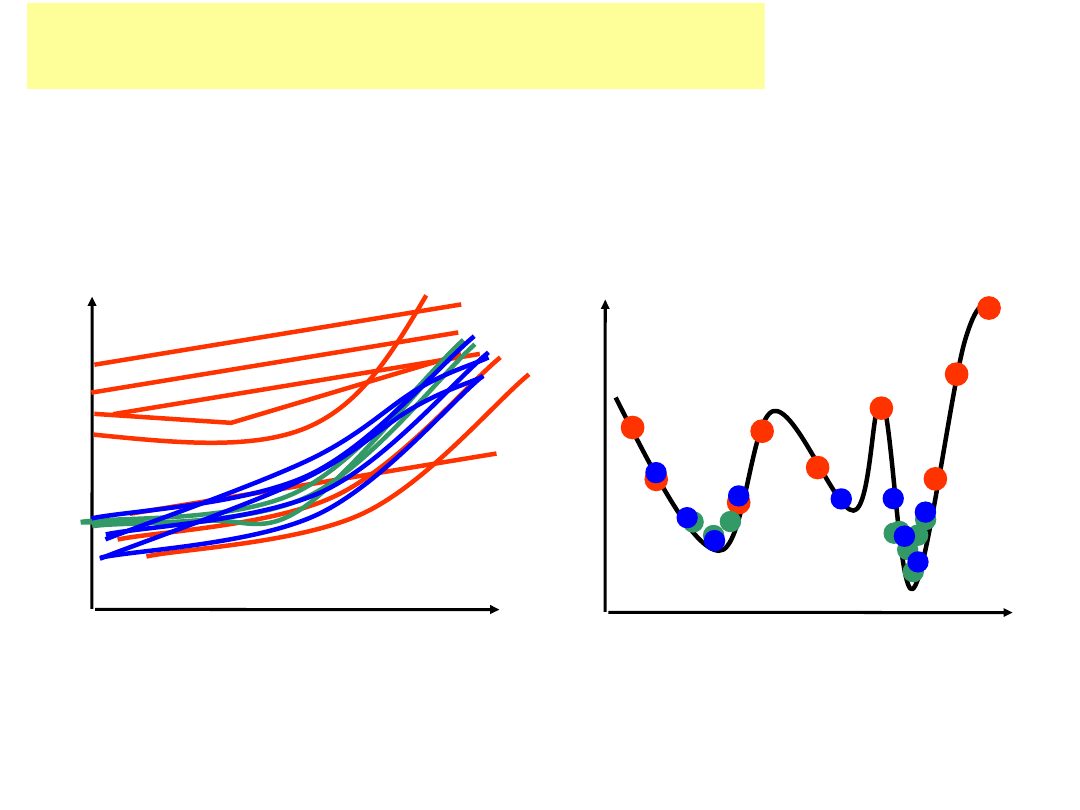
Definicja funkcji błędu dopasowania (FBD)

































































2

1

1

2

2

2

2

2

1

2

1

1

1

1

1

1

2

1

N

i

i

e

i

t

i

e

N

i

i

e

i

t

i

e

y

y

y

N

y

y

y

N

FBD

 

1

,

0

1

1

1

1

2

1

1

0

d

d

2

1

2

1

1

2

2

2

2

1

2

1

1

1

2

1

2

2

2

1

1

1

1







































































N

i

i

e

i

t

N

i

i

e

i

t

N

i

i

e

i

t

N

i

i

e

i

t

y

y

N

y

y

N

y

y

N

y

y

N

FBD

FBD





FBD

E

N

FP

SS

1

)

(



·y

t1

(x)

·y

t2

(x)

y

x

1

100

zmodyfikowana

metoda

najmniejszych

kwadratów

PLS

3

: x, yY

PL

,

 – czynnik geometryczny

27

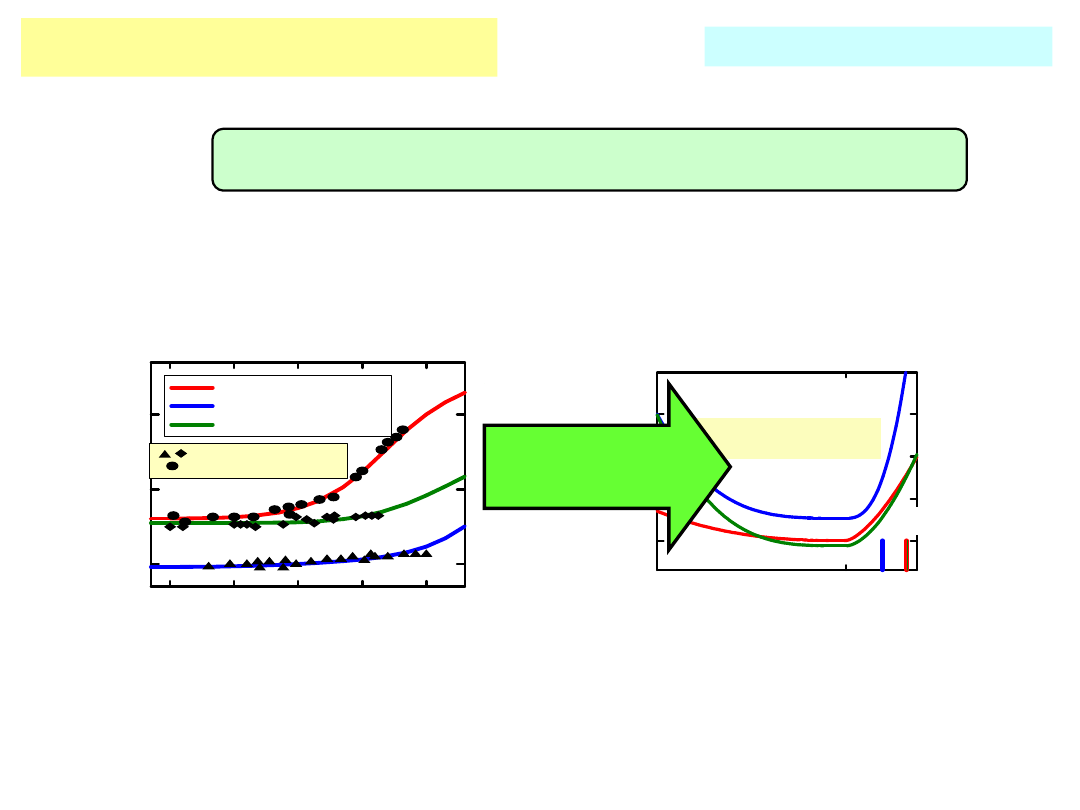
Proces dopasowania za pomocą

AG

FBD

5 parametrów N

ss

(E)

Y

PL



*

*

*

* * * *

pokolenie

pierwsze

końcowe

pośrednie

28

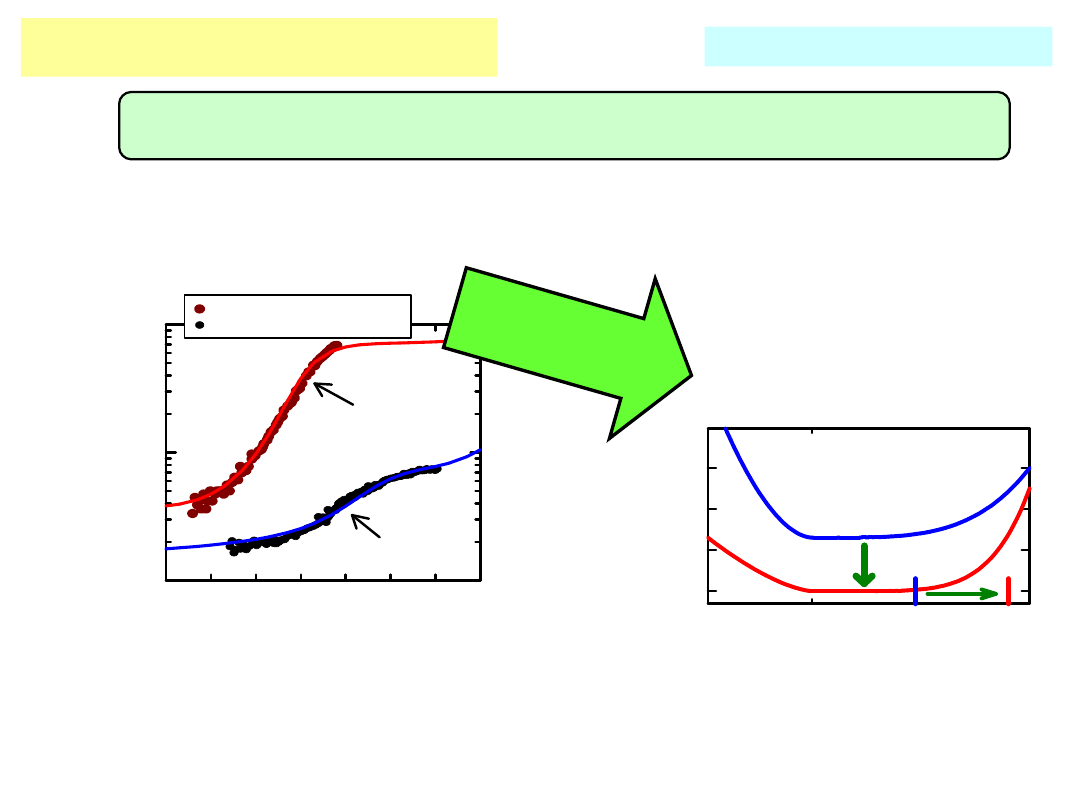
Przykłady dopasowań

F [foton cm

-2

s

-1

]

10

20

10

21

10

22

10

23

10

24

Y

P

L

[j

ed

n.

w

zg

l�

dn

e]

10

-3

10

-2

10

-1

polerowana
bombardowana
wygrzewana w As

Moison i inni

Appl. Phys. Lett. 1986

N

SS

[eV

-1

cm

-2

]

10

11

10

12

10

13

10

14

E

C

E

HO

E

V

s

n

=10

-14

cm

2

s

n

=s

p

=10

-13

cm

2

E

Fs

dopasowani

e

Powierzchnia InP(100) poddana cyklowi obróbek

M. Miczek: praca doktorska

29

Przykłady dopasowań

Powierzchnia GaAs(100) przed i po siarkowaniu w Na

2

S

(aq)

N

SS

[eV

-1

cm

-2

]

10

11

10

12

10

13

10

14

E

C

E

V

E

HO

E

Fs

F [foton cm

-2

s

-1

]

10

16

10

18

10

20

10

22

Y

PL

0.1

1.0

10.0

przed Na

2

S

po Na

2

S

Liu, Kauffman

Appl. Phys. Lett. 1995

dopasow

ani

e

M. Miczek: praca doktorska

30

4a. Podsumowanie

+ odporność na lokalne ekstrema
+ niepotrzebna wstępna wiedza

(punkt startowy)
+ słabe założenia co do FP
+ wydajność
+ prostota pojęciowa

Zalety AG

– słabsza podbudowa teoretyczna

– kodowanie (czasem konieczność
naprawy chromosomów)

– często koniecznośc skalowania FP

Wady AG



rozpoznawanie obrazów



synteza i optymalizacja układów

(mechanicznych, elektronicznych)



sterowanie



strategia gier



klasyfikacja i automatyczne wnioskowanie



analiza danych (dopasowanie, modelowanie)

Zastosowania

sztuczny

mózg

… ale na razie

ostatnie słowo

ma człowiek.

31

Literatura

1.

D. E. Goldberg, Algorytmy genetyczne i ich zastosowania, WNT, Warszawa,

1998

2.

Z. Michalewicz, Algorytmy genetyczne + struktury danych = programy

ewolucyjne, WNT, Warszawa, 1996

3.

J. Arabas, Wykłady z algorytmów ewolucyjnych, WNT, Warszawa, 2001.