1

Pełzanie

Pełzanie

– zwiększające się z upływem czasu

odkształcenie plastyczne pod wpływem stałego
obciążenia. Pełzanie staje się istotne przy temperaturach
(0,30,5)T

m

.

Granica pełzania

– wartość stałego naprężenia

nominalnego 

n

, które po upływie określonego czasu w

danej temperaturze spowoduje spowoduje trwałe
wydłużenie próbki o pewną określoną wartość.
(odpowiednik granicy plastyczności R

e

)

Wytrzymałość na pełzanie

– wartość stałego

naprężenia nominalnego 

n

, które po upływie

określonego czasu w danej temperaturze spowoduje
zerwanie próbki (odp. wytrzymałości na rozciąganie R

m

)

2

Pełzanie – oznaczenia granic pełzania

Granica pełzania

R

e/t/T

gdzie: e [%] – wart. wydłużenia trwałego; t [h]– czas; T – temp.
[ºC] np.

R

0,2/10000/500

oznacza =0,2% po czasie 10000h w temp. 500 ºC

Wytrzymałość na pełzanie

R

z/t/T

gdzie t i T jak wyżej. Np.

R

z/10000/500

oznacza wytrzymałość po czasie 10000h w temp. 500 ºC

3

Pełzanie – porównanie temperatur topnienia

(

)

, ,

t

f

T

e

s

=

Temperatura, przy której materiał
zaczyna pełzać to:

Dla Metali

T > (0,3  0,4) T

m

Dla Ceramik

T > (0,4  0,5) T

m

T

m

– temperatura topnienia

Pełzanie oznacza zależność
odkształcenia nie tylko od naprężenia,
ale także od temperatury oraz przede
wszystkim czasu.

4

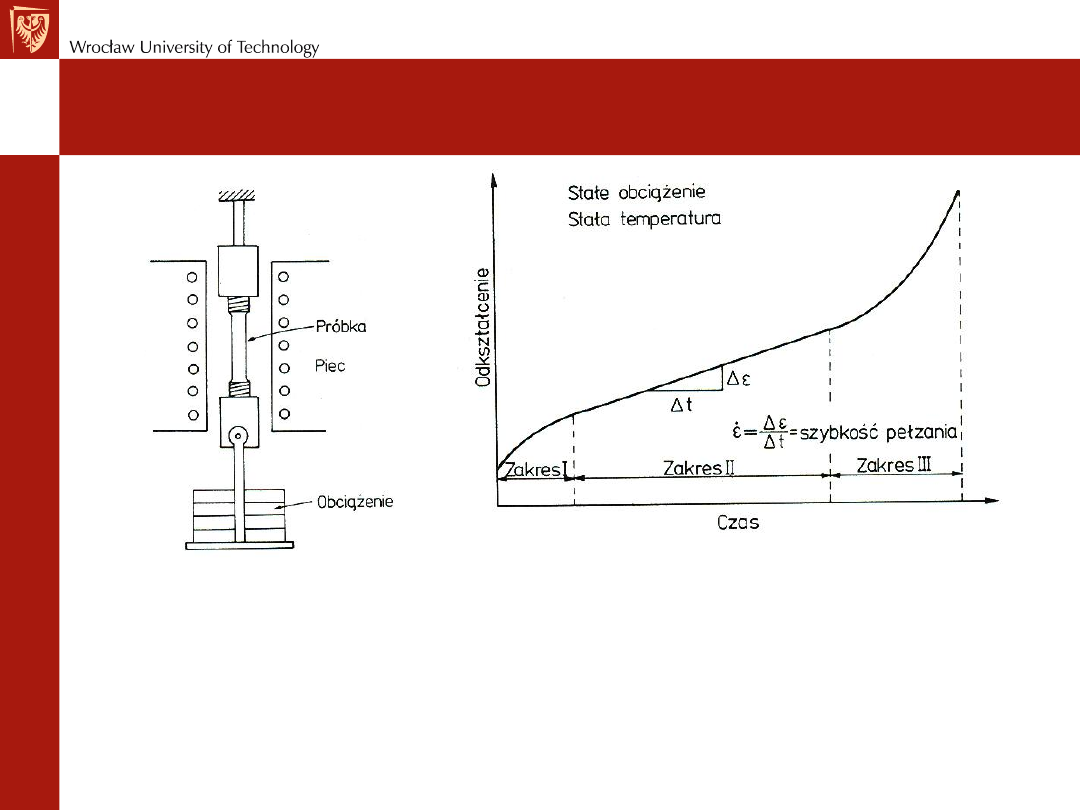
Pełzanie – przebieg w czasie

I –

pełzanie wstępne

(krótka faza – efekt umocnienia odkształceniowego powoduje

zmieszanie szybkości pełzania)

II –

pełzanie ustalone

(kontrolowane dyfuzją regularne uwalnianie dyslokacji

zakotwiczonych na wydzieleniach skutkuje ustaloną szybkością pełzania)

III –

pełzanie nieustalone

szybkość rośnie wykładniczo (efekt powstawania

mikropęknięć)

5

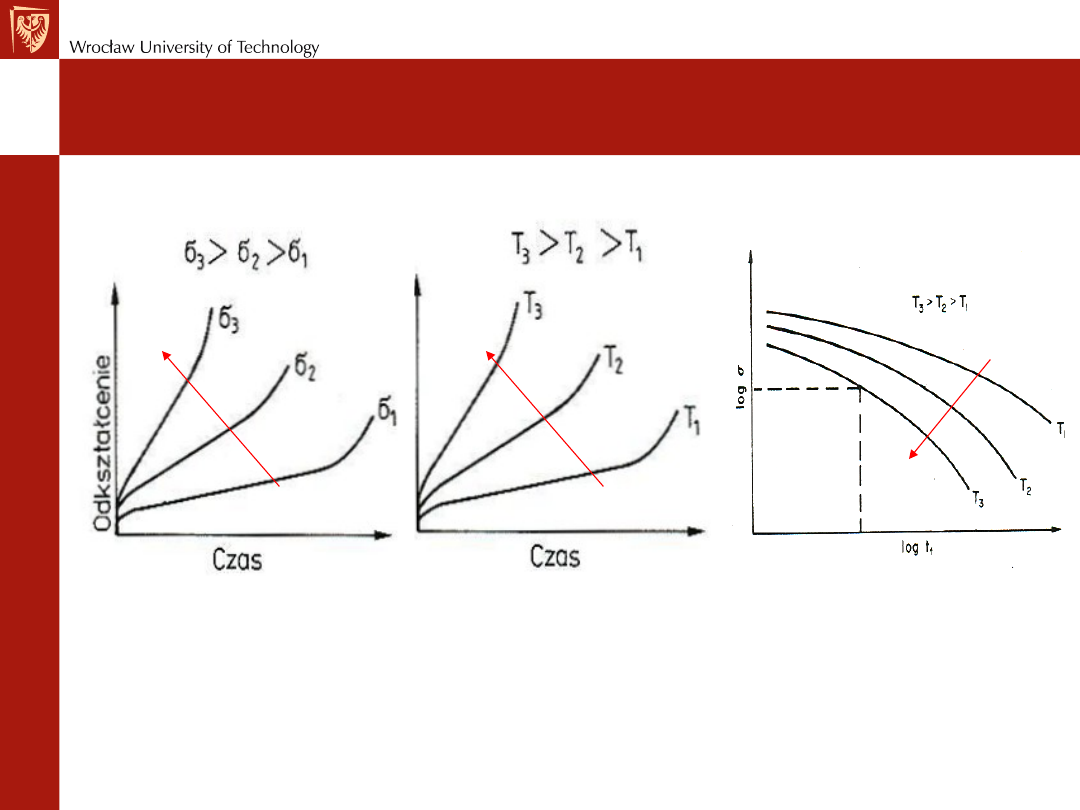
Pełzanie – krzywe

Zmiana kształtu krzywej pełzania spowodowana zmianą
a)

obciążenia;

b)

temperatury

c)

naprężenie dopuszczalne w dla czasu obciążenia przy różnych
temperaturach

c)

a)

b)

6

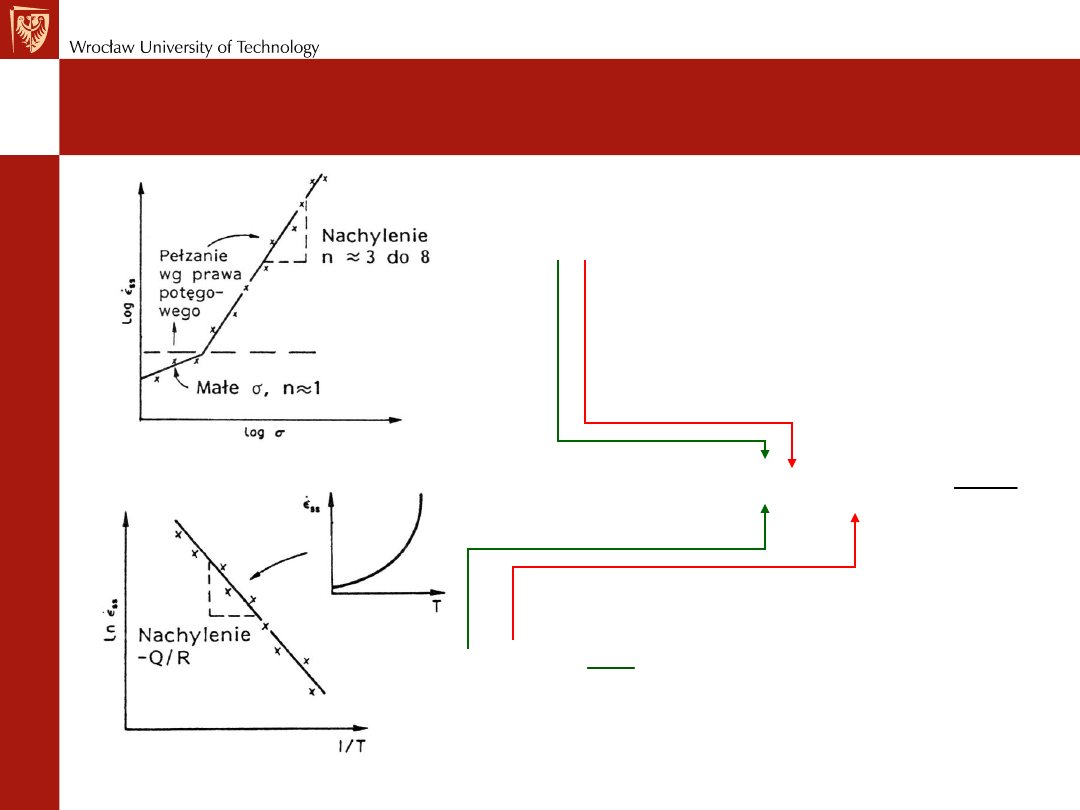
Pełzanie –szybkość pełzania w II stadium

exp

p

n

Q

A

RT

e

s

�

�

=

-

�

�

�

�

�

�

&

A, B, C, n – stałe
materiałowe, Q

p

– energia

aktywacji pełzania, R –
uniwersalna stała gazowa

Zmiana szybkości pełzania w funkcji  (T=

const)

Zmiana szybkości pełzania w funkcji T (



=const)

n

B

e

s

=

&

exp

p

Q

C

RT

e

�

�

= �

-

�

�

�

�

�

�

&

Doświadczalnie stwierdzono, że
przy stałej temperaturze szybkość
pełzania opisana jest

funkcją

potęgową

naprężania

zaś przy stałym naprężeniu

funkcją wykładniczą typu
Arrheniusa

.

Ostatecznie połączenie tych
zależności prowadzi do wzoru:

7

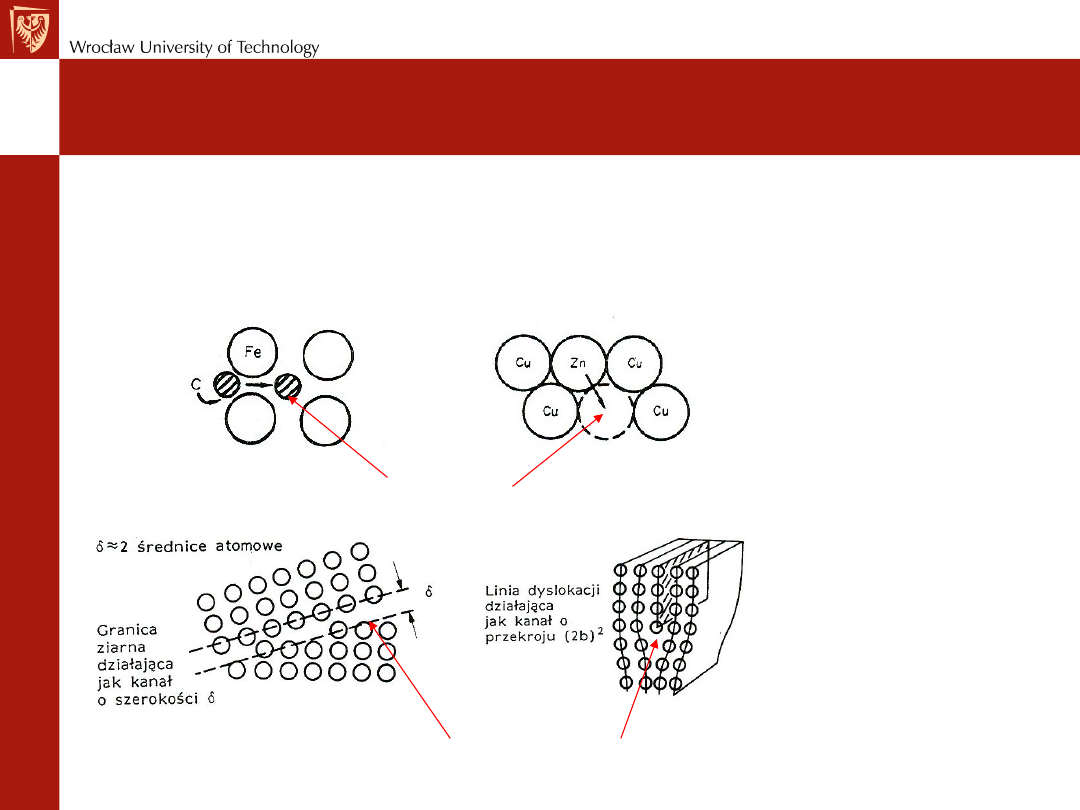
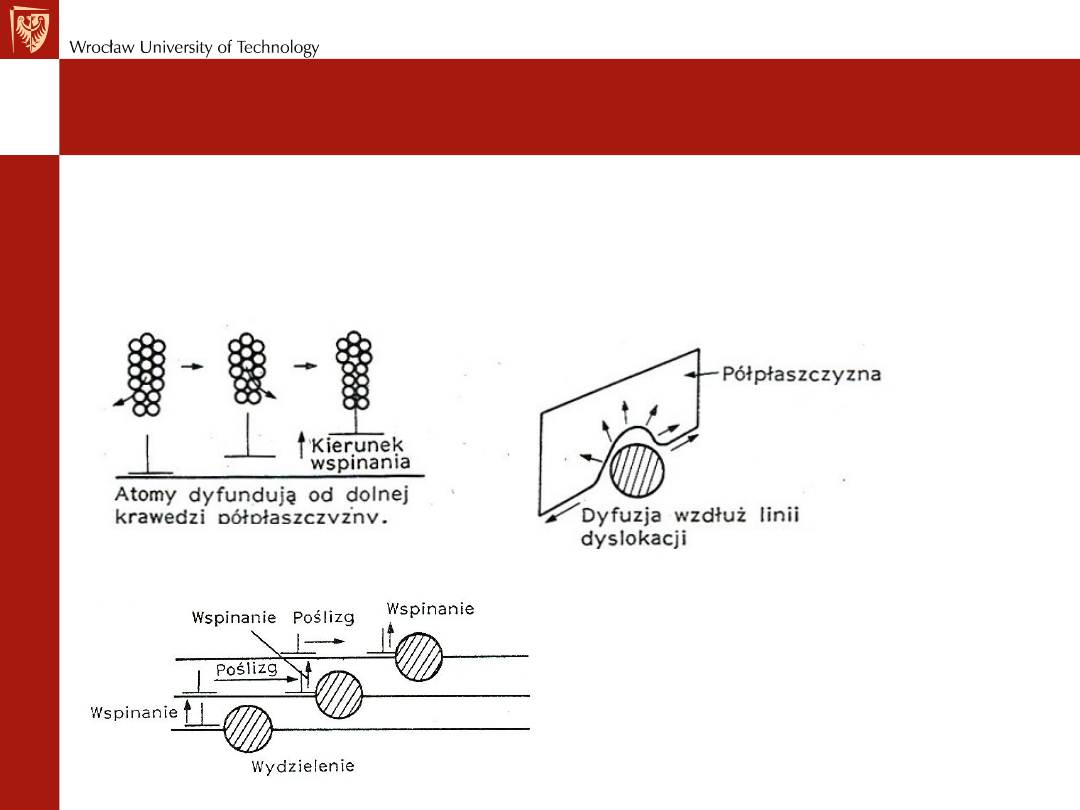
Pełzanie – mechanizm dyfuzji w ciałach stałych

Dyfuzja objętościowa: międzywęzłowa i wakansowa

Drogi szybkiej dyfuzji: po granicach ziaren i wzdłuż linii dyslokacji

W pełzaniu znaczącą rolę odrywa dyfuzja atomów w ciałach stałych.

1. Umożliwia ona dyslokacjom krawędziowym wspinanie się na przeszkody i ich
omijanie co powoduje stały wzrost odkształcenia plastycznego

2. Powoduje zmianę kształtu ziaren, które wydłużając się w kierunku działania
naprężenia relaksują naprężenia wewnętrzne

8

Pełzanie – wspinanie się dyslokacji na
przeszkody

Odkształcenia plastyczne są spowodowane ruchem dyslokacji krawędziowych. Zakotwiczenie
dyslokacji na przeszkodach uniemożliwia odkształcenia plastyczne.

Dyfuzja wzdłuż linii dyslokacji sprawia, że dyslokacja dopasowuję się kształtem do wydzielenia co
pozwala jej ominąć je i kontynuować proces odkształcenia plastycznego, aż do napotkania następnej
przeszkody. Ten efekt nazywa się

wspinaniem dyslokacji

.

Ponieważ dyfuzja w danej temperaturze odbywa
się ze stałą prędkością więc ze stałą szybkością
odbywa się wspinanie dyslokacji, co prowadzi do
stałej prędkości uwalniana dyslokacji i w efekcie
do stałej szybkości odkształcenia plastycznego

9

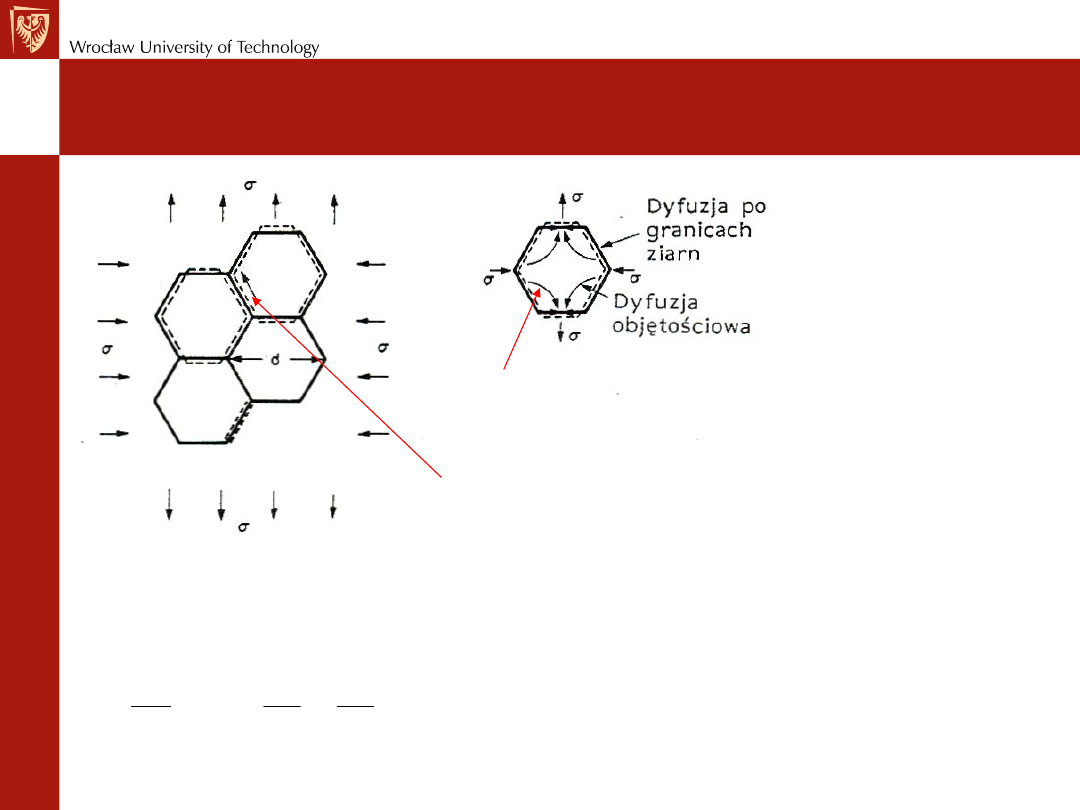
Pełzanie – zmiana kształtu ziaren

Dla mniejszych T/T

M

decyduje dyfuzja wzdłuż granicy ziaren (o

szybkości wciąż proporcjonalnej do naprężenia) co w konsekwencji
prowadzi do poślizgu po granicach ziaren.

/

2

2

1

Q RT

d

D

e

dt

d

d

e

s

s

-

:

:

Dla dużych T/T

M

zachodzi dyfuzja objętościowa wywołana

naprężeniem (działa ono jak gradient stężenia dc/dx) co
prowadzi do wydłużenia się ziarna.

Szybkość dyfuzji zmienia się z rozmiarem
ziarna d. (jak 1/d

2

). Bo dla większych d

transport dyfuzyjny odbywa się po większej
drodze.

Dyfuzja objętościowa i po granicach ziaren doprowadza do zmiany kształtu ziarna, które
wydłużają się w kierunku działania naprężenia, które ulega relaksacji. Jest to skutek dążenia
układu do zmniejszenia energii.

10

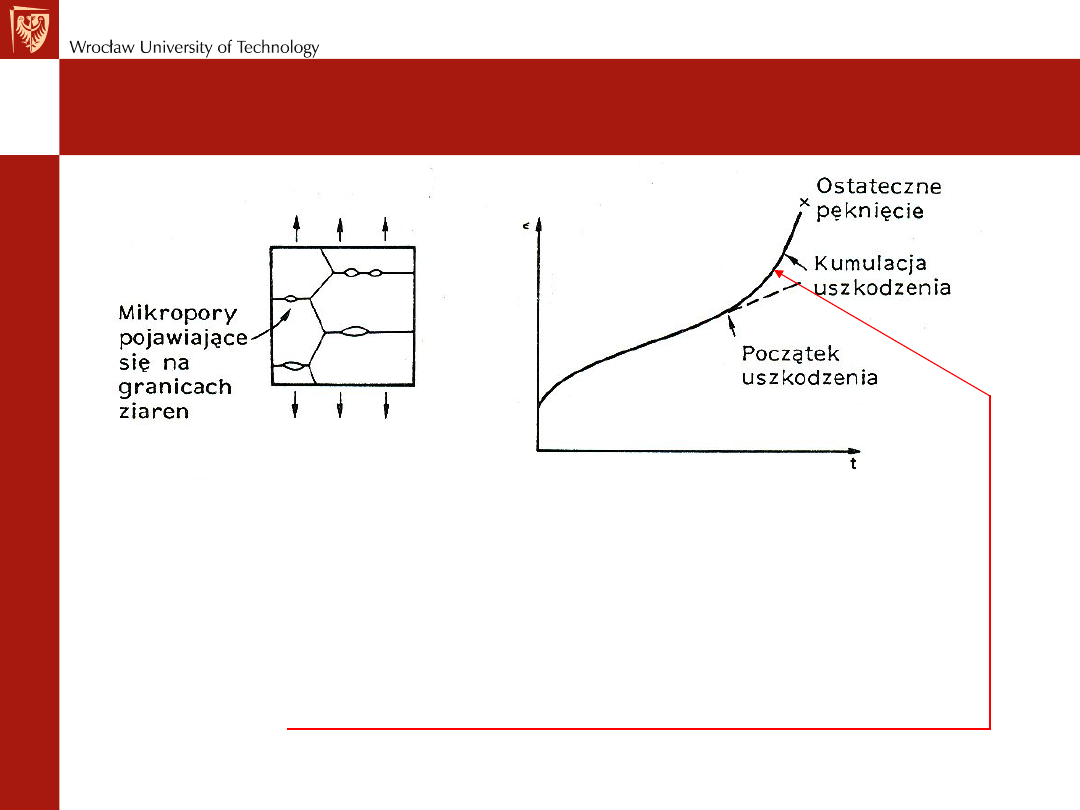
Pełzanie – uszkodzenie i pękanie

W III stadium pełzania wydłużenia ziaren są już tak duże, że wewnątrz
materiału pojawiają się mikropory. Mikropory zmniejszają przekrój próbki i w
konsekwencji (przy stałym obciążeniu) wzrasta naprężenie. Ponieważ

n

e s

&:

więc szybkość pełzania wzrasta szybciej niż naprężenie co prowadzi do
ekspotencjalnego wzrostu d

/dt

11

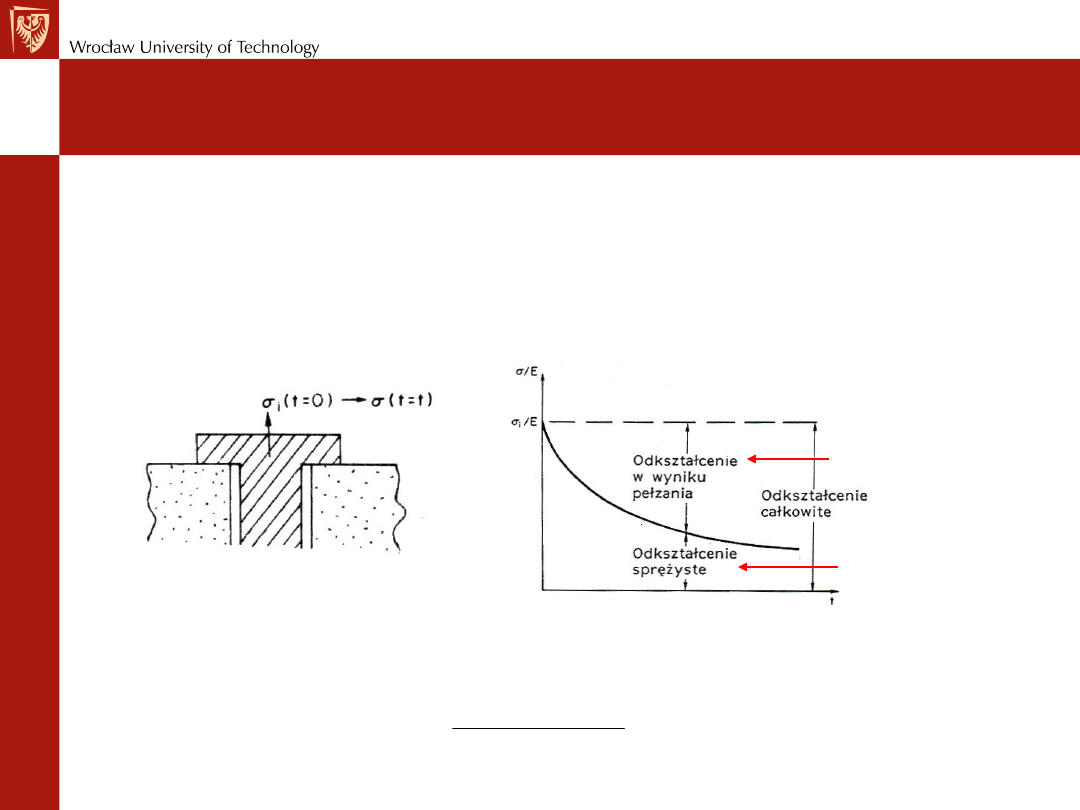
Pełzanie – konsekwencje

a)

Przy stałym naprężeniu odkształcenie rośnie z upływem czasu –
skutek wydłużanie się elementów

b)

Przy stałym odkształceniu naprężenie ulega relaksacji z upływem
czasu – skutek to luzowanie się elementów (np. śrub, które trzeba
okresowo dokręcać)

p

e











1

1

2

1

(

1)

n

r

n

o

t

n

BEs

-

-

-

=

-

Czas relaksacji naprężeń – czas niezbędny do zrelaksowania naprężeń o
połowę

p

e

e

e

12

Pełzanie – wybór materiału

(a) Wybrać materiał o dużej wartości temperatury topnienia T

M

(bo

szybkość pełzania zależy od T/T

M

)

(b) Maksymalnie utrudnić ruch dyslokacji przez utworzenie roztworów
stałych (stabilne wydzielenia dyspersyjne utrudniające ruch dyslokacji)

(c) Wybierać w miarę możliwości materiał o typie sieci stwarzającej
największy opór (wiązania kowalencyjne) (ceramika – tlenki, krzemiany,
węgliki krzemu, azotki krzemu ...)

(d) Stworzyć warunki powstania dużego ziarna (wydłuża drogę dyfuzji)

(e) Stworzyć warunki powstania wydzieleń na granicach ziaren
(ograniczenie poślizgu granic ziaren)

13

Pełzanie – przykład materiału odpornego na
pełzanie

(b) Wprowadzenie do roztworu stałego dużej
ilości obcych atomów (Co, W, Cr ....) –
utrudnia ruch dyslokacji

Nadstopy niklu

Typowy skład w procentach

Ni

50

Co, W

10

Cr

9

Al.

5,5

Ta, Ti, Hf
1,5-2.5
Mo, C, Si, Mn

0,1-0,25

Cu, Zr, B, S, Pb

<0,05

(b,e) Utworzenie stabilnych i twardych
wydzieleń faz: Ni

3

Al, Ni

3

Ti, MoC, TaC –

utrudnia ruch dyslokacji

oraz poślizg ziaren

Utworzenie ochronnej warstwy Cr

2

O na

powierzchni stopu ogranicza dodatkowo
korozję

Nadstopy niklu są odporne na pełzanie w temp. 850°C czyli do poziomu,
aż 72% temperatury topnienia niklu.

Dla przypomnienia w metalach pełzanie zaczyna się już na poziomie 30
– 40 % temperatury topnienia materiału.

14

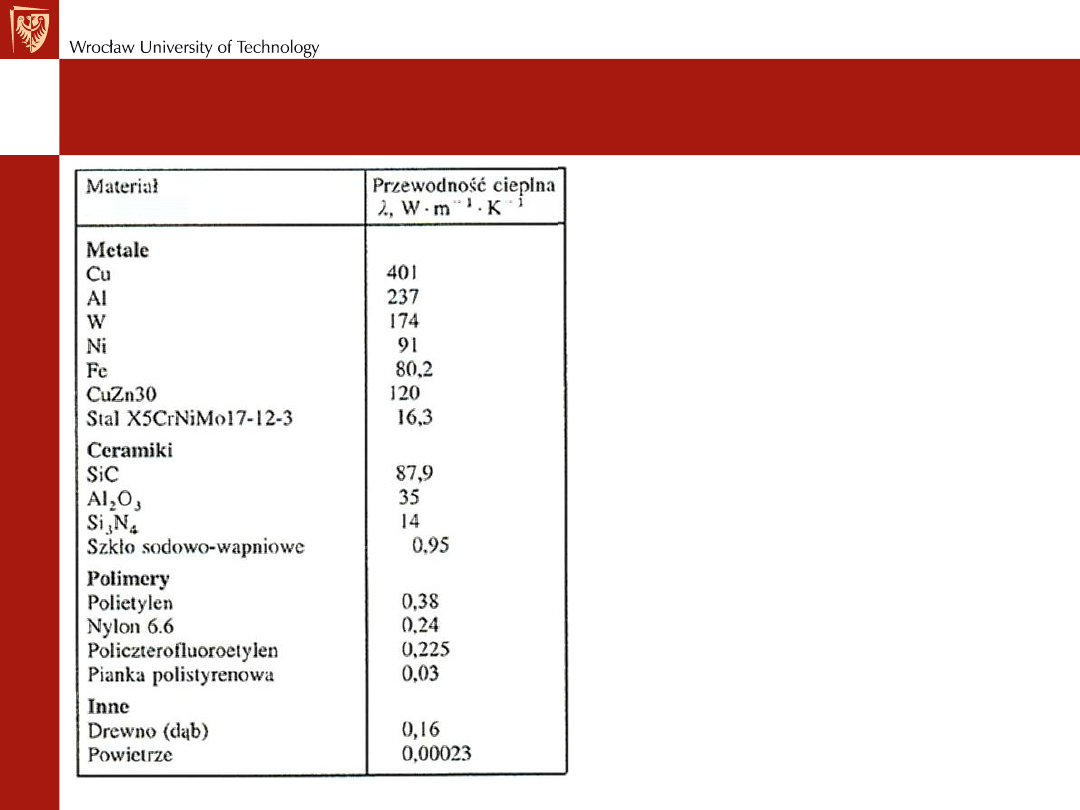
Własności termiczne

• Właściwa pojemność cieplna c
• Przewodność cieplna



• Rozszerzalność cieplna 
• Temperatury topnienia T

M

• Ciepło topnienia r

Atomy w ciałach w temp. powyżej 0 K drgają wokół położeń równowagi.
Nagrzewanie materiału powoduje wzrost amplitudy drgań.

Drgania poprzez sprężystość wiązań przenoszą się na sąsiednie atomy powodując
powstawanie fal sprężystych rozchodzących się z prędkością dźwięku. Przez
analogię do fal świetlnych fale te traktuje się jak cząstki zwane fononami. Ich
energia E = hv/ = h

Do parametrów termicznych mających znaczenie przy wyborze materiału
zaliczamy:

15

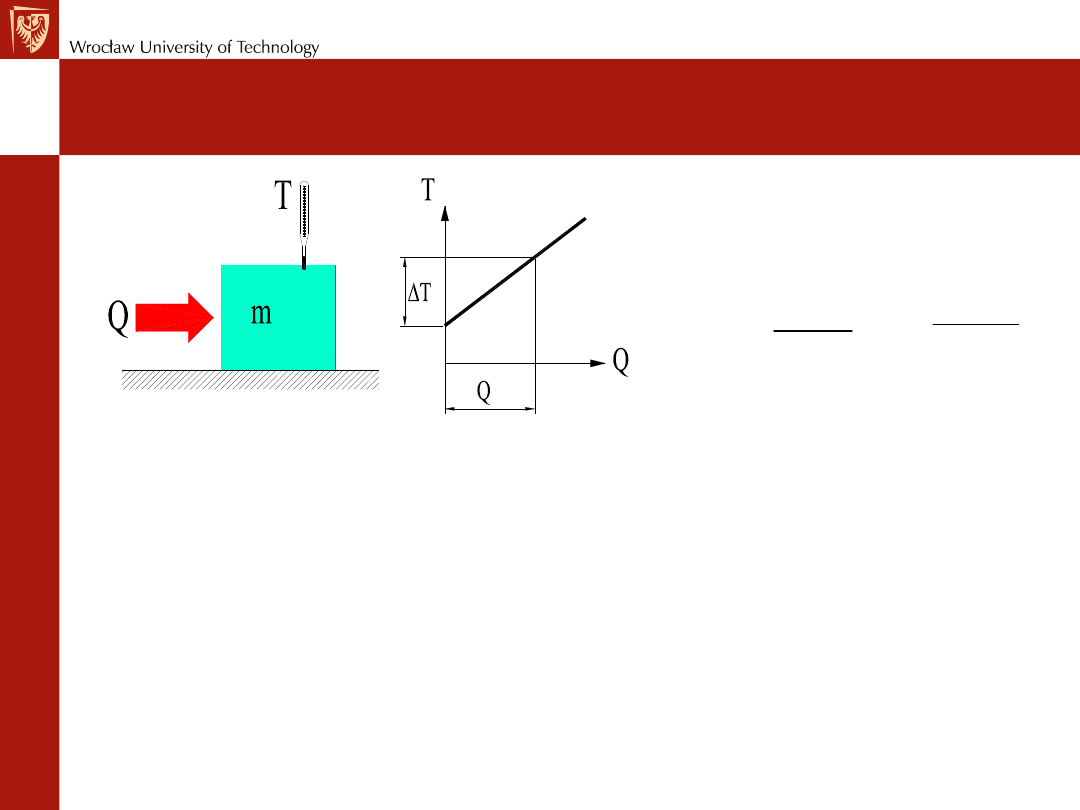
Właściwa pojemność cieplna

Q

c

m T

=

D

J

kg K

�

�

�

�

�

�

�

Właściwa pojemność cieplna.
Wzór ogólny

Wzrost amplitudy drgań wskutek nagrzewanie materiału wymaga dostarczenia energii,
która jest ostatecznie gromadzona w materiale w postaci energii kinetycznej i
potencjalnej ruchu oscylacyjnego.

W przypadku gazów nagrzewanie powoduje wzrost energii kinetycznej ruchu ruchu
postępowego oraz w zależności od kształtu cząstki ruchów oscylacyjnych oraz
rotacyjnych.

Wyróżnia się ciepło właściwe przy stałej objętości c

v

oraz stałym

ciśnieniu c

p

. Dla gazów doskonałych zachodzi zależność (R –

uniwersalna stała gazowa, M – masa molowa)

p

v

c

c

c

� =

Dla ciał stałych i cieczy

/

p

v

c c

R M

-

=

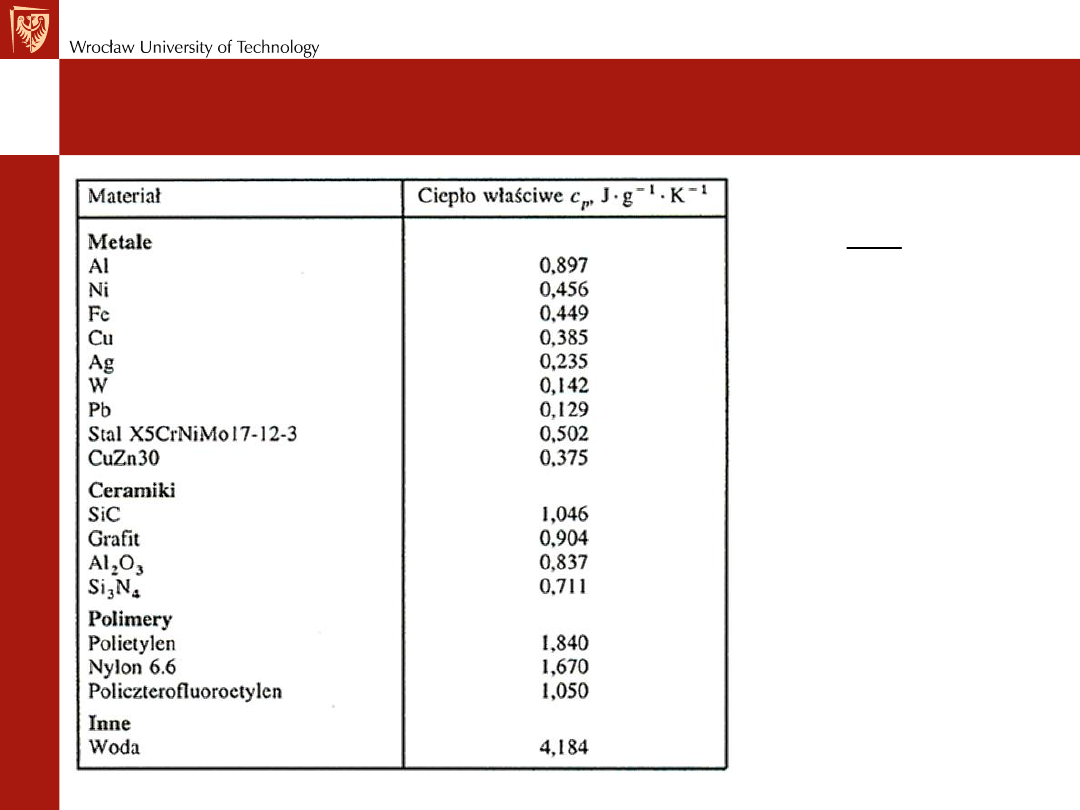
16

Właściwa pojemność cieplna

Q

C

n T

=

D

Ciepło molowe (n – liczba
moli)

p

v

c

c

c

� =

C cM

=

Związek między ciepłem
molowym C a właściwym c.

p

v

C

C

R

-

=

Dla gazów doskonałych

C jest funkcją
temperatury (i ciśnienia
dla gazów).

Mikrostruktura ma mały
wpływ na jej wartość.

Istotny wpływ ma
struktura krystaliczna.
Podczas przemian
polimorficznych
następuje skokowa
zmiana C

17

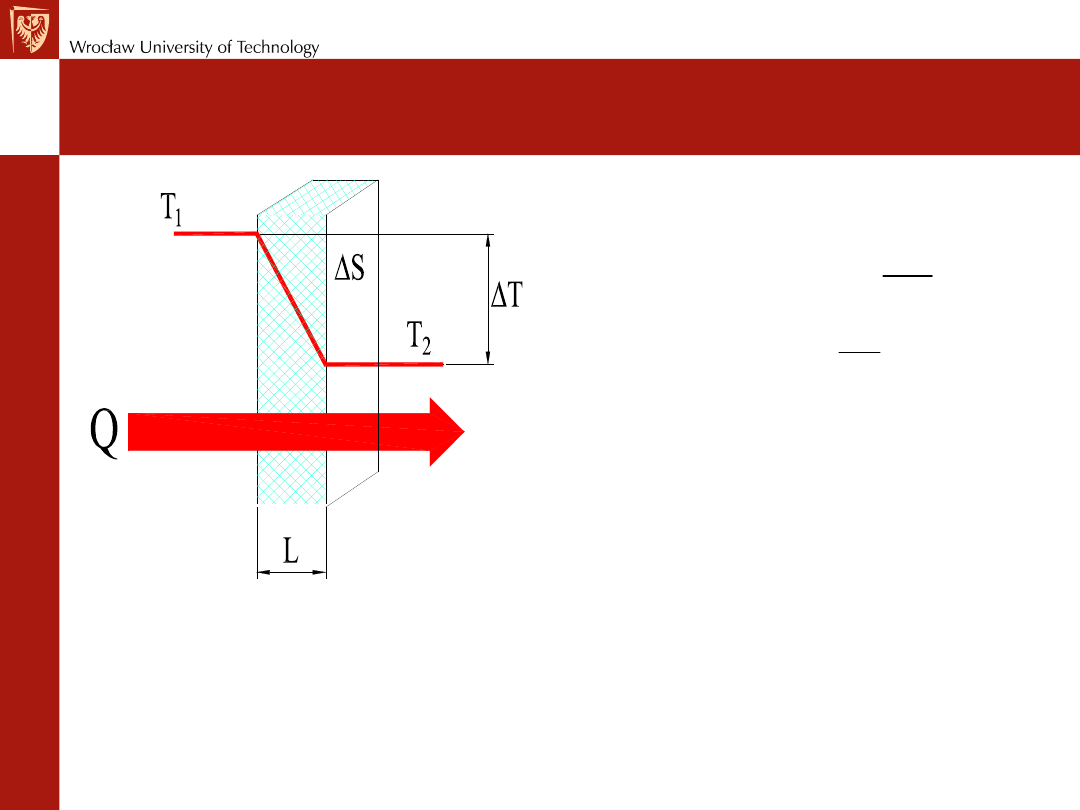
Przewodność cieplna

T

Q

S

L

l

D

=- D

&

Prawo Fouriera

 – współczynnik przewodzenia

ciepła W/(m·K)

dT

dQ

dydz

dx

l

=-

&

Transfer ciepła odbywa się za pośrednictwem
elektronów (głównie metale) i fononów (reszta
materiałów).

18

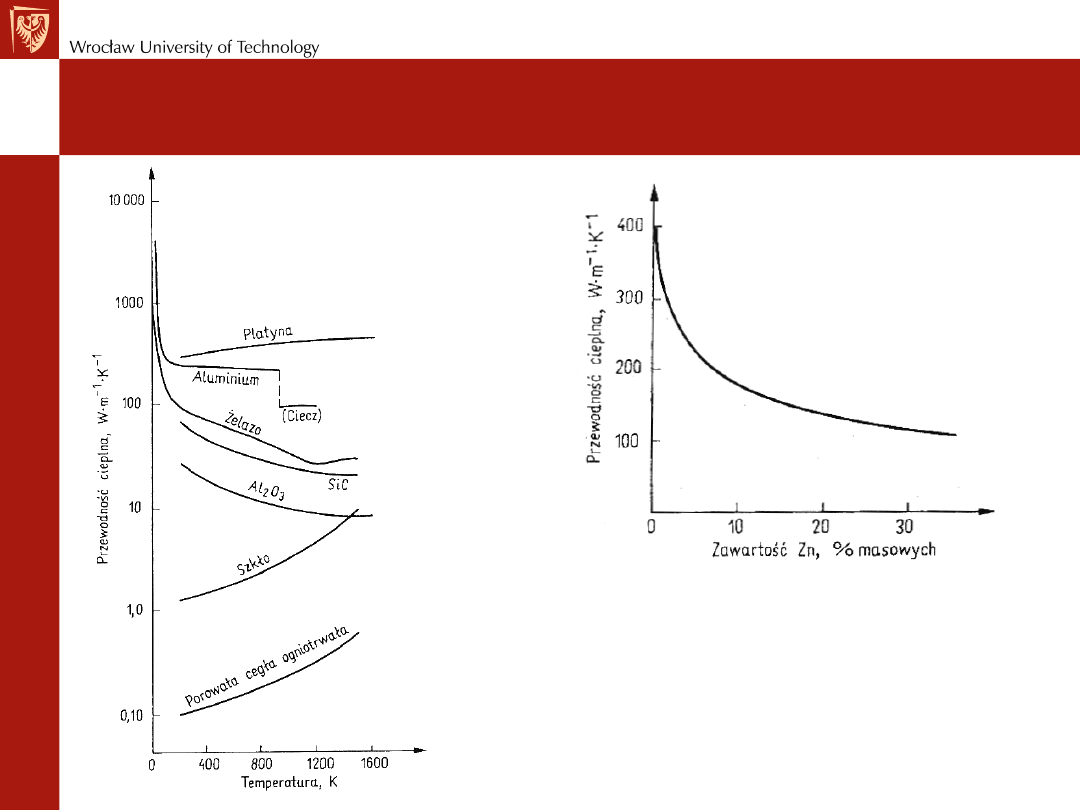
Przewodność cieplna

Metale - transfer ciepła 90 ÷ 99%
odbywa się za pośrednictwem
elektronów. Wraz ze wzrostem T rośnie
liczba elektronów i fononów i
jednocześnie zmniejsza się ich ruchliwość
na skutek zwiększania amplitudy drgań.
Sumaryczny wpływ jest różny dla
poszczególnych metali.

Ceramika - transfer ciepła gównie za
pośrednictwem fononów. Fonony nie są
dobrym nośnikiem ciepłą ze względu na
ich rozpraszanie na defektach struktury
krystalicznej. Wzrost ich rozpraszania
wraz z T (wpływ amplitudy drań)
sprawia, że

 maleje wraz ze wzrostem T.

Dodatkowy udział w złym
przewodnictwie mają pory.

Polimery – podobnie jak ceramika.
Wzrost

 towarzyszy wzrostowy udziału

fazy krystalicznej (regularne ułożenie
atomów sprzyja przemieszczaniu się
fononów) Podobnie obecność porów
zmniejsza

.

19

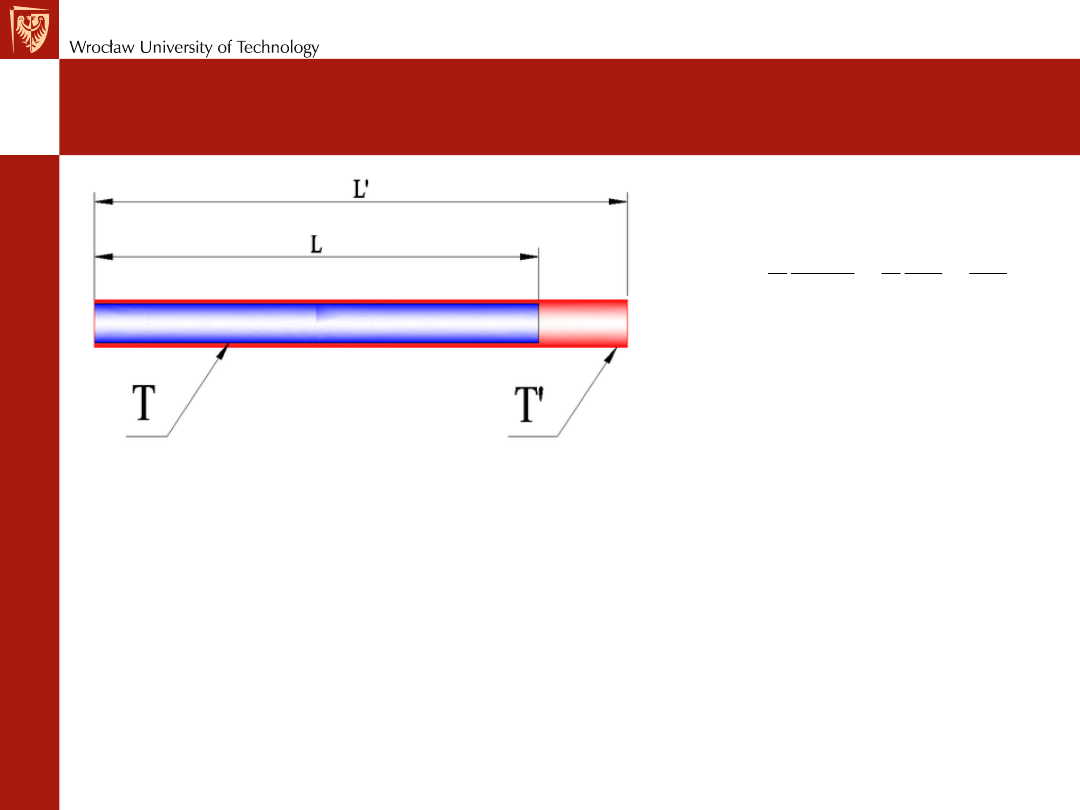
Przewodność cieplna – wpływ temperatury

Przewodność cieplna stopu Cu – Zn

20

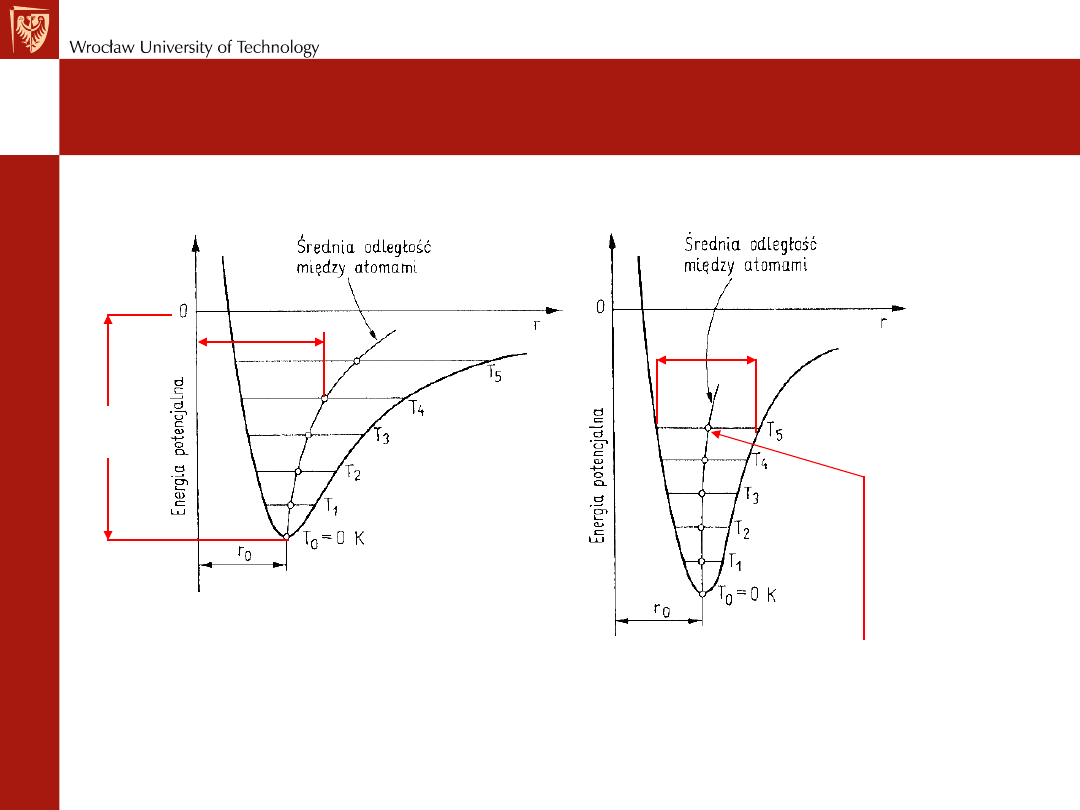
Rozszerzalność cieplna

1 '

1

'

T

L L

L

LT T

L T

T

e

a

-

D

=

=

=

-

D

D

Współczynnik rozszerzalności
cieplnej

Utwierdzenie elementu i jego nagrzanie wywołuje

naprężenia termiczne

. Są one

skutkiem wydłużania się elementu. Unieruchomienie elementu nie pozwala na jego
wydłużenie, które jest kompensowane przez naprężenie  dążące do utrzymania

wymiarów. Zgodnie z prawem Hooka naprężenie to wynosi

T

T

e

a

= D

T

E

s

e

=

E

T

s

a

=

D

a po uwzględnieniu wydłużenia termicznego

21

Rozszerzalność cieplna – wpływ energii wiązania

Materiał o dużej rozszerzalności
cieplnej mała energia wiązania E

w

Materiał o małej rozszerzalności
cieplnej, duża energia wiązania E

w

Wraz ze wzrostem temperatury amplituda A drgań atomów równowagi rośnie.

Położenie równowagi

jest

wówczas wyznaczone w połowie między skrajnymi położeniami atomu w czasie jego oscylacji. Położenie
równowagi wyznacza średnią odległość między atomami r

sr

. Ze względu na specyficzny kształt przebiegu

energii potencjalnej wiązania w zależności od odległości między atomami r średnia odległość miedzy
atomami rośnie wraz ze wzrostem temperatury. Da wiązań słabych (lewy rys) ten wzrost odległości jest
szybszy niż dla mocnych do przekłada się na większy współczynnik rozszerzalności cieplnej

A –

amplituda drań

E

w

r

sr

22

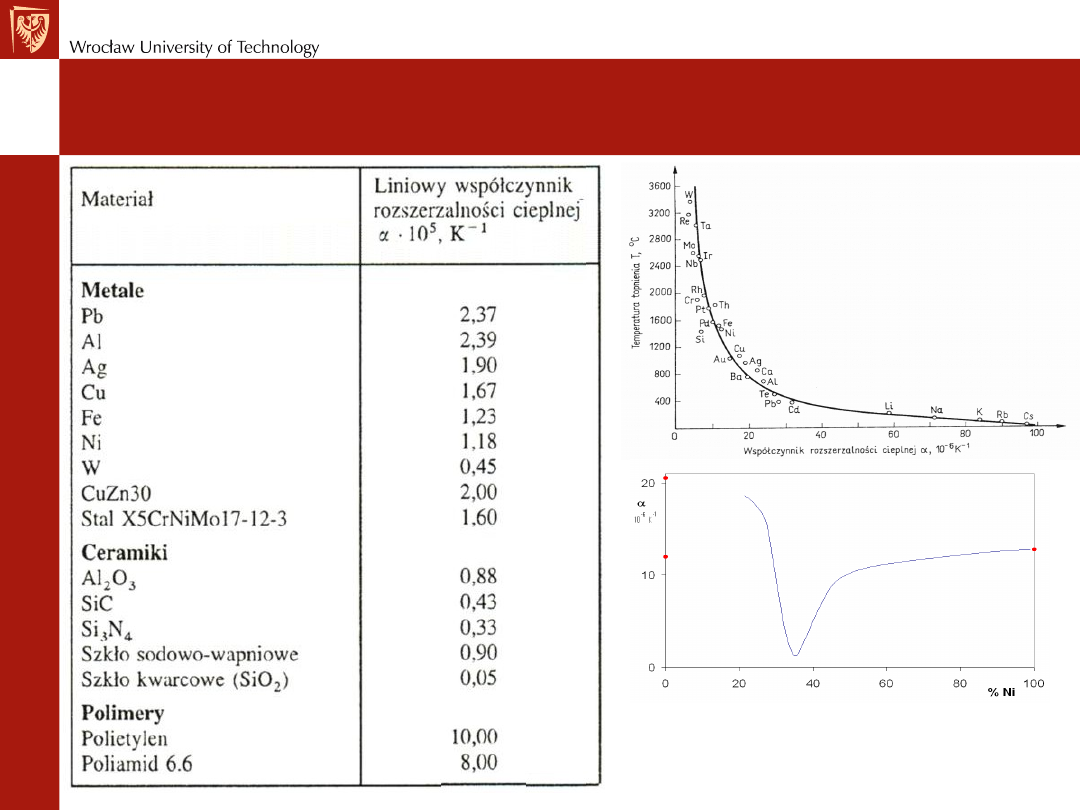
Rozszerzalność cieplna

Invar Fe(64%)
Ni(36%)

 = 0.55 ÷

1.2 × 10

–6

K

–1

(0.55÷1.2

ppm/°C).

Invar materiał o b. małym współczynniku
rozszerzalności cieplnej wynaleziony 1896 przez
Szwajcara Charles Édouard Guillaume

23

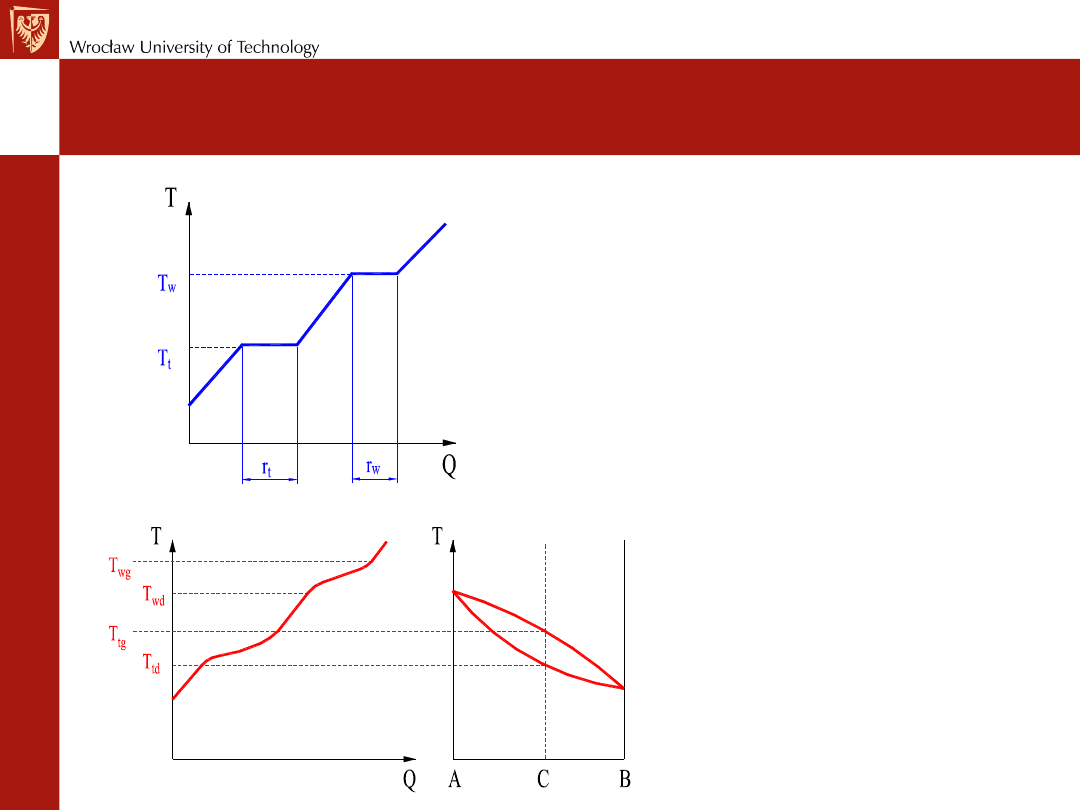
Topnienie, wrzenie

Krzywa przemian fazowych
dla materiałów
„jednorodnych”

Krzywa przemian fazowych
dla materiałów
„niejednorodnych” np.
stopów

24

Koniec

Dziękuję za

uwagę