Wpływ ordynacji wyborczej

na decyzje grupowe

Autor: Wojciech

Czaplejewicz

Plan prezentacji:

1. Systemy wyborcze

2. Jednomandatowe okręgi wyborcze

3. Dzielenie mandatów

4. Listy partyjne

5. Podsumowanie

Systemy wyborcze:

Na świecie:

W Australii przyjęto system większości bezwzględnej, w Wielkiej

Brytanii – system większości względnej i okręgi jednomandatowe,

natomiast w innych krajach są używane różne warianty

proporcjonalności. Warto dodać, że w ramach systemów list

partyjnych są stosowane formuły wyborcze(np. d`Hondta lub Sainte

– Lague).

Korzystną dla partii słabszych jest metoda Imperiali, praktykowana

we Włoszech. Kolejną popularną formułą wyborczą jest system

Sainte – Lague sprzęgnięty z zasadą wyrównawczej dystrybucji

miejsc, a więc rozwiązań preferujących do pewnego stopnia

ugrupowania zyskujące niewielkie poparcie, szczególnie popularny w

krajach nordyckich(Szwecja, Norwegia, Dania).

Systemy wyborcze:

W polskim parlamentaryzmie mamy do czynienia z ordynacją

proporcjonalną w wyborach do sejmu i większościową w wyborach

do senatu.

Często przy wszelkiego rodzaju sporach dotyczących ordynacji

proporcjonalnej, używa się argumentu iż tak naprawdę akt

wyborczy w znacznej mierze ma charakter losowy,

Partie dzięki odpowiednio ułożonej liście wyborczej potrafią

niemalże w 100% zagwarantować uzyskanie mandatu osobie,

która wyborach opierających się na ordynacji większościowej nie

miałaby większych szans. Dzieje się tak chociażby, dzięki

wystawianiu na szczycie list partyjnych osób cieszących się dużą

popularnością, rozpoznawalnych medialnie, które jako tzw.

”lokomotywy” generują wysokie poparcie dla danej listy wyborczej,

dzięki czemu osoby uzyskujące relatywnie małą ilość głosów, mają

szanse zdobyć mandat poselski, kosztem kandydata komitetu

konkurencyjnego mimo tego iż owy kandydat zdobył większą ilość

głosów.

Systemy wyborcze:

Kolejnym czynnikiem wpływającym na decyzje grupowe jest

istnienie klauzuli zaporowej.

Próg wyborczy, wynoszący u nas 5% dla partii i komitetów

wyborczych, oraz 8% dla koalicji partii, jest niezbędnym

warunkiem służącym racjonalizacji parlamentaryzmu, ponieważ

uniemożliwia dostęp do areny parlamentarno – gabinetowej

partią marginalnym, które nie cieszą się dużą społeczną

legitymacją. Próg wyborczy może ułatwiać zawieranie koalicji

rządowych partią relewantym na arenie politycznej bez udziału

„uciążliwych” z reguły partii marginalnych, które nie uzyskują

dostatecznej ilości głosów. Istnienie progów wyborczych

oscylujących w granicach 5 – 7% sprzyja, - aczkolwiek nie

gwarantuje – stabilności koalicji rządowych. Praktyka pokazuje,

że większa ilość partii wchodzących w skład gabinetu, zazwyczaj

wiąże się z jego mniejszą stabilnością.

Jednomandatowe okręgi wyborcze:

- Zmiana prowadziłaby do powstania zdecydowanie większej ilości

okręgów wyborczych, co w konsekwencji determinowałoby mniejszą

ilość wyborców w danym okręgu( np. 80 – 100tys.)

- Zapewne komitety wyborcze aby maksymalizować zyski

wystawiałyby po jednym kandydacie.

- Nie dochodziłoby do „bratobójczych” pojedynków między

kandydatami z jednej listy wyborczej, tak jak ma to miejsce w

obecnie.

- Wyborcy wiedzieliby na kogo oddają swój głos.

- Partie którym zależałoby na zwycięstwie wystawiałyby tylko i

wyłącznie osoby cieszące się społeczną atencją. Np. osoby popularne

w danym środowisku, działające od dawna na rzecz społeczności

zamieszkującej dany okręg.

- Największe szanse na zdobycie mandatu miałyby osoby starsze –

znane w danym środowisku, chociażby. ze względu na swoją

wcześniejszą działalność np. w samorządzie.

Dzielenie mandatów:

Sumuje się wyniki uzyskane w wyborach przez wszystkich

kandydatów danej listy wyborczej – czyli bierze się początkowo

pod uwagę wyłącznie wynik listy wyborczej np. jeżeli w wyborach

brały udział listy wyborcze: A,B,C,D – podsumowuje się

następująco ich wyniki wyborcze. W dalszej analizie uwzględnia

się tylko wyniki list, które w skali kraju przekroczą próg wyborczy

(jeżeli istnieje), często owe progi wyborcze nie stosują się do

komitetów mniejszości narodowych. Wyniki list dzieli się następnie

przez dzielniki, które wyznacza odpowiednia ordynacja wyborcza.

Jeżeli ordynacja stosuje metodę d`Hondta – tak jak w Polsce –

która zazwyczaj preferuje duże ugrupowania wyborcze,

dzielnikami są kolejne liczby naturalne, czyli 1,2,3,4,5 itd..

Inną metodą bardziej sprawiedliwą dla małych ugrupowań jest

metoda Sainte – Lague, dzielnikami są 1,3,5,7,9 i dalej kolejne

liczby nieparzyste. Wynikiem dzielenia jest otrzymanie listy

ilorazów. Podział mandatów dokonuje się przez wyodrębnienie

odpowiedniej liczby(równej ilości mandatów do zdobycia w danym

okręgu wyborczym) największych ilorazów. Ostatni etap podziału

mandatów polega na ich przydzieleniu konkretnym kandydatom w

ramach list wyborczych. Mandaty w ramach list zdobywają w

kolejności osoby które uzyskały najlepszy wynik wśród

kandydatów danej listy.

Dzielenie mandatów:

Inną metodą podziału mandatów, nie stosowaną jeszcze w Polsce

jest metoda Hare – Niemeyera.

Podobnie jak w wyżej opisanych metodach pierwszym etapem

podziału głosów jest zsumowanie wyników list wyborczych oraz

odrzucenie list które nie przekroczą stosownego progu.

Następnie konieczne jest obliczenie procentowego wyniku

pozostałych list wyborczych (stosunku głosów oddanych na daną

listę wyborczą do zsumowanych wyników wszystkich list

wyborczych, ale tylko tych które uczestniczą w podziale

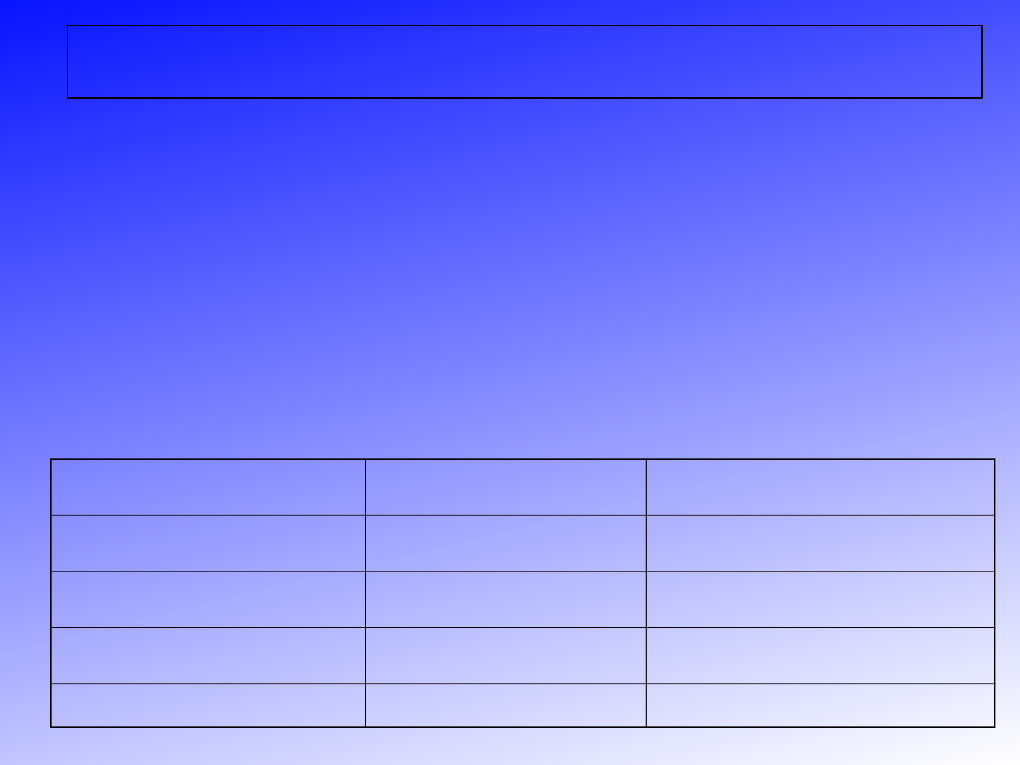
mandatów), procedurę tę ilustruje przykład poniżej:

Nazwa listy:

Suma głosów:

Procentowy udział:

A

1200

(1200/7700)*100%=15,58%

B

2000

(2000/7700)*100%=25,97%

C

4500

(4500/7700)*100%=58,44%

SUMA

7700

100%

Dzielenie mandatów:

Następnie procentowe udziały należy pomnożyć przez ilość mandatów

w okręgu w poniższym przykładzie jest to 7:

Pierwszego rozdania mandatów dokonuje się poprzez odrzucenie w

powstałych iloczynach cyfr po przecinku, jeśli suma tak podzielonych

mandatów jest mniejsza mandatów w okręgu, brakujące mandaty

rozdziela się w kolejności ugrupowaniom które miały największą

wartość ułamkową iloczynów.

Nazwa

listy

Suma głosów Proc. udz. Pr. Udz. * il. mandatów

A

B

C
SUMA

1200

2000

4500
7700

15,58%

25,97%

58,44%
100%

1.0906

1.8179

4.0908
7

Nazwa listy

Proc. Udz * il. mandatów

Podz. mandatów

A

B

C

1.0906

1.8179

4.0908

1

1+1

4

Dzielenie mandatów:

Opisywana metoda Hare – Niemeyera została zastosowana w Polsce

w wyborach do parlamentu europejskiego w 2004r. Została jednak

powiązana z metodą d`Hondta. Procedura podziału była następująca:

- Mandaty w skali kraju dzieli się przy pomocy metody d`Hondta.

- Ilość mandatów w okręgu nie jest stała – wylicza się ją w oparciu o

bezwzględną ilość głosów oddaną na dane ugrupowanie w okręgu, w

stosunku do ilości głosów jaka padła na dane ugrupowanie w całym

kraju. Stosuje się następujący wzór:

Część całkowita z powstałego wyniku oznacza ilość mandatów

przypadających danemu ugrupowaniu w okręgu w pierwszym rozdaniu.

Ilość mandatów zdobytych przez ufupowanie w okręgu =

(bezwględna liczba głosów oddanych na dane ugrupowanie w

okręgu / bezwzględnia liczba głosów oddanych na dane

ugrupowanie w kraju)*ilość mandatów przypadających

ugrupowaniu w kraju wynikających z podziału metoda d’Hondta

Listy partyjne:

Głosowanie polega na tym, iż wyborca oddaje swój głos na

poszczególne listy partyjne. Występują dwie metody takiego

głosowania. Pierwsza z nich pozwala wyborcy na dokonywanie

preferencji w ramach listy, co powoduje, że mandaty z listy otrzymują

kolejno kandydaci, którzy uzyskali największe liczby głosów w ramach

listy. Druga metoda popularna w Ameryce Łacińskiej nie pozwala na

preferowanie kandydatów, a o uzyskaniu mandatu decyduje wyłącznie

kolejność umieszczenia kandydata na liście. Występują również

rozwiązania pośrednie, gdzie co do zasady decyduje miejsce na liście,

chyba, że na kandydata oddano co najmniej określoną ustawowo,

procentową liczbę głosów (np. Republika Czeska).

FORMUŁA D’HONDTA: polega na tym, że liczby głosów oddane na

poszczególne listy dzieli się przez kolejne liczby naturalne (1,2,3,4), w

ilości równej ilości mandatów do obsadzenia; mandaty otrzymują te

listy, które posiadają kolejne największe ilorazy. System stosowany jest

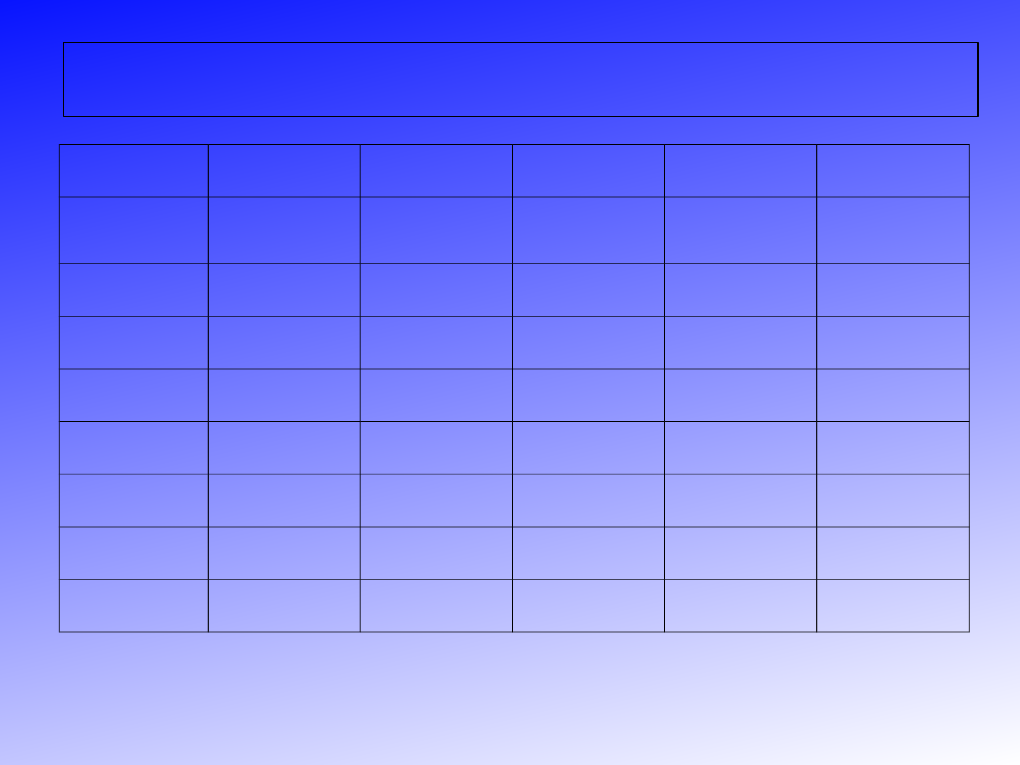
np. w Holandii, Belgii, Austrii, Hiszpanii, Portugalii i Grecji. Poniższy

przykład przedstawia podział mandatów zgodnie z formułą d’Hondta w

okręgu siedmiomandatowym:

Listy partyjne:

W powyższym przypadku partia A uzyska 3 mandaty, partia B  - 2

mandaty, a partie C i D po 1 mandacie.

 

Partia A

Partia B

Partia C

Partia D

Partia E

wynik

uzyskany

120000

105000

80000

45000

25000

/ 1

120000

105000

80000

45000

25000

/ 2

60000

52500

40000

22500

12500

/ 3

40000

35000

26667

15000

8333

/ 4

30000

26250

20000

11250

6250

/ 5

24000

21000

16000

9000

5000

/ 6

20000

17500

13333

7500

4167

/ 7

17143

15000

11429

6429

3571

Listy partyjne:

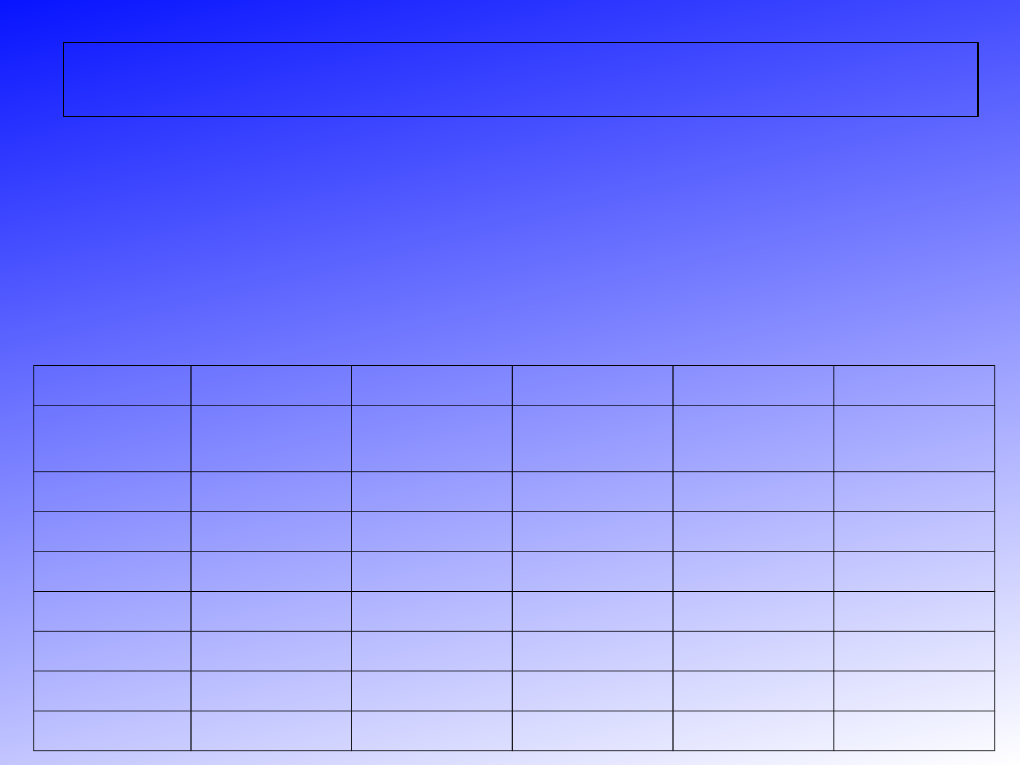
FORMUŁA ST. LAGUE: polega na tym, że liczby głosów oddane

na poszczególne listy dzieli się przez kolejne liczby nieparzyste (1,

3, 5, 7), w ilości równej ilości mandatów do obsadzenia; mandaty

otrzymują te listy, które posiadają kolejne największe ilorazy.

Stosowany jest np. na Łotwie i w Izraelu. Poniższy przykład

przedstawia podział mandatów zgodnie z formułą St. Lague w

okręgu siedmiomandatowym.

 

Partia A

Partia B

Partia C

Partia D

Partia E

wynik

uzyskany

120000

105000

80000

45000

25000

/ 1

120000

105000

80000

45000

25000

/ 3

40000

35000

26667

15000

8333

/ 5

24000

21000

16000

9000

5000

/ 7

17143

15000

11429

6429

3571

/ 9

13333

11667

8889

5000

2778

/ 11

10909

9545

7273

4091

2273

/ 13

9231

8077

6154

3461

1923

Listy partyjne:

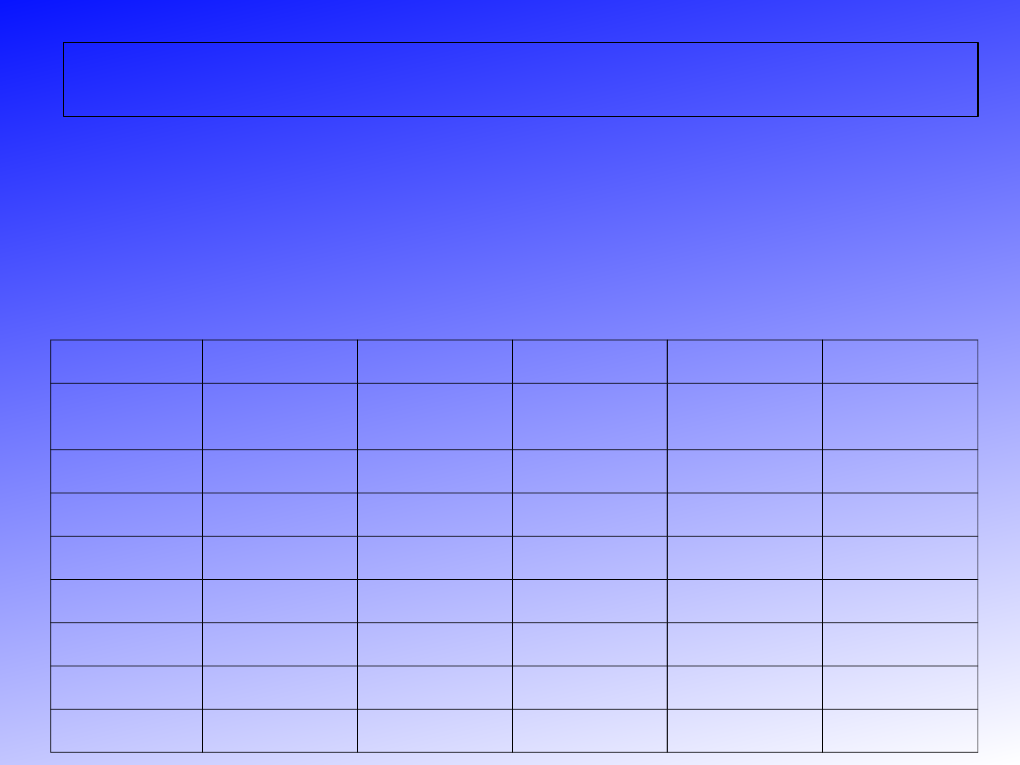
FORMUŁA HUNTINGTONA: polega na tym, że liczby głosów oddane

na poszczególne listy dzieli się przez pierwiastek z liczby n*(n-1),

przy czym n jest kolejną liczbą naturalną począwszy od 2, w ilości

równej ilości mandatów do obsadzenia; mandaty otrzymują te listy,

które posiadają kolejne największe ilorazy:

 

Partia A

Partia B

Partia C

Partia D

Partia E

wynik

uzyskany

120000

105000

80000

45000

25000

/ 1,4

85714

75000

57143

32143

17857

/ 3

40000

35000

26667

15000

8333

/ 5

24000

21000

16000

9000

5000

/ 7

17143

15000

11429

6429

3571

/ 9

13333

11667

8889

5000

2778

/ 11

10909

9545

7273

4091

2273

/ 13

9231

8077

6154

3461

1923

Listy partyjne:

FORMUŁA HAGENBACH – BISCHOFFA: zgodnie z tą metodą

wyniki poszczególnych list partyjnych dzieli się poprzez dzielnik

wyborczy, którym jest iloraz liczby ważnie oddanych głosów oraz

ilości mandatów do obsadzenia powiększonej o jeden mandat

fikcyjny; liczby całkowite z tego działania oznaczają liczbę mandatów

uzyskanych przez poszczególne listy. W sytuacji, gdy pozostaną

mandaty nieobsadzone stosuje się metodę największej reszty,

zgodnie z którą mandaty dodatkowe przyznaje się kolejno

ugrupowaniom, które posiadają największe reszty z danego

dzielenia. Stosowany do roku 2000 w Republice Czeskiej. Poniższy

przykład przedstawia podział mandatów zgodnie z formułą

Hagenbach - Bischoffa w okręgu siedmiomandatowym.

Łączna liczba ważnie oddanych głosów - 375000

partia A – 120000 głosów, partia B – 105000 głosów, partia C –

80000 głosów, partia D – 45000 głosów i partia E – 25000 głosów

partia A: 120000/(375000/7+1) = 2,56, czyli 2 mandaty

partia B: 105000/(375000/7+1) = 2,24, czyli 2 mandaty

partia C: 80000/(375000/7+1) = 1,71,czyli 1 mandat

partia D: 45000/(375000/7+1) = 0,96, czyli 0 mandatów

partia E: 25000/(375000/7+1) = 0,53, czyli 0 mandatów

Listy partyjne:

FORMUŁA HARE’A – NIEMEYERA: zgodnie z tą metodą wyniki

poszczególnych list partyjnych dzieli się poprzez dzielnik wyborczy,

którym jest iloraz liczby ważnie oddanych głosów oraz ilości mandatów

do obsadzenia; liczby całkowite z tego działania oznaczają liczbę

mandatów uzyskanych przez poszczególne listy. W sytuacji, gdy

pozostaną mandaty nieobsadzone możliwe są dwa sposoby ich podziału.

Pierwszy to metoda największej reszty. Druga sposób to metoda

największej średniej, która polega na przyznaniu dodatkowych mandatów

ugrupowaniom, które uzyskają kolejne największe średnie, czyli

posiadają największy stosunek liczby uzyskanych głosów do liczby

zdobytych mandatów w pierwszej fazie powiększonej o jeden mandat

fikcyjny. Stosowany jest np. w Niemczech i we Włoszech.

Łączna liczba ważnie oddanych głosów - 375000

partia A – 120000 głosów, partia B – 105000 głosów, partia C – 80000

głosów, partia D – 45000 głosów i partia E – 25000 głosów

partia A: 120000/(375000/7) = 2,24, czyli 2 mandaty

partia B: 105000/(375000/7) = 1,96, czyli 1 mandat

partia C: 80000/(375000/7) = 1,49, czyli 1 mandat

partia D: 45000/(375000/7) = 0,84, czyli 0 mandatów

partia E: 25000/(375000/7) = 0,47, czyli 0 mandatów

Listy partyjne:

FORMUŁA IMPERIALI: zgodnie z tą metodą wyniki poszczególnych list

partyjnych dzieli się poprzez dzielnik wyborczy, którym jest iloraz liczby

ważnie oddanych głosów oraz ilości mandatów do obsadzenia

powiększonej o dwa mandaty fikcyjne; liczby całkowite z tego działania

oznaczają liczbę mandatów uzyskanych przez poszczególne listy. W

sytuacji, gdy pozostaną mandaty nieobsadzone stosuje się metodę

największej reszty, zgodnie z którą mandaty dodatkowe przyznaje się

kolejno ugrupowaniom, które posiadają największe reszty z danego

dzielenia. Analogicznie postępuje się, gdy mandatów rozdzielonych

będzie zbyt dużo. Wtedy odejmuje się je ugrupowaniom, które posiadają

najmniejsze reszty. Stosowany we Włoszech do 1993 roku.

partia A – 120000 głosów, partia B – 105000 głosów, partia C – 80000

głosów, partia D – 45000 głosów i partia E – 25000 głosów

partia A: 120000/(375000/7+2) = 2,88, czyli 2 mandaty

partia B: 105000/(375000/7+2) = 2,52, czyli 2 mandaty

partia C: 80000/(375000/7+2) = 1,92,czyli 1 mandat

partia D: 45000/(375000/7+2) = 1,08, czyli 1 mandat

partia E: 25000/(375000/7+2) = 0,60, czyli 0 mandatów

Koniec:

Dziękuję za uwagę!