
T11. Kinematyka punktu
materialnego
Opis ruchu punktu materialnego.
Składanie ruchów.
Prędkość i przyspieszenie.
Równania ruchu punktu
materialnego.
Przyspieszenie dośrodkowe i
styczne.
Prędkość i przyspieszenie kątowe.
Szczególne przypadki ruchu punktu
materialnego.
Prędkość i przyspieszenie w ruchu
względnym

Kinematyka
– dział mechaniki zajmujący się
opisem ruchu ciał materialnych, bez wnikania w
przyczynę ruchu.
Dynamika
– dział mechaniki zajmujący się opisem
ruchu ciał materialnych pod wpływem sił
działających na te ciała.
Kinematyka i dynamika dostarczają nam narzędzi
obliczeniowych do przewidywania, jak w czasie
zmieniają swoje
położenie w przestrzeni
ciała
poddane działaniu sił.
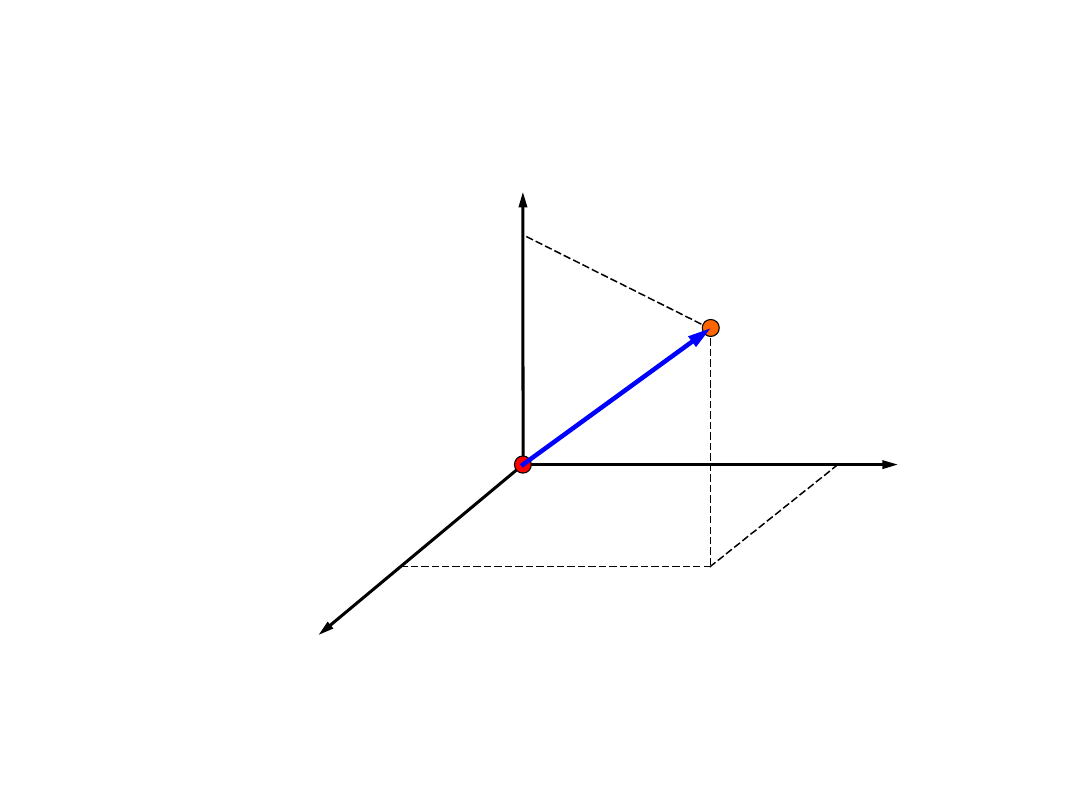
Opis ruchu punktu
materialnego
Położenie punktu
w przestrzeni w chwili czasu t
charakteryzujemy za pomocą wektora, zwanego
promieniem wodzącym, poprowadzonego z początku
wybranego układu współrzędnych
0
Punktem
materialnym
nazywamy
ciało
materialne o wymiarach pomijalnie małych w
porównaniu z wielkością obszaru przestrzeni, w
którym ruch tego ciała rozpatrujemy.
( )
r t
r
( )
y t
( )
x t
( )
z t
x
y
z
( ( ), ( ), ( ))
r x t y t z t
r
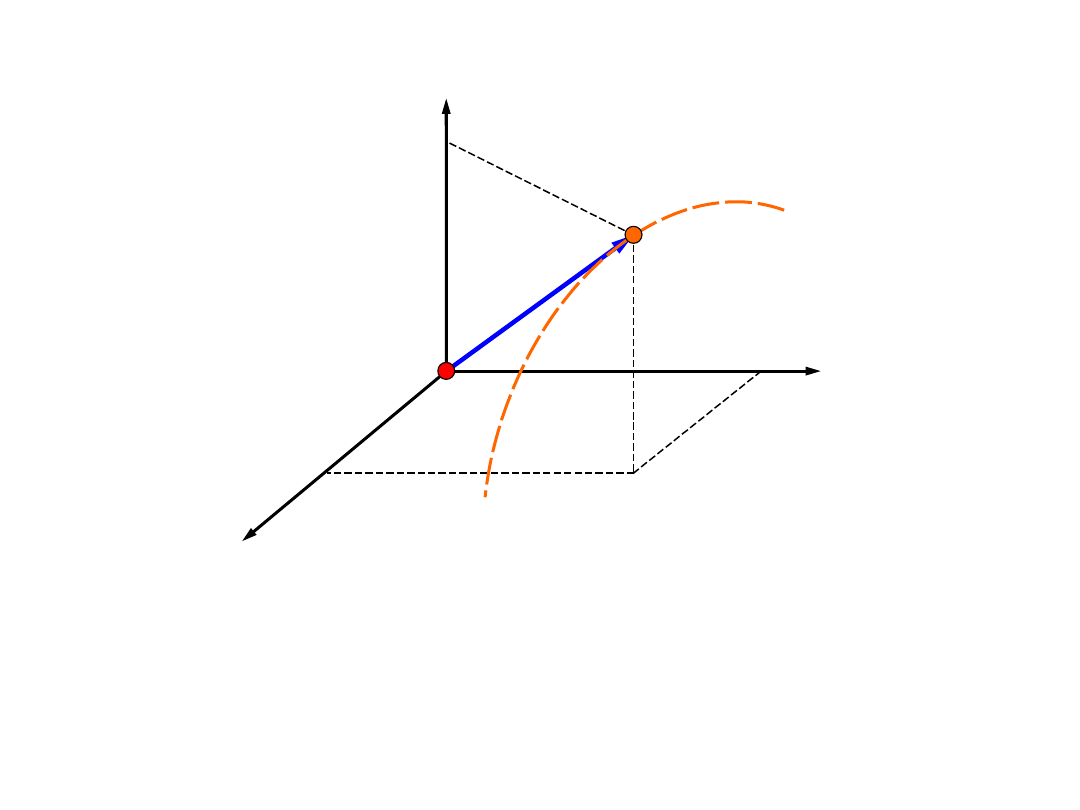
Opis ruchu punktu
materialnego
Trajektorią punktu
nazywamy miejsce geometryczne
położeń
punktu
materialnego
w
kolejnych
momentach czasu. Trajektorię punktu zadają trzy
funkcje x(t), y(t), z(t).
Torem punktu
nazywamy krzywą geometryczną, o
kształcie trajektorii punktu.
0
( )
r t
r
( )
y t
( )
x t
( )
z t
x
y
z
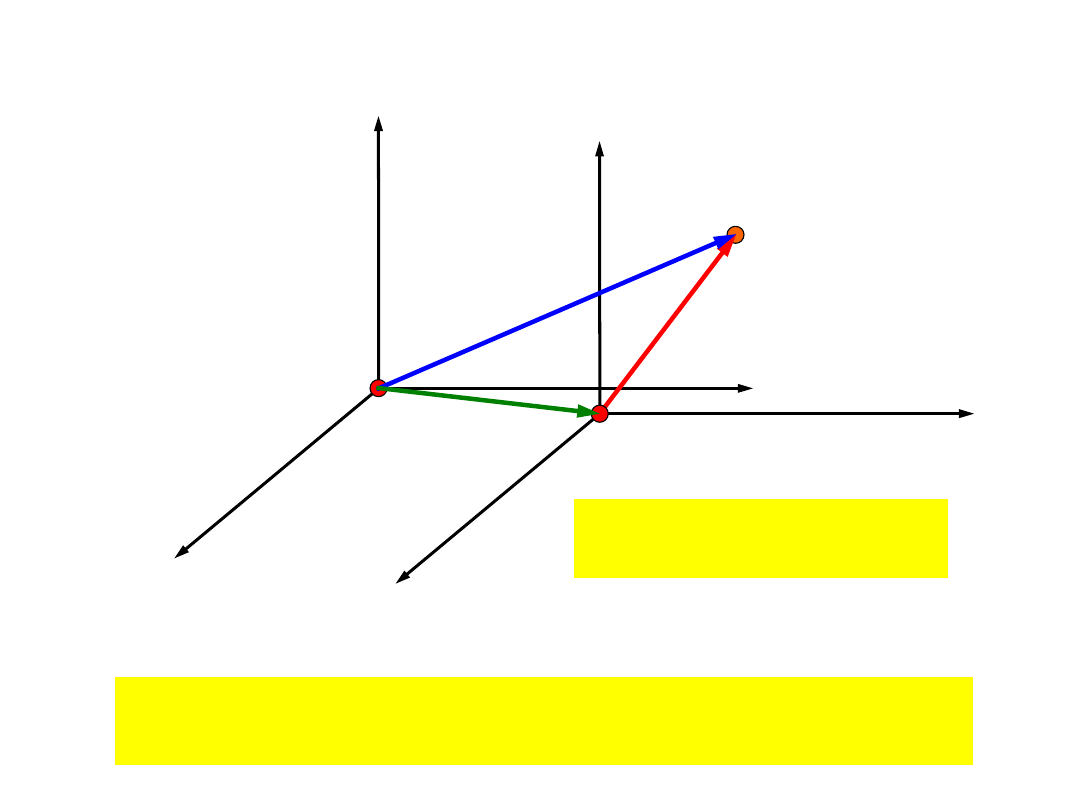
Składanie
ruchów
0
( )
r t
r
x
y
z
z
1
y
1
x
1
0
( )
r t
r
0
1
1
( )
r t
r
1
0
( )
( )
( )
r t
r t
r t
=
+
r
r
r
(
)
1
0
1
0
1
0
( )
( ), ( )
( ), ( )
( )
r x t
x t y t
y t z t
z t
+
+
+
r
Przy tej samej orientacji przestrzennej osi układu
współrzędnych:
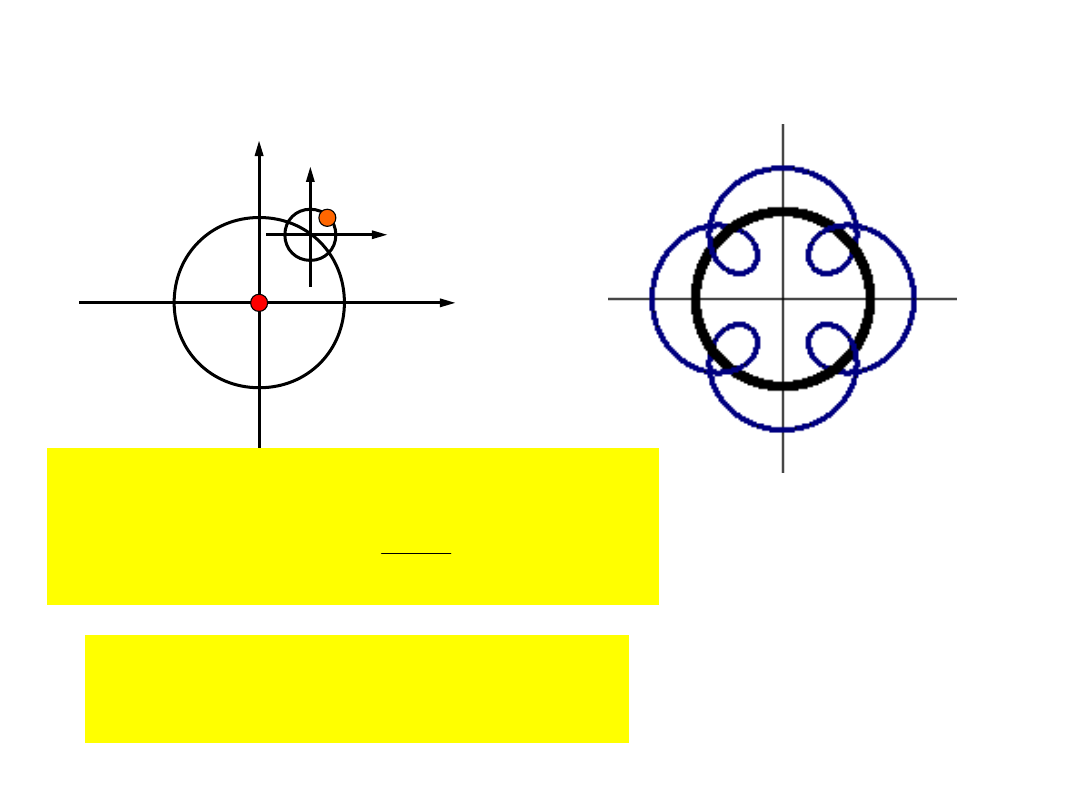
Składanie
ruchów
x
y
x
1
y
1
0
Epicykloid
a
1
= 5
0
(
)
(
)
1
1
1
1
1
1
1
1
1
1
1
( )
cos
,
( )
sin
(0)
arctg
(0)
x t
r
t
y t
r
t
y
x
w
j
w
j
j
=
+
=
+
�
�
=
�
�
�
�
(
)
(
)
(
)
(
)
1
1
1
0
0
0
1
1
1
0
0
0
( )
cos
cos
( )
sin
sin
x t
r
t
r
t
y t
r
t
r
t
w
j
w
j
w
j
w
j
=
+
+
+
=
+
+
+
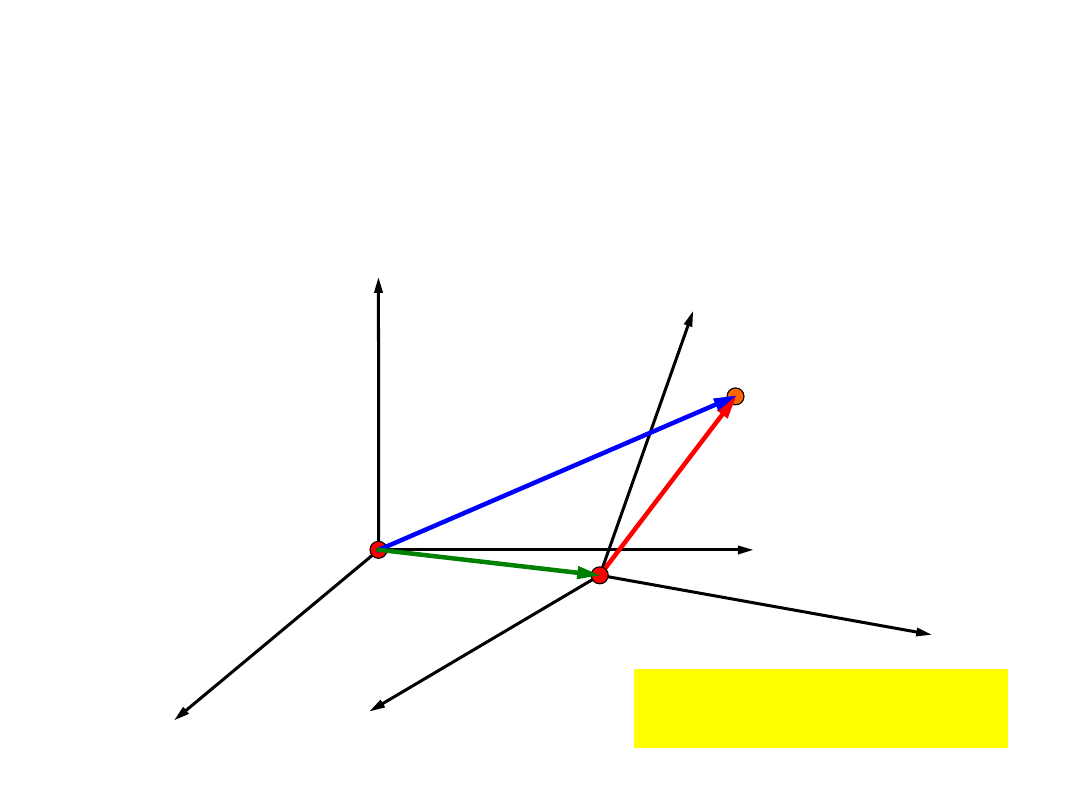
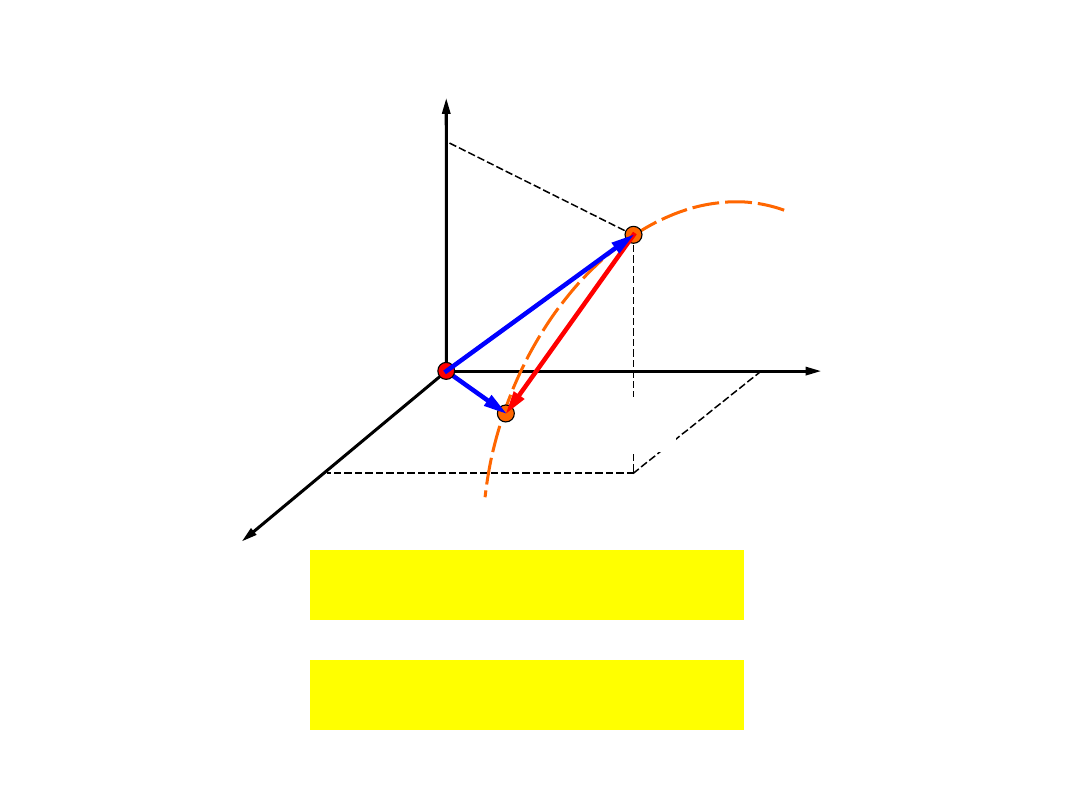
Składanie
ruchów
Ruch względem układu nieruchomego nazywamy
ruchem bezwzględnym
. Ruch względem układu
ruchomego nazywamy
ruchem względnym
.
0
( )
r t
r
x
y
z
z
1
y
1
x
1
0
( )
r t
r
0
1
1
( )
r t
r
1
0
( )
( )
( )
r t
r t
r t
=
+
r
r
r
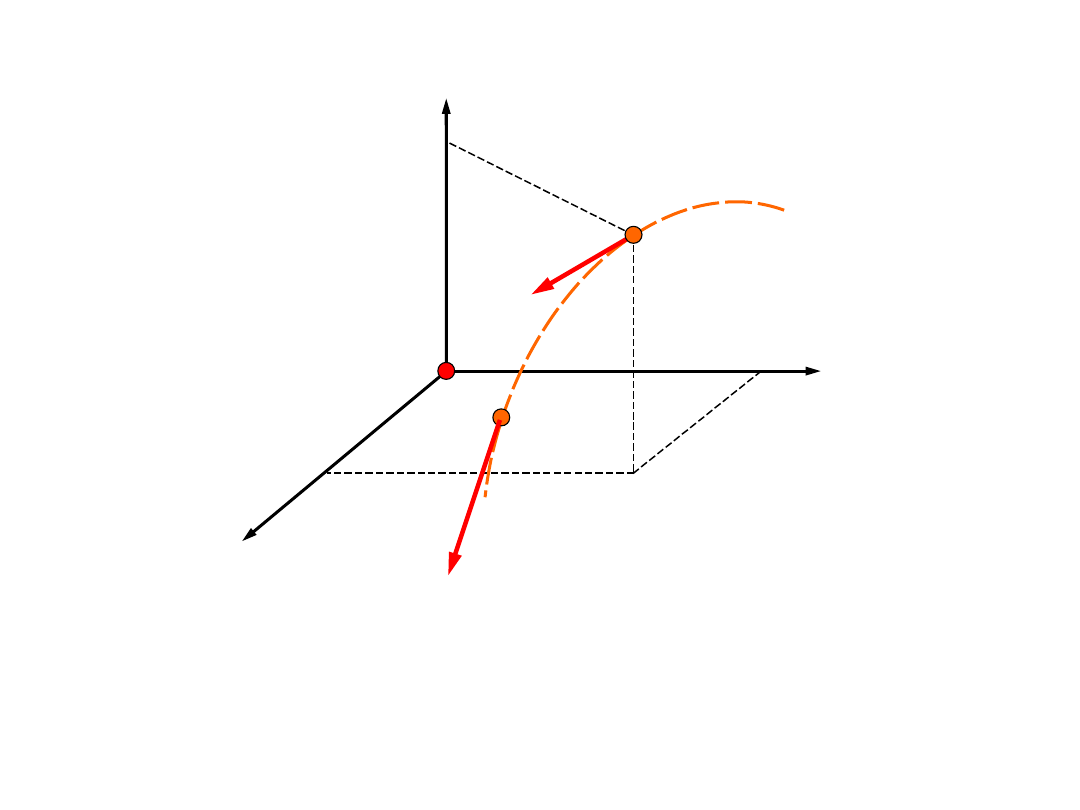
Prędkość i
przyspieszenie
0
( )
r t
r
( )
y t
( )
x t
( )
z t
x
y
z
(
)
r t
t
+D
r
r
D
r
(
)
( )
r t
t
r t
r
+D =
+D
r
r
r
(
)
( )
r r t
t r t
D =
+D -
r r
r
A
B

Prędkość i
przyspieszenie
(
)
( )
AB
s t
t
s t
u
t
+D -
=
D
s(t) – droga przebyta przez punkt materialny do
punktu A
s(t+t) - droga przebyta przez punkt materialny do
punktu B
Średnia prędkość na odcinku toru
AB
:
0
(
)
( )
lim
t
s t
t
s t
ds
u
t
dt
D �
+D -
=
=
D
Chwilowa prędkość w punkcie toru
A
:
( )
( )
0
t
s t
u
d
t t
=
�

Prędkość i
przyspieszenie
0
0
(
)
( )
lim
lim
t
t
r
r t
t
r t
dr
u
t
t
dt
D �
D �
D
+D -
=
=
=
D
D
r
r
r
r
r
Prędkością
punktu
materialnego
nazywamy
granicę do której dąży stosunek wektora przyrostu
promienia wodzącego do przyrostu czasu, gdy
przyrost czasu dąży do zera. Prędkość jest
wektorem o kierunku i zwrocie zgodnym z
kierunkiem
i
zwrotem
wektora
przyrostu
promienia wodzącego.
Dla scharakteryzowania zmiany położenia punktu
materialnego wprowadza się pojęcie prędkości
jako wektora
Prędkość i
przyspieszenie
( )
( )
( )
( )
r t
i x t
j y t
k z t
=
+
+
r
r
r
r
0
0
0
(
)
( )
(
)
( )
(
)
( )
lim
lim
lim
t
t
t
x t
t
x t
y t
t
y t
z t
t
z t
u i
j
k
t
t
t
D �
D �
D �
+D -
+D -
+D -
=
+
+
D
D
D
r
r
r
r
dx
dy
dz
u i
j
k
dt
dt
dt
=
+
+
r
r
r
r
,
,
x
y
z
dx
dy
dz
u
u
u
dt
dt
dt
=
=
=
Składowe wektora prędkości wyrażają się jako
pochodne po czasie składowych promienia
wodzącego

Prędkość i
przyspieszenie
Wektor przyrostu promienia wiodącego stanowi
sieczną toru. W granicy staje się styczny do toru.
Wektor prędkości ma ten sam kierunek co wektor
przyrostu promienia, zatem
jest styczny do toru
.
Dla odpowiednio małych t :
2
2
2
s
r
x
y
z
D @D = D +D +D
r
zatem:
0
0
0
lim
lim
lim
t
t
t
r
s
r
u
u
t
t
t
D �
D �
D �
D
D
D
=
=
=
=
D
D
D
r
r
r
2
2
2
x
y
z
u
u
u
u
=
+ +
Prędkość chwilowa równa jest wartości wektora
prędkości.
Prędkość i
przyspieszenie
0
( )
u t
r
( )
y t
( )
x t
( )
z t
x
y
z
(
)
u t
t
+D
r
A
B

Prędkość i
przyspieszenie
(
)
( )
AB
u t
t u t
a
t
+D -
=
D
Średnie przyspieszenie na odcinku
toru AB
:
0
(
)
( )
lim
s
t
u t
t u t
du
a
t
dt
D �
+D -
=
=
D
Chwilowe przyspieszenie w punkcie
toru A
:
( )
( )
( )
0
0
t
s
u t
u
a
d
t t
-
=
�
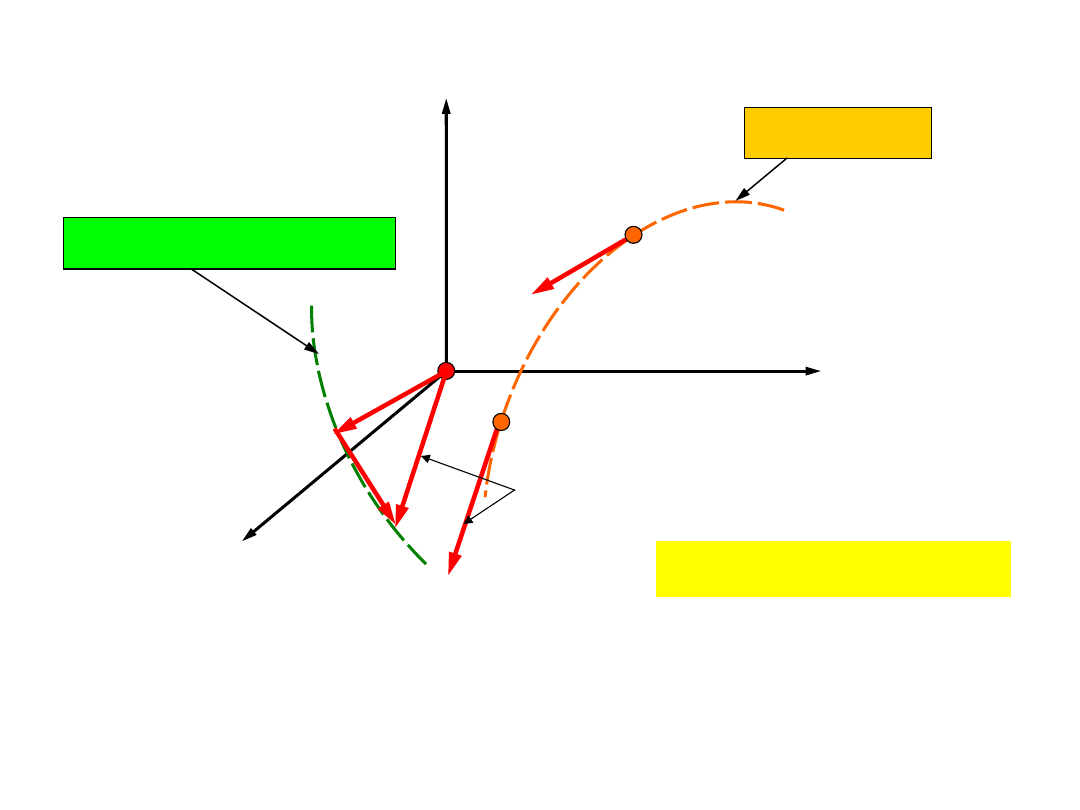
Prędkość i
przyspieszenie
0
( )
u t
r
x
y
z
(
)
u t
t
+D
r
A
B
( )
u t
r
hodograf prędkości
tor punktu
Hodografem prędkości
nazywamy miejsce geometryczne
końców wektora prędkości dla różnych chwil czasu, gdy
początek wektora prędkości jest ustalony w początku układu
współrzędnych
(
)
( )
u u t
t u t
D =
+D -
r r
r
u
D
r

Prędkość i
przyspieszenie
0
0
(
)
( )
lim
lim
t
t
u
u t
t u t
du
a
t
t
dt
D �
D �
D
+D -
=
=
=
D
D
r
r
r
r
r
Przyspieszeniem punktu materialnego
nazywamy
granicę do której dąży stosunek wektora przyrostu
prędkości do przyrostu czasu, gdy przyrost czasu
dąży do zera. Przyspieszenie jest wektorem o
kierunku i zwrocie zgodnym z kierunkiem i
zwrotem wektora przyrostu prędkości.
Dla scharakteryzowania zmiany wartości i
kierunku wektora prędkości wprowadza się
przyspieszenie jako wielkość wektorową
Równania ruchu punktu
materialnego
( )
( )
,
dr
du
u t
a t
dt
dt
=
=
r
r
r
r
( )
( )
( )
( )
( )
( )
,
,
,
,
x
y
z
y
x
z
x
y
z
dx
dy
dz
u t
u t
u t
dt
dt
dt
du
du
du
a t
a t
a t
dt
dt
dt
=
=
=
=
=
=
( )
( )
( )
( )
( )
( )
0
0
0
0
0
0
0
,
0
,
0
0
,
0
,
0
x
x
y
y
z
z
x
x
y
y
z
z
u
u
u
u
u
u
=
=
=
=
=
=
Warunek początkowy:
Równania ruchu punktu
materialnego
d dr
du
dt dt
dt
� �=
� �
� �
r
r
( )
( )
( )
2
2
2
2
2
2
,
,
x
y
z
d x
d y
d z
a t
a t
a t
dt
dt
dt
=
=
=
( )
( )
( )
( )
( )
( )
0
0
0
0
0
0
0
,
0
,
0
0
,
0
,
0
x
y
z
x
x
y
y
z
z
dx
dy
dz
u
u
u
dt
dt
dt
=
=
=
=
=
=
Warunek początkowy:
( )
2
2
d r
a t
dt
=
r
r
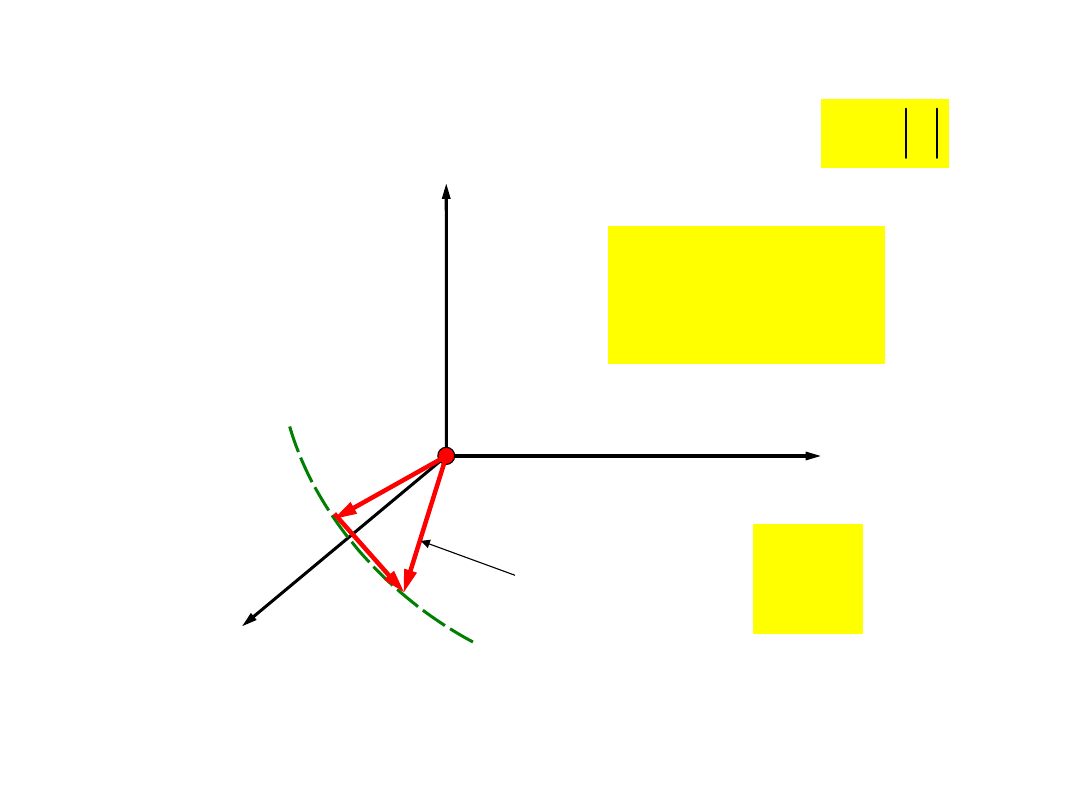
Czy podobnie jak dla prędkości, zachodzi relacja
?
s
a
a
=
r
( )
(
)
( )
(
)
u t
u t
t
u t
u t
t
=
+D
�
+D
r
r
0
0
s
a
a
=
�
r
Przyspieszenie dośrodkowe i
styczne
0
x
y
z
(
)
u t
t
+D
r
B
( )
u t
r
u
D
r
Chwilowe przyspieszenie
nie jest równe
wartości
wektora przyspieszenia.
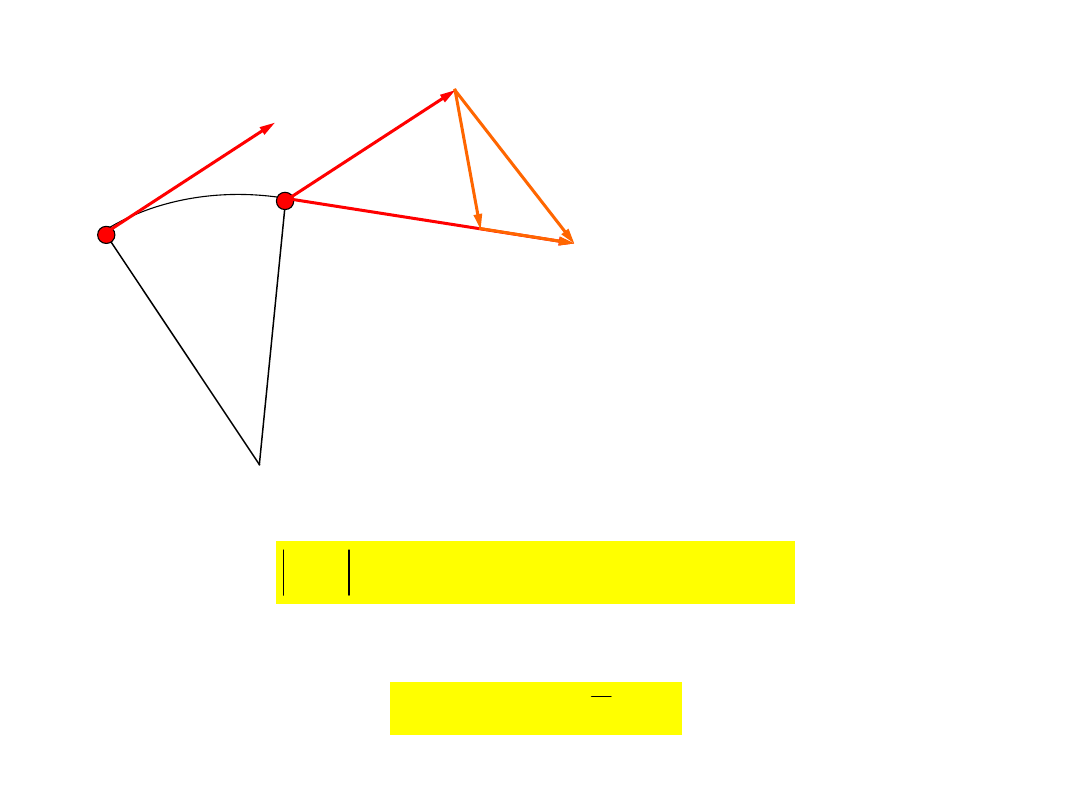
Przyspieszenie dośrodkowe i
styczne
A
B
( )
u t
r
(
)
u t
t
+D
r
( )
u t
D
r
(
)
2 ( )sin
/ 2
( )
n
u
u t
u t
a
a
D =
D
@
D
r
( )
s
u t
D
r
( )
n
u t
D
r
C
D
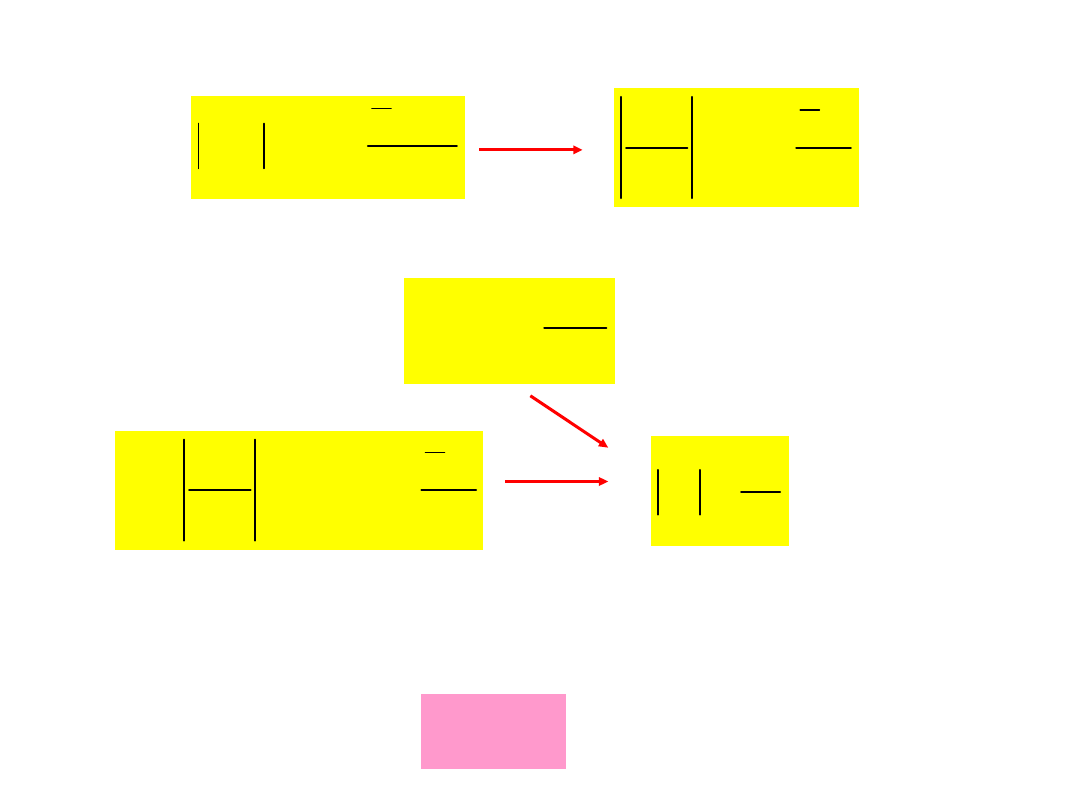
Trójkąt BCD jest trójkątem równoramiennym,
zatem
:
a
D
( )
n
u t
D
r
przyrost prędkości związany ze zmianą
kierunku wektora prędkości
( )
s
u t
D
r
przyrost prędkości związany ze zmianą
długości wektora prędkości
a
D
Przybliżamy odcinek toru AB łukiem okręgu o
promieniu
AB
s
u
t
r a
D = D =
D
t
–
promień krzywizny toru
( )
AB
n
u
t
u
u t
r
D
D =
r
0
0
lim
lim ( )
n
AB
t
t
u
u
u t
t
r
D �
D �
D
=
D
r
0
lim
n
n
t
u
a
t
D �
D
=
D
r
r
Wprowadzamy wielkość wektorową zdefiniowaną
wzorem:
( )
n
AB
u
u
u t
t
r
D
=
D
r
2
n
u
a
r
=
r
Gdy t dąży do zera, dąży do zera również kąt . Zatem
wektor przyrostu prędkości u
n
staje się prostopadły do
wektora prędkości, z czego wynika, że:
n
a
u
^
r
r
Przyspieszenie dośrodkowe i
styczne
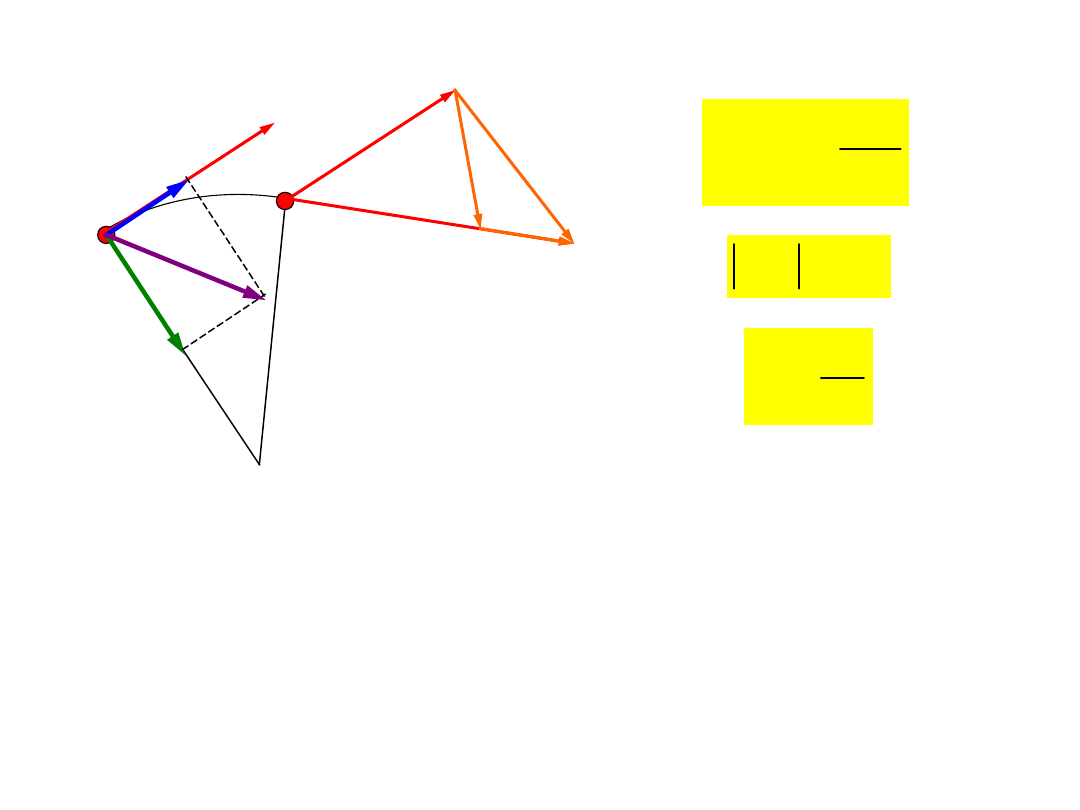
A
B
( )
u t
r
(
)
u t
t
+D
r
( )
u t
D
r
n
a
r
( )
s
u t
D
r
( )
n
u t
D
r
Ponieważ wektor wielkości skierowany jest w
stronę środka krzywizny toru, wielkość tą
nazywamy
przyspieszeniem dośrodkowym
.
( )
n
a t
r
0
lim
s
s
t
u
a
t
D �
D
=
D
r
r
s
u
u
D =D
r
s
du
a
dt
=
Wielkość nazywamy
przyspieszeniem
stycznym
. Długość tego wektora równa jest
pochodnej po czasie długości wektora prędkości.
( )
s
a t
r
( )
a t
r
s
a
r
Przyspieszenie dośrodkowe i
styczne
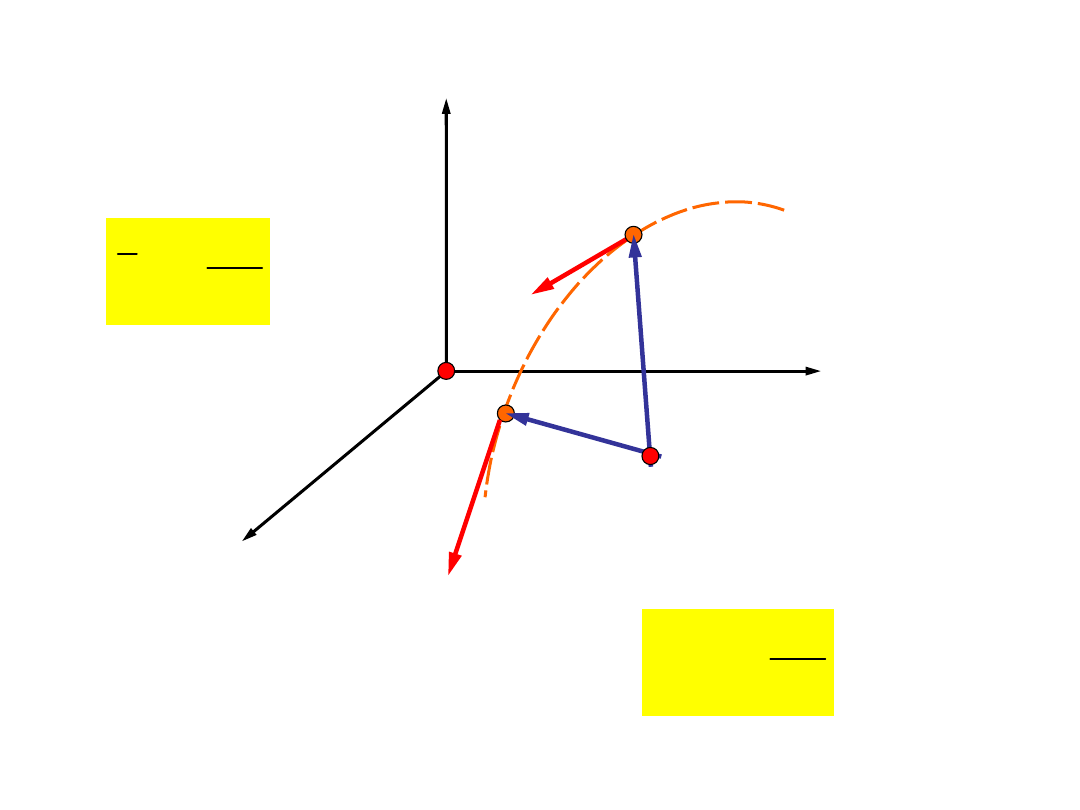
0
x
y
z
A
B
a
D
0
lim
t
t
a
w
D �
D
=
D
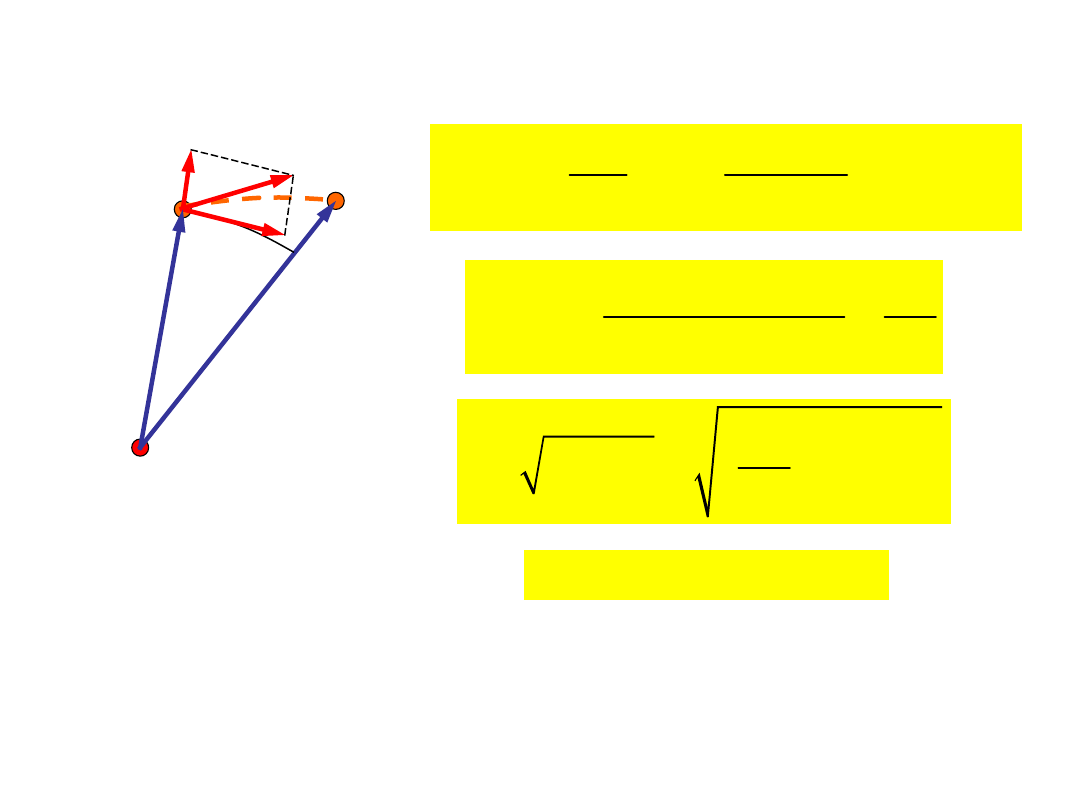
Prędkość i przyspieszenie
kątowe
Chwilowa prędkość
kątowa:
AB
t
a
w
D
=
D
Średnia prędkość
kątowa:
0
1
( )
t
r
r
(
)
t
t
r +D
r
Prędkość i przyspieszenie
kątowe
( )
t
r
(
)
t
t
r +D
A
B
a
D
C
u
r
r
u
a
r
( )
u t
r
0
0
( )
lim
lim
( ) ( )
t
t
AC
t
u
t
t
t
t
a
r
a
r
w
D �
D �
D
=
=
=
D
D
(
)
0
( )
lim
t
t
t
t
d
u
t
dt
r
r
r
r
D �
+D -
=
=
D
2
2
2
2
2
d
u
u
u
dt
r
a
r
r w
� �
=
+
=
+
� �
� �
gdy
const u
r
r w
=
=
0
1
0
x
y
z
A
( )
t
w
r
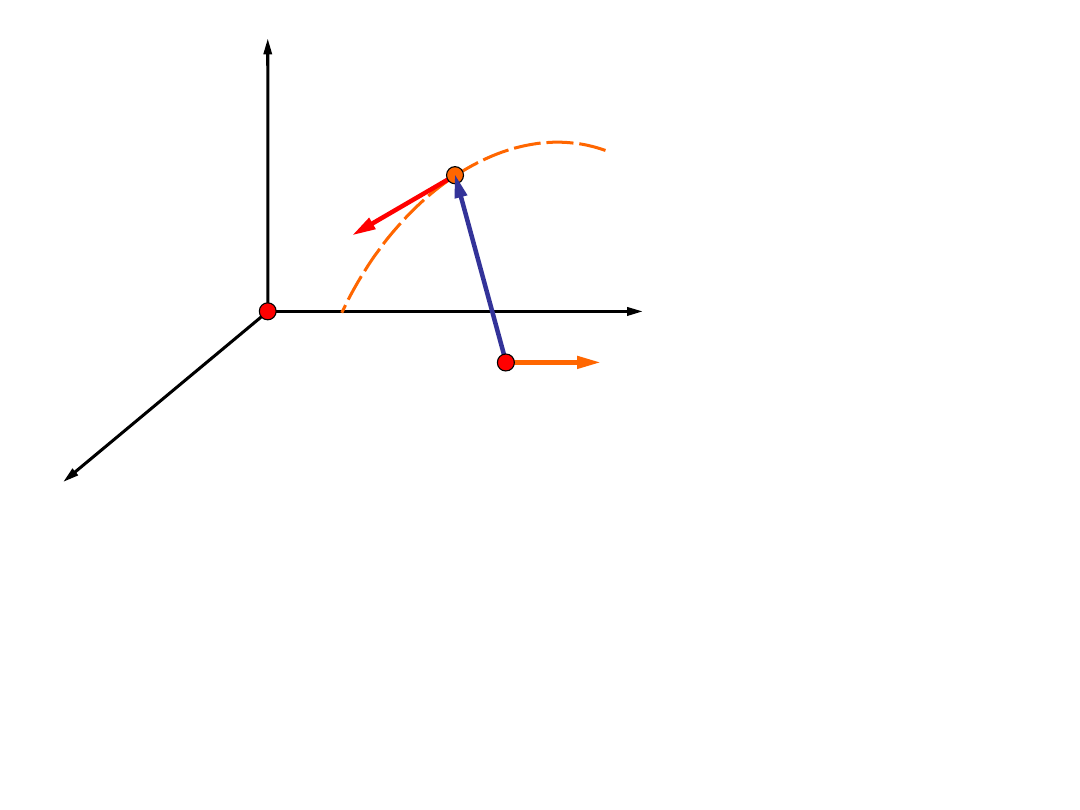
Prędkość i przyspieszenie
kątowe
Chwilowa prędkość kątowa charakteryzuje ruch w płaszczyźnie
wyznaczonej przez wektor promienia i wektor prędkości. Aby
scharakteryzować położenie tej płaszczyzny wystarczy podać
punkt, przez który przechodzi (punkt 0
1
), i wektor do którego
jest prostopadła. Dlatego wprowadza się prędkość kątową jako
wielkość wektorową.
0
1
( )
t
r
r
( )
u t
r
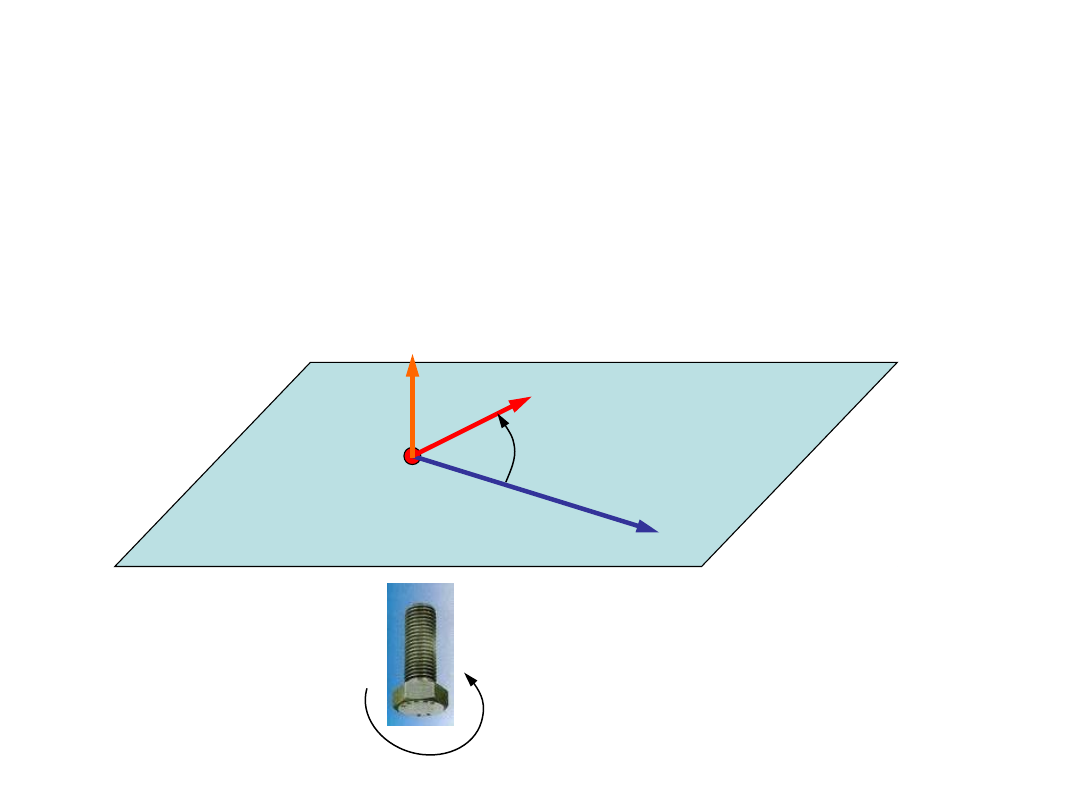
Prędkość i przyspieszenie
kątowe
Prędkością kątową
nazywamy wielkość wektorową o wartości
równej chwilowej prędkości kątowej, o kierunku prostopadłym
do płaszczyzny utworzonej przez wektor promienia wodzącego i
wektor
prędkości,
o zwrocie określonym regułą śruby prawoskrętnej.
0
1
( )
t
r
r
( )
u t
r
( )
t
w
r
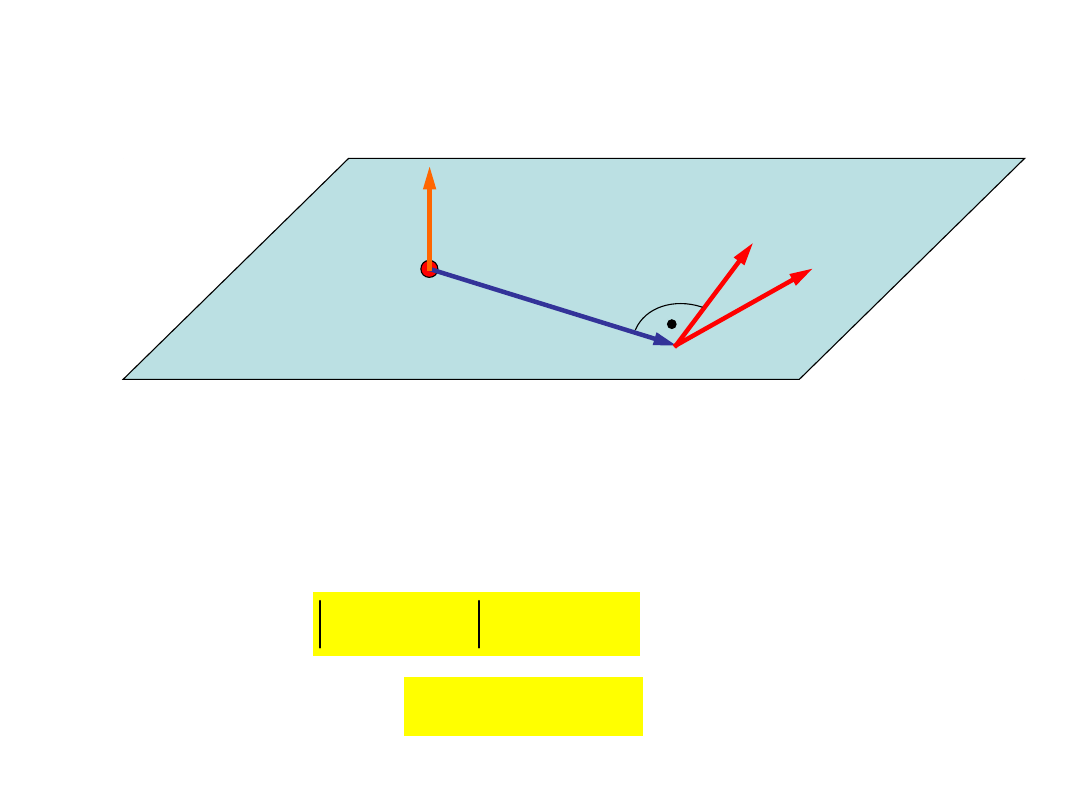
Prędkość i przyspieszenie
kątowe
0
1
( )
t
r
r
( )
u t
r
( )
t
w
r
( )
u t
a
r
( )
, ( ), ( )
t
t u t
a
r
w
r
r
r
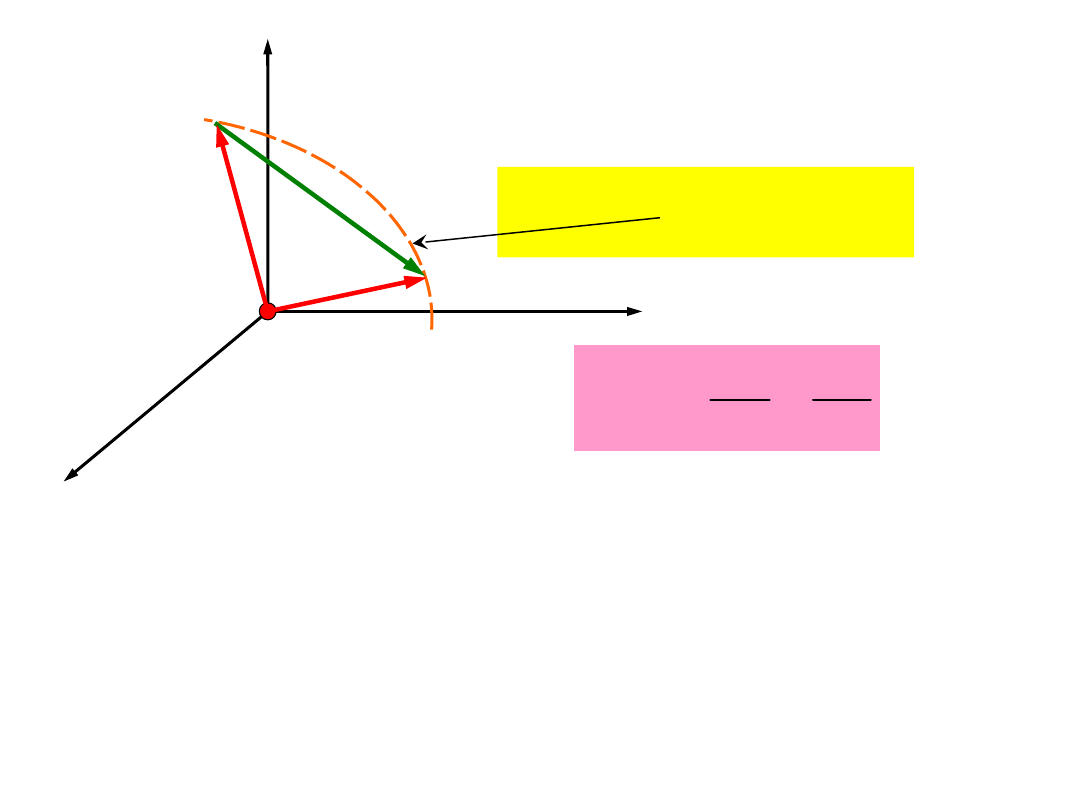
Wektory są wzajemnie prostopadłe. Zatem
kierunek wektora pokrywa się z kierunkiem iloczynu
wektorowego wektorów . Ponieważ te wektory są
prostopadłe, zachodzi:
( )
u t
a
r
( )
, ( )
t
t
r
w
r
r
( )
( )
t
t
u
a
w
r
wr
�
=
=
r
r
zatem:
( )
( )
u
t
t
a
w
r
=
�
r
r
r
0
x
y
z
( )
t
w
r
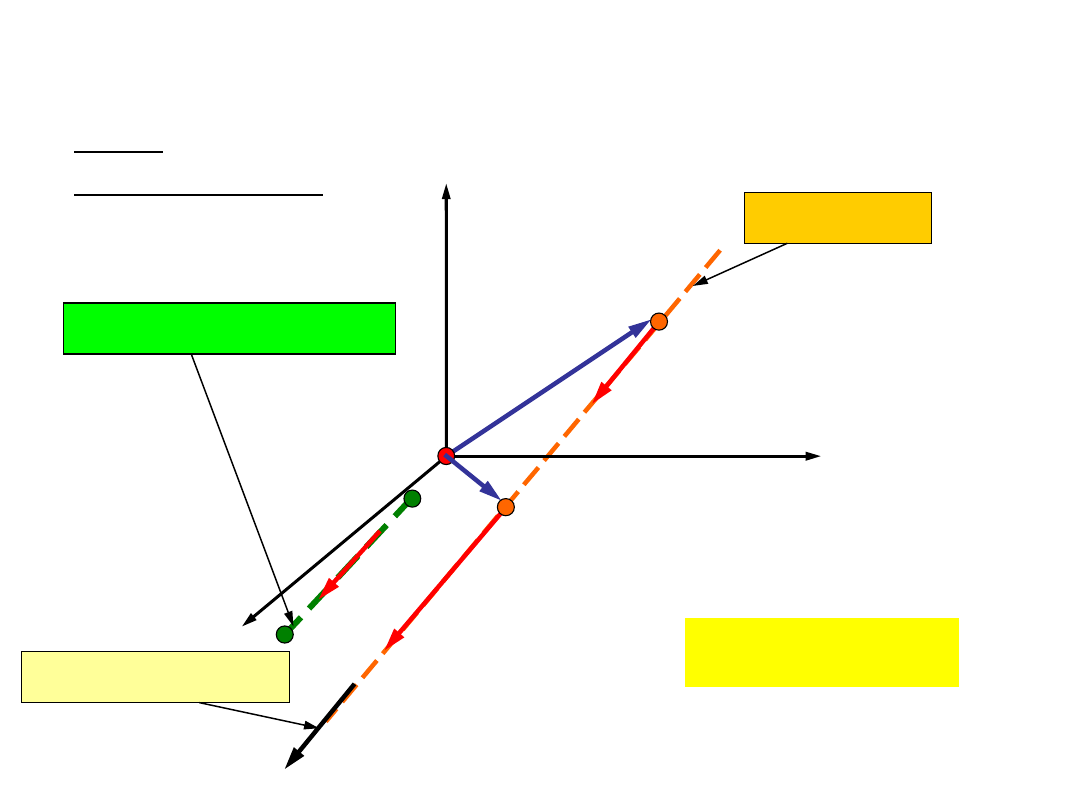
Prędkość i przyspieszenie
kątowe
hodograf
prędkości
kątowej
(
)
t
t
w +D
r
w
D
r
0
lim
t
d
t
dt
w
w
e
D �
D
=
=
D
r
r
r
Przyspieszeniem kątowym
nazywamy granicę do
której dąży stosunek wektora przyrostu prędkości
kątowej do przyrostu czasu, gdy przyrost czasu
dąży do zera. Przyspieszenie kątowe jest
wektorem o kierunku i zwrocie zgodnym z
kierunkiem i zwrotem wektora przyrostu prędkości
kątowej.
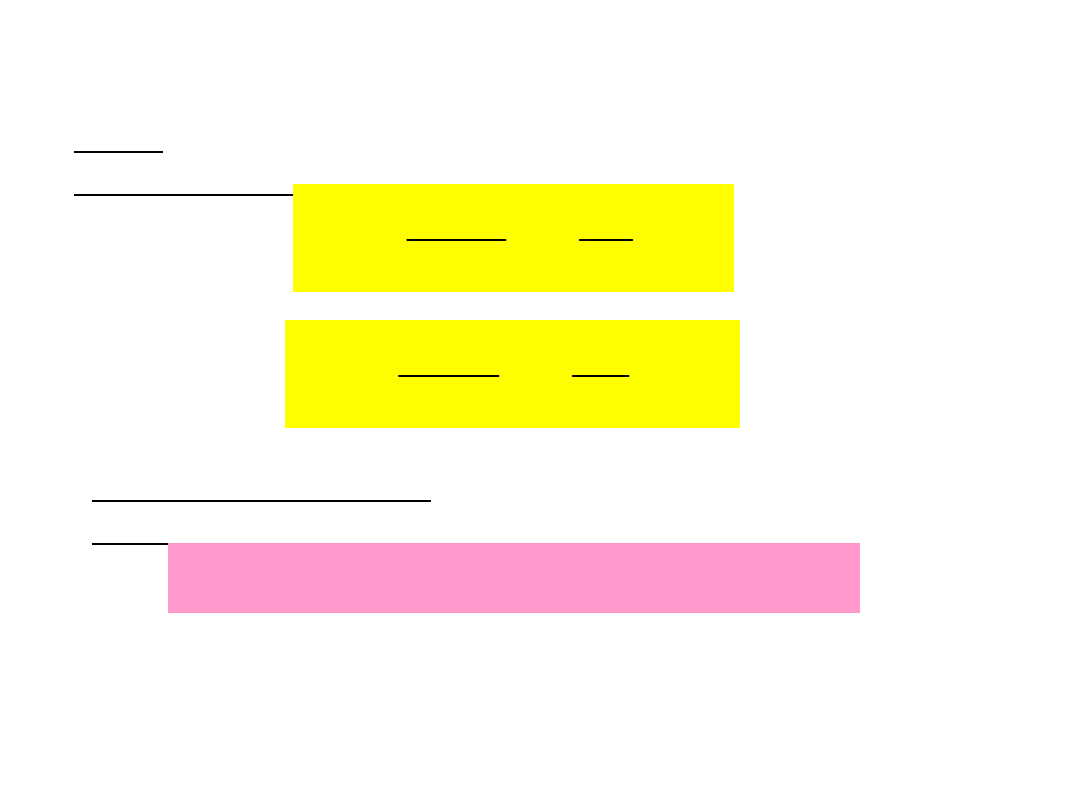
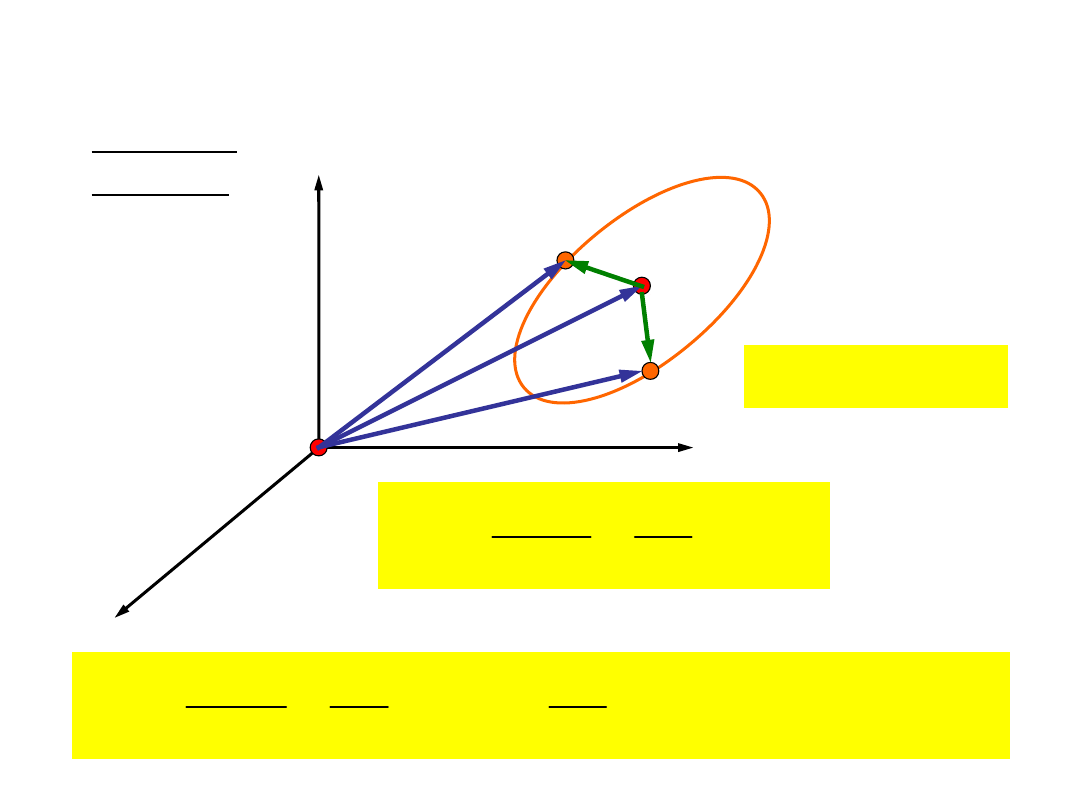
Szczególne przypadki ruchu punktu
materialnego
Ruch
prostoliniowy:
0
( )
u t
r
x
y
z
(
)
u t
t
+D
r
A
B
hodograf prędkości
tor punktu
u
D
r
0
r
r
r
r
k
r
Wektor jednostkowy
0
( )
( )
r t
r k s t
= +
r
r
r
Szczególne przypadki ruchu punktu
materialnego
Ruch
prostoliniowy:
( )
( )
dr t
ds
u t
k
ku
dt
dt
=
=
=
r
r
r
r
( )
( )
s
du t
du
a t
k
ka
dt
dt
=
=
=
r
r
r
r
Ruch prostoliniowy
jednostajny:
0
,
0,
,
u const a
s ut r r kut
=
=
=
= +
r
r r
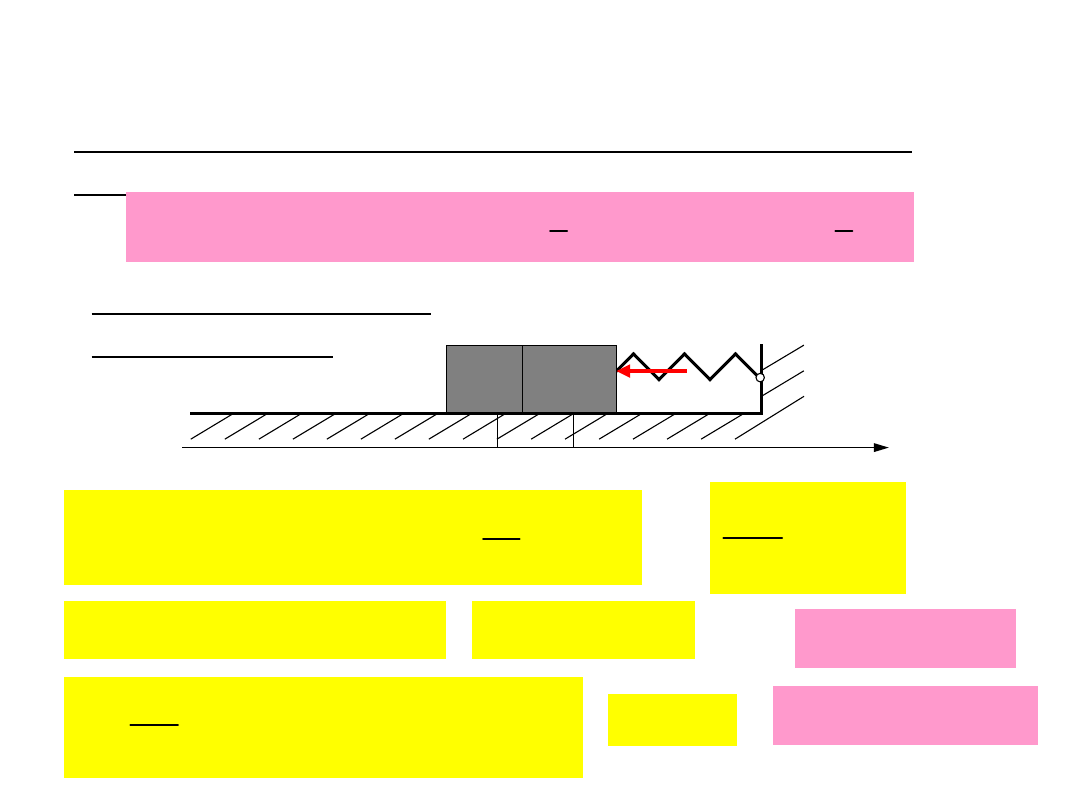
Szczególne przypadki ruchu punktu
materialnego
Ruch prostoliniowy jednostajnie przyspieszony
(opóźniony):
Ruch prostoliniowy
harmoniczny:
2
2
1
1
0
2
2
,
,
,
a const u at s
at
r r k at
=
=
=
= +
r
r r
x
0
x
0
F
2
kx
ma
F
kx
a
w x
m
=-
=-
�
=-
=-
2
2
2
d x
w x
dt
=-
( )
( )
sin
cos
x A
wt
B
wt
=
+
0
(0)
x
x
B
= =
( )
( )
cos
sin
d x
u
Aw
wt
Bw
wt
dt
=
=
-
0 Aw
=
( )
0
cos
x x
wt
=
( )
0
cos
u
wx
wt
=-
Szczególne przypadki ruchu punktu
materialnego
Ruch po
okręgu:
x
y
z
0
0
1
0
r
r
( )
r t
r
01
r
r
( )
t
r
r
0
r
r
( )
( )
dr t
d
u t
dt
dt
r
w r
=
=
= �
r
r
r r
r
01
( )
( )
r t
r
t
r
= +
r
r
r
( )
( )
s
n
du t
d
d
a t
u a a
dt
dt
dt
w
r
r w
e r w
=
=
� + �
= � + � = +
r
r
r
r r
r r r
r
r r
r

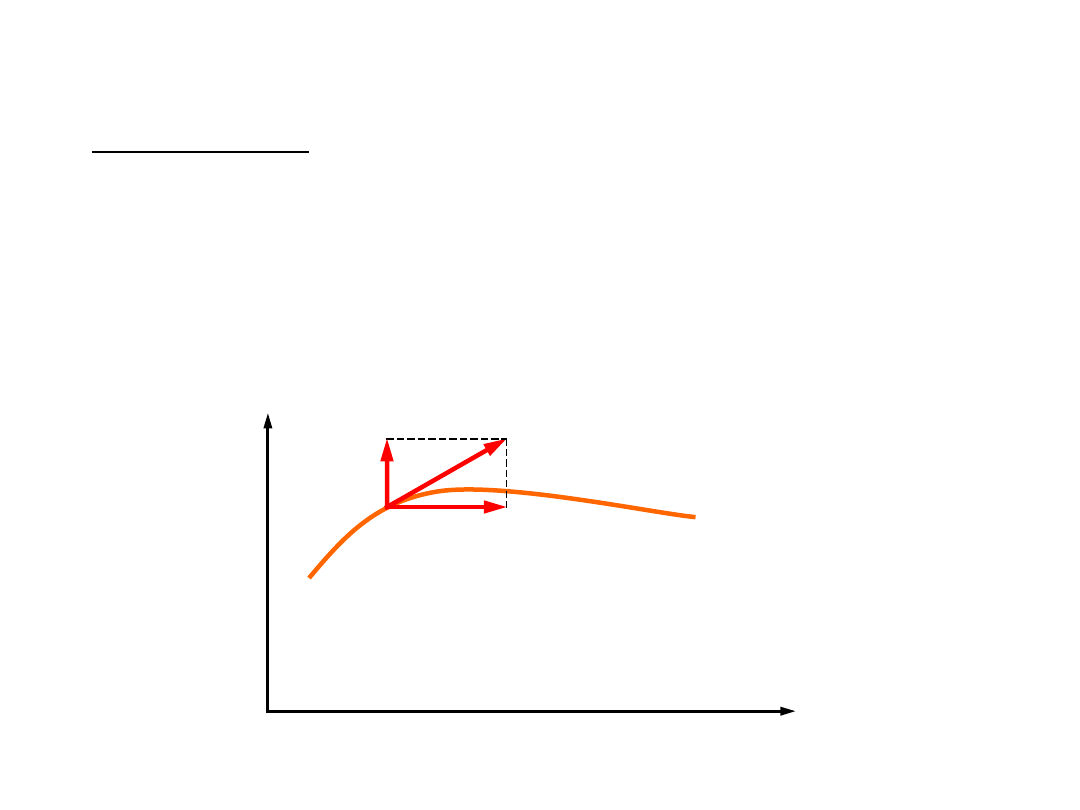
Szczególne przypadki ruchu punktu
materialnego
Ruch jednostajny po
okręgu:
0
0
,
,
0
d
dk
const
k
dt
dt
w
w
w
w
e
w
=
=
=
=
=
r
r
r
r
r
n
a
u a
w
= � =
r
r
r r
- wektor jednostkowy prostopadły do płaszczyzny
okręgu
k
r
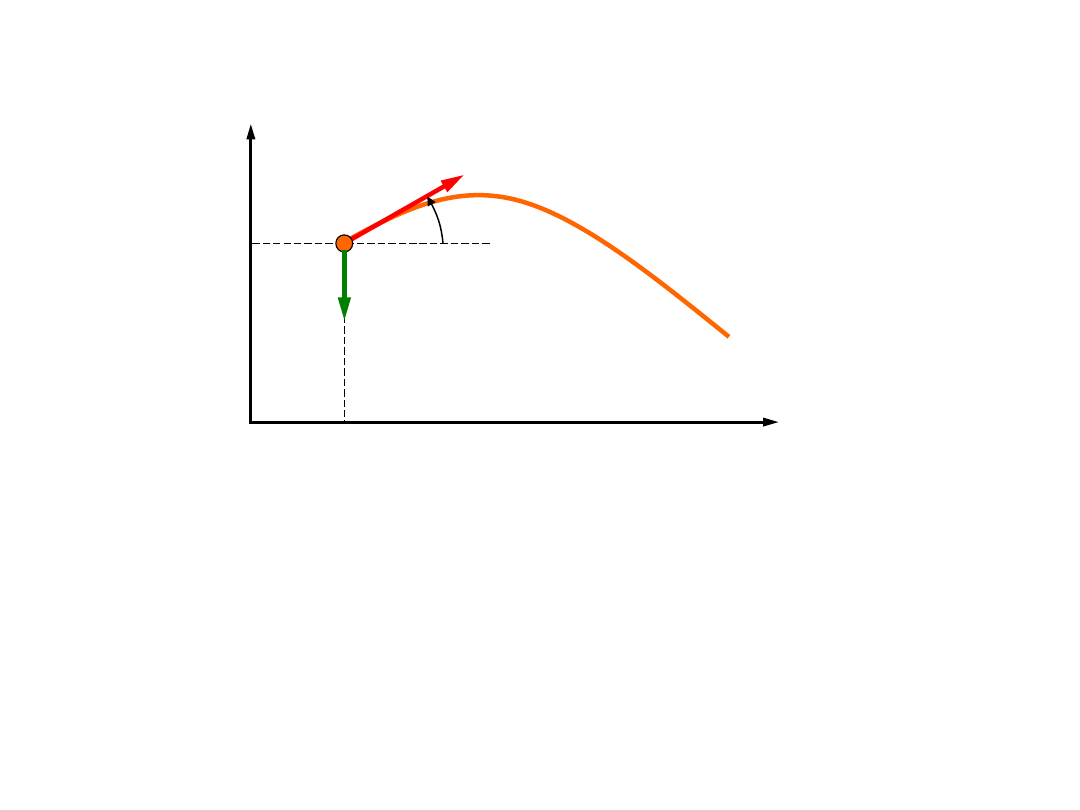
Szczególne przypadki ruchu punktu
materialnego
Ruch płaski:
Ruchem płaskim
nazywamy ruch, którego tor leży
w jednej płaszczyźnie.
Ruch prostoliniowy i ruch po okręgu są
szczególnymi przypadkami ruchu płaskiego
x
y
( )
u t
r
y
u
x
u
Szczególne przypadki ruchu punktu
materialnego
g
y
0
u
r
x
0
y
0
Dane:
wyjściowe położenie punktu
x
0
, y
0
wartość prędkości
początkowej u
0
kąt rzutu
przyspieszenie grawitacyjne g
Szukane:
funkcje opisujące trajektorię
punktu x(t), y(t)
a

Szczególne przypadki ruchu punktu
materialnego
( ),
( ),
0,
y
x
x
y
du
du
dx
dy
u t
u t
g
dt
dt
dt
dt
=
=
=
=-
0
0
0
( )
(0) 0
t
t
x
x
x
du
dt
dt
u t u
dt
=
�
-
=
�
�
0
( )
(0)
cos
x
x
u t
u
u
a
=
=
0
0
( )
(0)
t
t
y
y
y
du
dt
gdt
u t u
gt
dt
=-
�
-
=-
�
�
0
( )
(0)
sin
y
x
u t
u
gt u
gt
a
=
-
=
-
0
0
0
0
cos
( )
(0)
cos
t
t
dx
dt
u
dt
x t
x
u t
dt
a
a
=
�
-
=
�
�
0
0
( )
cos
x t
x u t
a
= +
(
)
2
1
0
0
2
0
0
sin
( )
(0)
sin
t
t
dy
dt
u
gt dt
y t
y
u t
gt
dt
a
a
=
-
�
-
=
-
�
�
2
1
0
0
2
( )
sin
y t
y u t
gt
a
= +
-
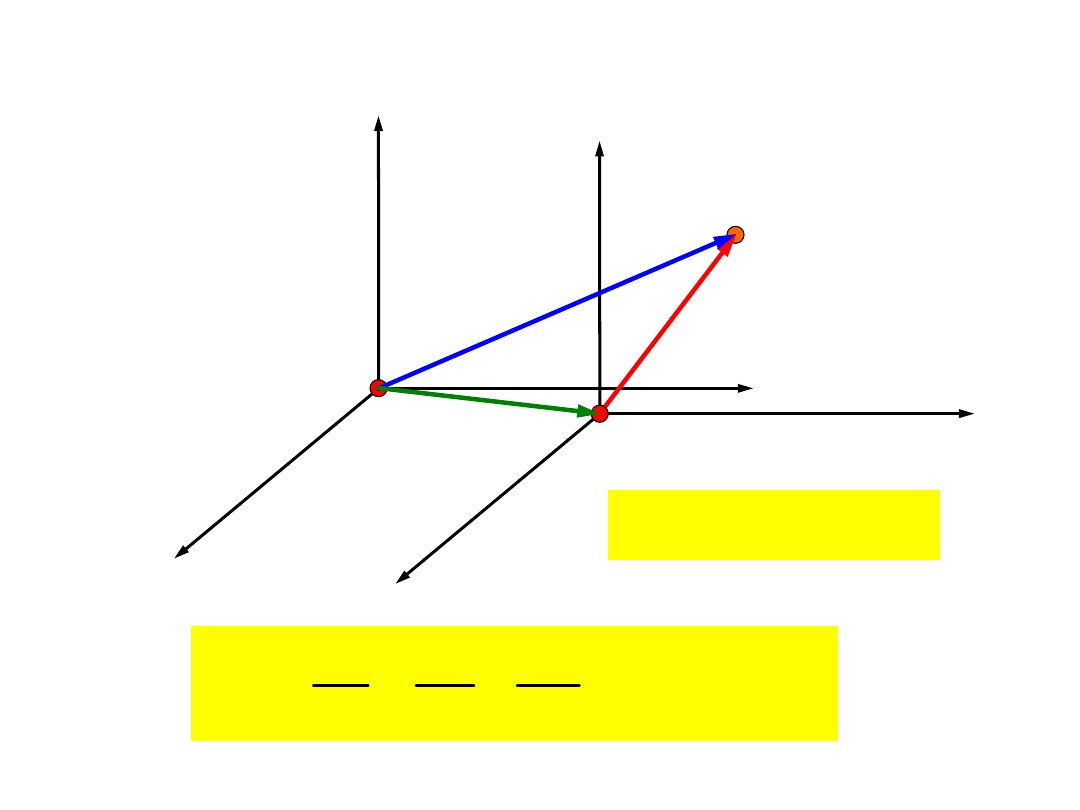
Prędkość i przyspieszenie w ruchu
względnym
0
( )
r t
r
x
y
z
z
1
y
1
x
1
0
( )
r t
r
0
1
1
( )
r t
r
1
0
( )
( )
( )
r t
r t
r t
=
+
r
r
r
0
1
1
0
( )
( )
( )
dr
dr
dr
u t
u t u t
dt
dt
dt
=
=
+
=
+
r
r
r
r
r
r
A

Prędkość i przyspieszenie w ruchu
względnym
Wniosek:
Prędkość w ruchu bezwzględnym (
prędkość
bezwzględna
) równa jest sumie prędkości punktu
materialnego, w przypadku gdyby pozostawał
nieruchomy
względem
ruchomego
układu
współrzędnych (
prędkość unoszenia
), i prędkości
punktu względem układu ruchomego (
prędkość
względna
).
prędkość bezwzględna
=
prędkość unoszenia
+
prędkość względna
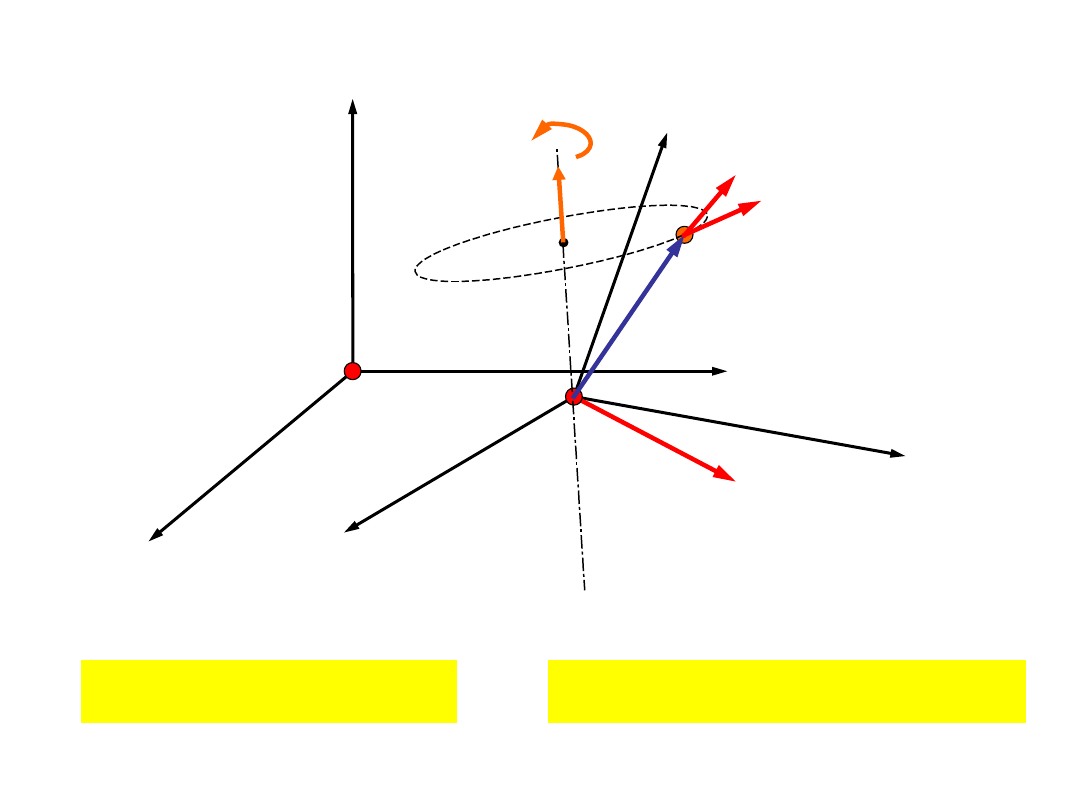
Prędkość i przyspieszenie w ruchu
względnym
0
0
( )
u t
r
x
y
z
z
1
y
1
x
1
0
1
1
( )
r t
r
( )
t
w
r
1
( )
( )
t r t
w �
r
r
Prędkość
unoszenia:
0
1
( )
( )
( )
e
u t
u
t r t
w
= +
�
r
r
r
r
0
1
1
( )
( )
( )
( )
u t
u
t r t u t
w
= +
�
+
r
r
r
r
r
Prędkość
bezwzględna:
1
( )
u t
r
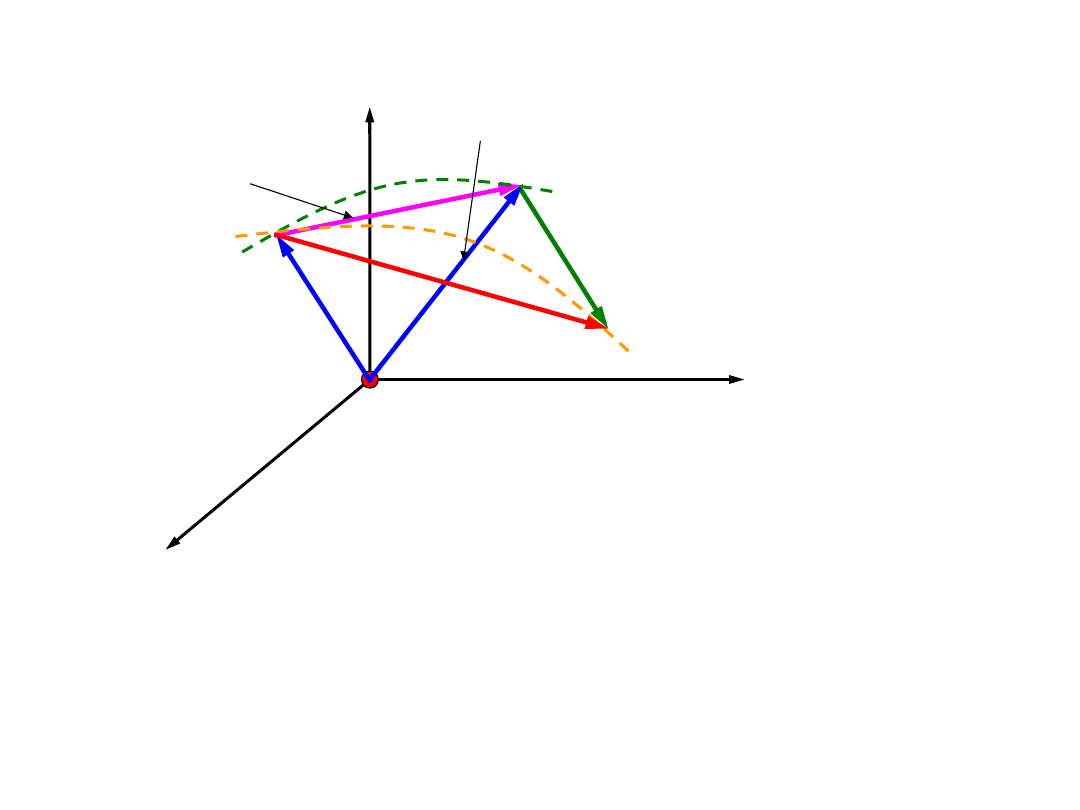
Prędkość i przyspieszenie w ruchu
względnym
z
1
y
1
x
1
0
1
1
( )
r t
r
1
(
)
r t
t
+D
r
1
( )
w
r t
D
r
1
( )
r t
D
r
1
( )
r
r t
D
r
1
( )
w
r t
D
r
przyrost promienia wodzącego
w układzie ruchomym
1
( )
r t
D
r
przyrost promienia wodzącego
w układzie nieruchomym
1
( )
r
r t
D
r
przyrost promienia wodzącego
na skutek obrotu układu
ruchomego
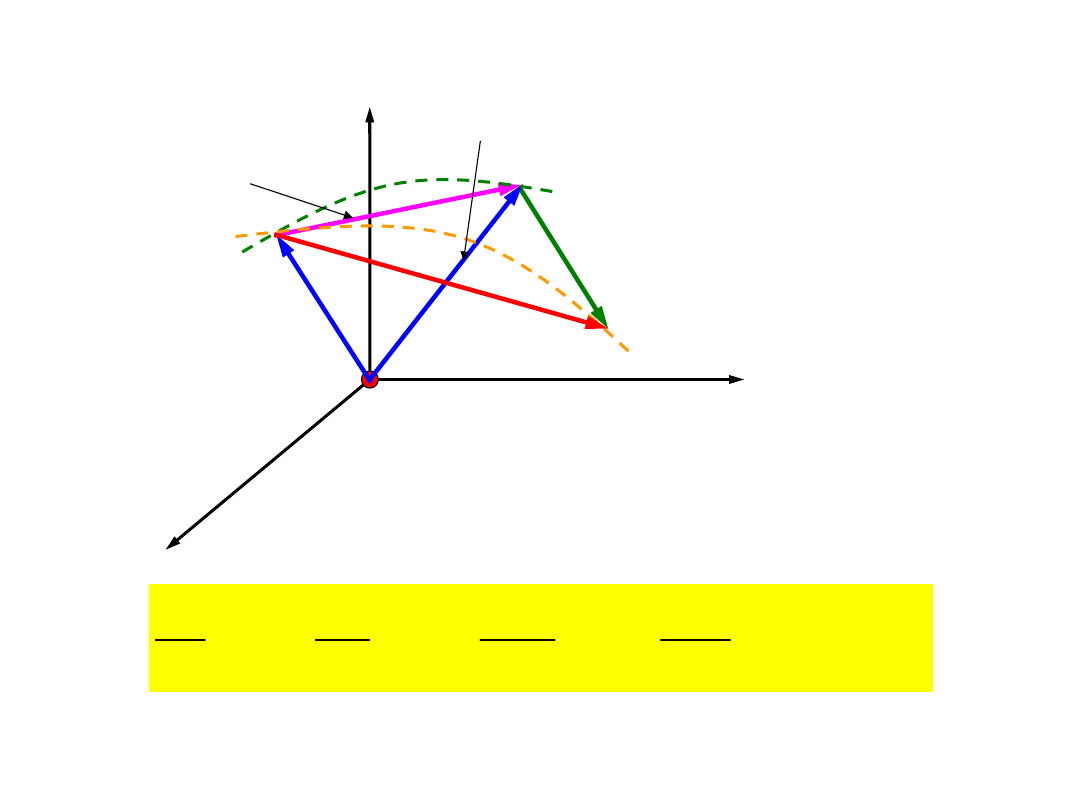
Prędkość i przyspieszenie w ruchu
względnym
z
1
y
1
x
1
1
1
1
1
1
1
0
0
0
lim
lim
lim
w
r
t
t
t
r
dr
r
r
u
r
dt
t
t
t
w
D �
D �
D �
D
D
D
=
=
+
= + �
D
D
D
r
r
r
r
r
r
r
0
1
1
( )
r t
r
1
(
)
r t
t
+D
r
1
( )
w
r t
D
r
1
( )
r t
D
r
1
( )
r
r t
D
r
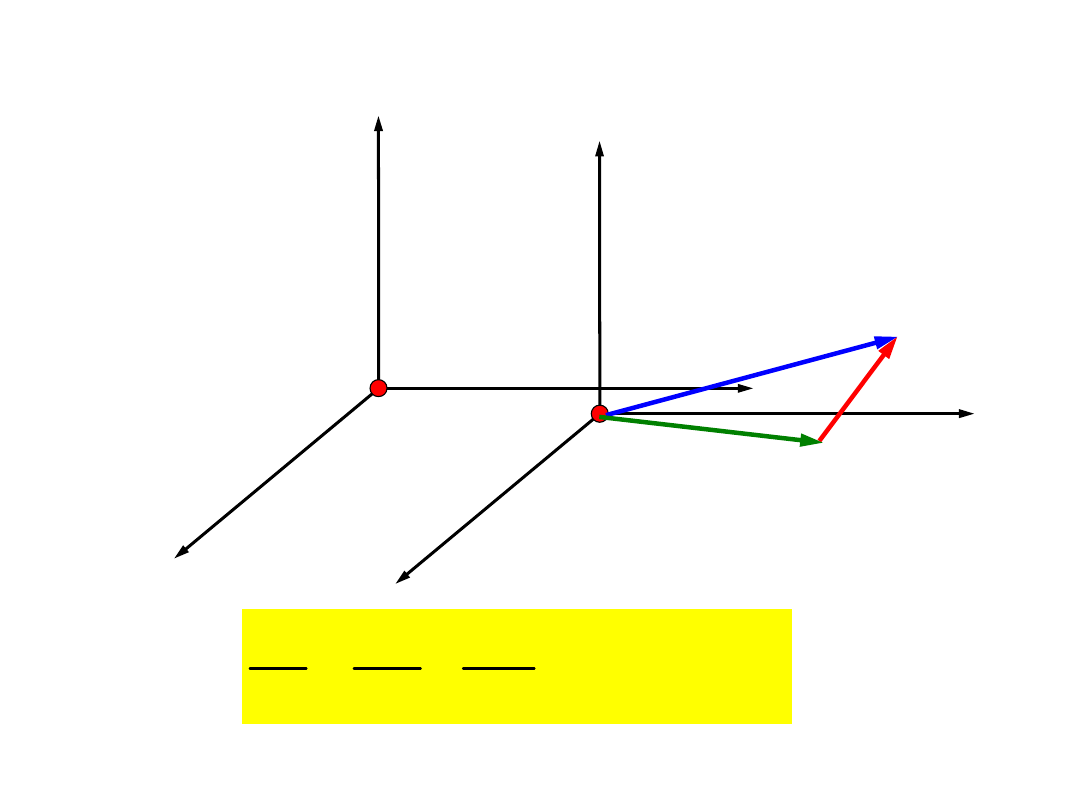
Prędkość i przyspieszenie w ruchu
względnym
0
( )
a t
r
x
y
z
z
1
y
1
x
1
0
( )
a t
r
0
1
1
( )
a t
r
0
1
1
0
( )
( )
du
du du
a t
a t
dt
dt
dt
=
+
=
+
r
r
r
r
r
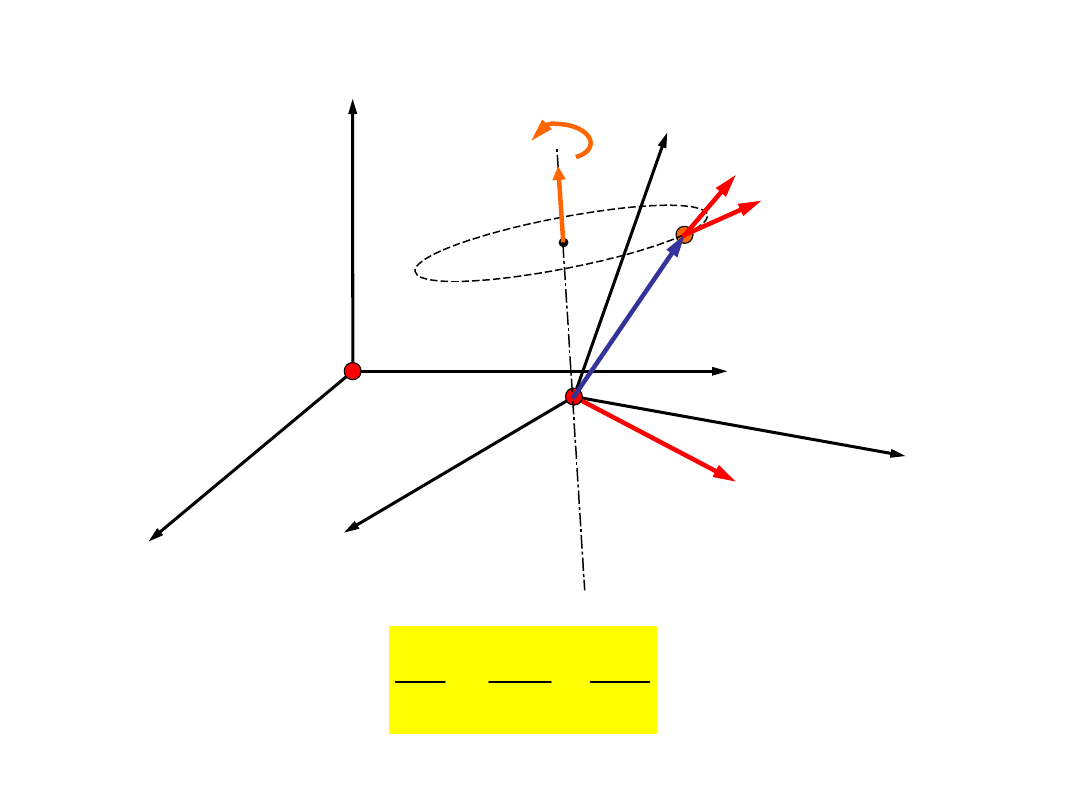
Prędkość i przyspieszenie w ruchu
względnym
0
0
( )
u t
r
x
y
z
z
1
y
1
x
1
0
1
1
( )
r t
r
( )
t
w
r
1
( )
( )
t r t
w �
r
r
1
e
du
du
du
dt
dt
dt
=
+
r
r
r
1
( )
u t
r

Prędkość i przyspieszenie w ruchu
względnym
0
1
1
( )
( )
e
du
du
d
dr
r t
t
dt
dt
dt
dt
w
w
=
+
�
+
�
r
r
r
r
r
r
(
)
0
1
1
1
( )
( )
( )
( )
( )
e
du
a
r t
t
u t
t r t
dt
e
w
w
= + �
+
�
+
�
r
r
r
r
r
r
r
r
(
)
0
1
1
1
( )
( )
( )
( )
( )
e
du
a
r t
t
t r t
t u
dt
e
w
w
w
= + �
+
�
�
+
�
r
r
r
r
r
r
r
r
r
(
)
0
1
1
( )
( )
( )
( )
( )
e
e
du
a
t r t
t
t r t
a
dt
e
w
w
= +
�
+
�
�
=
r
r
r
r
r
r
r
r
Gdy
1
( ) 0
u t =
r
1
( )
( )
( )
e
e
du
a t
t u t
dt
w
=
+
�
r
r
r
r
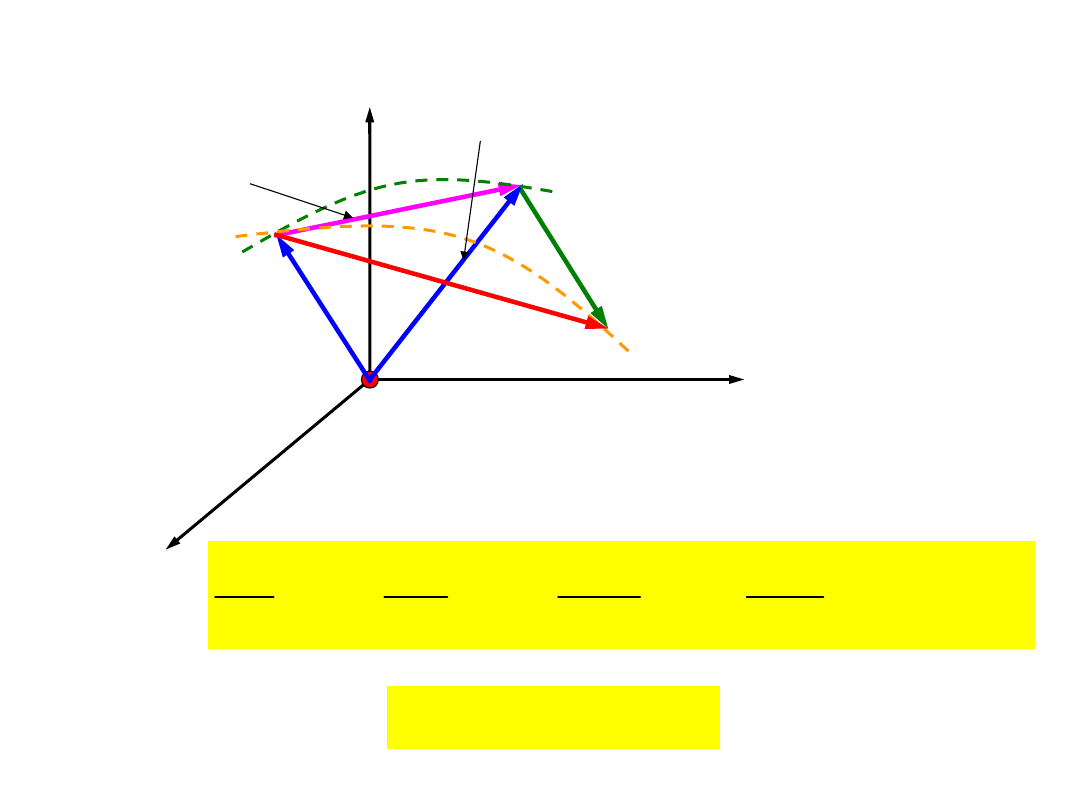
Prędkość i przyspieszenie w ruchu
względnym
z
1
y
1
x
1
1
1
1
1
1
1
0
0
0
lim
lim
lim
w
r
t
t
t
u
du
u
u
a
u
dt
t
t
t
w
D �
D �
D �
D
D
D
=
=
+
= + �
D
D
D
r
r
r
r
r
r
r
0
1
1
( )
u t
r
1
(
)
u t
t
+D
r
1
( )
w
u t
D
r
1
( )
u t
D
r
1
( )
r
u t
D
r
1
1
2
e
a a a
u
w
= + +
�
r
r r
r
r
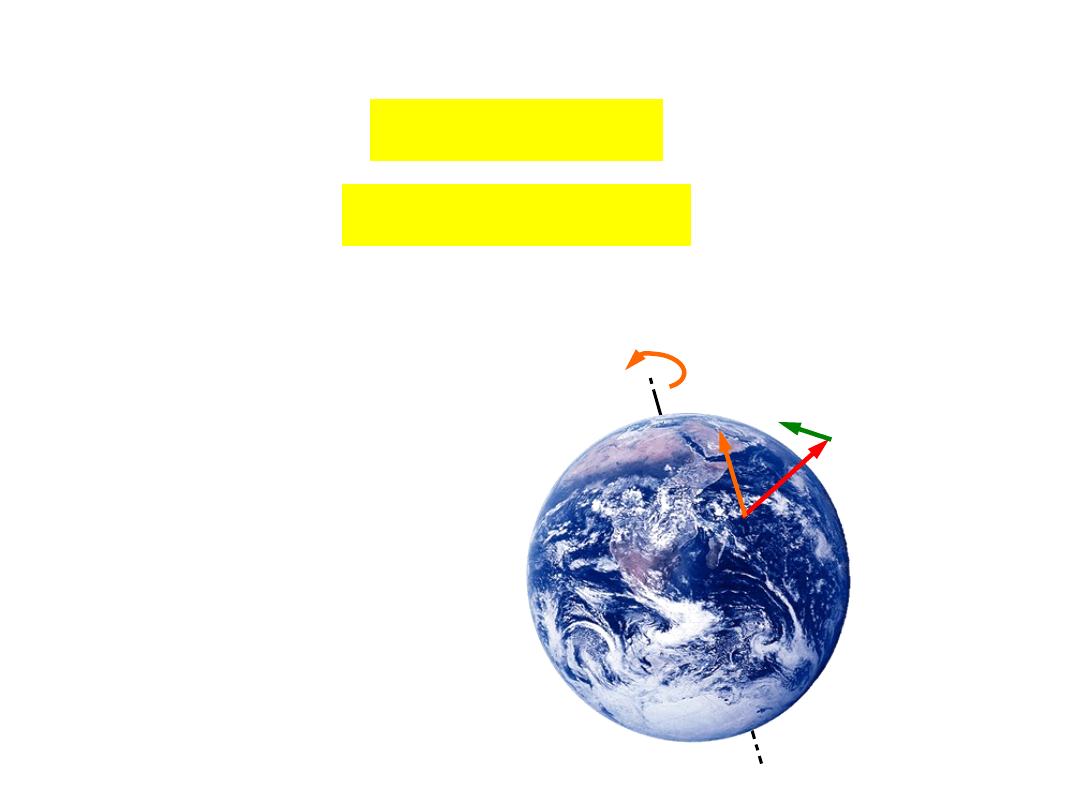
Prędkość i przyspieszenie w ruchu
względnym
Dodatkowe przyspieszenie punktu materialnego,
wynikające z obrotu układu ruchomego nazywamy
przyspieszeniem Coriolisa
1
2 ( )
( )
c
a
t u t
w
=
�
r
r
r
1
2 ( ) ( )sin
c
a
t u t
w
a
=

Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
Wyszukiwarka
Podobne podstrony:
Hydrodynamika środowiskowa z elementami mechani technicznej 23.11.2007, Inżynieria Ochrony Środowisk
Mechanika Techniczna I Skrypt 3 11
Mechanika techniczna(12)
Mechanika techniczna(1)
Mechanika Techniczna I Skrypt 2 4 Kinematyka
Mechanika Techniczna I Skrypt 4 2 4 Układ belkowy złożony
Ostwald M Podstawy mechaniki Mechanika techniczna
Tarcie, Materiały, Inżynieria Środowiska, Semestr 2, Mechanika techniczna, egzaminy
Maszyny-koło projekt, Technologia chemiczna, Maszynoznawstwo i mechanika techniczna, ogólne materiał
TARCIE, PW Transport, Gadżety i pomoce PW CD2, MECHANIKA, MECHANIKA !!, mechanika techniczna - labor
Mechanika Techniczna I Opracowanie 06
Mechanika Techniczna I Skrypt 1 2 1 Okreslenie i rodz
Mechanika Techniczna I Statyka Płaski Układ Sił
mechanika techniczna, kolo mohra
opracowanie 4 mechana, Studia - Mechatronika, III semestr, Mechanika Techniczna
Mechanika techniczna podstawy
Mechanika techniczna (150dpi)
Mechanika Techniczna I Skrypt 5 03
więcej podobnych podstron