Analiza obwodów

liniowych pobudzanych

okresowymi

przebiegami

niesinusoidalnymi

Prądy i napięcia mogą być
okresowe niesinusoidalne.

Aby uprościć analizę obwodów
z takimi prądami i napięciami
będziemy je przedstawiać
w postaci szeregu Fouriera.

 





k

k

mk

t

k

A

A

t

f

















0

1

0

sin

gdzie

T





2

0



jest pulsacją przebiegu rozkładanego na szereg Fouriera.
Rozpatrzmy przykład:

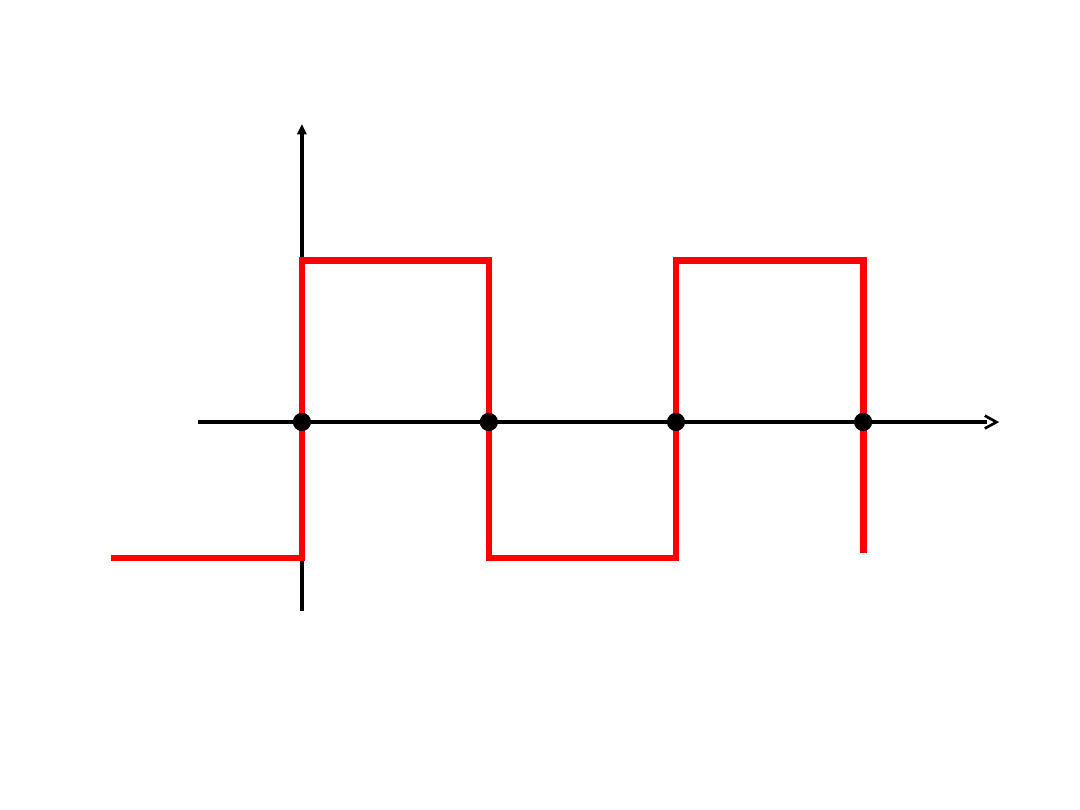
f(ωt)

ωt

0

π

2π

3π

A

m

-A

m

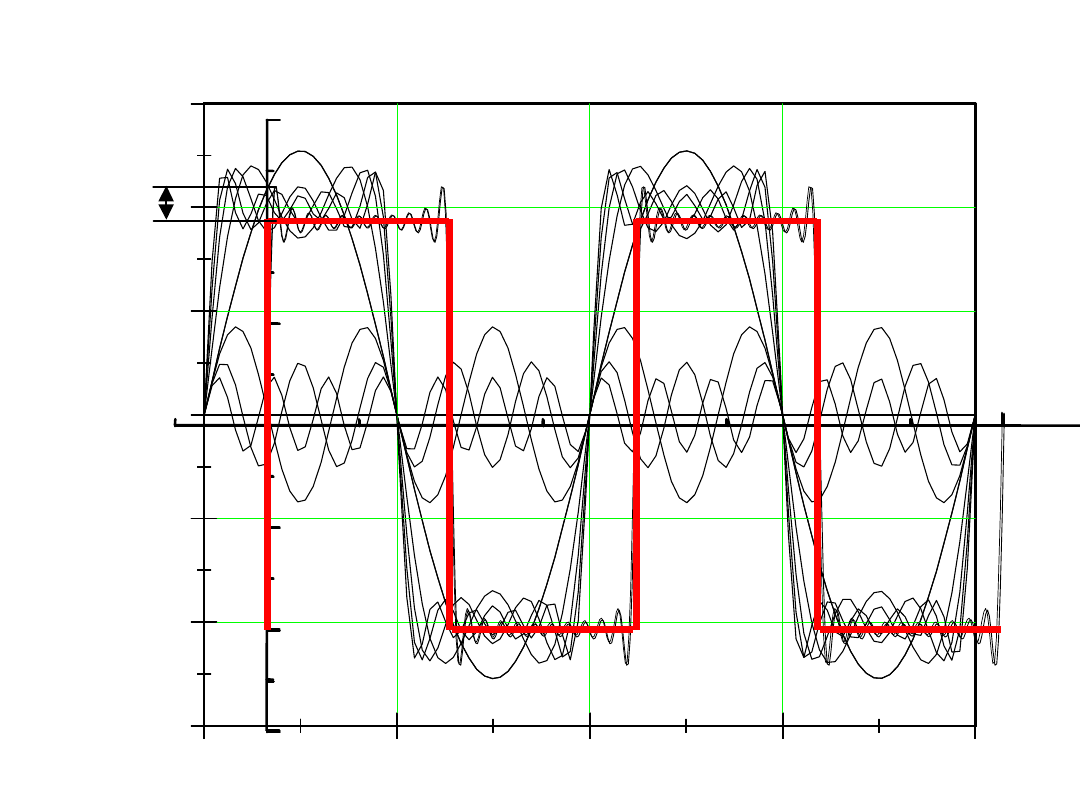
W praktyce możemy przyjąć do obliczeń
skończoną liczbę składników szeregu,
zwanych harmonicznymi.
Suma szeregu daje wówczas
wartość przybliżoną funkcji czasu.

Dodanie kolejnej harmonicznej
poprawia dokładność,
tzn. przybliżenie jest coraz lepsze.
Ilustruje to przykład:

0,0

0,5

1,0

1,5

2,0

-15

-10

-5

0

5

10

15

0,0

0,5

1,0

1,5

2,0

-15

-10

-5

0

5

10

15

0,0

0,5

1,0

1,5

2,0

-15

-10

-5

0

5

10

15

0,0

0,5

1,0

1,5

2,0

-15

-10

-5

0

5

10

15

0,0

0,5

1,0

1,5

2,0

-15

-10

-5

0

5

10

15

0,0

0,5

1,0

1,5

2,0

-15

-10

-5

0

5

10

15

0,0

0,5

1,0

1,5

2,0

-15

-10

-5

0

5

10

15

0,0

0,5

1,0

1,5

2,0

-15

-10

-5

0

5

10

15

9% Am

efekt
Gibbsa

Szereg Fouriera

• Czy każdą funkcję okresową można

przedstawić w postaci szeregu
Fouriera?

Z matematyki wiadomo, że musi ona
spełniać pewne warunki:

WARUNKI
DIRICHLETA

1. W każdym przedziale o długości T funkcja

jest bezwzględnie całkowalna

 

t

f

 







t

t

f

T

d

3. Funkcja może mieć w przedziale T co

najwyżej skończoną liczbę punktów
nieciągłości, przy czym w każdym punkcie
nieciągłości istnieją granice –

lewostronna

i

prawostronna

 

t

f

2. W każdym przedziale o długości T funkcja

ma skończoną liczbę maksimów i
minimów

 

t

f

 





k

k

mk

t

k

A

A

t

f

















0

1

0

sin

gdzie

f

T







2

2

0





jest pulsacją przebiegu rozkładanego na szereg Fouriera.

2

0

0

C

A 

- składowa stała,

nazywana

harmoniczną zerową





1

0

sin

1







t

A

m

- funkcja sinusoidalna o
takiej samej pulsacji jak
funkcja niesinusoidalna

 

t

f

nosi nazwę pierwszej lub podstawowej

harmonicznej

Rozpatrzymy k-tą

harmoniczną









k

m

t

k

A

k





0

sin

t

k

A

t

k

A

k

m

k

m

k

k

0

0

sin

cos

cos

sin













Oznaczymy:









k

m

t

k

A

k





0

sin

k

m

k

k

A

C



sin



k

m

k

k

A

B



cos



i otrzymujemy:

t

k

B

t

k

C

k

k

0

0

sin

cos









wówczas:

 

















1

0

0

0

cos

sin

2

k

k

k

t

k

C

t

k

B

C

t

f





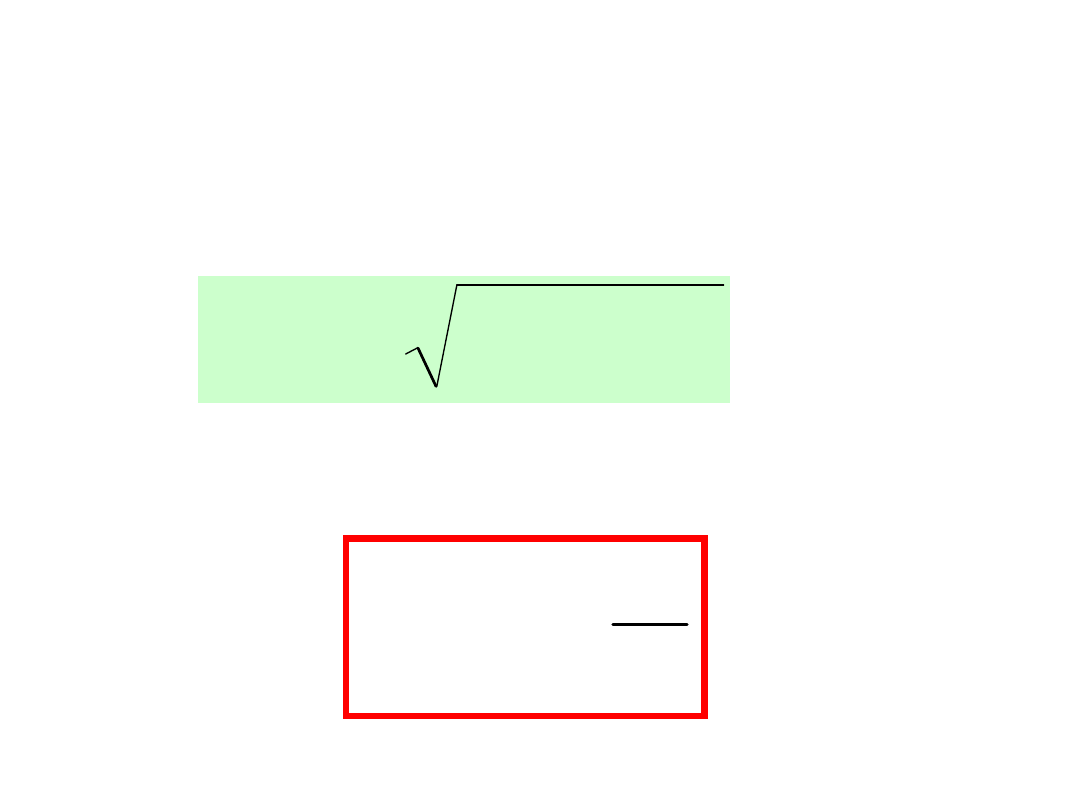
Z tych zależności wynika:

2

2

k

k

m

C

B

A

k





k

k

k

B

C

ctg

ar





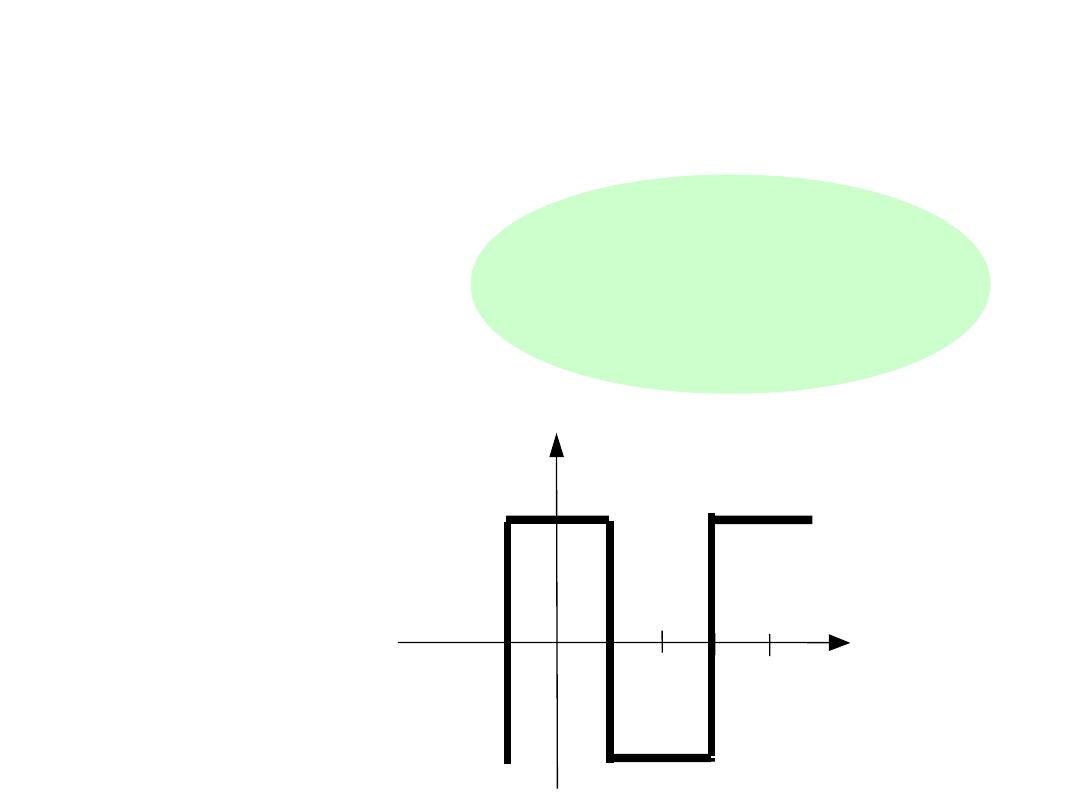
PEWNE RODZAJE

SYMETRII:

1.FUNKCJE

PRZEMIENNE

Spełniają
warunek:

 

0

d

0





t

t

f

T

wartość średnia
za okres równa
się zeru.

t

f (t)

0

T

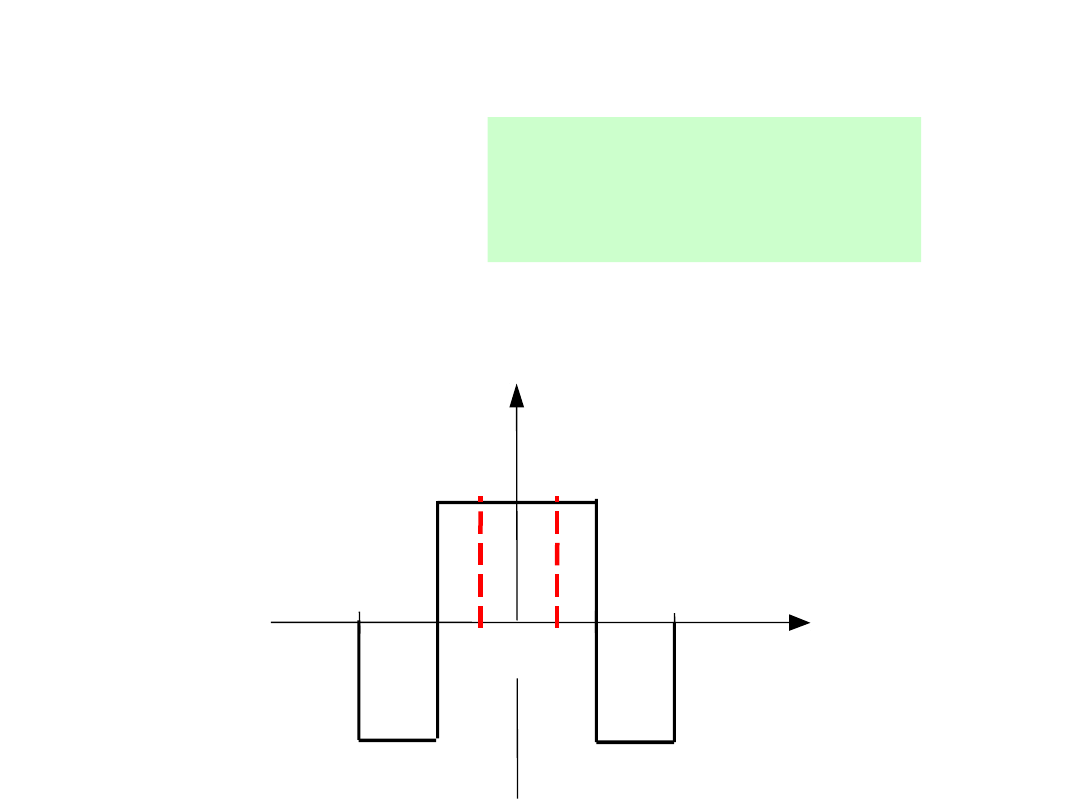
Spełniają
warunek:

2.FUNKCJE PARZYSTE

0



k

B

 

 

t

f

t

f





wówcza
s:

dla



,

2

,

1

,

0



k

t

f (t)

0

-t

t

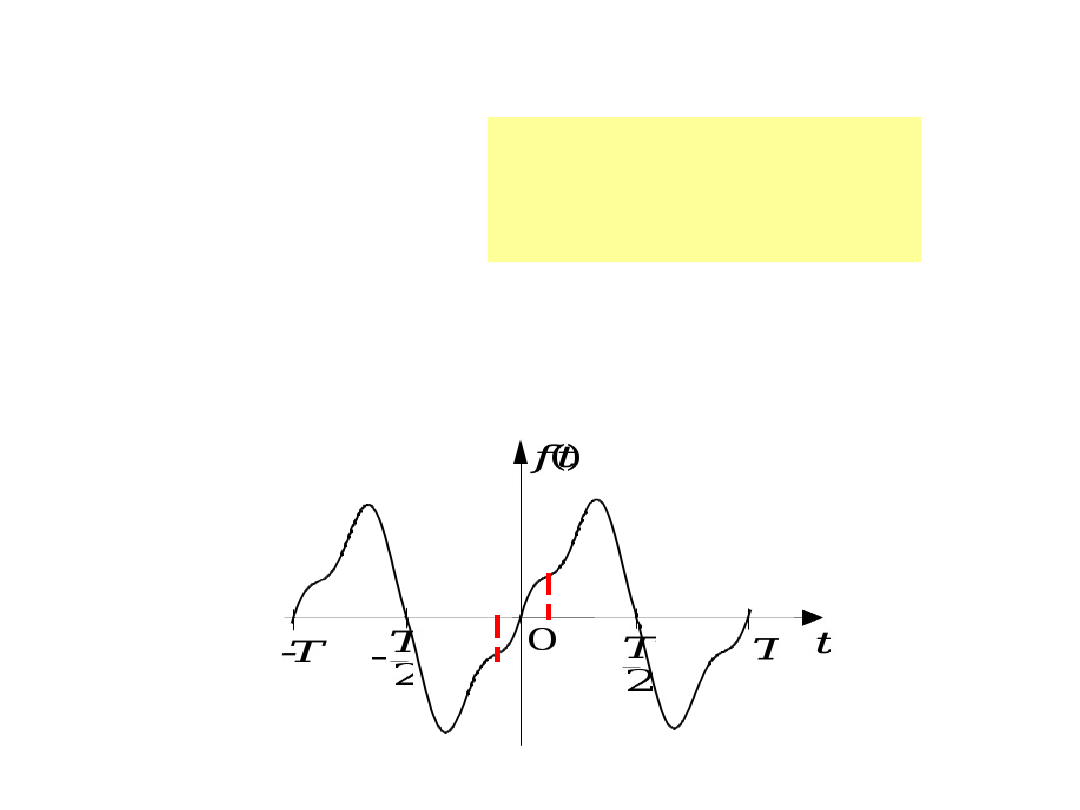
Spełniają
warunek:

3.FUNKCJE

NIEPARZYSTE

0



k

C

 

 

t

f

t

f







wówcza
s:

dla



,

2

,

1

,

0



k

-t

t

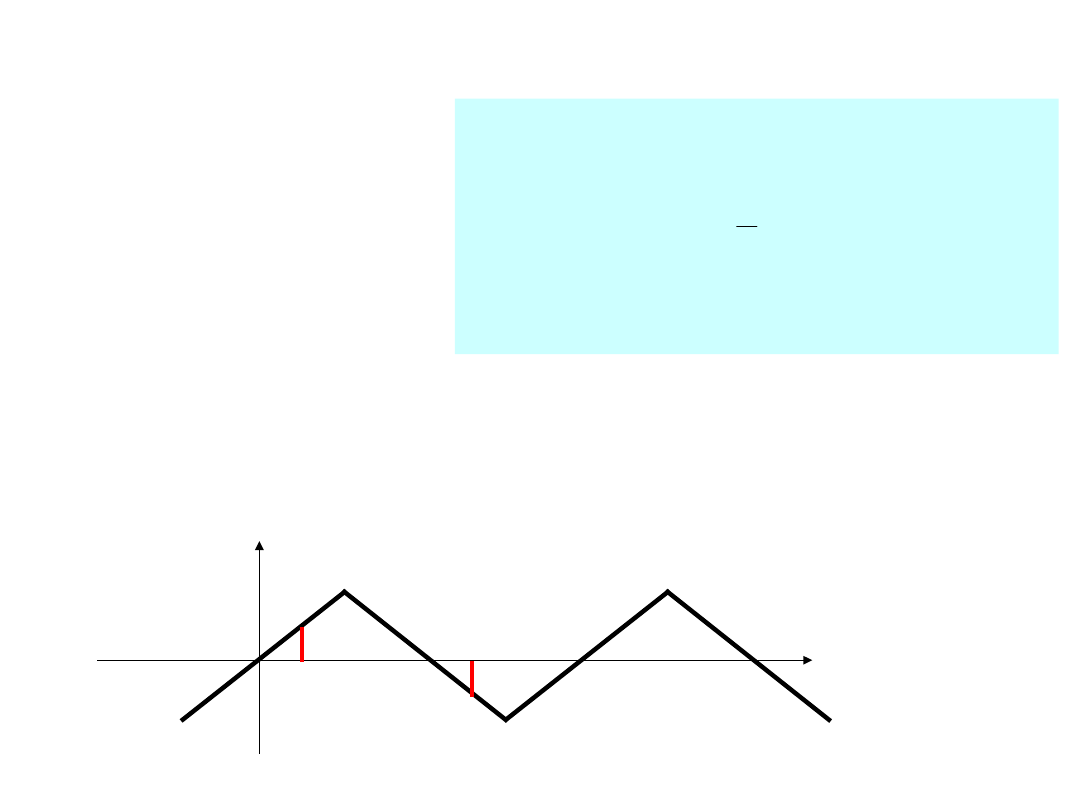
Spełniają
warunek:

4.FUNKCJE ANTYSYMETRYCZNE

,

0

0



C

 

t

f

T

t

f















 

2

wówcza
s:

dla



,

2

,

1

,

0



k

,

0

2



k

B

0

2



k

C

f(t)

t

0

π

2π

t

t+T/2

Obliczanie współczynników

szeregu Fouriera

 

;

d

2

0

0

t

t

f

T

C

T





2

0

0

C

A 

 

;

d

1

2

0

0

0

t

t

f

T

C

A

T







 

t

t

k

t

f

T

C

T

t

t

k

d

cos

2

0

0

0









 

t

t

k

t

f

T

B

T

t

t

k

d

sin

2

0

0

0









Funkcje

parzyste

Funkcje

nieparzyste

Funkcje

antysymetr.

F. parzysta

i antysyme-

tryczna

oraz

F.

nieparzysta

i antysyme-

tryczna

oraz

 

 

t

f

t

f





 

 

t

f

t

f







 

t

f

T

t

f















 

2

 

 

t

f

t

f





 

t

f

T

t

f















 

2

 

t

f

T

t

f















 

2

 





2

0

0

d

cos

4

T

k

t

t

k

t

f

T

C



 





2

0

0

d

cos

4

T

k

t

t

k

t

f

T

C



 





2

0

0

,

d

cos

4

T

k

t

t

k

t

f

T

C



 





4

0

0

d

cos

8

T

k

t

t

k

t

f

T

C



 





4

0

0

d

cos

8

T

k

t

t

k

t

f

T

B





,

2

,

1



k



,

3

,

1



k



,

3

,

1



k



,

2

,

1



k

 





2

0

0

d

sin

4

T

k

t

t

k

t

f

T

B





,

3

,

1



k

 

 

t

f

t

f







 





k

k

mk

t

k

A

A

t

f

















0

1

0

sin

 

















1

0

0

0

cos

sin

2

k

k

k

t

k

C

t

k

B

C

t

f





Mamy dwie równoważne postaci szeregu Fouriera:

Wykładnicza postać szeregu Fouriera

 

















1

0

0

0

cos

sin

2

k

k

k

t

k

C

t

k

B

C

t

f





j

e

e

t

k

t

jk

t

jk

2

sin

0

0

0













2

cos

0

0

0

t

jk

t

jk

e

e

t

k













 



























1

0

0

0

2

2

2

k

t

jk

k

k

t

jk

k

k

e

jB

C

e

jB

C

C

t

f





V

k

V

-k

....

2

,

1

,

0

2







k

dla

jB

C

V

k

k

k

....

2

,

1

,

0

2













k

dla

jB

C

V

k

k

k

k

k

k

k

B

B

C

C



















k

k

k

k

V

jB

C

V

2

 





















1

1

0

0

0

k

k

t

jk

k

t

jk

k

e

V

e

V

V

t

f















k

t

jk

k

e

V

0



 

,...

2

,

1

,

0

0

















k

dla

e

V

t

f

k

t

jk

k



Współczynniki V

k

obliczamy jako:

 

dt

e

t

f

T

V

t

jk

T

k

0

0

1









Widmo:

Amplitudowe – wykres modułu V

k

Fazowe – wykres argumentu V

k

dla wszystkich wartości k

Twierdzenie Parsevala

Jeżeli i są funkcjami okresowymi o
tym samym okresie T spełniającymi warunki
Dirichleta, to zachodzi zależność:

 

t

f

 

t

g

   

k

k

k

k

k

k

T

t

t

g

f

g

f

t

t

g

t

f

T





























d

1

0

0

w szczególności gdy

 

 

t

g

t

f



 















k

k

T

t

t

f

t

t

f

T

2

2

d

1

0

0

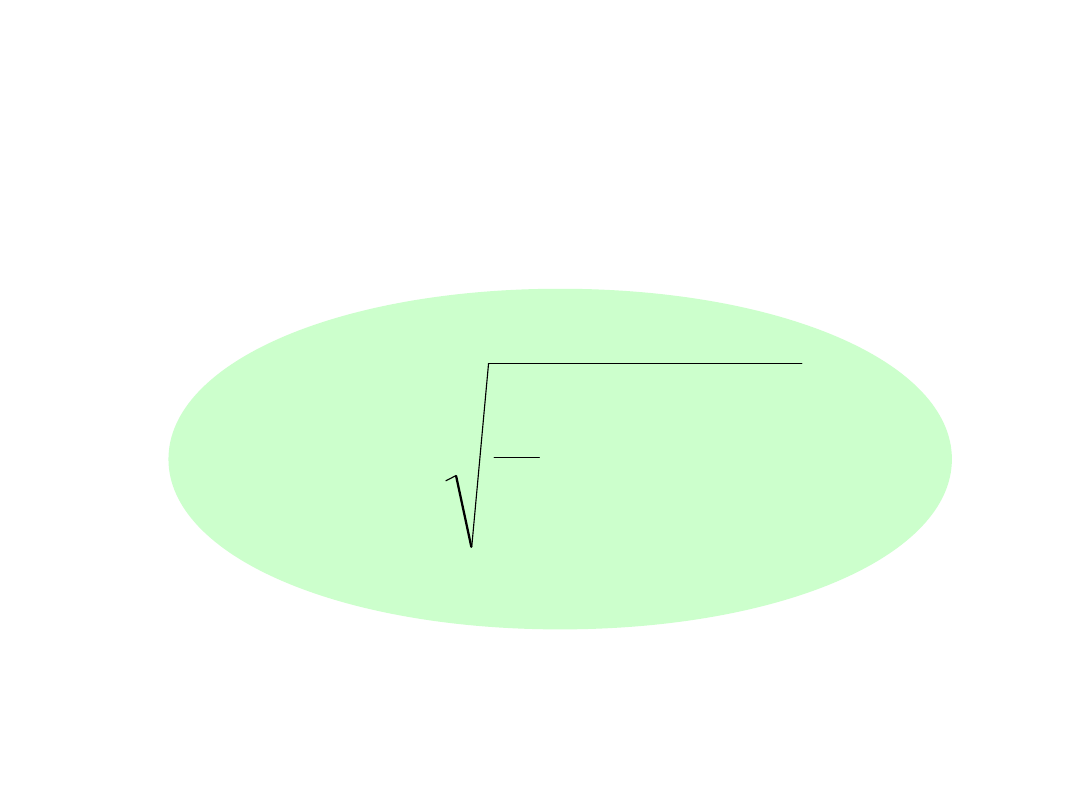
Wartość skuteczna funkcji

okresowej niesinusoidalnej:

 





T

sk

t

t

f

T

A

0

2

d

1

Wartość skuteczna k-tej

harmonicznej:

2

k

m

k

A

A 

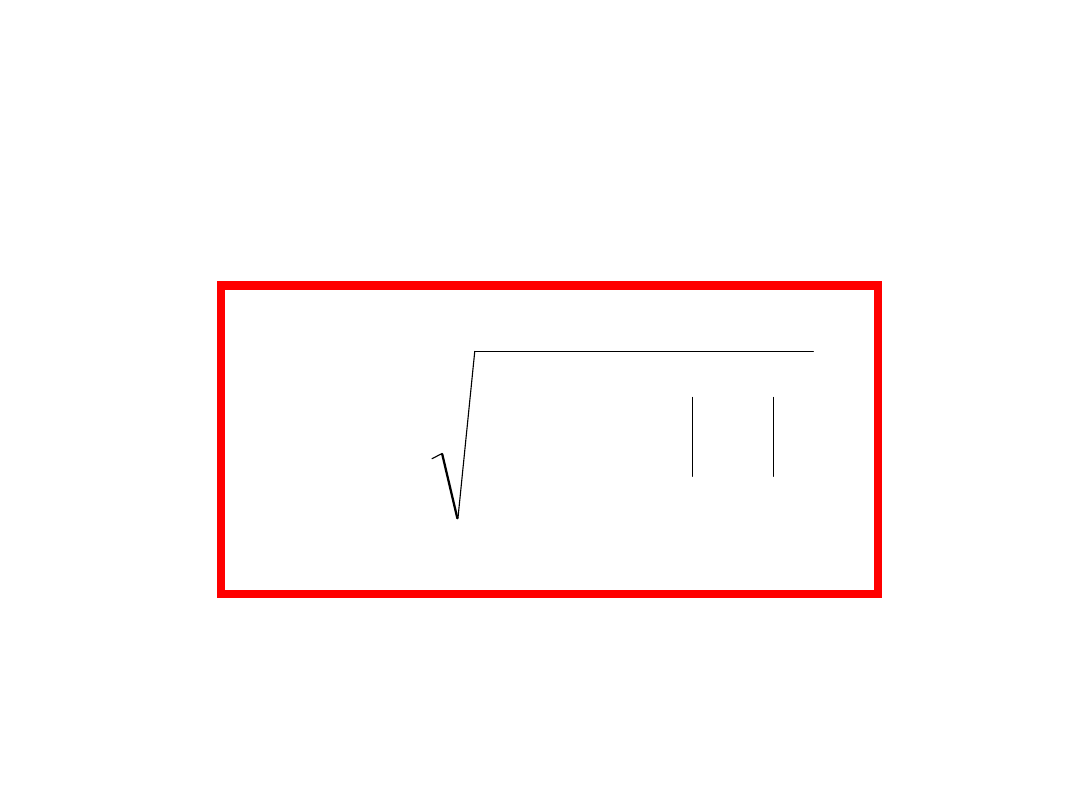
Wartość skuteczna funkcji
:

 

t

f











1

2

0

k

k

sk

A

A

A

Wartość średnia za okres

funkcji :

 

t

f

 

t

t

f

T

A

T

d

1

0

0





 

t

t

f

T

A

T

śr

d

1

0





Wartość średnia z modułu

funkcji :

 

t

f

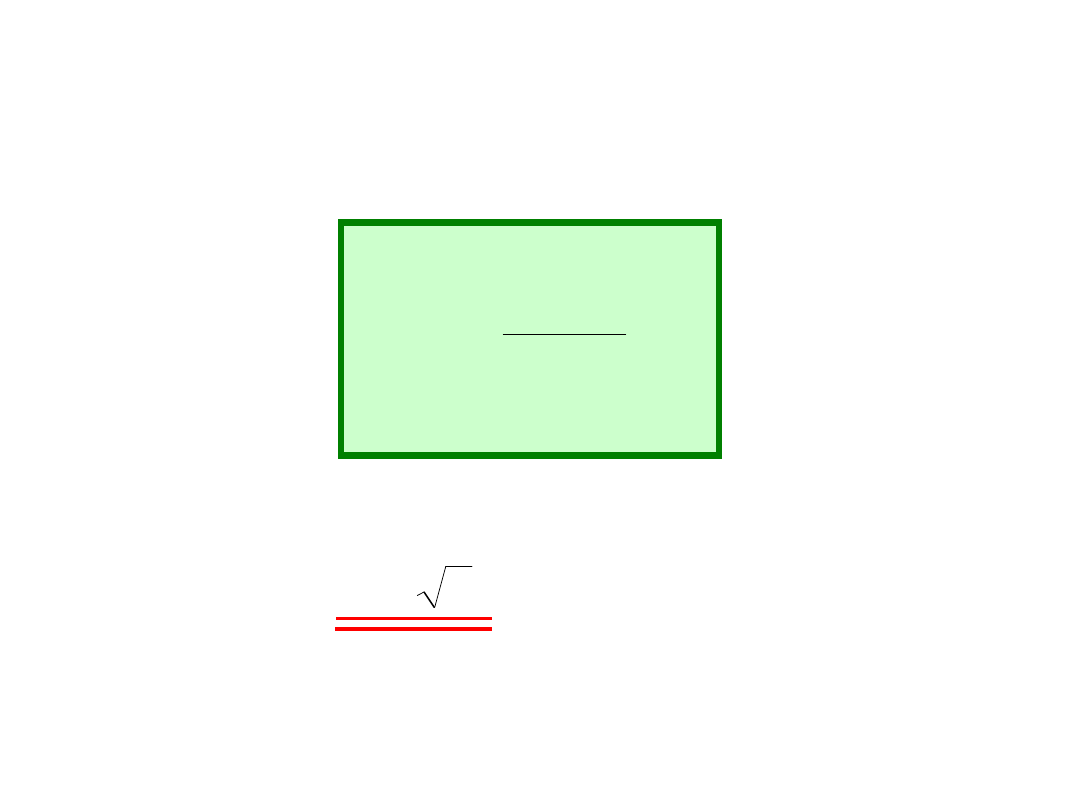
Współczynnik szczytu s

sk

A

A

s

max



dla sinusoidy

2



s

Współczynnik kształtu k:

śr

sk

A

A

k 

dla sinusoidy 11

,

1



k

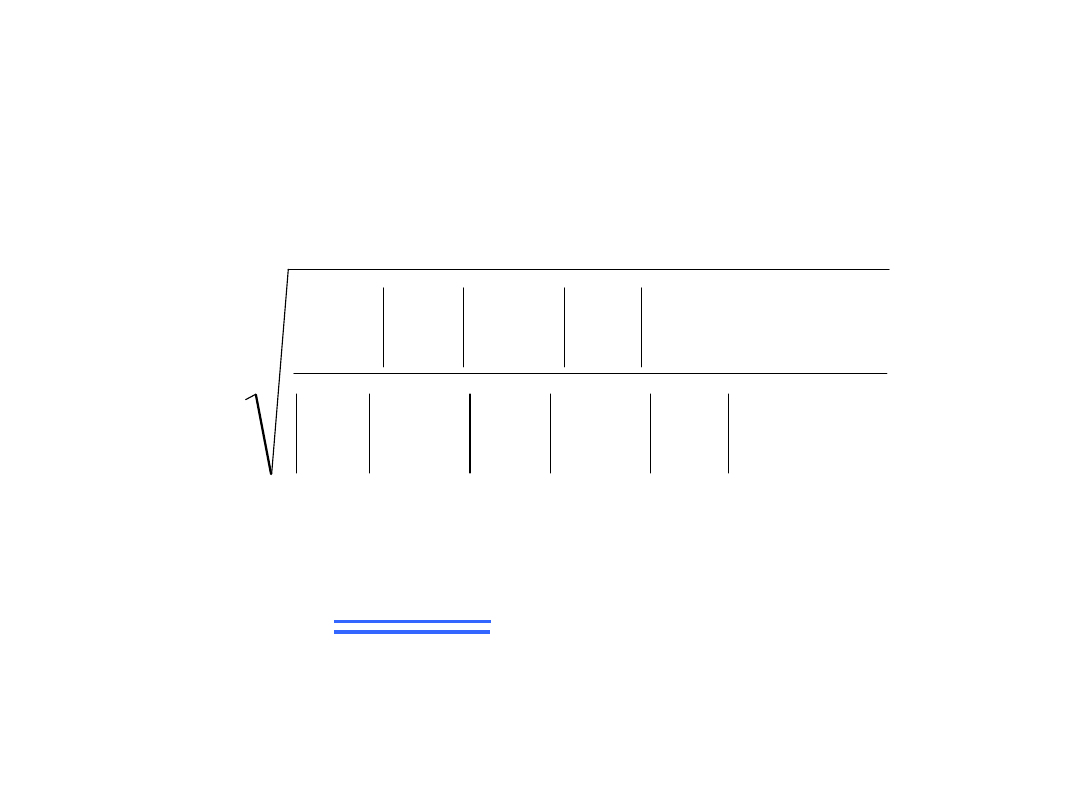
Współczynnik zawartości

harmonicznych h:

















2

3

2

2

2

1

2

3

2

2

A

A

A

A

A

h

dla sinusoidy 0



h

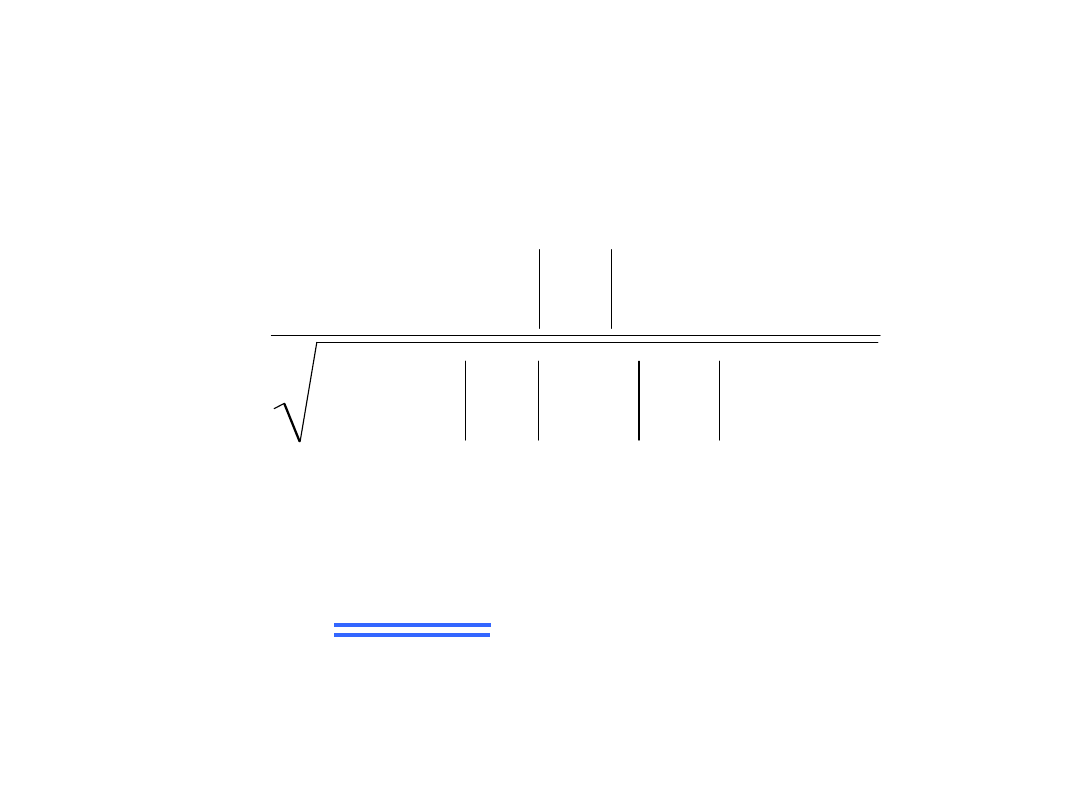
Współczynnik odkształcenia

k

0

:











2

2

2

1

2

0

1

0

A

A

A

A

k

dla sinusoidy 1

0



k

Współczynnik zawartości k-

tej harmonicznej h

k

:

1

A

A

h

k

k



Obwody liniowe zasilane

odkształconymi napięciami

i prądami źródłowymi

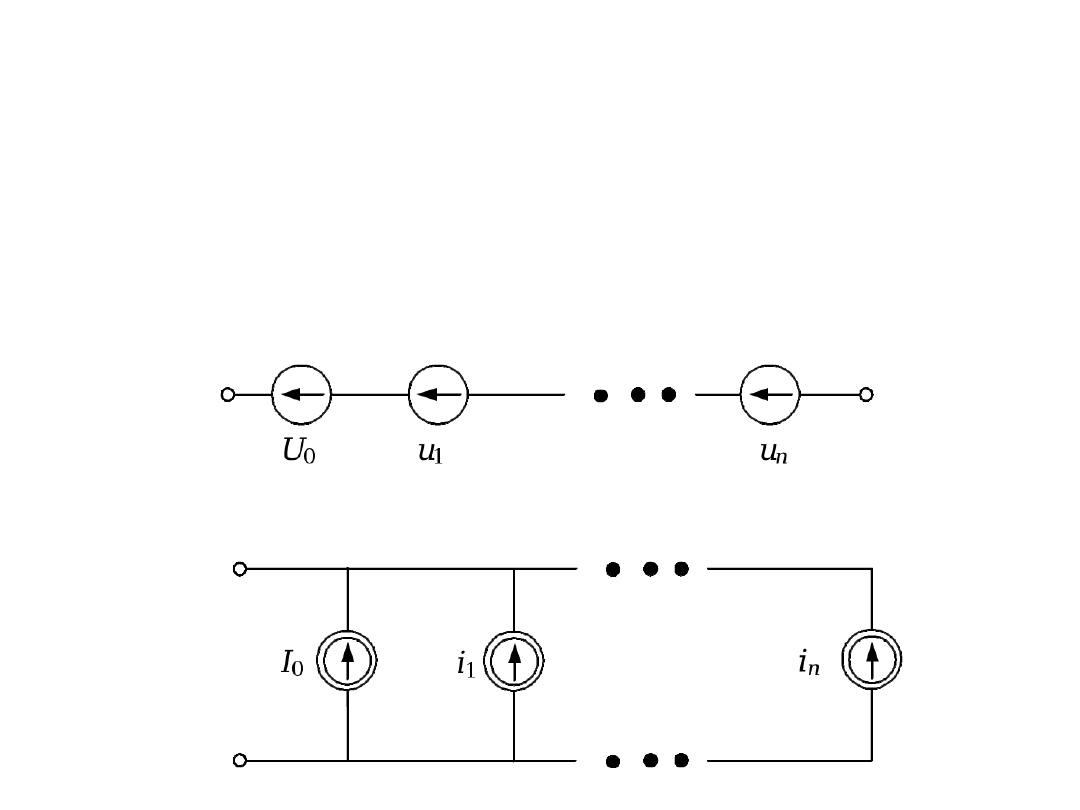
Jeżeli

















l

0

0

sin

k

u

m

k

k

t

k

U

U

u









k

k

i

k

m

t

k

I

I

i

















0

l

0

sin

ora
z

to

ora
z

Rozwiązanie obwodu tak zasilanego
polega na zastosowaniu zasady superpozycji
i rozwiązaniu obwodu dla każdej harmonicznej
oddzielnie.

1.Rozwiązujemy obwód dla składowej stałej,

kondensatory stanowią przerwę, a cewki – zwarcie.

2 Rozwiązujemy obwód dla kolejnych harmonicznych

metoda symboliczną, przy czym:

C

k

j

Z

L

k

j

Z

C

L

0

0

1











3. Przechodzimy do wartości chwilowych
dla poszczególnych harmonicznych

4. Po dodaniu wszystkich harmonicznych

otrzymujemy szereg Fouriera
dla szukanych prądów i napięć.

Wpływ indukcyjności i pojemności

na wyższe harmoniczne prądu i

napięcia

Liniowa cewka o indukcyjności L

k

U

U

U

L

L

k

U

I

I

m

m

m

m

m

m

k

k

k

1

1

1

1

0

0













dla wyższych harmonicznych k >1,
więc

1

1

m

m

m

m

U

U

I

I

k

k



Wniosek: Indukcyjność działa tłumiąco na
wyższe harmoniczne prądu i pobudzająco
na wyższe harmoniczne napięcia

Liniowy kondensator o pojemności
C:

1

1

1

1

1

0

0

m

m

m

m

m

m

m

m

m

m

U

U

I

I

U

U

k

C

U

C

k

U

I

I

k

k

k

k

k











Wniosek: pojemność działa tłumiąco na
wyższe harmoniczne napięcia i pobudzająco
na wyższe harmoniczne prądu

Moc okresowych

prądów

niesinusoidalnych

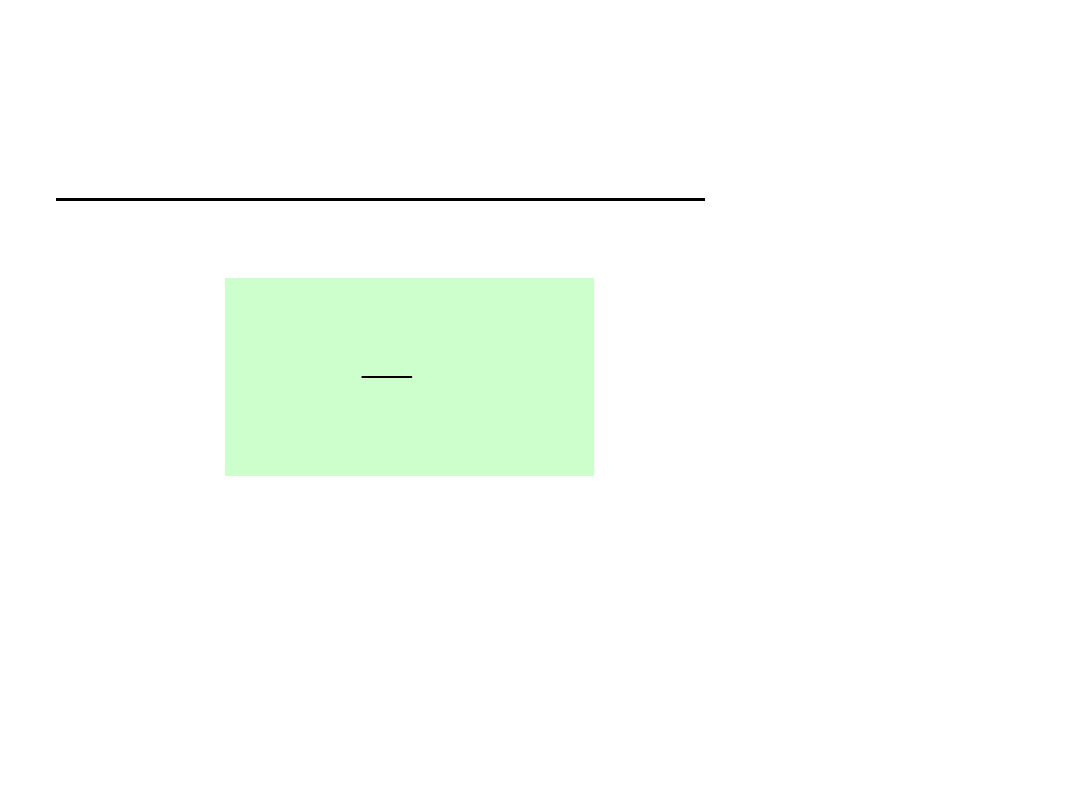
Moc czynną

– definiuje

wzór:

dla prądów okresowych





T

t

p

T

P

0

d

1

i

u

p





moc
chwilowa

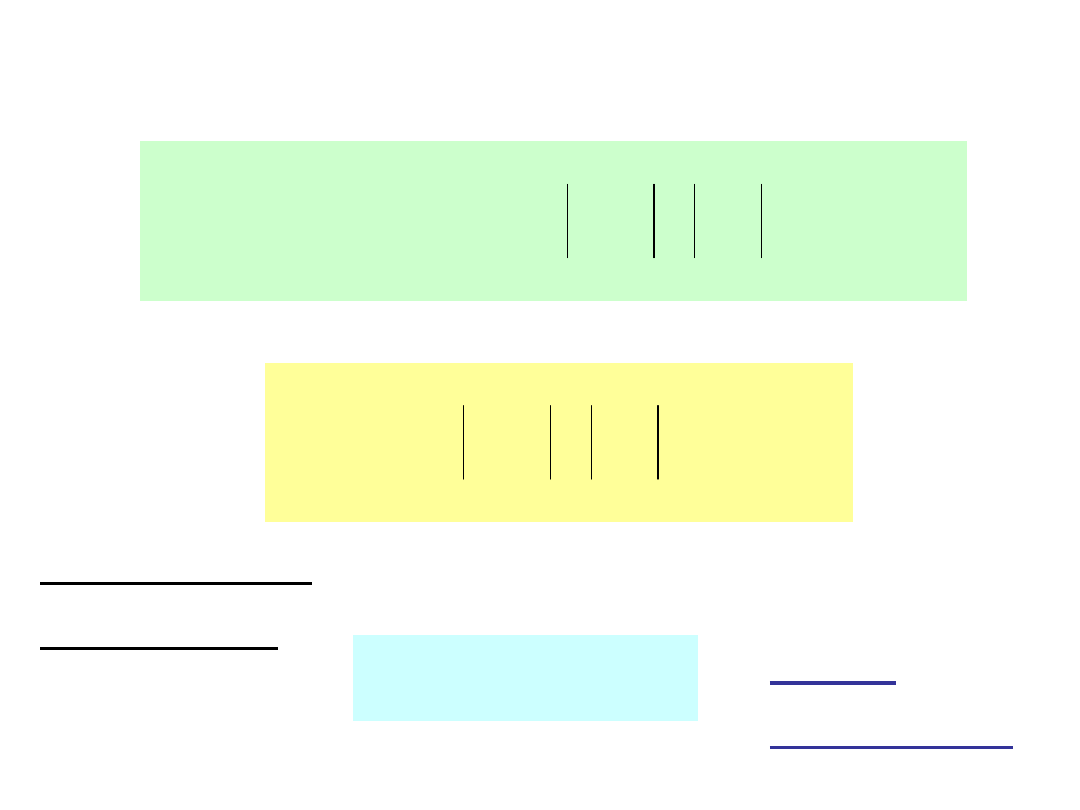
k

k

k

k

I

U

I

U

P



cos

1

0

0

















Podobnie moc bierna:

k

k

k

k

I

U

Q



sin

1













Def. mocy
pozornej

sk

sk

p

I

U

S





moc
pozorna

Moc czynna jest wynikiem współdziałania tych samych harmonicznych
prądu i napięcia:

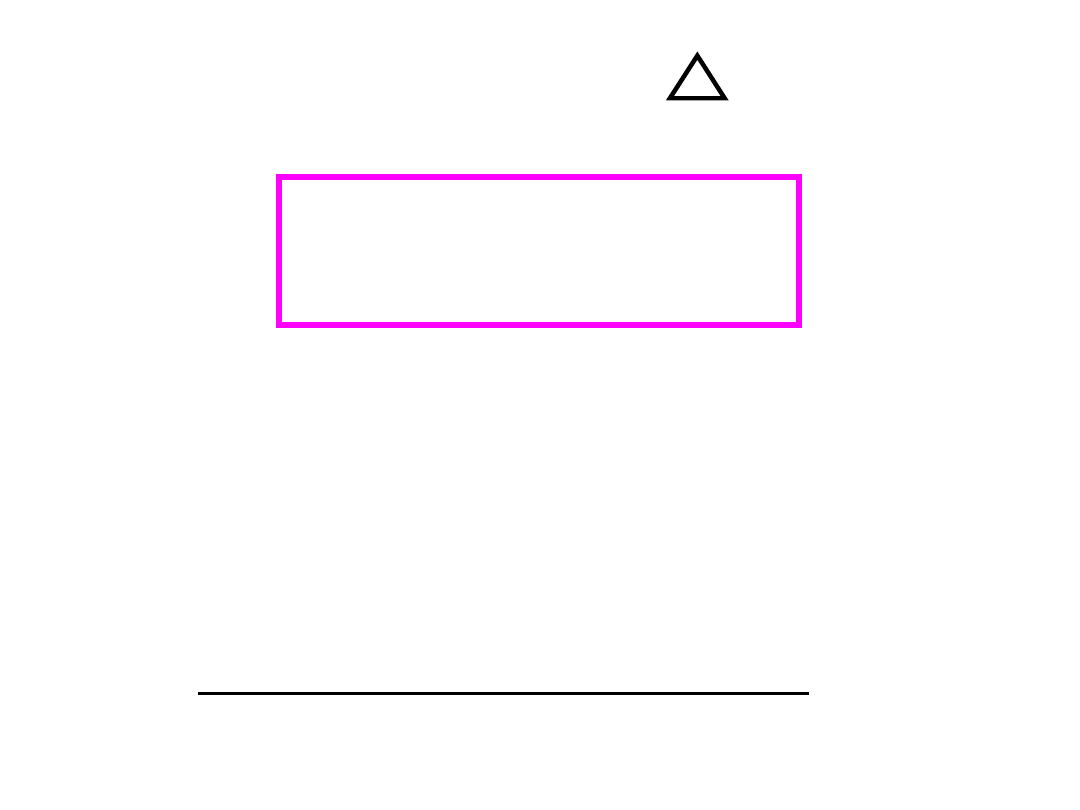
Jednak tu nie obowiązuje

mocy

2

2

2

p

S

Q

P





2

2

2

2

p

S

T

Q

P







T – moc zniekształcenia