1

Geomatyka – T. 1: Wiadomości 
wstępne

Pojęcie geomatyki 

(geoinformatyki)

Geomatyka (geoinformatyka) – jest to dziedzina wiedzy 
ściśle powiązana 
z informatyką i dotyczy problemów związanych z 
pozyskiwaniem, przesyłaniem, analizą, przetwarzaniem i 
udostępnianiem informacji geoprzestrzennych 
(geograficznych). 
Zadania te realizowane są przy użyciu oprogramowania 
Systemu Informacji Geograficznej (GIS – Geographics 
Information System)
Dyscypliny związane z tworzeniem informacji przestrzennych 
to: geodezja, fotogrametria, teledetekcja, kartografia, 
ewidencja gruntów i budynków (kataster) i inne.

Przedmiot 

Geomatyka

 ujmuje pojęcie geomatyki 

szerzej i umożliwia:
- poznanie logicznej struktury powiązań pomiędzy 
podstawowymi
  przedmiotami kierunku geodezja i kartografia;
- pełniejsze przyswojenie przedmiotów podstawowych oraz 
zarządzania
  pracami geodezyjnymi.

2

Geomatyka – T. 1: Wiadomości 
wstępne

Podstawowa literatura do przedmiotu 

Geomatyka

Baran L. W.: Teoretyczne podstawy opracowania wyników pomiarów 
geodezyjnych. 
                      Warszawa 1999
Geodezja inżynieryjna. Praca zbiorowa. Warszawa 1979
Jagielski A.: Geodezja I. Kraków 2005
Jagielski A.: Geodezja II. Kraków 2003
Jagielski A.: Przewodnik do ćwiczeń z geodezji I. Kraków 2004
Jagielski A.: Ćwiczenia z geodezji II. Kraków 2002
Jasiak A., Lelonkiewicz H., Wójcik M., Wyczałek I.: Przewodnik do ćwiczeń 
terenowych 
                       z geodezji. Poznań 1999
Kowalczyk K.: Wybrane zagadnienia z rysunku map. Olsztyn 2004
Lazzarini T.: Geodezja. Geodezyjna osnowa szczegółowa. Warszawa – 
Wrocław 1990
Saliszczew K. A.: Kartografia ogólna. Warszawa 1984
Teledetekcja, pozyskiwanie danych. Praca zb. pod red. J. Saneckiego. 
Warszawa 2006
Skórczyński A.: Podstawy obliczeń geodezyjnych. Warszawa 1983
Skórczyński A.: Lokalna triangulacja i trilateracja. Warszawa 2004
Skórczyński A.: Poligonizacja. Warszawa 2000
Szymański J.: Instrumentoznawstwo geodezyjne cz. I-III. Warszawa 1972
Werner P.: Wprowadzenie do systemów geoinformacyjnych. Warszawa 
2004
Wiśniewski Z.: Rachunek wyrównawczy w geodezji. Olsztyn 2005
Wysocki J.: Geodezja z fotogrametrią dla ochrony środowiska i 
budownictwa. Warszawa 2000

3

Geomatyka – T. 1: Wiadomości 
wstępne

GEODEZJA – nauką o 

Ziemi

Nauki o 

Ziemi - 

Geodezja

Geografia
Geologia
Geofizyka
Geomorfologia
Oceanologia
Geotechnika
Gleboznawstwo
Ekologia
Hydrologia i inne

Nauki o Ziemi – ich zadaniem jest 
gromadzenie, przetwarzanie 
i przekazywanie wiedzy o naszej 
planecie.  

Podstawy teoretyczne geodezji 
oparte są na naukach ścisłych, takich 
jak: matematyka, fizyka, astronomia, 
geografia, informatyka, mechanika i 
inne.

4

Geomatyka – T. 1: Wiadomości 
wstępne

Geodezja – jedną z najstarszych 

dziedzin nauki

Znaleziska archeologiczne – gliniane 
tabliczki i opisy 
prac pomiarowych w starożytnym Egipcie z 
okresu 
XX wieku p.n.e. sporządzone na papirusach

Nazwa geodezja, wprowadzona przez 
Arystotelesa, pochodzi od słów greckich: geo – 
Ziemia i daiso – będę dzielił, co dosłownie 
oznacza podział Ziemi, czyli pomiar 
i dzielenie na mniejsze fragmenty posiadłości 
ziemskich.

Także obecnie podziały nieruchomości stanowią 
jedno 
z ważniejszych zadań geodezyjnych. 

Wraz z rozwojem cywilizacji oraz nowymi odkryciami 
geograficznymi zadania geodezji ulegały 
stopniowemu poszerzeniu: sporządzano mapy nowych 
terenów, wyznaczano kształt i wielkość całej Ziemi.

5

Geomatyka – T. 1: Wiadomości 
wstępne

Współczesna definicja geodezji

Geodezja  jako nauka i dziedzina techniki zajmuje się 
uzyskiwaniem informacji 
o elementach środowiska geograficznego, kształcie i wymiarach 
części lub całości powierzchni Ziemi oraz określaniem na niej 
położenia wybranych obiektów, jak również zastosowaniem 
wyników tych opracowań do rozwiązywania różnych zagadnień o 
charakterze badawczym i projektowym lub gospodarczym 
związanych z wieloma dyscyplinami nauki, planowania, inżynierii 
i gospodarki.

Zadania geodezji: 

1.

Badanie kształtu, rozmiarów Ziemi oraz stanu i zmian 
środowiska geograficznego.

2.

Sporządzenie modelu matematycznego i mechanicznego bryły 
ziemskiej.

3.

Dostarczanie danych dla systemów informacji przestrzennej.

4.

Wykorzystanie informacji o terenie dostarczanych poprzez 
pomiary i dokumentację geodezyjną dla potrzeb ochrony 
środowiska oraz sporządzania różnych projektów i planowania 
przestrzennego.

5.

Gospodarka nieruchomościami i ustalanie ich granic dla celów 
prawnych i rozliczeń finansowych.

6.

Przenoszenie projektów i planów w teren podczas pomiarów 
realizacyjnych, badanie za pomocą techniki geodezyjnej budowli 
i urządzeń technicznych.

7.

Sporządzanie i gromadzenie dokumentacji geodezyjnej w celach 
archiwalnych i użytkowych oraz jej udostępnianie 
zainteresowanym instytucjom i osobom fizycznym.

6

Geomatyka – T. 1: Wiadomości 
wstępne

Podstawowe czynności zawodowe 

geodetów

Do zakresu podstawowych czynności zawodowych 
geodetów należą:

- prace polowe (terenowe) realizowane podczas 
różnorodnych pomiarów 
  i wywiadów;

- prace kameralne (biurowe) obejmujące: obliczenia i 
sporządzanie map,
  szkiców, rysunków, dokumentacji opisowej, protokołów, 
rejestrów itp.

Do prac geodezyjnych zalicza się (

Ustawa – Prawo geodezyjne i 

kartograficzne

):

- projektowanie i wykonywanie pomiarów geodezyjnych,

- dokonywanie obliczeń,

- sporządzanie dokumentacji geodezyjnej,

- zakładanie i aktualizacja baz danych,

- sporządzanie zdjęć, pomiary i opracowania 
fotogrametryczne,
  grawimetryczne, magnetyczne i astronomiczne związane z 
realizacją zadań
  z dziedziny geodezji i kartografii oraz krajowego systemu 
informacji 
  o tereni (SIT)

7

Geomatyka – T. 1: Wiadomości 
wstępne

Działy geodezji

Geodezja ogólna

 – (d. geodezja niższa lub miernictwo) zajmuje się pomiarami i 

sporządzaniem wielkoskalowych map małych obszarów, które można odnosić do 
płaszczyzny, bez konieczności uwzględniania krzywizny Ziemi.

Geodezja wyższa

 – zajmuje się badaniem kształtu i wymiarów Ziemi i pomiarami 

znacznych jej obszarów z uwzględnieniem krzywizny powierzchni, do której odnosi się 
pomiary.

Kartografia

 – jest nauką o mapach, metodach ich sporządzania i sposobach 

wykorzystania.

Topografia

 – zajmuje się wykonywaniem map ogólnogeograficznych w skalach 1:5000, 

1:10000, 1:25000, 1:50000, 1:100000 sporządzonych w oparciu o opracowania 
wielkoskalowe lub odrębną technikę pomiarową.

Fotogrametria

 – zajmuje się techniką wykonywania, opracowaniem i wykorzystaniem 

zdjęć naziemnych, lotniczych i satelitarnych dla celów pomiarowych oraz 
kartograficznych.

Instrumentoznawstwo geodezyjne

 – zajmuje się konstrukcją, badaniem, 

użytkowaniem i konserwacją przyrządów geodezyjnych.

Rachunek wyrównawczy

 – zajmuje się metodami obliczeń geodezyjnych, 

wyrównaniem wyników pomiarów i szukanych wielkości w celu określenia ich najbardziej 
prawdopodobnych wartości liczbowych, oceną dokładności pomiarów i wielkości 
wyrównanych, optymalizacją prac geodezyjnych.

Geodezja gospodarcza

 – obejmuje szeroki zakres zastosowań metod geodezyjnych w 

takich dziedzinach gospodarki jak: administracja, przemysł, komunikacja, rolnictwo, 
leśnictwo, górnictwo, koleje. Wyróżniamy geodezję: inżynieryjno-przemysłową, urządzeń 
rolnych, leśną, górniczą, kolejową.

Astronomia geodezyjna

 – zajmuje się określaniem położenia punktów i orientacją 

kierunków na powierzchni Ziemi za pomocą obserwacji ciał niebieskich.

Geodezja dynamiczna

 – zajmuje się wyznaczaniem kształtu i położenia 

przestrzennego geoidy w oparciu o pomiary grawimetryczne, których celem jest badanie 
przyspieszenia i potencjału siły ciężkości w różnych punktach powierzchni Ziemi.

8

Geomatyka – T. 1: Wiadomości 
wstępne

Powierzchnia odniesienia

Ziemia jest nieregularną bryłą, której 

rzeczywistego kształtu nie da się przedstawić w sposób 
ścisły, tzn. za pomocą równania matematycznego.
W celu zdefiniowania układu odniesienia niezbędnego 
do określania lokalizacji punktów potrzebna jest 
regularna powierzchnia dająca się opisać 
matematycznie, zbliżona kształtem do fizycznej 
powierzchni Ziemi.

Powierzchnia odniesienia to regularna powierzchnia, na którą 

rzutuje się 

punkty pomierzone sytuacyjnie.

Ziemia jest nieregularną bryłą, której rzeczywistego kształtu 

nie da się przedstawić w sposób ścisły, tzn. za pomocą równania 
matematycznego.
W celu zdefiniowania układu odniesienia niezbędnego do określania 
lokalizacji punktów potrzebna jest regularna powierzchnia dająca się 
opisać matematycznie, zbliżona kształtem do fizycznej powierzchni 
Ziemi.
W zależności od wielkości obszaru podlegającego pomiarowi 
powierzchnię tę może stanowić: płaszczyzna, kula lub elipsoida 
obrotowa. 

9

Geomatyka – T. 1: Wiadomości 
wstępne

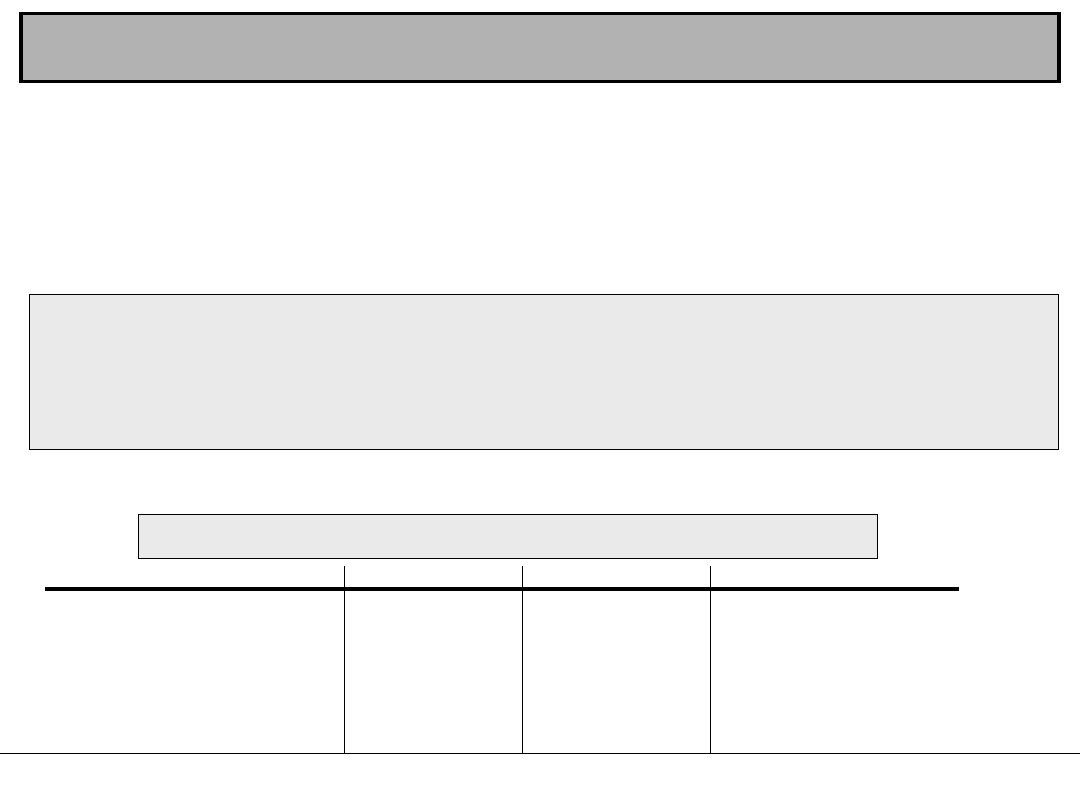
Geoida jest teoretyczną powierzchnią ciągłą powstałą w 

wyniku przedłużenia średniej powierzchni  mórz i oceanów w 
stanie spoczynku pod lądami i nad depresjami. Geoida najlepiej 
oddaje rzeczywisty kształt powierzchni Ziemi. Określana jest 
również jako powierzchnia stałego potencjału grawitacyjnego na 
poziomie morza, do której w każdym jej punkcie kierunek linii 
pionu jest zawsze prostopadły.

Już w XVII w. wiedziano, że kształt Ziemi nie jest ściśle 

kulisty, lecz zbliżony do symetrycznej bryły powstałej w wyniku 
obrotu elipsy wokół jej mniejszej osi, czyli tzw. elipsoidy 
obrotowej, przypominającej kulę spłaszczoną na biegunach. 
Równoleżniki Ziemi mają postać kolistą, zaś południki są 
krzywymi o kształcie zbliżonym do elips, zaś jednostopniowy łuk 
południka posiada zmienną długość. 
Spłaszczenie biegunowe Ziemi wynika ze skończonej sztywności 
globu i działania siły odśrodkowej ruchu obrotowego.

W 1873 r. uczony niemiecki Listing wprowadził pojęcie 

geoidy.

Geoida

Ze względu na niejednolity rozkład mas wewnątrz Ziemi bryła ta 

ma nieregularny kształt, niemożliwy do opisania równaniem 
matematycznym. Z tego powodu Listing zaproponował, aby jako 
powierzchnię odniesienia przyjąć tzw. elipsoidę ziemską.

10

Geomatyka – T. 1: Wiadomości 
wstępne

Współcześnie geoida pełni funkcję powierzchni odniesienia dla 

pomiarów wysokościowych. Jako powierzchnia o stałym potencjale siły 
ciężkości (ekwipotencjalna) geoida jest w każdym swym punkcie 
prostopadła do jej kierunku. Siła ciężkości stanowi wypadkową siły 
przyciągania i siły odśrodkowej. Zależnie od przyjętej wartości 
potencjału istnieją różne powierzchnie ekwipotencjalne. Lustro wód w 
stanie spoczynku jest naturalną geoidą. Powierzchnia ta jednak ulega 
ciągłym zmianom wskutek wiatrów i działania grawitacyjnego Słońca i 
Księżyca powodujące przypływy i odpływy. Z tych względów jako 
powierzchnię podstawową przyjmuje tzw. geoidę zerową.

Geoida zerowa jest to taka geoida, która przechodzi przez 

średni poziom morza w określonym punkcie Ziemi i jest wyznaczana 
poprzez wieloletnie obserwacje dla pewnej epoki czasowej. Wybór 
punktu zerowego wysokości ma bardzo istotne znaczenie dla pomiarów 
niwelacyjnych kraju, w którym obowiązuje.

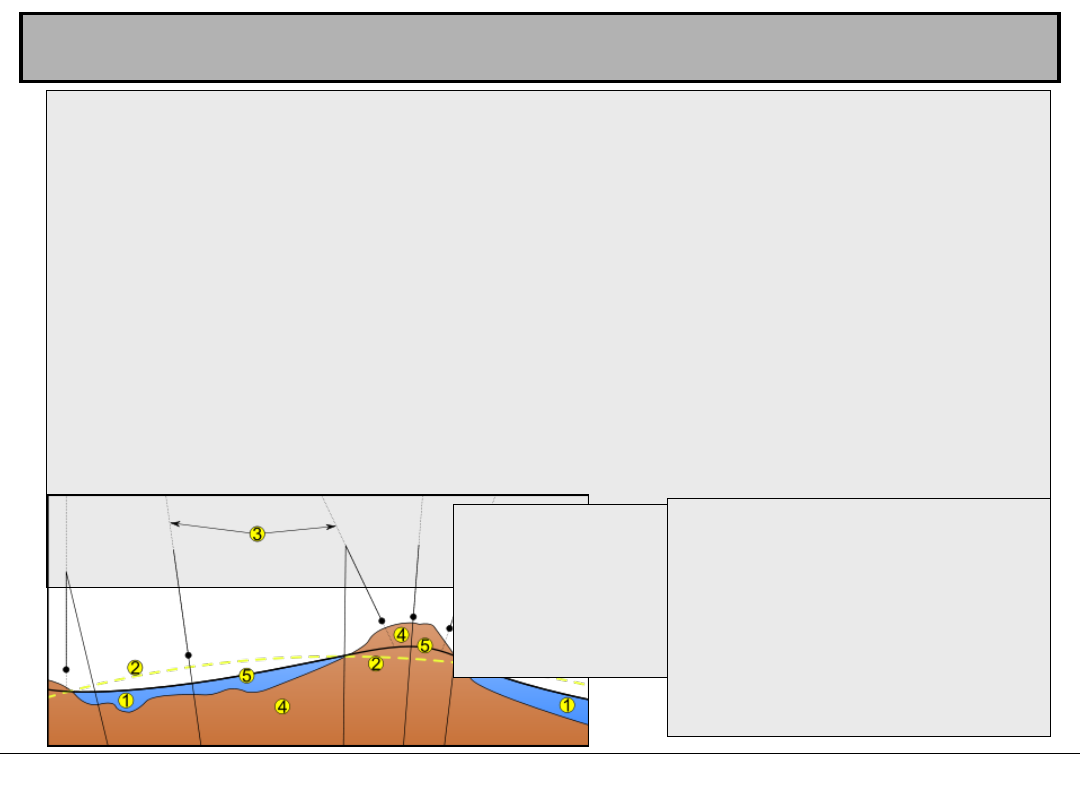
Geoida

 1. Ocean
2. Elipsoida
3. Pion lokalny
4. Kontynent
5. Geoida

Obecnie obowiązującym 
dla Polski jest poziom 
morza określony przez 
zero łaty wodowskazowej 
stacji mareograficznej w 
Kronsztadzie
k. Sankt Petersburga. 

11

Geomatyka – T. 1: Wiadomości 
wstępne

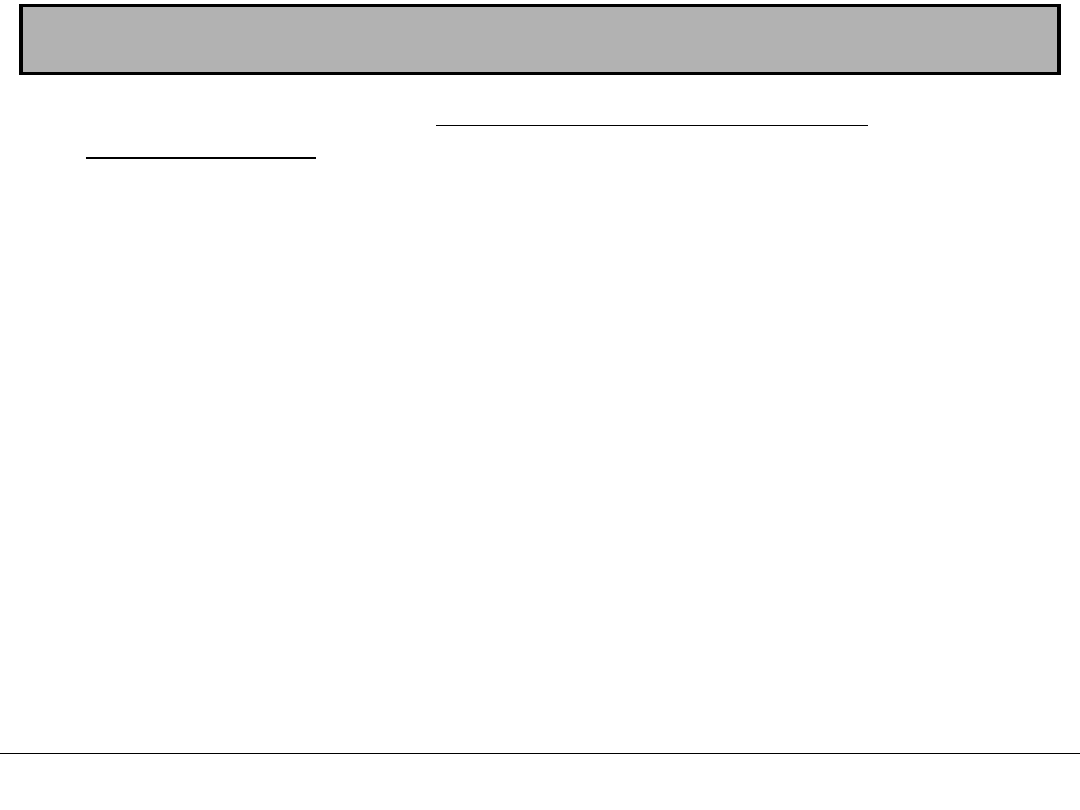
Elipsoida ziemska to taka elipsoida obrotowa 

spłaszczona, której objętość jest równa objętości geoidy, zaś 
suma wzajemnych odchyleń powierzchni obu brył jest minimalna. 
Jej mała oś pokrywa się z osią obrotu Ziemi.

Elipsoida ziemska

Wymiary i położenie geoidy są więc potrzebne do ustalenia 

parametrów elipsoidy ziemskiej. Geoida nie może być 
wykorzystywana jako powierzchnia odniesienia dla określania 
położenia sytuacyjnego punktów Ziemi. Do tego celu wykorzystuje 
się elipsoidę odniesienia i związany z nią układ współrzędnych 
kątowych o symbolach B, L.

Parametrami opisującymi elipsoidę ziemską są: długość 

półosi większej równikowej a i spłaszczenie s = (a-b)/a, gdzie b - 
półoś mniejsza biegunowa. 

Wymiary elipsoidy ziemskiej wg ważniejszych badań

   Autor (rok)                             a                             b                             
s
Bessel (1841)                    6377397 m             6356079 m              
1:299,15
Clarke (1880)                    6378249 m             6356515 m              
1:293,50
Hayford (1909)                 6378388 m             6356912 m              
1:297,00
Krasowski (1940)             6378245 m             6356863 m               
1:298,30
Elipsoida GRS 80 (1980) 6378137 m             6356752 m               
1:298,26

12

Geomatyka – T. 1: Wiadomości 
wstępne

Geodezyjny system odniesień 

przestrzennych

Na jednolity dla całego kraju państwowy system odniesień 

przestrzennych składają się:

1. Geodezyjny układ odniesienia określający geometryczne i geofizyczne 

parametry Ziemi, niezbędny do wyznaczenia współrzędnych B i L.

2. Układ i system wysokości, w którym wyznacza się wysokości punktów 

względem przyjętego poziomu odniesienia.

3. Układ współrzędnych prostokątnych płaskich.

Podstawowym zadaniem geodezji jest wyznaczenie 

przestrzennego położenia punktów na powierzchni Ziemi. Wymaga to 
powiązania używanego systemu odniesień przestrzennych z elementami 
charakteryzującymi Ziemię, a w szczególności z jej osią obrotu i 
rozkładem siły ciężkości.

Położenie sytuacyjne punktów na powierzchni Ziemi wyznaczają 

współrzędne geograficzne (geodezyjne) B, L na elipsoidzie, zaś w 
uproszczeniu wysokość H można uważać za odległość pionową danego 
punktu P od geoidy zerowej.

Wobec tego pomiary dzielimy na sytuacyjne i wysokościowe.
W geodezji stosowane są układy globalne obejmujące całą 

Ziemię oraz układy odnoszące się do pewnego fragmentu jej 
powierzchni, który można uznać za płaski.

Układy globalne to układy współrzędnych geograficznych 

(astronomiczny (,) i geodezyjny (B,L)) oraz kartezjański geocentryczny 

układ współrzędnych prostokątnych.

Do mniejszych obszarów wykorzystuje się układy prostokątne 

płaskie, czasem układ współrzędnych biegunowych.

13

Geomatyka – T. 1: Wiadomości 
wstępne

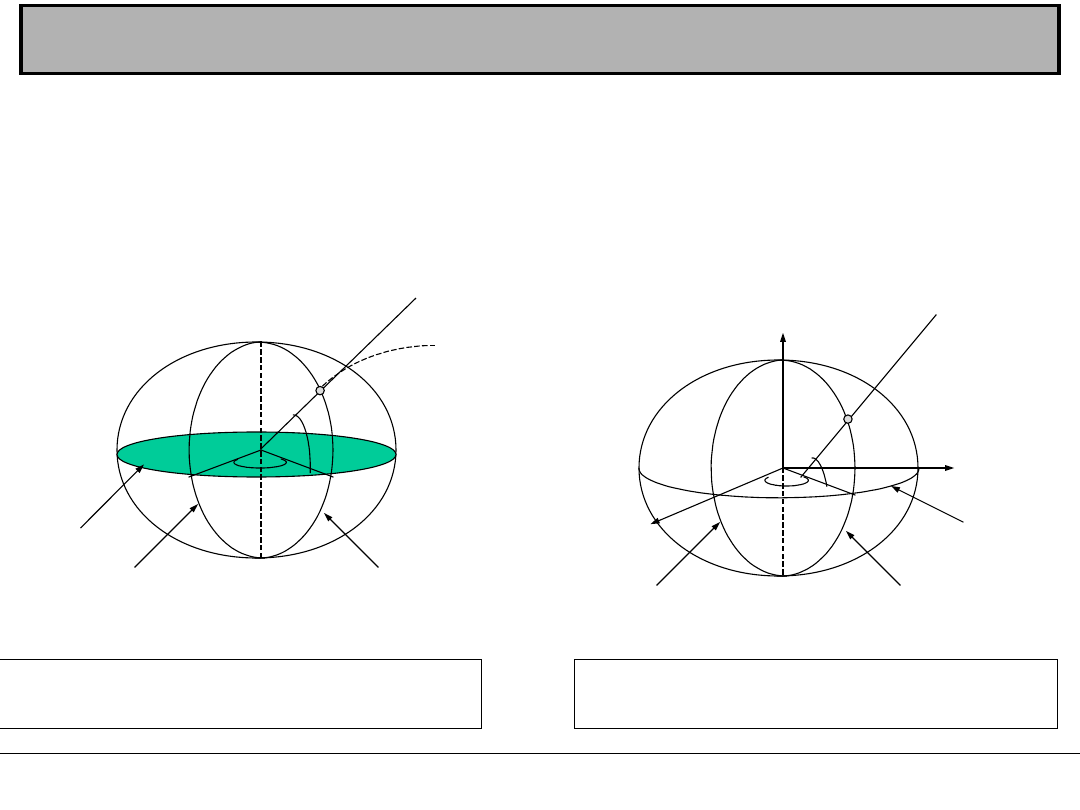
Współrzędne geograficzne związane są z osią obrotu Ziemi i linią pionu.
Współrzędne geograficzne podlegają redukcji na geoidę, redukcja ta 
polega na wprowadzeniu do współrzędnych wyznaczonych z pomiarów 
astronomicznych poprawek ze względu na ruchy bieguna i wpływ 
zakrzywienia linii pionu. 
Zredukowane współrzędne przeniesione z geoidy na elipsoidę 
odniesienia przez rzutowanie wzdłuż normalnych do elipsoidy obrotowej 
dają w ostateczności  współrzędne geograficzne geodezyjne B,L.



południk zerowy 
Greenwich

południk miejsca 
obserwacji

st

yc

zn

a 

do

 l.

 p

io

nu

l.pionu

B

B

południk zerowy 
Greenwich

południk miejsca 
obserwacji

no

rm

al

na

 d

o 

el

ip

so

id

y

równik

x

y

z

Układ współrzędnych geograficznych 

astronomicznych ,

Układ współrzędnych geograficznych 

geodezyjnych B,L

O

L

B

eli

ps

oid

a

ge

oi

da

Układ współrzędnych geograficznych

φ

równik

P

P

14

Geomatyka – T. 1: Wiadomości 
wstępne

Szerokość geograficzna φ jest kątem zawartym 

pomiędzy kierunkiem pionu (promieniem kuli) w danym punkcie 
P a płaszczyzną równika. Szerokość geograficzna zmienia się w 
przedziale od 0

0

 do +90

0

 na północ od równika 

i od 0

0

 do -90

0

 na południe od równika.

Długość geograficzna λ jest to kąt dwuścienny zawarty 

pomiędzy płaszczyzną południka zerowego Greenwich a 
płaszczyzną południka przechodzącego przez dany punkt P. 
Długość geograficzna zmienia się w przedziale od 0

0

 do +180

0 

 w 

kierunku na wschód od południka zerowego 
i w przedziale od 0

0

 do -180

0

 na zachód od tego południka.

Szerokość geograficzna (geodezyjna) B punktu P to 

kąt B, jaki tworzy normalna do elipsoidy obrotowej (w punkcie 
rzutu punktu P na powierzchnię elipsoidy) z płaszczyzną równika.

Długość geograficzna (geodezyjna) L to kąt 

dwuścienny zawarty pomiędzy południkiem zerowym a 
południkiem zawierającym punkt P. Płaszczyzna południka 
geodezyjnego zawiera normalną do elipsoidy w punkcie P 
i przechodzi przez oś obrotu elipsoidy.

Układ współrzędnych geograficznych

15

Geomatyka – T. 1: Wiadomości 
wstępne

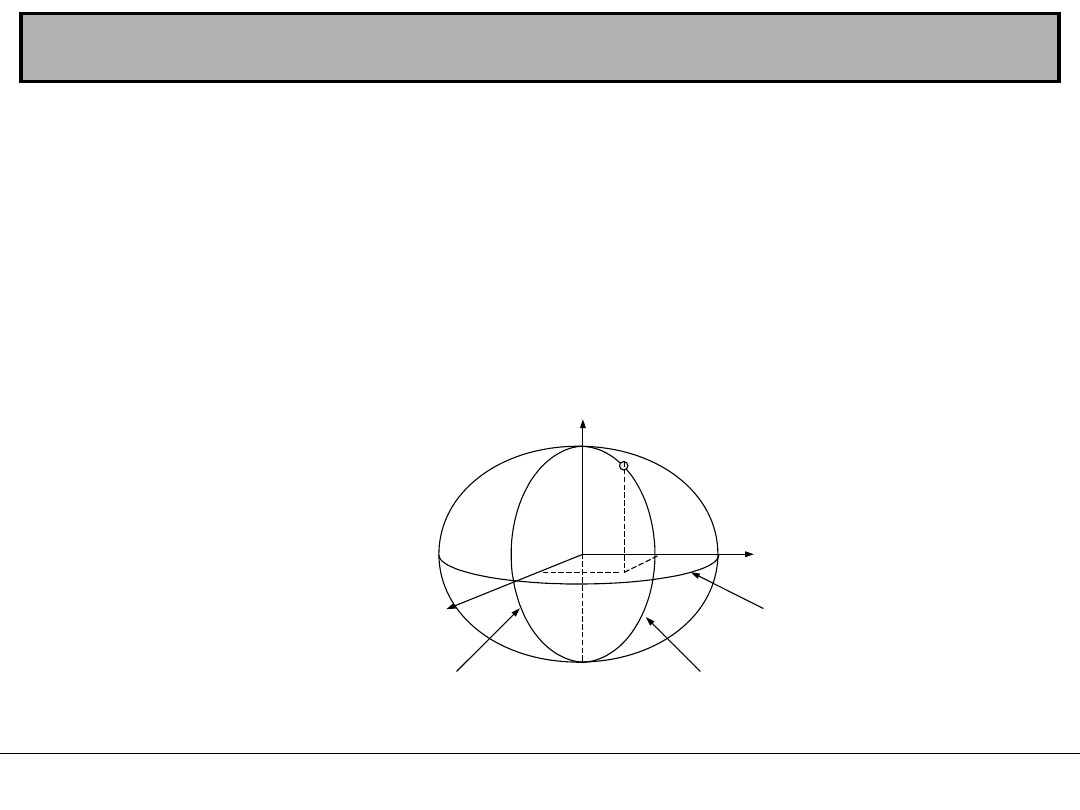
Układ geocentryczny

południk zerowy 
Greenwich

równik

x

y

z

O

eli

ps

oi

da

P

Y

P

X

P

Z

P

Układ współrzędnych przestrzennych X, Y, Z zwany jest 

również układem geocentrycznym. 

Początek tego układu O znajduje się w środku ciężkości 

masy Ziemi znajdującym się w płaszczyźnie równika. Oś x 
układu powstaje na przecięciu płaszczyzn: równika i południka 
zerowego, zaś oś y na przecięciu płaszczyzn: równika i 
południka 90

0

, tworząc z pozostałymi osiami układ 

prawoskrętny, natomiast oś z pokrywa się z osią obrotu 
elipsoidy.

Położenie punktu P jest zdefiniowane przez podanie 

trzech współrzędnych X

P

, y

P

, Z

P

.

16

Geomatyka – T. 1: Wiadomości 
wstępne

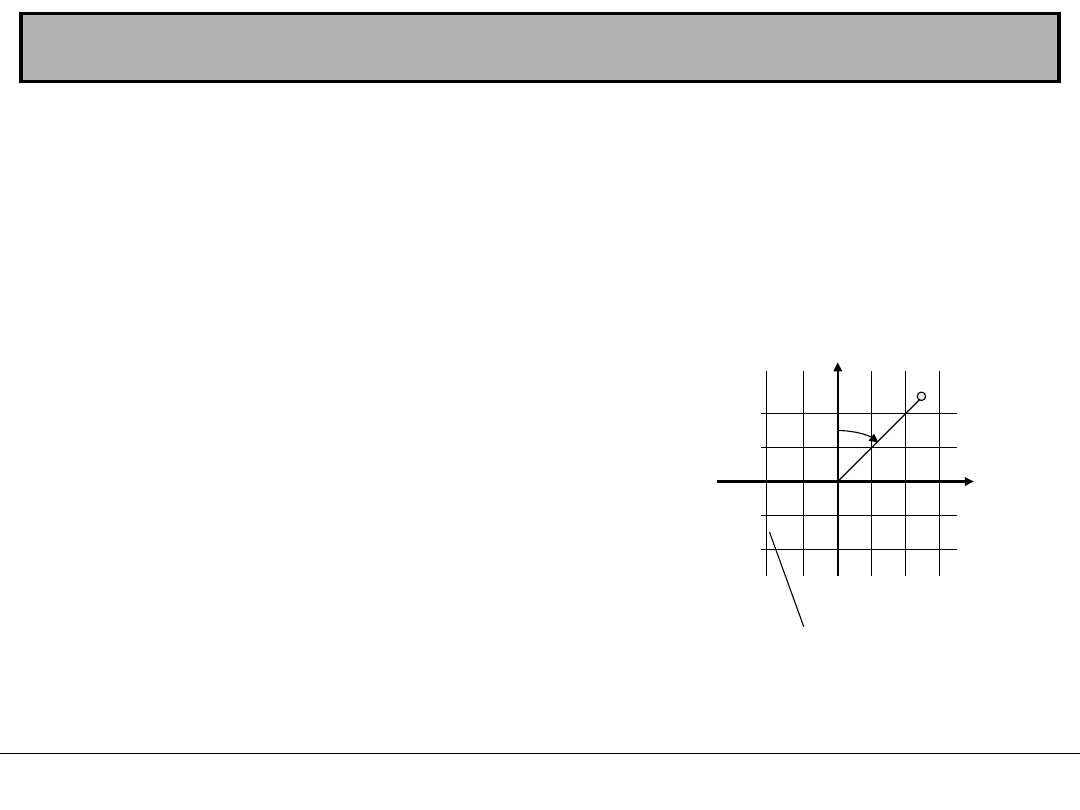
Układ współrzędnych prostokątnych na 

płaszczyźnie

Układ współrzędnych wykorzystywany w geodezji różni się od 

analogicznego układu stosowanego w matematyce usytuowaniem osi x, 
y i kierunkiem liczenia kątów, a tym samym kierunkiem liczenia 
ćwiartek układu.
Układ matematyczny jest lewoskrętny, zaś geodezyjny – prawoskrętny.
Powodem wprowadzenia powyższych zmian w układzie geodezyjnym 
jest konieczność nadania orientacji osiom układu w stosunku do stron 
świata, aby dodatni kierunek osi x wskazywał północ, zaś +y wschód.

+y

+x

N

E

W

S

O

P

linie siatki kilometrowej

I ćw.

II ćw.

III ćw.

IV ćw.

A

OP

Zgodnym z kierunkiem północnej części 

południka przechodzącego przez początek 
układu jest z reguły kierunek osi x, zaś dla 
małego obszaru pozostałe południki można 
traktować jako linie proste wzajemnie 
równoległe, tworzące wraz z równoleżnikami 
prostokątną siatkę (kilometrową).
Położenie sytuacyjne punktu określają 
współrzędne prostokątne płaskie X, Y, zaś 
orientację odcinka OP jego azymut A

OP

, który 

jest kątem liczonym w prawo od kierunku 
północy przechodzącego przez dany punkt P do 
kierunku odcinka OP.

Przy pomiarach dużych obszarów trzeba uwzględniać krzywiznę 

Ziemi, co wiąże się z problemem przedstawiania jej zakrzywionej 
powierzchni na płaszczyźnie.

17

Geomatyka – T. 1: Wiadomości 
wstępne

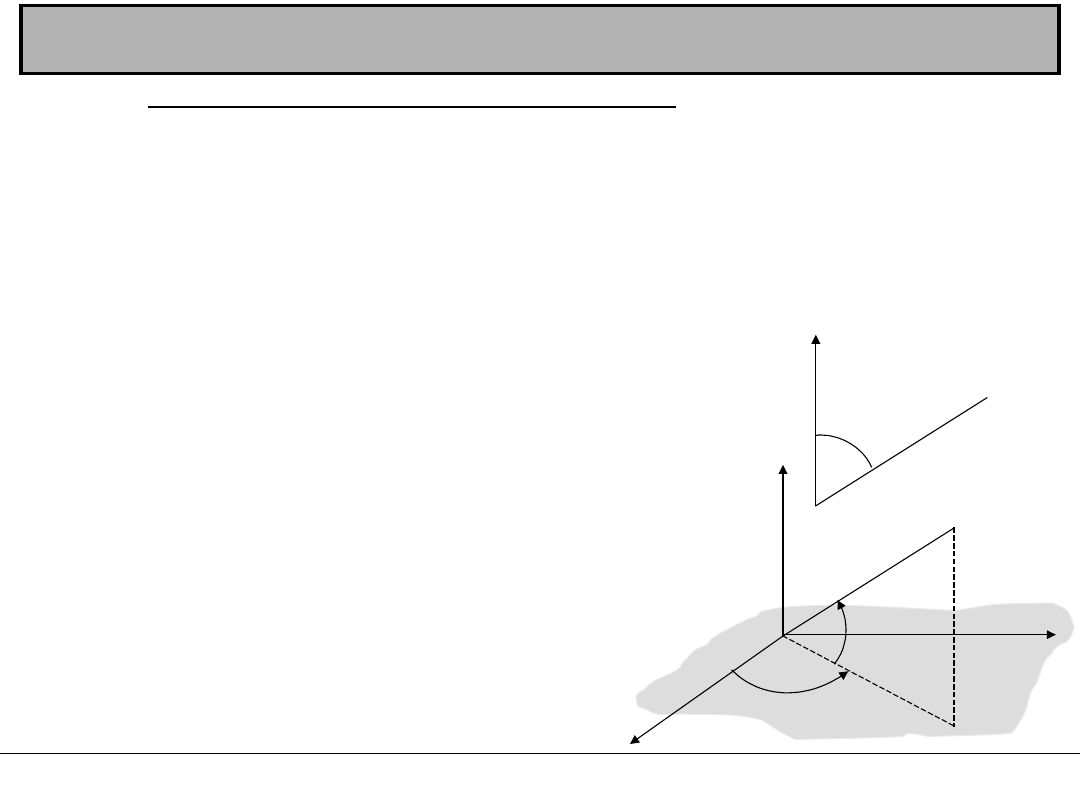
Układ współrzędnych biegunowych jest w geodezji często 

wykorzystywany jako układ lokalny. Dotyczy to szczególnie określania 
położenia punktów sytuacyjnych względem boków osnowy poziomej 
podczas pomiaru sytuacyjnego metodą biegunową. 

Układ biegunowy płaski tworzą: znany punkt B – początek 

układu, czyli biegun i wychodząca z niego półprosta x zwana osią 
biegunową.

Współrzędnymi biegunowymi wybranego 

punktu P są: promień wodzący r, czyli odległość d

BP

 

pomiędzy wyznaczanym punktem P a biegunem B i 
kąt kierunkowy β, zawarty między osią biegunową a 
promieniem wodzącym, mierzony od osi w prawo, 
czyli zgodnie z ruchem wskazówek zegara.

Do zdefiniowania stosowanego w geodezji 

przestrzennego układu współrzędnych 
biegunowych konieczne jest ustalenie poziomej 
płaszczyzny π, na której znajdują się: biegun B oraz 
oś biegunowa x. Przestrzenne położenie dowolnego 
punktu P w układzie biegunowym określają trzy 
wielkości: kąt poziomy β, długość promienia 
wodzącego r 
oraz kąt pionowy α , który promień wodzący r 
tworzy z płaszczyzną poziomą π. 
Rolę płaszczyzny spełnia w trakcie pomiarów 
horyzont instrumentu kątomierczego.  

Układ współrzędnych biegunowych

x

r

P

β

B

x

y

z

r

P

P
`

α

β

π

B