
1.Cyfry znaczące i miejsca po przecinku.
1,274501
1,2735
2,39951
Zaokrągl wartości do 3 cyfr po przecinku oraz do 3 cyfr znaczących
=1,275
=1,274
=2,400
=1,27
=1,27
=2,40
1
2,1514 2,15
2
0,16152
0,162
3
0,01204
0,0120
4
1,225
1,22
5
-0,0015281
-
0,00153
6
-392,85
-393
7
0,1545
0,154
8
0,003922
0,00392
9
625,55
626
10
94,525 94,5
Symbole rachunkowe prof. Hausbrandta
3
4
2
5
8
3
4
2
5
0
6
3
18
1
0
2
sin
cos
y
x
n
n
n
n
d
c
b
a
d
c
b
a
d
c
b
a
f
2
2
2
2
1
1
1
1
Przykłady form
lub
lub
Definicja formy:
Funkcja pierwsza (iloczyn wyznacznikowy)
i
i
i
i
n
n
n
n
c
b
d
a
c
b
d
a
c
b
d
a
c
b
d
a
f
...
2
2
2
2
1
1
1
1
1
Funkcja druga (iloczyn kolumnowy)
i
i
i
i
n
n
n
n
d
b
c
a
d
b
c
a
d
b
c
a
d
b
c
a
f
...
2
2
2
2
1
1
1
1
2
Funkcja zerowa (iloraz główny)
i
i
i
i
i
i
i
i
d
b
c
a
c
b
d
a
f
f
f
2
1
0

;
1
1
i
i
d
c
f
f
;
2
2
i
i
d
c
f
f
;
1
1
i
i
b
a
f
f
;
2
2
i
i
b
a
f
f
;
2
2
1
1
i
i
d
c
f
f
;
2
2
2
2
i
i
d
c
f
f
;
2
2
1
1
i
i
b
a
f
f
;
2
2
2
2
i
i
b
a
f
f
Funkcje względne proste
Funkcje względne kwadratowe
Przykład
8
4
7
5
6
7
3
4
F
oblicz wszystkie funkcje formy
Mając daną formę
71
7
)
4
(
8
5
7
3
6
4
8
4
7
5
6
7
3
4
1
1
F
82
8
7
)
4
(
5
6
3
7
4
8
4
7
5
6
7
3
4
2
2
F
82
71
8
4
7
5
6
7
3
4
0
0
F
17647
,
4
17
71
8
4
6
7
71
1
F
73684
,
3
19
71
7
5
3
4
71
1
F
82353
,
4
17
82
8
4
6
7
82
2
F
31579
,
4
19
82
7
5
3
4
82
2
F
4303
,
0
165
71
8
4
6
7
71
2
2
2
2
1
F
7172
,
0
99
71
7
5
3
4
71
2
2
2
2
1
F
49697
,
0
165
82
8
4
6
7
82
2
2
2
2
2
F
8283
,
0
99
82
7
5
3
4
82
2
2
2
2
2
F
= 3,7
= 4,2
= 4,82
= 4,32
= 0,4
= 0,7
= 0,5
= 0,9
Zaokrągl wyniki 1 szych funkcji względnych
do 2 cyfr znaczących
Zaokrągl wyniki 2-ich funkcji względnych
do 2 cyfr po przecinku
Zaokrągl wyniki 1-ych funkcji względnych
Kwadratowych do 1 cyfry znaczącej
Zaokrągl wyniki 2-ich funkcji względnych
kwadratowych do 1 cyfry znaczącej w górę
C
P
L
0
CP
CP
CL
CL
Y
X
Y
X
tg
ZASTOSOWANIE SYMBOLI RACHUNKOWYCH W OBLICZENIACH GEODEZYJNYCH
Rachunek kątów:
0
0
79
5
3
15
3
3
)
2
(
3
3
)
2
(
3
3
3
2
3
3
tg
0
0
45
1
15
15
3
3
0
5
tg
0
0
56
5
,
1
10
15
0
5
3
2
tg
X=5
Y=7
X=3
Y=1
0-
X=8
Y=1
0
ZADANIE
Mając dane współrzedne wierzchołków trójkąta oblicz jego kąty
2
,
1
sin
cos
,
b
d
y
x
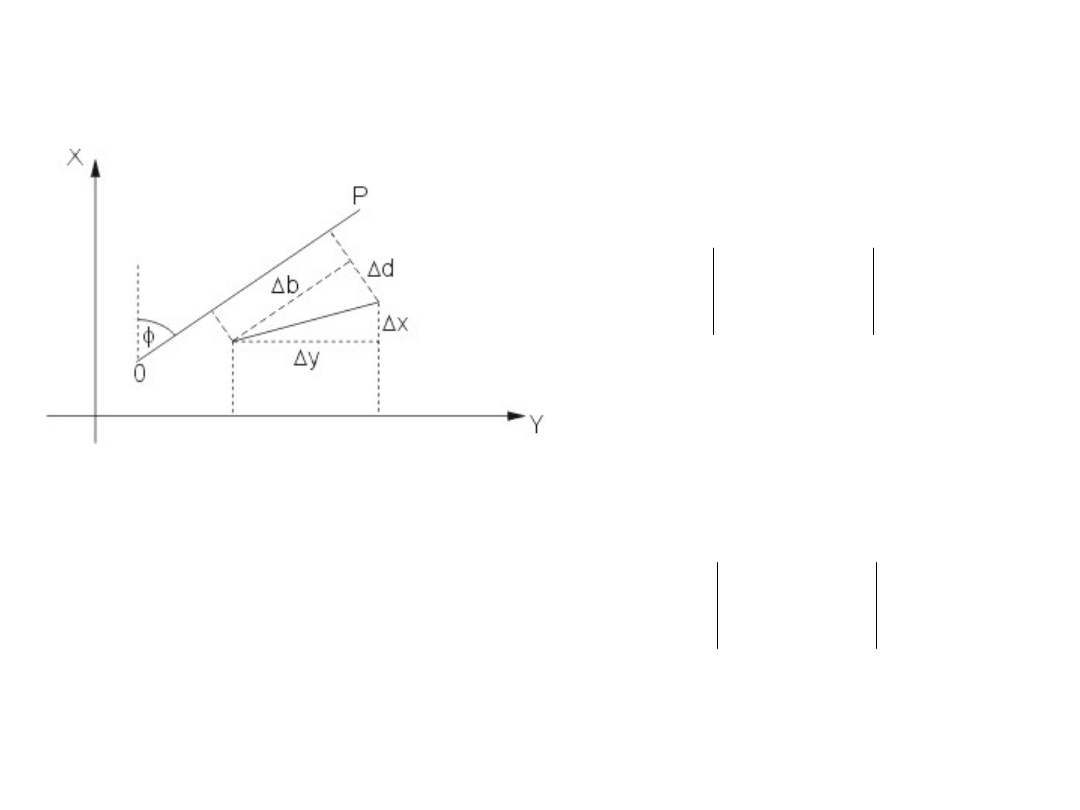
Przekształcanie współrzędnych:
a)Zamiana współrzędnych lokalnych na terenowe
b) Zamiana współrzędnych terenowych na lokalne
2
,
1
sin
cos
,
y
x
b
d
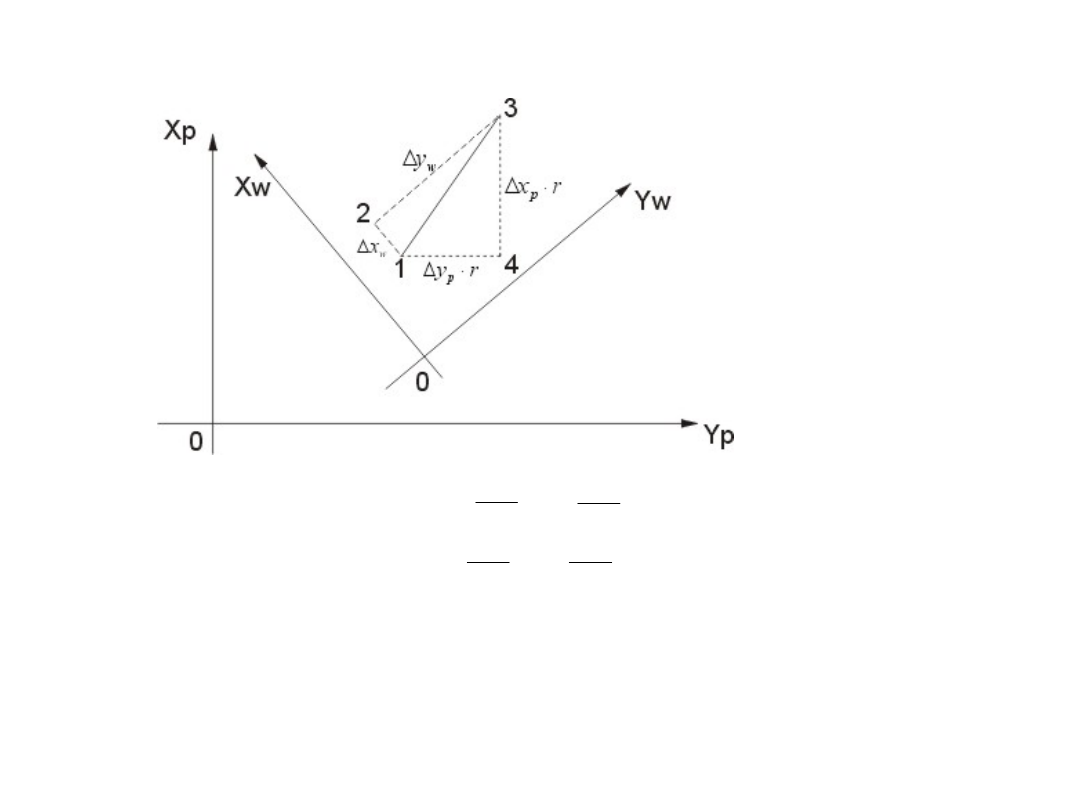
c)Zmiana współrzędnych terenowych na terenowe
p
x
p
y
w
x
w
y
p
x
p
y
w
x
w
y
Przyrosty miedzy punktami dostosowania oznaczamy:
W układzie pierwotnym
W układzie wtórnym
,
Przyrosty między dowolnymi punktami:
W układzie pierwotnym
W układzie wtórnym

0
w
w
p
p
y
x
y
x
v
u
tgP
Współczynniki transformacji u,v
2
,
1
,
v
u
y
x
y
x
p
p
w
w
2
,
1
,
w
w
p
p
y
x
y
x
v
u
Kąt skrętu
Współczynnik redukujący
2
2
2
v
u
r
Mając współrzędne pięciu punktów w układzie sieci poligonowej przeliczyć
je na układ sieci triangulacyjnej. Współrzędne punktów 1 i 5
dane są w obydwu układach
ZADANIE
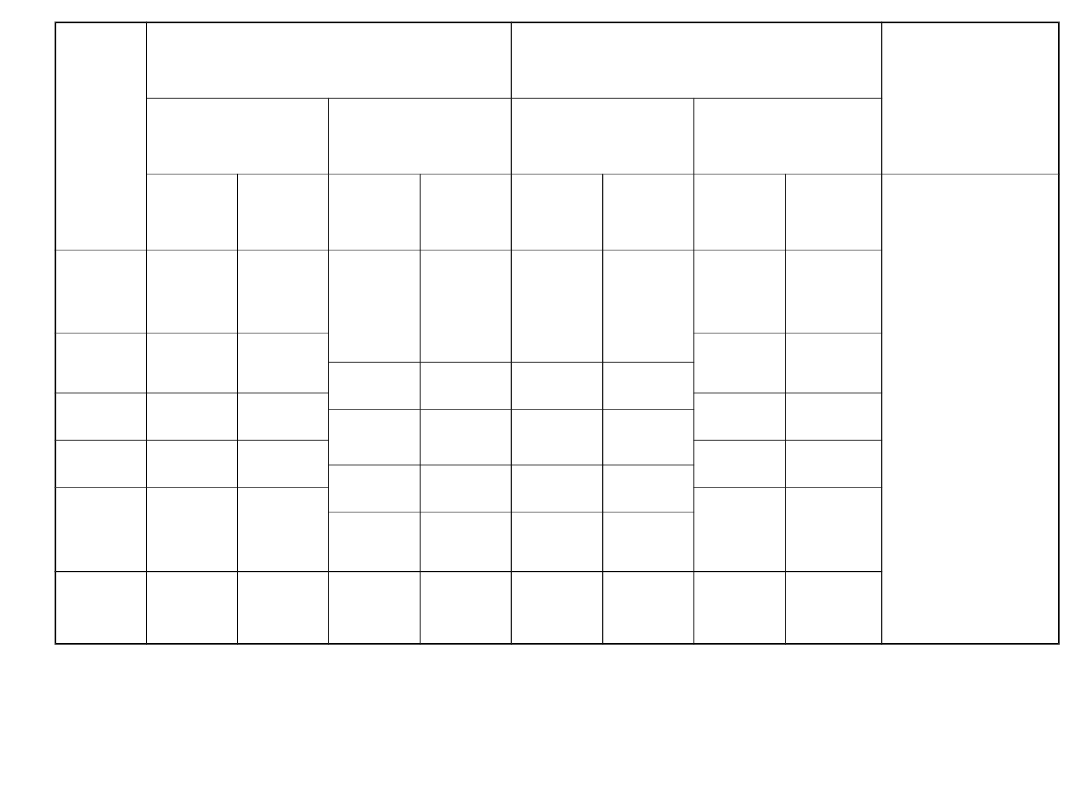
Nr
pkt.
Układ sieci poligonowej
Układ sieci
triangulacyjnej
UWAGI
współrzędn
e
przyrosty
przyrosty
współrzędn
e
x
p
y
p
x
p
y
p
x
w
y
w
x
w
y
w
Wylicz
najpierw
współczyn
niki u i v
a
następnie
kolejne
przyrosty
wsp.
Układu
wtórnego
1
540 270
356
2
243
4
2
590 290
3
630 320
4
670 365
5
732 436
361
6
268
2
1-5 192 166
54
248
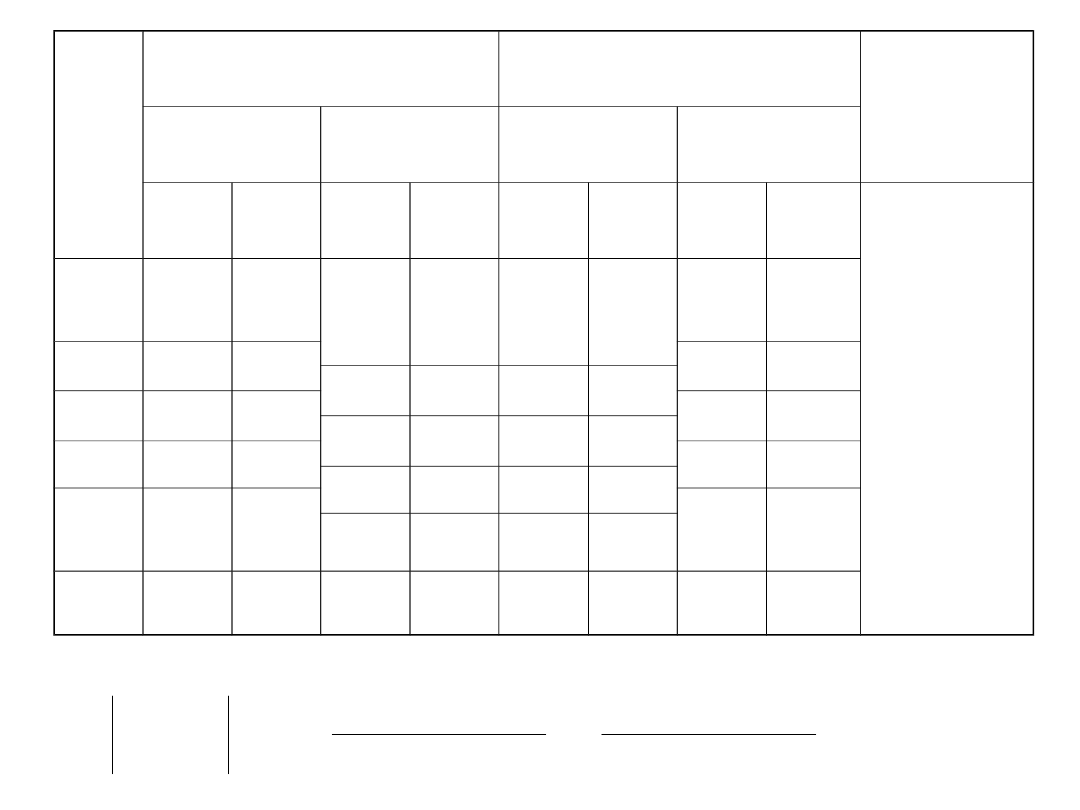
Nr
pkt.
Układ sieci poligonowej
Układ sieci
triangulacyjnej
UWAGI
współrzędn
e
przyrosty
przyrosty
współrzędn
e
x
p
y
p
x
p
y
p
x
w
y
w
x
w
y
w
Wylicz
najpierw
współczy
nniki u i v
a
następnie
kolejne
przyrosty
wsp.
Układu
wtórnego
1
540 270
50
20
356
2
243
4
2
590 290
40
30
3
630 320
40
45
4
670 365
62
71
5
732 436
361
6
268
2
1-5 192 166 192 166
54
248
u = 0,6
v = 0,8
2
2
2
2
2
,
1
166
192
248
166
54
192
166
192
166
54
248
192
;
248
54
166
192
)
,
(
v
u
v
u

2
,
1
12
12
12
12
,
v
u
y
x
y
x
p
p
w
w
2480
46
2434
3590
28
3562
46
8
,
0
20
6
,
0
50
28
6
,
0
20
8
,
0
50
;
8
,
0
6
,
0
20
50
,
12
1
2
12
1
2
12
12
2
,
1
12
12
w
w
w
w
w
w
w
w
w
w
y
y
y
x
x
x
y
x
y
x
2
,
1
23
23
2
,
1
23
23
23
23
8
,
0
6
,
0
30
40
,
,
w
w
p
p
w
w
y
x
v
u
y
x
y
x
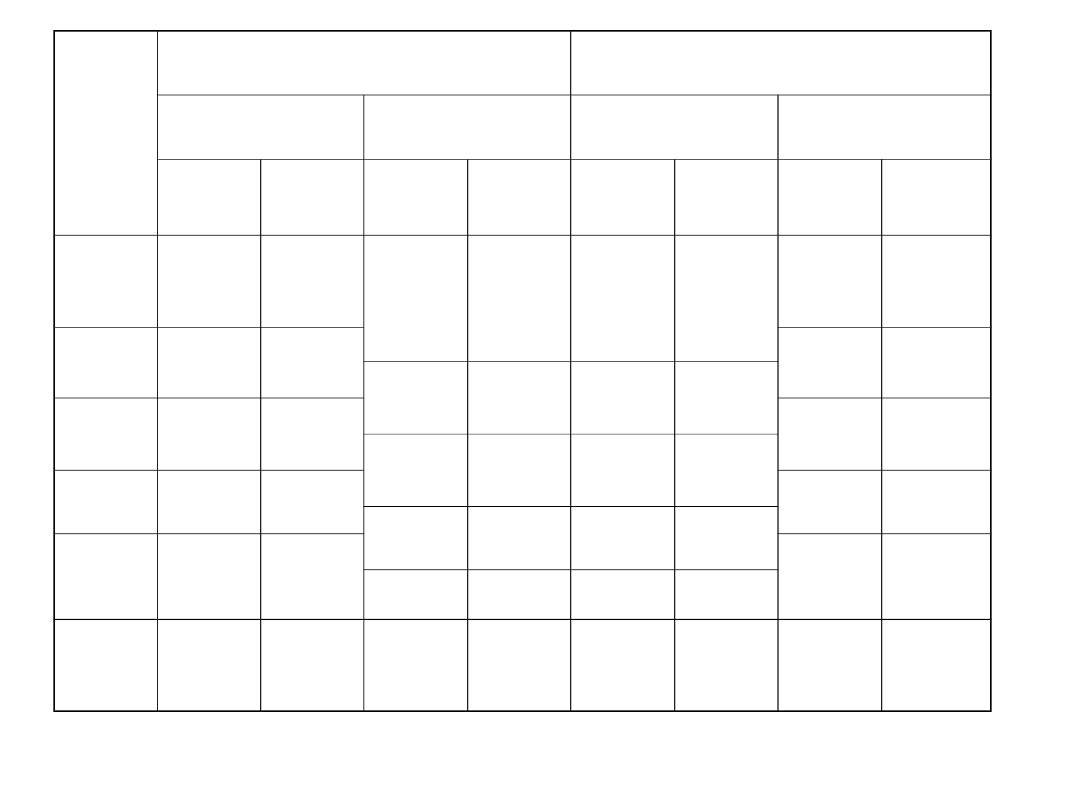
Nr
pkt.
Układ sieci poligonowej
Układ sieci triangulacyjnej
współrzędne
przyrosty
przyrosty
współrzędne
x
p
y
p
x
p
y
p
x
w
y
w
x
w
y
w
1
540
270
50
20
28
46
356
2
2434
2
590
290
3590 2480
40
30
3
630
320
40
45
4
670
365
62
71
5
732
436
361
6
2682
1-5
192
166
192
166
54
248
Nr
pkt.
Układ sieci poligonowej
Układ sieci triangulacyjnej
współrzędne
przyrosty
przyrosty
współrzędne
x
p
y
p
x
p
y
p
x
w
y
w
x
w
y
w
1
540
270
50
20
28
46
356
2
2434
2
590
290
3590 2480
40
30
14
48
3
630
320
3604 2528
40
45
5
60
4
670
365
3609 2588
62
71
7
94
5
732
436
361
6
2682
1-5
192
166
192
166
54
248
54
248
Wcięcia
Wcięcie kątowe w przód
A
B
C
)
2
,
1
(
1
1
,
ctg
y
x
ctg
y
x
y
x
B
B
A
A
C
Obliczyć współrzędne punktu 15, według danych z rysunku
13
14
15
x=9000
y=3000
x=3000
y=6000
x=?
y=?
arc ctg 1
arc ctg 2
2
,
1
2
1
3000
9000
1
1
6000
3000
,
y
x
x = 8000 y = 6000
Liniowe wcięcie w przód
B
A
C
a
c
b
A
C
C
B
B
A
C
B
A
A
B
B
B
A
A
C
C
C
C
C
C
C
P
c
b
a
C
b
c
a
C
a
c
b
C
C
P
y
x
C
P
y
x
y
x
4
4
4
,
2
2
2
2
2
2
2
2
2
2
,
1
;
4
;
4
;
4
P
C
ctg
P
C
ctg
P
C
ctg
C
B
A
Przykład
Obliczyć współrzędne punktu 17, według danych na rysunku
16
15
17
c
b
x=8000
y=6000
x=4000
y=6000
x=?
y=?
2
1000
6
6
6
6
2
6
6
2
6
6
2
10
8
4
24
8
4
8
24
10
4
;
10
4
;
10
16
;
10
8
;
10
10
;
10
24
;
10
2
P
C
c
C
b
C
a
C
B
A
10
1000
2
,
1
2
,
1
6
6
6
6
24
8
6000
8000
8
8
6000
4000
10
24
10
8
6000
8000
10
8
10
8
6000
4000
,
y
x
x=7000
y=7000
Wcięcie wstecz
0
1
2
C
1
2
C
C
x
F
F
f
f
x
ctg
y
x
ctg
y
x
f
F
0
0
0C
1
0
2
1
0
2
02
02
1
01
01
y
;
1
;
1
1
,
Obliczyć współrzędne punktu 20 mając współrzędne punktów 17,18,19
podane na rysunku oraz kąt =45
0
i =90
0
17
18
19
20
x=4000
y=1000
x=5000
y=3000
x=3000
y=5000
x=?
y=?

2000
4000
;
1
1
4000
1000
1
1
2000
1000
2
1
F
F
F
Rozwiązanie
2800
1400
2
1400
5
7000
1
2
3000
1000
1
y
x
;
3800
;
2600
y
x
Zadanie Hansena
Mając dane dwa punkty 1,2 oraz kąty A,B,C,D pomierzonejak na
rysunku na dwu punktach P i Q, możemy zadanie to rozwiązać przez
dwukrotne wcięcie w przód z podstawy 1, 2, po wcześniejszym
wyznaczeniu wcinających kątów . Kąty te można łatwo obliczyć,
jeśli przedtem określimy kąt
, który wyznacza wzór
P
Q
1
2
D
C
A B
ctg
ctgD
ctgC
ctgB
ctgA
ctg
1
Krakowiany
1. Mnożenie krakowianów
3
0
1
c
;
3
5
2
b
;
4
1
6
2
3
2
0
2
1
a
Krakowiany można mnożyć jeżeli mają taką samą ilość wierszy.
Rozmiar krakowiana wynikowego
• ilość kolumn taka jak ilość kolumn pierwszego krakowiana
• ilość wierszy taka jak ilość kolumn drugiego krakowiana
b
a
c
c
a
b
Kolejność mnożenia jest ważna
e
b
a
d
e
d
b
a
c
Zadanie
Podaj wyniki mnożenia krakowianów
c
b
3
2
4
3
c
;
4
3
2
2
1
3
b
;
1
2
1
a
d
a
64
45
3
2
4
3
12
7
3
2
4
3
4
3
2
2
1
3
1
2
1
d
b
c
;
1
0
0
0
1
0
0
0
1
-
;
1
0
0
0
1
0
0
0
1
3
1
2
1
3
1
2
5
4
0
1
3
c
;
3
1
4
2
b
;
1
0
2
2
3
1
4
1
2
a
d
a
r
3
1
4
2
3
3
4
1
2
1
1
2
5
0
1
3
1
0
2
2
3
1
4
1
2
d
3
1
4
2
25
3
10
23
13
3
7
18
17
3
8
13
164
106
112
2. Obliczanie pierwiastka krakowianowego
Aby obliczyć pierwiastek krakowianowy krakowian musi być symetryczny
Schemat Banachiewicza
Oblicz pierwiastek krakowiana
11
9
2
9
13
6
2
6
4
a
schemat
a
4
6
2
6
13
9
2
9
11
2
3
1
0
2
3
0
0
1
a
r
r
r
;
1
0
0
3
2
0
1
3
2
3. Obliczanie układów równań
Rozwiąż układ równań przy pomocy
pierwiastka krakowianowego
schemat
r
a
L
L’
1
x
0
29
9
2
2
0
13
2
17
0
9
2
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
1
-1
2
-9
-1
17
2
13
2
2
9
-29
1
-1
2
-9
0
4
1
1
0
0
2
-6
x1
x2
x3
1
3
0
6
2
3
3
x
x
1
0
1
3
4
0
1
4
2
2
3
2
x
x
x
x
2
0
9
6
1
0
9
2
1
1
3
2
1
x
x
x
x
x
Rozwiązać symetryczny układ równań liniowych stosując transformację Banachiewicza
4
-4
2
0
22
-4
20
-18
16
-102
2
-18
18
-18
94
0
16
-18
36
-102
1
1
3
2
4
3
2
1
x
x
x
x
3. Obliczanie odwrotności krakowiana symetrycznego
r
a
r
-1
1
1
2
1
1
)
(
r
r
r
a

Podstawowe informacje o błędach
Błędem prawdziym
i
, i-tej obserwacji l
i
nazywamy różnicę między
wartością prawdziwą L mierzonej wielkości, a wartością
zaobserwowaną:
i
i
l
L
Błędem pozornym
i
, albo poprawką i-tej obserwacji nazywamy różnicę
między wartością najprawdopodobniejszą L
0
mierzonej wielkości, a
wartością zaobserwowaną l
i
i
i
l
L
0
W geodezji jako kryterium dokładności obserwacji przyjmuje się błąd średni
1
-
n
;
m
n
m
N
n
m
Wzór ogólny na błąd średni
Pomiary nadmiarowe
Błąd średni średniej arytmetycznej
1
n
n
n
m
M
m (błąd średni)
Prawdopodobieńst
wo
Bł. średni m
-
68,27%
Bł. przec. t
0,8 m
57,53%
Bł. prawd. r
0,67 m (2/3
m)
50,00%
Bł. gran. g
2 m
95,45%
Bł. gran. g
3 m
99,73%

Zaokrąglanie błędów końcowych
Jeżeli końcowy wynik obliczeń błędu ma więcej niż jedną cyfrę znaczącą
należy go odpowiednio zaokrąglić.
Końcowy wynik błędu może mieć tylko jedną lub dwie cyfry
znaczące
Najpierw wynik zaokrąglamy do jednej cyfry znaczącej w górę i
przeprowadzamy test.
%
100
1
w
w
W
T
Jeżeli T jest mniejsze niż 10% to wynik pozostawiamy z jedną cyfrą znaczącą W1
Jeżeli więcej to wynik zaokrąglamy do 2 cyfr znaczących w górę
1
W
Wynik w zaokrąglony do jednej cyfry znaczącej w górę
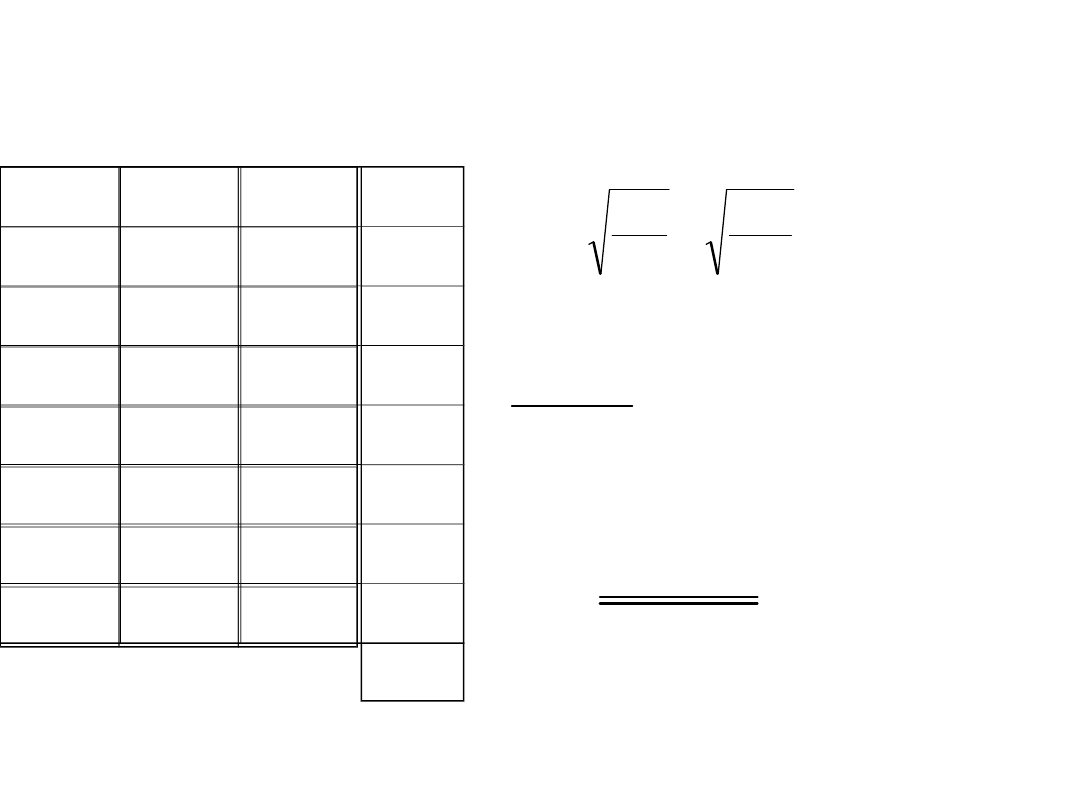
Pewne obliczenia wykonano dwukrotnie, raz za pomocą
arytmometru, a drugi raz za pomocą suwaka. Znaleźć średni błąd
rachunku suwakiem w zastosowaniu do tych obliczeń.
A
S
548,4
548
572,6
571
551,3
552
562,7
564
567,2
567
558,9
558
560,5
562
A
S
548,4
548
+0,4
572,6
571
+1,6
551,3
552
-0,7
562,7
564
-1,3
567,2
567
+0,2
558,9
558
+0,9
560,5
562
-1,5
07
,
1
7
00
,
8
n
m
%
10
%
87
%
100
07
,
1
07
,
1
2
Test:
1
,
1
m
0,16
2,56
0,49
1,69
0,04
0,81
2,25
8,00
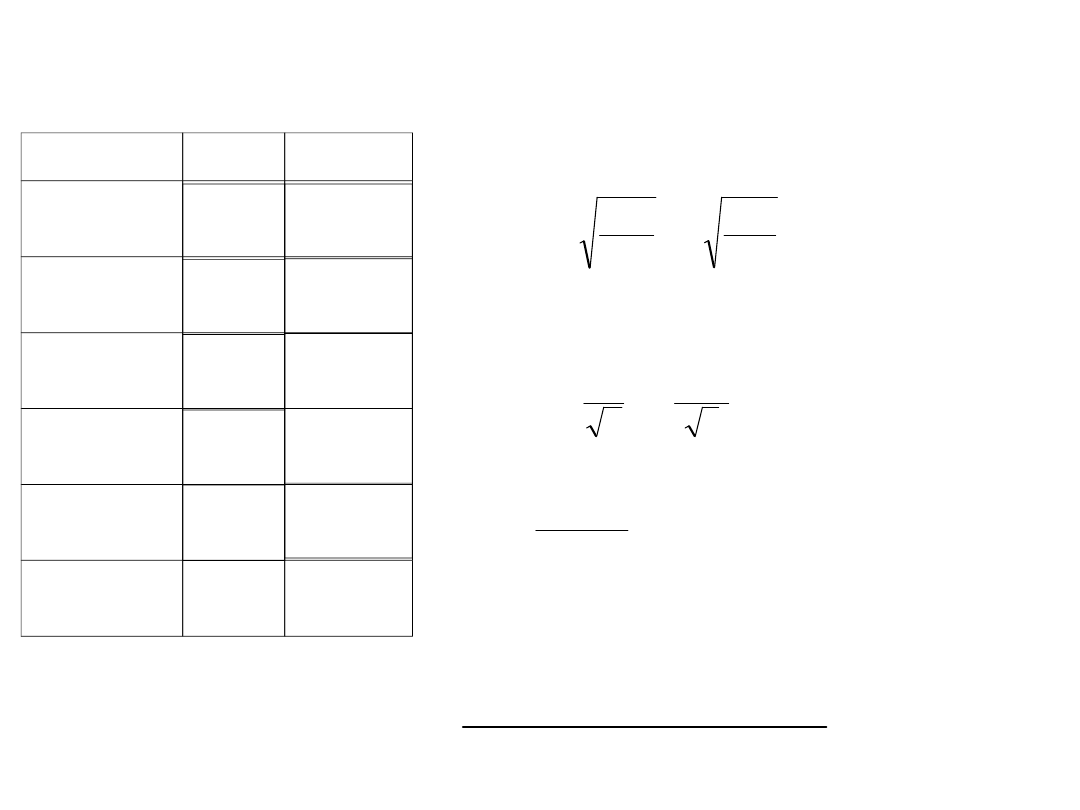
Pole pewnej figury pomierzono pięciokrotnie planimetrem uzyskując
wyniki w metrach, zamieszczone w poniższej tabelce. Obliczyć
najprawdopodobniejszą wartość pola i jej błąd średni
Pi[m
2
]
v
i
[m
2
] v
i
2
[m
4
]
9456
52
53
55
51
Pśr=9453
,4
-2,6
1,4
0,4
-1,6
2,4
6,76
1,96
0,16
2,56
5,76
[v]=0
[vv]=17,20
]
[
07
,
2
4
2
,
17
1
2
0
m
n
vv
m
Średni błąd jednokrotnego pomiaru pola
Średni błąd średniej arytmetycznej
]
[
93
,
0
5
07
,
2
2
0
m
n
m
M
test
%
10
%
7
%
100
93
,
0
93
,
0
1
2
)
1
9453
(
m
P
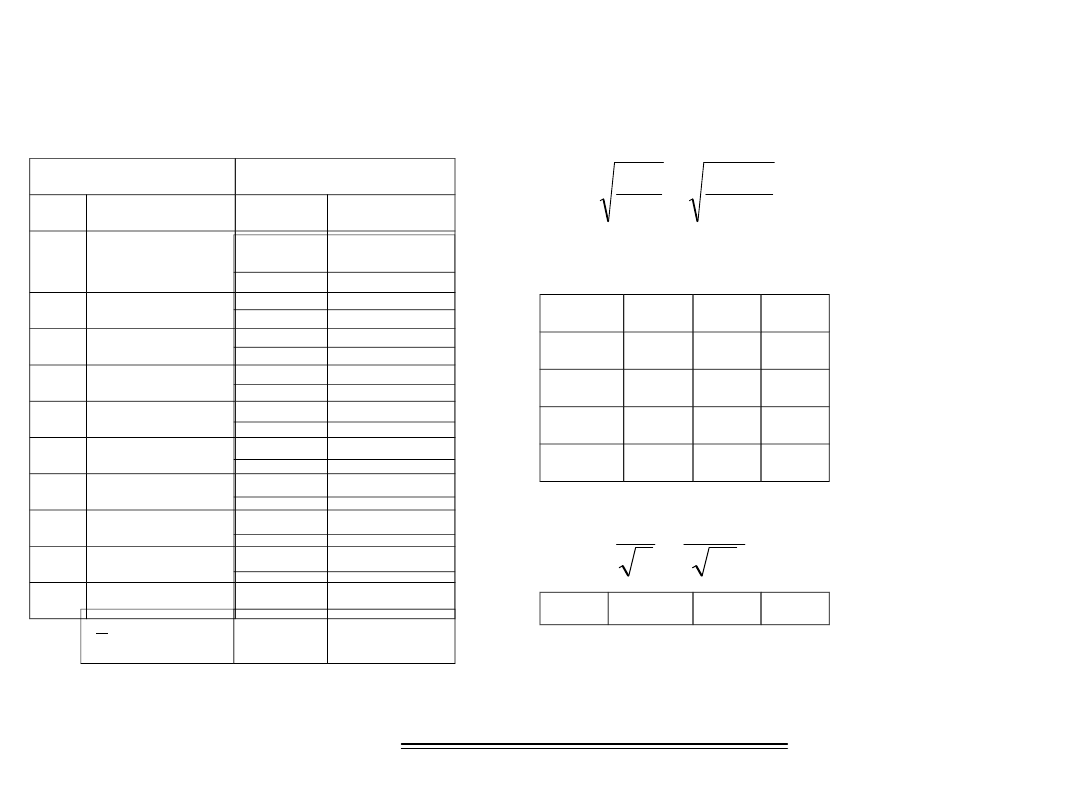
Pewien kąt pomierzono 10 razy uzyskując zamieszczone w poniższej
tabeli wyniki. Wyznaczyć najprawdopodobniejszą wartość kąta, oraz jego
błąd średni, przeciętny, prawdopodobny oraz graniczny
Obserwacje
Obliczenia
i
v
vv
1
39o38'27,2
"
2
31,4
3
28,5
4
26,3
5
32,7
6
30,6
7
25,6
8
29,8
9
28,7
10
28,8
=39
o
38'28,
96"
1,76
-2,44
0,46
2,66
-3,74
-1,64
3,36
-0,84
0,26
0,16
[v]=0
3,098
5,954
0,212
7,076
13,988
2,690
11,290
0,706
0,068
0,026
[vv]=
45,104
"
24
,
2
9
104
,
45
1
]
[
0
n
vv
m
m0= 2,24 34% 2,3”
t= 1,79 12% 1,8”
r= 1,49 34% 1,5”
g= 4,48 12% 4,5”
g= 6,72
4%
7”
test wynik
"
7084
,
0
10
"
24
,
2
0
0
n
m
M
M0=
0,7084
13%
0,71
"
71
,
0
"
96
,
28
'
38
39
0

Prawo przenoszenia się błędów pomiarów niezależnych i zależnych
n
xn
x
x
n
l
x
l
x
l
x
l
m
m
m
x
l
x
l
x
l
m
2
1
2
2
2
2
1
2
1
2
0
0
0
0
0
0
Jeżeli wielkość fizyczna jest wyznaczana za pomocą pomiarów innych wielości
mierzalnych, to błąd wyznaczanej wielkości możemy wyznaczyć znając błędy
poszczególnych pomierzonych wielkości
)
,...,
,
(
2
1
n
x
x
x
f
l
Zapis krakowianowy
n
xn
x
x
n
l
x
l
x
l
x
l
m
m
m
x
l
x
l
x
l
m
2
1
2
2
2
2
1
2
1
2
0
0
0
0
0
0
Zapis macierzowy
2
2
2
2
2
2
2
1
2
1
...
xn
n
x
x
l
m
x
l
m
x
l
m
x
l
m
Ten sam wzór
Dla pomiarów niezależnych
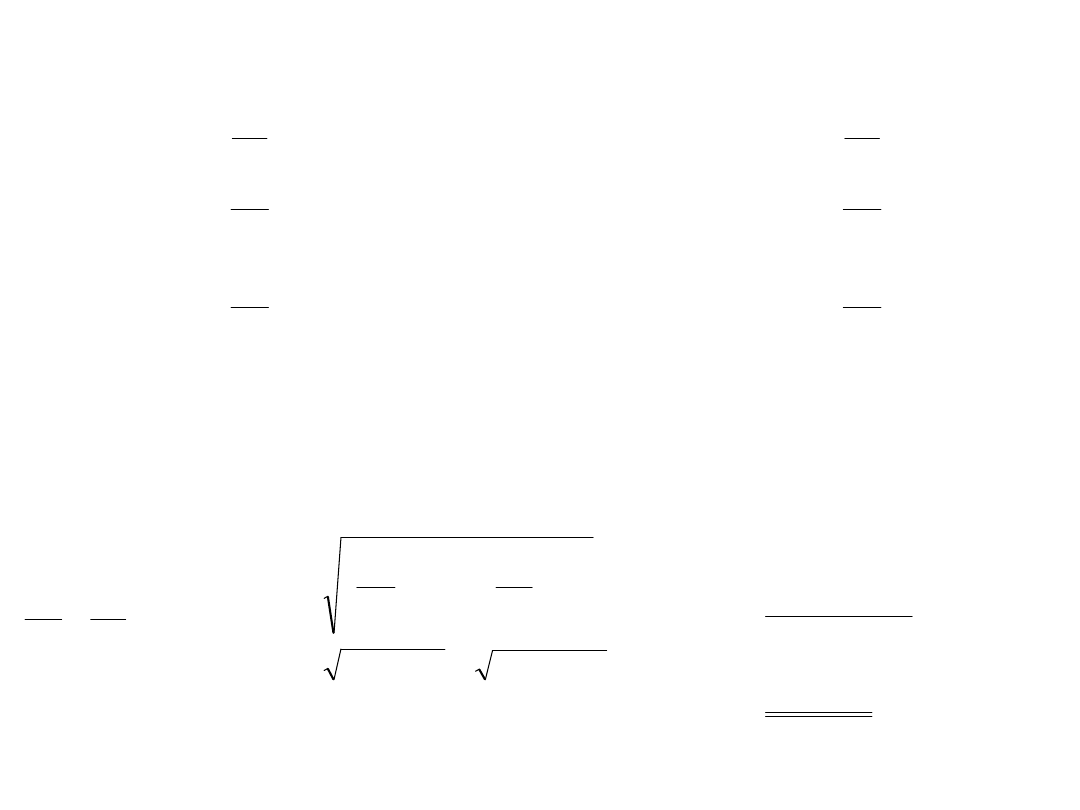
Dla pomiarów zależnych
n
xn
xn
x
n
xn
x
n
xn
x
n
x
x
x
xn
x
n
x
x
x
n
l
x
l
x
l
x
l
m
m
m
r
m
m
r
m
m
r
m
m
m
r
m
m
r
m
m
r
m
x
l
x
l
x
l
m
2
1
2
2
2
1
1
2
2
2
2
2
1
12
1
1
2
1
12
2
1
2
1
2
Zadanie
Oblicz średni błąd kąta , wyznaczonego z sumy pozostałych dwóch
kątów i trójkąta, znając błędy tych kątów m=10” i m=16”
1
180
"
868
,
18
256
100
16
10
2
2
2
2
2
2
m
m
m
m
"
20
%
6
%
100
868
,
18
868
,
18
20
m
test
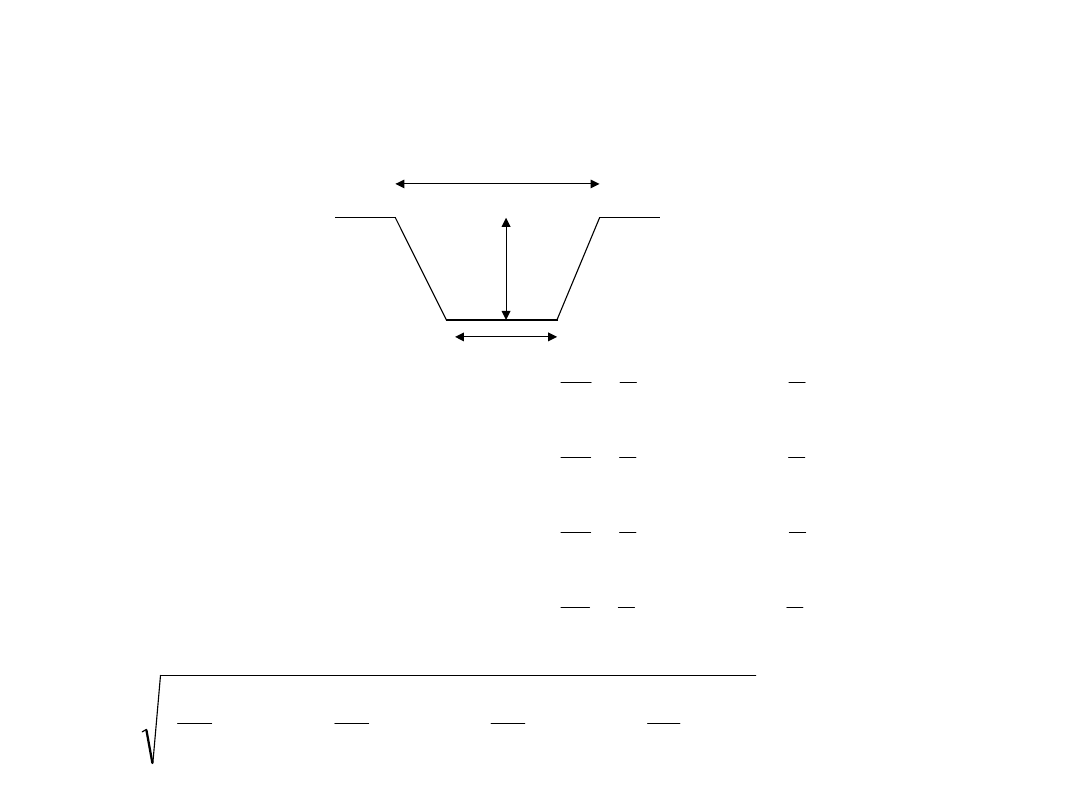
Szerokość dna rowu wynosi a=1[m] z błędem średnim ma=0,2[m];
głębokość h=2[m], mh=0,2[m], a długość l=1000[m], przy czym ml=1[m].
Obliczyć objętość v tego rowu i jej błąd średni, jeżeli szerokość rowu w
koronie jest równa b=3[m], mb=0,3[m].
Wskazać wielkość, której błąd średni ma największy wpływ na dokładność
wyznaczenia objętości
a
h
b
3
4000
1000
2
3
1
2
/
1
2
/
1
m
v
l
h
b
a
v
2
2
2
2
4
2
4
2
1
2
1
2000
1000
4
2
1
2
1
1000
1000
2
2
1
2
1
1000
1000
2
2
1
2
1
m
h
b
a
l
v
m
l
b
a
h
v
m
l
h
b
v
m
l
h
a
v
2
2
2
2
l
h
b
a
v
m
l
v
m
h
v
m
b
v
m
a
v
m

3
4
2
2
2
2
2
2
2
2
2
2
2
52
,
538
10
29
4
10
4
10
3
10
2
1
4
2
,
0
2000
3
,
0
1000
2
,
0
1000
m
m
v
3
540
4000
%
11
%
100
52
,
538
52
,
538
600
m
v
test
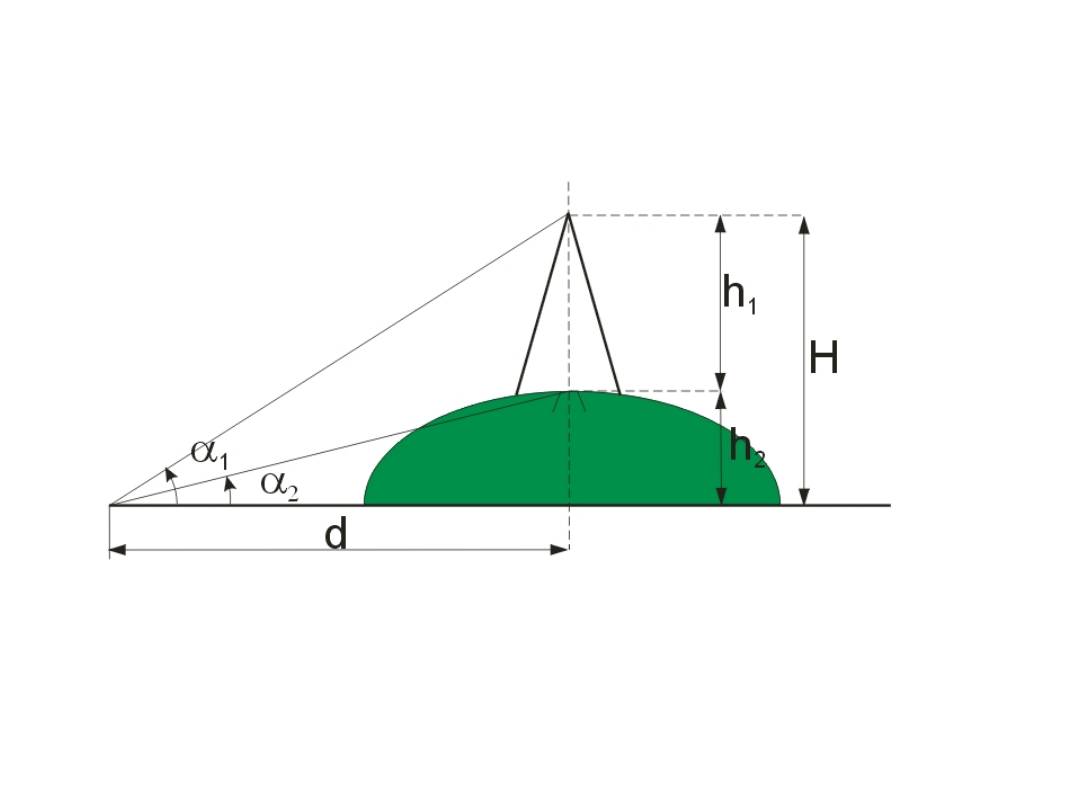
W celu wyznaczenia wysokości h
1
wieży triangulacyjnej nad głowicą
słupa, pomierzono odległość d oraz dwa kąty pionowe
1
i
2
Obliczyć błąd średni tej wysokości, jeśli
d = 40,00 m
1
= 28
o
05’
2
= 2
o
32’
m
d
= 0,02 m m
1
= 1’
m
2
= 1’
Przyjąć’=3440’
m
d
h
m
d
h
tg
tg
d
h
tg
tg
d
h
1
,
40
998
,
0
40
;
cos
4
,
51
778
,
0
40
;
cos
0,490
;
2
2
2
1
1
2
1
1
2
1
1
2
1
1
m
m
m
m
m
h
h
h
2
2
4
2
2
2
2
2
2
2
10
2
,
2
10
133
,
2
10
5
5
,
4
0117
,
0
)
0149
,
0
(
0098
,
0
'
3440
'
1
1
,
40
'
3440
'
1
4
,
51
02
,
0
490
,
0
1
1
1
Obserwacje niejednakowo dokładne
Waga obserwacji:
2
1
m
p
Błąd średni obserwacji o wadze jedność
p
m
m
p
m
m
p
m
n
p
m
f
f
f
0
0
0
0
;
1
-
n
;
k
k
f
p
l
f
p
l
f
p
l
f
m
m
1
...
1
1
2
2
2
2
1
2
1
0
Błąd wielkości mierzonej
Prawo przenoszenia się błędów
pomiarów niezależnych
niejednakowo dokładnych
Ogólna średnia arytmetyczna
(średnia z wagami)
]
[p
pl
X
Jeżeli wagi
są identyczne
n
l
X

Kąt pomierzono kilkakrotnie trzema różnymi metodami uzyskując
wyniki zestawione w tabelce. Obliczyć najprawdopodobniejszą wartość
kąta i jego błąd średni
I metoda
II metoda
III metoda
87
0
40’29”
87
0
40’31”
87
0
40’28”
27
32
26
32
27
31
26
30
29
28
27
30
Najpierw musimy obliczyć najprawdopodobniejsze wartości kąta
dla poszczególnych metod i średnie błędy tych wartości
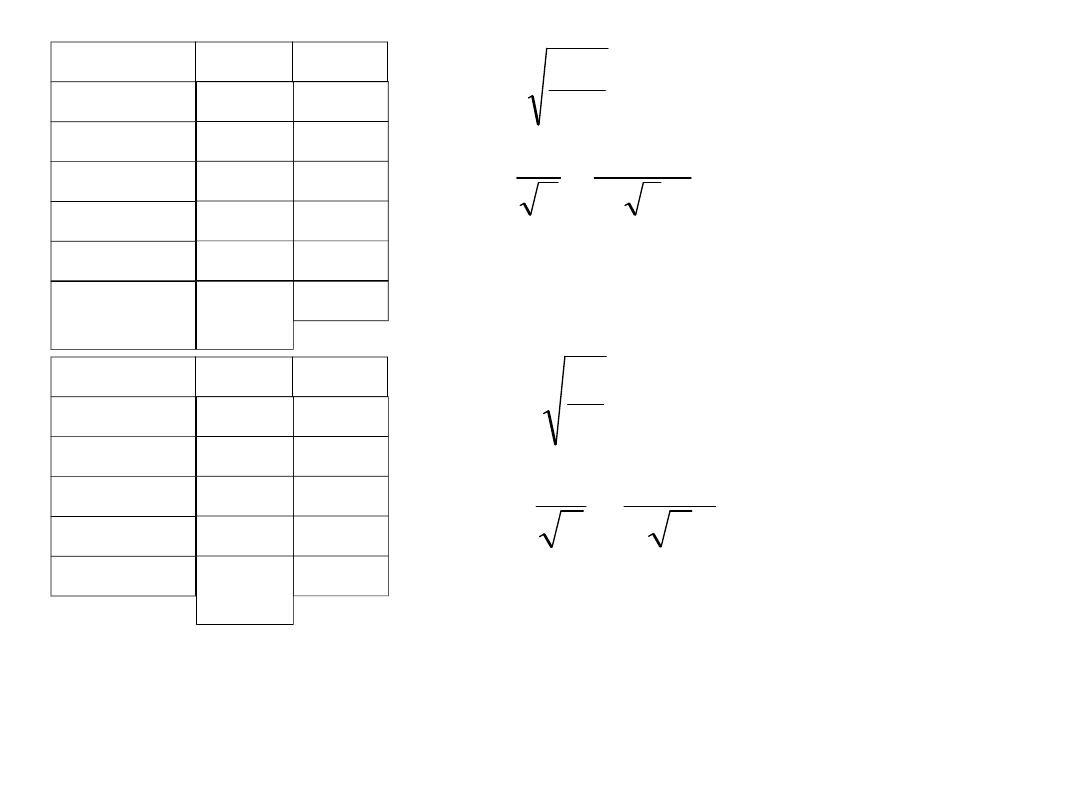
l
29
27
32
26
28
87
0
40’28,
4”
v["]
vv
-0,6
1,4
-3,6
2,4
0,4
[v]=0
,0
0,36
1,96
12,96
5,76
0,16
21,20
I metoda
l
31
32
27
30
87
0
40’30”
v["]
vv
-1,0
-2,0
3,0
0,0
[v]=0
,0
1,0
4,0
9,0
0
14,0
II metoda
"
03
,
1
5
302
,
2
"
302
,
2
4
2
,
21
0
0
n
m
M
m
I
"
08
,
1
4
16
,
2
"
16
,
2
3
14
0
0
n
m
M
m
II
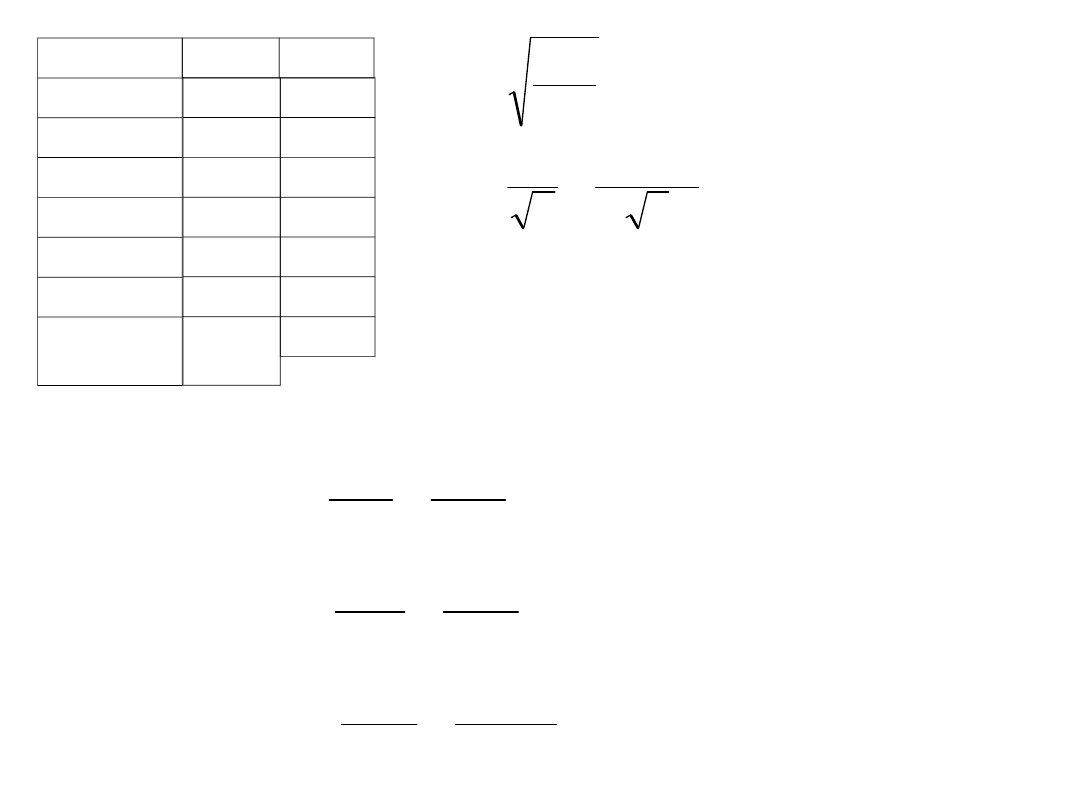
l
28
26
31
29
27
30
87
0
40’28,
5”
v["]
vv
0,5
2,5
-2,5
-0,5
1,5
-1,5
[v]=0
,0
0,25
6,25
6,25
0,25
2,25
2,25
17,50
III metoda
"
764
,
0
6
871
,
1
"
871
,
1
5
5
,
17
0
0
n
m
M
m
III
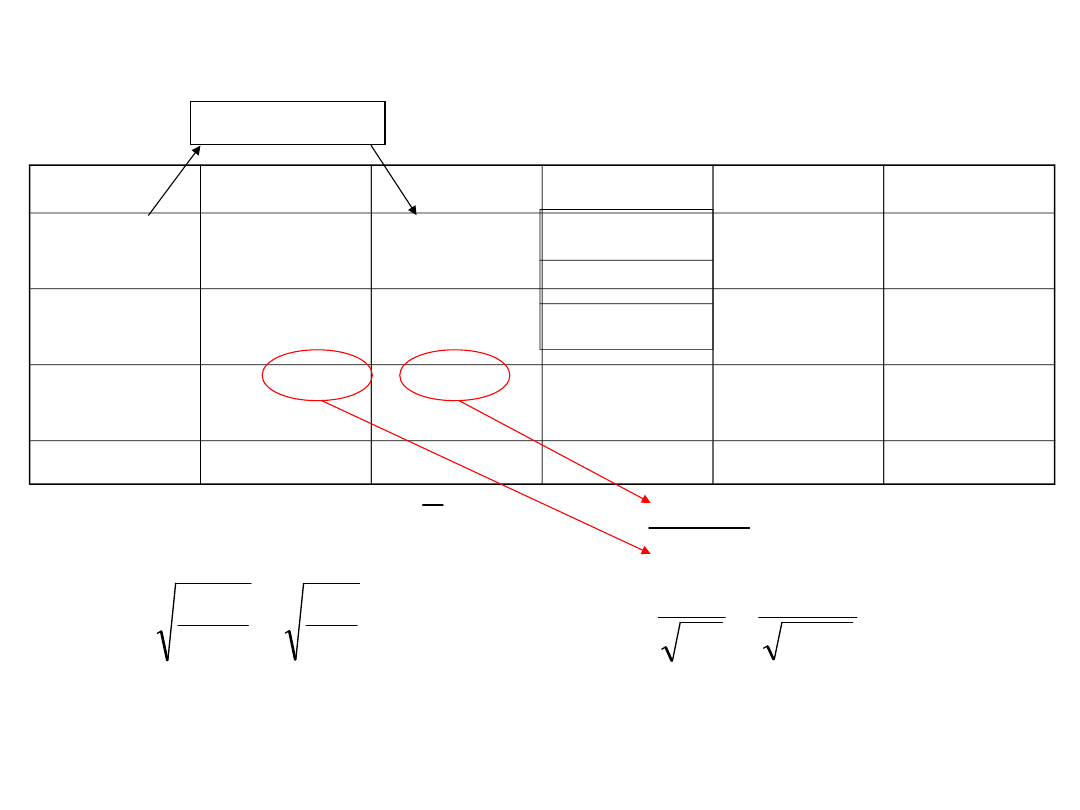
Następnie
obliczamy
wagi
otrzymanych
wartości
najprawdopodobniejszych z poszczególnych metod odnosząc je np. do
spostrzeżenia o średnim błędzie +- 1”
713
,
1
764
,
0
0
,
1
8573
,
0
08
,
1
0
,
1
9426
,
0
03
,
1
0
,
1
2
2
2
2
0
2
2
2
2
0
2
2
2
2
0
III
III
II
II
I
I
M
m
p
M
m
p
M
m
p
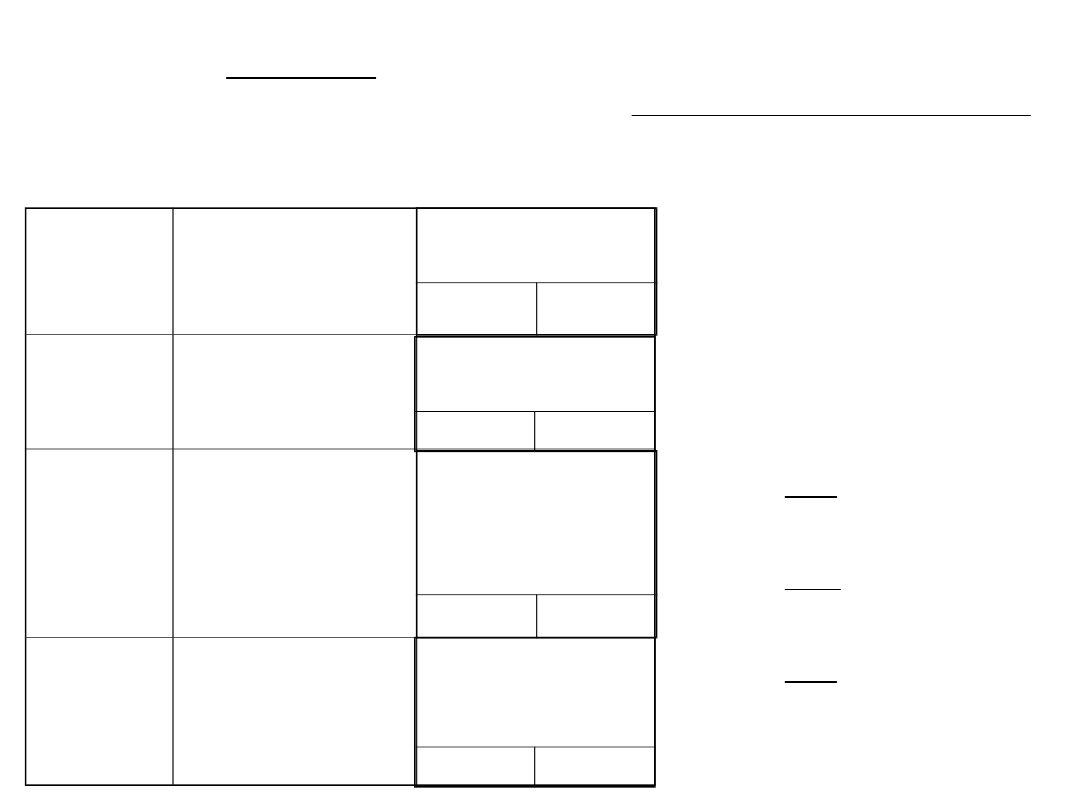
Mając obliczone wagi przystępujemy do wyznaczenia ogólnej średniej
arytmetycznej oraz błędu średniego średniej arytmetycznej
l
i
p
pl
v = L - l
i
pv
pvv
87
o
40’28,4
”
87
o
40’30,0
”
87
o
40’28,5
”
[p]=
[pv]=0,0
9426
,
0
8573
,
0
713
,
1
Dla ułatwienia obliczeń wydzielamy jakąś część wspólną średnich np.: 87
o
40’20”
3,513
7,918
8,573
14,56
2
8,4*0,9426=
31,054
Ogólna średnia arytmetyczna:
"
84
,
28
'
40
87
513
,
3
054
,
31
"
20
'
40
87
0
0
L
0,44
-1,16
0,34
0,41
-0,99
0,58
0,18
1,15
0,20
1,5
3
"
8758
,
0
2
53
,
1
1
]
[
0
n
pvv
m
0,467"
513
,
3
"
8758
,
0
]
[
0
p
m
M
Test:
%
7
%
100
467
,
0
467
,
0
5
,
0
"
5
,
0
"
8
,
28
'
40
87
0
Obliczyć średni błąd pomiaru taśmą odcinka stumetrowego opierając się na
wynikach wielokrotnych pomiarów odcinków A, B, C, podanych w tabeli
Odcinek
Wyniki pomiarów
wielokrotnych
A
średnia
110,20
110,16
110,18
B
średnia
250,10
250,20
250,15
250,15
250,15
C
średnia
170,10
170,12
170,17
170,13
Błędy pozorne v
(w centymetrach)
[vv]
i
p
i
5
-5
0
0
50
-2
2
8
3
1
-4
26
Przy pomiarach taśmą przyjmuje
się proporcjonalność błędu
średniego do pierwiastka z
długości. Wagi będą więc
odwrotnie proporcjonalne do
długości, czyli przy przyjęciu
wagi pomiaru odcinka
stumetrowego za jedność
otrzymamy:
588
,
0
170
100
400
,
0
250
100
909
,
0
110
100
A
B
A
p
p
p
0,909
0,400
0,588
]
[
66
,
2
6
56
,
42
3
9
588
,
0
26
400
,
0
50
909
,
0
8
0
cm
m
[cm]
66
,
2
1
66
,
2
1
100
100
p
;
100
100
0
M
p
m
M
Test:
%
13
%
100
66
,
2
66
,
2
3
[cm]
7
,
2
M

Pary spostrzeżeń
n
pdd
n
pdd
m
2
1
2
0
0
Średni błąd pojedynczej obserwacji o wadze jedność
Średni błąd podwójnego spostrzeżenia o wadze jedność
Z pomiaru długości uzyskano wyniki podane w tabeli. Jaki jest średni
błąd podwójnego pomiaru odcinka długości 150 [m] a jaki 200 [m]
Zadanie
I pomiar
II pomiar
125,182
125,186
122,365
122,386
111,413
111,451
93,637
93,684
99,178
99,180
117,410
117,414
110,536
110,534
107,413
107,381
96,337
96,301
104,438
104,454
125,358
125,404
154,175
154,170
d
[mm]
4
21
38
47
2
4
-2
-32
-36
16
46
-5
pdd
D
p
100
0,800
0,820
0,901
1,064
1,010
0,855
0,901
0,935
1,042
0,962
0,800
0,649
12,8
361,5
1300,9
2350,0
4,0
13,7
3,6
957,0
1350,0
246,2
1692,8
16,2
[pdd]=7955
[mm]
21
,
18
24
7955
0
m
[mm]
87
,
12
48
7955
0
Odcinkowi o długości 150 m
odpowiada waga:
667
,
0
150
100
150
p
Odcinkowi o długości 200 m
odpowiada waga:
5
,
0
200
100
200
p

]
[
21
,
18
5
,
0
87
,
12
]
[
77
,
15
667
,
0
87
,
12
200
0
200
150
0
150
mm
p
mm
p
Test:
]
[
16
]
[
20
%
9
,
9
%
100
21
,
18
21
,
18
20
150
200
mm
mm
Prawo przenoszenia się błędów pomiarów zależnych
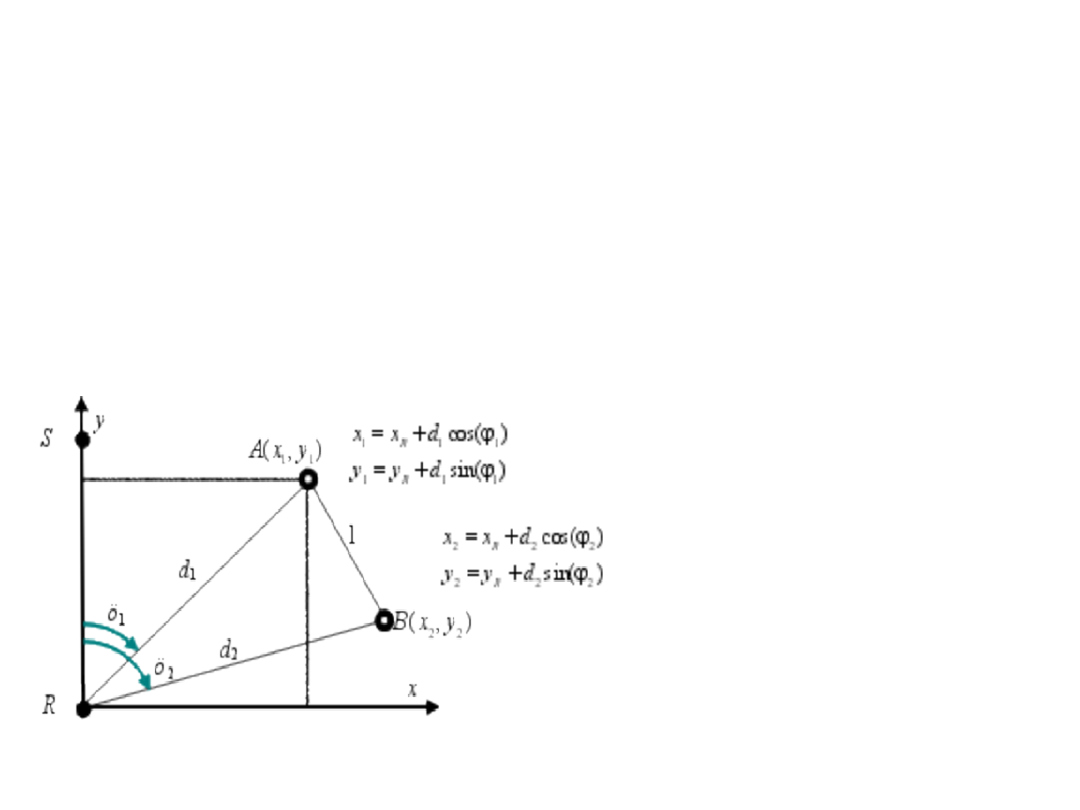
Metodą biegunową wyznaczono współrzędne (x
2
=20,y
2
=5) punktu B i
niezależnie (wcześniej) tą samą metodą współrzędne (x
1
=15,y
1
=10)
punktu A (współrzędne punktu R uważamy za dokładne). Oznacza to,
że x
1
,y
1
, są zależne - ich dokładność określa macierz kowariancji C
x1,y1
.
Jednocześnie pomiary x
2
,y
2
, są też zależne - ich dokładność określa
macierz kowariancji C
x2,y2
.
(Pary wielkości x
1
,y
1
i x
2
,y
2
są niezależne). Wyznaczyć błąd średni
odległości l między punktami A i B.
09
,
0
012
,
0
012
,
0
01
,
0
09
,
0
03
,
0
03
,
0
04
,
0
2
,
2
1
,
1
y
x
y
x
C
C
2
2
2
1
2
1
(
)
(
)
x
x
y
y
=
-
+
-
l
1
1 1
1 1
1
2
2 2
2 2
2
1
2
2
1
2
2
1
1
2
2
2
2
2
0
0
0
0
.
0
0
0
0
x
x y
x y
y
x
x y
x y
y
x
m
m
m
m
y
m
x
y
x
y
m
m
x
m
m
y
�
� �
� �
�
� �
�
� �
� �
�
�� �
�
�
��
�
�
�
�
�
� �
=
�
�
�
��
�� �
�
�
�
�
�
�
��
�� �
�
�
�� �
�
�
� �
�
� �
�
� �
l
l
l
l
l
l
l
l
l
2
2
1
1
2
2
2
2
2
2
2
2
2
1
1
1
1
1
2
1
2
2
1
1
2
0
0
0
0
0
0
0
0
y
l
x
l
y
l
x
l
m
m
m
m
m
m
m
m
y
l
x
l
y
l
x
l
m
y
y
x
y
x
x
y
y
x
y
x
x
l
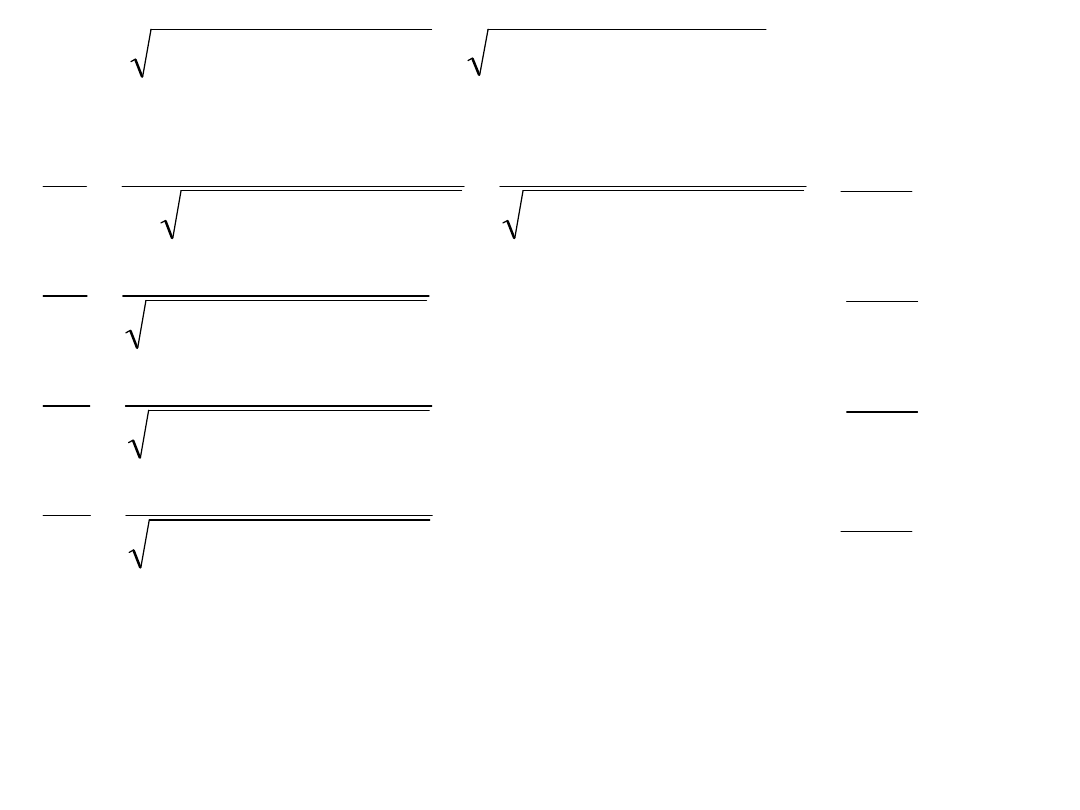
2
1
2
2
1
2
1
2
2
2
1
2
2
1
2
1
2
2
2
1
2
2
1
2
2
1
1
2
1
2
2
1
2
2
1
2
1
2
2
1
2
1
2
1
2
1
2
y
y
x
x
y
y
y
l
y
y
x
x
x
x
x
l
y
y
x
x
y
y
y
l
y
y
x
x
x
x
y
y
x
x
x
x
x
l
7,071
7,071068
10
5
15
20
2
2
2
1
2
2
1
2
y
y
x
x
l
-0,70711
071
,
7
5
0,70711
071
,
7
5
-0,70711
071
,
7
5
0,70711
071
,
7
5
0,7071
-
0,7071
0,7071
0,7071
-
09
,
0
012
,
0
0
0
012
,
0
01
,
0
0
0
0
0
09
,
0
03
,
0
0
0
03
,
0
04
,
0
0,7071
-
0,7071
0,7071
0,7071
-
2
l
m
0,0730
0,7071
-
0,7071
0,7071
0,7071
-
0,05515
-
0,00141
-
0,04243
0,00707
-
2
l
m
%
11
%
100
0,2702
0,2702
-
0,3
0,2702
0,0730
l
m
0,28
7,07
l
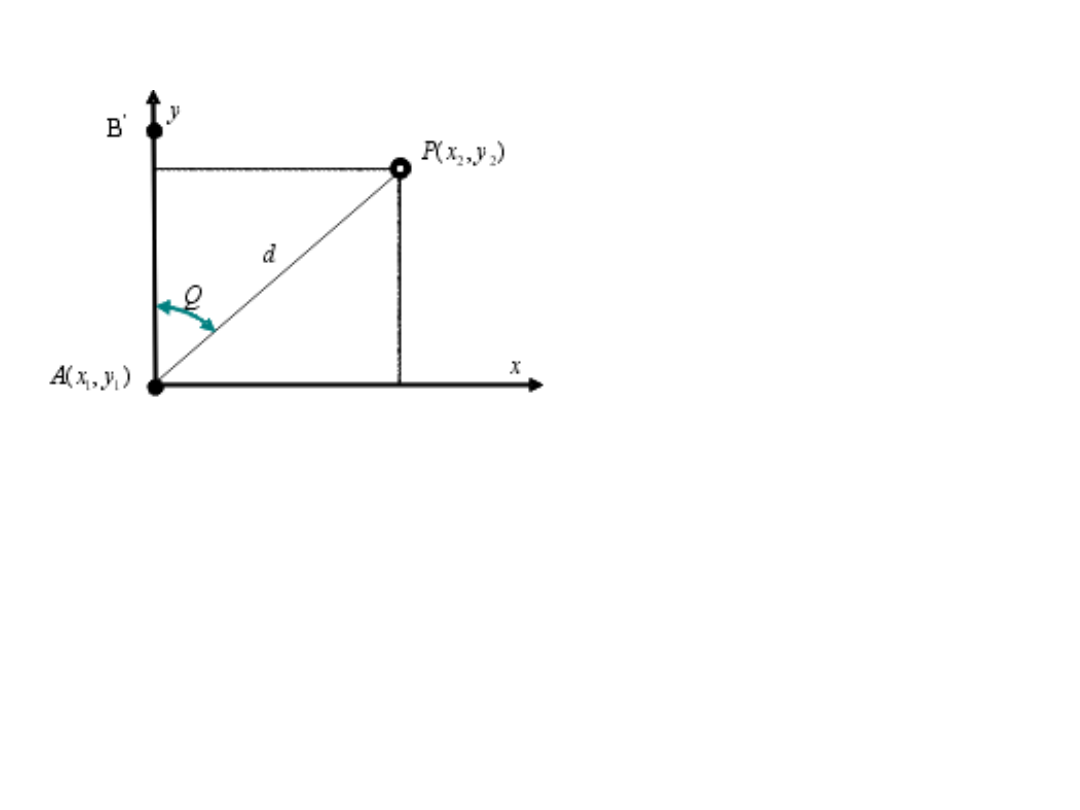
Przykład. Wyznaczyć kowariancję i błędy średnie współrzędnych x
2
i y
2
:
)
sin(
)
cos(
1
2
1
2
Q
d
y
y
Q
d
x
x
Dane:
x
1
= 1,0 m
x1
= 0,2
y
1
= 1,0 m
y1
= 0,1
m
x1y1
= 0,01
d= 20,0 m
d
= 0,4
Q= 30
o
0’ m
Q
= 1’
11,00
5
,
0
20
1
18,32
0,866025
20
1
2
2
y
x

1
1 1
2
2 2
1 1
1
2
2
2 2
2
2
2
1
2
2
2
2
2
2
2
2
2
1
1
1
1
,
2
2
2
2
2
2
2
2
2
1
1
2
2
0
0
0
0
0
0
0
0
0
0
x
x y
x
x y
x y
y
x y
x y
y
d
x
y
x
m
m
x
x
x
x
x
y
m
m
x
y
d
m
m
y
y
y
y
y
y
m
m
x
y
m
x
y
d
d
d
m
x
y
j
j
j
j
j
j
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
� �
�
�
�
�
�
�
�
�
�
�
=
=
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
�
��
��
�
�
�
�� �
�
�
C
�
�
�
�
�
�
�
1
1 1
1 1
1
2
2
2
2
,
2
2
0
0
1
0
0
0
1 0 cos
sin
0
1
0 1 sin
cos
cos
sin
0
0
0
sin
cos
0
0
0
x
x y
x y
y
x y
d
m
m
m
m
d
d
m
d
d
m
j
j
j
j
j
j
j
j
j
�
��
�
�
��
�
-
�
��
��
�
=�
��
��
�
�
��
��
�
-
�
��
�
�
�
C
cos
sin
sin
cos
cos
sin
sin
cos
1
0
0
1
0
0
0
0
0
0
0
0
0
0
2
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
1
1
1
1
d
m
d
m
m
m
m
m
m
m
d
d
m
m
m
m
m
m
d
d
y
y
x
y
x
x
d
y
y
x
y
x
x
1
1 1
1 1
1
2
2
1
1 1
1 1
1
2
2
,
2
2
2
2
2
2
2
2 2
2
2
2 2
2
2 2
2
2
2
1 0 cos
sin
0 1 sin
cos
cos
sin
sin
cos
cos
sin
sin cos
sin cos
sin cos
sin cos
sin
x
x y
x y
y
x y
d
d
x
d
x y
d
x y
d
y
d
m
m
m
m
d
d
m
m
m d
m d
m
m
m d
m
m
m d
m
m
m d
m
m
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
�
�
�
�
-
�
��
�
=
=
�
��
�
�
��
�
�
�
-
�
�
+
+
+
-
+
-
+
+
C
2 2
2
cos
m d
j
j
�
�
�
�
�
�
�
�
0
2
2
2
0
2
2
2
0
0
2
2
0
0
2
0
0
2
2
0
0
2
0
2
2
2
0
2
2
2
30
cos
20
'
3440
'
1
30
sin
4
,
0
1
,
0
30
sin
30
cos
20
'
3440
'
1
30
sin
30
cos
4
,
0
01
,
0
30
sin
30
cos
20
'
3440
'
1
30
sin
30
cos
4
,
0
01
,
0
30
sin
20
'
3440
'
1
30
cos
4
,
0
2
,
0
0,75
0,116279
0,25
16
,
0
01
,
0
5
,
0
0,866025
0,116279
5
,
0
0,866025
16
,
0
01
,
0
5
,
0
0,866025
0,116279
5
,
0
0,866025
16
,
0
01
,
0
0,25
0,116279
75
,
0
16
,
0
04
,
0
0,137209
0,028932
0,028932
0,21035
2
,
2 y
x
C
0,370418
137209
,
0
0,45864
21035
,
0
2
2
y
x
m
m
0,4
0,5
2
2
y
x
m
m
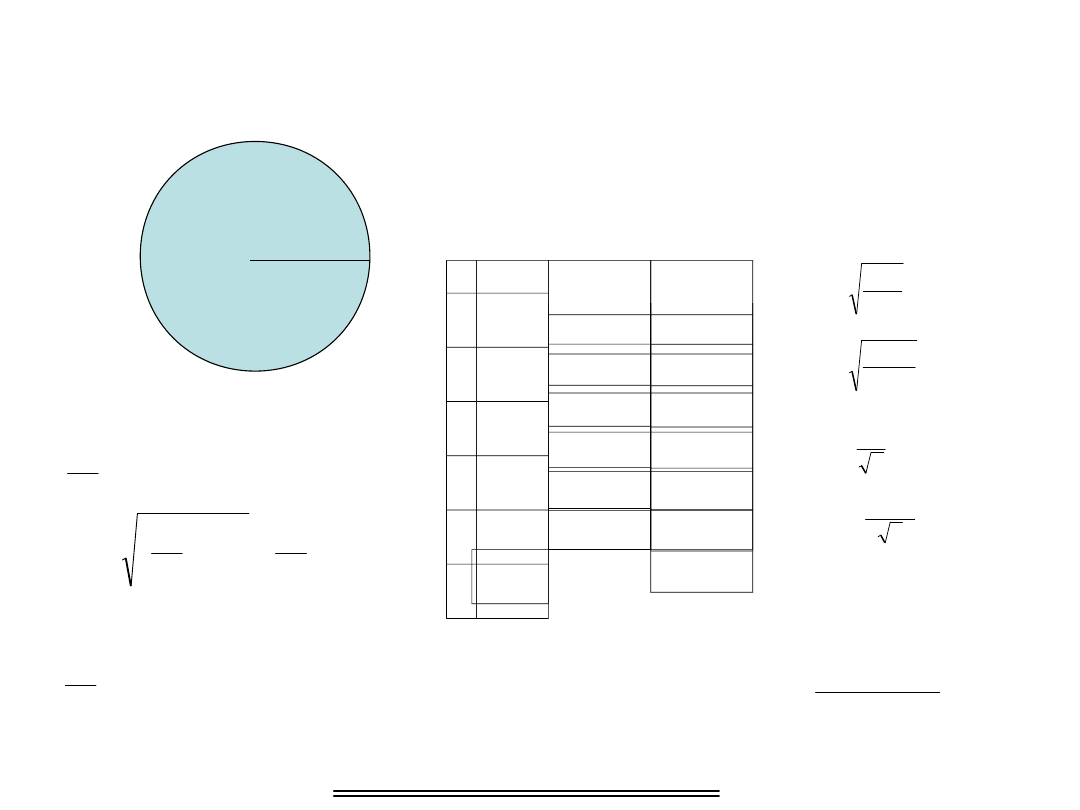
Powtórzenie
R
Oblicz pole koła oraz jego błąd. Promień
pomierzono 6 razy
R[m]
1
123,
4
2
123,
8
3
122,
9
4
124,
2
5
123,
8
6
123,
2
123,
55
Rśr=
v[cm]
vv[cm2
]
15
-25
65
-65
-25
35
225
625
4225
4225
625
1225
11150
1
0
n
vv
m
]
[
22
,
47
5
11150
0
cm
m
n
m
M
0
]
[
2112
,
0
]
[
12
,
21
6
22
,
47
m
M
cm
M
47955,16
2
R
P
R
R
P
m
R
P
m
R
P
m
R
R
P
2
2
M
m
R
]
163,95[m
2112
,
0
55
,
123
2
1415
,
3
śr
2
2
m
m
M
R
m
R
P
m
R
P
%
22
%
100
95
,
163
95
,
163
200
2
)
170
47960
(
m
P
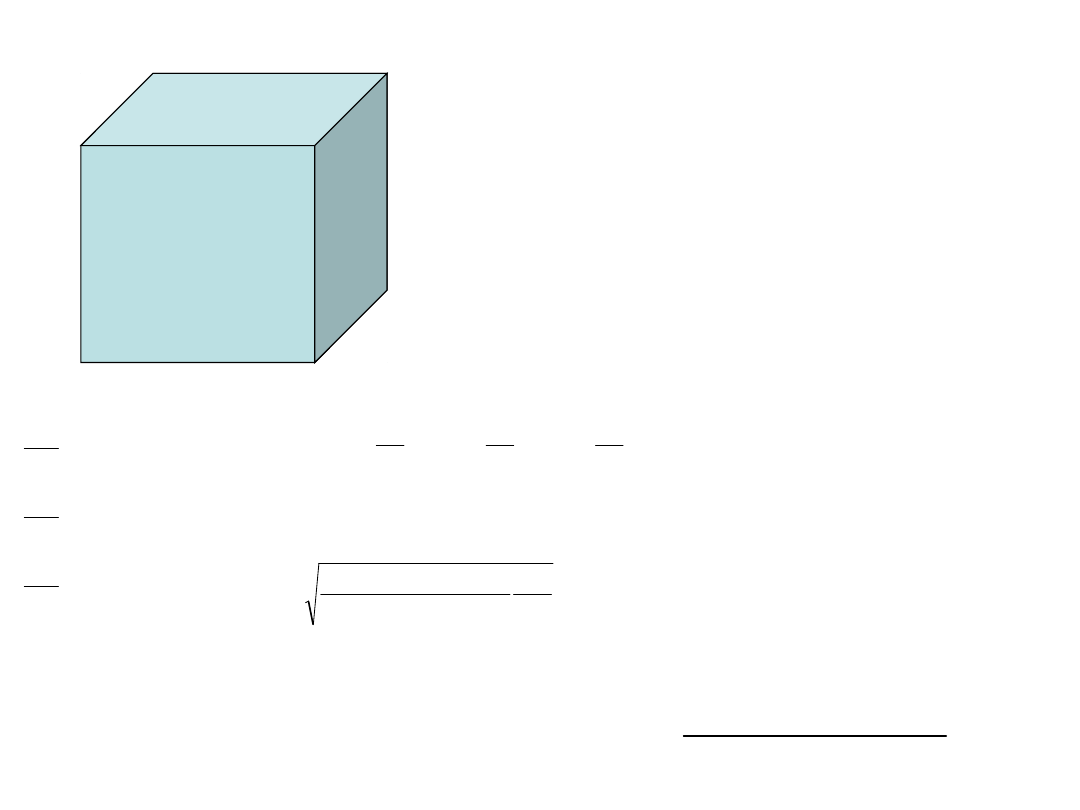
Z jaka dokładnością należy pomierzyć boki
a,b,c aby błąd objętości V nie przekraczał
200m
3
. przyjmij że błędy odległości są równe
m
0
m
c
m
b
m
a
18
25
20
a
b
c
c
b
a
V
2
2
2
500
360
450
m
a
b
c
V
m
c
a
b
V
m
c
b
a
V
2
2
2
2
c
b
a
V
m
c
V
m
b
V
m
a
V
m
0
4
6
2
2
2
2
2
0
4
2
2
2
2
2
0
2
2
0
2
2
0
2
6
2
)
500
360
450
(
200
500
360
450
200
500
360
450
200
m
m
m
m
m
m
m
m
m
m
m
m
m
0,26213
0
m
m
0,26
0
m
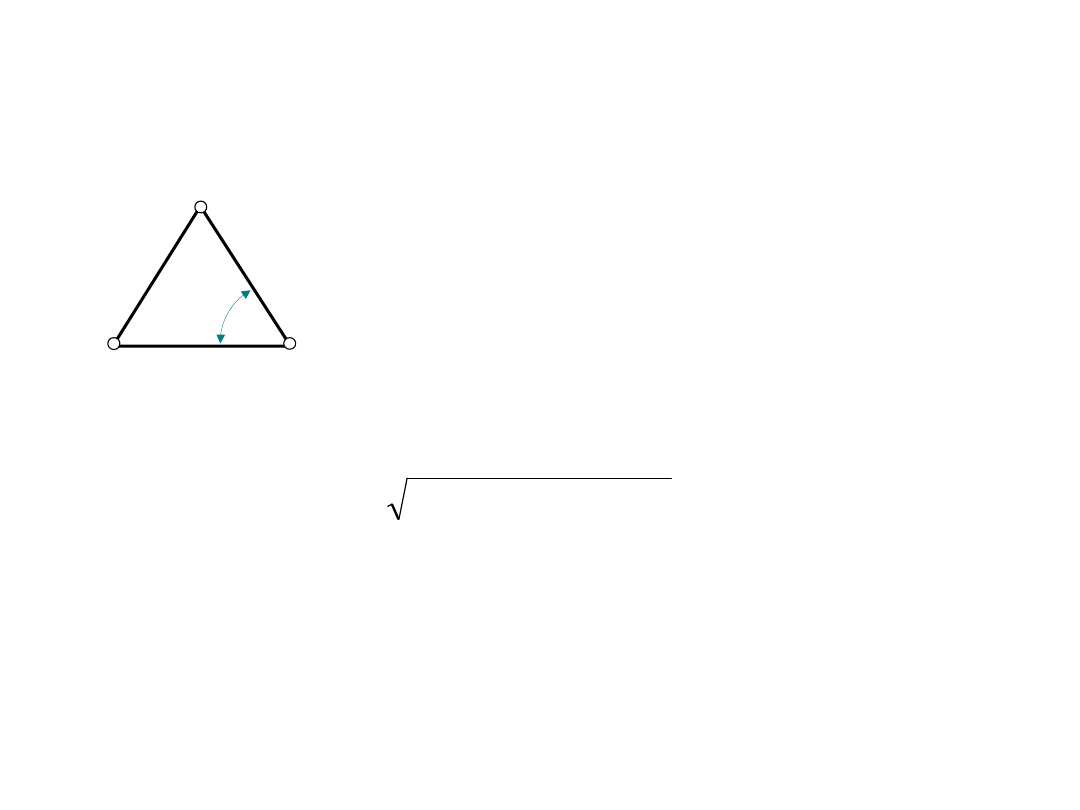
B
C
c
a
b
B
A
Obliczyć wartość boku
trójkąta oraz jego
błąd średni błąd dla danych
b
AC
m
c
120
m
m
C
2
,
0
m
a
80
m
m
a
2
,
0
0
1
150
o
B
5
B
m
Długość boku b wyznaczamy z twierdzenia kosinusów (tw. Carnota)
)
cos(
2
2
2
B
ac
c
a
b
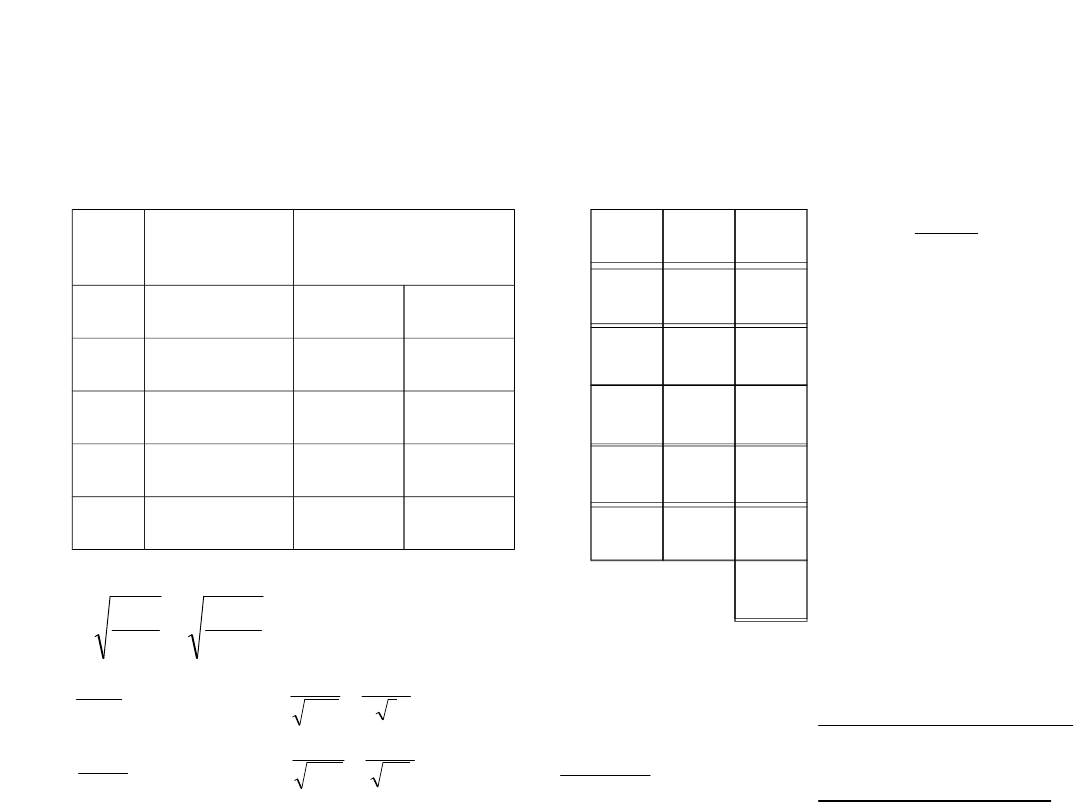
Obliczyć średni błąd niwelacji odcinka o długości 1 kilometra i
odcinka 2km opierając się na wynikach podwójnej niwelacji tras A,B,
...,E, dokonanych tym samym narzędziem i w analogicznych
warunkach. Wyniki niwelacji i długości tras podano w tabeli.
Tras
a
Długość trasy
w
kilometrach
Wyniki niwelacji w
milimetrach
A
1,3
125
121
B
0,8
134
136
C
1,7
43
47
D
2,6
410
420
E
1,5
400
412
p
d
pdd
km
D
km
p
1
1
2
L
L
d
p
d
pdd
0,77
-4
12,3
1
1,25
2
5,00
0,59
4
9,41
0,38
10
38,4
6
0,67
12
96,0
0
161,
2
]
[
014
,
4
5
2
2
,
161
2
0
mm
n
pdd
m
5
,
0
]
[
2
]
[
1
1
]
[
1
]
[
1
2
1
km
km
p
km
km
p
km
km
]
[
678
,
5
5
,
0
014
,
4
]
[
014
,
4
1
014
,
4
2
0
2
1
0
1
mm
p
m
m
mm
p
m
m
km
km
km
km
]
[
6
]
[
1
,
4
2
1
mm
m
mm
m
km
km
%
7
,
5
%
100
678
,
5
678
,
5
6
TEST
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
Wyszukiwarka
Podobne podstrony:
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
Ćwiczenia1 Elektroforeza
cwiczenia 9 kryzys
Ćwiczenia 1, cz 1
Ćwiczenie 8
9 ćwiczenie 2014
Cwiczenie 1
Ćwiczenie 2 Polska w europejskim systemie bezpieczeństwa
11 CWICZENIE 1 SEMESTR LETNIid 12747 ppt
więcej podobnych podstron