2. Termiczne równanie stanu,

2. Termiczne równanie stanu,

przemiana termodynamiczna

przemiana termodynamiczna

Pod pojęciem stanu rozumiemy
zwykle zespół wielkości, które mogą
przybierać różne wartości, a których
zmiana wiąże się ze zmianą stanu.

2.1. Stan termodynamiczny czynnika

2.1. Stan termodynamiczny czynnika

Stan termodynamiczny czynnika

określany jest zespołem

parametrów

stanu

- określane na podstawie

pomiarów lecz bez znajomości
historii układu.

Parametry stanu:



ilość substancji



objętość



ciśnienie



temperatura



składowe prędkości



współrzędna położenia



stężenia

objętość
właściwa

Objętość właściwa

2.2. Termiczne parametry stanu

2.2. Termiczne parametry stanu

Równania termodynamiki dogodniej
jest zapisywać za pomocą objętości
właściwej, podczas gdy w równaniach
mechaniki płynów, częściej występuje
gęstość.







1

m

V

v

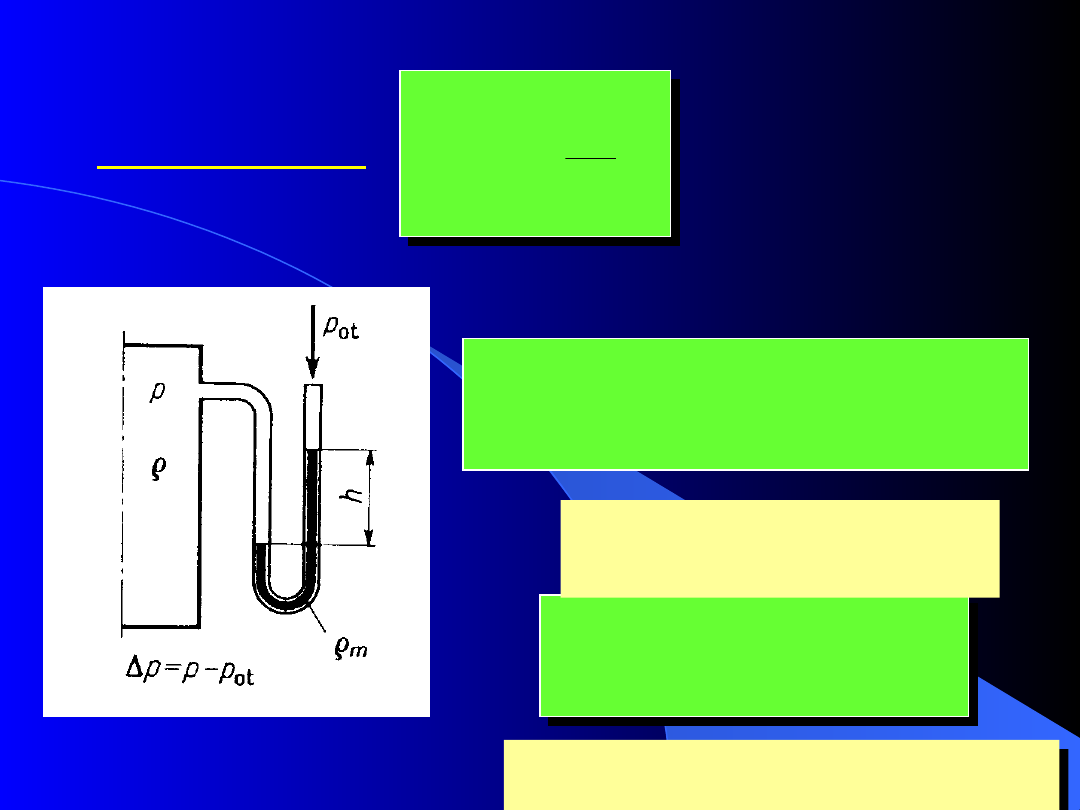
Ciśnienie:

A

F

p 





g

h

p

m

m









ot

m

p

p

p





ciśnienie
manometryczne

bezwzględne ciśnienie
statyczne

bezwzględne ciśnienie
statyczne

ot

m

p

p

p





ot

m

p

p

p





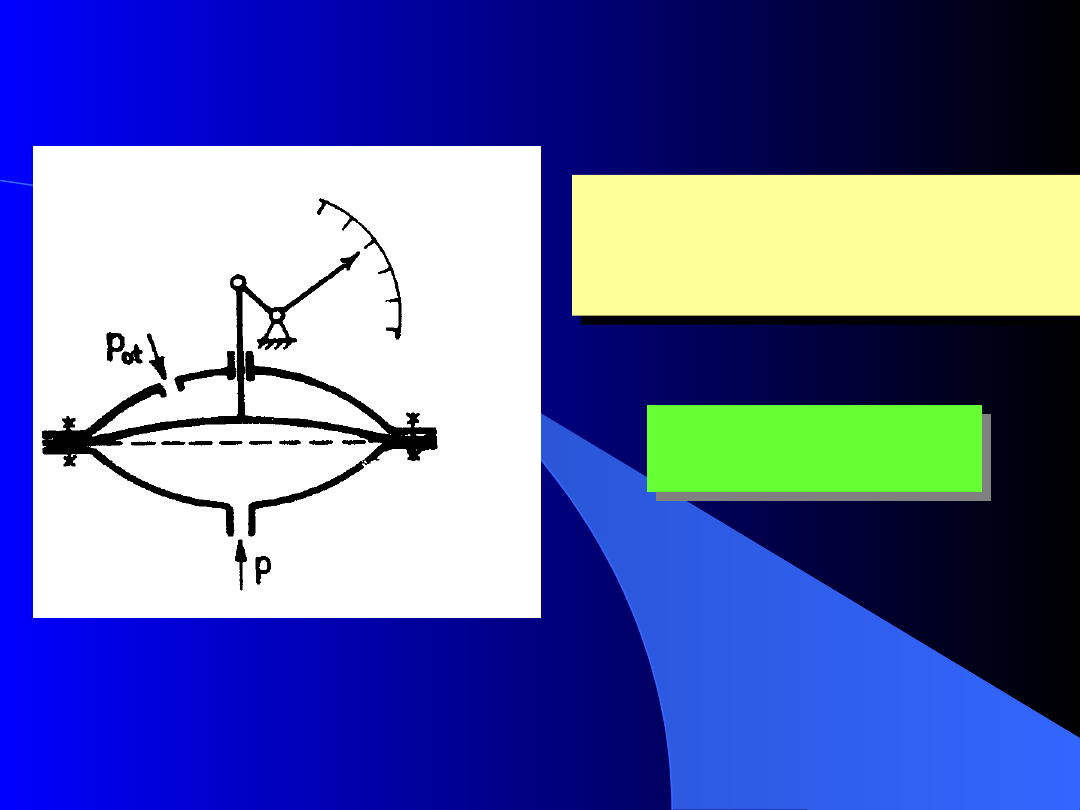
Membrana reaguje na

różnicę

ciśnień

Membrana reaguje na

różnicę

ciśnień

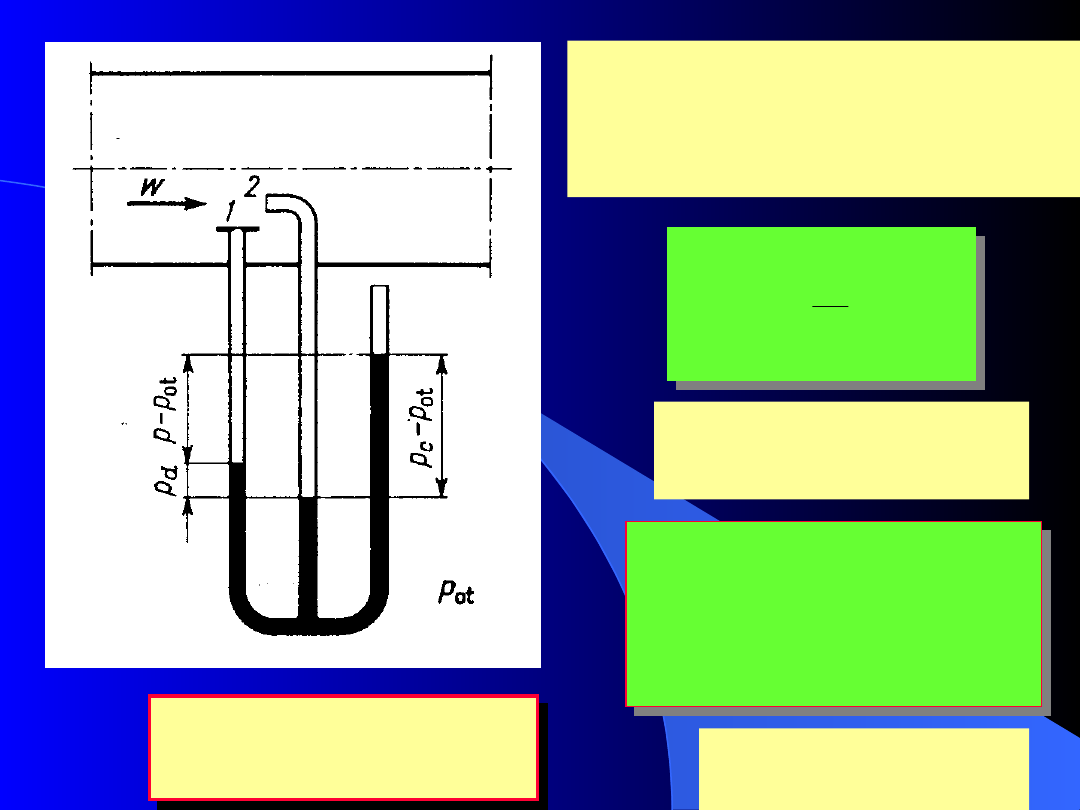
Rurka Pitota służy

do pomiaru

prędkości płynu

2

2

1

w

p

d





2

2

1

w

p

d





d

ot

m

d

s

c

p

p

p

p

p

p













d

ot

m

d

s

c

p

p

p

p

p

p













ciśnienie
dynamiczne

ciśnienie
całkowite

parametr stanu to
p

s

parametr stanu to
p

s

Temperatura

Pojęcie to nie zostało wprowadzone przez mechanikę
i jest
wielkością typowo termodynamiczną.

Istnienie parametru termicznego zwanego

temperaturą

wynika

z tzw.

zerowej zasady termodynamiki

lub

tranzytywności równowagi termicznej

.

A

B

C

A

C

R

R

R

Nie każde dwa stany termiczne ciał są stanami wzajemnej
równowagi. Oznacza to, że wystąpienie równowagi stanowi
ograniczenie wyboru parametrów p

A

, v

A

, p

B

, v

B

tych ciał.

Równowaga termiczna

to stan, w którym pomiędzy ciałami nie

jest przekazywana żadna energia, a parametry termiczne nie
zmieniają się.

A

B

R





0

,

,

,

f

1



B

B

A

A

v

p

v

p





0

,

,

,

f

2



C

C

B

B

v

p

v

p





0

,

,

,

f

3



C

C

A

A

v

p

v

p













C

C

B

B

A

A

v

p

v

p

v

p

,

,

,

3

2

1











W celu zmierzenia temperatury należy doprowadzić do
równowagi termometru i danego ciała. Jednocześnie przyjmuje
się dla wzorcowej substancji termometrycznej funkcję , dla

rtęci

Dla każdego ciała istnieje jednoznaczna funkcja ciśnienia i
objętości
właściwej, przy czym dla ciał w stanie równowagi wartości
tej funkcji są sobie równe.

b

at

v





temperatura
empiryczna

temperatura
empiryczna

t



Różne substancje i funkcje oznaczają różne skale
termometryczne.

Bezwzględna skala

15

.

273



t

T

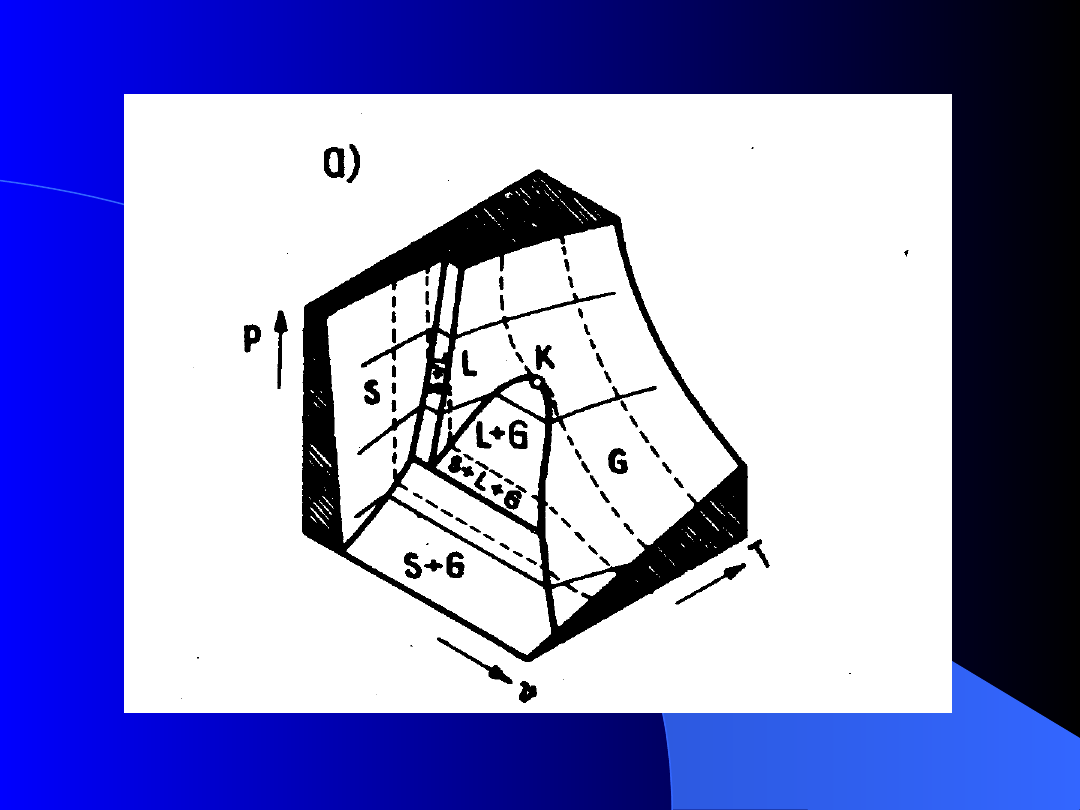
2.3. Termiczne równanie stanu

2.3. Termiczne równanie stanu

Każda substancja ma swoje własne
równanie stanu. Termodynamika
zajmuje się głównie gazami oraz
cieczami.





v

p

t

,









v

p

t

,





Z zerowej zasady termodynamiki
wynika nie tylko istnienie temperatury,
ale również istnienie zależności
pomiędzy parametrami stanu.





0

,

,

F



T

v

p





0

,

,

F



T

v

p

dwa stopnie
swobody

2.4. Termiczne równanie stanu

2.4. Termiczne równanie stanu

gazu

gazu

doskonałego i

doskonałego i

półdoskonałego

półdoskonałego



cząsteczki gazu są punktami materialnymi (nie

posiadają objętości własnej)



cząsteczki gazu nie oddziałują na siebie



cząsteczki poruszają się ruchem postępowym i

obrotowym

W

celu

uproszczenia

rozważań

termodynamika

stosuje

model

gazu

doskonałego

i

półdoskonałego

(odpowiedniki

modelu punktu materialnego i bryły sztywnej
w mechanice)

Gaz doskonały

Gaz doskonały



cząsteczki gazu są punktami

materialnymi

(nie posiadają

objętości własnej)



cząsteczki gazu nie oddziałują na

siebie



cząsteczki poruszają się ruchem

postępowym,

obrotowym i

drgającym

Gaz półdoskonały

Gaz

doskonały

Gaz

doskonały

ma

stałą

pojemność

cieplną

właściwą

(ciepło właściwe), podczas gdy
pojemność cieplna właściwa

gazu

gazu

półdoskonałego

półdoskonałego

zależy

od

temperatury.

Kiedy gaz można traktować jak doskonały i/lub
półdoskonały?

Gaz rzeczywisty tym bardziej zbliża się do
modelu gazu doskonałego im ma:

• mniejsze ciśnienie

• wyższą temperaturę
Wymagania te są tym ostrzejsze im
większe są cząsteczki.

• 1-atomowe - gazy doskonałe

• 2-atomowe - do temp. ok 100

o

C gazy doskonałe,

dla wyższych półdoskonałe

• 3-atomowe - gazy półdoskonałe lub rzeczywiste

Równanie

Równanie

Clapeyron’a

Clapeyron’a

RT

pv 

RT

pv 

p - ciśnienie
v - objętość właściwa
T - temperatura bezwzględna
R - indywidualna stała
gazowa
R=idem

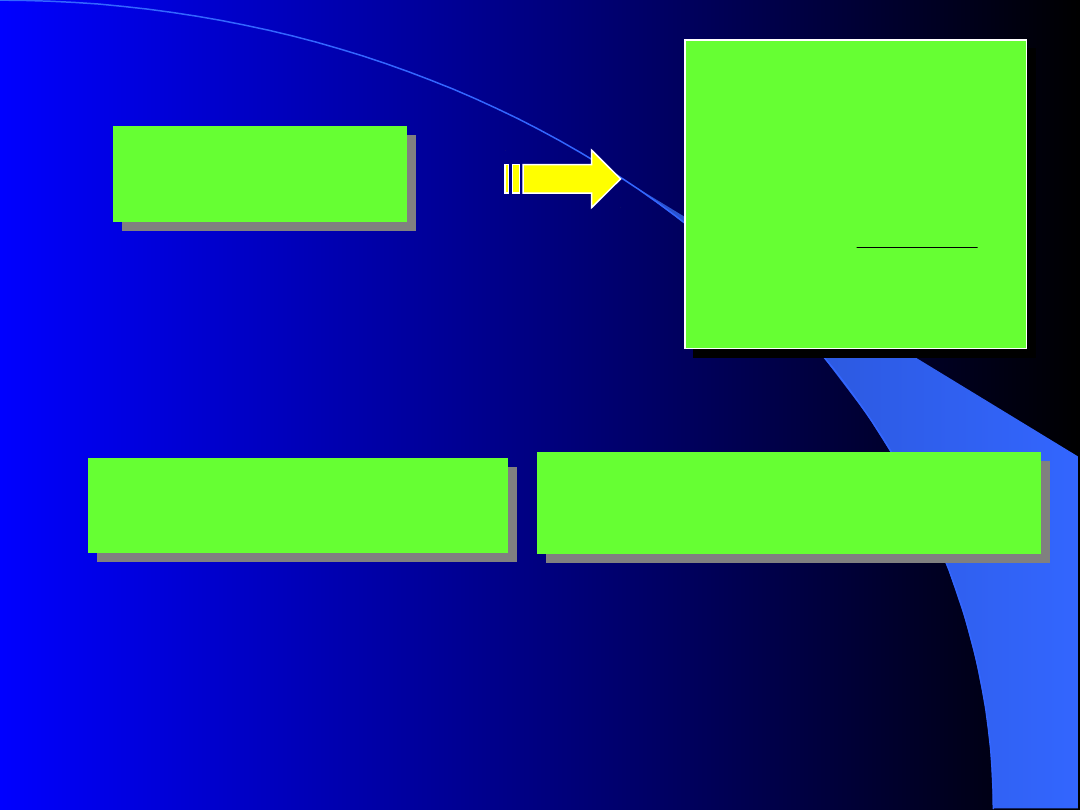
RT

pv 

RT

pv 

(MR) = 8314.4 kJ/kmol K = const

uniwersalna stała gazowa

RT

p

RT

p









MRT

pMv 

MRT

pMv 

  



T

MR

Mv

p



  



T

MR

Mv

p



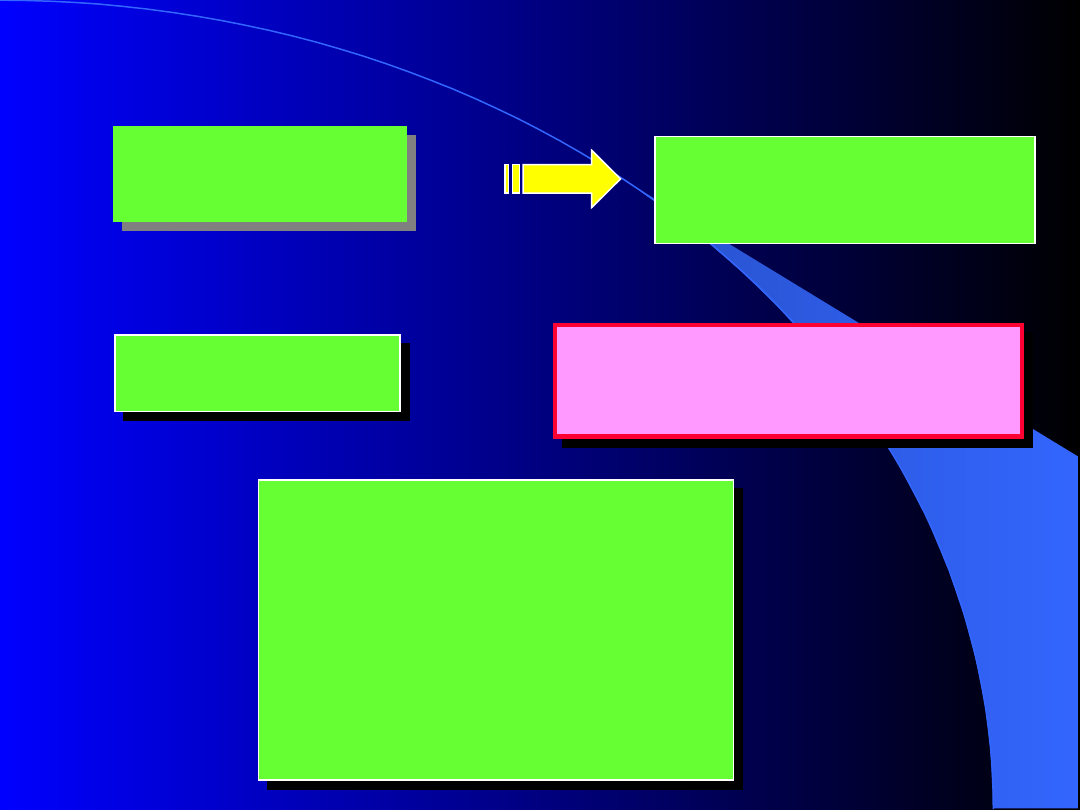
RT

pv 

RT

pv 

mRT

pV 

nM

m 





T

MR

n

pV 





T

MR

n

V

p

RT

m

V

p













2.5. Termiczne równanie stanu

2.5. Termiczne równanie stanu

gazu

gazu

rzeczywistego

rzeczywistego







RT

v

v

p

p

















RT

v

v

p

p















RT

b

v

v

a

p















 

2





RT

b

v

v

a

p















 

2



 



RT

b

v

b

v

v

T

a

p























 



RT

b

v

b

v

v

T

a

p





















Równanie Van der Waalsa

Równanie Redlich - Kwonga

Z

Z

RT

pv









1

...

1

2









v

C(T)

v

B(T)

RT

pv

Równania wirialne

...

)

(

)

(

1

2













p

T

C

p

T

B

RT

pv

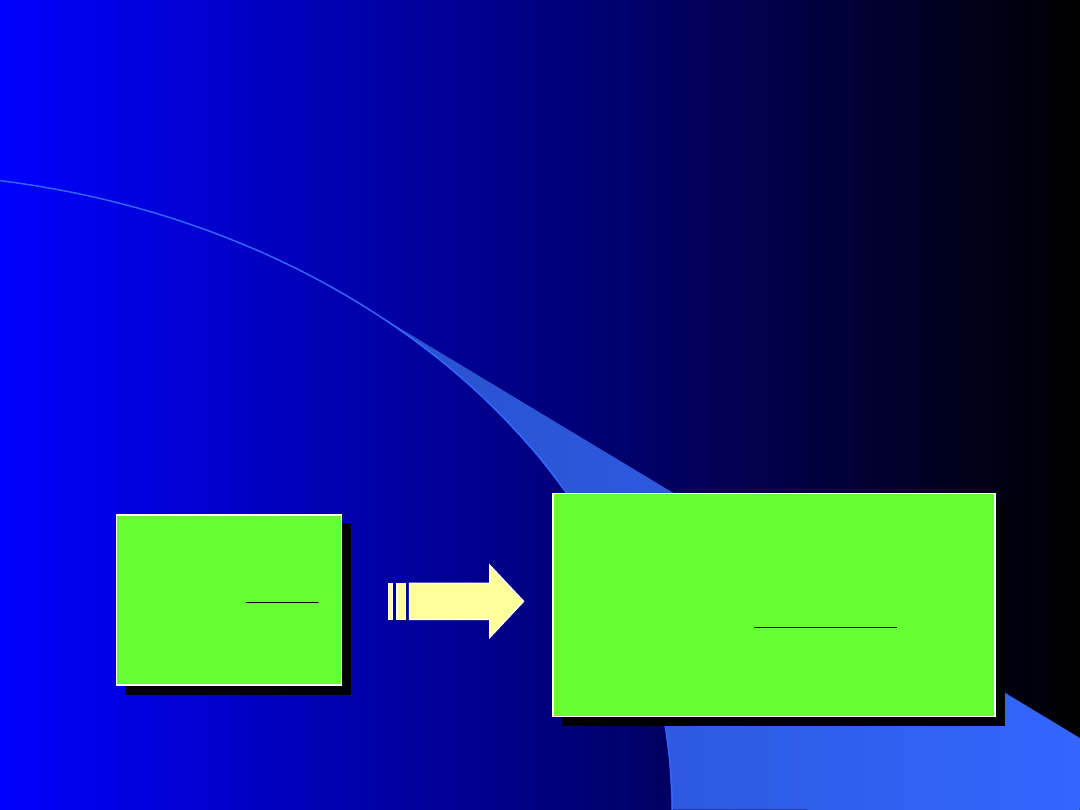
2.6. Roztwory gazów doskonałych i

2.6. Roztwory gazów doskonałych i

półdoskonałych

półdoskonałych

Udział masowy (gramowy, wagowy)

Informacją podstawową o roztworze
jest jego skład

m

m

g

i

i



1









m

m

g

i

i

i

i

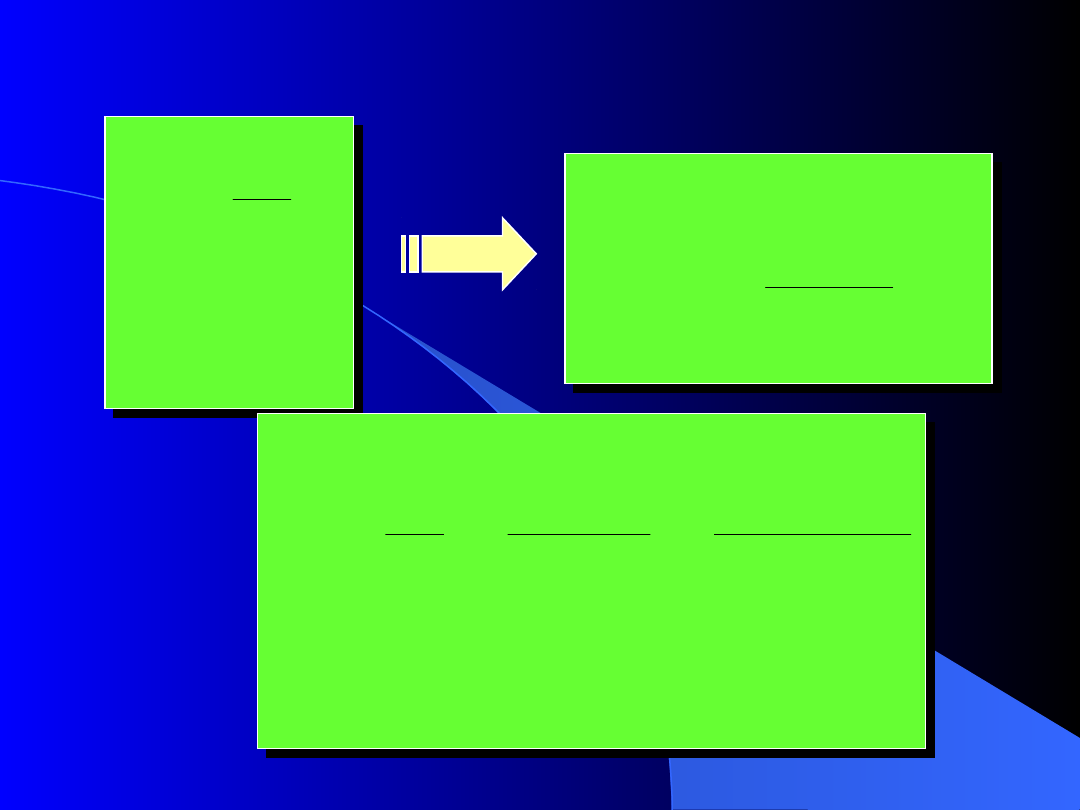
Udział molowy







i

i

i

i

n

n

n

n

z

1









n

n

z

i

i

i

i















i

i

i

i

i

i

i

i

M

z

M

n

n

M

n

m

n

m

M

Np. powietrze:

84

.

28

28

79

.

0

32

21

.

0

2

2

2

2

















N

N

O

O

a

M

z

M

z

M

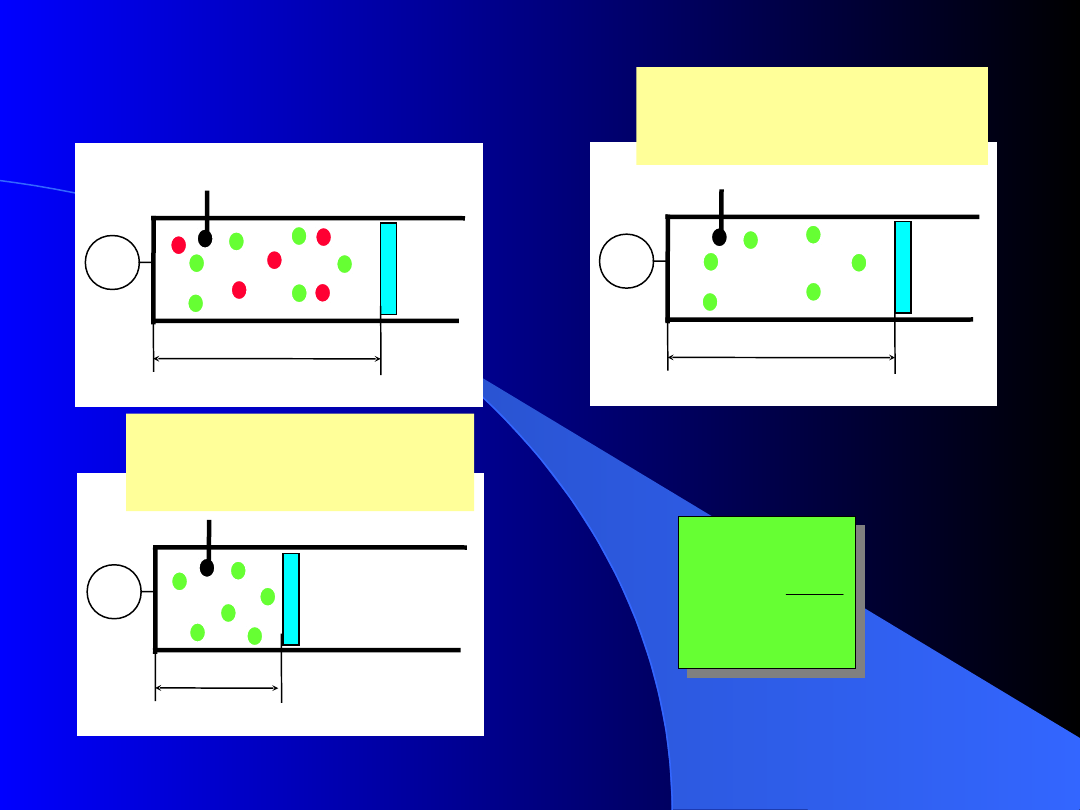
Udział objętościowy

V

V

r

i

i



V

V

r

i

i



p

V

T

p

i

V

T

p

V

i

T

ciśnienie
cząstkowe

objętość
cząstkowa





i

i

p

p





i

i

p

p

Prawo
Daltona

i

i

pV

V

p



i

i

pV

V

p



p

r

V

V

p

p

i

i

i





1





i

i

r





T

MR

n

V

p

i

i







T

MR

n

V

p

i

i



Dla pojedynczego
składnika

Sumując dla wszystkich składników otrzymujemy





T

MR

n

V

p

i

i

i

i



































T

MR

n

V

p

i

i

i

i



































T

MR

n

pV 





T

MR

n

pV 

T

R

m

V

p

i

i

i



T

R

m

V

p

i

i

i



Dla pojedynczego
składnika

Sumując dla wszystkich składników otrzymujemy

mRT

pV 

mRT

pV 

T

R

m

m

m

T

R

m

V

p

i

i

i

i

i

i

i

i































































i

i

i

R

g

R

















i

i

i

R

g

R

zastępcza stała
gazowa





T

MR

n

V

p

i

i







T

MR

n

V

p

i

i



Dla pojedynczego
składnika

Sumując dla wszystkich składników otrzymujemy

n

n

p

p

i

i



n

n

p

p

i

i







T

MR

n

pV 





T

MR

n

pV 

i

i

z

r 

i

i

z

r 

T

R

m

V

p

i

i

i



Dla pojedynczego
składnika

Sumując dla wszystkich składników otrzymujemy

R

R

m

m

p

p

i

i

i



mRT

pV 

R

R

g

r

i

i

i











i

i

i

i

i

i

i

M

M

g

MR

M

M

MR

g

R

R

g

r















i

i

i

i

i

i

i

M

M

g

MR

M

M

MR

g

R

R

g

r







M

M

r

g

i

i

i



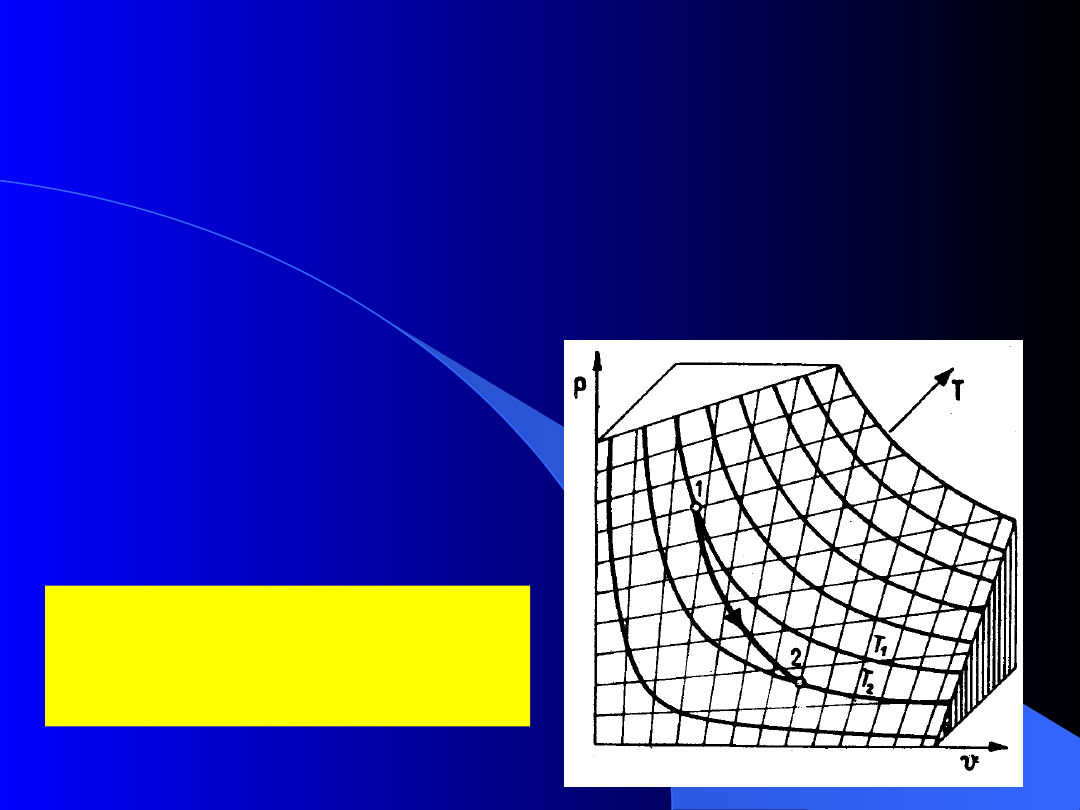
2.7. Przemiana termodynamiczna

2.7. Przemiana termodynamiczna

Obrazem przemiany jest
linia na powierzchni
stanów

Przemiana termodynamiczna

to

zmiana stanu termicznego czynnika
(od stanu początkowego do
końcowego) przez kontinuum stanów
pośrednich.

 

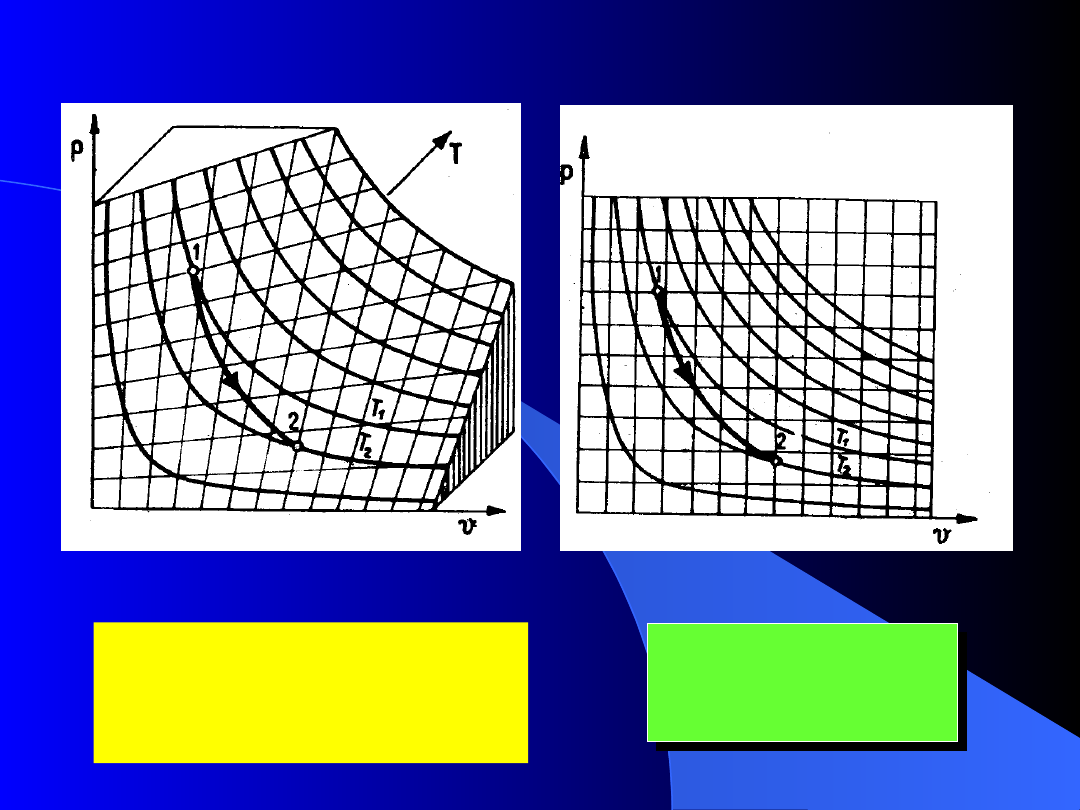
v

p h



Równanie przemiany
ma jeden stopień
swobody

Równanie

przemiany

termodynamicznej

to

dodatkowe

równanie więzów na parametry
stanu, np. w przypadku izotermy
gazu doskonałego mamy:

idem



T

idem

idem



R

pv

RT

pv 

sprężanie

rozpręża
nie
izobara

Przebieg ciśnienia w układzie:

Zmiany objętości właściwej w układzie:



dv > 0



dv < 0



dv = 0



dp >

0



dp <

0



dp =

0

ekspansja
kompresja
izochora

Przemiany mogą przebiegać jako:



nieodwracalne



odwracalne



pseudoodwracalne

p

v

0

d

dp



v

Przy opisie matematycznym przemian musimy
korzystać z następujących praw:



zasada zachowania ilości

substancji



I zasada termodynamiki

(zasada zachowania energii)



II zasada termodynamiki

związki
ilościowe

związki
jakościowe