Analiza wariancji

Opracowała:
Aneta Jordan

Analiza wariancji

(analysis of variance – ANOVA)

Metoda analizy wariancji zapoczątkowana przez R.A. Fishera,
służy do weryfikacji hipotezy równości wartości średnich
wielu prób.

Analiza

wariancji

to

parametryczne

narzędzie

pozwalające porównać więcej niż dwie badane grupy

wydzielone przez kategorie jednej zmiennej (analiza

jednoczynnikowa)

lub

wielu

zmiennych

(analiza

wieloczynnikowa).

2

ANOVA - zastosowanie

Analiza wariancji wykorzystywana jest gdy np. w różnych

warunkach wykonuje się kilka serii pomiarowych. W procesie

kontroli jakości produkcji często pobierane są próby, na które

składa się kilka elementów wyprodukowanych przy użyciu

różnych maszyn. Istotną sprawą jest wykrycie możliwego

wpływu zmiennych zewnętrznych (warunki doświadczenia,

nr maszyny itp.) na własności próby.

3

ANOVA - podział

Możemy podzielić analizę wariancji na trzy grupy analiz:

 jednoczynnikowa analiza wariancji -

wpływ jednego czynnika między grupowego na zmienną zależną,

 wieloczynnikowa analiza wariancji -

wpływ kilku czynników międzygrupowych na zmienną zależną,

 analiza wariancji dla czynników wewnątrzgrupowych -

wpływ czynnika wewnątrzgrupowego na zmienną zależną, tzw.

„powtarzane pomiary”.

4

Jednoczynnikowa analiza wariancji

Polega ona na porównaniu wariancji wewnątrz grupowej

do wariacji między grupowej. Dobrze jeśli wariancja

międzygrupowa jest duża, natomiast wariancja wewnątrz

grupowa jak najmniejsza (możliwie małe różnice w

zakresie badanej zmiennej zależnej „wewnątrz” jednej

grupy).

5

ANOVA - podstawowe założenia

Wyniki uzyskane metodą analizy wariancji mogą być
uznane za prawidłowe, gdy spełnione są założenia:

 Każda populacja musi mieć rozkład normalny,
 Pobrane do analizy próby są niezależne,
 Próby pobrane z każdej populacji myszą być losowymi

próbami prostymi,

 Wariancje w populacji są równe.

W przypadku, gdy założenia analizy wariacji nie są spełnione
należy posługiwać się testem Kruskala-Wallisa.

6

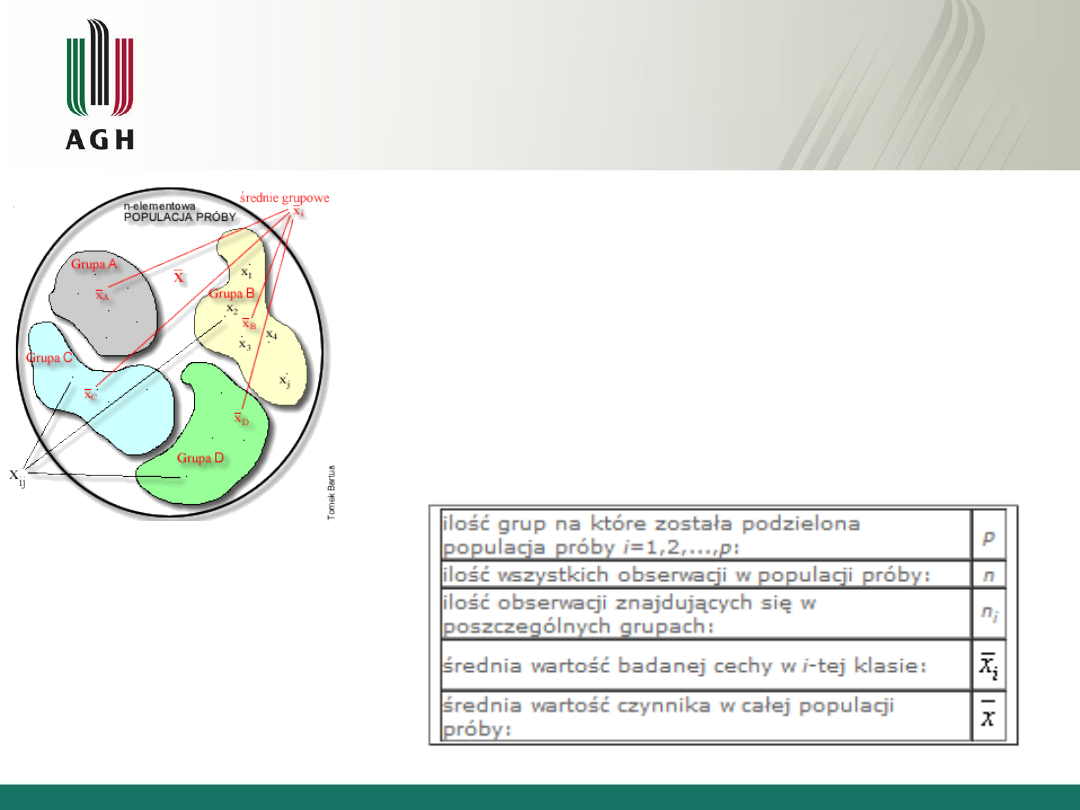
Jednoczynnikowa analiza wariancji

Mamy do czynienia tylko z jednym czynnikiem
i chcemy sprawdzić czy ma on wpływ na
mierzoną zmienną zależną.

(np. temperatura

spiekania, atmosfera spiekania itp.)

n – elementowa populacja próby, którą możemy
podzielić ze względu na pewien czynnik na p grup
(klas). Do każdej z nich trafi pewna liczba n

i

: 1, 2, 3,

…, i.

7

ANOVA – jednoczynnikowa - hipotezy

 Hipoteza zerowa – średnie porównywanych populacji są

równe,
H

0

: m

1

=m

2

=…=m

r

 Hipoteza alternatywna (eksperymentalna) – istnieję co

najmniej dwie takie populacje, których porównywane średnie
są różne)
H

1

: nie wszystkie m

1

są sobie równe (i=1,…,r)

8

Weryfikacja hipotezy

Do weryfikacji hipotezy oblicza się wartość statystyki F:

Gdzie:
• MSTR – oznacza średni kwadratowy błąd „zabiegowy”
• MSE – oznacza średni kwadratowy błąd losowy

Przy założeniu prawidłowości H

0

statystyka F ma rozkład

F-Snedecora z r-1 stopniami swobody w liczniku i n-r stopniami swobody w
mianowniku. Obszar krytyczny jest w postaci:

Q={F:F≥F

a

}

Gdzie:

• F

a

–

jest wartością krytyczną odczytywaną z tablic rozkładu F-Snedecora dla

(r-1, n-r) stopni swobody

9

Test Snedecora

W analizie wariancji wykorzystuje się test F Snedecora. Ma on
postać ilorazu dwóch niezależnie oszacowanych wariancji. W liczniku
- wariancja międzygrupowa, na której maksymalizacji nam zależy.
W mianowniku - wariancja wewnątrzgrupowa czyli ważona średnia
wariancji

w

poszczególnych

grupach,

nazywana

jest

często wariancją błędu. Wielkość tej wariancji chcielibyśmy z kolei
minimalizować, ponieważ jest to ta część całkowitej wariancji
zmiennej zależnej, której nie jesteśmy w stanie wyjaśnić efektem
wpływu zmiennej niezależnej.

10

Wnioskowanie

 Jeżeli obliczona

wartość statystyki F należy do

obszar krytycznego Q to hipotezę H

0

odrzucamy

na korzyść hipotezy alternatywnej i

wnioskujemy, że badane średnie nie są jednorodne.

 Jeżeli obliczona

wartość statystyki F nie należy

do obszaru krytycznego Q to nie ma podstaw
do odrzucenia H

0

i wnioskujemy, że badane

średnie są jednorodne.

11

Tablica analizy wariancji

12

Wnioskowanie

Gdy

odrzucamy hipotezę H

0

mówimy:

 Stwierdzono statystycznie istotny wpływ czynnika A na

badaną cechę,
albo:

 Czynnik A wpływa istotnie różnicująco na badaną cechę.
Gdy

nie odrzucimy hipotezy H

0

mówimy:

 Nie stwierdzono statystycznie istotnego wpływu

czynnika A na badaną cechę,
albo:

 Czynnik A nie wpływa istotnie różnicująco na badaną

cechę.

13

Jednoczynnikowa analiza wariancji -
podsumowanie

Analiza wariancji daje informację tylko o tym czy między

grupami występują istotne statystycznie różnice. Nie mówi

ona,

które

populacje

różnią

się

między

sobą.

Przeprowadzając jednoczynnikową analizę wariancji można

stwierdzić, że np. między wydajnością maszyn występują

różnice, jednak nie można powiedzieć, które maszyny mają

tę samą wydajność, a które różnią się między sobą. W celu

uzyskania takich informacji przeprowadza się następny krok

analizy wariancji tzw. testy post hoc, np. test Tukey'a.

14

Wieloczynnikowa analiza wariancji

W przypadku wieloczynnikowej analizy wariancji mamy do

czynienia z przynajmniej dwoma czynnikami. Najczęstszy jest

model dwuczynnikowy (dwuczynnikowa analiza wariancji),

chociaż może być o wiele więcej czynników. Analiza wariancji

z klasyfikacją wielokrotną pozwala zbadać jaki wpływ na

populację mają kombinacje czynników.
Np. dla ANOV’y dwuczynnikowej kombinacje czynników
A i B

15

ANOVA wieloczynnikowa - założenia

 Normalność i identyczna wariancja rozkładu ze

względu na badaną cechę w każdej grupie

 Obserwacje pochodzą z losowych prób

 Liczba obserwacji o poszczególnych

kombinacjach poziomów czynników jest

identyczna

16

Efekty analizy dwuczynnikowej

Efekt swoisty

– (czynnika A oraz B) efekt działania

każdego z czynników z osobna (bez względu na poziom

drugiego czynnika).

Efekt interakcji (AB)

- występuje, gdy efekt uzyskany

przy danym poziomie jednego czynnika zależy od poziomu

drugiego; nie miałby miejsca bez połączenia dwóch

czynników na danym poziomie.

17

Analiza dwuczynnikowa

 Badamy daną cechę populacji (jej natężenie -

średnią) w podgrupach ze względu na działanie

dwóch czynników A i B.

 Otrzymujemy n x k kombinacji poziomów (gdyż

istnieje n poziomów czynnika A i k poziomów

czynnika B)

 Jako pierwszą sprawdzamy zawsze hipotezę

dotyczącą interakcji, gdyż interpretacja wyników

testów na efekty swoiste zależy od tego, czy

czynniki są addytywne, czy nie.

18

Testowanie hipotez

 Test na efekt swoisty czynnika A

H

o

: dla każdego i=1,2,...,n a

i

=0

H

1

: istnieje i, dla którego a

i

≠ 0

Test sprawdza, czy istnieją statystycznie istotne różnice między

średnimi badanej cechy, wynikające z zastosowania czynnika A

na określonym poziomie

 Test na efekt swoisty czynnika B

(analogicznie)

 Test na interakcje czynników AB

H

o

: dla każdego i=1,2,...,n oraz j=1,2,...,k (ab)

ij

=0

H

1

: istnieje i oraz j, dla którego (ab)

ij

≠ 0

19

• Efekty swoiste:

- czynnika A

F=MSA/MSE, df: (n-1) i nk(N-1)

- czynnika B

F=MSB/MSE, df: (k-1) i nk(N-1)

• Efekt interakcji:

F=MS(AB)/MSE df: (n-1)(k-1) i nk(N-1)

Gdzie:
MSA=SSA/(n-1),
MSB=SSB/(k-1),
MS(AB)=SS(AB)/(n-1)(k-1),
MSE=SSE/nk(N-1)

20

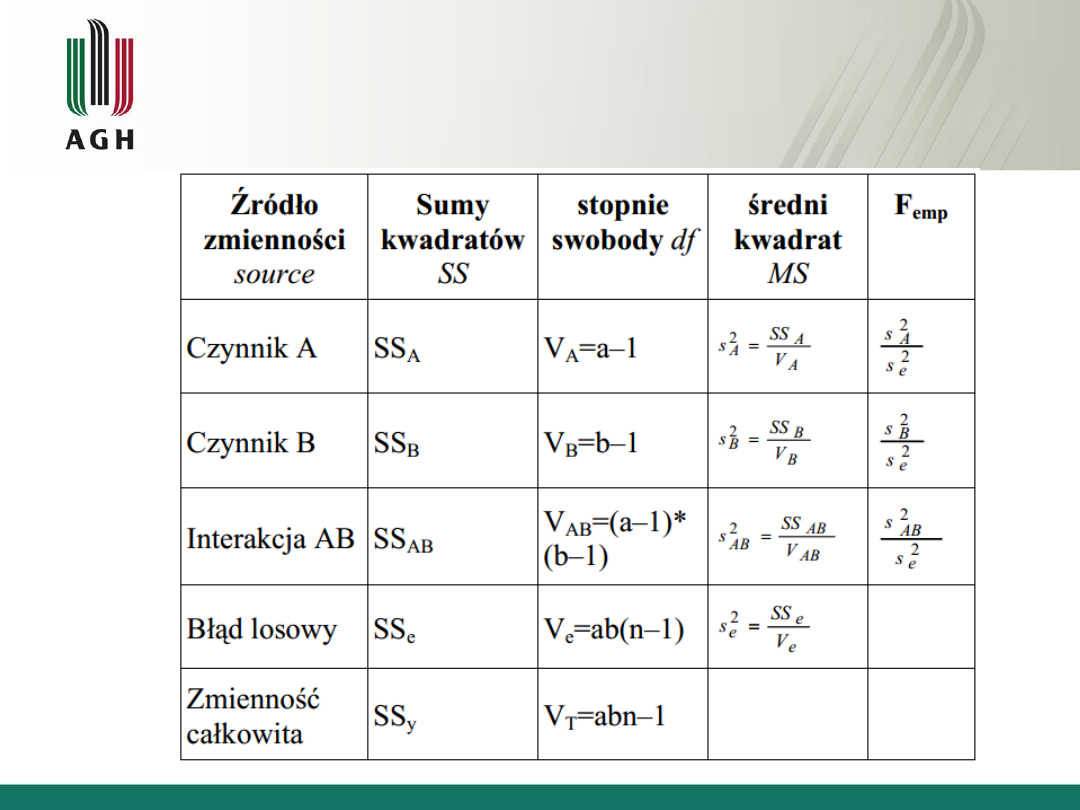
Dwuczynnikowa ANOVA - tablica analizy
wariancji

21

Porównanie

 W dwuczynnikowej analizie wariancji postępowanie jest

zbliżone do jednoczynnikowej analizy wariancji, jednak
oceniamy jednocześnie wpływ dwóch czynników
doświadczalnych.

 Jedną z ważnych różnic w dwuczynnikowej analizy

wariancji w stosunku do jednoczynnikowej analizy
wariancji jest ocena współdziałania dwóch czynników. Jeśli
występuję współdziałanie oznacza to, że jeden czynnik
modyfikuje wpływ drugiego na badaną zmienną.

22

Bibliografia

• W. Volk; Statystyka stosowana dla inżynierów; Wyd.

Naukowo-Techniczne; Warszawa 1973,

• Cz. Szmigiel, J. Mercik; Ekonometria, WSZiF; Wrocław

2000,

• B. Kamys; Statystyczne metody opracowania pomiarów;

2007/8

23