A K A D E M I A G Ó R N I C Z O - H U T N I C Z A

i m. S t a n i s ł a w a S t a s z i c a

WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI, INFORMATYKI i ELEKTRONIKI

Z a k ł a d E l e k t r o e n e r g e t y k i

SIECI ELEKTROENERGETYCZNE

SIECI ELEKTROENERGETYCZNE

Wykład 7

Wykład 7

Asymetria w układach trójfazowych

Asymetria w układach trójfazowych

Opracował: W. Szpyra

Opracował: W. Szpyra

/na podstawie: Praca zbiorowa pod red. Kujszczyk Sz.:

/na podstawie: Praca zbiorowa pod red. Kujszczyk Sz.:

Elektroenergetyczne sieci rozdzielcze. Wyd. Naukowe PWN,

Elektroenergetyczne sieci rozdzielcze. Wyd. Naukowe PWN,

Warszawa 1994, tom 2. [1] /

Warszawa 1994, tom 2. [1] /

Kraków, kwiecień 2002

Kraków, kwiecień 2002

Literatura

1. Praca zbiorowa pod red. Kujszczyk Sz.: Elektroenergetyczne sieci rozdzielcze.

Tom 1 i 2. Wyd. Naukowe PWN, Warszawa 1994

8. Rozporządzenie Ministra Gospodarki z dnia 21 października 1998 r. w sprawie

szczegółowych warunków przyłączania podmiotów do sieci
elektroenergetycznych, pokrywania kosztów przyłączania, obrotu energią,
świadczenia usług przesyłowych, ruchu sieciowego i eksploatacji sieci oraz
standardów jakościowych obsługi odbiorców (Dz. U. Nr 135 poz. 881)

7. Praca zbiorowa: Wytyczne programowania rozwoju sieci rozdzielczych. Instytut

Energetyki Zakład Sieci Rozdzielczych, Warszawa-Katowice 1986

2. Marzecki J., Parol M.: Komputerowe projektowanie rozdzielczych sieci

elektroenergetycznych. Oficyna Wydawnicza Politechniki Warszawskiej,
Warszawa 1994

3. Marzecki J.: Miejskie sieci elektroenergetyczne. Oficyna Wydawnicza Politechniki

Warszawskiej, Warszawa 1996

4. Popczyk J., Żmuda K.: Sieci elektroenergetyczne. Ocena stanu i optymalizacja

według podejścia probabilistycznego. Skrypty Uczelniane Pol. Śląskiej, nr 1612
Gliwice 1991

5. Praca zbiorowa: Poradnik Inżyniera Elektryka. Wydawnictwa Naukowo-

Techniczne Warszawa 1996

6. Borowczyk B.: Wskazówki ustalania obciążeń elektrycznych odbiorców

komunalno-bytowych w miejskich sieciach osiedlowych. ENERGOPROJEKT
Poznań 1989

9. Wskazówki projektowania sieci elektroenergetycznych w zakładach

przemysłowych, BISTYP 1974

Literatura

10. Norma PN-IEC60038:1999 Napięcia znormalizowane

12. Kowalski Z.: Asymetria w układach elektroenergetycznych. PWN

Warszawa 1974

11. Kochel M.: Niesymetryczne obciążenia w miejskich sieciach

elektroenergetycznych. Praca doktorska, Warszawa 1966

13. PN-EN 50160 Parametry napięcia zasilającego w publicznych sieciach

rozdzielczych. Polski Komitet Normalizacyjny, październik 1998.

Asymetria układów wielofazowych

W obliczeniach sieci elektroenergetycznych przyjmuje się zazwyczaj
założenie symetrii impedancji wzdłużnych oraz symetrii prądów
odbiorów i napięć zasilających. Przyjęcie tego założenia w znacznym
stopniu ułatwia wykonanie obliczeń. Jednak w rzeczywistości w
ustalonych stanach pracy sieci należy rozróżnić dwa rodzaje
asymetrii:

1) asymetrię wewnętrzną (własną) elementów sieci (linii i

transformatorów), powodowaną niejednakowymi impedancjami
własnymi i wzajemnymi poszczególnych faz, np. w liniach
napowietrznych,

2) asymetrię

zewnętrzną:

a) w punktach zasilających, polegającą na tym, że napięcie

trójfazowe
w tych punktach sieci jest asymetryczne,

b) w punktach odbioru miejscową, polegającą na tym, że odbiory

przyłączone w poszczególnych punktach sieci mają w każdej
fazie
różne moce,

c) w punktach odbioru przestrzenną, polegającą na tym, że do

sieci przyłączone są w różnych punktach odbiory jednofazowe.

Najistotniejsze znaczenie praktyczne ma asymetria zewnętrzna w
punktach odbioru i to zarówno miejscowa jak i przestrzenna

Asymetria układów wielofazowych

Asymetria napięć i prądów w układzie trójfazowym określona jest
przez współczynniki niezrównoważenia napięć i prądów:

(7.1

)

gdzie

U

1

, U

2

, U

0

–

wartości skuteczne składowych symetrycznych

kolejności zgodnej, przeciwnej i zerowej napięć,

I

1

, I

2

, I

0

–

wartości skuteczne składowych symetrycznych

kolejności zgodnej, przeciwnej i zerowej prądów

 kolejności

przeciwnej:

Przy obciążeniu sieci elektroenergetycznej odbiornikami
asymetrycznymi
spadki i straty napięcia są różne w różnych fazach, a zatem napięcia
przyłożone do zacisków odbiorników są asymetryczne. Napięcia te
różnią się wartościami modułów napięć fazowych, a wektory są
przesunięte są względem siebie o kąty inne niż 120°

,

1

2

2

U

U

n

U



,

1

0

0

U

U

n

U



 kolejności

zerowej:

,

1

2

2

I

I

n

I



,

1

0

0

I

I

n

I



Asymetria układów wielofazowych

Odbiornikami powodującymi asymetrię napięć w sieci są:

 zespoły odbiorników jednofazowych przyłączonych do linii

trójfazowej, np. piece indukcyjne, spawarki transformatorowe,
trakcja jednofazowa;

 odbiorniki trójfazowe o asymetrycznym obciążeniu chwilowym, jak

np. piece łukowe w okresie topienia wsadu;

 liczne, nierównomiernie rozmieszczone odbiorniki jednofazowe

włączone między przewody fazowe i neutralny, występujące np. u
odbiorców komunalnych zasilanych z sieci niskiego napięcia.

Asymetryczne włączenie odbiorów do sieci powoduje obciążenie jej
mocą pozorną, różną od mocy pozornej, jaka byłaby pobierana z
sieci przy symetrycznym włączeniu tych samych odbiorów

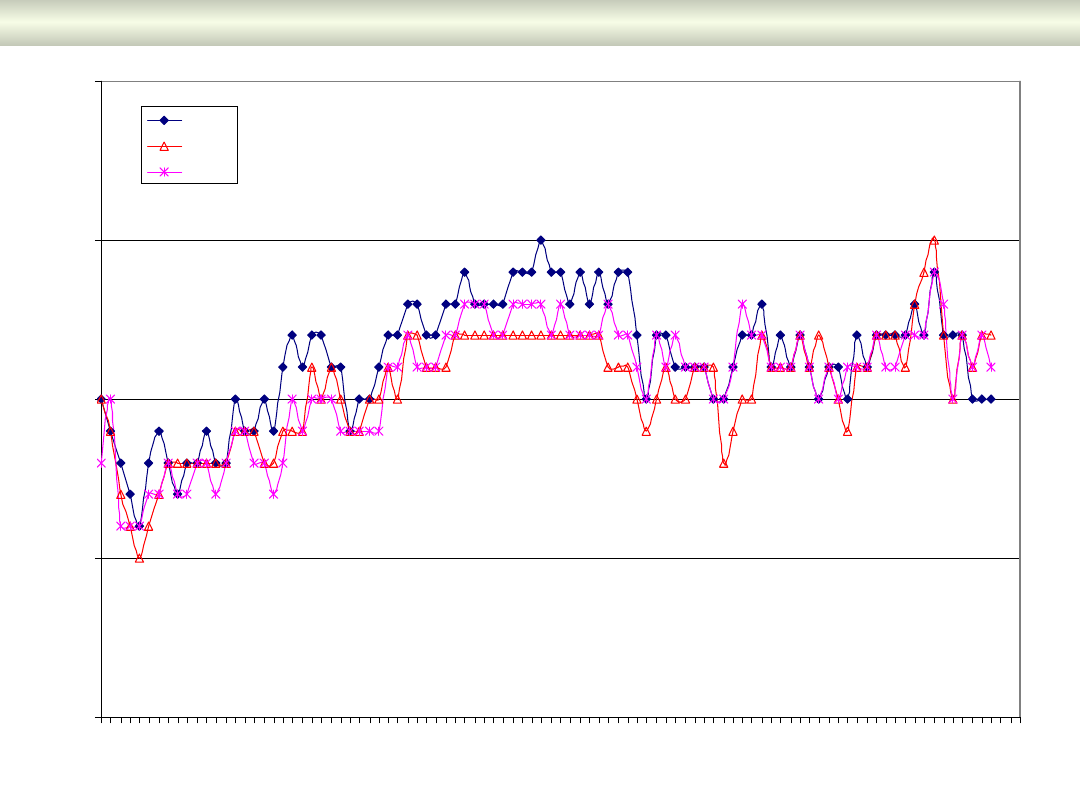
Asymetria napięcia w stacji 15/0.4 kV

215

220

225

230

235

16 17 18 19 20 21 22 23 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16

Godzina

N

ap

ię

ci

e,

w

V

Faza R
Faza S
Faza T

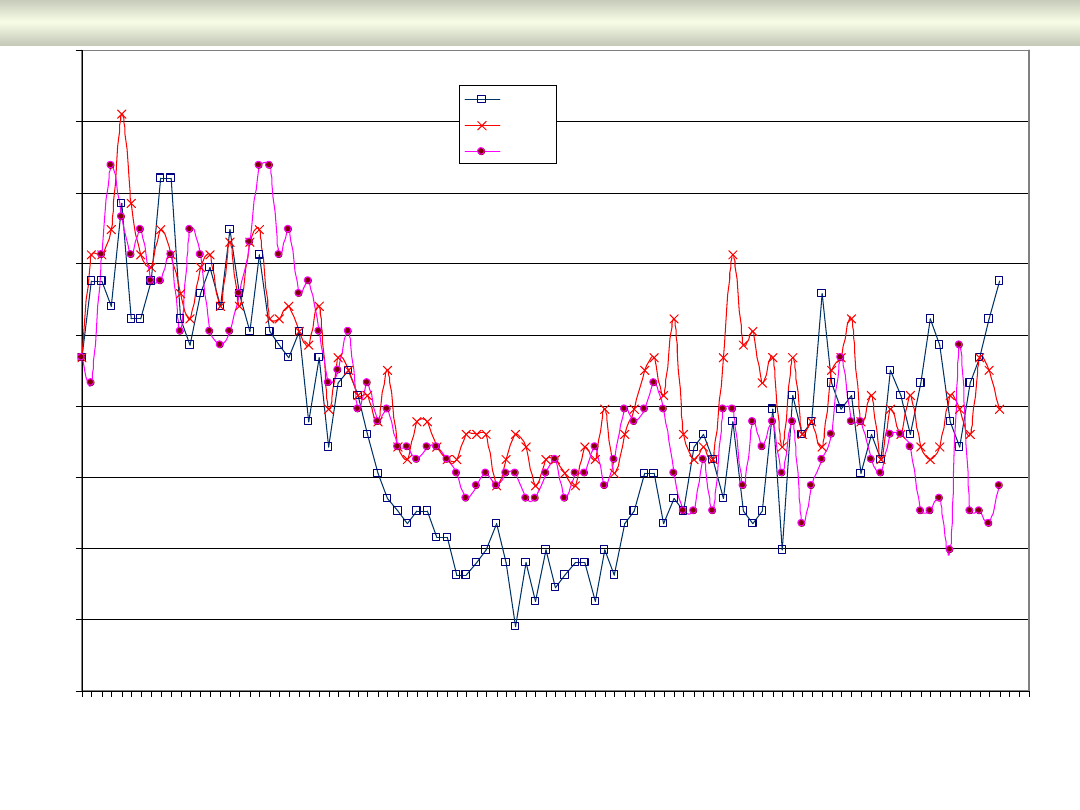
Asymetria prądu w stacji 15/0.4 kV

0

10

20

30

40

50

60

70

80

90

16 16 17 18 19 19 20 21 22 22 23 00 01 01 02 03 04 04 05 06 07 07 08 09 10 10 11 12 13 13 14 15 16

Godzina

P

rą

d,

w

A

Faza R
Faza S
Faza T

Moc obwodu trójfazowego obciążonego

asymetrycznie

Moc pozorna

S

S

przesyłana symetryczną linią trójfazową przy

sinusoidalnych przebiegach napięcia

U

U(t)

i prądu

I

I(t)

,

zmieniających się z jednakową częstotliwością, określona jest
wzorem:















cos

3

2

2

P

Q

P

I

U

S

Moc czynna pobierana przez odbiór symetryczny równa jest sumie
trzech mocy o jednakowej wartości

P

f

pobieranych przez każdą

fazę odbiornika:





















cos

3

cos

3

3

I

U

I

U

P

P

f

f

f

Przy asymetrycznym obciążeniu linii trójfazowej kąt przesunięcia
może być inny w każdej fazie, dlatego powyższy wzór nie wiąże mocy
czynnej z mocą pozorną - współczynnik mocy asymetrycznego
odbioru trójfazowego nie jest więc równy cosinusowi kąta
przesunięcia między prądem a napięciem

(7.2)

(7.3)

Moc asymetrii

Moc pozorną

S

A

odbioru asymetrycznego można obliczyć z

zależności:

Gdzie

D

jest mocą asymetrii pobieraną dodatkowo z linii przez odbiór

asymetryczny
Moc pozorną odbioru asymetrycznego można także wyrazić za
pomocą składowych symetrycznych asymetrycznego układu prądów
i napięć:

D

Q

P

I

I

I

U

U

U

S

T

s

R

T

s

R

A

2

2

2

2

2

2

2

2

2





















 







2

2

0

2

0

2

2

2

1

2

2

2

1

9

3

3























I

I

I

I

U

U

S

D

Gdzie



2

-

stosunek rezystancji przewodu neutralnego

R

N

do

rezystancji przewodu fazowego

R

:

R

R

N





2

(7.4
)

(7.5
)

(7.6)

Moc asymetrii

Moc asymetrii

D

w zależności od składowych symetrycznych

asymetrycznego układu napięć i prądów fazowych przy dowolnej
asymetrii kątowej i asymetrii modułów wektorów fazowych napięć
zasilających oraz przy dowolnej asymetrii kątowej i asymetrii
modułów wektorów prądów fazowych odbioru zasilanego linią
trójfazową czteroprzewodową można wyrazić wzorem:





















0

2

0

0

2

2

0

1

0

0

1

1

2

1

2

2

1

1

2

2

0

2

2

2

2

0

2

1

2

0

2

2

2

0

2

1

2

0

2

0

2

1

2

2

2

1

2

1

cos

cos

cos

18

3

3

3































































































I

U

I

U

I

U

I

U

I

U

I

U

I

U

I

U

I

U

I

U

I

U

I

U

I

U

D

(7.7)

gdzie



1

, 

2

, 

0

–

kąty przesunięcia fazowego między składowymi

symetrycznymi napięcia i prądu odpowiednio kolejności
zgodnej, przeciwnej i zerowej

Powyższe równanie znacznie się upraszcza gdy wektory fazowych
napięć zasilających tworzą zamknięty trójkąt - gdyż wtedy składowa
symetryczna kolejności zerowej układu napięć zasilających jest równa
zeru

U

0

= 0

,

natomiast gdy odbiornik trójfazowy zasilany jest linią

trójfazową, trójprzewodową, wtedy

U

0

= 0

oraz

I

0

= 0

.

Moc asymetrii

W przypadku gdy napięcie zasilające jest symetryczne tj. gdy
moduły wektorów napięć fazowych są sobie równe a wektory są
przesunięte
o kąt

120°

wówczas składowa symetryczna przeciwna napięcia

U

2

=

0 .

Moc asymetrii

D

przesyłaną linią zasilającą czteroprzewodową

można wówczas obliczyć ze wzoru:





2

2

0

2

2

3

1

3

















I

I

U

D

f

(7.8)

W przypadku linii zasilającej trójprzewodowej

I

0

= 0

i wtedy stosuje się

wzór:

(7.9

)

Po podstawieniu do równania

(7.7)

współczynników

niezrównoważenia napięć i prądów określonych wzorami

(7.1)

równanie na moc asymetrii przyjmie postać:

2

3

I

U

D

f





























 



2

2

2

0

2

0

1

2

2

2

1

2

2

2

2

2

2

1

1

3

1

1

cos

cos

cos

2

3

0

0

0

0

2

2

0

0

2

2

0

0

2

2





































































I

I

I

U

I

U

U

I

U

I

u

I

U

I

n

n

n

n

n

n

n

n

n

n

n

n

n

n

I

U

D

W praktyce, dla dość szerokiego zakresu asymetrii obciążeń
prądowych

można przyjąć (nie popełniając zbyt wielkiego błędu), że

trójkąt napięć zasilających jest równoboczny,

(

tj.:

U

2

= 0

oraz

=

0

)

.

2

U

n

(7.10)

Moc asymetrii

Założenie to jest dopuszczalne dla obliczeń praktycznych, gdyż
stopień niezrównoważenia napięć jest bardzo mały w porównaniu ze
stopniem niezrównoważenia prądów.

Przy tym założeniu moc

asymetrii

D

w linii czteroprzewodowej oblicza się z uproszczonego

wzoru:

Natomiast w trójprzewodowej linii zasilającej składowa symetryczna
zerowa prądu równa jest zeru

I

0

=

0

oraz , wówczas moc

asymetrii

D

można obliczyć korzystając z uproszczonej zależności:

0

0



I

n





2

2

2

1

1

3

1

3

0

2



















I

I

n

n

I

U

D

(7.11)

(7.12)

2

1

1

2

3

I

n

I

U

D









Straty mocy czynnej w obwodzie trójfazowym obciążonym

symetrycznie

Przy jednakowym obciążeniu trzech faz straty mocy czynnej w linii
są funkcją mocy czynnej i biernej, przesyłanych do odbioru. Oblicza
się je ze wzoru

[11]

:

r

a

n

n

n

P

P

R

U

Q

R

U

P

R

U

S

R

I

P





























2

2

2

2

2

2

2

3

(7.13)

gdzie

R

- rezystancja fazy elementu sieci

S

- moc pozorna płynąca przez element sieci

U

n

- napięcie znamionowe międzyprzewodowe

P

a

- straty mocy czynnej spowodowane przepływem mocy

czynnej

P

r

- straty mocy czynnej spowodowane przepływem mocy

biernej

Przy asymetrycznym obciążeniu linii straty mocy są sumą strat mocy
w poszczególnych przewodach

gdzie

Straty mocy czynnej w obwodzie trójfazowym obciążonym

asymetrycznie





D

r

a

N

L

L

L

P

P

P

R

I

I

I

I

P





























2

2

2

2

2

3

2

1

(7.14)

3

2

1

,

,

L

L

L

I

I

I

- prądy płynące w przewodach fazowych

I

N

- prąd płynący w przewodzie neutralnym

Straty mocy przy asymetrycznym obciążeniu w wyrażone
powyższym wzorem są większe od strat mocy wyrażonych wzorem

(7.13)

przy przesyle symetrycznie obciążoną linią mocy czynnej

równej sumie mocy czynnych przesyłanych w poszczególnych fazach
przy obciążeniu asymetrycznym. Wzrost strat jest spowodowany
przesyłem mocy asymetrii

D

R

U

D

P

D







2

2

P

D

-

straty mocy czynnej spowodowany przesyłem mocy

asymetrii

D

wyrażone wzorami

7.7 ÷ 7.12

(7.15

)

Straty mocy czynnej w obwodzie trójfazowym obciążonym

asymetrycznie

Asymetryczne obciążenie linii powoduje niejednakowe spadki napięć

w poszczególnych fazach, więc napięcia międzyprzewodowe nie
tworzą trójkąta równobocznego, dlatego do obliczeń strat mocy
występujących wg wzorze

(7.15)

za kwadrat napięcia

międzyprzewodowego należy przyjmować średnią wartość
kwadratów napięć międzyprzewodowych wyrażoną wzorem:





2

,

2

,

2

,

2

1

3

3

2

2

1

3

1

L

L

L

L

L

L

U

U

U

U









(7.16)

Dzieląc równanie

(7.15)

przez

(7.13)

i dokonując przekształceń,

można wykazać, że współczynnik wzrostu strat mocy czynnej

P

w

linii obciążonej asymetrycznie w stosunku do strat mocy czynnej przy
obciążeniu symetrycznym wyraża się wzorem:

2

2

2

1

Q

P

D

P









(7.17

)

Straty mocy czynnej w linii obciążonej asymetrycznie są zwiększone
proporcjonalnie do kwadratu mocy asymetrii podzielonego przez
sumę kwadratów mocy czynnej i biernej pobieranej z linii przez odbiór
asymetryczny

Straty mocy czynnej w obwodzie trójfazowym obciążonym

asymetrycznie

Dla znalezienia współczynnika wzrostu

P

strat mocy czynnej przy

obciążeniu asymetrycznym w stosunku do strat przy symetrycznym
obciążeniu linii należy wyrażenia na moc asymetrii

D

(wzory

7.10

,

7.11

i

7.12

) podstawić do wzoru

(7.17)

, oraz uwzględnić, że:

.

9

2

1

2

1

2

2

I

U

Q

P









W efekcie otrzymuje
się:

(7.18

)

 dla asymetrii dowolnej:

























}

{

2

2

2

0

2

0

1

2

1

2

2

2

2

3

1

1

cos

cos

cos

2

1

2

0

0

0

2

2

0

0

2

2

0

0

2

2









































































U

I

I

U

I

U

I

U

I

U

I

U

I

U

n

n

n

n

n

n

n

n

n

n

n

n

n

n

P

;

 dla linii czteroprzewodowej zasilanej symetrycznym napięciem przy

asymetrycznych prądach poszczególnych faz:

 dla linii trójprzewodowej zasilanej symetrycznym napięciem przy

asymetrycznych prądach poszczególnych faz:

2

2

1

I

n

P











2

2

2

3

1

1

0

2

















I

I

n

n

P

;

(7.19

)

(7.20

)

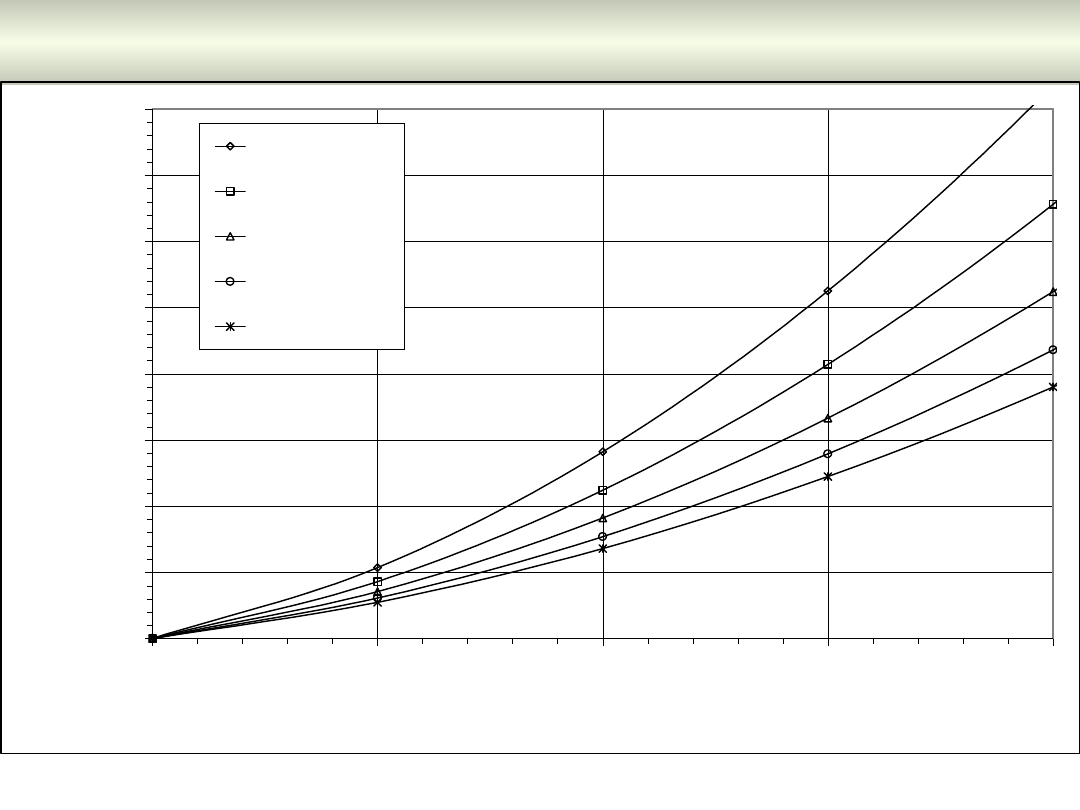
Straty mocy czynnej w obwodzie trójfazowym obciążonym

asymetrycznie

1.0

1.5

2.0

2.5

3.0

3.5

4.0

4.5

5.0

0.0

0.5

1.0

1.5

2.0

Stosunek prądu w przewodzie neutralnym do średniego prądu w przewodach fazowych I

N

/Ī

L

s

N

/s

f

= 0.5

s

N

/s

f

= 0.7

s

N

/s

f

= 1.0

s

N

/s

f

= 1.4

s

N

/s

f

= 1.9

St

os

un

ek

s

tr

at

p

rz

y

ob

ci

ąż

en

iu

n

ie

sy

m

et

ry

cz

ny

m

d

o

st

ra

t

pr

zy

o

bc

ią

że

ni

u

sy

m

et

ry

cz

ny

m





P

as

ym



P

as

ym

/

P

sy

m

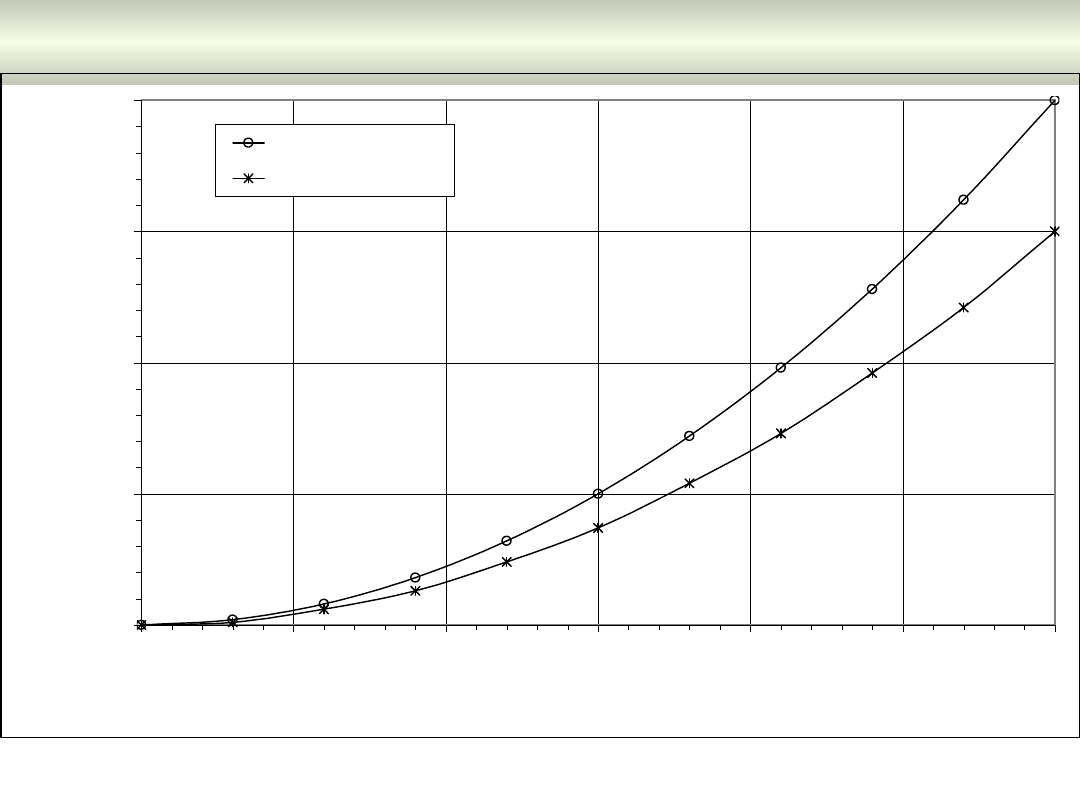
Rys. 7.1. Wpływ asymetrii obciążenia linii niskiego napięcia na wzrost strat

mocy w linii

Straty mocy czynnej w obwodzie trójfazowym obciążonym

asymetrycznie

1.0

1.5

2.0

2.5

3.0

0.0

0.5

1.0

1.5

2.0

2.5

3.0

Układ połączeń Yy0
Układ połączeń Yz5

St

os

un

ek

s

tr

at

p

rz

y

ob

ci

ąż

en

iu

n

ie

sy

m

et

ry

cz

ny

m

d

o

st

ra

t

pr

zy

o

bc

ią

że

ni

u

sy

m

et

ry

cz

ny

m





P

as

ym



P

as

ym

/

P

sy

m

Stosunek prądu w przewodzie neutralnym do średniego prądu w przewodach fazowych

I

N

/Ī

L

Rys. 7.2. Wpływ asymetrii obciążenia na wzrost strat mocy w transformatorze

Straty mocy czynnej w obwodzie trójfazowym obciążonym

asymetrycznie

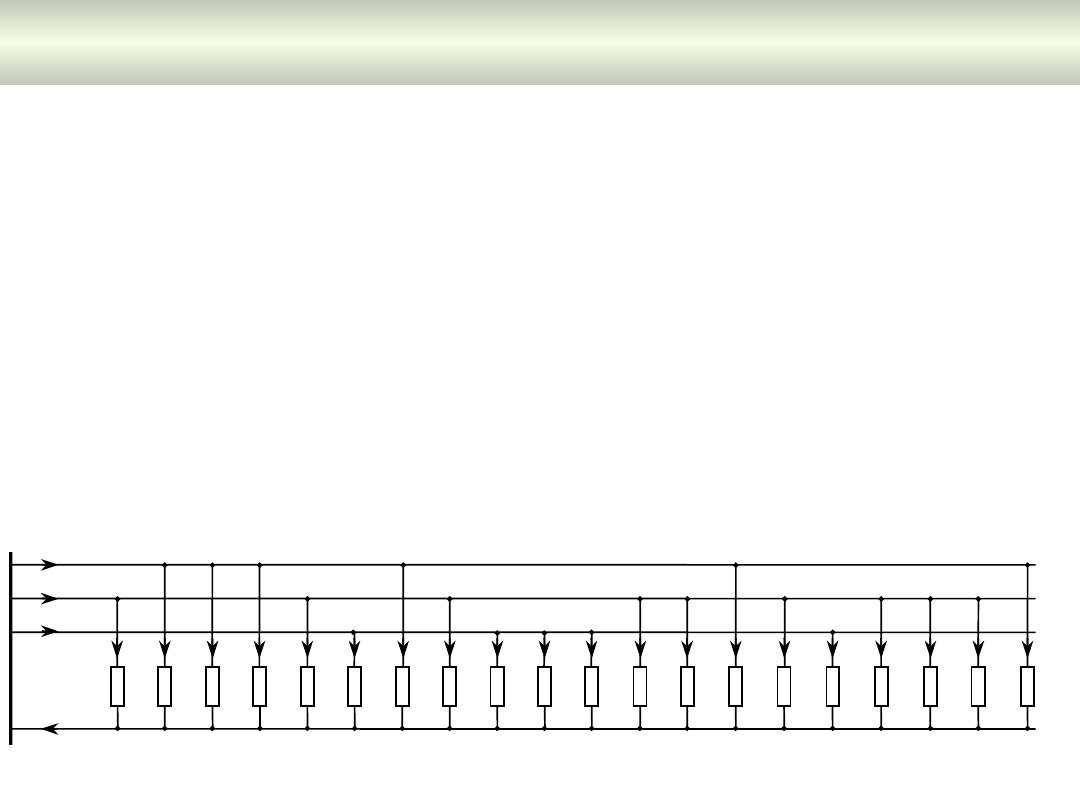
Przykład.
Linia niskiego napięcia o długości 700 m z przewodami aluminiowymi
o przekrojach

3×50+35

mm

2

zasila

20

jednofazowych

odbiorów

rozmieszczonych w równych odstępach. Prądy pobierane przez odbiory w
szczycie obciążenia oraz fazy, z których poszczególne odbiory są zasilane
pokazano na rys. 7.3. Dla uproszczenia przyjęto, że prądy maja tylko
składową czynną. Łącznie odbiory pobierają moc

P

o

= 36.7 kW

. Linia

zasilana jest z transformatora o mocy

S

n

=63

kVA, dla którego znamionowe

obciąże-niowe straty mocy czynnej wynoszą

P

Cu

 = 1.28 kW

. Układ połączeń

uzwojeń trans-formatora Yz5. Spadki napięcia w poszczególnych fazach
wynoszą:

U

R

= 1.4%

,

U

S 

=21.9%

oraz  

U

T 

=-5.8%,

natomiast straty mocy w

linii są równe

P

asym

=3 170 W

(w tym w przewodach fazowych

P

f

=1 970 W

,

w przewodzie neutralnym

P

N

=1 200 W

). Przyjmując czas trwania strat

maksymalnych

 = 2 000

 godz./rok, straty energii w ciągu roku wynoszą

E

asym

 = 6 340 kWh/rok

.

I

T

=
23A

I

R

= 55A

I

S

= 89A

I

N

= 57A

13A

O

1

O

2

O

3

O

7

O

6

O

5

O

4

O

8

O

9

O

10

O

11

O

12

O

13

O

14

O

15

O

16

O

17

O

18

O

19

O

20

8A

13A

4A

8A

3A

11A

11A 4A 4A 3A 9A 3A 8A 10A 4A 12A 13A 15A 11A

Rys. 7.3. Schemat linii niskiego napięcia do przykładu

Straty mocy czynnej w obwodzie trójfazowym obciążonym

asymetrycznie

Straty mocy i energii jakie wystąpiłyby w analizowanym obwodzie przy
obciążeniu symetrycznym zostaną określone dwoma sposobami:

A. Przy założeniu, że wszystkie odbiory są trójfazowe i pobierają z sieci taką

samą moc jak jednofazowe;

B. Na podstawie stosunku prądu w przewodzie neutralnym do średniej

wartości prądów w przewodach fazowych - przy wykorzystaniu wykresu z
rys. 7.1;

Ad A. Stosunek prądu w przewodzie neutralnym do średniej wartości prądów

w przewodach fazowych jest równy:











T

S

R

N

f

N

I

I

I

I

I

I

3

03

.

1

23

89

55

57

3









Z wykresu na rys. 1 wynika, że dla stosunku przekroju przewodu neutralnego
do przekroju przewodu fazowego równego

s

N

/s

f

= 35/50=0.7

stosunek strat

występujących przy obciążeniu asymetrycznym do strat jakie wystąpiłyby
przy obciążeniu symetrycz-nym wynosi

P

asym

 = 2.15

. Oznacza to, że straty

przy obciążeniu symetrycznym byłyby ok.

2.15

razy mniejsze i wyniosłyby

ok.:

P

sym

= P

asym

/P

asym

 = 3 170/2.15 = 1 475 W.

Straty energii byłyby równe:

E

sym

 = P

sym

·



 = 1 475×2 000 = 2 950 kWh/rok.

Straty mocy czynnej w obwodzie trójfazowym obciążonym

asymetrycznie

Spowodowany asymetrią obciążenia wzrost strat energii w ciągu roku wynosi:

E

asym

 = E

asym

 – E

sym

 = 6 340 – 2 950 = 3 390 kWh/rok.

Przy cenie energii równej

C

E

= 0.3 zł/kWh,

koszty dodatkowych strat energii

wyniosą około:

K

Easym

= E

asym

·C

E

= 3 390×0.3 = 1 017 zł/rok.

Ad. C. Straty mocy obliczone przy założeniu, że odbiory przyłączone w
poszczególnych punktach obwodu trójfazowe i pobierają z sieci taką samą
moc jak przyłączone w tych punktach odbiory jednofazowe wynoszą:

P

sym

=

1 410 W.

Straty energii przy tym założeniu były by równe:

E

sym

= P

sym

 ·  = 1 410×2 000 = 2 820 000 Wh = 2 820 kWh.

Spowodowany asymetrią obciążenia wzrost strat energii w ciągu roku wynosi:

E

asym

 = E

asym

 – E

sym

 = 6 340 – 2 820 = 3 520 kWh/rok.

Przy cenie energii równej C

E

= 0.3 zł/kWh, koszty dodatkowych strat energii

wyniosą około:

K

Easym

= E

asym

·C

E

= 3 520×0.3 = 1 056 zł/rok.

Straty mocy czynnej w obwodzie trójfazowym obciążonym

asymetrycznie

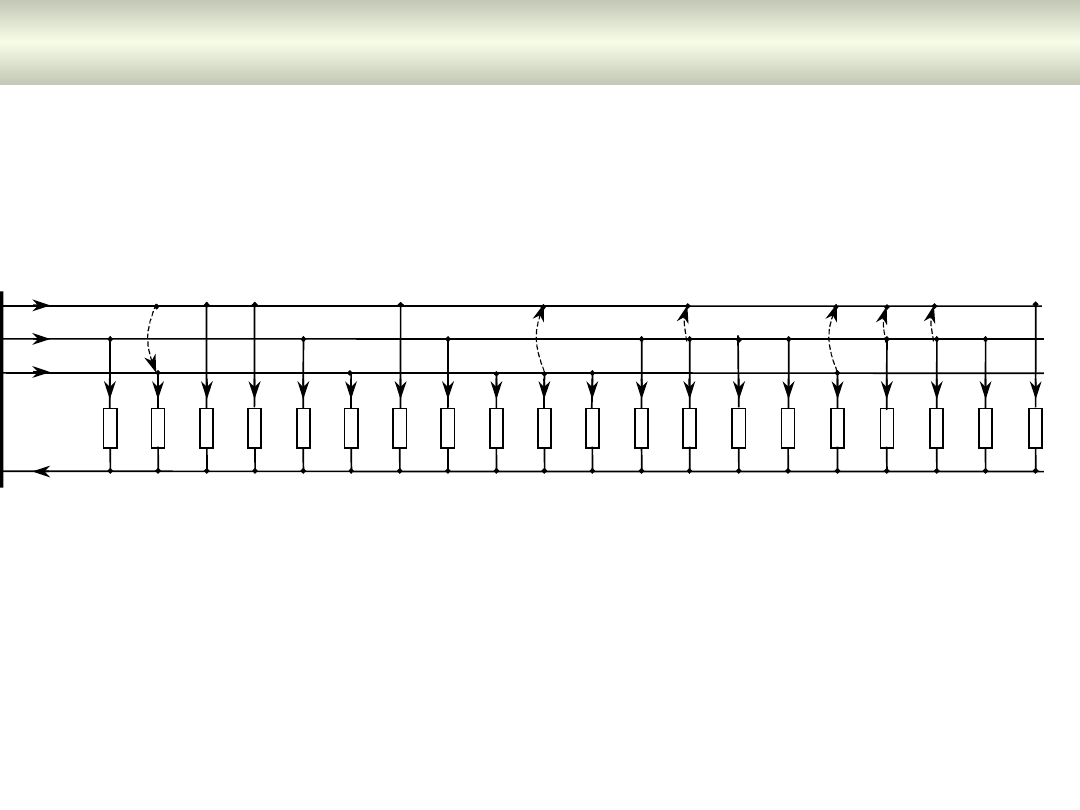
Na podstawie obliczeń symulacyjnych stwierdzono, że przełączenie zasilania
6 odbiorów na inne fazy pozwoliłoby zmniejszyć asymetrię obciążenia
poszczególnych faz tak, że stosunek prądu w przewodzie neutralnym do
średniej wartości prądów w przewodach fazowych zmaleje do wartości

I

N

/Ī

f

=

0.1

. Sposób przełączenia odbiorów pokazano na rys. 7.4 – linie przerywane

zakończone strzałkami wskazują które odbiory i na które fazy należy
przełączyć.

I

T

= 53A

I

R

= 55A

I

S

= 59A

I

N

= 5.3A

13A

O

1

O

2

O

3

O

7

O

6

O

5

O

4

O

8

O

9

O

10

O

11

O

12

O

13

O

14

O

15

O

16

O

17

O

18

O

19

O

20

8A

13A

4A

8A

3A

11A

11A 4A 4A 3A 9A 3A 8A 10A 4A 12A 13A 15A 11A

Rys. 7.4. Sposób przełączenia odbiorów w linii z przykładu

W efekcie przełączenia nastąpi zmniejszenie strat mocy w linii do około:

P = 1 500 W

(w tym w przewodach fazowych

P

f

= 1 440 W

, w przewodzie

neutralnym

P

N

= 60 W

).

Spadki napięcia w poszczególnych fazach zmienią się do wartości:

U

R

= 4.1 V

,

U

S 

= 5.9

V

oraz  

U

T 

= 7.5 V

.

Straty mocy czynnej w obwodzie trójfazowym obciążonym

asymetrycznie

Przy czasie trwania strat maksymalnych

 = 2 000

godz./rok

, straty energii w

ciągu roku po dokonaniu przełączenia odbiorów na inne fazy wyniosłyby:

E

asym

 = 3 000 kWh/rok

.

Zmniejszenie strat wyniosłoby więc:

E = 6 340 – 3 000 = 3 340 kWh/rok

.

Przy przeciętnej cenie energii

C

E

= 0.3

zł/kWh

oszczędność na stratach

energii wyniosłaby:

Z



E

= C

E

·E = 0.3 × 3 340



1002 zł/rok

.

Dzięki przełączeniu 6 odbiorów na inne fazy można zaoszczędzić około

1000

zł

. Jest to równowartość około

5 godzin

pracy ekipy pogotowia

energetycznego. Wykonanie przełączenia odbiorów na inne fazy jest w takim
czasie realne. Zanim przełączenie odbiorów zostanie wykonane, konieczne
jest:
– dokonanie pomiarów obciążeń w dłuższym okresie czasu,
– wykonanie obliczeń i analiz,
– wytypowanie odbiorów, które powinny być przełączone na inne fazy.

Koszty wykonania pomiarów i analiz są trudne do oszacowania i mogą być

Koszty wykonania pomiarów i analiz są trudne do oszacowania i mogą być

wielokrotnie większe niż oszczędność na stratach energii, którą można

wielokrotnie większe niż oszczędność na stratach energii, którą można

osiągnąć w ciągu roku.

osiągnąć w ciągu roku.

Współczynnik mocy w asymetrycznym obwodzie

trójfazowym

W symetrycznym obwodzie trójfazowym współczynnik mocy równy
jest liczbowo cosinusowi kąta przesunięcia fazowego między
napięciami i prądami. Kąty te w każdej fazie są jednakowe.
Współczynnik mocy wyraża się wzorem:

S

P

Q

P

P

k

S

S











2

2

cos

(7.21

)

W asymetrycznym obwodzie trójfazowym prądy, napięcia i
przesunięcia fazowe między prądami a napięciami są różne w
poszczególnych fazach. Dlatego też współczynnik mocy
asymetrycznego obwodu trójfazowego jest różny od współczynnika
mocy symetrycznego obwodu trójfazowego. Wyznaczenie
współczynnika mocy w przypadku odbioru asymetrycznego napotyka
trudności. Można go zdefiniować przez analogię do odbioru
symetrycznego (wzór

7.20

) jako stosunek całkowitej mocy czynnej do

całkowitej mocy pozornej pobieranej przez odbiór:

2

2

2

2

2

2

2

2

1

1

cos

Q

P

D

Q

P

P

D

Q

P

P

k

A

D





















(7.22

)

Współczynnik mocy odbioru asymetrycznego

k

D

można więc wyrazić

jako iloczyn współczynnika mocy odbioru symetrycznego

k

S

oraz

współczynnika nierównomierności obciążenia

k

Dr

.

Współczynnik mocy w asymetrycznym obwodzie

trójfazowym

Współczynnik

k

S

określa wzrost mocy pozornej w stosunku do mocy

czynnej pobieranej przez odbiór spowodowany przesunięciem
fazowym między napięciami a prądami w poszczególnych fazach
symetrycznego odbioru trójfazowego i jest nazywamy
współczynnikiem przesunięcia.

Współczynnik

k

Dr

określa wzrost mocy pozornej w stosunku do mocy

pobieranej przez odbiór na skutek niejednakowego rozdziału obciążeń
na poszczególne fazy odbioru i dlatego jest nazywany
współczynnikiem nierównomierności obciążenia.

Zatem zgodnie ze wzorem (

7.22

) można napisać:

Dr

S

D

k

k

k





(7.23

)

Oczywiście

k

S

 1

oraz

k

Dr

< 1

.

Z powyższego wynika, że

współczynnik mocy przy obciążeniu

asymetrycznym jest mniejszy od jedności, nawet wówczas gdy to
obciążenie ma charakter czysto rezystancyjny

przy czym

2

2

2

1

1

Q

P

D

k

Dr







(7.24

)

Współczynnik mocy w asymetrycznym obwodzie

trójfazowym

Należy zauważyć, że wyrażenie pod pierwiastkiem we wzorze na
wartość współczynnika nierównomierności

k

Dr

, określa wzrost strat

mocy

P

określony zależnością

(7.17)

. Można więc napisać, że:

P

k

Dr





1

(7.25

)

Po podstawieniu do wzoru

(7.25)

zależności na

P

(wzory

7.18 ÷

7.20

) otrzymamy wzory wyrażające współczynnik

k

Dr

w funkcji

współczynników niezrównoważenia napięć i prądów

Spadki napięć w linii trójfazowej czteroprzewodowej

obciążonej asymetrycznie

Obciążenia asymetryczne najczęściej występują w linii trójfazowej
czteroprzewodowej, zasilającej odbiory komunalno-bytowe niskiego
napięcia.

Przy symetrycznym napięciu zasilającym linię

trójfazową

czteroprzewodową obciążoną asymetrycznym odbiorem o
charakterze rezystancyjnym, ogólne wzory na spadek napięcia w
poszczególnych fazach są następujące:





















































































2

1

3

3

3

1

2

2

3

2

1

1

2

1

2

1

2

1

L

L

N

N

L

N

L

L

L

N

N

L

N

L

L

L

N

N

L

N

L

I

I

R

R

R

I

U

I

I

R

R

R

I

U

I

I

R

R

R

I

U

(7.26

)

Największy spadek napięcia wystąpi w fazie najbardziej obciążonej.
Przy szczególnie dużej asymetrii obciążenia spadek napięcia w fazie
najmniej obciążonej może mieć wartość ujemną,

a więc może w tej

fazie wystąpić wzrost napięcia

. Natomiast przy obciążeniu

symetrycznym Spadek napięcia
jest w każdej fazie taki sam i wynosi:

R

I

U







sym

(7.27)

Spadki napięć w linii trójfazowej czteroprzewodowej

obciążonej asymetrycznie

max

I

I

k

pośr

pośr



- współczynnik obciążenia
pośredniego;

Oznaczając , , oraz wprowadzając
oznaczenia:

pośr

I

I

L



2

max

I

I

L



1

min

I

I

L



3

max

min

I

I

k

min



- współczynnik obciążenia
minimalnego,

(7.28

)

wzory na spadki napięcia w poszczególnych fazach można zapisać w
postaci:























































































































pośr

min

max

min

pośr

max

pośr

pośr

k

R

R

R

k

I

U

k

R

R

R

k

I

U

k

k

R

R

R

I

U

N

N

N

N

N

N

1

2

1

1

2

1

2

1

min

min

max

max

(7.29

)

Spadki napięć w linii trójfazowej czteroprzewodowej

obciążonej asymetrycznie

Dla określenia wpływu asymetrii obciążenia na spadki napięcia należy
porównać spadek napięcia przy obciążeniu symetrycznym ze
spadkiem napięcia przy obciążeniu asymetrycznym. Można tu
wyróżnić dwa przypadki:

1. Suma mocy czynnych odbieranych z trzech faz jest taka sama

przy obciążeniu symetrycznym jak przy obciążeniu
asymetrycznym.
Wtedy prąd występujący we wzorze

(7.27)

będzie równy:





min

max

3

1

I

I

I

I









pośr

2. Moc czynna odbierana na końcu linii ulega zmniejszeniu przez

zmniejszenie obciążeń faz

L

2

i

L

3

natomiast obciążenie fazy

L

1

pozostaje bez zmian.
Wtedy prąd występujący we wzorze

(7.27)

będzie równy:

max

I

I 

(7.30)

(7.31)

Dzieląc równanie

(7.29)

przez równanie

(7.27)

i uwzględniając

odpowiednio zależność

(7.30)

lub

(7.31)

otrzymamy współczynniki

U

określające krotność wzrostu fazowych spadków napięcia przy

obciążeniu asymetrycznym
w stosunku do spadków napięcia przy obciążeniu symetrycznym:

Spadki napięć w linii trójfazowej czteroprzewodowej

obciążonej asymetrycznie

w

przypadku

1:

























































 







































 







































 













pośr

min

sym

min

min

pośr

sym

pośr

pośr

pośr

sym

k

R

R

R

R

k

I

I

U

U

U

k

R

R

R

R

k

I

I

U

U

U

k

k

R

R

R

R

I

I

U

U

U

N

N

N

N

N

N

1

2

1

1

2

1

2

1

max

min

max

min

max

max

max

















































 





























 





























 











pośr

min

sym

min

min

pośr

sym

pośr

pośr

pośr

sym

k

R

R

R

R

k

U

U

U

k

R

R

R

R

k

U

U

U

k

k

R

R

R

R

U

U

U

N

N

N

N

N

N

1

2

1

1

2

1

2

1

min

min

max

max

w

przypadku 2:

(7.32

)

(7.33

)

Spadki napięć w linii trójfazowej czteroprzewodowej

obciążonej asymetrycznie

Podane równania mogą być także zastosowane do obliczania
spadków napięcia w czteroprzewodowej linii niskiego napięcia z
asymetrycznie włączonymi odbiorami wzdłuż linii.

Do obliczeń spadków napięć w sieciach prądy wyznaczane są
zwykle na podstawie podanych mocy odbiorów, przy założeniu że w
punktach odbiorów napięcie równe jest napięciu znamionowemu
Fazowy spadek napięcia, wyrażony w procentach w odcinku linii
obciążonym symetrycznie mocą

P

f

w każdej fazie, można obliczyć

ze wzoru:

R

U

P

U

fn

f









2

100

sym%

(7.34

)

W celu wyznaczenia fazowych spadków napięć w linii obciążonej
asymetrycznie należy najpierw obliczyć spadek napięcia przy
założeniu obciążenia symetrycznego, posługując się wzorem

(7.34)

, a

następnie otrzymaną wartość pomnożyć przez współczynniki

U

,

wyrażone przez jeden z zespołów równań

(7.32)

lub

(7.33)

Obliczanie sprowadza się do sumowania w każdej fazie spadków
napięcia
w poszczególnych odcinkach wywołanych prądem obliczonym przy
założeniu, że na początku każdego odcinka napięcia są symetryczne

Spadki napięć w linii trójfazowej czteroprzewodowej

obciążonej asymetrycznie









































min

%

%

min

%

%

max

%

%

max

U

U

U

U

U

U

U

U

U

sym

pośr

sym

pośr

sym

(7.35)

Obliczając spadki napięć często posługujemy się rozpływem mocy, w
takim przypadku współczynniki obciążenia pośredniego

k

pośr

i

obciążenia minimalnego

k

min

określone zależnościami

(7.28),

można

wyrazić w przybliżeniu za pomocą stosunków mocy płynących w
poszczególnych fazach:

max

max

P

P

k

P

P

k

min

min

pośr

pośr

,





(7.36

)

Obliczając współczynniki

U

występujące we wzorach

(7.35)

, należy

we wzorach

(7.32)

lub

(7.33)

podstawić współczynniki obliczone z

zależności

(7.36)

, przyjmując jednocześnie w równaniach

(7.32)

, że:

P

P

I

I

max

max



Otrzyma się wtedy wyrażenia na fazowe spadki napięć w linii
obciążonej asymetrycznie:

Wpływ asymetrii napięcia na pracę silnika

indukcyjnego

Moment napędowy

M

n

silnika asynchronicznego zasilanego

napięciem symetrycznym wywołany jest polem magnetycznym o
strumieniu



wirującym zgodnie z kierunkiem obrotów wirnika

W przypadku napięcia zasilającego asymetrycznego występują dwa
strumienie: zgodny



1

, wirujący w kierunku ruchu obrotowego wirnika

wywołującego moment obrotowy

M

1

, oraz przeciwny



2

, wywołujący

moment

M

2

o kierunku przeciwnym do

M

1

. Użyteczny moment

napędowy silnika będzie więc mniejszy od momentu znamionowego:

M = M

1

-

M

2

(7.37

)

W praktycznie spotykanych wartościach asymetrii napięć
zasilających zmniejszenie momentu napędowego oraz mocy silnika
asynchronicznego jest niewielkie i wynosi kilka procent

Zmianie (zmniejszeniu) ulega także moc silnika asynchronicznego
zasilanego napięciem asymetrycznym w stosunku do mocy silnika
zasilanego napięciem symetrycznym. Sposób postępowania w celu
wyznaczenia dopuszczalnej mocy, którą można obciążyć silnik
zasilany napięciem asymetrycznym, podano
w pracy

[12]

.

12. Kowalski Z.: Asymetria w układach elektroenergetycznych. PWN

Warszawa 1974

Obciążalność transformatora przy obciążeniu

asymetrycznym

Najczęściej przy asymetrycznym obciążeniu trójfazowych elementów
sieci ich obciążalność nie jest w pełni wykorzystana

Dotyczy to gównie obciążalności transformatorów trójfazowych, dla
których dopuszczalne obciążenie wynika zazwyczaj z warunku
nieprzekroczenia wartości prądu znamionowego w najbardziej
obciążonej fazie. W takim przypadku ilość ciepła wydzielającego się w
tej fazie jest taka sama, jak przy znamionowym symetrycznym
obciążeniu. Jednak całkowita ilość ciepła wydzielającego się
w transformatorze jest mniejsza. Istnieje więc możliwość zwiększenia
obciążenia najbardziej obciążonej fazy powyżej prądu znamionowego,
przy niedociążeniu faz pozostałych w ten sposób, aby łączna ilość
ciepła wydzielonego w transformatorze była taka sama jak przy
symetrycznym znamionowym obciążeniu. Zagadnienie to jest
przedstawione w pracach

[11]

i

[12]

11. Kochel M.: Niesymetryczne obciążenia w

miejskich sieciach elektroenergetycznych.
Praca doktorska, Warszawa 1966

Metody ograniczania asymetrii

Ograniczanie asymetrii prądów i napięć w układach
elektroenergetycznych ma za zadanie zmniejszenie niekorzystnych
skutków w pracy sieci i odbiorników, powodowanych
asymetrycznymi obciążeniami

Wyeliminowanie obciążeń asymetrycznych jest niemożliwe, a więc
jedynym sposobem przeciwdziałania ich skutkom jest symetryzacja.

Szereg metod symetryzacji obciążeń asymetrycznych przedstawiono
np. w pracy

[12]

Symetryzację obciążeń jednofazowych przeprowadza się zazwyczaj
stosując układy statyczne sprzężone:

 elektrycznie

- złożone zwykle z elementów pojemnościowych i

indukcyjnych,

 elektromagnetycznie

- złożone z dławików oraz specjalne

transformatorów lub autotransformatorów

Istnieje wiele rodzajów układów symetryzujących, różniących się
sposobem połączenia, liczbą elementów oraz charakterem sprzężenia
między tymi elementami

Symetryzacja obciążeń jednofazowych

Przy wyborze i opracowaniu układów symetryzujących odbiory
jednofazowe należy brać pod uwagę następujące wymagania:

1. Moc elementów symetryzujących powinna być jak najmniejsza.

2. Układ powinien zapewnić uzyskanie możliwie dużej wartości

współczynnika mocy sieci trójfazowej przy wysokim stopniu
skompensowania obciążenia

3. Układ powinien być wykonany ze standardowych elementów

(kondensatory, dławiki)

4. Układ powinien być prosty w konstrukcji i niezawodny

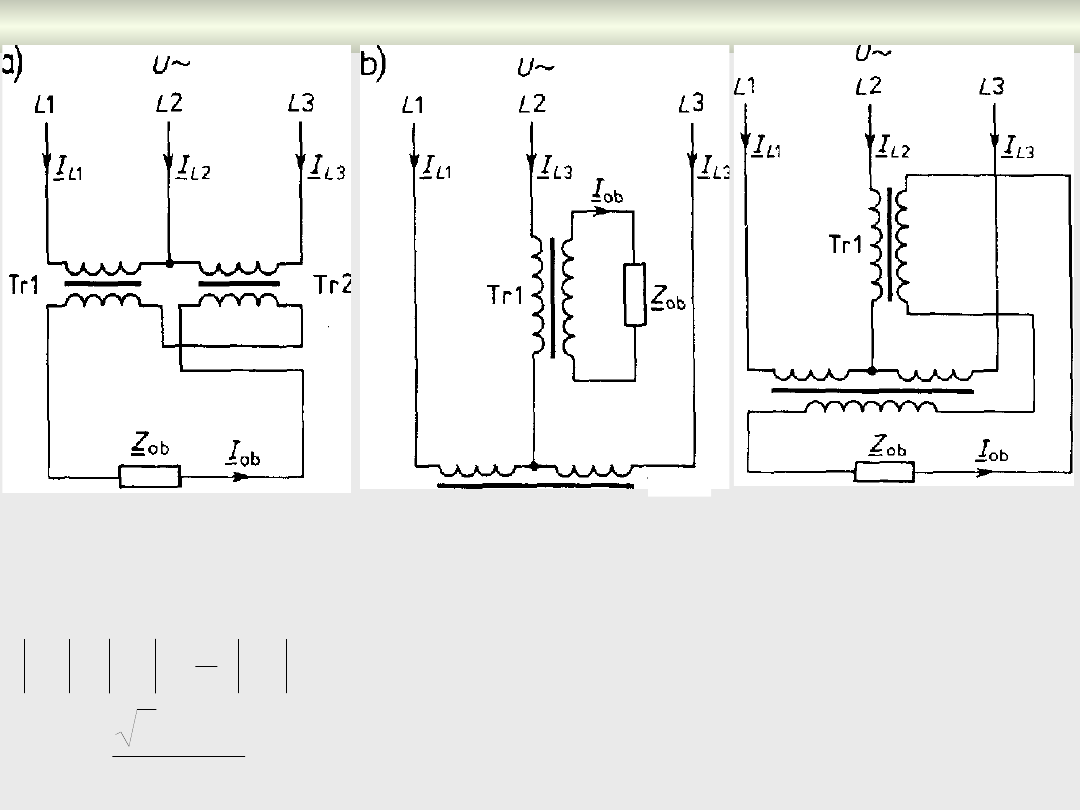
Transformatorowe układy symetryzujące

Tr2

Tr2

c)

Rys. 7.5. Transformatorowe układy symetryzujące do zasilania

odbiorów jednofazowych z sieci trójfazowej: a) układ V, b)
układ T, c) układ L.

W układzie T

(rys. 7.5a)

między prądami fazowymi zachodzi

zależność:

2

3

1

2

1

L

L

L

I

I

I







, a wartość prądu obciążenia jest
równa:

ob

ob

Z

U

I









3

(7.38
)

Transformatorowe układy symetryzujące

W układzie

V

(rys. 7.5a)

oraz

T

(rys. 7.5b)

między prądami

fazowymi zachodzi związek:

2

3

1

2

1

L

L

L

I

I

I







, a wartość prądu obciążenia jest
równa:

ob

ob

Z

U

I









3

gdzi
e



- przekładnia transformatorów

Tr1

i

Tr2

U

- napięcie międzyprzewodowe po stronie

pierwotnej

W układzie

V

:

W układzie

T

(

Scotta):

ob

ob

Z

U

I











2

3

1

gdzi
e



1

- przekładnia transformatora

Tr1

(przekładnia transformatora

Tr2:



2

= 1

)

(7.39

)

(7.40)

Układy symetryzujące jednofazowe

W innym rozwiązaniu układu Scotta

(rys. 7.5c)

przekładnie uzwojeń

transformatorów Tr1 i Tr2 dobiera się tak aby napięcia ich stron
wtórnych były jednakowe, tj.:

2

1

3

2









Między prądami fazowymi w tym układzie zachodzi związek:

2

3

1

38

.

1

L

L

L

I

I

I







Prąd obciążenia w tym układzie
wynosi:

ob

ob

Z

U

I











2

6

1

Istnieje wiele rozwiązań będących modyfikacjami układów z rys.
7.5

Najbardziej rozpowszechniony jest jednak układ Steinmetza (rys.
7.6)

Sumaryczna moc elementów symetryzujących

L

i

C

jest równa

1.16·P

ob

, (mocą czynnej obciążenia). Układ ten umożliwia uzyskanie

właściwych efektów jedynie przy symetryzacji obciążenia o
charakterze rezystancyjnym

(7.41

)

(7.43
)

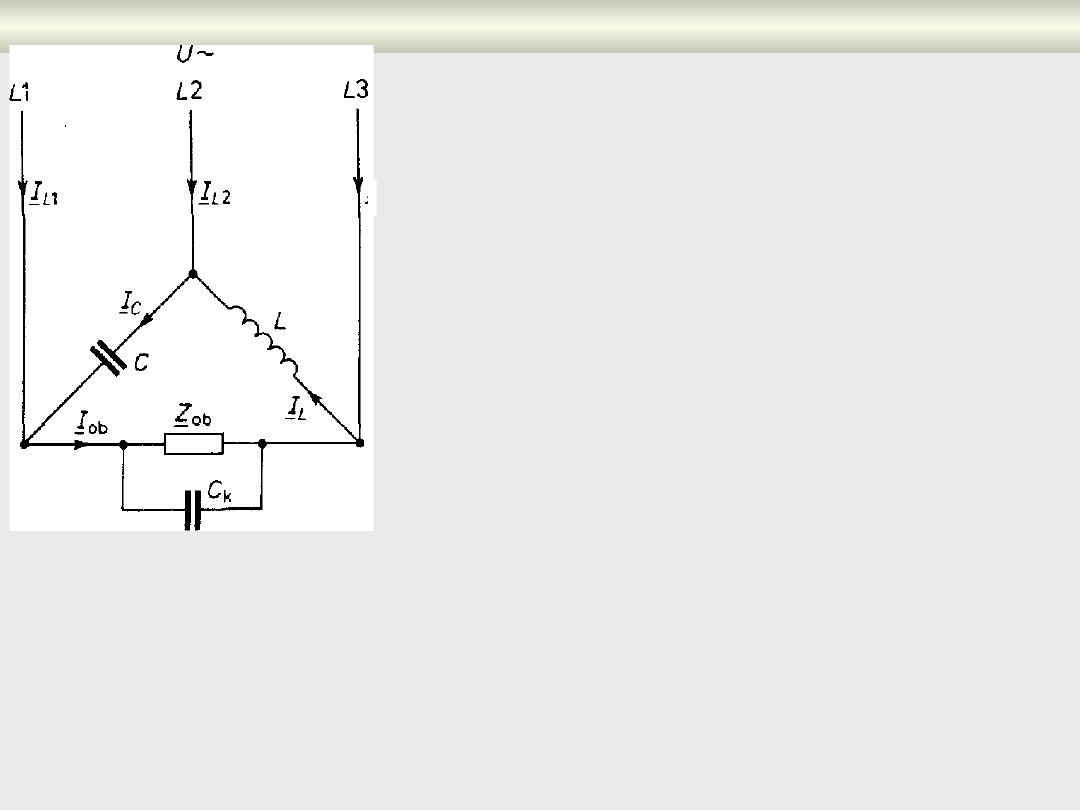
Układy symetryzujące jednofazowy Steinmetza

W przypadku gdy obciążenie ma charakter
indukcyjny, w układzie Steinmetza należy
skompensować współczynnik mocy
odbiornika

Z

ob

do wartości równej jedności przez
zastosowanie kondensatora

C

k

, co

powoduje wzrost strat mocy przeznaczonej
na symetryzację sieci trójfazowej.

I

L2

Rys. 7.6. Układ
Steinmetza

Układ Steinmetza umożliwia także
symetryzację jednofazowego obciążenia
rezystancyjno-indukcyjnego
nieskompensowanego, jednak powoduje to
znaczne zmniejszenie wartości
współczynnika mocy w sieci trójfazowej

Układ z sekcjonowanymi uzwojeniami dławika (rys. 7.7) umożliwia
symetryzację obciążeń rezystancyjno-indukcyjnych.

Współczynnik sprzężenia indukcyjne

M

, między sekcjami dławika

powinien być zbliżony do jedności

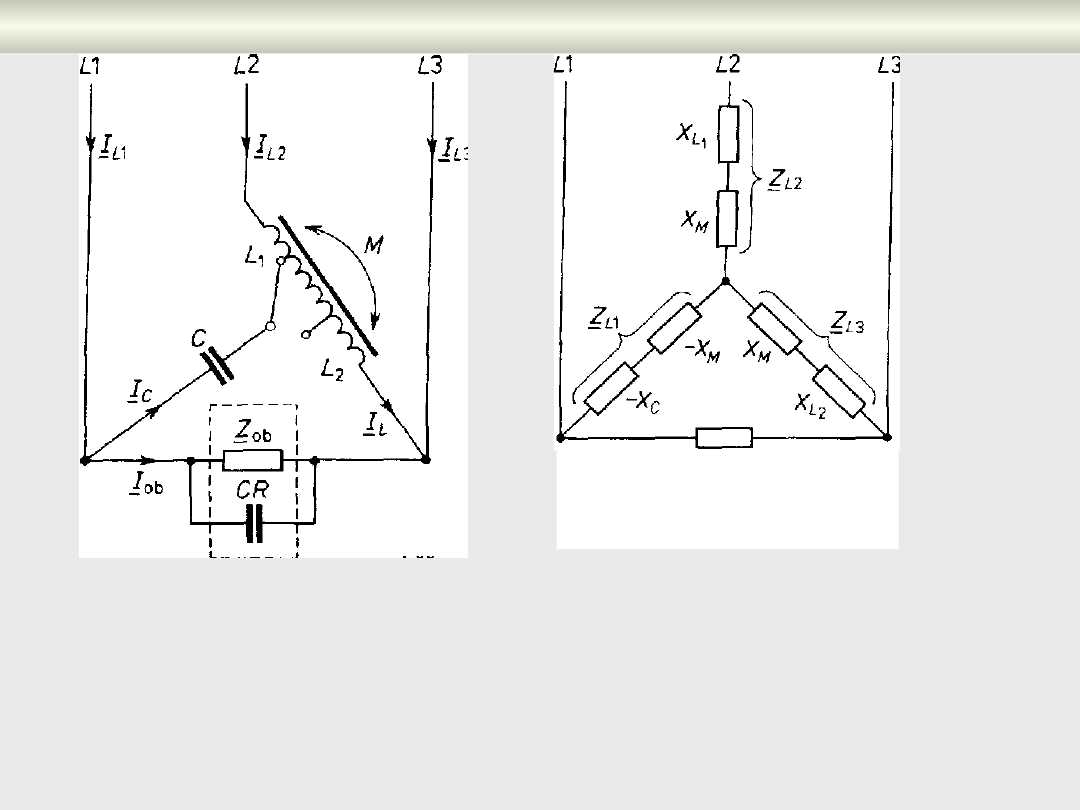
Odbiory mocy biernej

W czasie symetryzacji rezystancyjno-indukcyjnego odbiornika każdej
wartości kąta fazowego



ob

, obciążenia odpowiada dołączenie

kondensatora

C

do jednego z odczepów dławika. Występuje tu

problem określenia takiej wartości kąta



ob

, przy którym suma strat

mocy przeznaczonej na kompensację
i symetryzację obciążenia będzie najmniejsza.

R

ob

·cos



ob

R

ob

·cos



ob

Rys. 7.7. Schemat układu symetryzującego z sekcjonowanymi
uzwojeniami

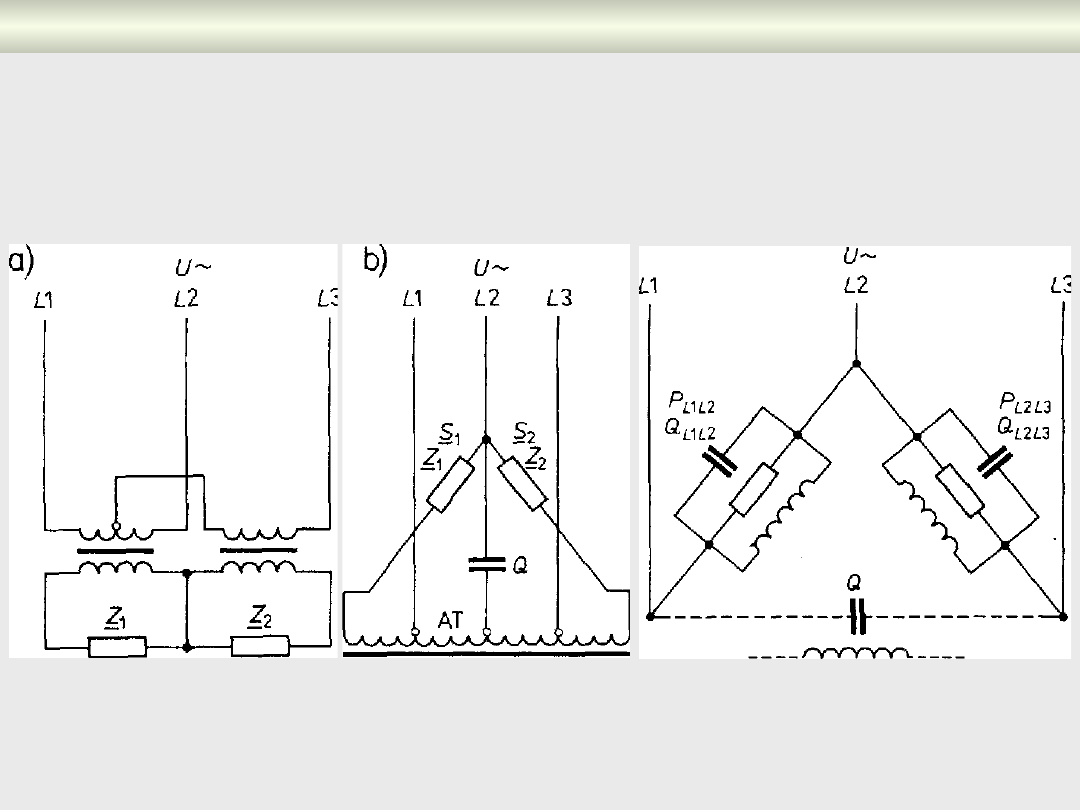
Symetryzacja obciążeń dwufazowych

Wybór układu symetryzującego

obciążeń

dwufazowych zależy od

charakteru obciążenia

Do symetryzacji odbiornika dwufazowego o jednakowym obciążeniu
obu faz stosuje się

trójfazowo-dwufazowe

transformatory Scotta

Rrys. 7.8. Schematy układów symetryzacji obciążenia dwufazowego:

a) układ Scotta, b) układ z kondensatorem i
autotransformatorem, c) układ dostrajalny

c)

Symetryzacja obciążeń dwufazowych

Układ pozwala na jednakowe rozłożenie obciążenia pomiędzy trzy
fazy sieci
z zachowaniem wartości współczynnika mocy równej jedności.

Do symetryzacji odbiorników dwufazowych, mających charakter
indukcyjny, najkorzystniejsze jest stosowanie układu dostrajalnego

(rys. 7.8c)

Oryginalne rozwiązanie stanowi układ z autotransformatorem, w
którym obciążenia są włączone w taki sposób, aby prądy kolejności
przeciwnej każdego z nich wzajemnie się kompensowały co pozwala
na zmniejszenie całkowitej mocy elementów symetryzujących w
stosunku do układu indywidualnej symetryzacji każdego z obciążeń.

Podsumowanie

1. Asymetria obciążenia linii niskiego napięcia może prowadzić do

znacznego wzrostu strat energii (głównie w liniach) oraz asymetrii napięć
w tej sieci.

2. W efekcie działań zmniejszających asymetrię można osiągnąć pewne,

niezbyt duże, oszczędności wynikające ze zmniejszenia strat energii.

3. Całkowite koszty dokonania przełączeń odbiorów na inne fazy w celu

zmniejszenia asymetrii są trudne do oszacowania ze względu na:



losowo zmieniający się w czasie rozkład obciążenia na poszczególne fazy,
oraz



brak informacji o tym, z których faz zasilane są instalacje jednofazowe u
odbiorców posiadających trójfazowe przyłącza (ustalenie, z których faz
zasilani są odbiorcy z przyłączami jednofazowymi jest stosunkowo
proste).

4. W przypadku stwierdzenia znacznej asymetrii obciążenia poszczególnych

faz w trakcie wykonywanych okresowo pomiarów (np. gdy stosunek prądu
w przewodzie neutral-nym do średniej wartości prądów w przewodach
fazowych

I

N

/I

f

> 1

) należałoby wykonać dokładniejsze pomiary obciążeń z

zastosowaniem przyrządów rejestrujących dla stwierdzenia rzeczywistej
skali problemu.

5. Zwiększenie przekroju przewodu neutralnego może również wpłynąć na

zmniejszenie strat.

Ze względu na koszty, działanie to powinno być

podejmowane już na etapie projektowania linii i powinno być poprzedzone
dokładną analizą techniczno-ekonomiczną.