Wstęp do Informatyki

Wykład 3

Cyfrowe układy logiczne

Autor: Dr hab. Marek J. Greniewski

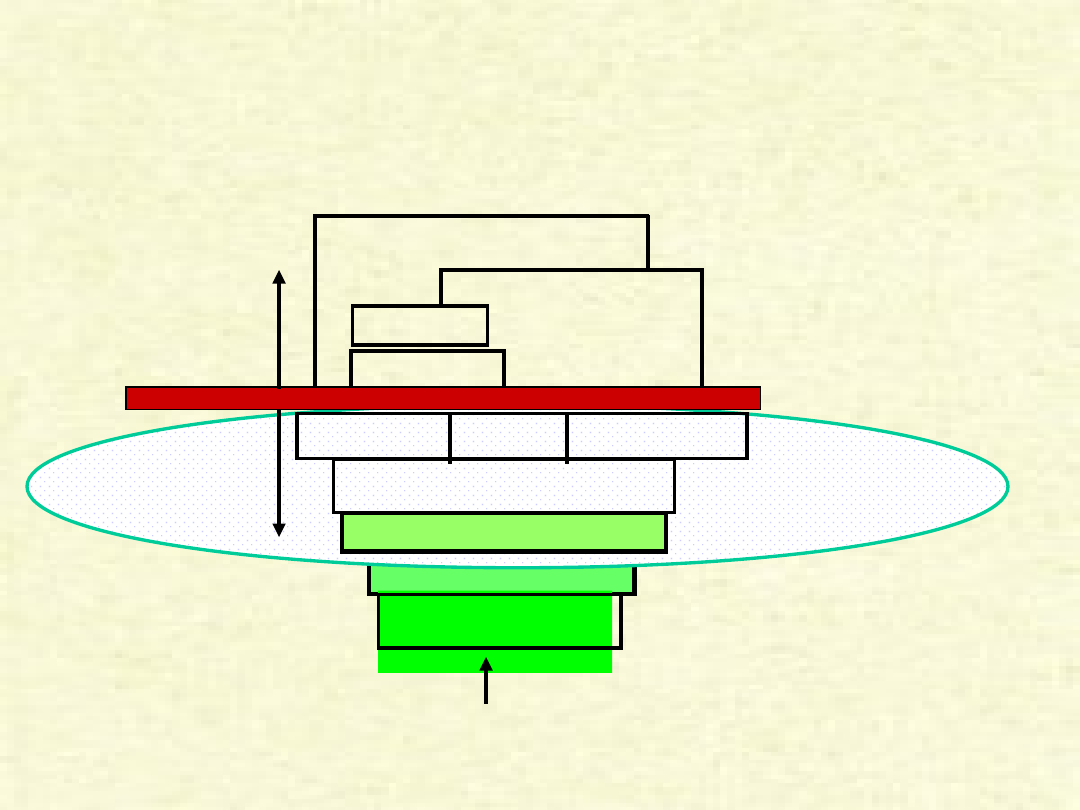
Podział na części architektoniczną i

układową współczesnego komputera

Układy we-wy

Procesor

Kompilator

System

operacyjny

(Windows 2K)

Aplikacje (np. Netscape)

Układy cyfrowe

Obwody

scalone

Lista rozkazów

określająca architekturę

Ścieżki danych i sterowanie

Bramki i

elementy

pamięci

Pamięć

Hardware

Software

Assemble
r

Cyfrowe układy logiczne

.

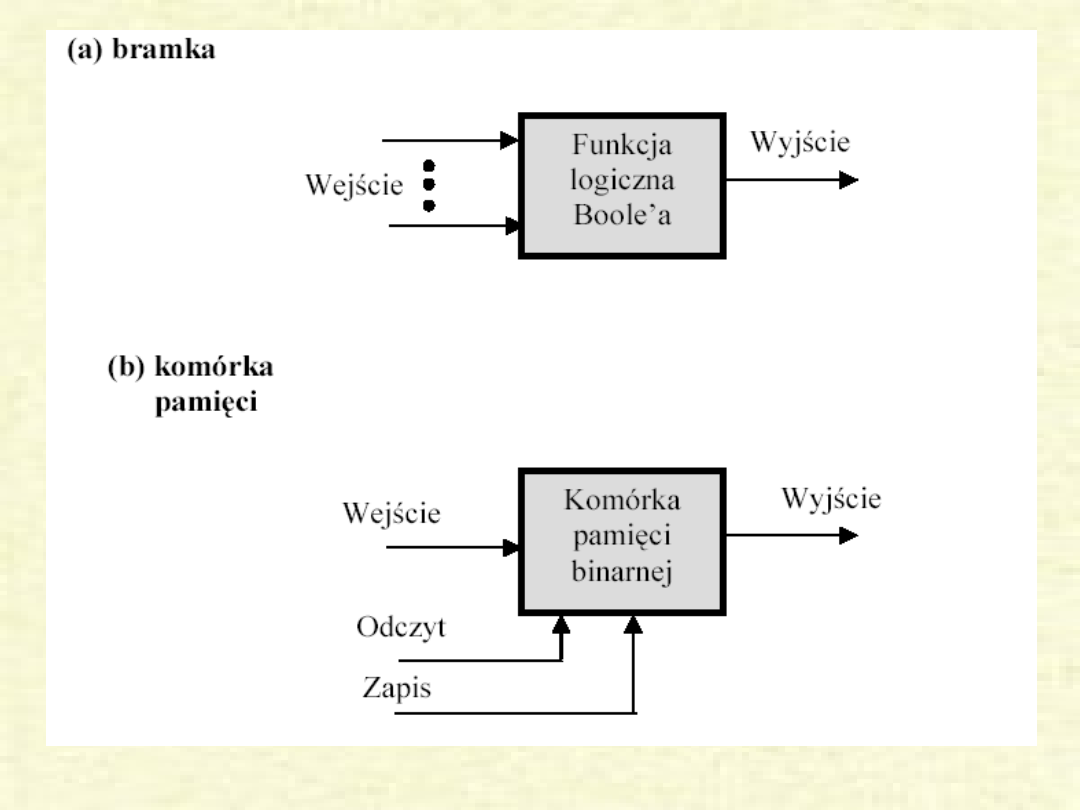
Elementy podstawowe

• Do realizacji funkcji przechowywania, przenoszenia,

przetwarzania i sterowania komputera potrzebne

są tylko

dwa typy elementów podstawowych:

– bramki
– komórki pamięci

.

• Bramka jest przyrządem, który realizuje prostą

funkcję logiczną, taką jak, AND, OR, NOT, NOR,

NAND

• Komórka pamięci jest przyrządem, który może

przechowywać pojedynczy bit danych - oznacza to,

że przyrząd ten w określonym czasie może

znajdować się w jednym z dwóch stabilnych stanów

2. Bramka AND (i) - iloczyn logiczny

3. Bramka OR (lub) - suma logiczna

4. Bramka NOT (nie) - negacja

5. Bramka NAND - negacja iloczynu

6. Bramka NOR - negacja sumy

7. Bramka XOR - równoważność

8. Bramka XNOR - nierównoważność

PODSTAWOWE BRAMKI LOGICZNE

9. BUFOR

1. Co to jest bramka?

• Kombinacyjne układy cyfrowe najczęściej

budowane są za pomocą tzw. bramek.

• Bramką (

gate

) nazywa się układ elektroniczny

realizujący funkcję boolowską, posiadający
określoną liczbę wejść i jedno wyjście.

• Jak każdy układ elektroniczny, tak i bramki

opisywane są wieloma parametrami zarówno
funkcjonalnymi (liczba wejść, liczba wyjść,
realizowana funkcja, przeznaczenie i in.), jak i
elektrycznymi (pobierana moc zasilania,
obciążalność prądem układów sterujących
wejściami, możliwość wysterowania wejść
innych układów itp.) oraz dynamicznymi
(czasy zmiany sygnału na wyjściu układu,
wnoszone opóźnienia i inne).

Co to jest BRAMKA?

(początek)

• Bramki produkowane są jako układy

scalone.

• Do produkcji układów scalonych były i są

stosowane różne technologie.

• Pierwsza z nich to technologia TTL

(

transistor-transistor

logic

),

jedną

z

następnych CMOS (

complementary MOS

).

W jednym układzie scalonym znajdowało

się początkowo kilka bramek.

• Przykładowo w jednym układzie scalonym

znajdowały się 4 bramki dwuwejściowe lub

trzy bramki trzy-wejściowe, lub dwie

bramki czterowejściowe, lub jedna bramka

ośmiowejściowa.

• Natomiast współczesne obwody scalone

wielkiej skali integracji - VLSI (czyli

Very

Large Scale Integration

) zawierają już

miliony bramek.

Co to jest BRAMKA?

(kontynuacja)

• Bramki AND, OR, NAND i NOR mogą

występować jako wielowejściowe.

• Bramki sumy modulo 2 XOR występują tylko jako

dwuwejściowe.

• Bramka NOT jest jednowejściowa.
• Spotyka się także bramki w wykonaniu

specjalnym. Mogą to być tzw. bramki z otwartym
kolektorem (

open collector

) - OC stosowane

celem uzyskania możliwości zwierania wyjść
bramek lub bramki trzystanowe (

three-state

logic

) wykorzystywane np. w magistralach

(szynach) komputera.

Co to jest BRAMKA?

(zakończenie)

BRAMKA

„AND”

Bramka AND realizuje iloczyn logiczny. Jeżeli na jej wejściach podane są jedynki
to na wyjściu jest jedynka, w każdym innym przypadku na wyjściu jest zero.

A

B

Y

Y=A•B

A

B

Y

1

0

1

0

1

0

Tablica zero-

jedynkowa

Y=A•B

A

B

Y

0

0

0

0

1

0

1

0

0

1

1

1

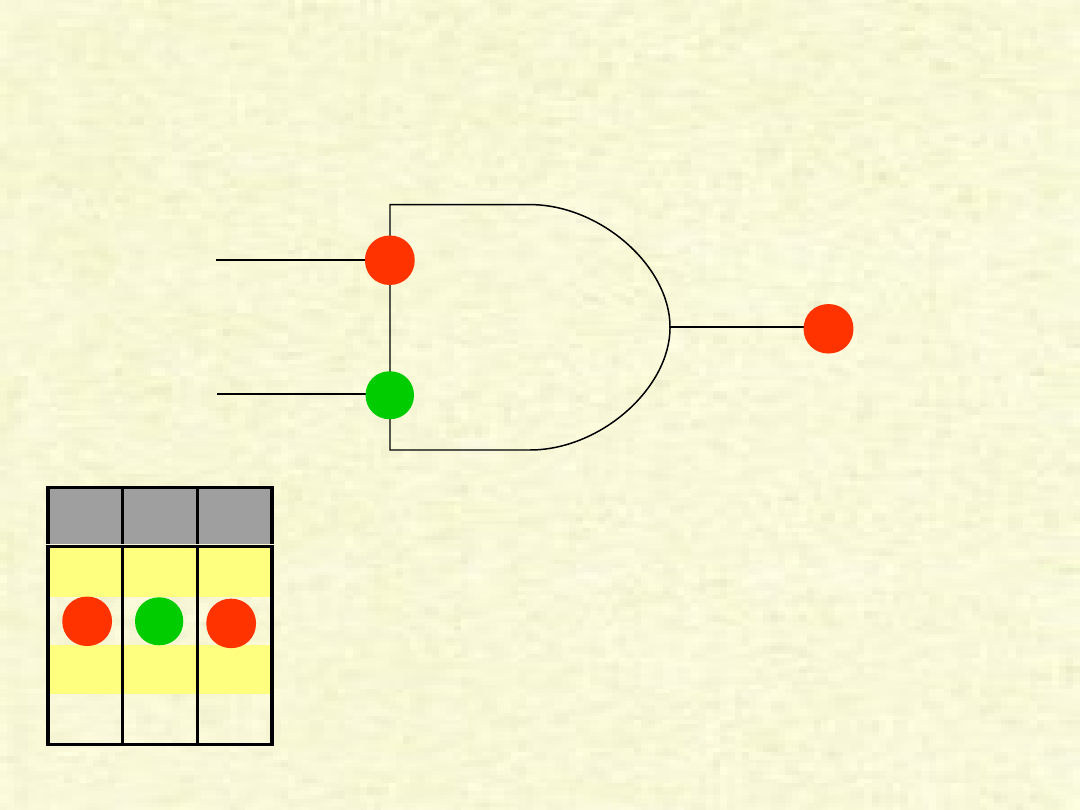
PRZYKŁAD BRAMKI „AND”

0



1

=

0

Przykład pokazuje przypadek, w którym na
wejścia (AB) zostały podane sygnały zero i jeden,
w wyniku czego na wyjściu (Y) otrzymujemy zero.

A

B

Y = A • B

0

1

0

A

B

Y

0

0

0

0

1

0

1

0

0

1

1

1

0

1

0

BRAMKA

„OR”

Bramka OR realizuje sumę logiczną. Jeżeli przynajmniej na jednym wejściu
podana jest jedynka, to na wyjściu (Y) jest jedynka.

A

B

Y

Y=A+B

Y=A+B

Tablica zero-

jedynkowa

A

B

Y

0

0

0

0

1

1

1

0

1

1

1

1

A

B

Y

1

0

1

0

1

0

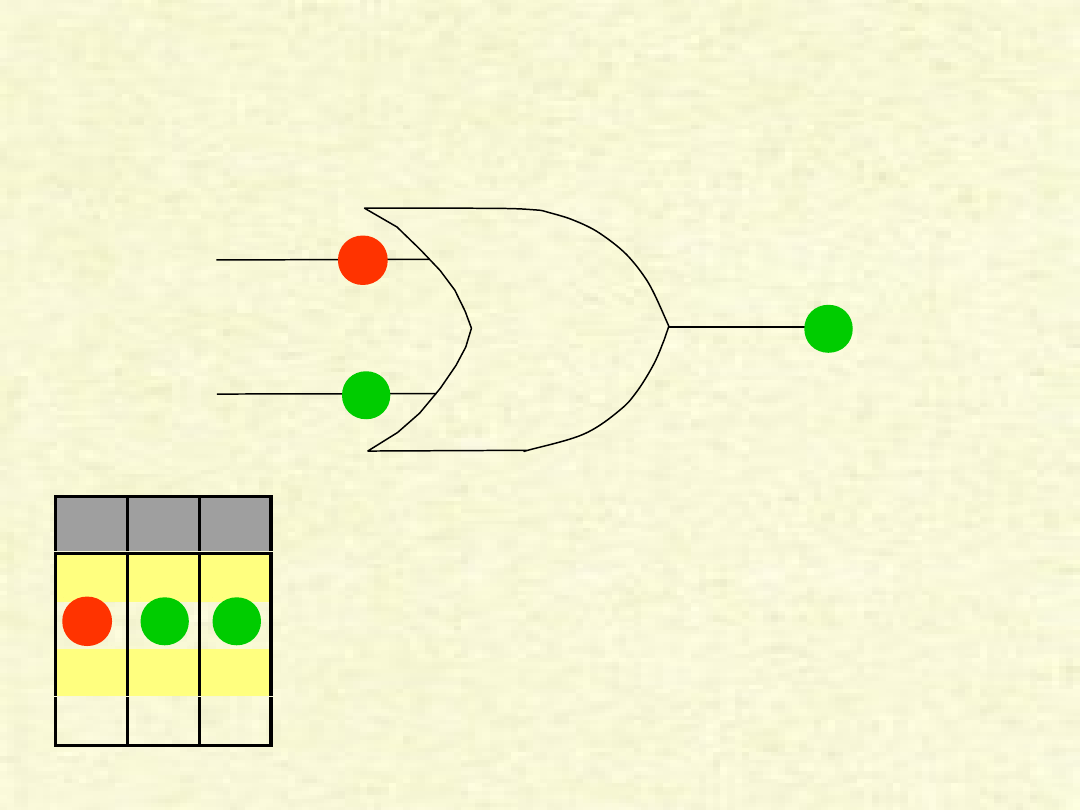
PRZYKŁAD BRAMKI „OR”

0

+

1

=

1

Przykład pokazuje przypadek, w którym
na wejścia (AB) zostały podane sygnały
zero i jeden,w wyniku czego na wyjściu
(Y) otrzymujemy jedynkę.

A

B

0

1

1

Y = A + B

A

B

Y

0

0

0

0

1

1

1

0

1

1

1

1

0

1

1

BRAMKA

„NOT”

A

Y

Y=A

Bramka NOT realizuje operację zaprzeczenia. Jeżeli na wejściu podana jest
jedynka, to na wyjściu (Y) będzie zero i odwrotnie.

Y=A

A

Y

0

1

1

0

Tablica zero-

jedynkowa

A

Y

1

0

1

0

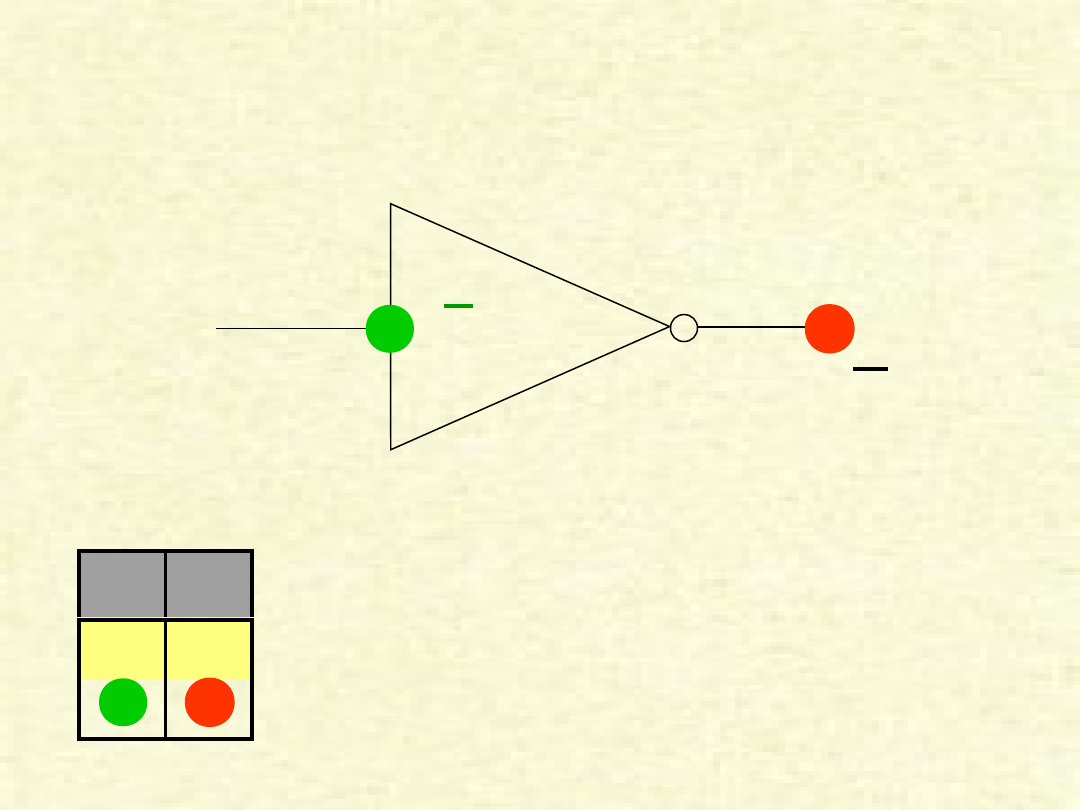
PRZYKŁAD BRAMKI „NOT”

1

Przykład pokazuje przypadek, w którym na
wejście (A) podana została jedynka, w wyniku
czego na wyjściu (Y) otrzymujemy zero.

A

1

=

0

0

Y = A

A

Y

0

1

1

0

0

1

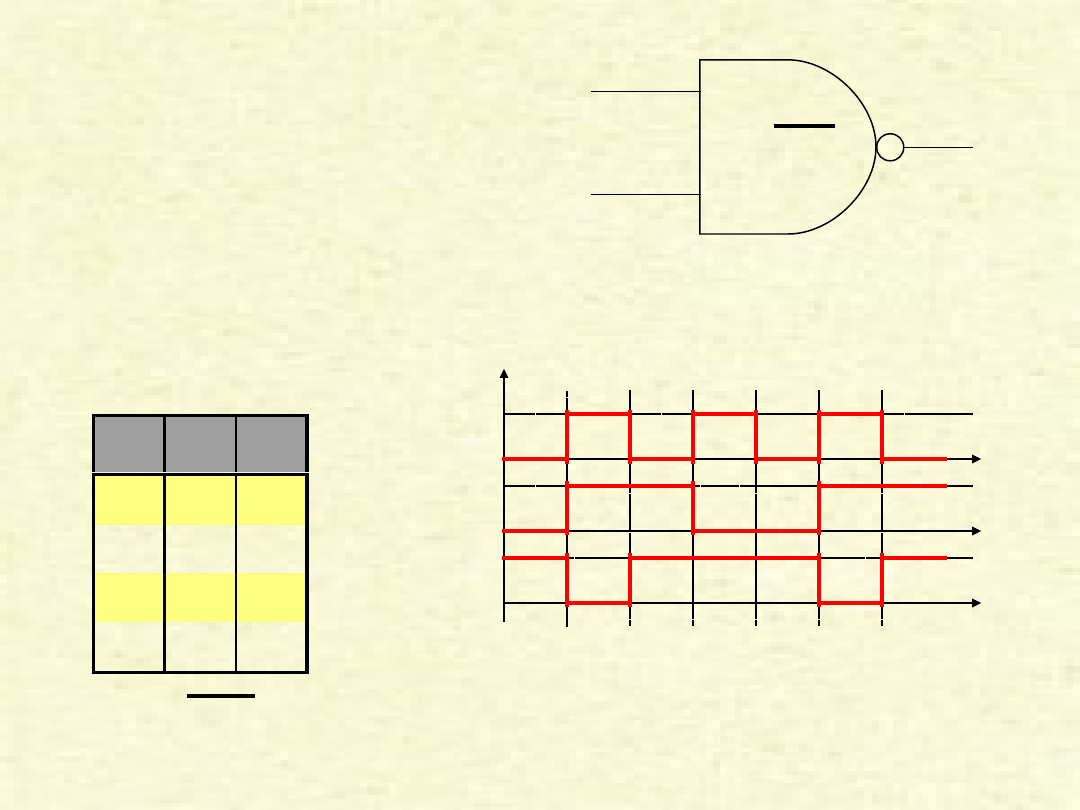
BRAMKA

„

NAND”

Bramka NAND jest złożona z bramek NOT i AND. Zasada działania jest taka sama
jak bramki AND z tą różnicą, że sygnał wyjściowy jest jeszcze negowany.

A

B

Y

Y=A•B

A

B

Y

1

0

1

0

1

0

Y=A•B

Tablica zero-

jedynkowa

A

B

Y

0

0

1

0

1

1

1

0

1

1

1

0

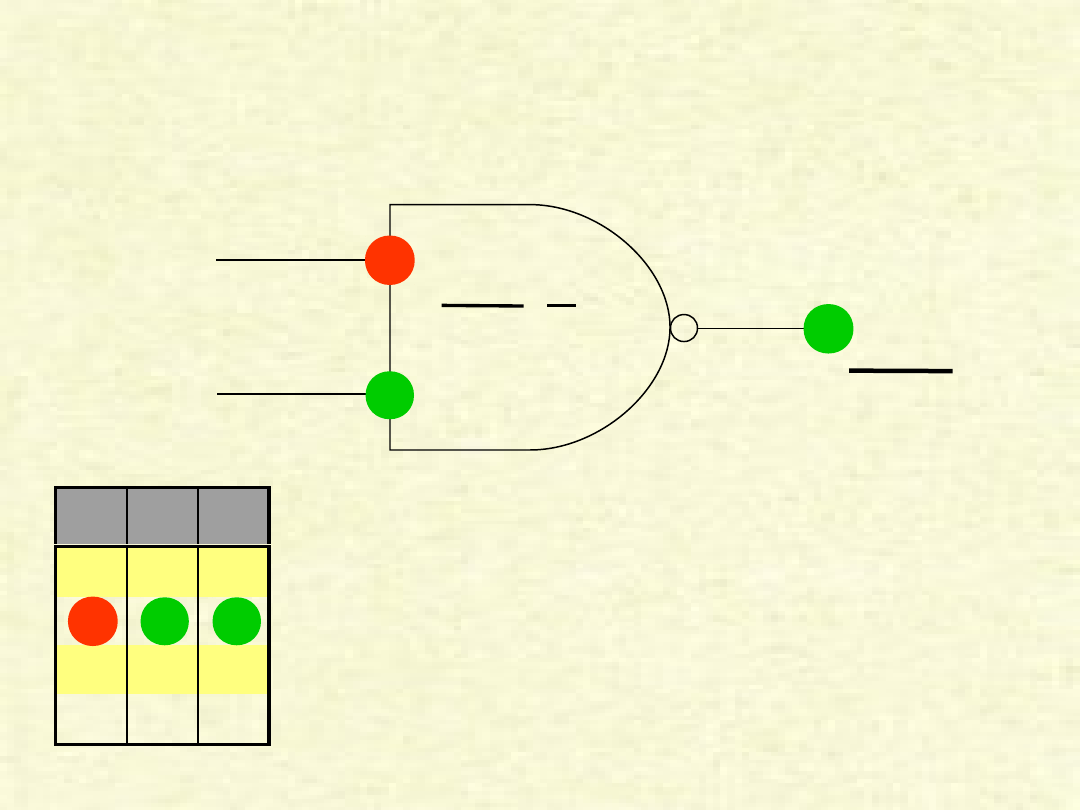
PRZYKŁAD BRAMKI „NAND”

Przykład pokazuje przypadek, w którym na
wejścia (AB) zostały podane sygnały zero
i jeden, w wyniku czego na wyjściu (Y)
otrzymujemy negację zera, czyli jedynkę.

A

B

0

1

1

0



1

=

0

=

1

Y = A • B

A

B

Y

0

0

1

0

1

1

1

0

1

1

1

0

0

1

1

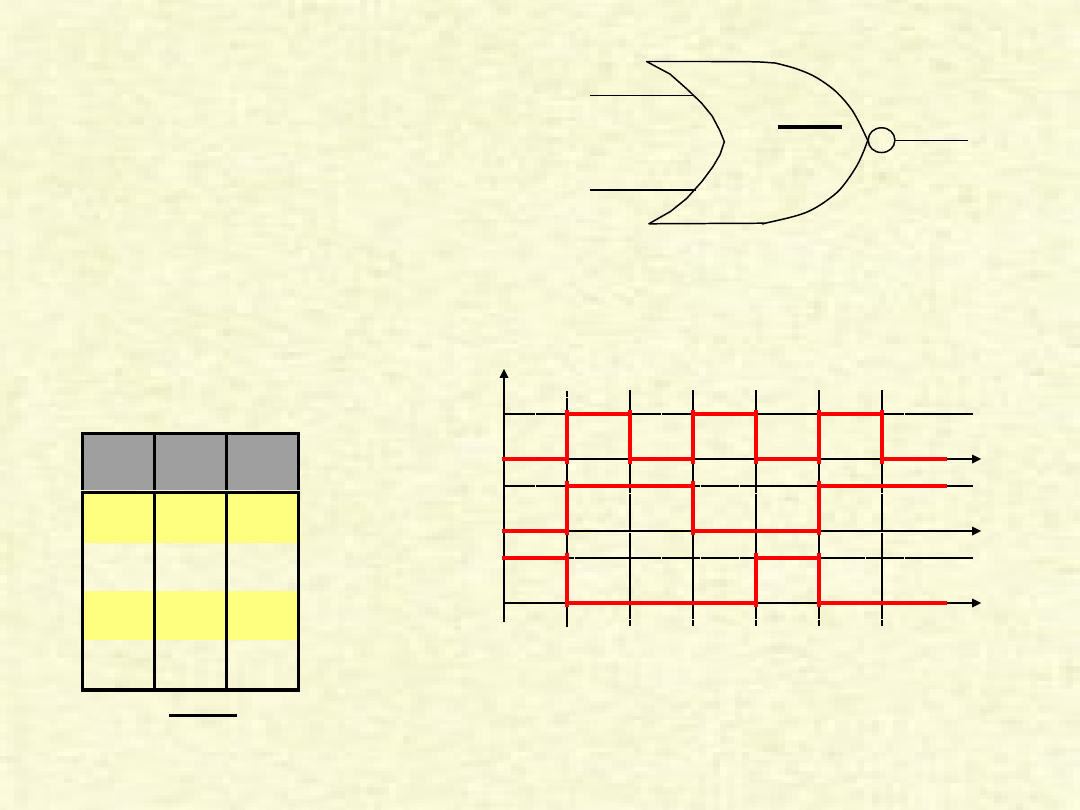
BRAMKA

„NOR”

Bramka NOR jest złożona z bramek: NOT i OR. Zasada działania jest taka sama jak
bramki OR z tą różnicą, że sygnał wyjściowy jest jeszcze negowany.

A

B

Y

Y=A+B

A

B

Y

1

0

1

0

1

0

Y=A+B

Tablica zero-

jedynkowa

A

B

Y

0

0

1

0

1

0

1

0

0

1

1

0

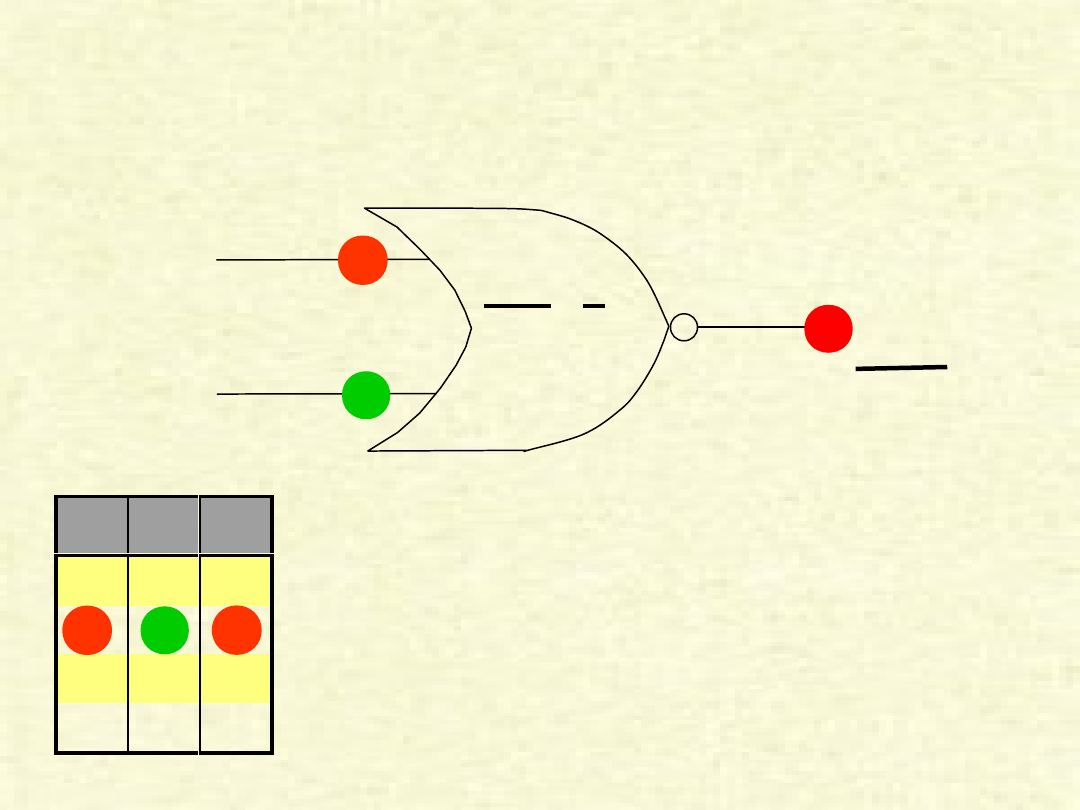
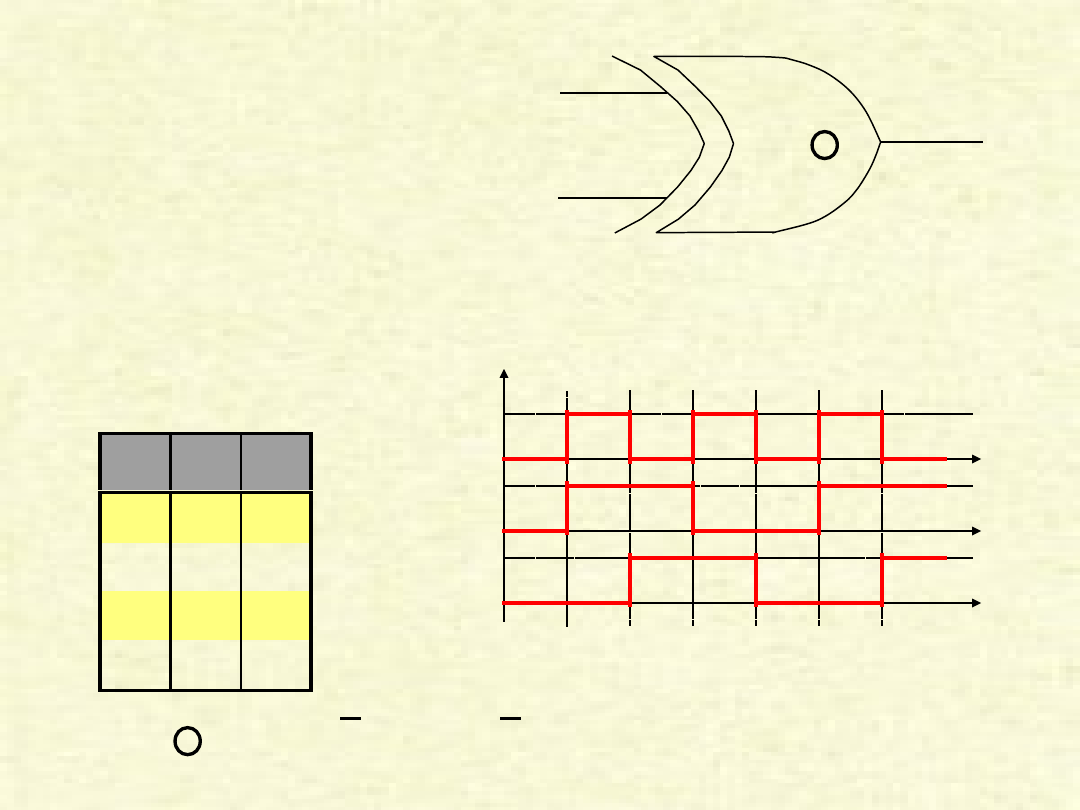
PRZYKŁAD BRAMKI „NOR”

Przykład pokazuje przypadek, w którym na wejścia
(AB) zostały podane sygnały zero i jeden, w wyniku
czego na wyjściu (Y) otrzymujemy jedynkę.

A

B

Y = A + B

0

+

1

=

1

=

0

0

1

0

A

B

Y

0

0

1

0

1

0

1

0

0

1

1

0

0

1

0

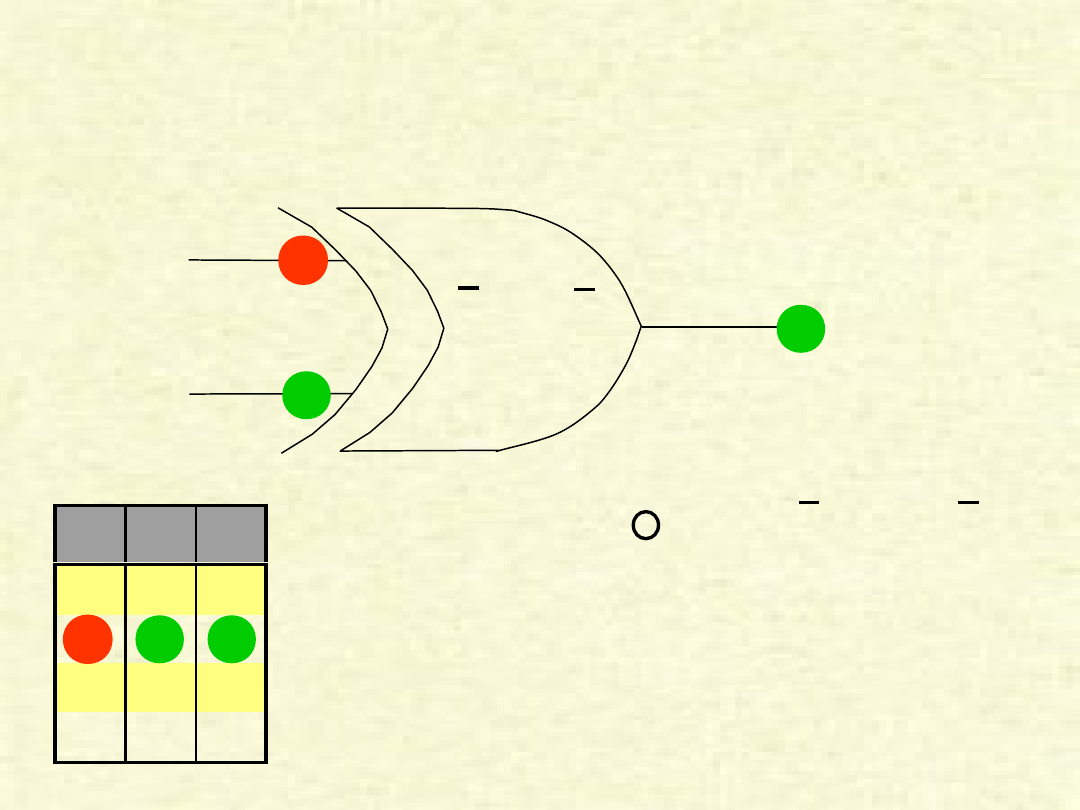
BRAMKA

„

XOR”

Jeżeli sygnały wejściowe są sobie równe (A=B=0 lub A=B=1),
to na wyjściu (Y) jest zero.

A

B

Y

Y=A + B

A

B

Y

1

0

1

0

1

0

Y=A + B



Y=A•B + A•B

Tablica zero-

jedynkowa

A

B

Y

0

0

0

0

1

1

1

0

1

1

1

0

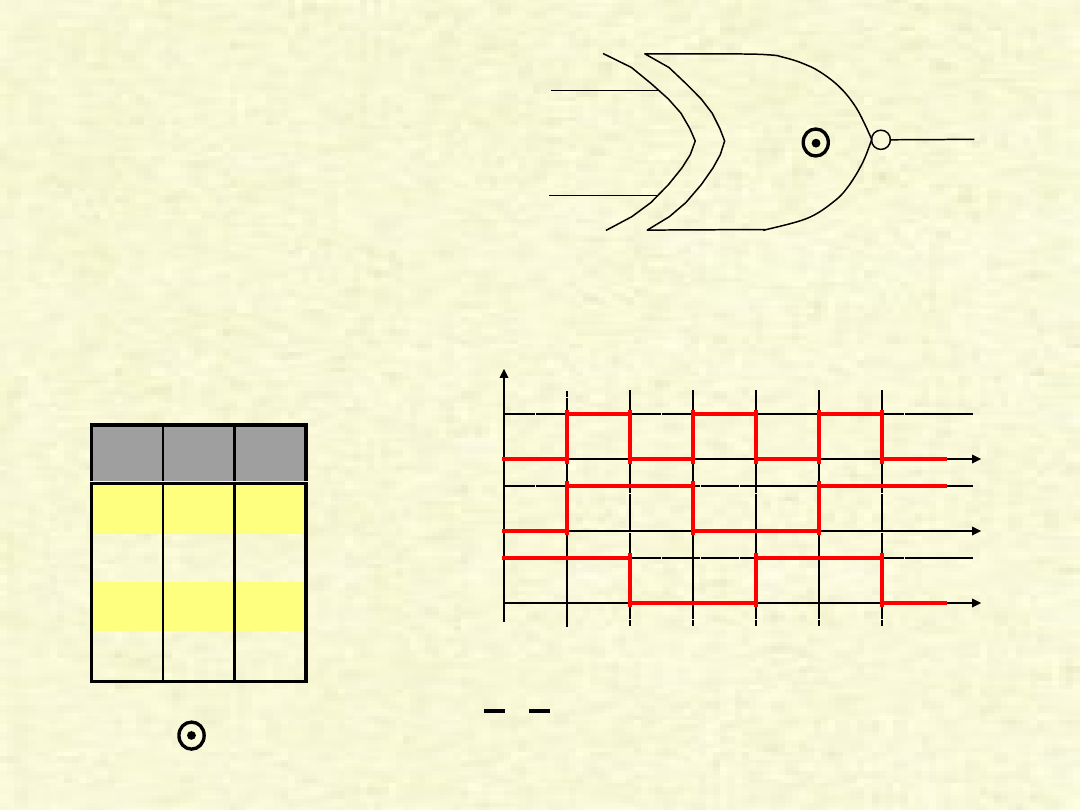
PRZYKŁAD BRAMKI „XOR”

Przykład pokazuje przypadek, w którym na wejścia
(AB) zostały podane sygnały zero i jeden, w wyniku
czego na wyjściu (Y) otrzymujemy jedynkę.

A

B

1

0

x

1

+

0

x

1

=

1

+

0

=

1

0

1

A

B

Y

0

0

0

0

1

1

1

0

1

1

1

0

Y=A + B



Y=A•B + A•B

0

1

1

Y

BRAMKA

„XNOR”

Jeżeli sygnały wejściowe są sobie równe (A=B=0 lub A=B=1),
to na wyjściu (Y) jest jedynka.

A

B

Y

Y=A B

A

B

Y

1

0

1

0

1

0

Y=A B



Y=A•B + A•B

Tablica zero-

jedynkowa

A

B

Y

0

0

1

0

1

0

1

0

0

1

1

1

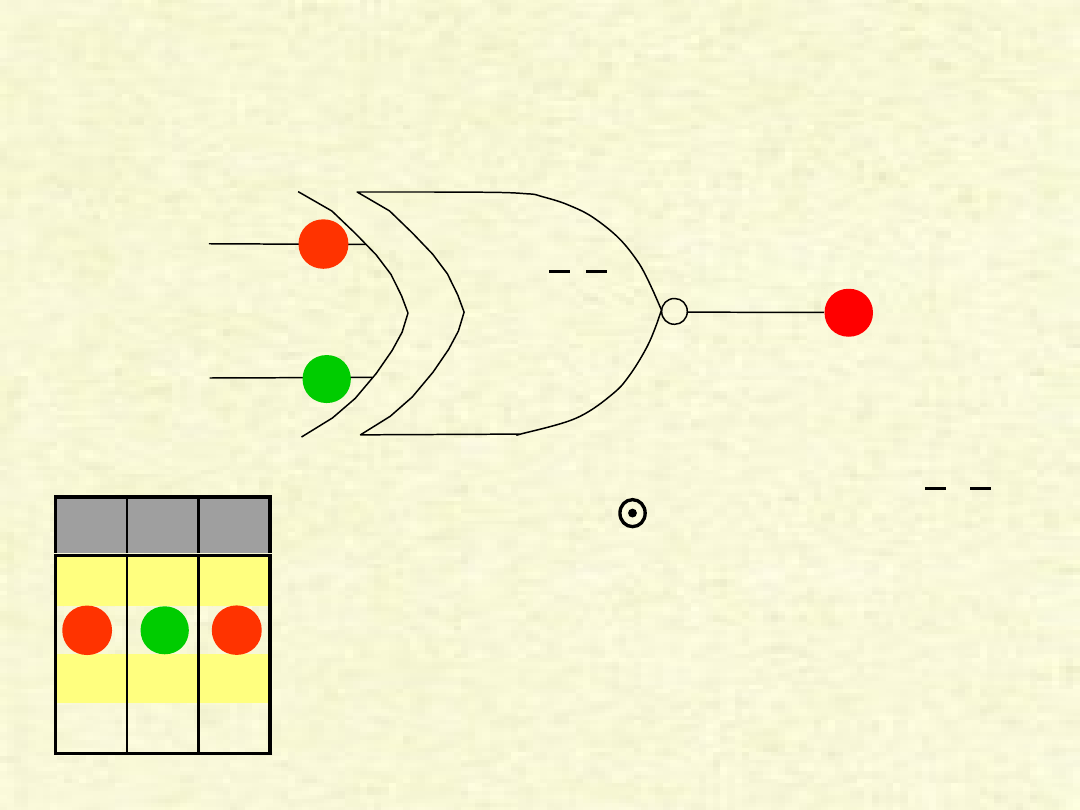
PRZYKŁAD BRAMKI „XNOR”

Przykład pokazuje przypadek, w którym na
wejścia (AB) zostały podane sygnały zero i jeden,
w wyniku czego na wyjściu (Y) otrzymujemy zero.

0

x

1

+

0

x

1

=

0

+

0

=

0

Y=A B



Y=A•B + A•B

A

B

Y

0

0

1

0

1

0

1

0

0

1

1

1

Y

0

1

0

A

B

0

1

0

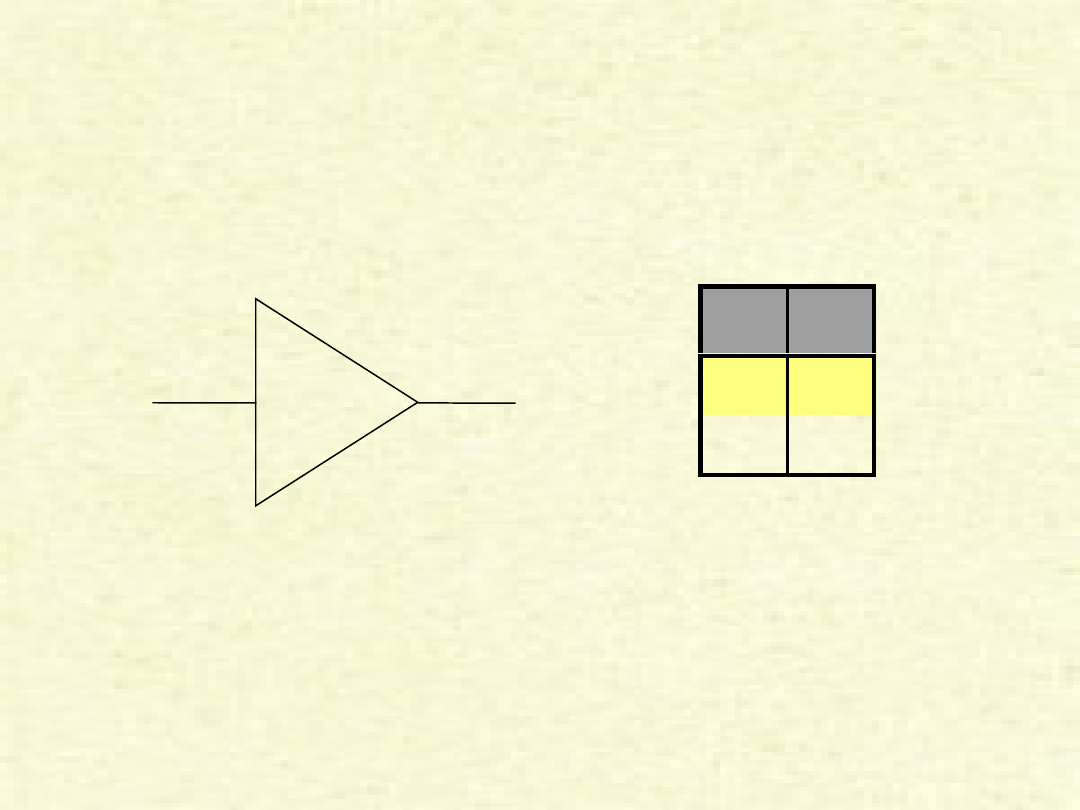
BUFOR czyli np. linia

opóźniająca

A

Y

Y=A

A

Y

0

0

1

1

Y=A

Tablica zero-

jedynkowa

Zastosowanie bramek

• Z bramek budowane są układy kombinacyjne,

takie jak:

– Multiplexery,

– Demultiplexery,

– Kodery,

– Dekodery.

• Z bramek budowane są przerzutniki – składowe

układów sekwencyjnych, takie jak

– Przerzutnik S-R,

– Przerzutnik synchroniczny S-R,

– Przerzutnik D,

– Przerzutnik J-K.

• Przerzutniki są wykorzystywane jako składowe:

– Rejestrów (np. równoległych i przesuwanych),

– Liczników (np. szeregowych, synchronicznych).

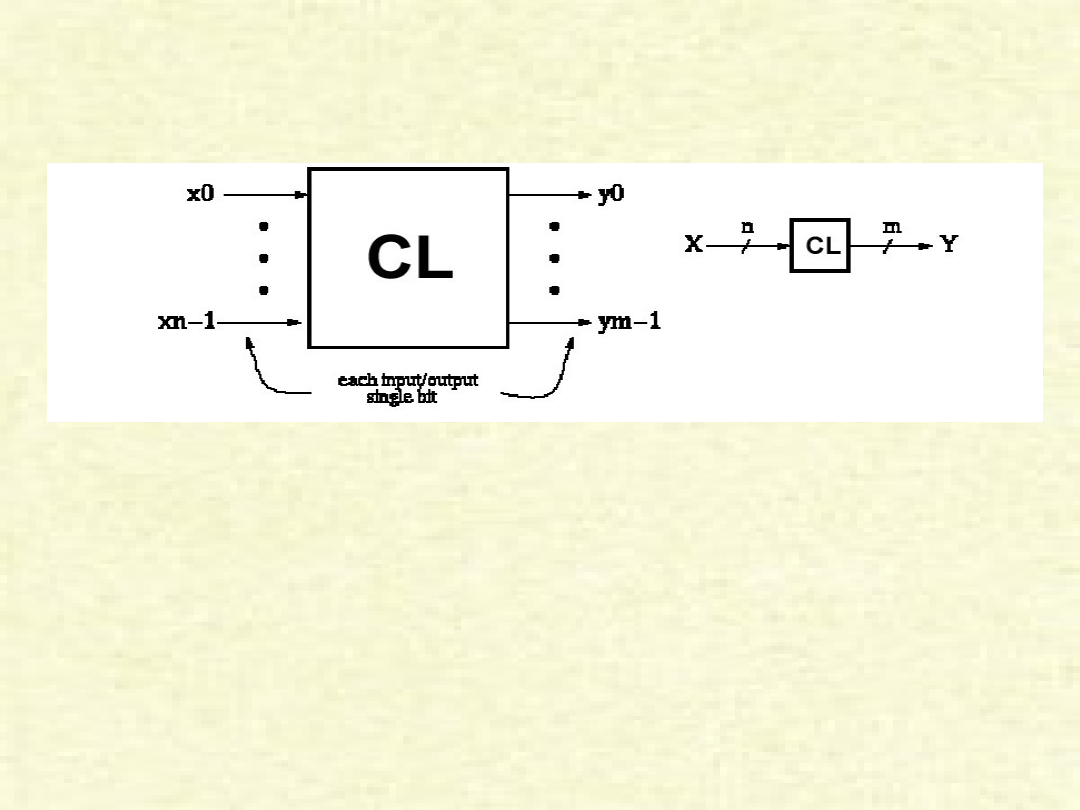
Logika kombinacyjna CL

• y

i

= f(x

0

, x

1

, ..., x

n-1

) gdzie x, y przyjmują wartości {0,

1}, zaś indeks i przyjmuje wartości {0, 1, 2, ..., n-1}

• y jest funkcją jedynie od x
• jeśli zmienimy wartości zmiennych x, to wartość y

zmieni się niemal natychmiast

• oznacza to, że czas propagacji układu

kombinacyjnego można pominąć!!!

Układy kombinacyjne

• Układ kombinacyjny jest zbiorem wzajemnie połączonych

bramek, którego stan wyjść w dowolnej chwili (kwancie

czasowym – określonym taktem zegara) jest wyłącznie funkcją

stanu wejść w tej samej chwili.

• Podobnie jak w przypadku pojedynczej bramki, po ustaleniu

stanu na wejściu – prawie natychmiast pojawia się sygnał na

wyjściu, przy czym występuje tylko opóźnienie bramkowe,

odpowiadające czasowi propagacji sygnału elektrycznego w

bramce.

• Ogólnie rzecz biorąc, układ kombinacyjny zawiera n wejść i m

wyjść binarnych i realizuje określone funkcje boolowskie.

• Układy kombinacyjne budowane są z bramek.
• Złożoność funkcji jest ograniczoną związkiem pomiędzy

długością sumy czasu propagacji najdłuższej ścieżki danych

binarnych układu kombinacyjnego – a długością sygnału

pojedynczego taktu zegara. Suma czasu propagacji sygnału w

układzie kombinacyjnym nie może przekraczać czasu trwania

pojedynczego sygnału taktującego zegara.

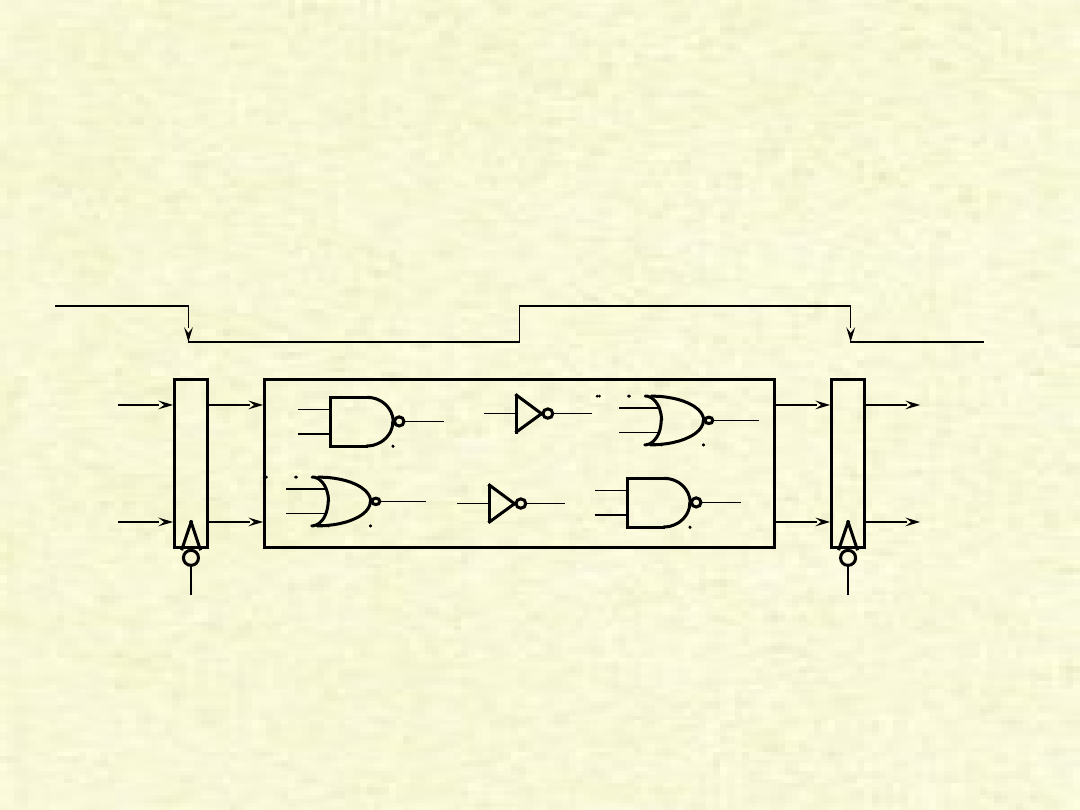
Zasada taktowania

zegarem

układu

kombinacyjnego

Zegar

.
.
.

.
.
.

.
.
.

.
.
.

Układ kombinacyjny

Algebra Boole’a

•

Do projektowania i analizowania cyfrowych układów

logicznych w komputerach i innych systemach cyfrowych

używana jest gałąź matematyki zwana algebrą Boole’a.

•

Nazwano ją tak dla uczczenia brytyjskiego matematyka

Georga’a Boole’a, który zaproponował podstawowe zasady

tej algebry w pracy zatytułowanej „An Investigation of the

Laws of Thought on Which to Found Mathematical Theories

of Logic and Probabilities (Badania praw myśli, które mogą

być podstawą matematycznych teorii logiki i

prawdopodobieństwa)”.

•

W roku 1938 Claude Shannon, wówczas asystent na

wydziale elektrycznym MIT (późniejszy twórca teorii

informacji), zasugerował zastosowanie algebry Boole’a do

rozwiązywania problemów projektowania układów

przekaźnikowych.

•

Metody Shannona zostały następnie użyte do analizowania

oraz projektowania elektronicznych układów cyfrowych.

Algebra Boole’a

• Podobnie jak inne rodzaje algebry, algebra Boole’a

używa zmiennych i operacji.

• W tym przypadku są to logiczne zmienne i

operacje, które mogą przyjmować wartości 1

(

Prawda

) i 0 (

Fałsz

), natomiast podstawowymi

operacjami logicznymi są

AND

(i),

OR

(lub) i

NOT

(nie).

• Trzy inne użyteczne operatory algebry Boole’a to

XOR

(albo – czyli lub wykluczające),

NAND

(nie-i)

oraz

NOR

(nie-lub).

• Operator

NAND

jest zdefiniowany jako:

a

NAND

b =

NOT

( a

AND

b)

• Operator

NOR

jest zdefiniowany jako:

a

NOR

b =

NOT

( a

OR

b)

• Natomiast operator

XOR

jest zdefiniowany jako:

a

XOR b

= ( a

AND

b)

OR

( a

NAND

b).

Algebra Boole’a

podstawowe tożsamości

a b

NOT

a a

AND

b a

OR

b a

XOR

b a

NAND

b a

NOR

b

0 0 1 0 0 0 1 1
0 1 1 0 1 1 1 0
1 0 0 0 1 1 1 0
1 1 0 1 1 0 0 0

Podstawowe postulaty
a * b = b * a a + b = b + a

Prawo przemienności

a * (b + c) = (a * b) + (a * c) a + (b * c) = (a + b) * (a + c)

Prawo rozdzielczości

1 * a = a 0 + a = a

Prawo tożsamości

Pozostałe tożsamości
a * NOTa = 0 a + NOTa = 1

Prawo odwrotności

0 * a = 0 1 + a = 1
a * (b * c) = (a * b) * c a + (b + c) = (a + b) + c

Prawo łączenia

NOT(a * b) = NOTa + NOTb NOT(a + b) = NOTa * NOTb

Twierdzenie DeMorgana

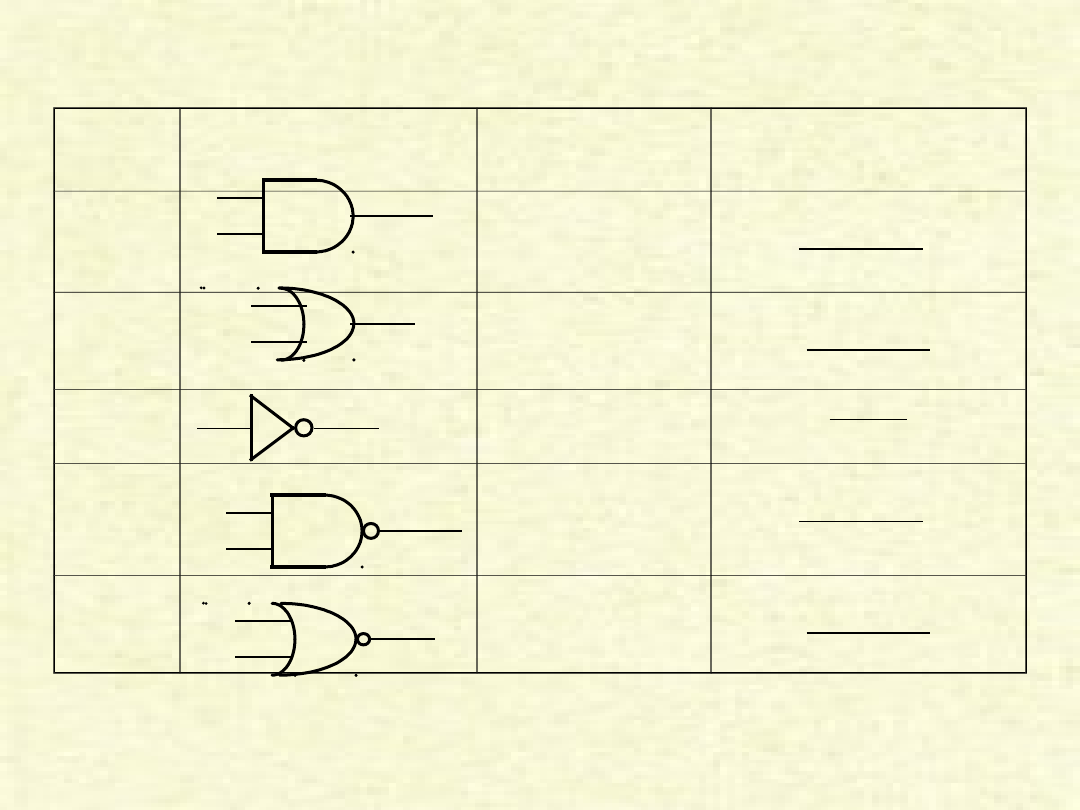
Podstawowe bramki logiczne

Nazwa Symbol graficzny

Funkcja

Boolowska

Tabelka funkcji

AND

F = A • B

lub

F = AB

A | 0 0 1 1

B | 0 1 0 1

F | 0 0 0 1

OR

F = A + B

A | 0 0 1 1

B | 0 1 0 1

F | 0 1 1 1

NOT

__

F = A

A | 0 1

F | 1 0

NAN

D

___

F = (A • B)

A | 0 0 1 1

B | 0 1 0 1

F | 1 0 0 0

NOR

_____

F = (A + B)

A | 0 0 1 1

B | 0 1 0 1

F | 1 0 0 0

A

B

A

B

F

F

A

B

A

B

F

F

A

F

F

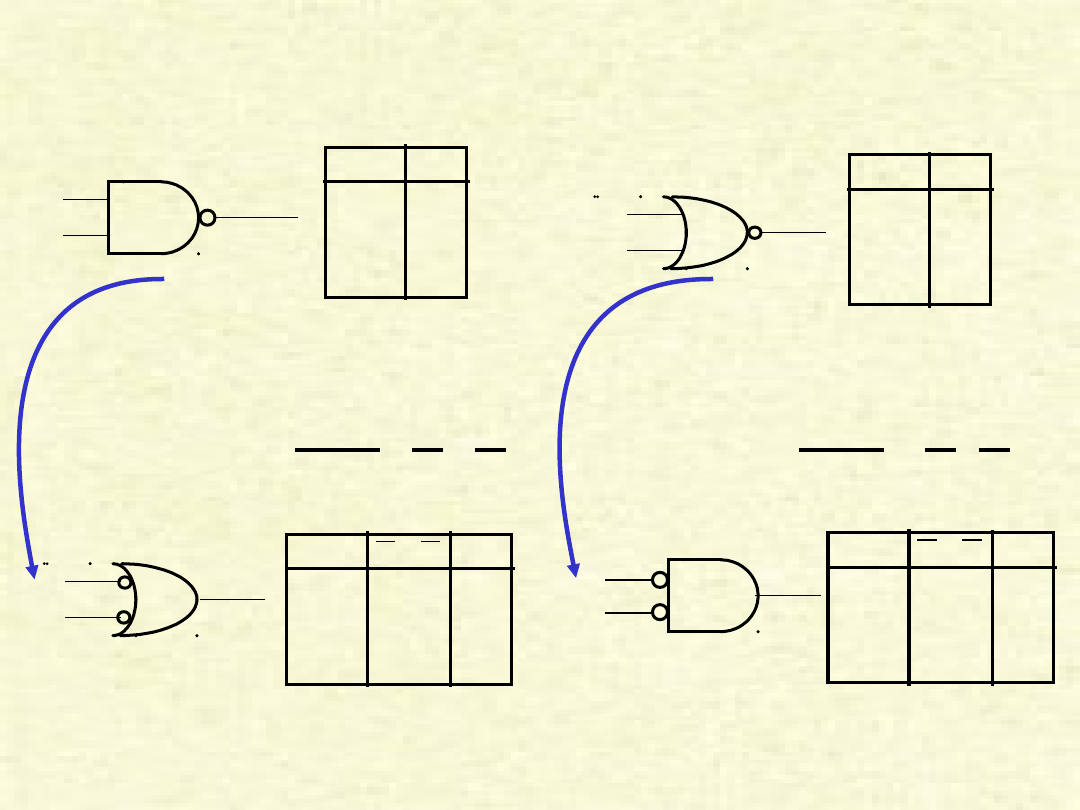
Twierdzenia DeMorgan’a

NAND Gate

NOR Gate

Out

A

B

A

B

Out

A B Out

1

1

1

0 0

0 1

1 0

1 1

0

A
B

Out

Out

A

B

Out = A • B = A + B

A B Out

0 0

1

0 1

0

1 0

0

1 1

0

A B Out

1 1

1

1 0

1

0 1

1

0 0

0

0 0

0 1

1 0

1 1

A B

A B Out

1 1

1

1 0

0

0 1

0

0 0

0

0 0

0 1

1 0

1 1

A B

Out = A + B = A • B

Układy kombinacyjne

• Realizacja funkcji Boole’a.
• Realizacja wszystkich funkcji boolowskich za

pomocą bramki NAND.

• Realizacja wszystkich funkcji boolowskich za

pomocą bramki NOR.

• Multipleksery.
• Dekodery.
• Sumatory.

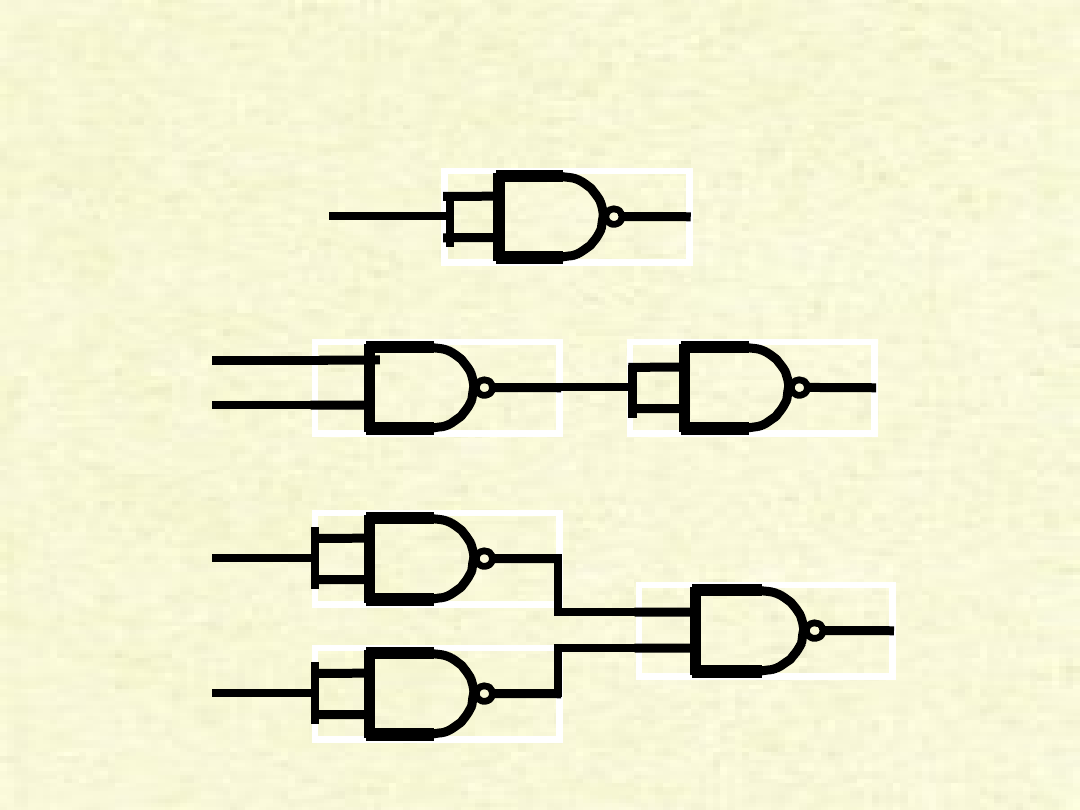
Zastosowanie bramki

NAND

A

A’

A

B

(A*B)’

A*B

A

B

A’

B’

A+B

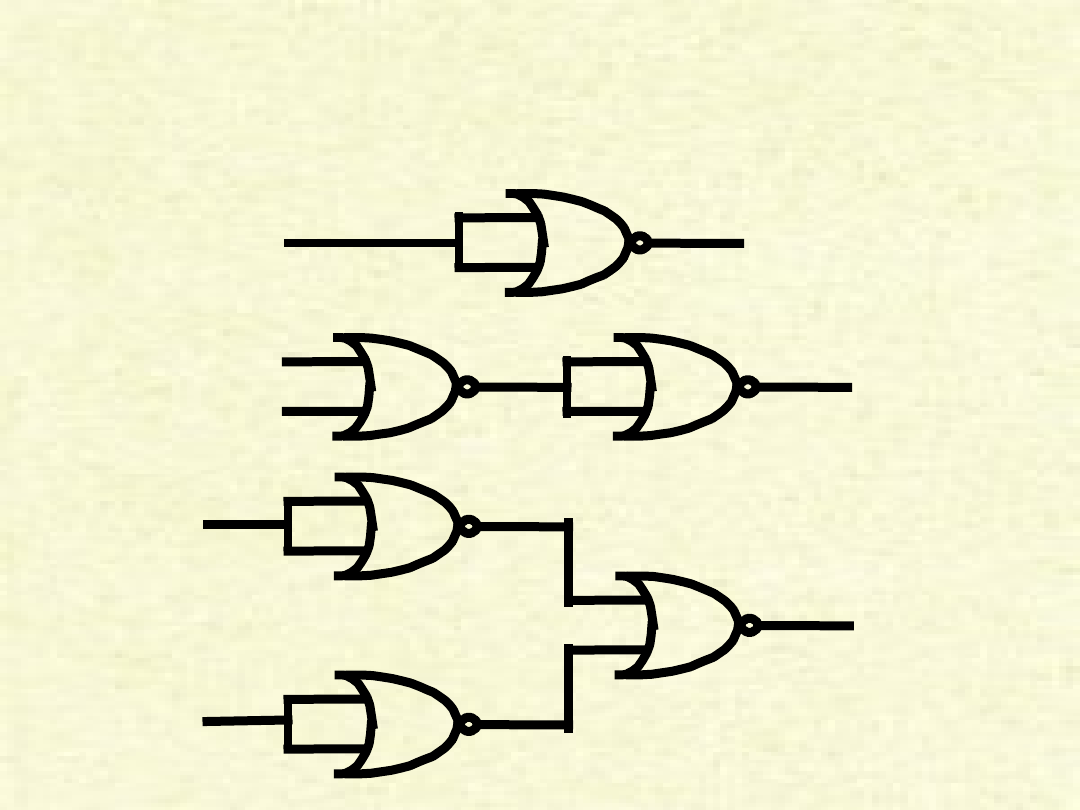
Zastosowanie bramki

NOR

A

A’

A

B

(A+B)’

A+B

A

B

A’

B’

A*B

Definiowanie układu

kombinacyjnego

• Układ kombinacyjny jest zbiorem wzajemnie

połączonych bramek, którego stan wyjść w dowolnej

chwili jest wyłącznie funkcją stanu wejść w tej samej

chwili.

• Układ kombinacyjny zawiera n wejść i m wyjść

binarnych

• Podobnie jak bramkę, układ kombinacyjny można

zdefiniować na jeden z trzech sposobów:

– Tablicą zero-jedynkową. Dla każdej z 2

n

możliwych

kombinacji sygnałów wejściowych podana jest wartość

binarna każdego z m sygnałów wyjściowych.

– Schematem graficznym – czyli schematem połączeń bramek
– Funkcjami Boole’owskimi – gdzie każdy sygnał wyjściowy

jest wyrażony jako funkcja sygnałów wejściowych.

Układ opisany tablicą zero-

jedynkową

A

B

C

F

0

0

0

0

0

0

1

0

0

1

0

1

0

1

1

1

1

0

0

0

1

0

1

0

1

1

0

1

1

1

1

0

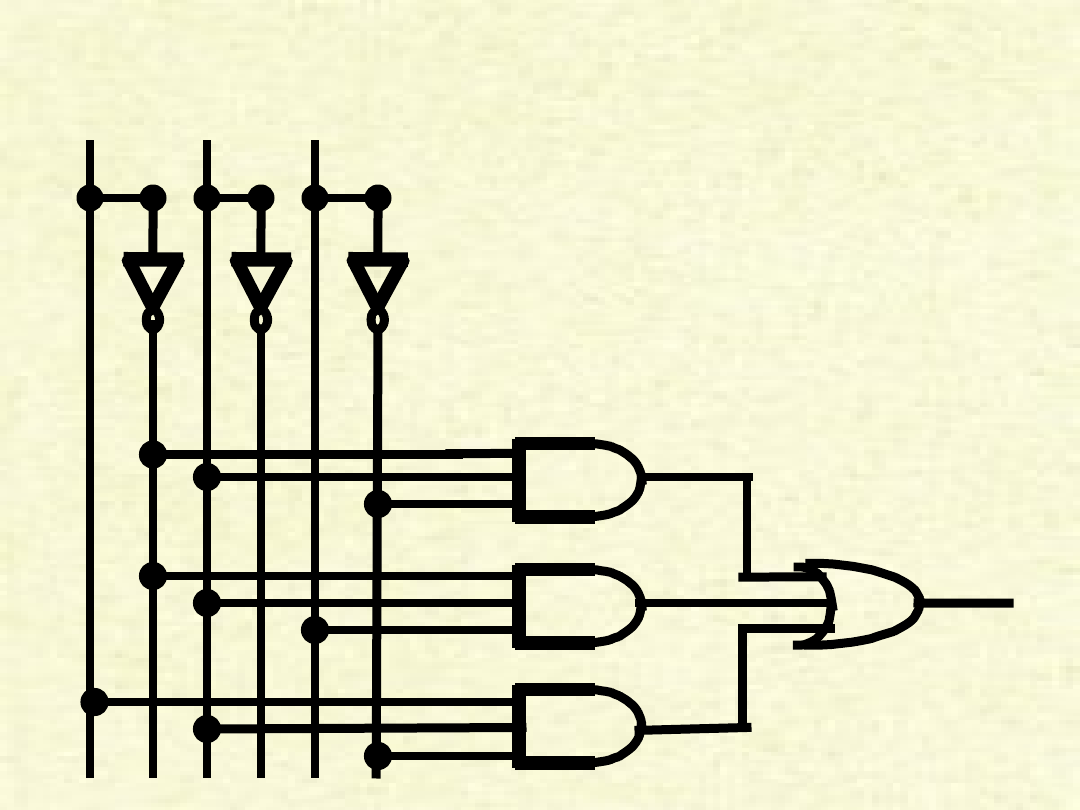
Układ opisany schematem

wersja (a)

A

B

C

F

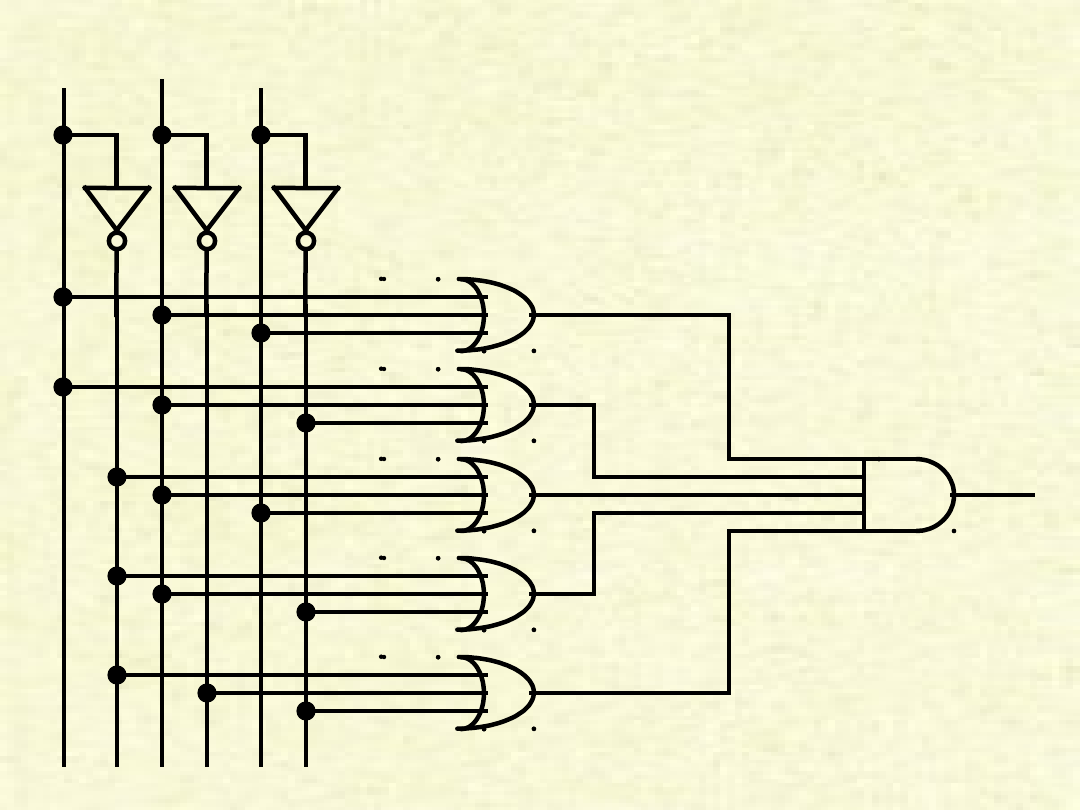
Układ opisany schematem

wersja (b)

A

B

C

F

Układ opisany funkcją

Boolea’owską

(a) F = A’ * B * C’ + A’ * B * C + A

* B * C’

(b) F =

(A+B+C)*(A+B+C’)*(A’+B+C)*(
A’+B’+C’)

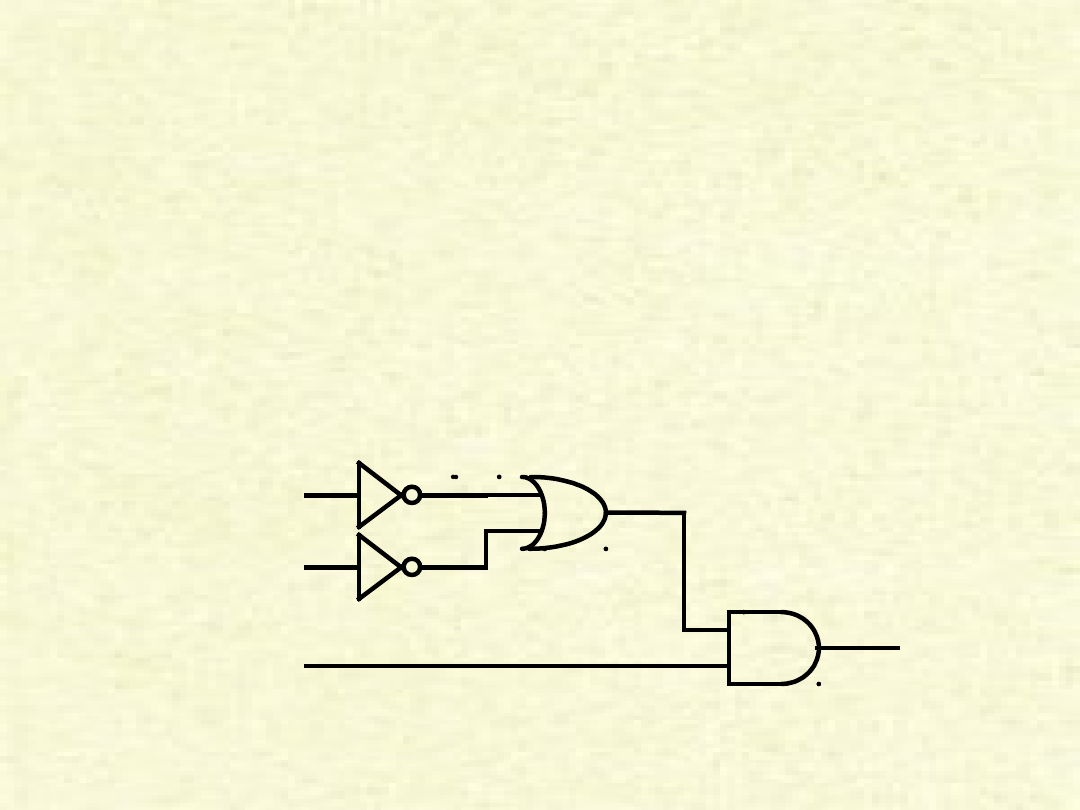
Uproszczenia

algebraiczne

F = (A’ * B + B * C’)

F = B * (A’ + C’)

A

C

B

F

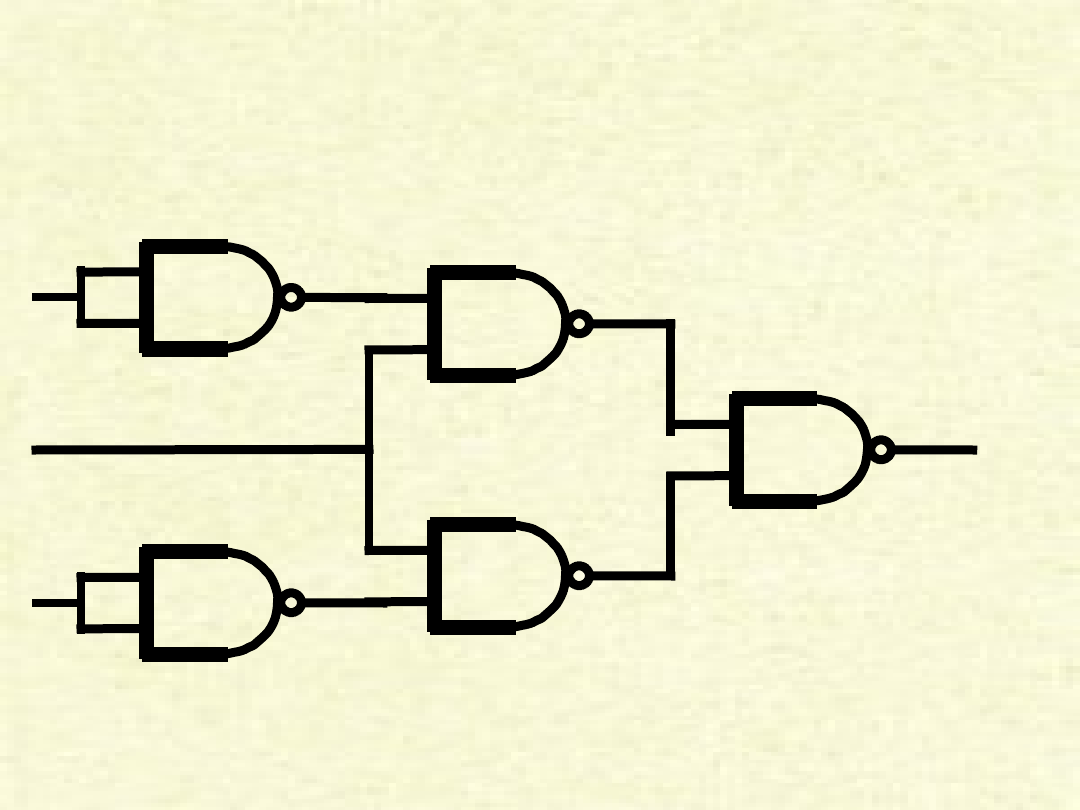
Realizacja układu z bramek

NAND

A

B

C

F

F = B * (A’ +
C’)

Multiplekser

• Multiplekser jest układem kombinacyjnym, który łączy wiele

wejść, (np. D0, D1, D2 i D3) z jednym wyjściem F, a o
którego działaniu decydują sygnały sterujące (np. S1 i S2).

• Na wyjście F multipleksera dostarczany jest sygnał z

jednego wybranego wejścia. Sygnały sterujące
multiplekserem decydują o wyborze wejścia.

• Multipleksery są używane w układach cyfrowych do

sterowania przepływem sygnałów i danych.

• Przykładem jest ładowanie licznika programu (PC). Liczba

wprowadzana do licznika programu, może pochodzić z
jednego z kilku źródeł:

– Układu pół-sumatora, jeśli stan PC ma być inkrementowany w celu

określenia adresu następnego rozkazu

– Rejestru rozkazu (IR), jeśli został właśnie wykonany rozkaz skokowy

używający adresu bezpośredniego

– Wyjścia ALU, jeśli rozkaz skokowy określa adres, używając trybu

indeksowego.

Tablica multipleksera

pokazująca jakim kombinacjom sygnałów

sterującym S1, S2 odpowiada przełączenie

poszczególnych wejść na wyjście

S2

S1

F

0

0

D0

0

1

D1

1

0

D2

1

1

D3

Symbol multipleksera

MUX

4 do 1

D0

D
1

D2

D3

F

S1

S2

W

e

jś

ci

a

Sterowanie

Wyjście

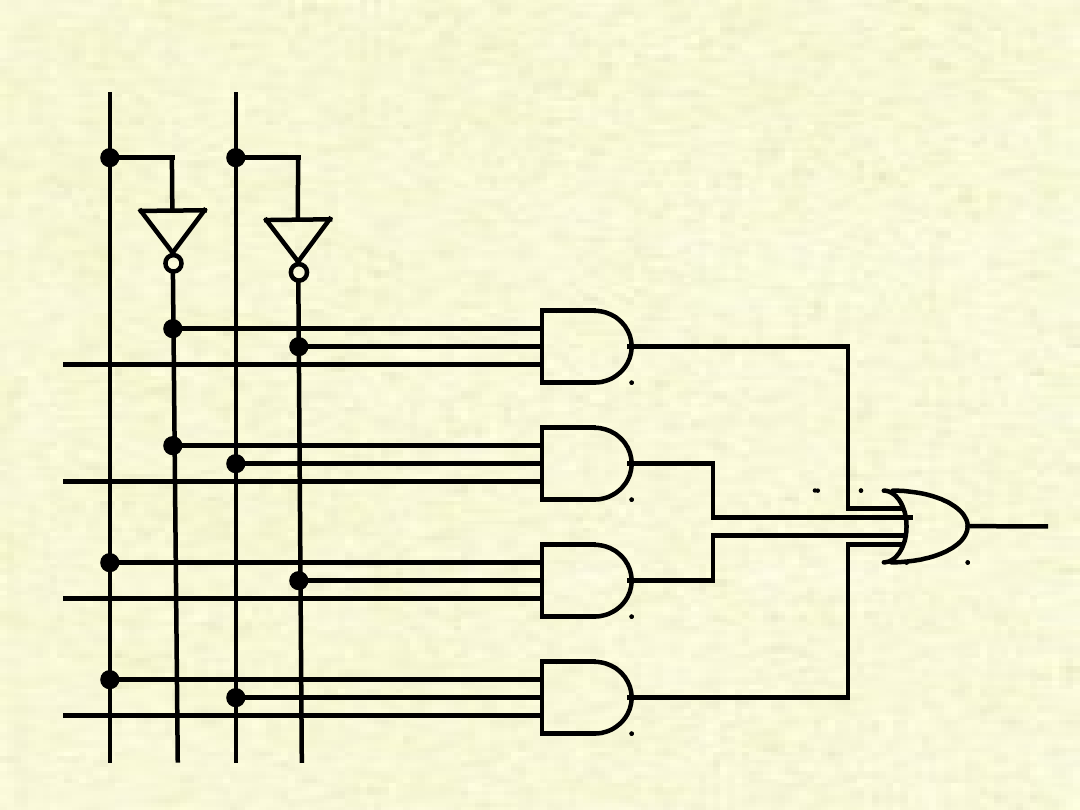
Schemat multipleksera

S1

S2

D0

D1

D2

D3

F

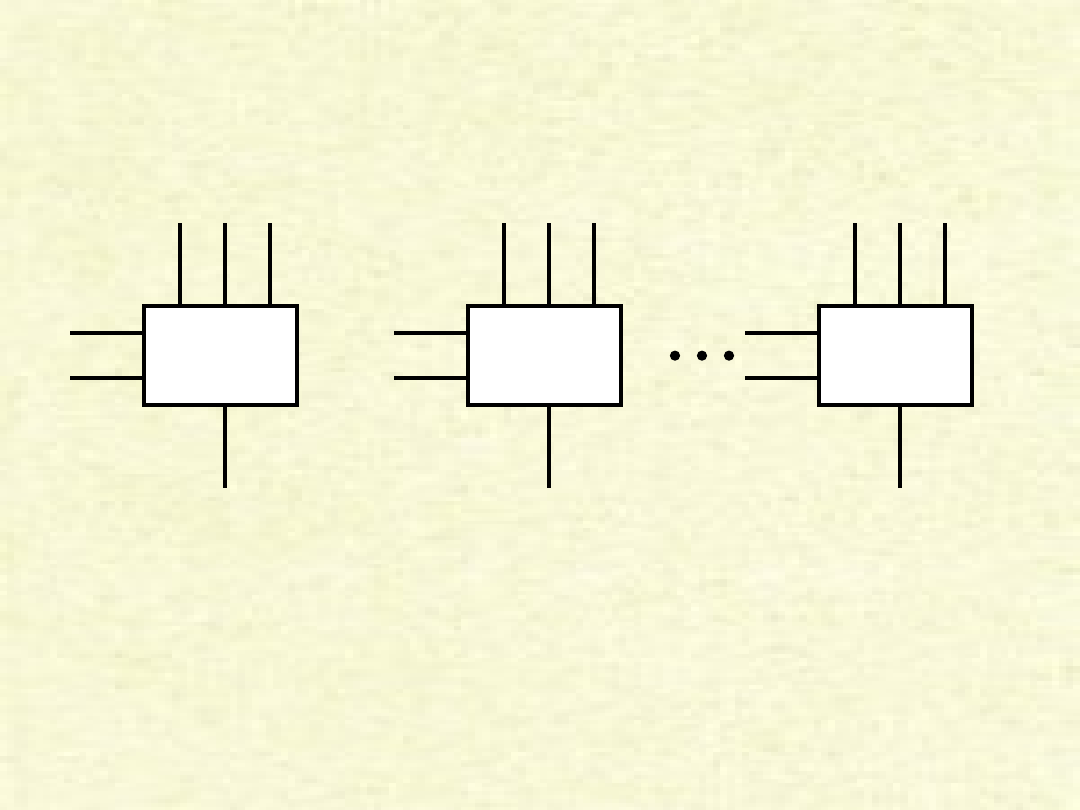
Wejście multiplekserowe

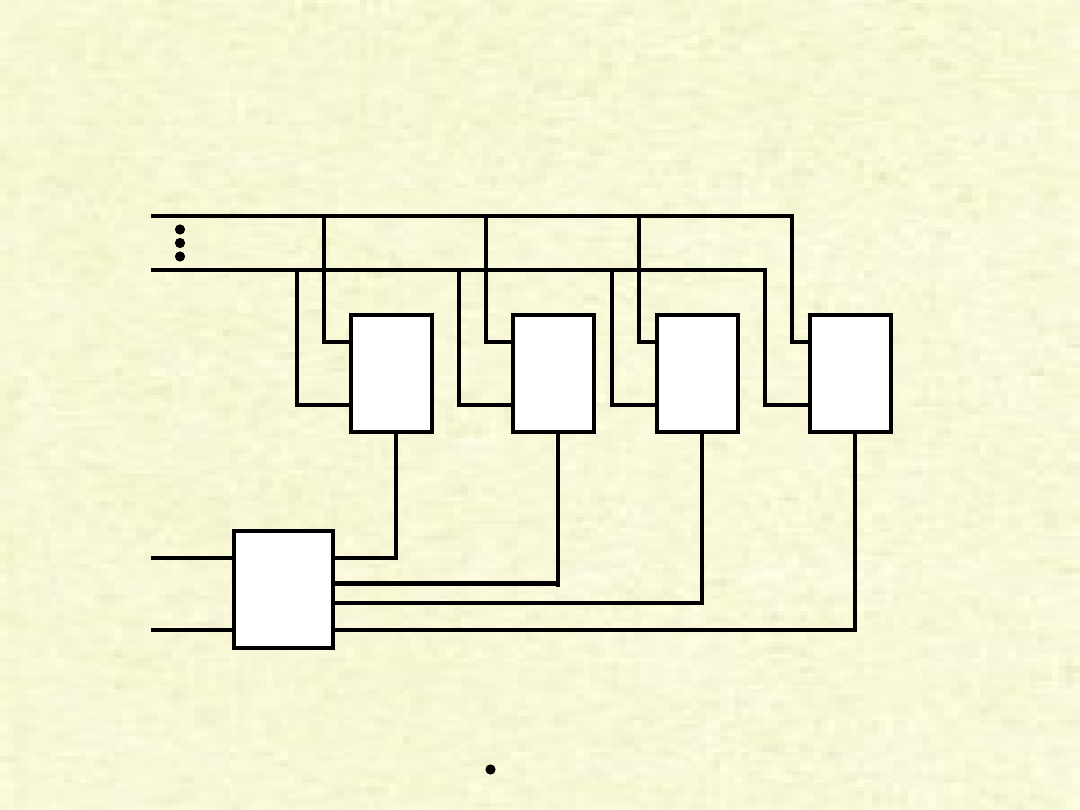
do PC

MUX

0

4 do 1

MUX

1

4 do 1

MUX

15

4 do 1

S1

S2

S1

S2

S1

S
2

PC

0

PC

1

PC

15

C

0

IR

0

ALU

0

C

1

IR

1

ALU

1

C

15

IR

15

ALU

15

Przykład dotyczący 16 bitowego adresu (PC

0

, PC

1

, ... , PC

15

).

Źródła (C

0

, C

1

, ... , C

15

), (IR

0

, IR

1

, ... , IR

15

) oraz ALU – są połączone

z liniami wejściowymi poszczególnych multiplekserów, zaś wyjścia tych
ostatnich – połączone są do poszczególnych bitów rejestru PC.

Dekoder

•

Dekoder jest układem kombinacyjnym o pewnej liczbie linii

wyjściowych, z których w określonej chwili sygnał może być

wysłany na jedynie jedną linię, zależnie od kombinacji

sygnałów na liniach wejściowych.

•

Ogólnie mówiąc, dekoder ma N wejść i

2

N

wyjść.

•

Dekodery znajdują wiele zastosowań w komputerach.

Jednym z przykładów zastosowań jest dekodowanie adresu.

•

Załóżmy dalej, że chcemy zbudować pamięć 1-kilobajtową

przy użyciu 4 układów RAM o pojemności 256x8 bitów

każdy. Przy czym, chcemy mieć jedną zunifikowaną

przestrzeń adresową, którą możemy podzielić następująco:

– Adresy szesnastkowe od 0000 do 00FF układ pamięciowy RAM 0
– Adresy szesnastkowe od 0100 do 01FF układ pamięciowy RAM 1
– Adresy szesnastkowe od 0200 do 02FF układ pamięciowy RAM 2
– Adresy szesnastkowe od 0300 do 03FF układ pamięciowy RAM 3

Tablica dekodera

Pokazuje jakiej kombinacji sygnałów

wejściowych A, B, C

- odpowiada pojawienie się sygnału x na jednym

z wyjść

A

B

C

Dan

e

D0 D1 D2 D3 D4 D5 D6 D7

0

0

0

x

x

0

0

0

0

0

0

0

0

0

1

x

0

x

0

0

0

0

0

0

0

1

0

x

0

0

x

0

0

0

0

0

0

1

1

x

0

0

0

x

0

0

0

0

1

0

0

x

0

0

0

0

x

0

0

0

1

0

1

x

0

0

0

0

0

x

0

0

1

1

0

x

0

0

0

0

0

0

x

0

1

1

1

x

0

0

0

0

0

0

0

x

Symbol dekodera

Dekoder

N do 2

N

N – bitowy

adres miejsca

przeznaczenia

Wejście
danych

2

N

wyjść binarnych

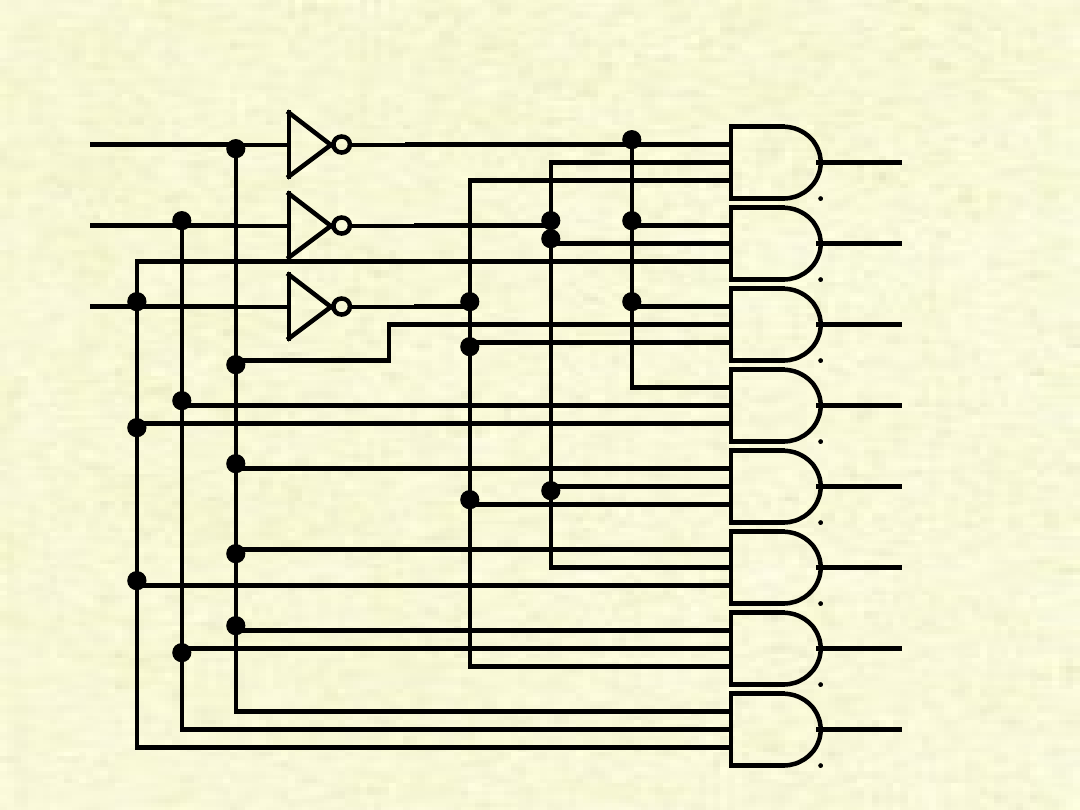
Przykład dekodowania

adresu

256x8

RAM

Dekoder

2 do 4

256x8

RAM

256x8

RAM

256x8

RAM

A0

A7

A8

A9

Zezwolenie

Zezwolenie

Zezwolenie

Zezwolenie

Schemat

dekodera

A

B

C

D0

D1

D2

D3

D4

D5

D6

D7

000

001

010

011

100

101

110

111

Pamięć stała ROM

• Układy kombinacyjne są często określane jako układy

„bez pamięci”, ponieważ ich wyjścia zależą jedynie od

bieżącego stanu ich wejść, a żadne informacje historyczne

o poprzednich stanach wejść nie są zachowywane.

• Istniej jednak pewien rodzaj pamięci, który jest

realizowany za pomocą układów kombinacyjnych, a

mianowicie pamięć stała ROM.

• ROM jest pamięcią, która umożliwia wykonanie wyłącznie

operacji odczytu. Informacja binarna zawarta w ROM jest

w związku z tym trwała. Jest ona zapisywana w pamięci

ROM w toku procesu wytwarzania modułu pamięci.

• Wobec tego określona kombinacja sygnałów wejściowych

ROM – podana na linie adresowe, prowadzi zawsze do tej

samej kombinacja sygnałów na liniach wyjściowych.

Tablica pamięci stałej

ROM

------Linie wejściowe------ ----- Linie

wyjściowe------

0

0

0

0

0

0

0

0

0

0

0

1

0

0

0

1

0

0

1

0

0

0

1

1

0

0

1

1

0

0

1

0

0

1

0

0

0

1

1

0

0

1

0

1

0

1

1

1

0

1

1

0

0

1

0

1

0

1

1

1

0

1

0

0

1

0

0

0

1

1

0

0

1

0

0

1

1

1

0

1

1

0

1

0

1

1

1

1

1

0

1

1

1

1

1

0

1

1

0

0

1

0

1

0

1

1

0

1

1

0

1

1

1

1

1

0

1

0

0

1

1

1

1

1

1

0

0

0

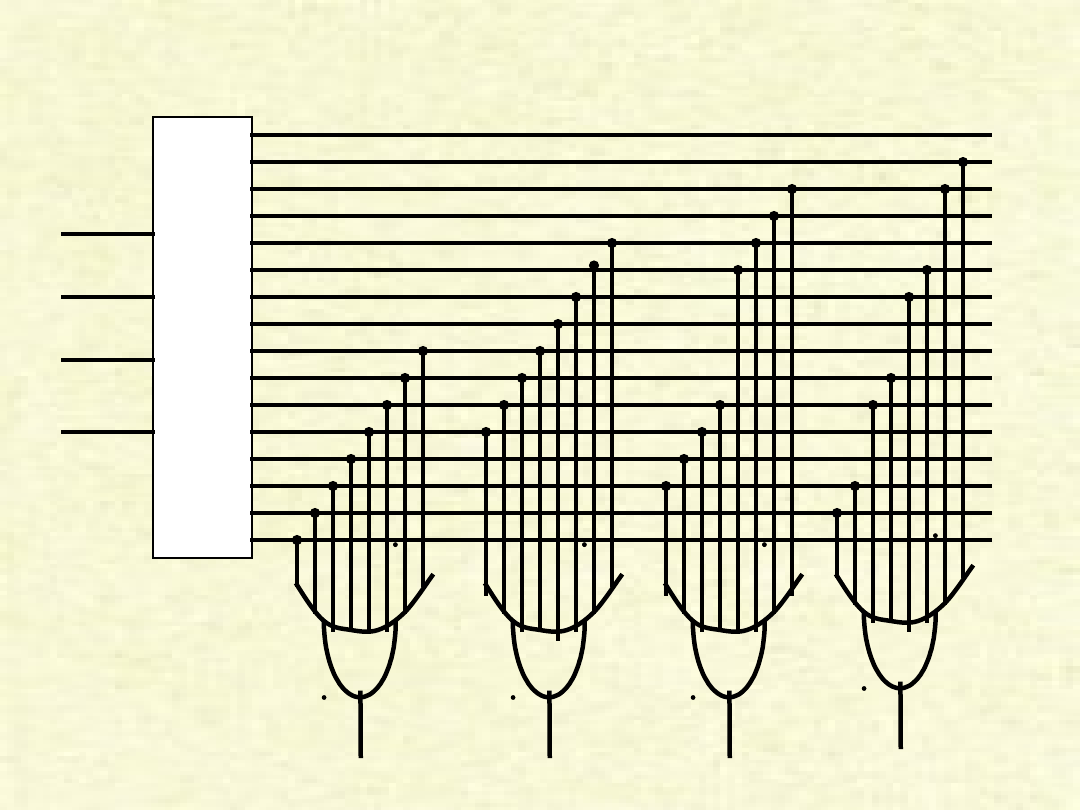
64-bitowa pamięć ROM

D

e

ko

d

e

r 4

x

1

6

X

1

X

2

X

3

X

4

Z

1

Z

2

Z

3

Z

4

0000

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

1100

1101

1110

1111

Sumatory

•

Obszarem o zasadniczym znaczeniu, którego

jeszcze nie rozpatrywaliśmy, są operacje

arytmetyczne.

•

Obecnie omówimy, jako przykład funkcję

dodawania binarnego liczb.

•

Suma binarna różni się tym od sumy w algebrze

Boole’a, że wynik obejmuje przeniesienie

pomiędzy pozycjami binarnymi dodawanych

liczb binarnych.

•

Dodawanie binarne można wyrazić za pomocą

wyrażeń algebry Boolea.

Tablica dodawania

binarnego

C

in

A

B

Suma

C

out

0

0

0

0

0

0

0

1

1

0

0

1

0

1

0

0

1

1

0

1

1

0

0

1

0

1

0

1

0

1

1

1

0

0

1

1

1

1

1

1

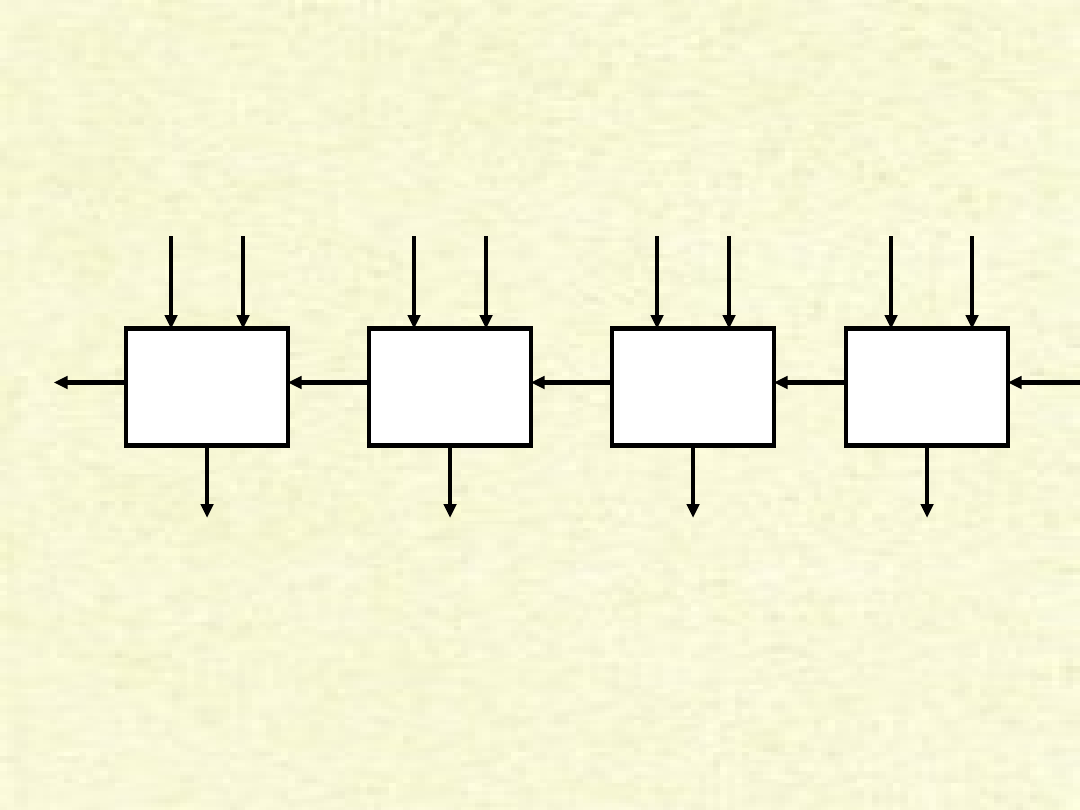
Sumator 4-bitowy

C

3

S

y

g

n

a

ł

p

rz

e

p

e

łn

ie

n

ia

C

in

C

2

C

in

C

1

C

in

C

0

C

in

0

S

3

S

2

S

1

S

0

A

3

B

3

A

2

B

2

A

1

B

1

A

0

B

0

Wzory na stany dwóch wyjść

sumatora

suma

= A’ * B’ * C + A’ * B * C’ + A * B * C + A * B’ * C’

= (A’ * B’ + A * B) * C + (A’ * B + A * B’) * C’

przeniesienie

= A * B + A * C + B * C

= A * B + (A + B) *C

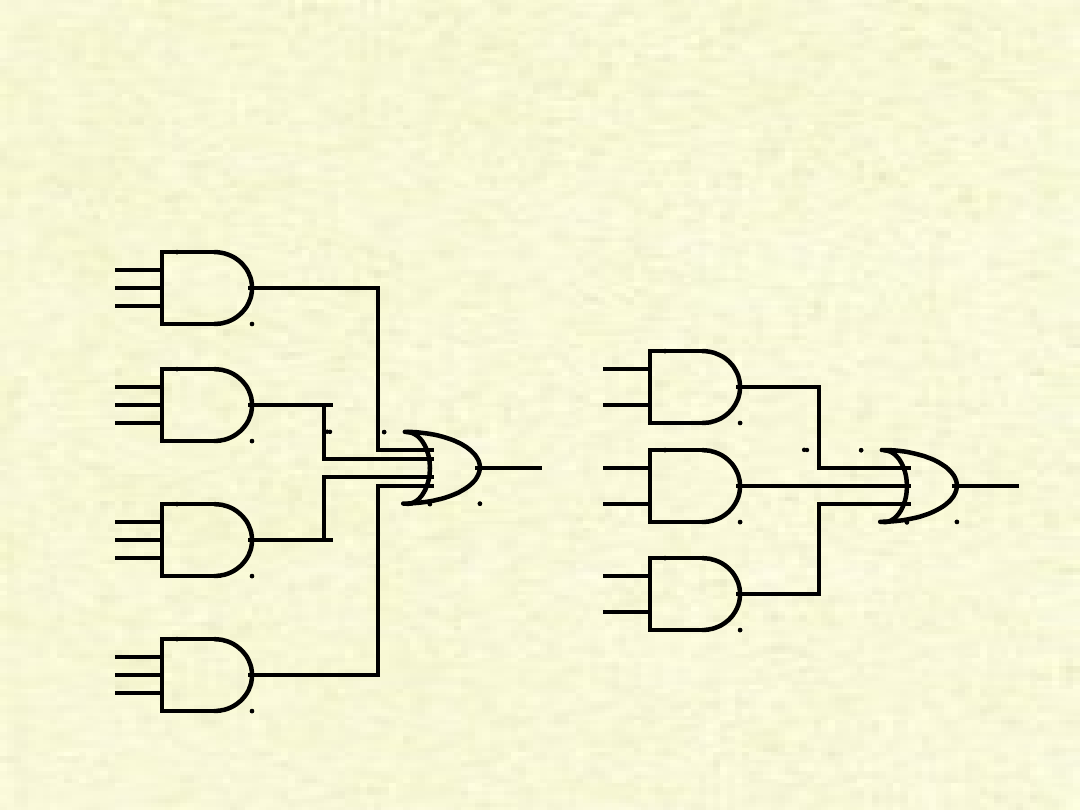
Schemat sumatora

suma

przeniesienie

A’

B’

C

A’

B

C’

A

B

C

A

B’

C’

A
B

A
C

B
C

Sumatory wielobitowe

• Dysponujemy więc układami logicznymi niezbędnymi do budowy

wielobitowego sumatora.

• Zauważmy, że ponieważ wartość wyjściowa każdego sumatora

zależy od przeniesienia z poprzedniego sumatora, istnieje
opóźnienie narastające od najmniej znaczącego do najbardziej
znaczącego bitu, ponieważ w każdym sumatorze jednobitowym
następują pewne opóźnienia bramkowe, które się kumulują.

• Gdyby wartości przeniesienia mogły być określone bez

przechodzenia przez wszystkie pośrednie szczeble, każdy
sumator jednobitowy mógłby działać niezależnie i opóźnienia by
się nie kumulowały.

• Można to osiągnąć, stosując rozwiązanie nazywane układem

przeniesienia na bardziej znaczące pozycje (

carry look-a-head

).

• Dla wyjaśnienia tego rozwiązania ponownie rozważmy sumator

4-bitowy.

Wzory na

carry look-a-

head

Chcemy więc otrzymać wyrażenia, które określają wartości na wejściu
Dowolnego szczebla sumatora, bez odnoszenia się do poprzednich

wartości przeniesienia:

(1)C

0

= A

0

* B

0

(2)C

1

= A

1

* B

1

+ (A

1

+ B

1

) * C

0

Podstawiając równości (1) do (2) otrzymamy:

(3)C

1

= A

1

* B

1

+ A

1

* A

0

* B

0

+ B

1

* A

0

* B

0

Powtarzając tę samą procedurę, otrzymujemy:

(4)C

2

= A

2

* B

2

+ A

2

* A

1

* B

1

+ A

2

* B

1

* A

0

* B

0

+ B

2

* A

1

* B

1

+ B

2

* A

1

* A

0

* B

0

+ B

2

* B

1

* A

0

* B

0

Postępowanie to możemy powtarzać dla dowolnie długich sumatorów.
Każdy składnik przeniesienia może być wyrażony w postaci sumy
iloczynów jako funkcja wyłącznie oryginalnych danych wejściowych,
bez zależności od przeniesień.

Układy sekwencyjne

• Układy kombinacyjne służą do wdrażania

podstawowych funkcji komputera. Jednak, poza

szczególnym przypadkiem pamięci ROM, nie

umożliwiają one zrealizowania układów pamięci lub

przechowywania informacji o stanie, które również

mają zasadnicze znaczenie dla działania komputera.

• Bieżący stan wyjścia układu sekwencyjnego zależy

nie tylko od bieżącego stanu wejścia, ale również od

historii stanu wejścia.

• Inaczej mówiąc, bieżący stan wyjścia układu

sekwencyjnego zależy od bieżącego stanu wejścia

oraz od bieżącego stanu samego układu

sekwencyjnego.

Przerzutniki

• Najprostszą formą układu sekwencyjnego jest

przerzutnik.

• Istnieje szereg rodzajów przerzutników, jednak wszystkie

mają następujące dwie własności:

– Przerzutnik jest układem dwustabilnym. Utrzymuje się w jednym

z dwóch stanów i bez sygnału wejściowego nie zmienia stanu.
Czyli przerzutnik działa jako pamięć jednobitowa.

– Przerzutnik ma dwa wyjścia, które zawsze dopełniają się

wzajemnie. Są one często oznaczane jako Q i Q’.

• W dalszym ciągu omówimy cztery rodzaje przerzutników:

– Przerzutnik zatrzaskowy S-R
– Synchronizowany przerzutnik S-R
– Przerzutnik D
– Przerzutnik J-K.

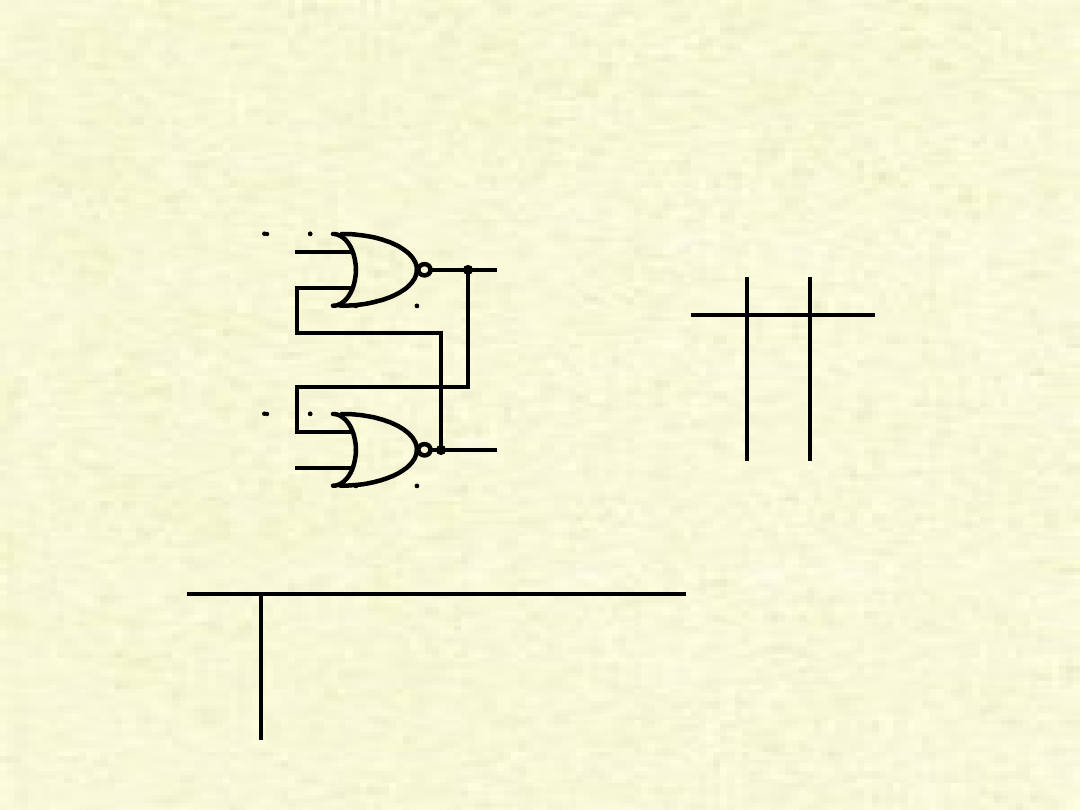
Przerzutnik zatrzaskowy

R

S

Q

Q’

S R Q

n+1

0 0 Q

n

0 1 0
1 0 1
1 1 ?

Odpowiedzi układu na serie wartości wejściowych

t 0 1 2 3 4 5 6 7 8 9
S 1 0 0 0 0 0 0 0 1 0
R 0 0 0 1 0 0 1 0 0 0
Q

n+1

1 1 1 0 0 0 0 0 1 1

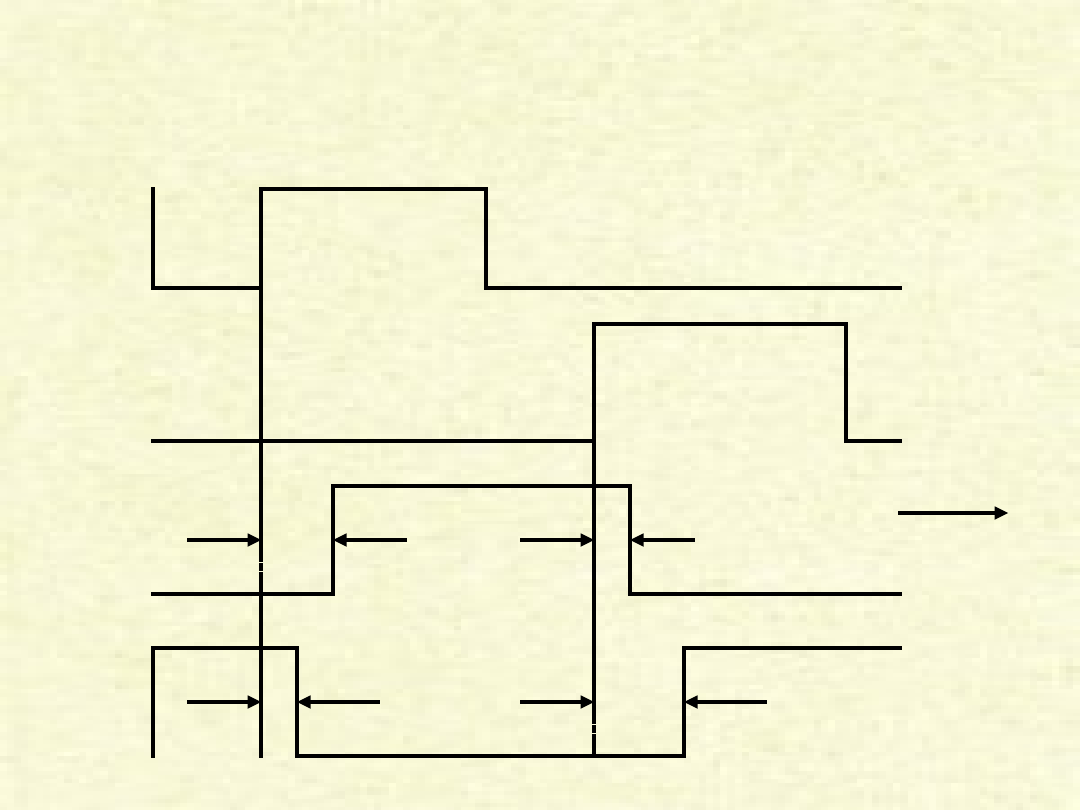
Przebiegi czasowe

przerzutnika S-R

1
S
0

1
R
0

0
Q
1

0
Q’
1

2Δt

Δt

2Δt

Δt

t

Synchronizacja

przerzutnika S-R

• Zmiana stanu wyjścia przerzutnika S-R następuje po

krótkim opóźnieniu, jako reakcja na zmianę stanu
wejścia. Określimy to jako

działanie asynchroniczne

.

• Częściej jednak, zdarzenia w komputerze są

synchronizowane impulsami zegara, zmiany stanu mogą
nastąpić tylko wtedy gdy pojawi się impuls zegarowy.

• Przerzutnik S-R synchronizowany impulsami zegara

nazywamy

synchronicznym przerzutnikiem S-R

.

• W synchronicznym przerzutniku S-R, stany wejść S i R są

doprowadzane do bramek NOR przerzutnika tylko
podczas trwania impulsu zegarowego.

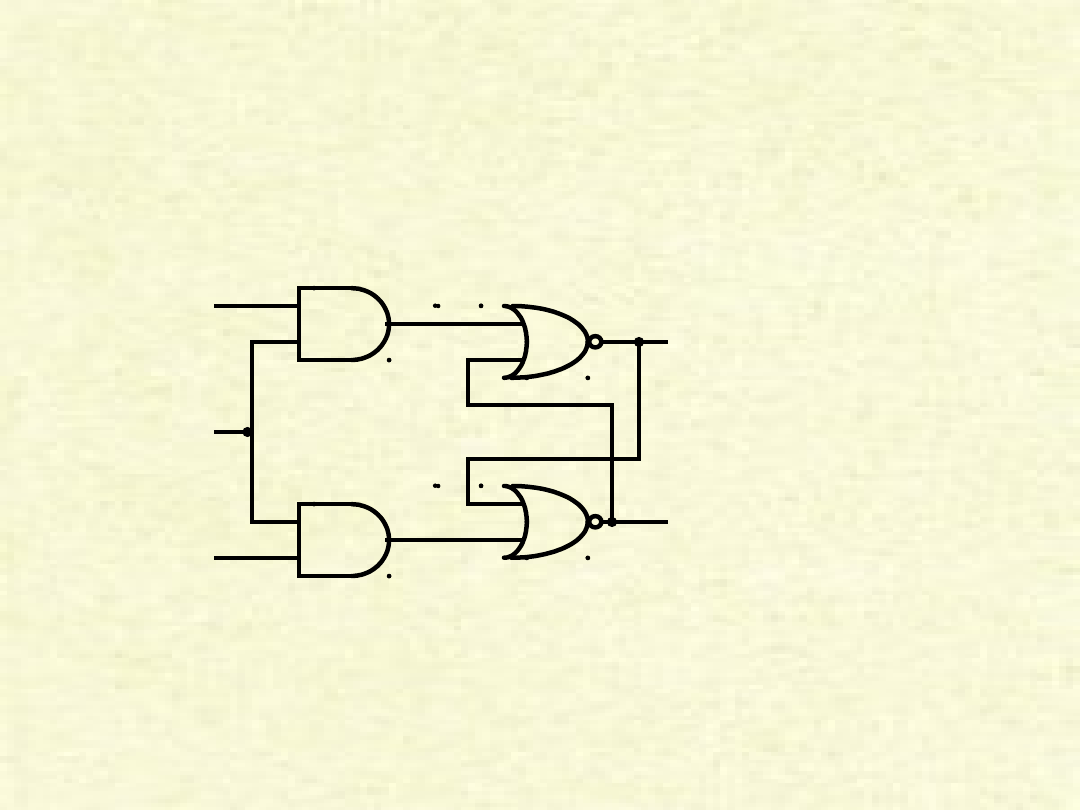
Synchronizowany

przerzutnik S-R

R

S

zegar

Q

Q’

Rozwiązywanie problemu

S-R

• W przypadku przerzutnika S-R problem jest to, że należy

zapobiegać powstawaniu sytuacji, w której równocześnie R =
1, S = 1.

• Jednym ze sposobów osiągnięcia tego jest pozostawienie tylko

jednego wejścia.

• Tak właśnie jest rozwiązany przerzutnik D, gdzie za pomocą

inwertora (funkcji negacji) zagwarantowano, że nie-zegarowe
wejścia do dwóch bramek AND dają stany, które są swoją
negacją.

• Stan na wyjściu przerzutnika D jest zawsze równy ostatniej

wartości stanu wejścia. Dlatego przerzutnik D jest często
określany jako linia opóźniająca, ponieważ pojawienie się na
wejściu 0 lub 1 – pojawia się na wyjściu z opóźnieniem jednego
cyklu zegara.

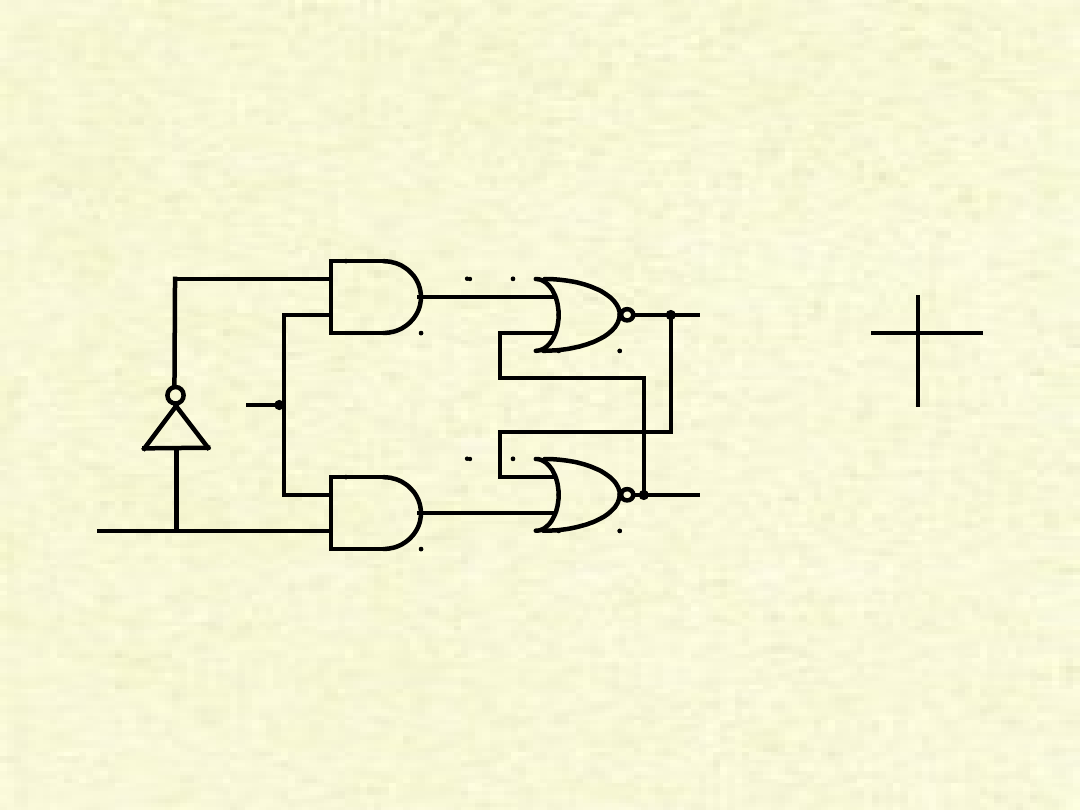
Przerzutnik D

zegar

D

Q

Q’

D Q

n+1

0 0
1 1

Inne rozwiązanie

problemu S-R

• Kolejnym użytecznym przerzutnikiem jest

przerzutnik J-K

.

• Podobnie jak przerzutnik S-R ma dwa wejścia. W odróżnieniu

jednak od przerzutnika S-R wszystkie możliwe kombinacje

stanów wejść przerzutnika J-K są dopuszczalne.

• Zauważmy, że pierwsze trzy kombinacje wartości wejść i

wyjść przerzutnika J-K są identyczne jak dla przerzutnika S-

R.

• Samo wejście J umożliwia realizację ustawienia na wejściu

wartości 1 (

set

), zaś samo wejście K realizuje kasowanie

(

reset

).

• Gdy oba wejścia (J i K) są równe 1, stan wyjścia ulega

zanegowaniu. Jeśli więc Q jest równe 1, to ustawienie

stanów wejść J = 1 i K = 1 powoduje zmianę stanu wyjścia Q

na 0. Jeśli zaś Q jest równe 0, to ustawienie stanów wejść J

= 1 i K = 1 powoduje zmianę stanu wyjścia Q na 1.

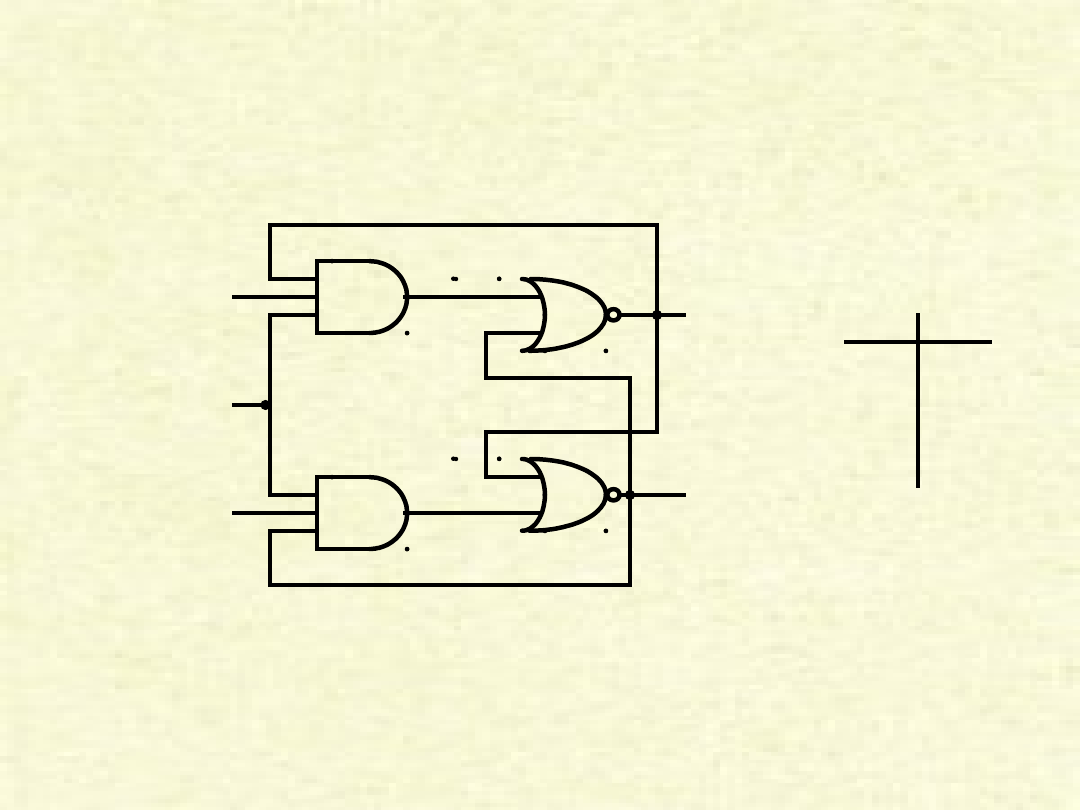
Przerzutnik J-K

K

zegar

J

Q

Q’

J K Q

n+1

0 0 Q

n

0 1 0
1 0 1
1 1 Q’

n

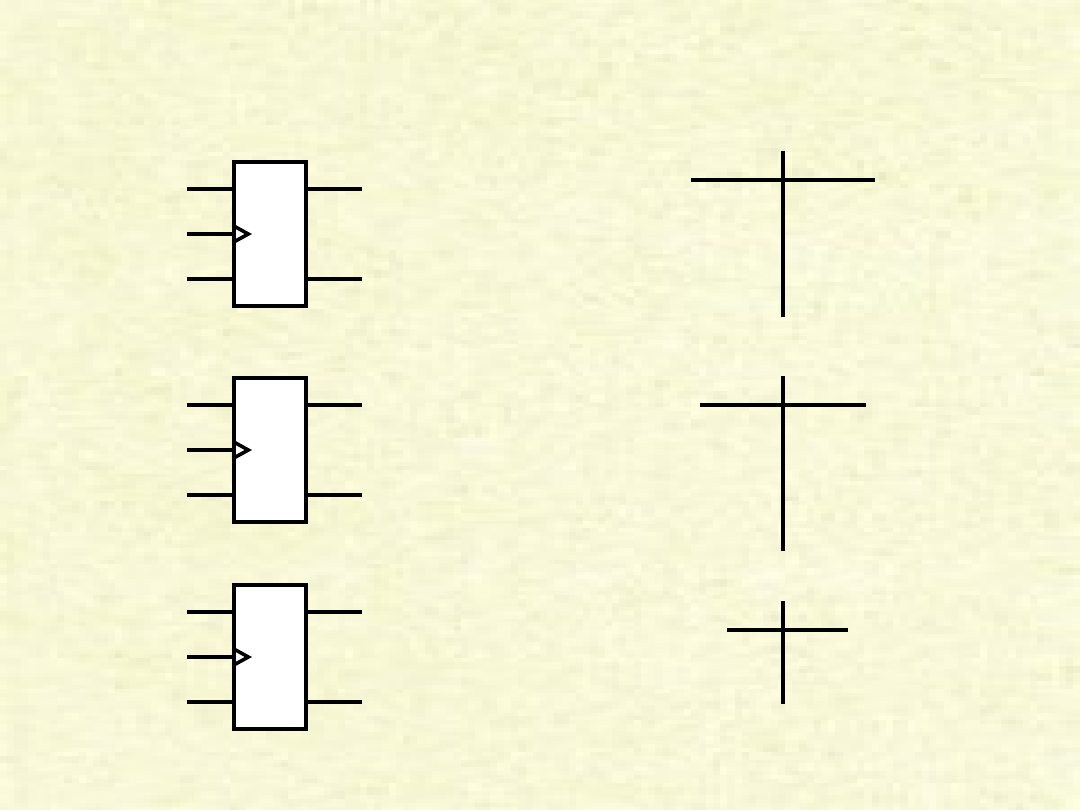
Symbole podstawowych

przerzutników

C

k

C

k

C

k

S Q

R Q’

J Q

K Q’

D Q

Q’

S R Q

n+1

0 0 Q

n

0 1 0
1 0 1
1 1

?

J K Q

n+1

0 0 Q

n

0 1 0
1 0 1
1 1 Q’

n

D Q

n+1

0 0
1 1

Rejestry

• Jako przykład zastosowania przerzutników,

przeanalizujemy jeden z zasadniczych
elementów procesora:

rejestr

.

• Jak wiemy, rejestr jest układem cyfrowym

używanym między innymi wewnątrz procesora
do przechowywania jednego lub wielu bitów
danych.

• Powszechnie używane są dwa rodzaje rejestrów:

– Rejestry równoległe
– Rejestry przesuwające.

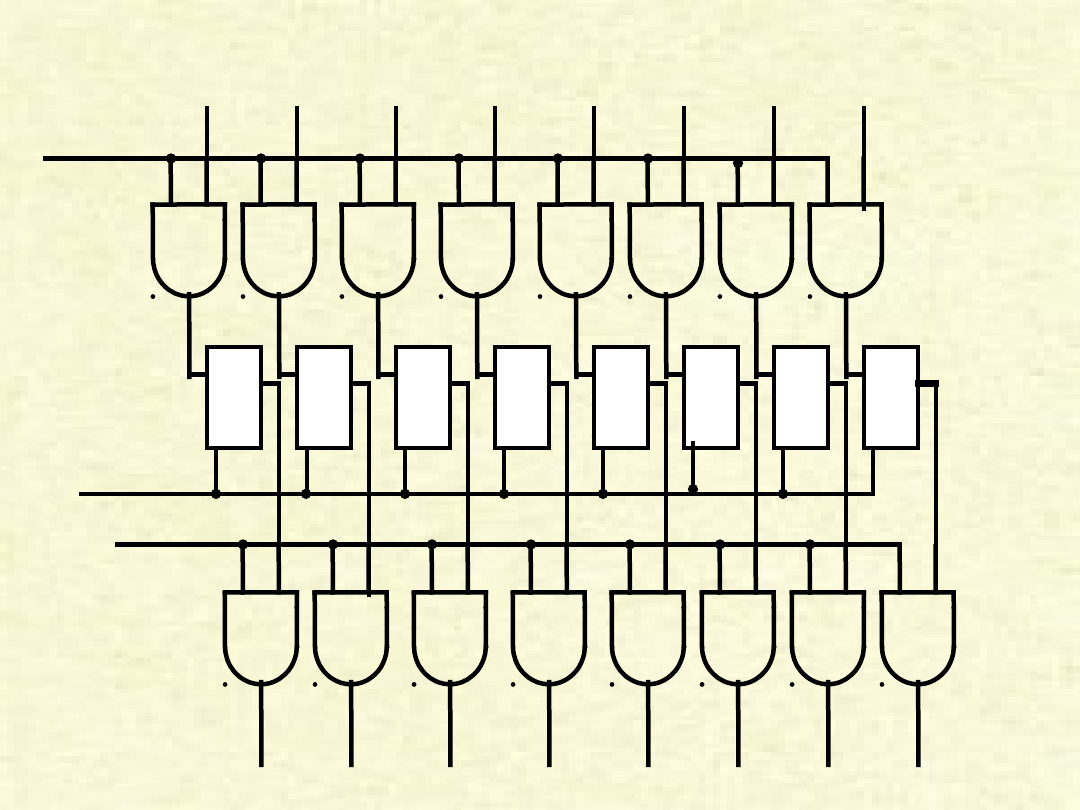
Rejestr równoległy

S Q

R

S Q

R

S Q

R

S Q

R

S Q

R

S Q

R

S Q

R

S Q

R

D

o7

D

o6

D

o5

D

o4

D

o3

D

o2

D

o1

D

o0

D

i7

D

i6

D

i5

D

i4

D

i3

D

i2

D

i1

D

i0

Input

strobe

Reset

Output

strobe

Linie wejścia

Linie wyjściowe

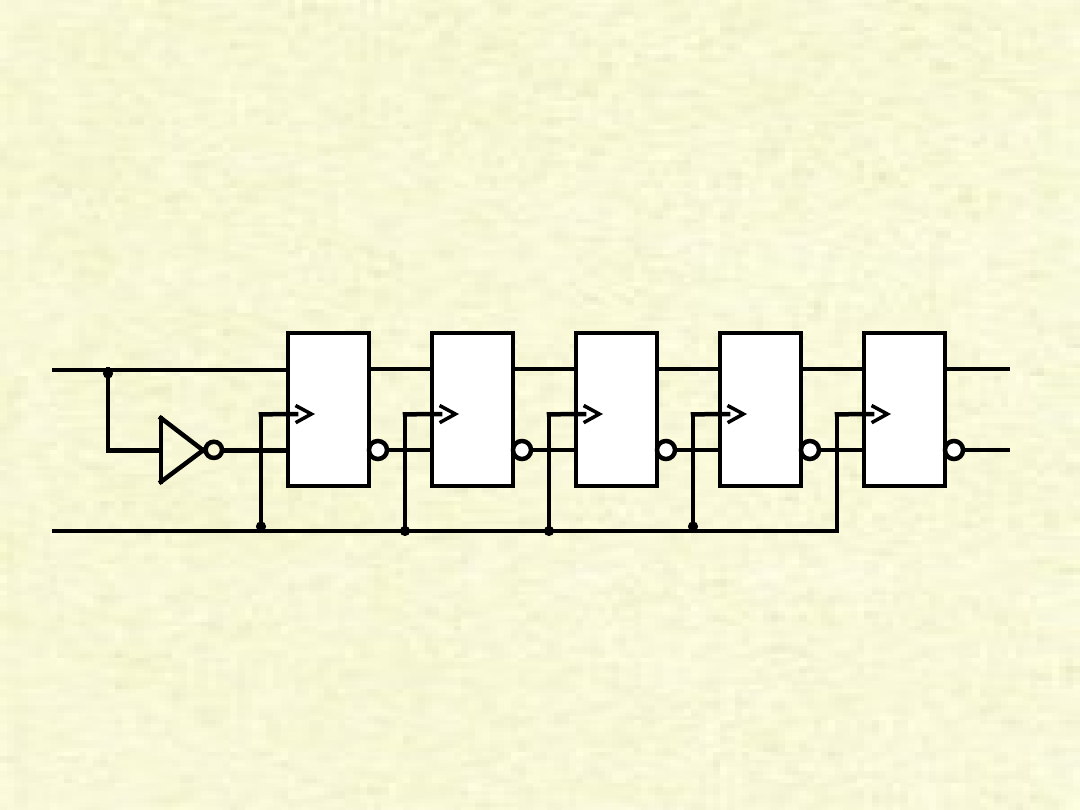
5-bitowy rejestr

przesuwający

S

5

Y

5

C

R

5

Y’

5

S

4

Y

4

C

R

4

Y’

4

S

3

Y

3

C

R

3

Y’

3

S

2

Y

2

C

R

2

Y’

2

S

1

Y

1

C

R

1

Y’

1

zegar

X

Liczniki

• Inną użyteczną kategorią układów sekwencyjnych są

liczniki

.

• Licznik jest rejestrem, którego zawartość może być z łatwością

inkrementowana 1 modulo pojemność rejestru.

• Rejestr wykonany z n przerzutników może liczyć od 0 do 2

n

– 1.

• Gdy zawartość licznika jest zwiększana poza jego wartość

maksymalną, jest on ustawiony na 0.

• Przykładem licznika występującego w procesorze jest licznik

programu IC.

• Liczniki mogą być projektowane jako

asynchroniczne

lub

synchroniczne

.

• Liczniki asynchroniczne są stosunkowo powolne, ponieważ

przerzutnik wyzwala zmianę stanu następnego przerzutnika.

• W liczniku synchronicznym wszystkie przerzutniki zmieniają stan

jednocześnie i dlatego są o wiele szybsze od liczników

asynchronicznych. Dlatego też, są one powszechnie stosowane

w procesorach.

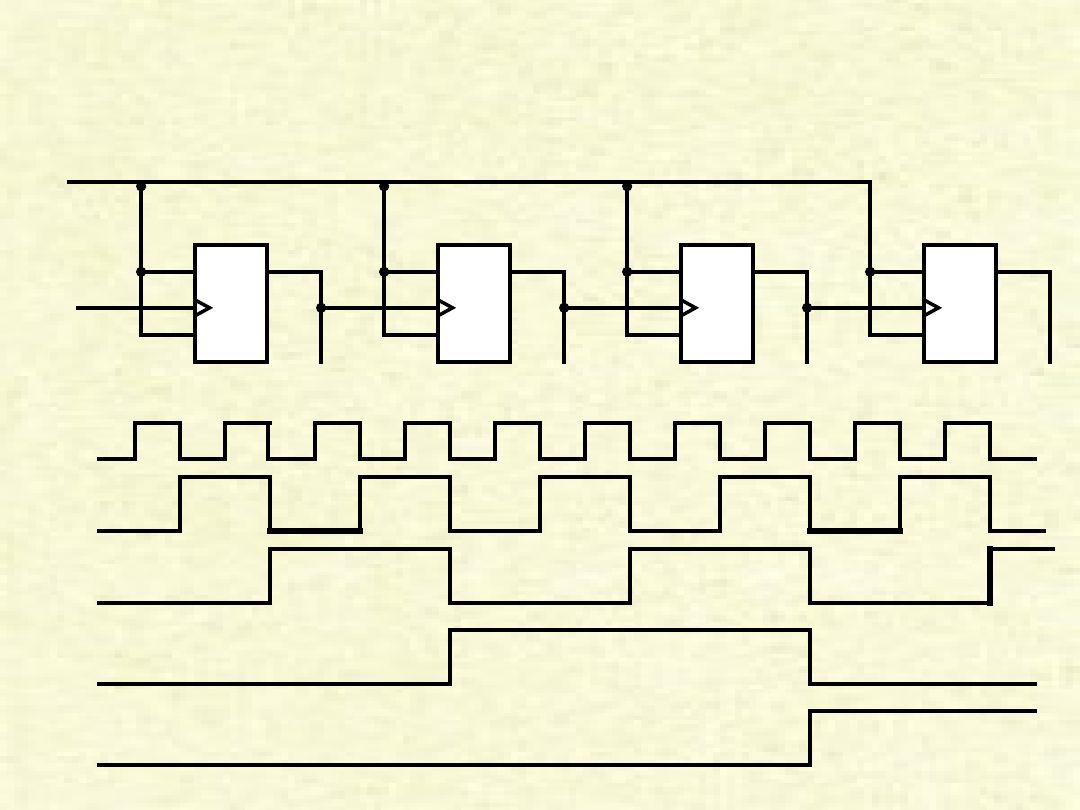
Licznik asynchroniczny

(szeregowy)

J Q

Ck

K Q’

J Q

Ck

K Q’

J Q

Ck

K Q’

J Q

Ck

K Q’

zegar

poziom
wysoki

Q

0

Q

1

Q

2

Q

3

zeg

ar

Q

0

Q

1

Q

2

Q

3

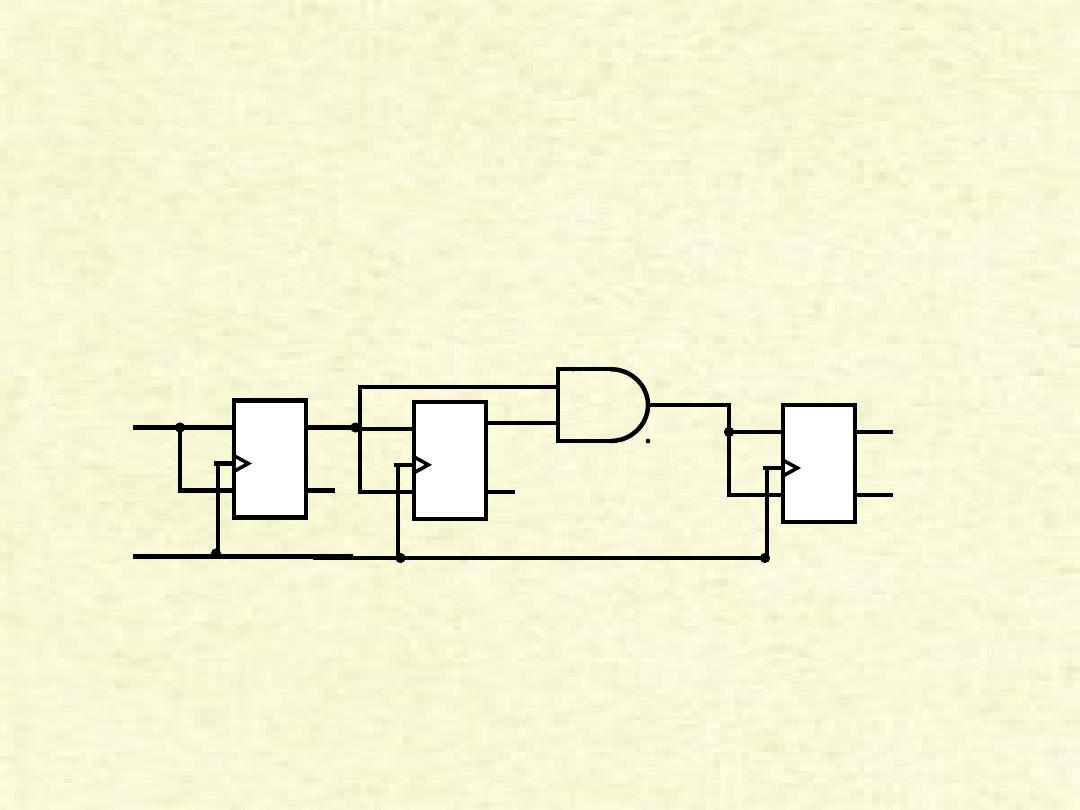
Licznik synchroniczny

J C

Ck

K C’

J B

Ck

K B’

J A

Ck

K A’

wysoki

zegar