Weryfikacja hipotez 
statystycznych, 
parametryczne testy 
istotności w populacji

Dr Joanna Banaś

Zakład Matematyki Stosowanej

Katedra Metod Sztucznej Inteligencji i Matematyki 

Stosowanej

Wykład

 

    

 

9

Metody probabilistyczne i statystyka

Wydział Informatyki Zachodniopomorskiego Uniwersytetu 

Technologicznego w Szczecinie

 

 

23. Weryfikacja hipotez 
statystycznych

 



Cel weryfikacji hipotez statystycznych – ustalenie, czy 

estymacja parametrów populacji (lub jej rozkładu) 

uzyskana na podstawie próbki jest do przyjęcia



Działanie



porównanie wyników otrzymanych z próbki z założeniami 

teoretycznymi



porównanie wyników otrzymanych z dwóch próbek

         Określamy przy tym, czy porównywane wyniki różnią się 

w sposób istotny, czy przypadkowy



Podstawowe pojęcia



hipoteza statystyczna



test statystyczny          

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

 

 

Podstawowe pojęcia

 



Hipoteza statystyczna – dowolne przypuszczenie o 

nieznanym rozkładzie badanej cechy populacji, o 

prawdziwości lub fałszywości którego wnioskuje się w 

oparciu o pobraną próbkę



Hipoteza nieparametryczna – przypuszczenie dotyczy postaci 

rozkładu cechy populacji



Hipoteza parametryczna – przypuszczenie dotyczy wartości 

parametrów rozkładu cechy populacji



Test statystyczny – reguła postępowania, która każdej 

możliwej realizacji próby (x

1

,…, x

n

) przyporządkowuje (z 

ustalonym prawdopodobieństwem) decyzję przyjęcia albo 

odrzucenia sprawdzanej hipotezy



Test parametryczny – dotyczy hipotezy parametrycznej



Test nieparametryczny (test zgodności) – dotyczy hipotezy 

nieparametrycznej

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

 

 

Elementy testu 
statystycznego



X – badana cecha populacji



H

0

 – pewna hipoteza statystyczna, dotycząca 

rozkładu cechy X, zwana hipotezą zerową



H

1

 – hipoteza alternatywna, którą będziemy skłonni 

przyjąć, gdyby H

0 

okazała się fałszywa



Statystyka testowa albo sprawdzian – statystyka U

n

 

= U

n

 (X

1

,…, X

n

), dobrana jako miernik rozbieżności 

między wynikami próby a postacią hipotetyczną



Obszar krytyczny – przedział liczbowy K, do którego 

prawie na pewno nie powinna należeć żadna 

realizacja statystyki U

n

, jeśli H

0

 jest prawdziwa

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

 

 

Błędy przy podejmowaniu 
decyzji

 



Dla próbki (x

1

,…, x

n

) wartości cechy X obliczamy u

n

 = U

n

 (X

1

,

…, X

n

) 

i podejmujemy jedną z decyzji:



odrzucamy  H

0

  i  przyjmujemy  H

1

,  jeśli  u

n

 K



przyjmujemy  H

0

  i  odrzucamy  H

1

,  jeśli  u

n

 K



Przy weryfikacji hipotezy w oparciu o wyniki próbki można 

popełnić dwa rodzaje błędów:



błąd pierwszego rodzaju – odrzucenie hipotezy H

0

, gdy jest ona 

prawdziwa (prawdopodobieństwo popełnienia tego błędu 

nazywamy poziomem istotności i oznaczamy przez )

(23.1)                                = P (U

n

 K / H

0

)



błąd drugiego rodzaju – przyjęcie hipotezy H

0

, gdy jest ona 

fałszywa (prawdopodobieństwo popełnienia oznaczamy przez )

(23.2)                     = P (U

n 

 K / H

1

) = 1 P (U

n 

 K / H

1

) 

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

 

 

Błędy przy podejmowaniu 
decyzji



Tablica 23.1. Decyzje słuszne i błędy przy podejmowaniu decyzji

 



Dla ustalonego (0,1) bliskiego zera, obszar krytyczny K dobiera się 

tak, aby  było możliwie najmniejsze (wówczas test jest najmocniejszy)

 



Ponieważ najczęściej  jest dość duże, albo nie jest znane, zamiast 

wysoce ryzykownej decyzji „przyjmujemy H

0

„ podejmujemy 

ostrożniejszą: 

                                 „nie ma podstaw do odrzucenia H

0

„



Testy istotności – testy, w których nie uwzględnia się błędu 2-go 

rodzaju

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

Sytuacja

Decyzja

H

0 

– prawdziwa

H

0 

– fałszywa

Przyjęcie H

0

decyzja słuszna

1 – 

błąd 2-go rodzaju



Odrzucenie H

0

błąd 1-go rodzaju



decyzja słuszna

1 – 

 

 

24

. Parametryczne testy istotności 

      w populacji



(24.1) Wartość oczekiwana (średnia)



Model 1 (rozkład normalny, znana wariancja)

         X – zmienna losowa o rozkładzie normalnym N(m,), 

wartość oczekiwana m = EX nie jest znana, 

wariancja  

2

 = D

2

X  jest znana

        Statystyka

        ma rozkład  N(0,1) przy założeniu prawdziwości 

hipotezy zerowej 

H

0

: m = m

0

        Dla przykładu pokażemy konstrukcję obszaru 

krytycznego dla hipotezy alternatywnej  H

1

: m > m

0

 

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

0

X m

U

n

-

=

s

 

 

Weryfikacja hipotezy dotyczącej 
wartości średniej – model 1

         Dla ustalonego (0,1) mamy

 = P (U K / m = m

0

)

         Obszar krytyczny K dobiera się tak, aby  było możliwie 

najmniejsze, 

tzn.   P (U

 

 K / H

1

)    było największe

         Ponieważ  H

1

: m > m

0

,  więc 

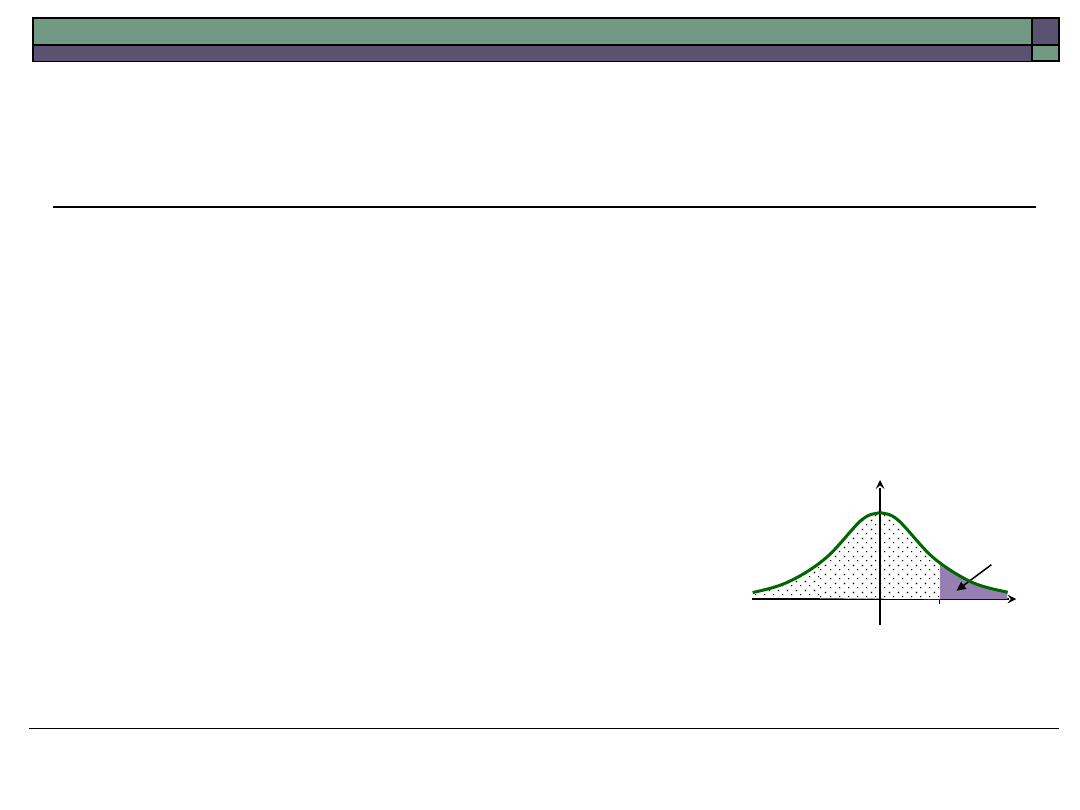
 = P (U  k) = 1  P (U < k) = 1  (k)     dla pewnego k

         Stąd  (k) = 1
         Oznacza to, że  k  jest kwantylem rzędu 1

  

i  będziemy go oznaczać przez  u(1)

         W rezultacie                          

K = u(1); )

         Dla pozostałych hipotez obszary krytyczne buduje się analogicznie

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

( )

f x

0

0.1

(0,1)

N

k

1- a

a

Rys.24.1. Gęstość rozkładu 

N(0,1)

 

 

Weryfikacja hipotezy dotyczącej 
wartości średniej – model 1

         

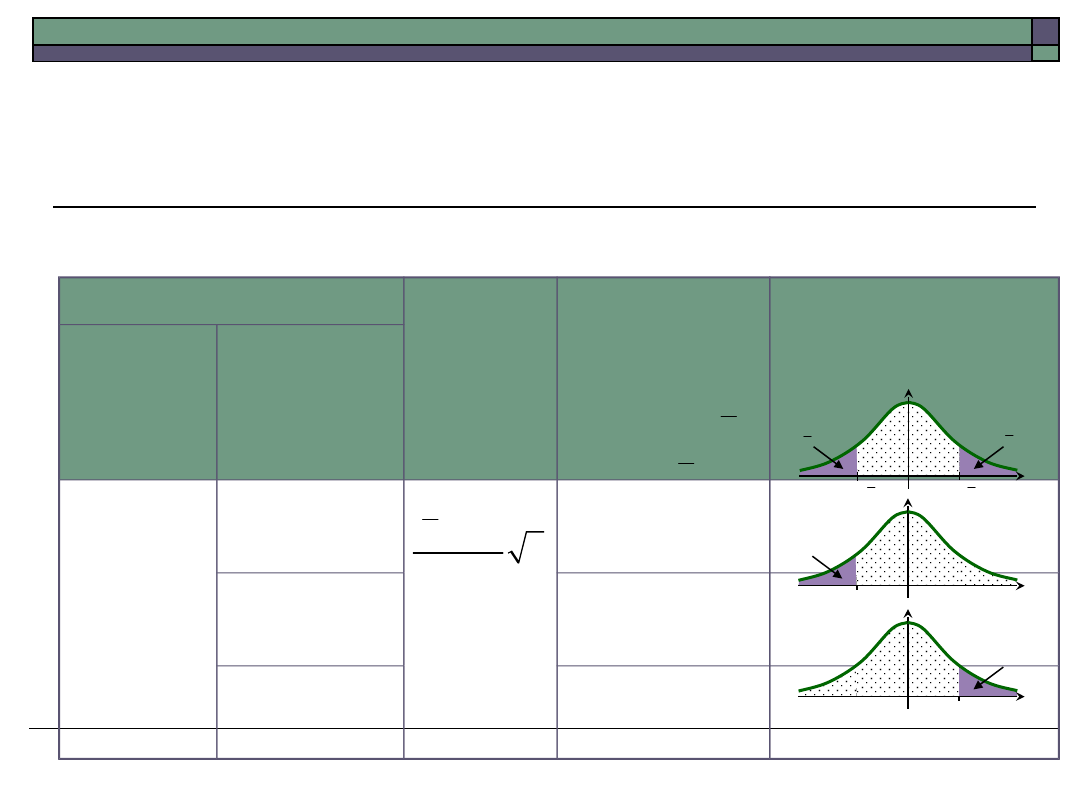
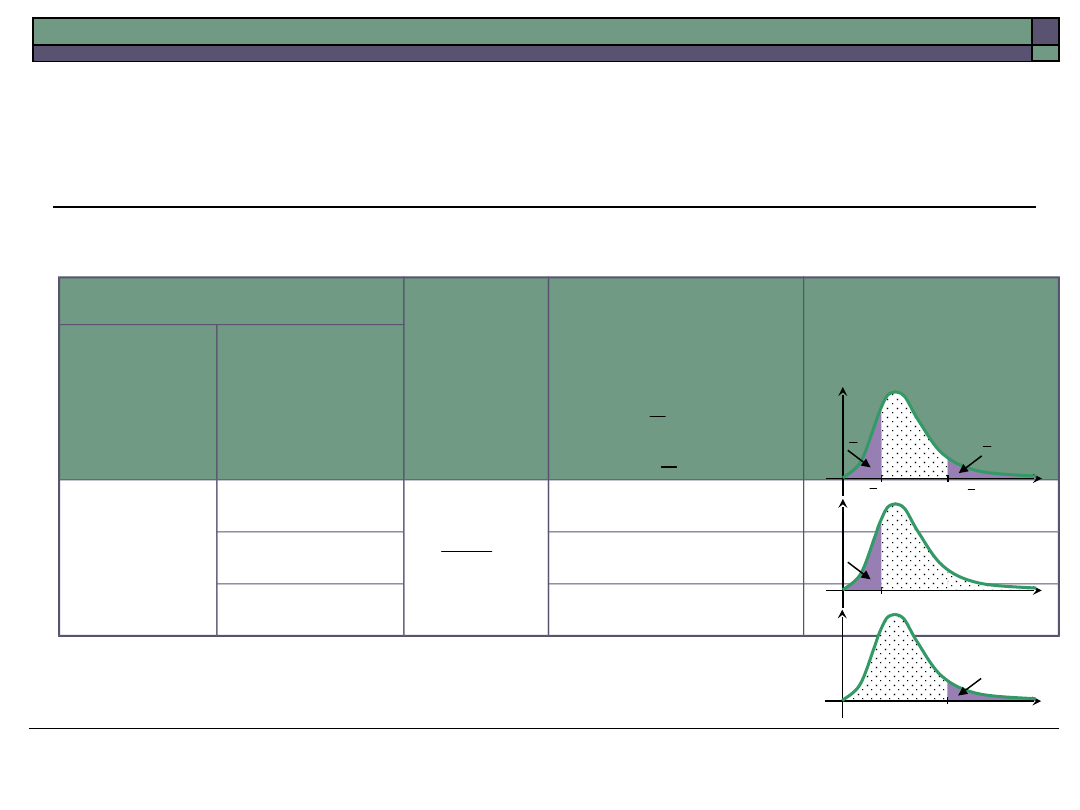
Tablica 24.1. Tablica testu dla średniej – model 1

 

 

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

Hipoteza

Statysty

ka 

testowa 

U

Obszar 

krytyczny K

Uwagi

zerowa

alternatyw

na

H

0

: m = 

m

0

H

1

: m  

m

0

H

1

: m < 

m

0

H

1

: m > 

m

0

0

X m n

-

s

2

2

(

; (1

)

(1

); )

u

u

a

a

- �-

-

�

�� -

�

0

0.1

(0,1)

N

2

(1

)

u

a

-

1- a

2

a

2

(1

)

u

a

-

-

2

a

0

0.1

(0,1)

N

(1

)

u - a

1- a

a

0

0.1

(0,1)

N

(1

)

( )

u

u

-

- a = a

1- a

a

(

; (1

)

u

- �-

- a �

(1

); )

u

� - a �

 

 

Weryfikacja hipotezy dotyczącej 
wartości średniej – model 1



Przykład (do modelu 1)



Norma przewiduje, że waga produkowanego wyrobu 

powinna wynosić 50 dag



Wysunięto przypuszczenie, że producent zawyża wagę 

wyrobów



Aby potwierdzić przypuszczenie wylosowano 16 

wyrobów, dla których średnia waga wynosiła 51 dag



Wiadomo, że odchylenie standardowe wynosi 1.1 dag



Waga wyrobów ma rozkład normalny

       Na poziomie istotności 0.05 zweryfikować 

hipotezę, że waga wyrobów według normy i 

waga rzeczywista są równe wobec hipotezy 

alternatywnej, że są różne

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

 

 

Weryfikacja hipotezy dotyczącej 
wartości średniej – model 2



Model 2 (rozkład normalny, parametry nieznane)

        X – zmienna losowa o rozkładzie normalnym N(m,), 

parametry m  i    nie są znane

       Statystyka

       ma rozkład Studenta z n1 stopniami swobody przy 

założeniu, że prawdziwa jest hipoteza zerowa  H

0

: m = 

m

0

       Ponieważ funkcja gęstości rozkładu Studenta ma 

podobne własności jak krzywa Gaussa, obszary 

krytyczne dla hipotez alternatywnych  H

1

: m  m

0

 ,  H

1

: 

m < m

0 

 oraz  H

1

: m > m

0

  buduje się podobnie jak w 

modelu 1

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

0

1

X m

t

n

S

-

=

-

 

 

Weryfikacja hipotezy dotyczącej 
wartości średniej – model 2

         

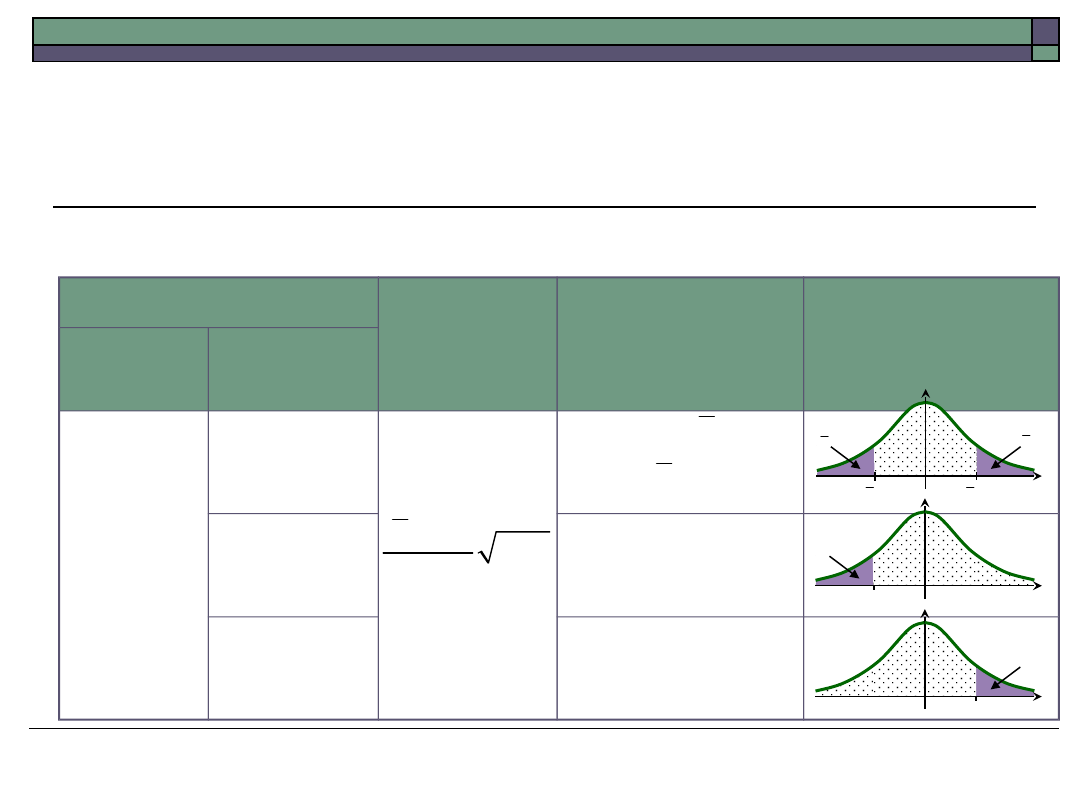
Tablica 24.2. Tablica testu dla średniej – model 2

 

 

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

Hipoteza

Statystyka 

testowa t

Obszar 

krytyczny K

Uwagi

zerowa

alternaty

wna

H

0

: m = 

m

0

H

1

: m  

m

0

H

1

: m < 

m

0

H

1

: m > 

m

0

0

1

X m n

S

-

-

2

2

(

; (1

,

1)

(1

,

1); )

t

n

t

n

a

a

- �-

-

- �

�� -

-

�

0

0.1

t

2

(1

,

1)

t

n

a

-

-

1- a

2

a

2

(1

,

1)

t

n

a

-

-

-

2

a

0

0.1

t

(1

,

1)

t

n

- a -

1- a

a

0

0.1

t

(1

,

1)

t

n

-

- a -

1- a

a

(

; (1

,

1)

t

n

- �-

- a - �

(1

,

1); )

t

n

� - a -

�

 

 

Weryfikacja hipotezy dotyczącej 

wartości średniej – model 2



Przykład (do modelu 2)



Norma przewiduje, że średni czas potrzebny na 

wykonanie pewnego detalu wynosi 1.5 h



Robotnicy skarżą się, że czas ten jest zbyt krótki



Aby sprawdzić zasadność skargi, zmierzono faktyczny 

czas produkcji 17 losowo wybranych detali i 

otrzymano wartość średniej z próbki 1.6 h, a 

odchylenia standardowego 0.2 h



Zakładamy, że czas potrzebny do wykonania detalu 

jest zmienną losową o rozkładzie normalnym

       Na poziomie istotności 0.05 stwierdzić, czy 

uzyskane wyniki stanowią podstawę do 

zwiększenia normy

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

 

 

Weryfikacja hipotezy dotyczącej 

wartości średniej – model 3



Model 3 (rozkład nieznany, duża próba  n  100 )

         X – zmienna losowa o nieznanym rozkładzie, istnieją wartość 

oczekiwana  

EX = m  i  wariancja  

2

 = D

2

X  > 0

         Jeśli próba jest duża  ( n  100 ),  to statystyka
       

         ma w przybliżeniu rozkład normalny N(0,1), a nieznaną wartość 

parametru  możemy oszacować za pomocą estymatora S, gdzie

         W rezultacie do weryfikacji hipotez stosujemy statystykę 

         przy założeniu, że prawdziwa jest hipoteza zerowa  H

0

: m = m

0

        Obszary krytyczne dla hipotez alternatywnych  H

1

: m  m

0

 ,  H

1

: m 

< m

0 

 oraz  H

1

: m > m

0

  wyznaczamy tak samo jak w modelu 1

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

X m

U

n

-

=

s

(

)

2

2

1

1

n

i

n

i

S

X

X

=

=

-

�

0

X m

U

n

S

-

=

 

 

Weryfikacja hipotezy dotyczącej 
wariancji – model 1



(24.2) Wariancja (lub odchylenie standardowe)



Model 1 (rozkład normalny, parametry nieznane)

         X – zmienna losowa o rozkładzie normalnym 

N(m,), 

 parametry m  i    nie są znane

        Statystyka

       ma rozkład  

2

  z  n



1  stopniami swobody przy 

założeniu, że prawdziwa jest hipoteza zerowa  

H

0

: 

2

 = 

02 

 ( lub  H

0

:  = 

0 

)

 

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

2

2

2

0

nS

c =

s

 

 

Weryfikacja hipotezy dotyczącej 
wariancji – model 1

         

Tablica 24.3. Tablica testu dla wariancji – model 1

 

 

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

Hipoteza

Statysty

ka 

testowa 



2

Obszar 

krytyczny K

Uwagi

zerowa

alternatyw

na

H

0

: 

2

 = 



0

2

H

1

: 

2

  

0

2

H

1

: 

2

 < 

0

2

H

1

: 

2

 > 

0

2

2

2

0

nS

s

2

2

2

2

0; ( ,

1)

(1

,

1); )

n

n

a

a

� c

- ��

�

c

-

-

�

2

a

1- a

2

2

( ,

1)

n

a

c

-

2

a

( )

f x

0

x

2

c

2

2

(1

,

1)

n

a

c

-

-

1- a

2

( ,

1)

n

c a -

a

( )

f x

0

x

2

c

x

2

0; ( ,

1)

n

� c a - �

2

(1

,

1); )

n

�

c

- a -

�

a

1- a

( )

f x

0

x

2

c

2

(1

,

1)

n

c

- a -

 

 

Weryfikacja hipotezy dotyczącej 
wariancji – model 1



Przykład (do modelu 1)



Dokonano 10 pomiarów pewnej wielkości



Otrzymano odchylenie standardowe z próbki 

1.5



W teorii pomiarów zakładamy, że wynik 

pomiaru jest zmienną losową o rozkładzie 

normalnym N(m,), zaś odchylenie 

standardowe jest miarą dokładności pomiarów

      Zweryfikować hipotezę  H

0

:  = 1.0  

wobec hipotezy alternatywnej  H

1

:  > 1.0 

 na poziomie istotności 0.05

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

 

 

Weryfikacja hipotezy dotyczącej 
wariancji – model 2



Model 2 (rozkład normalny, duża próba  n  50 )

         X – zmienna losowa o rozkładzie normalnym N(m,), 

 parametry m  i    nie są znane

         Jeśli próba jest duża  ( n  50 ),  to statystyka
       

        ma w przybliżeniu rozkład normalny N(0,1), przy 

założeniu, że prawdziwa jest hipoteza zerowa  H

0

: 

2

 = 



02 

 ( lub  H

0

:  = 

0 

)

 

        Obszary krytyczne dla hipotez alternatywnych  
        H

1

: 

2

  

02

,  H

1

: 

2

 < 

02  

oraz  H

1

: 

2

 > 

02  

        wyznaczamy tak samo jak w modelu 1 dla średniej

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

2

2

2

3

U

n

= c -

-

 

 

Weryfikacja hipotezy dotyczącej 
wariancji – model 3



Model 3 (rozkład nieznany, duża próba  n  100 )

         X – zmienna losowa o  dowolnym rozkładzie 

 o skończonej wariancji 

2

 > 0

         Jeśli próba jest duża  ( n  100 ),  to statystyka

       

        ma w przybliżeniu rozkład normalny N(0,1), przy 

założeniu, że prawdziwa jest hipoteza zerowa  H

0

: 

2

 = 



02 

 ( lub  H

0

:  = 

0 

)

 

        Obszary krytyczne dla hipotez alternatywnych  
        H

1

: 

2

  

02

,  H

1

: 

2

 < 

02  

oraz  H

1

: 

2

 > 

02  

        wyznaczamy tak samo jak w modelu 1 dla średniej

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

2

2

0

2

0

ˆ

2

S

n

U

- s

=

s

 

 

Weryfikacja hipotezy dotyczącej 
wariancji



Przykład



Wylosowano 200 robotników pewnego zakładu



Zbadano stopień wykonania normy [%]



Wyniki przedstawiono w szeregu rozdzielczym

      

       Na poziomie istotności 0.05 zweryfikować 

hipotezę, że odchylenie standardowe stopnia 

wykonania normy jest równe 10 % wobec 

hipotezy alternatywnej, że jest mniejsze od 10 %

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

Stopień wykonania 

normy [%]

70 80 90 100 110 120 130 140 150

Liczba 
pracowników

3

15 29 70 50 17 12

3

1

 

 

Weryfikacja hipotezy o 
wskaźniku struktury



(24.3) Wskaźnik struktury



Model (rozkład 0-1, parametr p nieznany, duża próba  n  100 )

         X – zmienna losowa o rozkładzie 0-1, parametr p nie jest znany
         Jeśli próba jest duża  ( n  100 ),  to statystyka

        

         gdzie M jest zmienną losową, której wartości są liczbami 

wyróżnionych elementów w n-elementowej próbce, ma rozkład w 

przybliżeniu normalny N(0,1), przy założeniu, że prawdziwa jest 

hipoteza zerowa  H

0

: p = p

0

        Obszary krytyczne dla hipotez alternatywnych  
        H

1

: p  p

0

,  H

1

: p < p

0

  oraz  H

1

: p > p

0

 

        wyznaczamy tak samo jak w modelu 1 dla średniej

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

0

0

0

(1

)

M

n

p

U

p

p

n

-

=

-

 

 

Weryfikacja hipotezy o 
wskaźniku struktury



Przykład



Zbadano 2000 pacjentów pewnego szpitala



8 % miało grupę krwi AB



25 % pacjentów z grupą krwi AB miało 

czynnik RH–

      Na poziomie istotności 0.01 

zweryfikować hipotezę, ze odsetek 

osób o grupie krwi AB RH– wynosi 3 % 

wobec alternatywnej, że jest mniejszy 

niż 3 %

Wykład 

 

9

Opracowała Joanna Banaś

Metody probabilistyczne i statystyka

 

 

Wykład

 

    

 

9

Metody probabilistyczne i statystyka

Dziękuję za uwagę

Opracowała Joanna Banaś