
WYKŁAD 5
WYKŁAD 5
1
1
BŁĘDY PRZYPADKOWE
BŁĘDY PRZYPADKOWE powstają w efekcie
oddziaływania czynników, które są
niezdeterminowane. Badaniem modeli takich
zjawisk zajmuje się rachunek prawdopodobieństwa
i statystyka matematyczna

WYKŁAD 5
WYKŁAD 5
2
2
BŁĘDY PRZYPADKOWE
Czy na podstawie zbioru wartości
Czy na podstawie zbioru wartości
uzyskanych w wyniku realizacji serii
uzyskanych w wyniku realizacji serii
n
n
pomiarów, można w jakikolwiek
pomiarów, można w jakikolwiek
sposób oszacować nieznaną wartość
sposób oszacować nieznaną wartość
rzeczywistą mierzonego stanu
rzeczywistą mierzonego stanu
q
q
wielkości Q, nasilenie występujących
wielkości Q, nasilenie występujących
w założonym pomiarze błędów
w założonym pomiarze błędów
przypadkowych oraz podać
przypadkowych oraz podać
jakakolwiek miarę jakości tych
jakakolwiek miarę jakości tych
oszacowań ?
oszacowań ?

WYKŁAD 5
WYKŁAD 5
3
3
BŁĘDY PRZYPADKOWE
Ocena wartości rzeczywistej mierzonego
Ocena wartości rzeczywistej mierzonego
stanu oraz nasilenia występujących w
stanu oraz nasilenia występujących w
danym pomiarze błędów przypadkowych,
danym pomiarze błędów przypadkowych,
jak też jakości tych oszacowań zależy
jak też jakości tych oszacowań zależy
przede wszystkim od rodzaju
przede wszystkim od rodzaju
prawa
prawa
probablistycznego
probablistycznego
, jakie tymi błędami
, jakie tymi błędami
rządzi.
rządzi.
Podstawową charakterystyką błędów
Podstawową charakterystyką błędów
przypadkowych jest ich tzw.
przypadkowych jest ich tzw.
rozkład
rozkład
prawdopodobieństwa
prawdopodobieństwa
, który określa
, który określa
zarówno wartości błędów mogących się
zarówno wartości błędów mogących się
pojawić w danym pomiarze, jak i
pojawić w danym pomiarze, jak i
odpowiadające tym wartościom szanse ich
odpowiadające tym wartościom szanse ich
pojawienia się.
pojawienia się.

WYKŁAD 5
WYKŁAD 5
4
4
BŁĘDY PRZYPADKOWE
BŁĘDY PRZYPADKOWE
OKREŚLENIA PODSTAWOWE
1. Populacja generalna (populacja wyników, liczność zbioru, ciągłość)
2. Próba losowa (liczność próby)
3. Sposób pobrania próby
4. Rozkład normalny (Gaussa)
5. Estymacja parametryczna:
- punktowa
- przedziałowa
6. Estymacja nieparametryczna

WYKŁAD 5
WYKŁAD 5
5
5
PRZYKŁAD:
Napięcie na zaciskach pewnego zasilacza zostało zmierzone
woltomierzem 21 razy. Uzyskano wyniki, które zestawiono w
załączonej tabeli.
Czy uzyskane wyniki podlegają prawom rządzącym błędami
przypadkowymi ?
► założenie: brak błędów systematycznych
►
pomiary zostały wykonane w tych samych warunkach
►
wyniki układają się wokół pewnej wartości, przy czym
liczba wyników
o wartościach mniejszych różni się niewiele od wyników
o wartościach większych
►
wyniki odbiegające niewiele od „średniej” pojawiają się
częściej niż
wyniki różniące się od niej znacznie
BŁĘDY PRZYPADKOWE
WYKŁAD 5
WYKŁAD 5
6
6
BŁĘDY PRZYPADKOWE
Nr
Nr
Wynik
Wynik
pomiaru
pomiaru
Błąd
Błąd
pomiar
pomiar
u
u
Kwadra
Kwadra
t błędu
t błędu
Nr
Nr
Wynik
Wynik
pomiar
pomiar
u
u
Błąd
Błąd
pomiar
pomiar
u
u
Kwadra
Kwadra
t błędu
t błędu
i
i
U
U
i
i
U
U
(U
(U
i
i
-
-
U)
U)
2
2
i
i
U
U
i
i
U
U
(U
(U
i
i
-
-
U)
U)
2
2
V
V
V
V
V
V
2
2
V
V
V
V
V
V
2
2
1
1
102,1
102,1
1,9
1,9
3,61
3,61
12
12
99,9
99,9
-0,3
-0,3
0,09
0,09
2
2
97.9
97.9
-2,3
-2,3
5,29
5,29
13
13
100,4
100,4
0,2
0,2
0,04
0,04
3
3
99,0
99,0
-1,2
-1,2
1,44
1,44
14
14
96,4
96,4
-3,8
-3,8
14,44
14,44
4
4
100,3
100,3
0,1
0,1
0,01
0,01
15
15
103,6
103,6
3,4
3,4
11,56
11,56
5
5
101,4
101,4
1,2
1,2
1,44
1,44
16
16
103,0
103,0
2,8
2,8
7,84
7,84
6
6
102,4
102,4
2,2
2,2
4,84
4,84
17
17
98,8
98,8
-1,4
-1,4
1,96
1,96
7
7
100,9
100,9
0,7
0,7
0,49
0,49
18
18
99,3
99,3
-0,9
-0,9
0,81
0,81
8
8
101,2
101,2
1,0
1,0
0,01
0,01
19
19
101,3
101,3
1,1
1,1
1,21
1,21
9
9
99,3
99,3
-0,9
-0,9
0,81
0,81
20
20
101,7
101,7
1,5
1,5
2,25
2,25
10
10
98,2
98,2
-2,0
-2,0
4,00
4,00
21
21
96,2
96,2
-4,0
-4,0
16,00
16,00
11
11
100,9
100,9
0,7
0,7
0,49
0,49
2104,2
2104,2
0,0
0,0
83,62
83,62
WYKŁAD 5
WYKŁAD 5
7
7
BŁĘDY PRZYPADKOWE
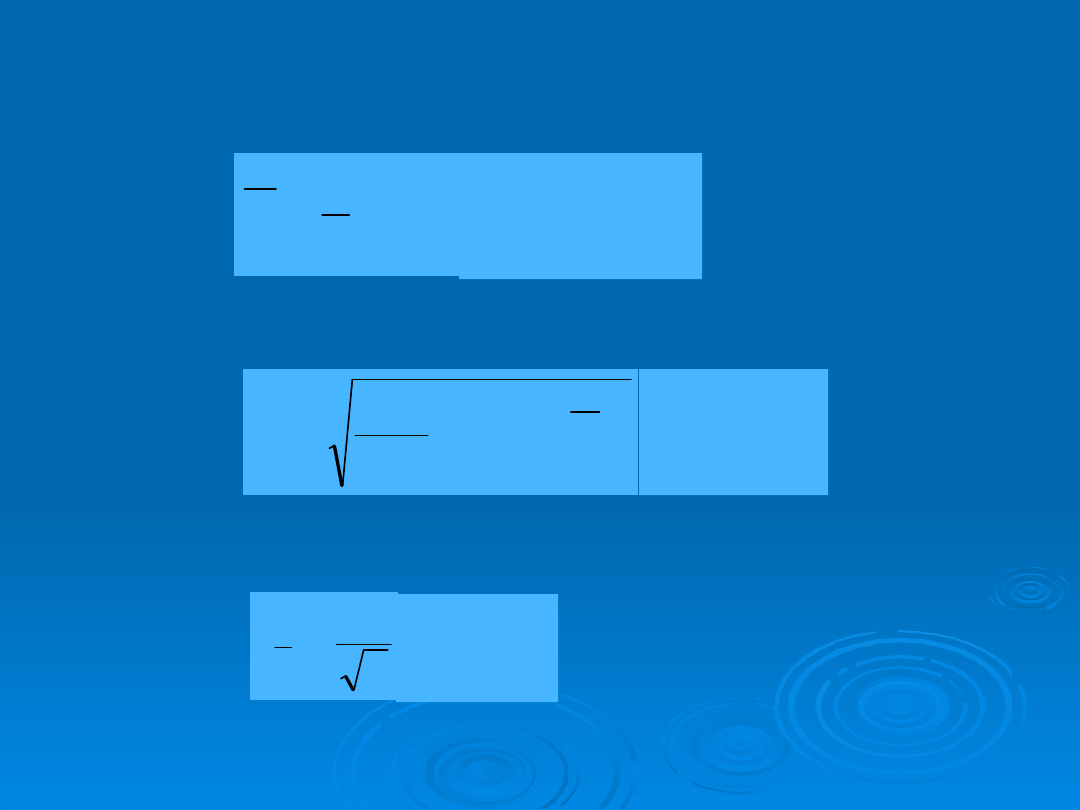
WARTOŚĆ ŚREDNIA
n
i
i
U
n
U
1
1
= 100,2
V
ODCHYLENIE STANDARDOWE
EMPIRYCZNE
n
i
i
U
U
U
n
s
1
2
1
1
= 2,04 V
ODCHYLENIE STANDARDOWE EMPIRYCZNE WARTOŚCI
ŚREDNIEJ
n
s
s
U
U
= 0,45
V
WYKŁAD 5
WYKŁAD 5
8
8
BŁĘDY PRZYPADKOWE
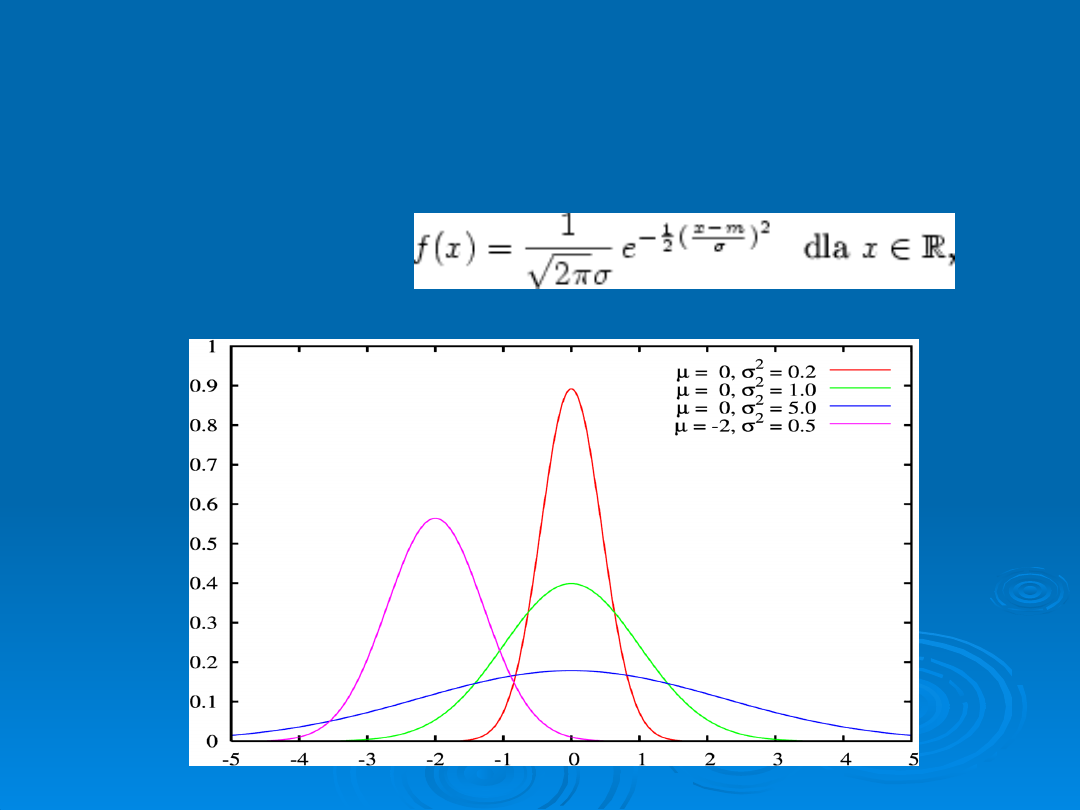
ROZKŁAD NORMALNY (Gaussa)
Rozkład nazywamy rozkładem normalnym, jeżeli istnieją takie liczby rzeczywiste
oraz , że funkcja , określona wzorem:
jest gęstością tego rozkładu.
WYKŁAD 5
WYKŁAD 5
9
9
BŁĘDY PRZYPADKOWE
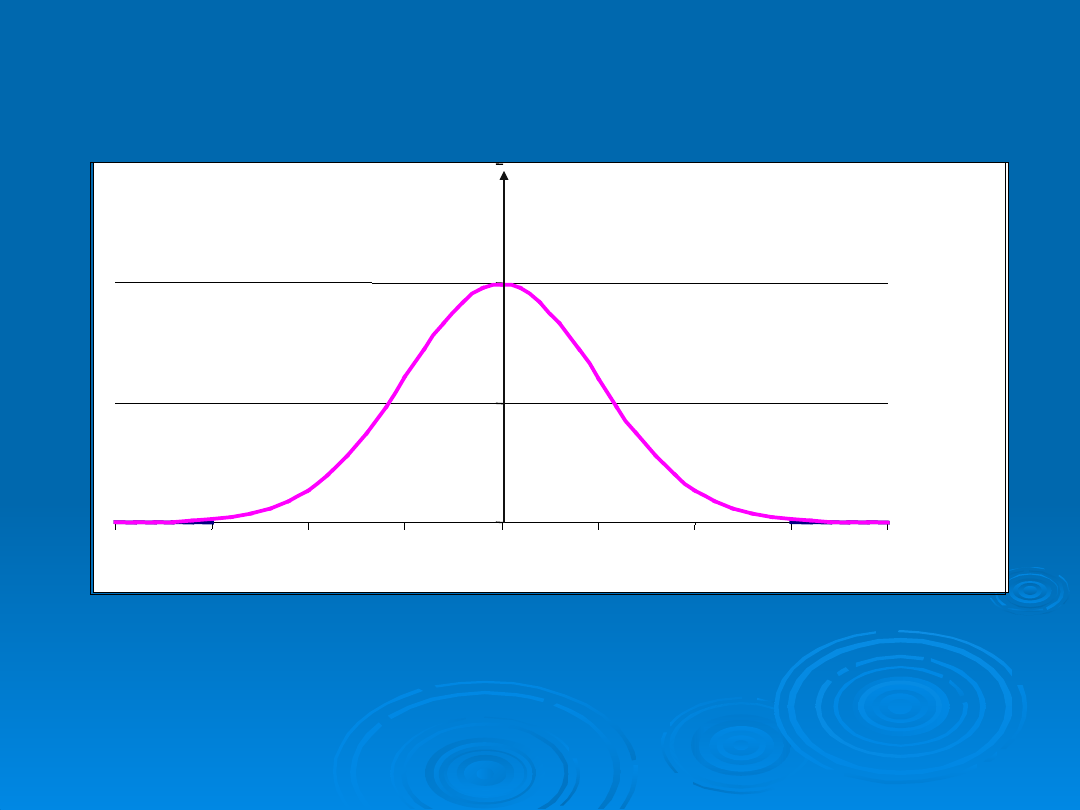
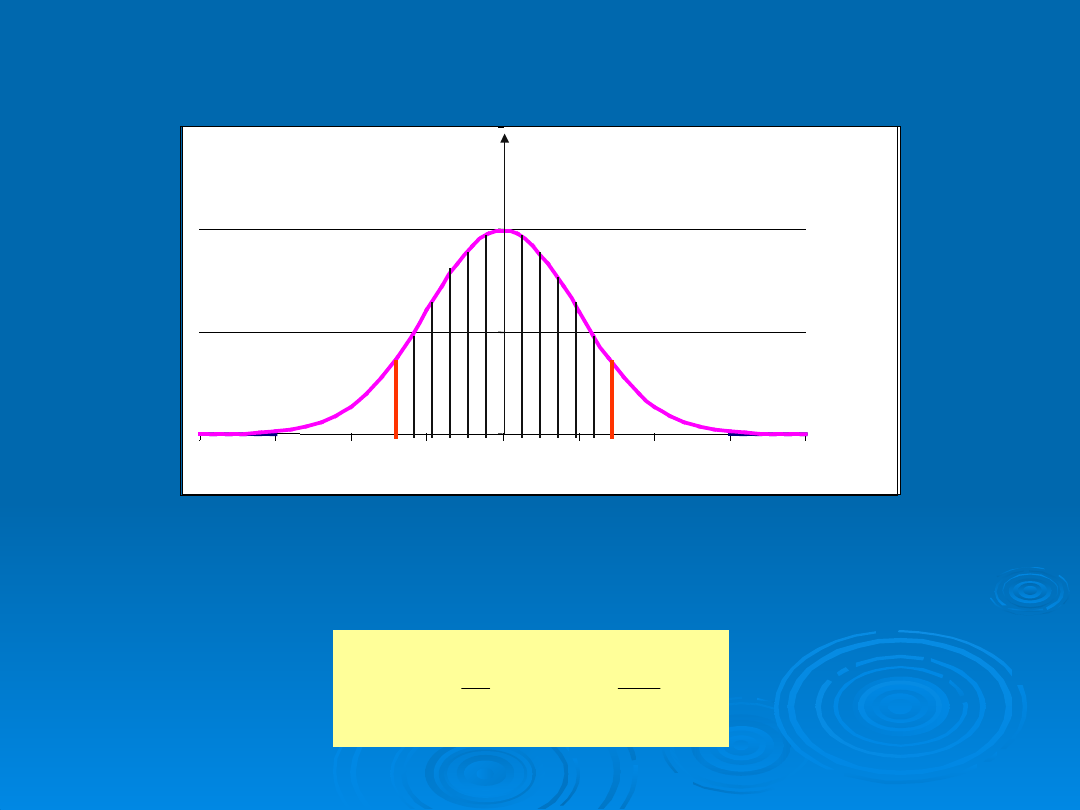
UNORMOWANY ROZKŁAD GAUSSA
0
0,2
0,4
-4
-3
-2
-1
0
1
2
3
4
N(0, 1) m = 0; =
1
WYKŁAD 5
WYKŁAD 5
10
10
BŁĘDY PRZYPADKOWE
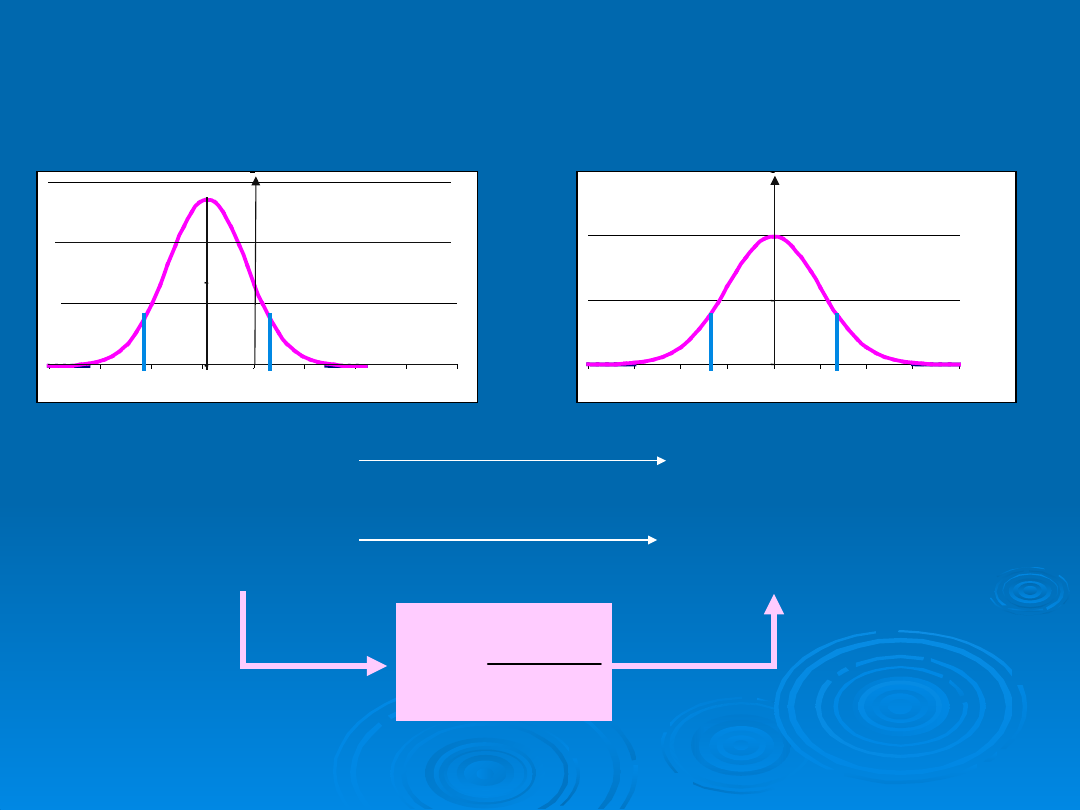
CAŁKA PRAWDOPODOBIEŃSTWA
0
0,2
0,4
-4
-3
-2
-1
0
1
2
3
4
y
0
-y
0
Całka prawdopodobieństwa (y
0
).
Część zakreskowana wyraża prawdopodobieństwo wyników
pomiarów w przedziale <-y
0
; y
0
>.
dy
y
y
y
0
0
2
0
2
exp
1
WYKŁAD 5
WYKŁAD 5
11
11
BŁĘDY PRZYPADKOWE
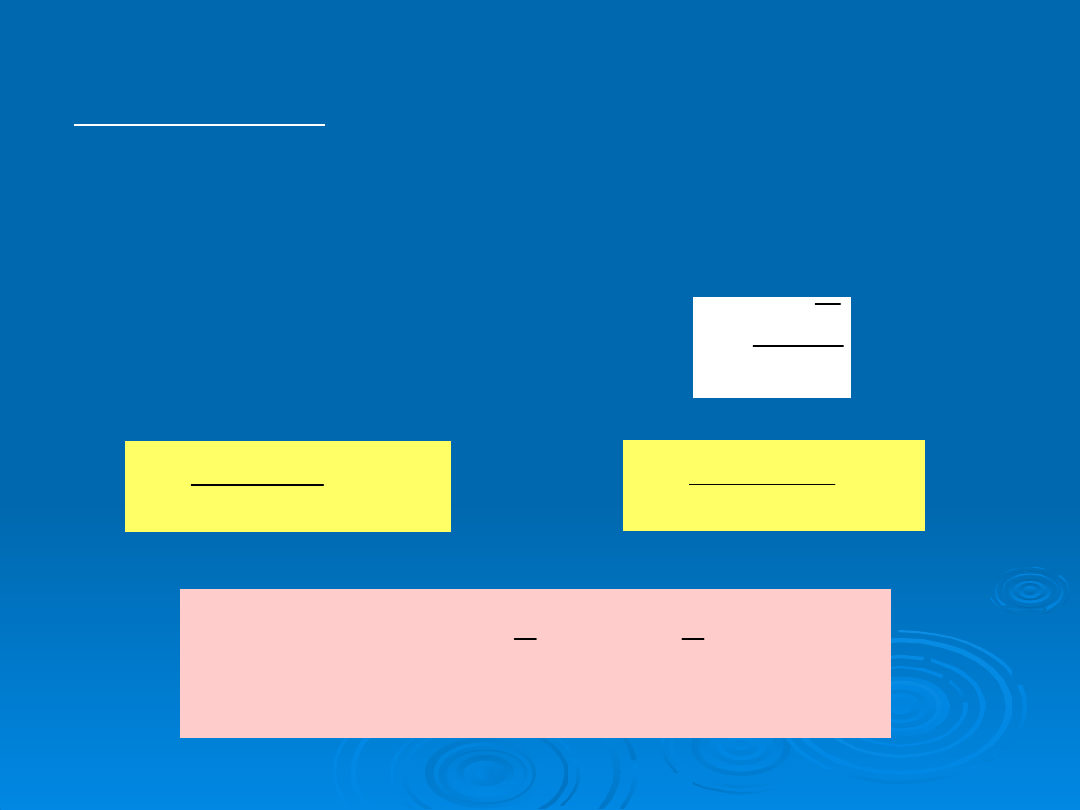
STANDARYZACJA
0
0,2
0,4
-4
-3
-2
-1
0
1
2
3
4
0
0,2
0,4
-4
-3
-2
-1
0
1
2
3
4
N(m, )
N(0, 1)
y
2
y
1
x
2
x
1
P(x
1
X x
2
)
P(y
1
Y y
2
)
m
x
y
i
1
f(x)
f(y)

WYKŁAD 5
WYKŁAD 5
12
12
BŁĘDY PRZYPADKOWE
UNORMOWANY ROZKŁAD GAUSSA -
tabelaryzacja
y = y
y = y
0
0
f(y)
f(y)
(y
(y
0
0
)
)
y = y
y = y
0
0
f(y)
f(y)
(y
(y
0
0
)
)
y = y
y = y
0
0
f(y)
f(y)
(y
(y
0
0
)
)
0,0
0,0
0,398
0,398
9
9
0,000
0,000
0
0
1,0
1,0
2,0
2,0
0,1
0,1
1,1
1,1
2,2
2,2
0,2
0,2
1,2
1,2
2,4
2,4
0,3
0,3
1,3
1,3
2,6
2,6
0,4
0,4
1,4
1,4
2,8
2,8
0,5
0,5
1,5
1,5
3,0
3,0
0,6
0,6
1,6
1,6
3,5
3,5
0,7
0,7
1,7
1,7
4,0
4,0
0,8
0,8
1,8
1,8
4,42
4,42
0,9
0,9
1,9
1,9
4,89
4,89
WYKŁAD 5
WYKŁAD 5
12
12
BŁĘDY PRZYPADKOWE
UNORMOWANY ROZKŁAD GAUSSA - tabelaryzacja
1
1
-
-
10
10
2,5
2,5
•
•
10
10
?
?
6
6
4,89
4,89
0,9426
0,9426
0,0656
0,0656
1,9
1,9
0,6319
0,6319
0,2661
0,2661
0,9
0,9
1
1
–
–
10
10
2,3
2,3
•
•
10
10
?
?
5
5
4,42
4,42
0,9281
0,9281
0,0790
0,0790
1,8
1,8
0,5763
0,5763
0,2897
0,2897
0,8
0,8
0,9999
0,9999
0,0001
0,0001
4,0
4,0
0,9109
0,9109
0,0940
0,0940
1,7
1,7
0,5161
0,5161
0,3123
0,3123
0,7
0,7
0,9995
0,9995
0,0009
0,0009
3,5
3,5
0,8904
0,8904
0,1109
0,1109
1,6
1,6
0,4515
0,4515
0,3332
0,3332
0,6
0,6
0,9973
0,9973
0,0044
0,0044
3,0
3,0
0,8664
0,8664
0,1295
0,1295
1,5
1,5
0,3829
0,3829
0,3521
0,3521
0,5
0,5
0,9949
0,9949
0,0079
0,0079
2,8
2,8
0,8385
0,8385
0,1497
0,1497
1,4
1,4
0,3108
0,3108
0,3683
0,3683
0,4
0,4
0,9907
0,9907
0,0136
0,0136
2,6
2,6
0,8064
0,8064
0,1714
0,1714
1,3
1,3
0,2358
0,2358
0,3814
0,3814
0,3
0,3
0,9836
0,9836
0,0224
0,0224
2,4
2,4
0,7699
0,7699
0,1942
0,1942
1,2
1,2
0,1595
0,1595
0,3910
0,3910
0,2
0,2
0,9722
0,9722
0,0355
0,0355
2,2
2,2
0,7287
0,7287
0,2179
0,2179
1,1
1,1
0,0797
0,0797
0,3970
0,3970
0,1
0,1
0,9545
0,9545
0,0540
0,0540
2,0
2,0
0,6827
0,6827
0,2420
0,2420
1,0
1,0
0,0000
0,0000
0,3989
0,3989
0,0
0,0
(y
(y
0
0
)
)
f(y)
f(y)
y = y
y = y
0
0
(y
(y
0
0
)
)
f(y)
f(y)
y = y
y = y
0
0
(y
(y
0
0
)
)
f(y)
f(y)
y = y
y = y
0
0

WYKŁAD 5
WYKŁAD 5
13
13
BŁĘDY PRZYPADKOWE
PRZYKŁAD (c.d.)
Obliczmy prawdopodobieństwo:
P(98 V U 103 V)
Standaryzujemy zmienną U wg. wzoru:
U
s
U
U
y
078
,
1
04
,
2
2
,
100
98
1
y
37
,
1
04
,
2
2
,
100
103
1
y

WYKŁAD 5
WYKŁAD 5
14
14
BŁĘDY PRZYPADKOWE
UNORMOWANY ROZKŁAD GAUSSA -
tabelaryzacja
y = y
y = y
0
0
f(y)
f(y)
(y
(y
0
0
)
)
y = y
y = y
0
0
f(y)
f(y)
(y
(y
0
0
)
)
y = y
y = y
0
0
f(y)
f(y)
(y
(y
0
0
)
)
0,0
0,0
0,398
0,398
9
9
0,000
0,000
0
0
1,0
1,0
2,0
2,0
0,1
0,1
1,1
1,1
2,2
2,2
0,2
0,2
1,2
1,2
2,4
2,4
0,3
0,3
1,3
1,3
2,6
2,6
0,4
0,4
1,4
1,4
2,8
2,8
0,5
0,5
1,5
1,5
3,0
3,0
0,6
0,6
1,6
1,6
3,5
3,5
0,7
0,7
1,7
1,7
4,0
4,0
0,8
0,8
1,8
1,8
4,42
4,42
0,9
0,9
1,9
1,9
4,89
4,89
WYKŁAD 5
WYKŁAD 5
12
12
BŁĘDY PRZYPADKOWE
UNORMOWANY ROZKŁAD GAUSSA - tabelaryzacja
1
1
-
-
10
10
2,5
2,5
•
•
10
10
?
?
6
6
4,89
4,89
0,9426
0,9426
0,0656
0,0656
1,9
1,9
0,6319
0,6319
0,2661
0,2661
0,9
0,9
1
1
–
–
10
10
2,3
2,3
•
•
10
10
?
?
5
5
4,42
4,42
0,9281
0,9281
0,0790
0,0790
1,8
1,8
0,5763
0,5763
0,2897
0,2897
0,8
0,8
0,9999
0,9999
0,0001
0,0001
4,0
4,0
0,9109
0,9109
0,0940
0,0940
1,7
1,7
0,5161
0,5161
0,3123
0,3123
0,7
0,7
0,9995
0,9995
0,0009
0,0009
3,5
3,5
0,8904
0,8904
0,1109
0,1109
1,6
1,6
0,4515
0,4515
0,3332
0,3332
0,6
0,6
0,9973
0,9973
0,0044
0,0044
3,0
3,0
0,8664
0,8664
0,1295
0,1295
1,5
1,5
0,3829
0,3829
0,3521
0,3521
0,5
0,5
0,9949
0,9949
0,0079
0,0079
2,8
2,8
0,8385
0,8385
0,1497
0,1497
1,4
1,4
0,3108
0,3108
0,3683
0,3683
0,4
0,4
0,9907
0,9907
0,0136
0,0136
2,6
2,6
0,8064
0,8064
0,1714
0,1714
1,3
1,3
0,2358
0,2358
0,3814
0,3814
0,3
0,3
0,9836
0,9836
0,0224
0,0224
2,4
2,4
0,7699
0,7699
0,1942
0,1942
1,2
1,2
0,1595
0,1595
0,3910
0,3910
0,2
0,2
0,9722
0,9722
0,0355
0,0355
2,2
2,2
0,7287
0,7287
0,2179
0,2179
1,1
1,1
0,0797
0,0797
0,3970
0,3970
0,1
0,1
0,9545
0,9545
0,0540
0,0540
2,0
2,0
0,6827
0,6827
0,2420
0,2420
1,0
1,0
0,0000
0,0000
0,3989
0,3989
0,0
0,0
(y
(y
0
0
)
)
f(y)
f(y)
y = y
y = y
0
0
(y
(y
0
0
)
)
f(y)
f(y)
y = y
y = y
0
0
(y
(y
0
0
)
)
f(y)
f(y)
y = y
y = y
0
0
WYKŁAD 5
WYKŁAD 5
15
15
BŁĘDY PRZYPADKOWE
PRZYKŁAD (c.d.)
Obliczmy prawdopodobieństwo:
P(98 V U 103 V)
Standaryzujemy zmienną U wg. wzoru:
U
s
U
U
y
078
,
1
04
,
2
2
,
100
98
1
y
37
,
1
04
,
2
2
,
100
103
1
y
77
,
0
72
,
0
5
,
0
82
,
0
5
,
0
)
078
,
1
(
2
1
)
37
,
1
(
2
1
)
37
,
1
078
,
1
(
Y
P

WYKŁAD 5
WYKŁAD 5
16
16
BŁĘDY PRZYPADKOWE
PRZYKŁAD (c.d.)
Obliczmy prawdopodobieństwo:
)
(
k
U
U
k
U
P
i
Dla rozkładu normalnego:
k
= 1
P =
68,27 %
k
= 2
P =
95,45 %
k
= 3
P =
99,73 %

WYKŁAD 5
WYKŁAD 5
17
17
BŁĘDY PRZYPADKOWE
POZIOM UFNOŚCI
k
k
k
k
k
k
0,00
0,00
0,05
0,05
0,10
0,10
0,15
0,15
0,20
0,20
0,25
0,25
0,30
0,30
0,35
0,35
0,40
0,40
0,45
0,45
0,50
0,50
0,000
0,000
0,063
0,063
0,55
0,55
0,60
0,60
0,92
0,92
0,94
0,94
0,95
0,95
0,96
0,96
0,98
0,98
0,99
0,99
0,999
0,999
Tabela wartości k
przy zadanych wartościach poziomu
ufności dla rozkładu normalnego
WYKŁAD 5
WYKŁAD 5
15
15
BŁĘDY PRZYPADKOWE
POZIOM UFNOŚCI
1,751
1,751
1,881
1,881
1,960
1,960
2,054
2,054
2,326
2,326
2,576
2,576
3,291
3,291
0,92
0,92
0,94
0,94
0,95
0,95
0,96
0,96
0,98
0,98
0,99
0,99
0,999
0,999
0,756
0,756
0,842
0,842
0,935
0,935
1,036
1,036
1,151
1,151
1,282
1,282
1,341
1,341
1,405
1,405
1,476
1,476
1,555
1,555
1,645
1,645
0,55
0,55
0,60
0,60
0,65
0,65
0,70
0,70
0,75
0,75
0,80
0,80
0,82
0,82
0,84
0,84
0,86
0,86
0,88
0,88
0,90
0,90
0,000
0,000
0,063
0,063
0,126
0,126
0,189
0,189
0,253
0,253
0,319
0,319
0,385
0,385
0,454
0,454
0,524
0,524
0,598
0,598
0,675
0,675
0,00
0,00
0,05
0,05
0,10
0,10
0,15
0,15
0,20
0,20
0,25
0,25
0,30
0,30
0,35
0,35
0,40
0,40
0,45
0,45
0,50
0,50
k
k
k
k
k
k
Tabela wartości k
przy zadanych wartościach poziomu ufności dla
rozkładu normalnego

WYKŁAD 5
WYKŁAD 5
18
18
BŁĘDY PRZYPADKOWE
PRZYKŁAD (c.d.)
Obliczmy szerokość przedziału U, dla
którego:
99
,
0
)
(
U
U
U
U
U
P
i
z tabeli k
= k
0,99
=
2,576
U = k
s
U
= 2,576 2,04
=5,26
tak więc: P( 96,94 U
i
105,46) = 0,99
WYKŁAD 5
WYKŁAD 5
19
19
BŁĘDY PRZYPADKOWE
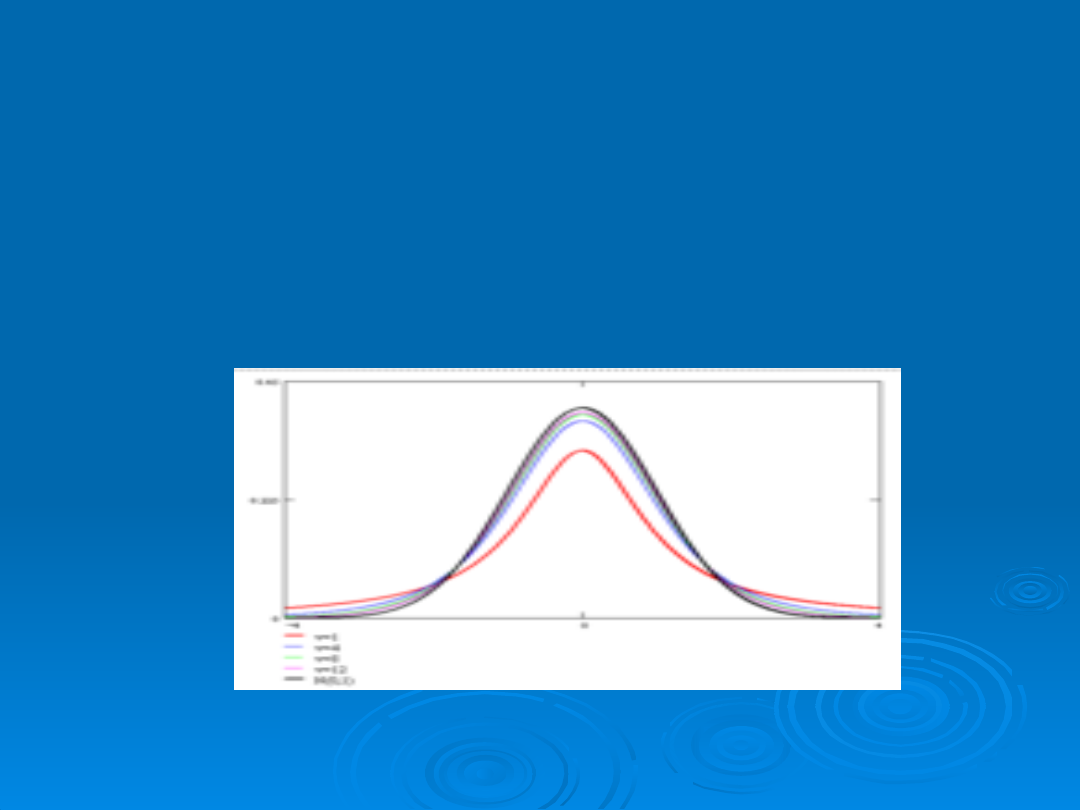
Poniższy wykres przedstawia gęstości rozkładu Studenta dla kilku
wartości liczby stopni swobody v w zestawieniu z gęstością
standardowego rozkładu normalnego N(0,1).
rozkłady Studenta porównane z rozkładem
normalnym
Rozkład Studenta jest symetryczny względem zera a jego ogólny
kształt jest podobny do kształtu standardowego
.
Jest to typ rozkładu najpowszechniej wykorzystywany w przypadku
testowania hipotez dotyczących wartości średniej określonej populacji.

WYKŁAD 5
WYKŁAD 5
20
20
Tabela wartości t
,n-1
przy zadanych wartościach
poziomu ufności dla rozkładu t Studenta (n – liczba
pomiarów)
n
n
n-1
n-1
t
t
,n-1
,n-1
= 0,90
= 0,90
=
=
0,95
0,95
=
=
0,99
0,99
=
=
0,99
0,99
=
=
0,999
0,999
5
5
6
6
7
7
8
8
9
9
10
10
11
11
12
12
13
13
14
14
15
15
16
16
17
17
19
19
21
21
31
31
51
51
81
81
101
101
4
4
5
5
6
6
7
7
8
8
9
9
10
10
11
11
12
12
13
13
14
14
15
15
16
16
18
18
20
20
30
30
50
50
80
80
100
100
2,132
2,132
2,015
2,015
1,943
1,943
1,895
1,895
1,860
1,860
1,833
1,833
1,812
1,812
1,796
1,796
1,782
1,782
1,771
1,771
1,761
1,761
1,753
1,753
1,746
1,746
1,734
1,734
1,725
1,725
1,697
1,697
1,676
1,676
1,664
1,664
1,660
1,660
1,645
1,645
2,776
2,776
2,571
2,571
2,447
2,447
2,365
2,365
2,306
2,306
2,262
2,262
2,228
2,228
2,201
2,201
2,179
2,179
2,160
2,160
2,145
2,145
2,131
2,131
2,120
2,120
2,103
2,103
2,084
2,084
2,042
2,042
2,008
2,008
1,990
1,990
1,984
1,984
1,960
1,960
3,747
3,747
3,365
3,365
3,143
3,143
2,998
2,998
2,896
2,896
2,821
2,821
2,764
2,764
2,718
2,718
2,681
2,681
2,650
2,650
2,624
2,624
2,602
2,602
2,583
2,583
2,552
2,552
2,528
2,528
2,457
2,457
2,403
2,403
2,374
2,374
2,364
2,364
2,326
2,326
4,604
4,604
4,032
4,032
3,707
3,707
3,499
3,499
3,355
3,355
3,250
3,250
3,169
3,169
3,106
3,106
3,055
3,055
3,012
3,012
2,977
2,977
2,947
2,947
2,921
2,921
2,878
2,878
2,845
2,845
2,750
2,750
2,677
2,677
2,639
2,639
2,626
2,626
2,576
2,576
8,610
8,610
6,589
6,589
5,959
5,959
5,405
5,405
5,041
5,041
4,781
4,781
4,587
4,587
4,487
4,487
4,318
4,318
4,221
4,221
4,140
4,140
4,073
4,073
4,015
4,015
3,922
3,922
3,850
3,850
3,646
3,646
3,497
3,497
3,416
3,416
3,391
3,391
3,291
3,291
WYKŁAD 5
WYKŁAD 5
21
21
BŁĘDY PRZYPADKOWE
)
(
1
,
1
,
U
n
i
U
n
s
t
U
U
s
t
U
P
Korzystając z rozkładu t Studenta można
obliczyć:
gdzie:
- poziom ufności
n-1- liczba stopni swobody
t
,n-1
s
U
- przedział ufności
PRZYKŁAD (c.d.)
Określić przedział, w którym z prawdopodobieństwem
0,99 znajdzie się kolejny wynik pomiaru

WYKŁAD 5
WYKŁAD 5
22
22
Tabela wartości t
,n-1
przy zadanych wartościach
poziomu ufności dla rozkładu t Studenta (n – liczba
pomiarów)
n
n
n-1
n-1
t
t
,n-1
,n-1
= 0,90
= 0,90
=
=
0,95
0,95
=
=
0,99
0,99
=
=
0,99
0,99
=
=
0,999
0,999
5
5
6
6
7
7
8
8
9
9
10
10
11
11
12
12
13
13
14
14
15
15
16
16
17
17
19
19
21
21
31
31
51
51
81
81
101
101
4
4
5
5
6
6
7
7
8
8
9
9
10
10
11
11
12
12
13
13
14
14
15
15
16
16
18
18
20
20
30
30
50
50
80
80
100
100
2,132
2,132
2,015
2,015
1,943
1,943
1,895
1,895
1,860
1,860
1,833
1,833
1,812
1,812
1,796
1,796
1,782
1,782
1,771
1,771
1,761
1,761
1,753
1,753
1,746
1,746
1,734
1,734
1,725
1,725
1,697
1,697
1,676
1,676
1,664
1,664
1,660
1,660
1,645
1,645
2,776
2,776
2,571
2,571
2,447
2,447
2,365
2,365
2,306
2,306
2,262
2,262
2,228
2,228
2,201
2,201
2,179
2,179
2,160
2,160
2,145
2,145
2,131
2,131
2,120
2,120
2,103
2,103
2,084
2,084
2,042
2,042
2,008
2,008
1,990
1,990
1,984
1,984
1,960
1,960
3,747
3,747
3,365
3,365
3,143
3,143
2,998
2,998
2,896
2,896
2,821
2,821
2,764
2,764
2,718
2,718
2,681
2,681
2,650
2,650
2,624
2,624
2,602
2,602
2,583
2,583
2,552
2,552
2,528
2,528
2,457
2,457
2,403
2,403
2,374
2,374
2,364
2,364
2,326
2,326
4,604
4,604
4,032
4,032
3,707
3,707
3,499
3,499
3,355
3,355
3,250
3,250
3,169
3,169
3,106
3,106
3,055
3,055
3,012
3,012
2,977
2,977
2,947
2,947
2,921
2,921
2,878
2,878
2,845
2,845
2,750
2,750
2,677
2,677
2,639
2,639
2,626
2,626
2,576
2,576
8,610
8,610
6,589
6,589
5,959
5,959
5,405
5,405
5,041
5,041
4,781
4,781
4,587
4,587
4,487
4,487
4,318
4,318
4,221
4,221
4,140
4,140
4,073
4,073
4,015
4,015
3,922
3,922
3,850
3,850
3,646
3,646
3,497
3,497
3,416
3,416
3,391
3,391
3,291
3,291

WYKŁAD 5
WYKŁAD 5
23
23
BŁĘDY PRZYPADKOWE
PRZYKŁAD (c.d.)
Z tabeli:
t
,n-1
= 2,845
a więc
100,2 – 2,845 2,04 U
i
100,2 2,845
94,4 U
i
106,0

WYKŁAD 5
WYKŁAD 5
24
24
POJĘCIA ZWIĄZANE Z OCENĄ
DOKŁADNOŚCI POMIARÓW
▀ PRECYZJA (Precision):
rozdzielczość
(discrimination) – zdolność narzędzia
pomiarowego do reagowania na małe zmiany wartości
wielkości mierzonej;
powtarzalność
(repeatability) - zgodność wyników w serii
pomiarów wykonanych w tych samych warunkach, w
krótkim okresie czasu;
odtwarzalność
(reproducibility) – zgodność wyników
w przypadku powtórzenia tego samego doświadczenia
pomiarowego po dowolnym okresie czasu.

WYKŁAD 5
WYKŁAD 5
25
25
POJĘCIA ZWIĄZANE Z OCENĄ
DOKŁADNOŚCI POMIARÓW
▀ DOKŁADNOŚĆ (Accuracy):
właściwość, która charakteryzuje narzędzie
pomiarowe pozwalające uzyskać wyniki pomiaru
odpowiadające prawdziwej wartości wielkości
mierzonej.

WYKŁAD 5
WYKŁAD 5
26
26
POJĘCIA ZWIĄZANE Z OCENĄ
DOKŁADNOŚCI POMIARÓW
▀
Wartość prawdziwa
(true value, actual value);
pojęcie umowne, abstrakcyjne; w praktyce
zastępowana przez wartość:
► poprawną (the conventional true value)
► nominalną (nominal value)
► oczekiwaną (średnią statystyczną) (mean value)
wyznaczoną na podstawie zbioru wartości
wyników pomiarów.

WYKŁAD 5
WYKŁAD 5
27
27
POJĘCIA ZWIĄZANE Z OCENĄ
DOKŁADNOŚCI POMIARÓW
▀ BŁĄD POMIARU (Measuring error)
miara dokładności pomiaru; różnica (lub
różnica względna) między wartością zmierzoną
(wynikiem pomiaru), a prawdziwą wartością
wielkości mierzonej.

WYKŁAD 5
WYKŁAD 5
28
28
KRYTERIA KLASYFIKACJI BŁĘDOW
POMIAROWYCH
W zależności od sposobu odniesienia wyniku
pomiaru x
M
do prawdziwej (poprawnej) wartości
wielkości mierzonej x
R
.
► bezwzględne ∆x = x
M
- x
R
► względne δx = (x
M
– x
M
)/x
R
,

WYKŁAD 5
WYKŁAD 5
29
29
KRYTERIA KLASYFIKACJI BŁĘDOW
POMIAROWYCH
W zależności od źródła powstawania
► przyrządu pomiarowego,
► metody pomiarowej:
□ pobrania
□ przetwarzania
□ ………………..
► obserwatora
► obliczeń i przetwarzania danych
► wynikające z wpływu otoczenia na:
□ źródło wielkości mierzonej,
□ układ pomiarowy,
□ obserwatora.

WYKŁAD 5
WYKŁAD 5
30
30
KRYTERIA KLASYFIKACJI BŁĘDOW
POMIAROWYCH
W zależności od regularności pojawiania się
błędów przy wielokrotnym powtarzaniu
pomiarów w tych samych warunkach
► systematyczne
□ stałe (właściwe)
□ zmienne (niewłaściwe)
► przypadkowe,
► nadmierne (pomyłki).

WYKŁAD 5
WYKŁAD 5
31
31
KRYTERIA KLASYFIKACJI BŁĘDOW
POMIAROWYCH
W zależności od charakteru zmienności
wielkości
mierzonej i typu reakcji układu pomiarowego
► statyczne,
► dynamiczne.
W zależności od warunków środowiska,
istniejących w momencie wykonania pomiaru
► podstawowe,
► dodatkowe

WYKŁAD 5
WYKŁAD 5
32
32
METODA NAJMNIEJSZYCH
KWADRATÓW
Zmienne y i x związane są zależnością
funkcyjną:
y = f(x, a
1
, a
2
, a
3
, . . . , a
m
)
gdzie:
- postać funkcji f jest znana,
- a
1
, a
2
, . . . , a
m
są stałymi
określonymi
na podstawie
pomiarów.
* * *
Niech para (x
i
, y
i
) ; i = 1, 2, 3, . . . , n będzie
wynikiem pomiaru

WYKŁAD 5
WYKŁAD 5
33
33
METODA NAJMNIEJSZYCH
KWADRATÓW
Wprowadzamy zmienną:
e
i
= y
i
- f(x
i
, a
1
, a
2
, a
3
, . . . , a
m
)
* * *
Dla m (liczba parametrów) i n (liczba
pomiarów)
1.n < m
– układ nieoznaczony
2.n = m
– może być rozwiązanie jednoznaczne
3.n > m
– liczba równań jest większa niż liczba
niewiadomych a
i
1.n < m
– układ nieoznaczony
2.n = m
– może być rozwiązanie jednoznaczne
3.n > m – liczba równań jest większa niż liczba
niewiadomych a
i

WYKŁAD 5
WYKŁAD 5
34
34
METODA NAJMNIEJSZYCH
KWADRATÓW
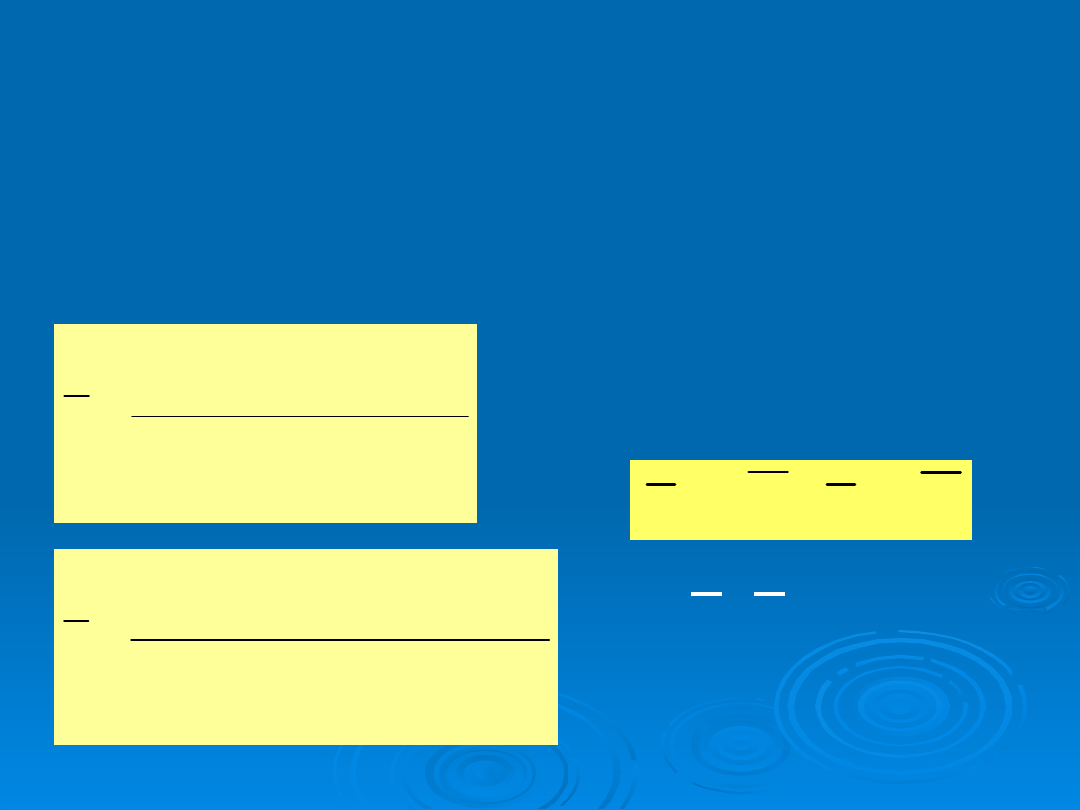
Poszukujemy takich parametrów a
i
, aby:
min
1
2
n
i
i
e
S
Ponieważ S =
(a
1
, a
2
, . . . , a
m
) , więc warunek
konieczny minimum ma postać:
m
i
a
S
i
,
3
,
2
,
1
;
0
Rozwiązanie powyższego układu równań zależy
od postaci funkcji f.
WYKŁAD 5
WYKŁAD 5
35
35
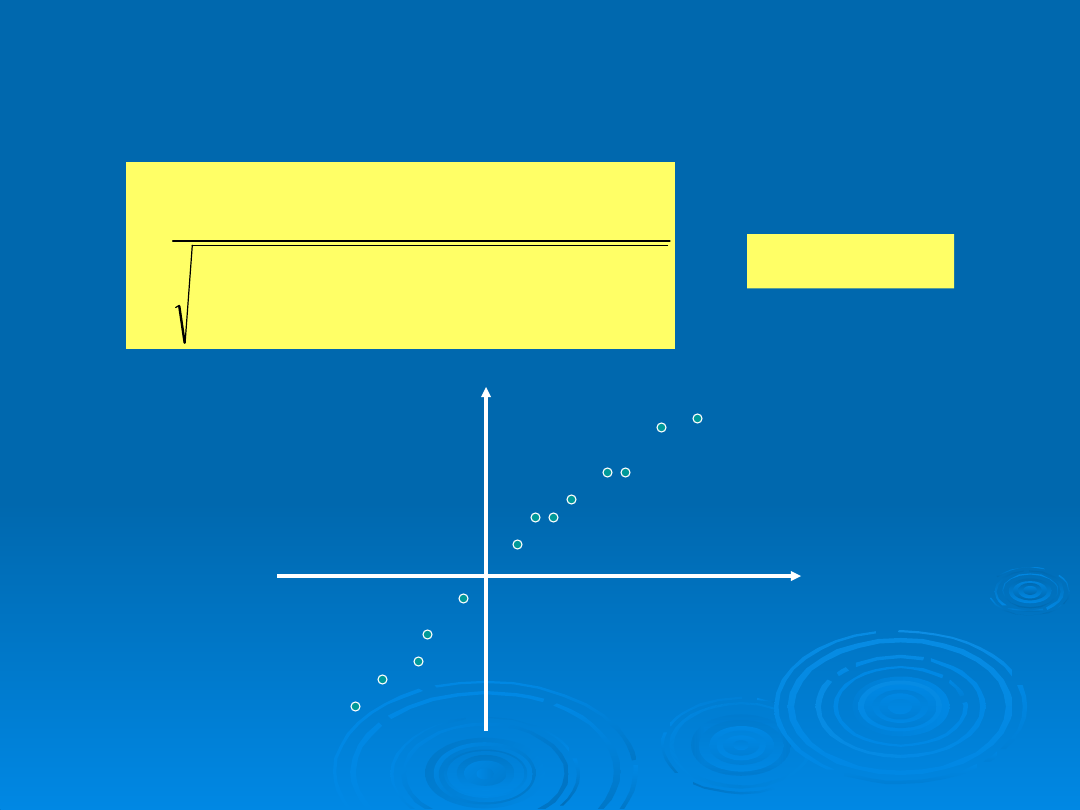
REGRESJA LINIOWA
Dla funkcji liniowej:
y = A x + B
Nieznane parametry A i B szacuje się, korzystając z
wyrażeń:
2
1
1
2
1
1
1
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
i
x
x
n
y
x
y
x
n
A
2
1
1
2
1
1
1
1
2
n
i
i
n
i
i
n
i
i
i
n
i
i
n
i
n
i
i
i
x
x
n
y
x
x
x
y
n
B
przy czym
gdzie x i y są
średnimi arytmetycznymi
wielkości x
i
i y
i
.
B
x
A
y
WYKŁAD 5
WYKŁAD 5
36
36
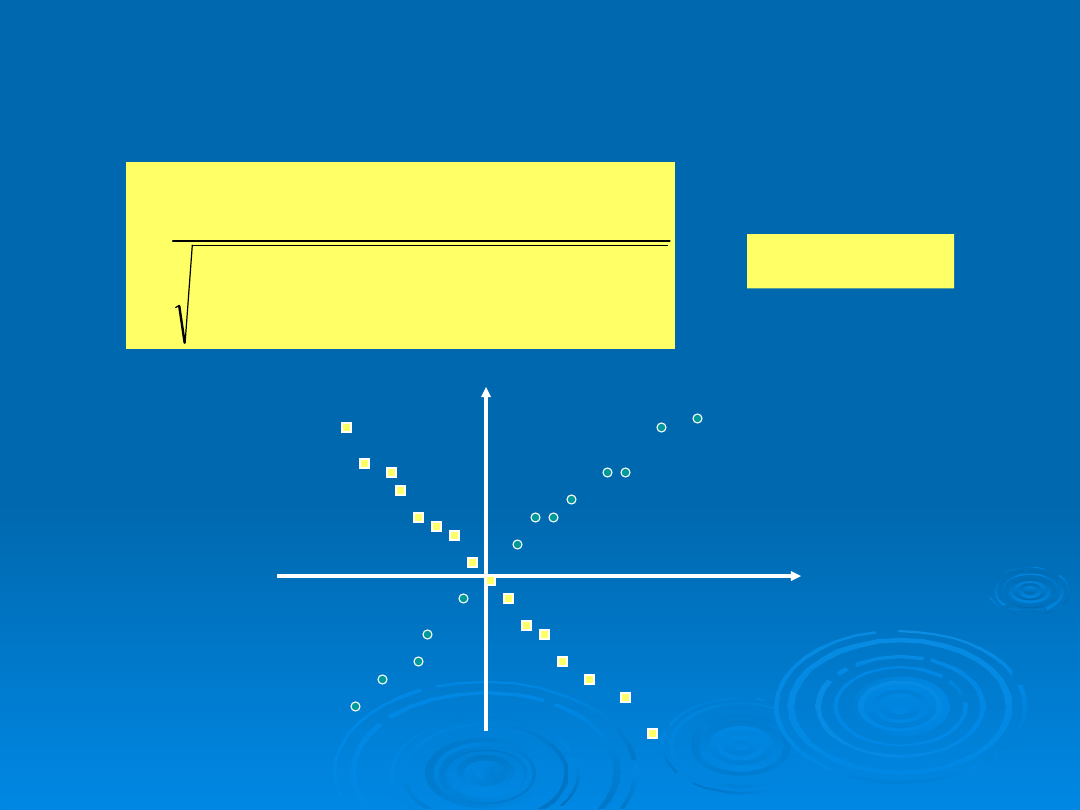
WSPÓŁCZYNNIK KORELACJI
Miara zależności liniowej między wielkościami X i
Y
2
1
1
2
2
1
1
2
1
1
1
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
i
y
y
n
x
x
n
y
x
y
x
n
r
-1 r 1
X
Y
WYKŁAD 5
WYKŁAD 5
37
37
WSPÓŁCZYNNIK KORELACJI
Miara zależności liniowej między wielkościami X i
Y
2
1
1
2
2
1
1
2
1
1
1
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
i
y
y
n
x
x
n
y
x
y
x
n
r
-1 r 1
X
Y
WYKŁAD 5
WYKŁAD 5
38
38
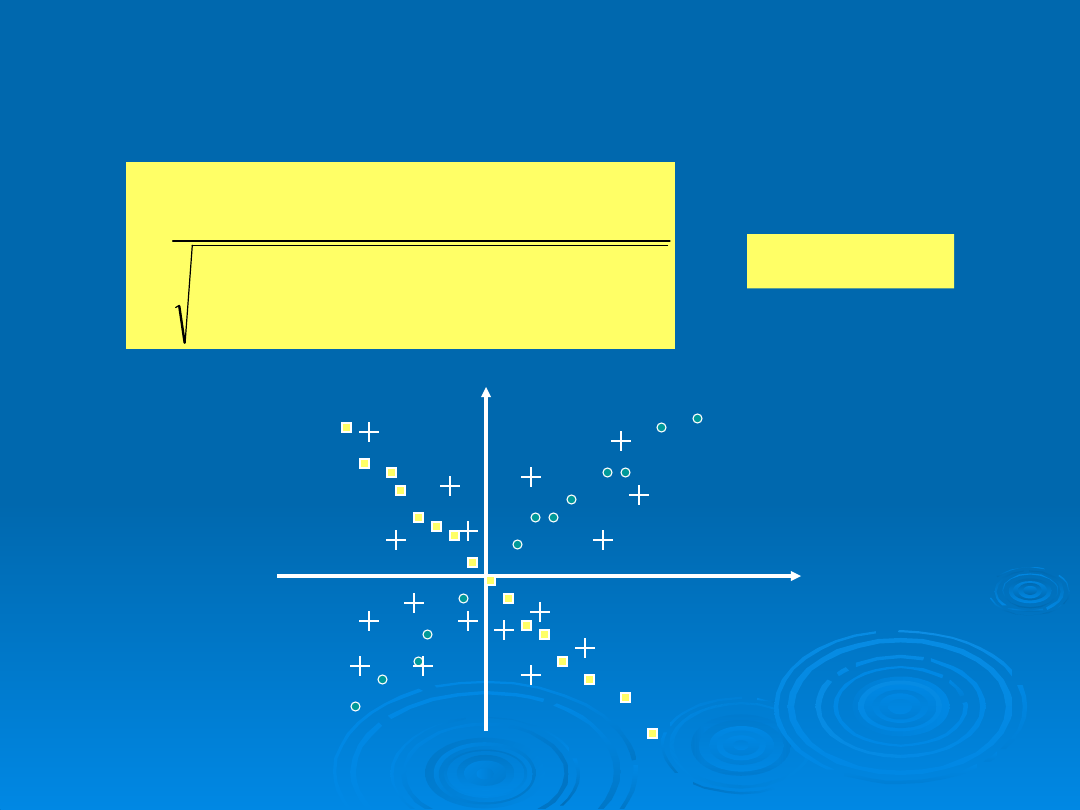
WSPÓŁCZYNNIK KORELACJI
Miara zależności liniowej między wielkościami X i
Y
2
1
1
2
2
1
1
2
1
1
1
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
i
y
y
n
x
x
n
y
x
y
x
n
r
-1 r 1
X
Y
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
Wyszukiwarka
Podobne podstrony:
Błędy przypadkowe w pomiarach pośrednich 3
Błędy przypadkowe w pomiarach pośrednich 2
METROLOGIA, laborki(metrol3), Błędy przypadkowe w pomiarach bezpośrednich
Błędy przypadkowe Metoda pośrednia, PWR Politechnika Wrocławska, podstawy metrologii, Wykłady 2011
bledy przypadkowe
Laboratorium z Metrologii - Błędy przypadkowe w pomiarach bezpośrednich, Metrologia
Błędy przypadkowe w pomiarach?zpośrednich
2 Błędy przypadkowe w pomiarach pośrednich
wyklad 04 bledy-przypadkowe, ŹRÓDŁA BŁĘDÓW, CHARAKTER BŁĘDÓW - BŁĘDY SYSTEMATYCZNE I PRZYPADKOWE
2012 03 28 metody przypadków ppt
bledy przypadkowe w pomiarach bezposrednich doc
bledy przypadkowe w pomiarach posrednich doc
Przypadek kliniczny nr 6 (2) ppt
W9 MPiS ppt
więcej podobnych podstron