Modelowanie
model związków encji

Wykład 3
Prowadzący: dr Paweł Drozda

dr Paweł Drozda

Modelowanie



Odwzorowanie obiektów rzeczywistych

w systemie informatycznym



Dwa typy modeli:



Konceptualny



Model związków encji



Model UML



Implementacyjny



Relacyjny



Obiektowy



Obiektowo-relacyjny

dr Paweł Drozda

Etapy projektowania systemu



Analiza – jakie wymagania (dane,

funkcjonalność) powstaje model

konceptualny



Projektowanie – zmiana modelu

konceptualnego w model

implementacyjny



Implementacja



Wdrożenie



Utrzymanie

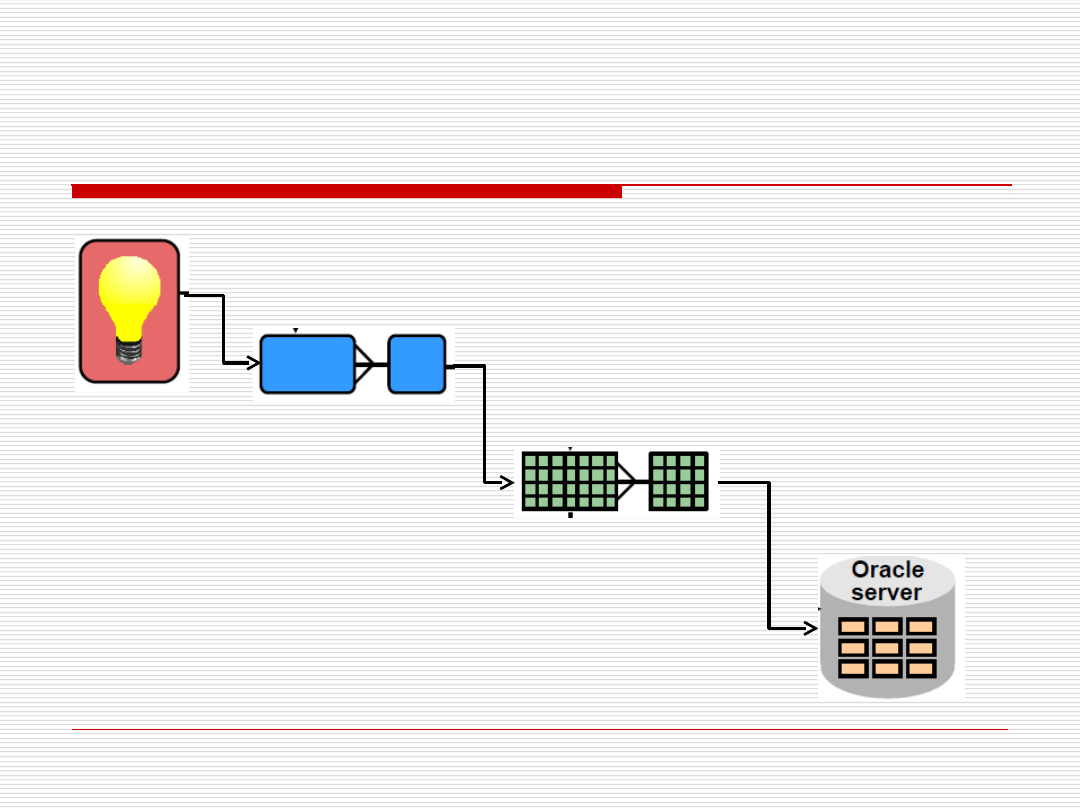
Etapy tworzenia bazy danych

dr Paweł Drozda

Model w
głowie

Zapis za pomocą
modelu związków encji

Model
relacyjny

Baza
danych

dr Paweł Drozda

Model związków encji



Część rzeczywistości zapisana za
pomocą encji (entities)



Atrybuty – właściwości encji



Powiązania w strukturze obiektów –
związki pomiędzy encjami

dr Paweł Drozda

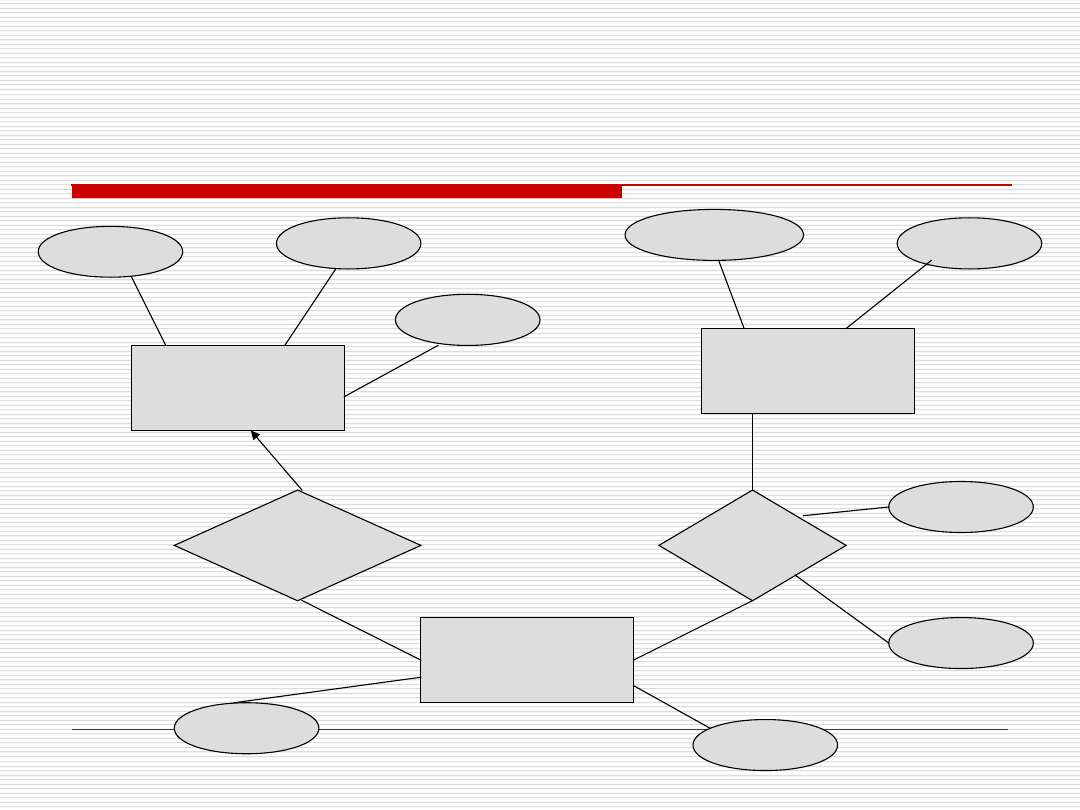
Model związków encji – przykład
– notacja Chena

pesel

Przedmiot

Egzamin

Pracownik

Student

Prowadzenie

nazwisko

nrindeksu

data

nazwisko

zarobki

nazwa

id

ocena

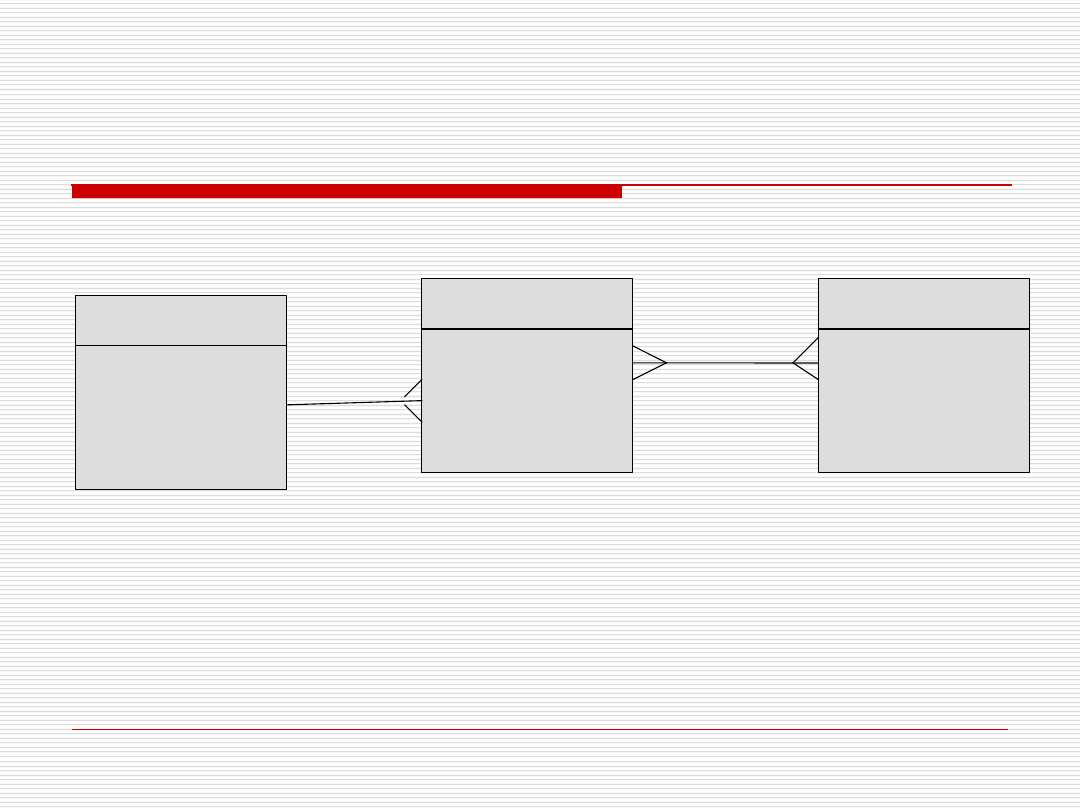
Przykład – notacja Barkera

dr Paweł Drozda

Pesel
Nazwisko
Zarobki

PRACOWNIK

NrIndeksu
Nazwisko

STUDENT

Id
Nazwa

PRZEDMIOT

prowadzi

zdaje

dr Paweł Drozda

Encja



Odpowiednik klasy w modelu obiektowym



Zbiór obiektów o tych samych cechach
(atrybuty, własności, związki)



Konkretny obiekt = wystąpienie encji

dr Paweł Drozda

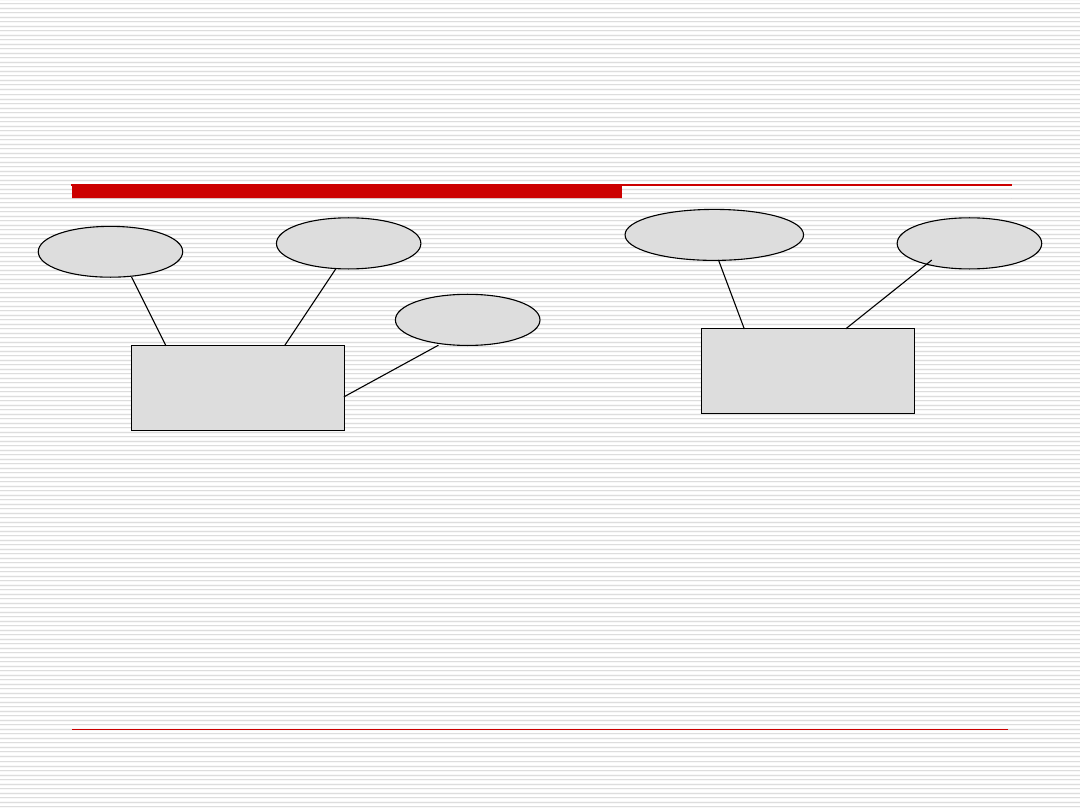
Encje – przykład Chen

pesel

Osoba

Pies

nazwisko

rasa

imię

płeć

Przykład wystąpienia
Osoba: 76040603149, Kucka, K
Osoba: 79072203350, Drozda, M

Pies: Kundel, Bury

Pies: Jamnik, Długi

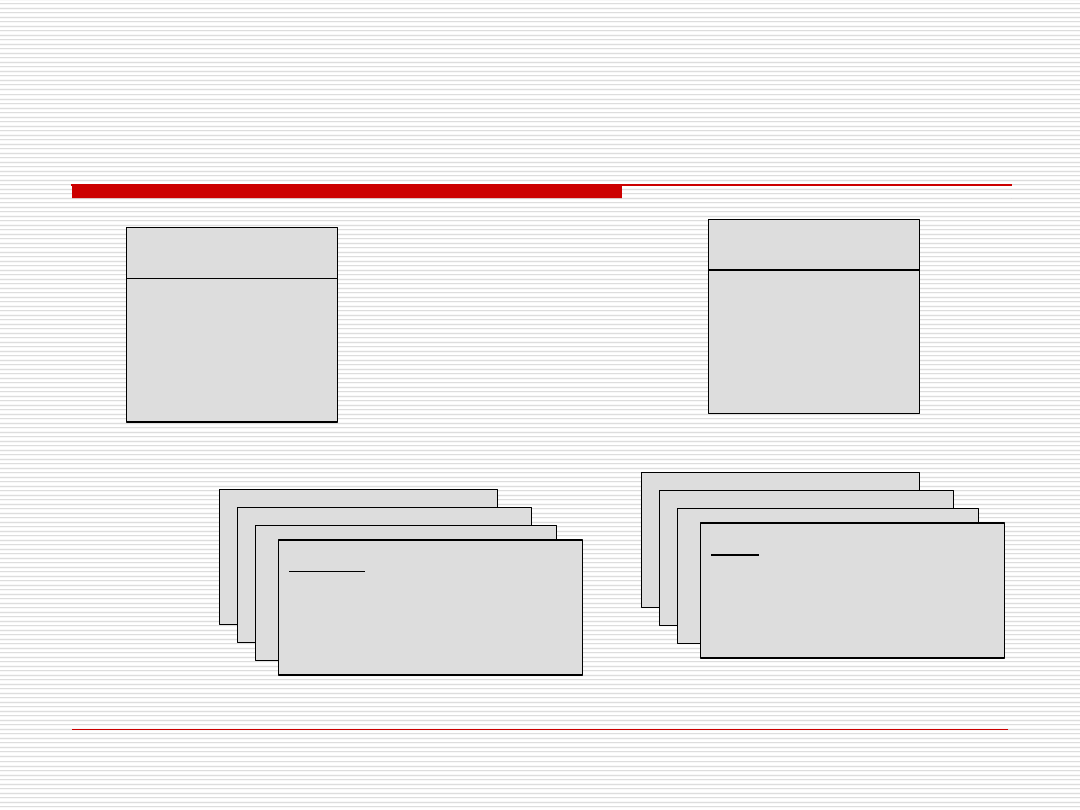
Przykład Barker

dr Paweł Drozda

Pesel
Nazwisko
Płeć

OSOBA

Rasa
Imię

PIES

Osoba
Pesel = 77021211111
Nazwisko = Kowalski
Płeć = Kobieta

Pies
Rasa = Kundel
Imię = Bury

dr Paweł Drozda

Reguły modelowania encji



Unikalność nazw



Atrybuty



Związki między encjami



Obiekt reprezentowany tylko przez
jedną encję



Nazwa – rzeczownik w liczbie
pojedynczej

dr Paweł Drozda

Atrybuty encji



Identyfikatory – jednoznacznie opisują wystąpienie
encji



Naturalne – PESEL, NrDowodu, itd.



Sztuczne – nrIdentyfikacyjny, idpracownika



Deskryptory – pozostałe atrybuty opisujące encję



Deklaracja atrybutu



Nazwa



Dziedzina (typ danych i max rozmiar, zbiór bądź
zakres dozwolonych wartości)



Opcja unikalności



Wartości puste (dozwolone lub nie)

dr Paweł Drozda

Rodzaje atrybutów - przykład

pesel

Osoba

Film

nazwisko

tytuł

rok

zarobki

adres

płeć

telefon

długość

gatunek

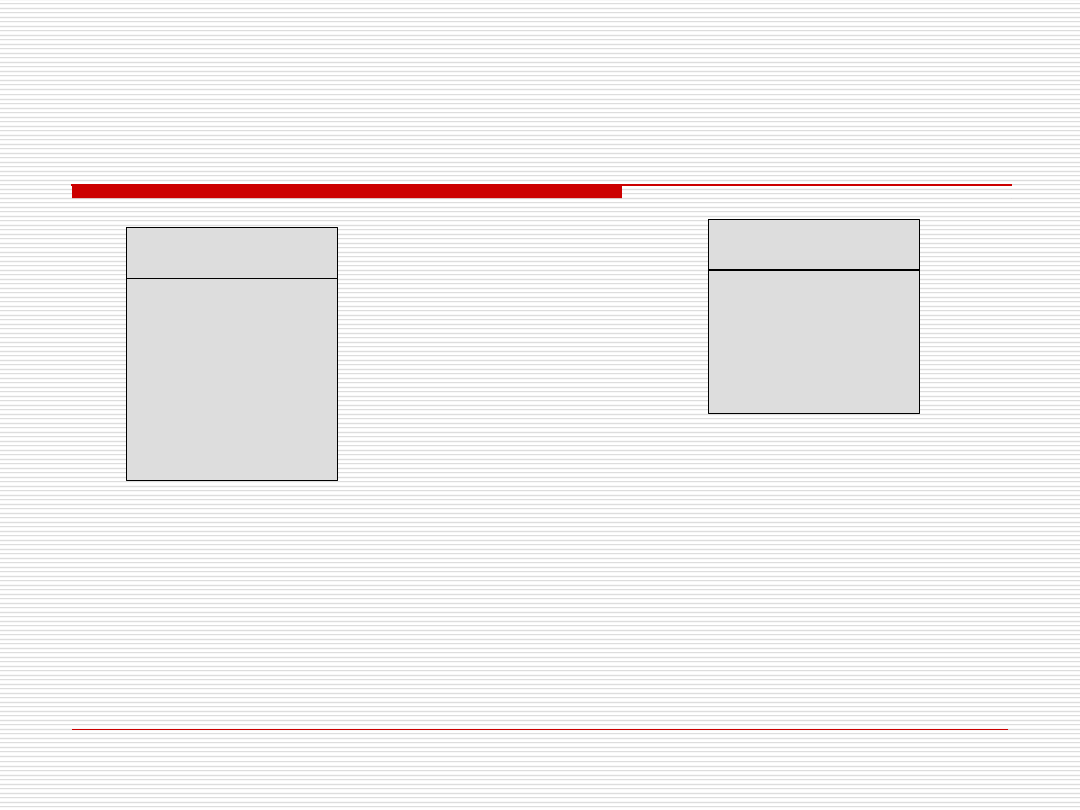
Przykład Barker

dr Paweł Drozda

# Pesel
* Nazwisko
* Płeć
* Zarobki
 Adres

 Telefon

OSOBA

# Tytuł
# Rok
(#) Gatunek
* Długość

Film

dr Paweł Drozda

Związki encji



Opisują połączenia pomiędzy encjami



Powiązane dwie lub więcej encji



Przykład:

STUDENT

WYKŁAD

uczestniczy

Przewidziany dla

Pytania:
W ilu wykładach uczestniczy student, dla ilu studentów
przewidziany jest wykład, czy wykład musi być przewidziany dla
studenta, czy student musi uczestniczyć w wykładzie

Cechy związku



Liczebność (unarny - rekursywny,
binarny, tetrarny, n-arny)



Istnienie (opcjonalny, obowiązkowy)



Karynalność



1:1 – jeden do jednego



1:M – jeden do wielu



N:M – wiele do wielu

dr Paweł Drozda

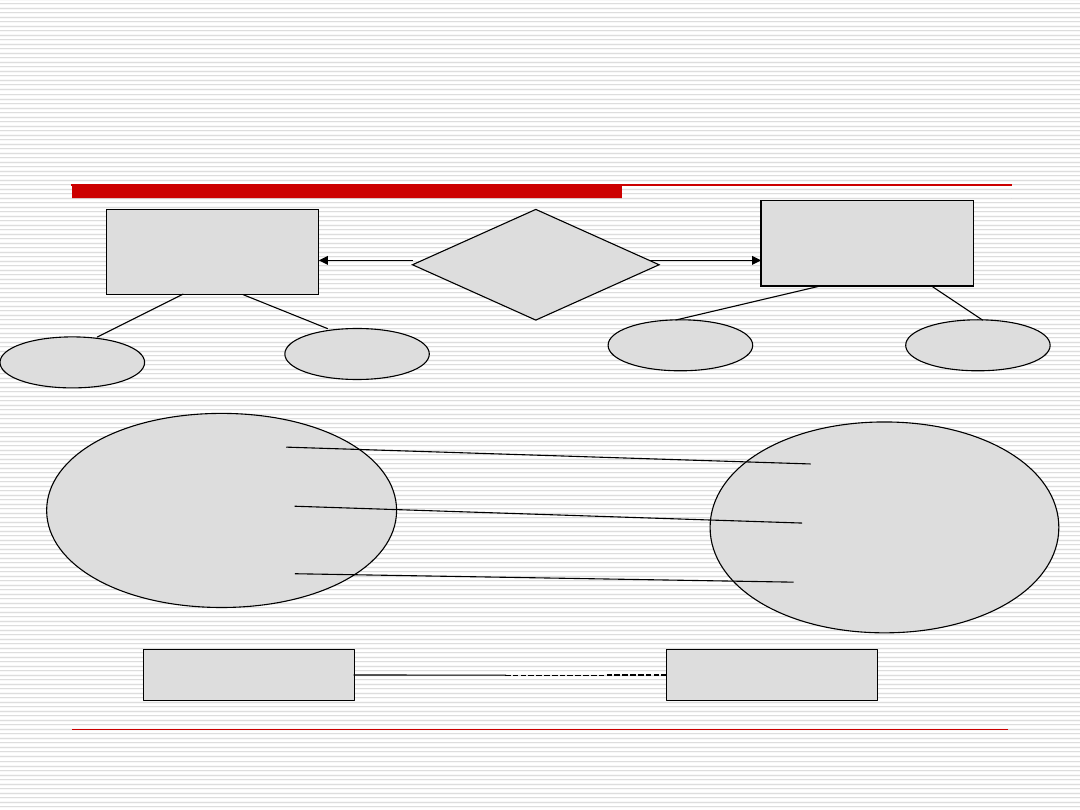
dr Paweł Drozda

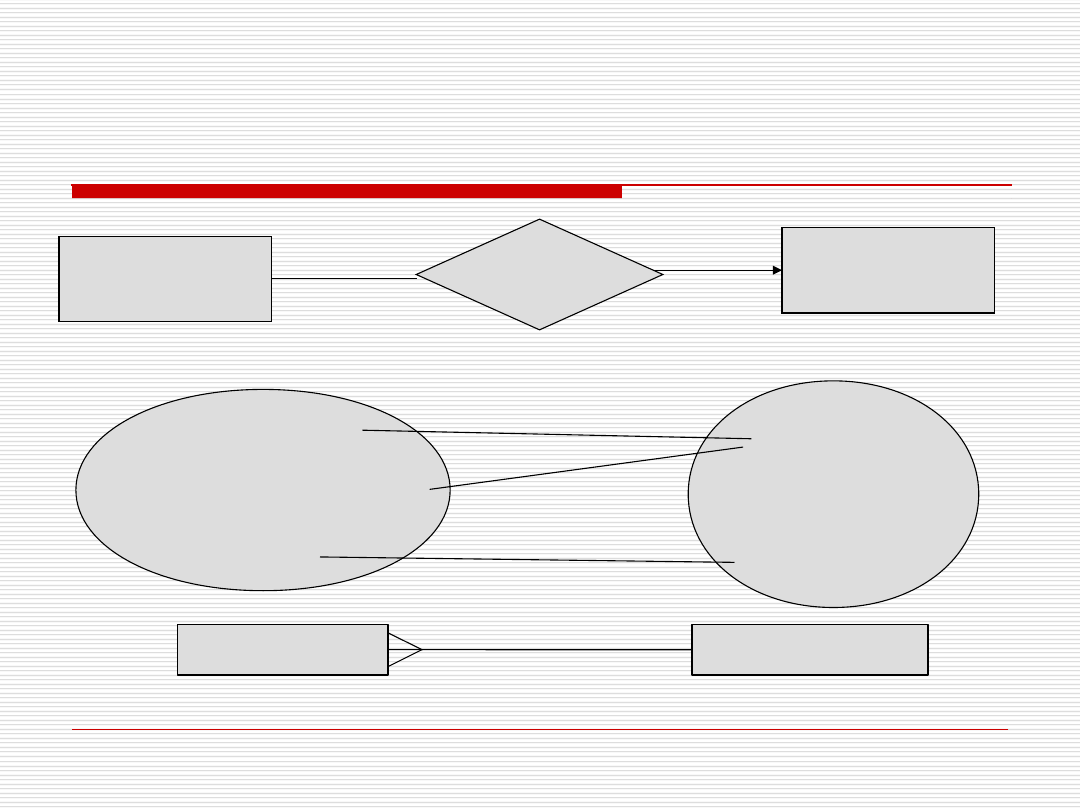
Związek 1:1 - Przykład

adres

nazwisko

Klasa

nazwa

sala

Nauczyciel

Wychowawca

1b

2c

6a

Jan Mucha

Marta Ącka

Stefan Kula

Wychowawca

KLASA

NAUCZYCIEL

wychowuje

ma wychowawcę

dr Paweł Drozda

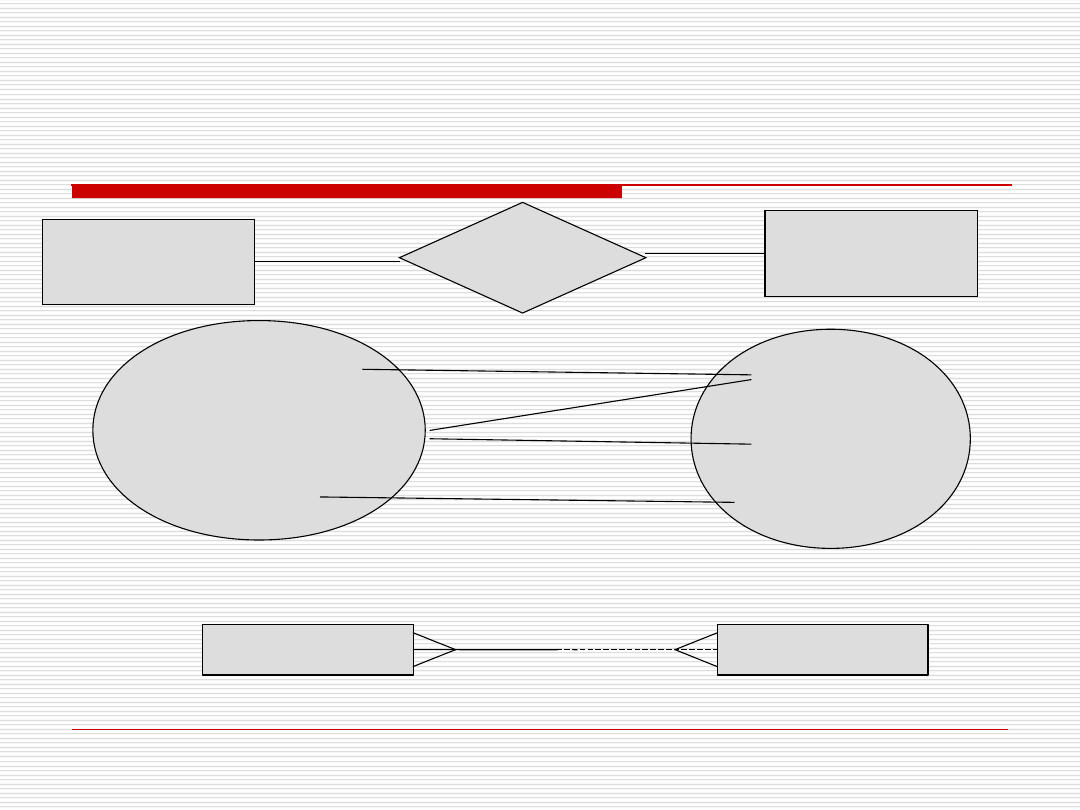
Związek 1:m - Przykład

Wykładowca

Prowadzenie

Przedmiot

Bazy danych

Analiza matematyczna

Logika

Jan Mucha

Marta Ącka

Stefan Kula

Prowadzenie

PRZEDMIOT

WYKŁADOWCA

prowadzi

Jest prowadzony

dr Paweł Drozda

Związek m:n - Przykład

Student

Egzamin

Przedmiot

Bazy danych

Analiza matematyczna

Logika

Jan Mucha

Marta Ącka

Stefan Kula

Egzamin

PRZEDMIOT

STUDENT

zdaje

Jest zdawany

dr Paweł Drozda

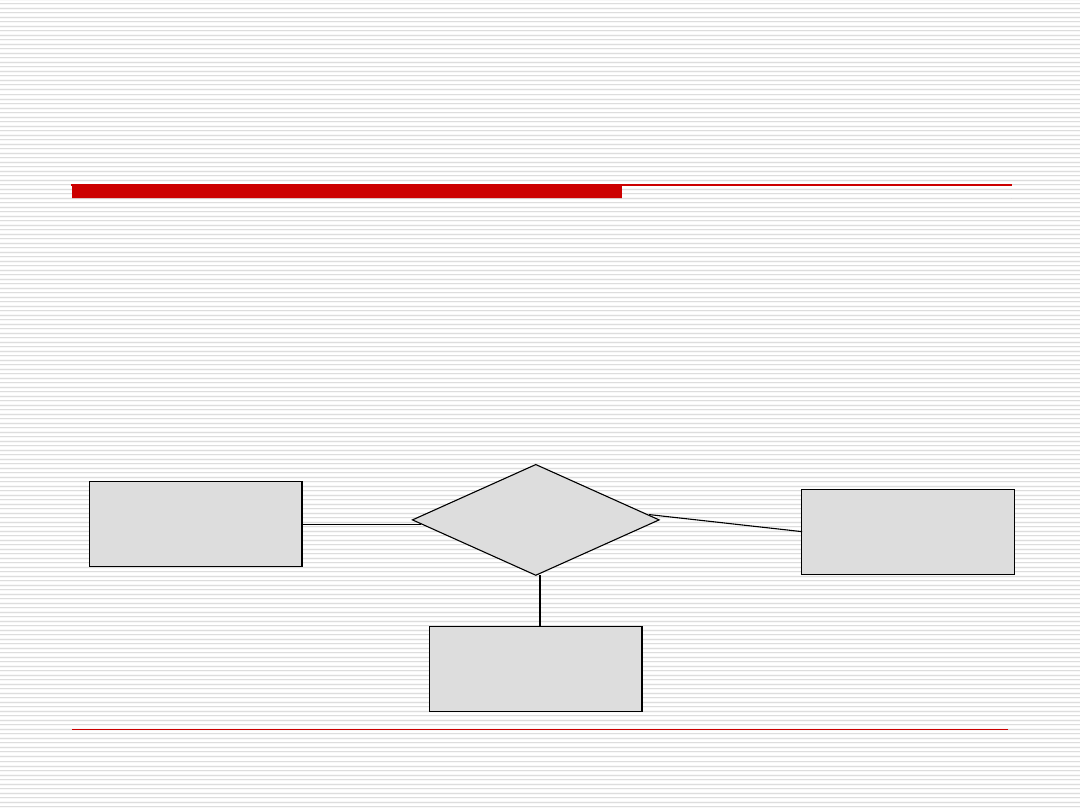
Związki wieloargumentowe (1)



Możliwość definicji związku
wieloargumentowego



Co najmniej 3 encje są związane

Kierowca

Policjant

Mandat

Wykroczenie

dr Paweł Drozda

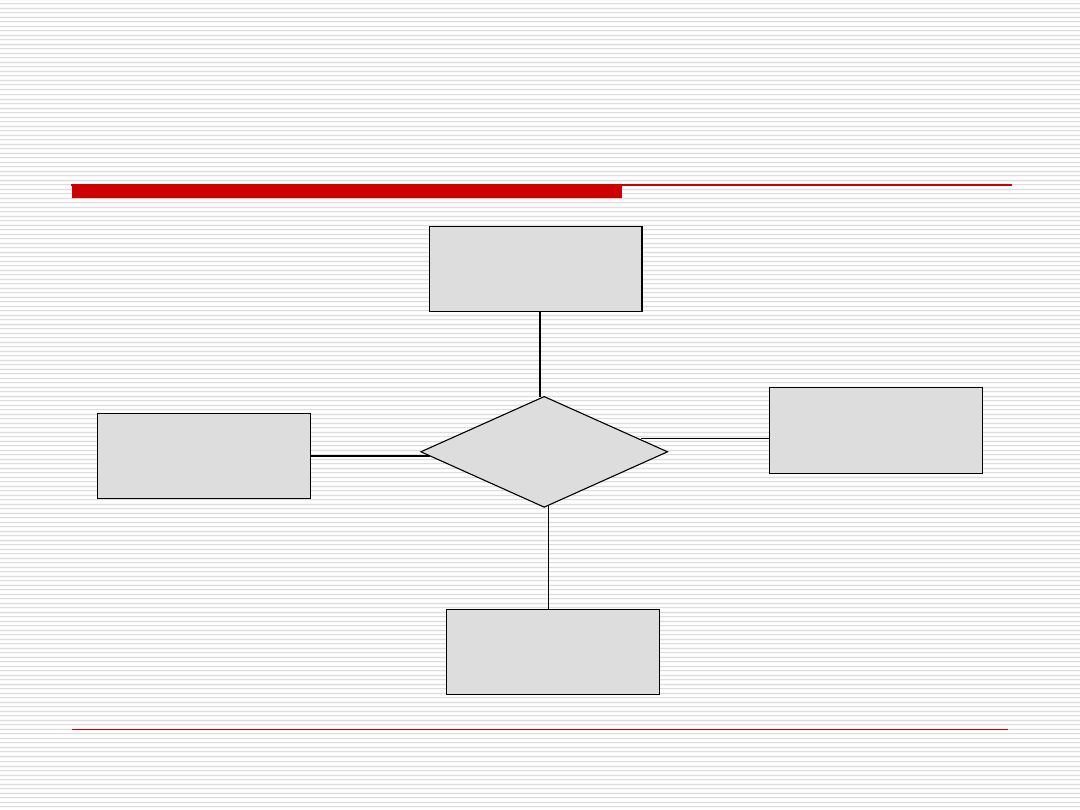
Związki wieloargumentowe (2)

Lekarz

Pielęgniarka

Operacja

Pacjent

Sala

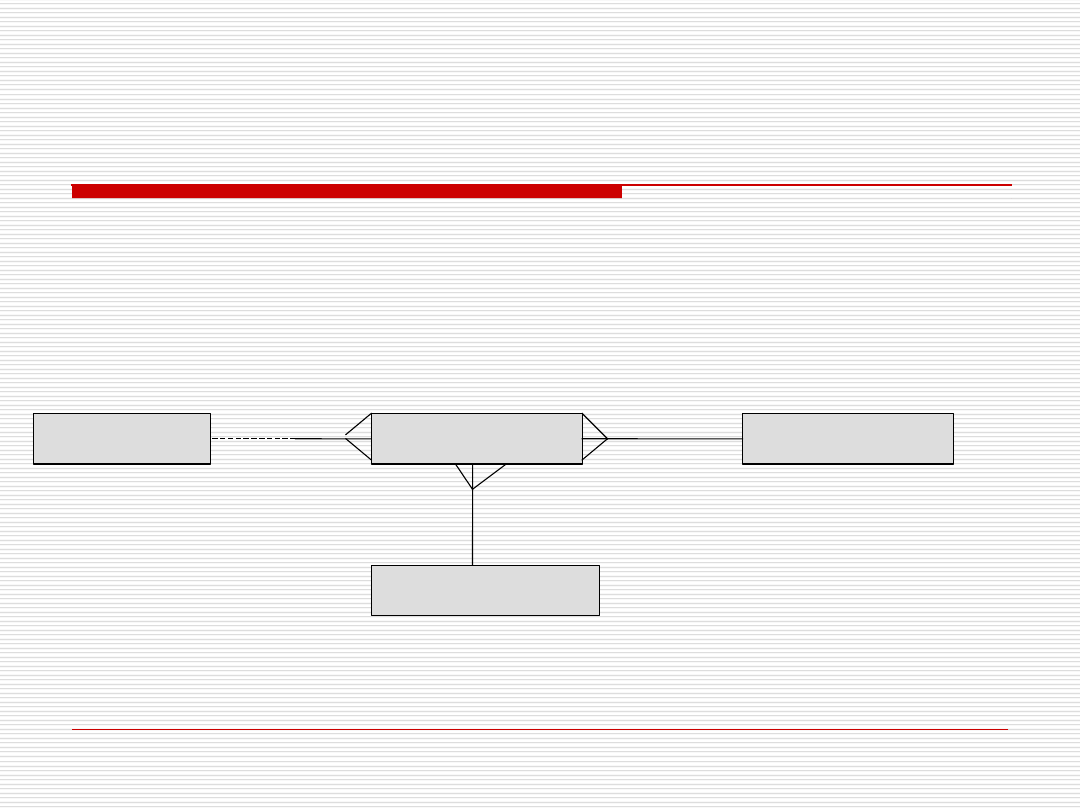
Związki wieloargumentowe –
notacja Berkera



Gdy związek wieloargumentowy –
zamienia się w encję

dr Paweł Drozda

Mandat

POLICJANT

KIEROWCA

WYKROCZENIE

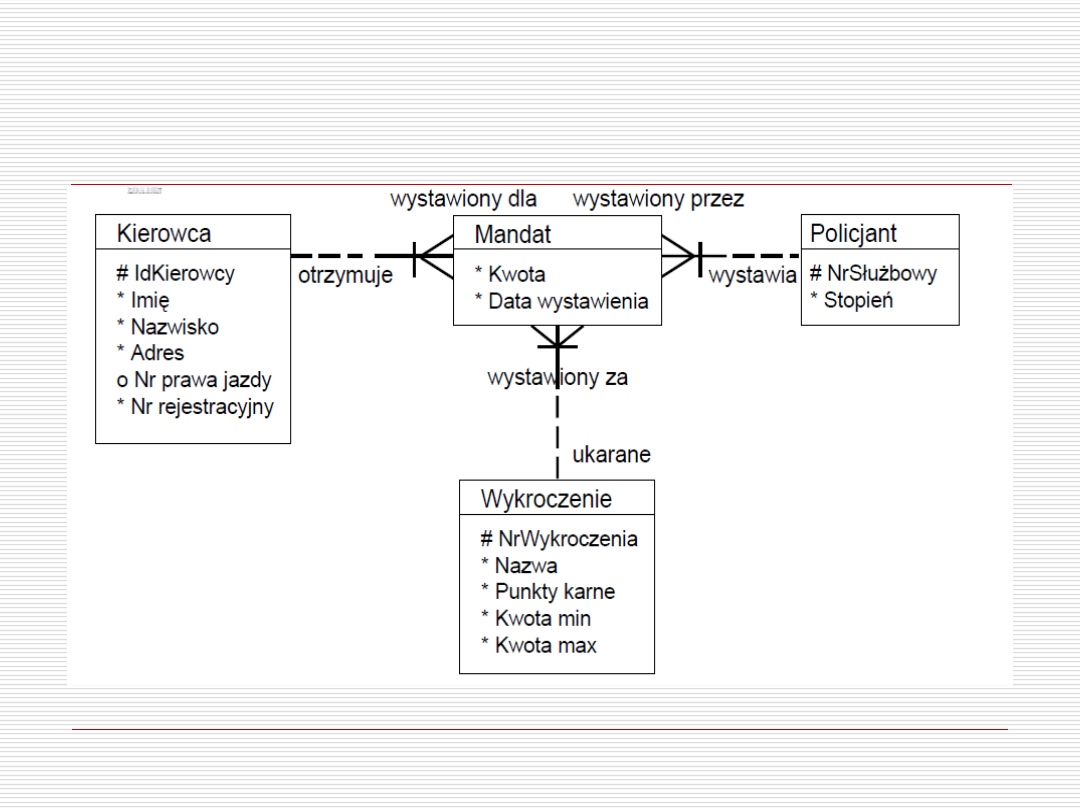
Rozszerzenie – poprzedni
przykład

dr Paweł Drozda

Ze strony ważniak

dr Paweł Drozda

Związek rekursywny



Podwójne wystąpienie encji w związku



Zarówno dla związków
dwuargumentowych jak i
wieloargumentowych

rodzic

Osoba

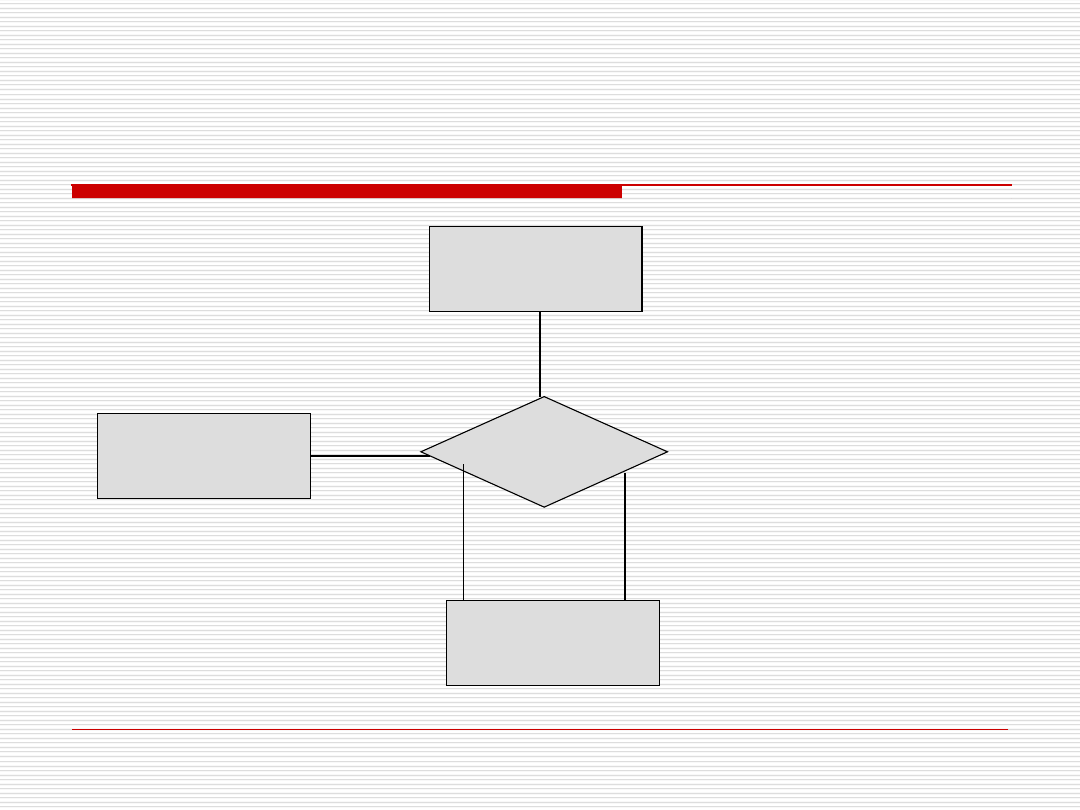
dr Paweł Drozda

Typy związków - podsumowanie

Stadion

Mecz

Drużyna

Sędzia

Gospodarze

Goście

dr Paweł Drozda

Atrybuty związków



Gdy związek posiada specyficzne
cechy



Można stworzyć encję dla związku z
atrybutami odnoszącymi się do
związku

dr Paweł Drozda

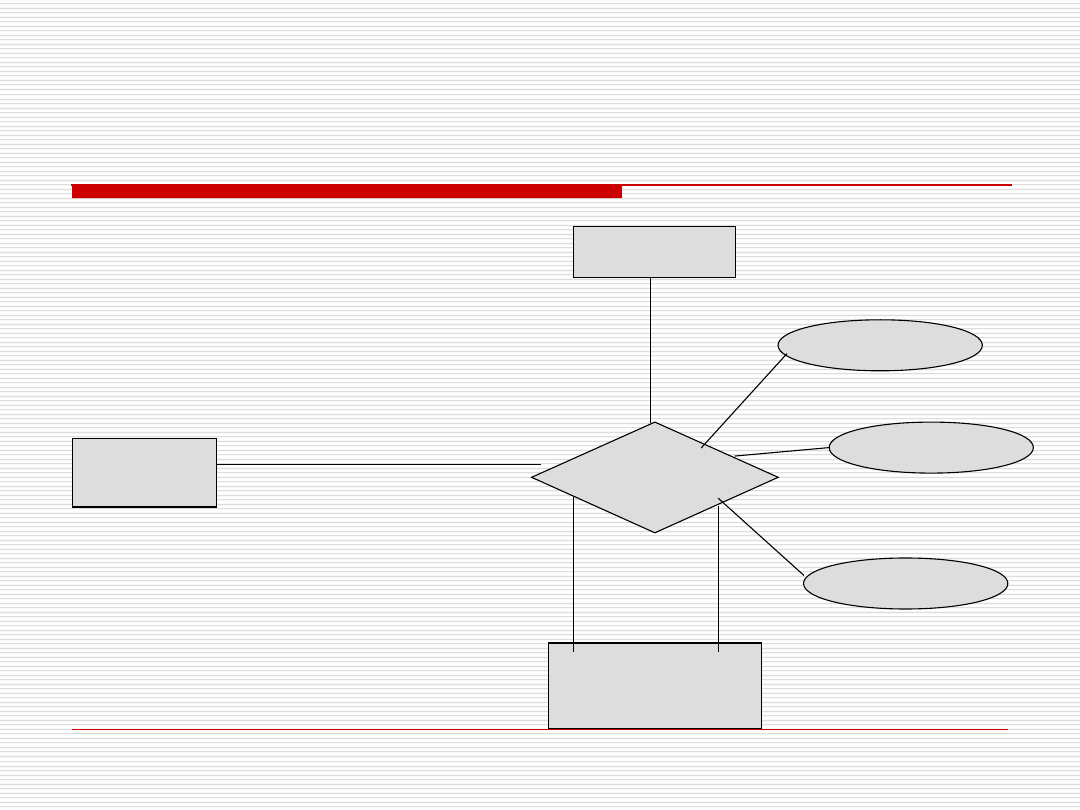
Atrybuty związku - przykład

Stadion

Drużyna

Sędzia

Mecz

liczba widzów

typ meczu

data

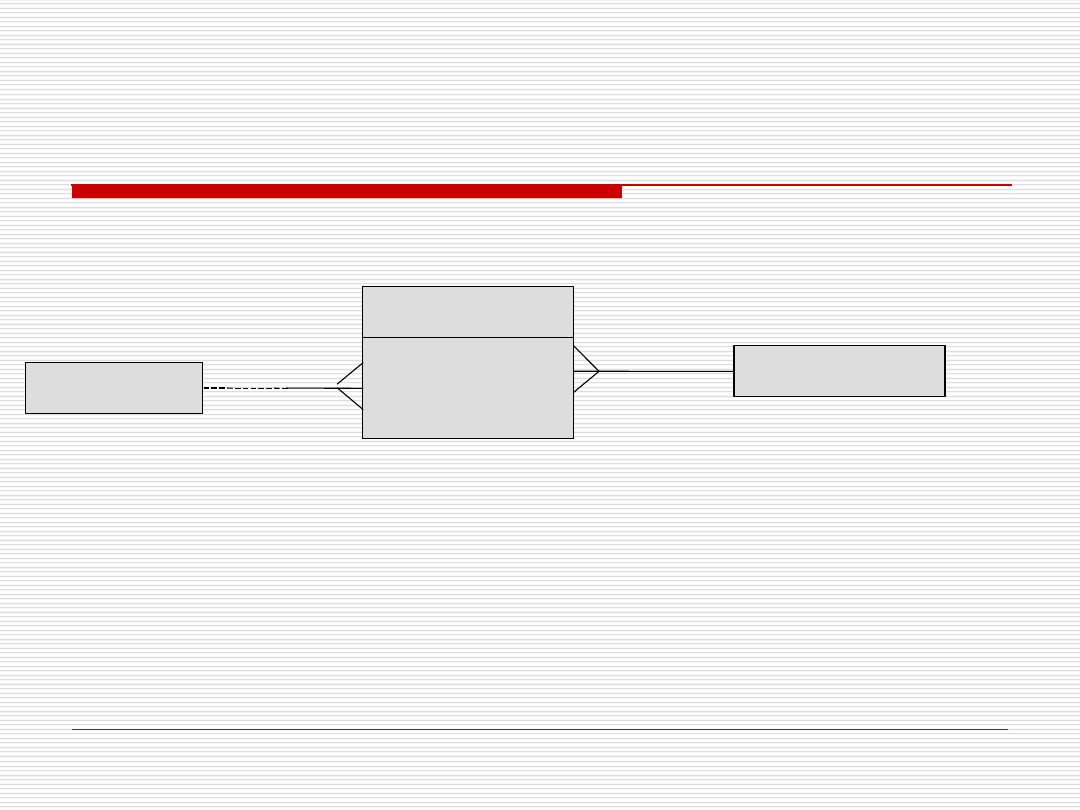
Przykład – atrybuty związku

dr Paweł Drozda

Gaża

Występuje

FILM

AKTOR

Gdy związek posiada atrybuty – konieczność wprowadzenia
dodatkowej encji
Pojawiają się związki typu wiele
Od strony związku – obowiązkowe

dr Paweł Drozda

Zamiana związków wielo-
argumentowych na binarne



Zamiana związku na encję



Każda encja związku
wieloargumentowego wchodzi w
związek binarny jeden do wielu z
nową encją

dr Paweł Drozda

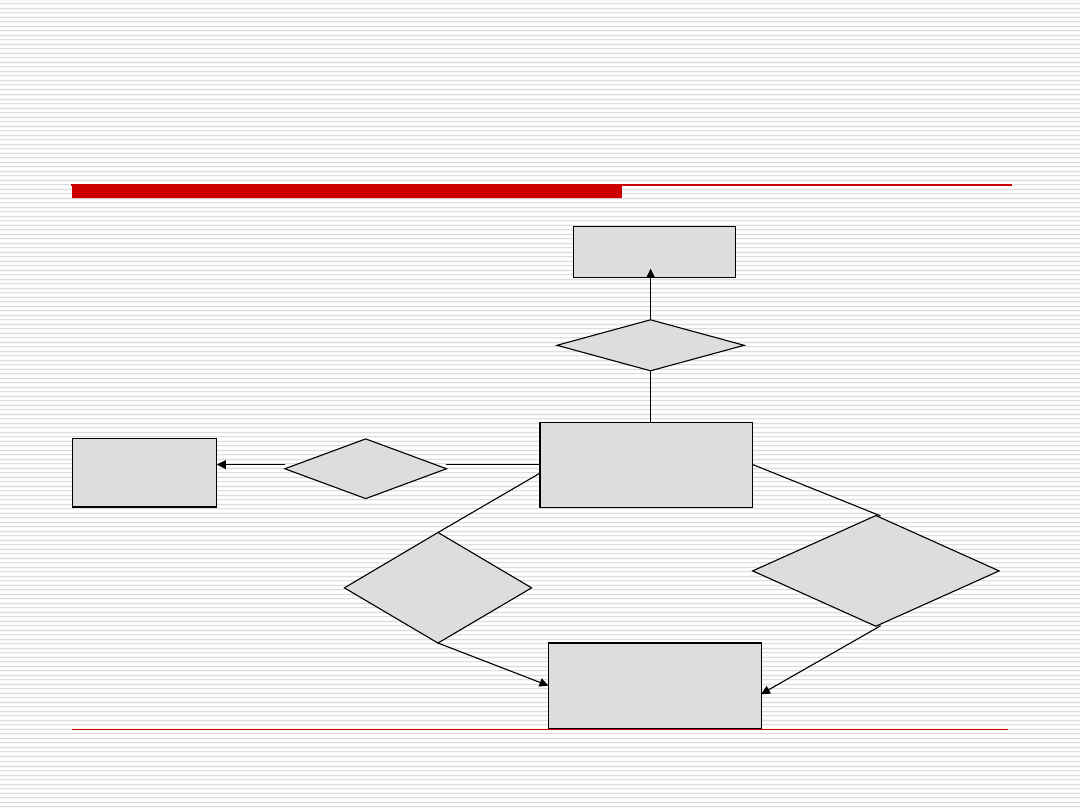
Zamiana związków wielo-
argumentowych na binarne -przykład

Stadion

Miejsce

Drużyna

Sędzia

Goście

Arbiter

Gospodarze

Mecz

dr Paweł Drozda

Zasady projektowania



Dokładność



Unikanie redundancji



Prostota



Dobór właściwych elementów

dr Paweł Drozda

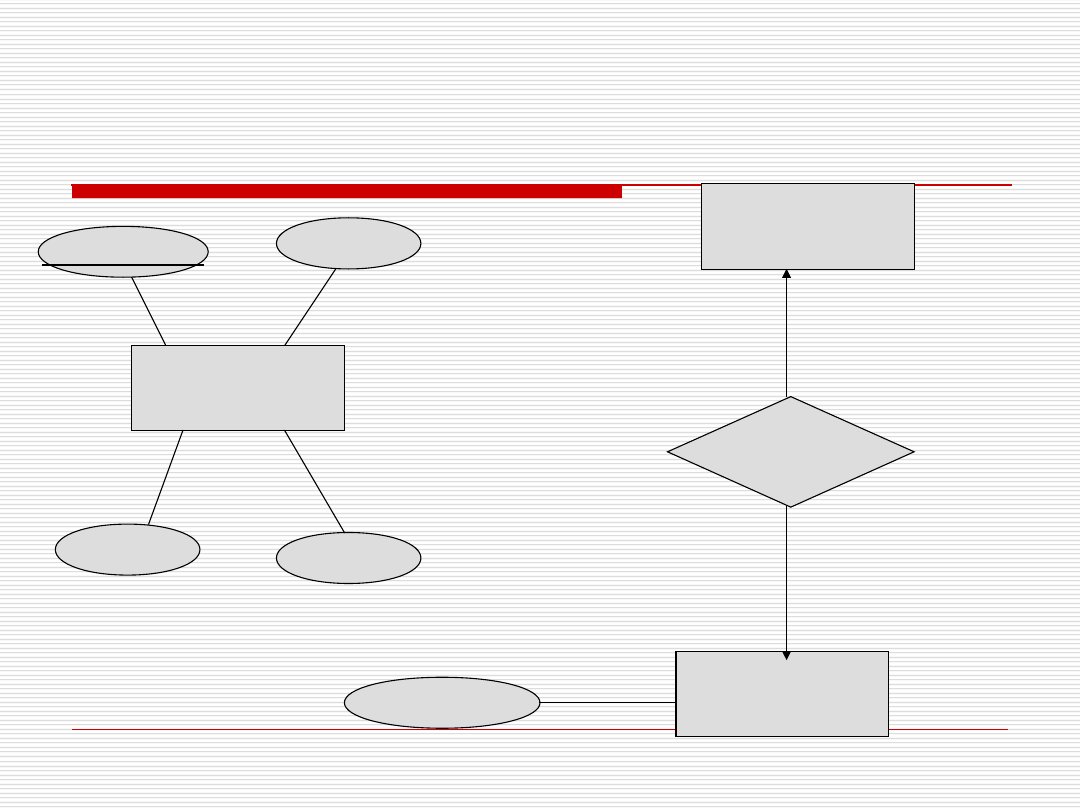
Projektowanie – przykład (1)

powirzchnia

Osoba

cylindry

płeć

telefon

Klasa

Nauczyciel

Wychowawca

Wychowawca

dr Paweł Drozda

Projektowanie – przykład (2)

Klasa

Nauczyciel

Wychowawca

Nauczyciel

Klasa

?

dr Paweł Drozda

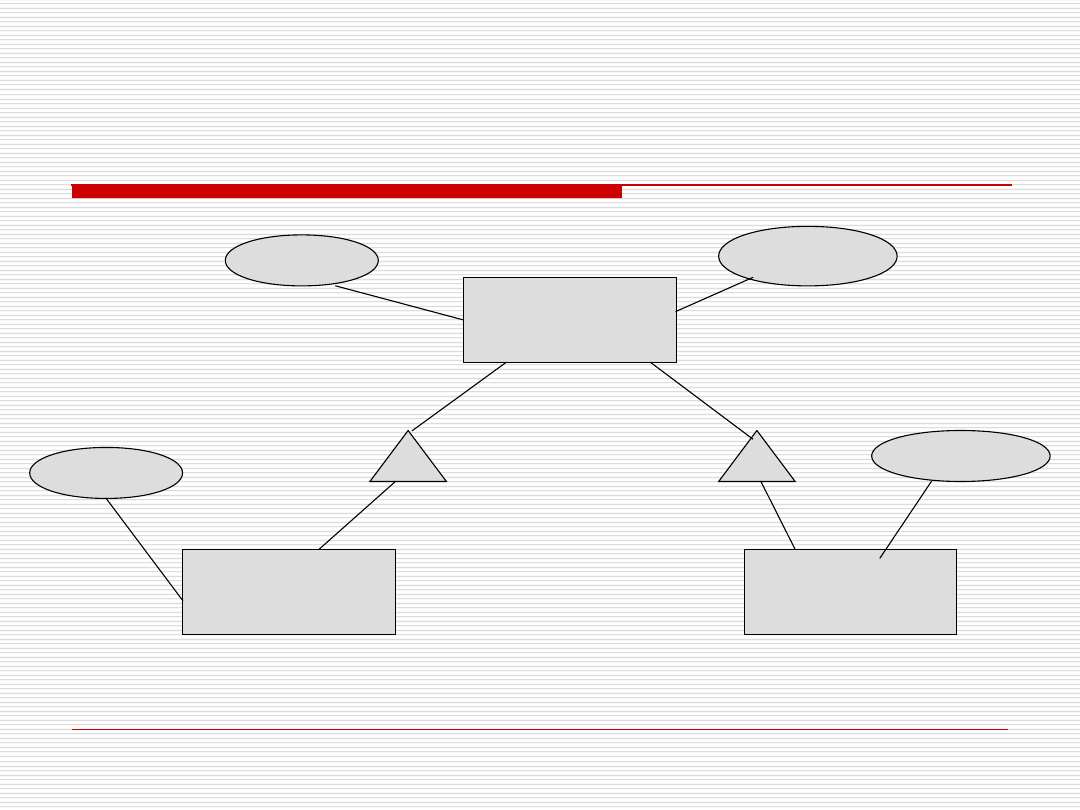
Podklasy/Nadklasy



Uszczegółowienie encji



Reprezentowane przez trójkąt na
krawędzi łączącej encje (często z
napisem isa)



Podział celu wyodrębnienia podgrup o
specyficznych cechach

Cechy hierarchizacji



Podencje dziedziczą atrybuty z
nadencji



Każde wystąpienie podencji jest
wystąpieniem nadencji i na odwrót



Podencje nie mają swoich
identyfikatorów – wspólny dla
wszystkich jest w nadencji

dr Paweł Drozda

dr Paweł Drozda

Podklasy - przykład

Student

Zaoczny

Dzienny

isa

isa

nrindeksu

nazwisko

stypendium

czesne

Model Berkera



Specjalizacja – dzieli encje na
podencje



Generalizacja łączy podencje w encje

dr Paweł Drozda

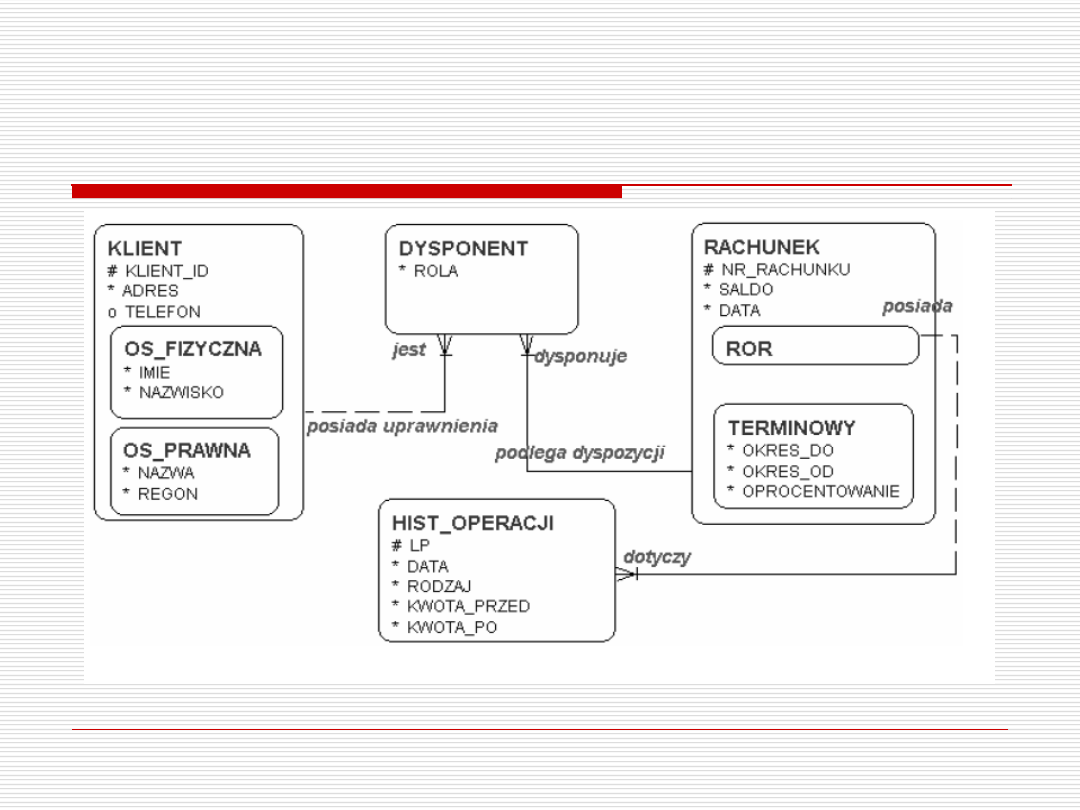
Przykład hierarchii

dr Paweł Drozda

Źródło: ważniak

dr Paweł Drozda

Zbiory słabych encji



Atrybuty klucza wybierane z innego
zbioru encji



Oznaczane przez podwójne linie



Przyczyny



Hierarchiczny układ zbiorów encji



Zbiory łączące eliminujące związki
wieloargumentowe

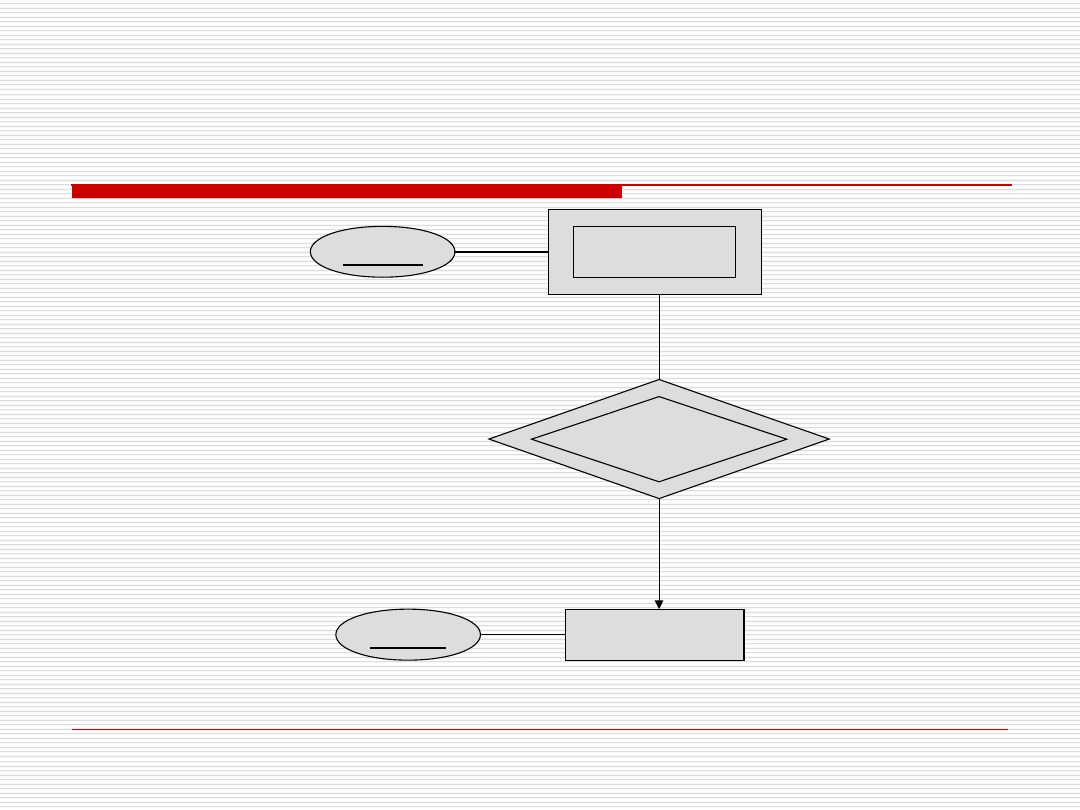
dr Paweł Drozda

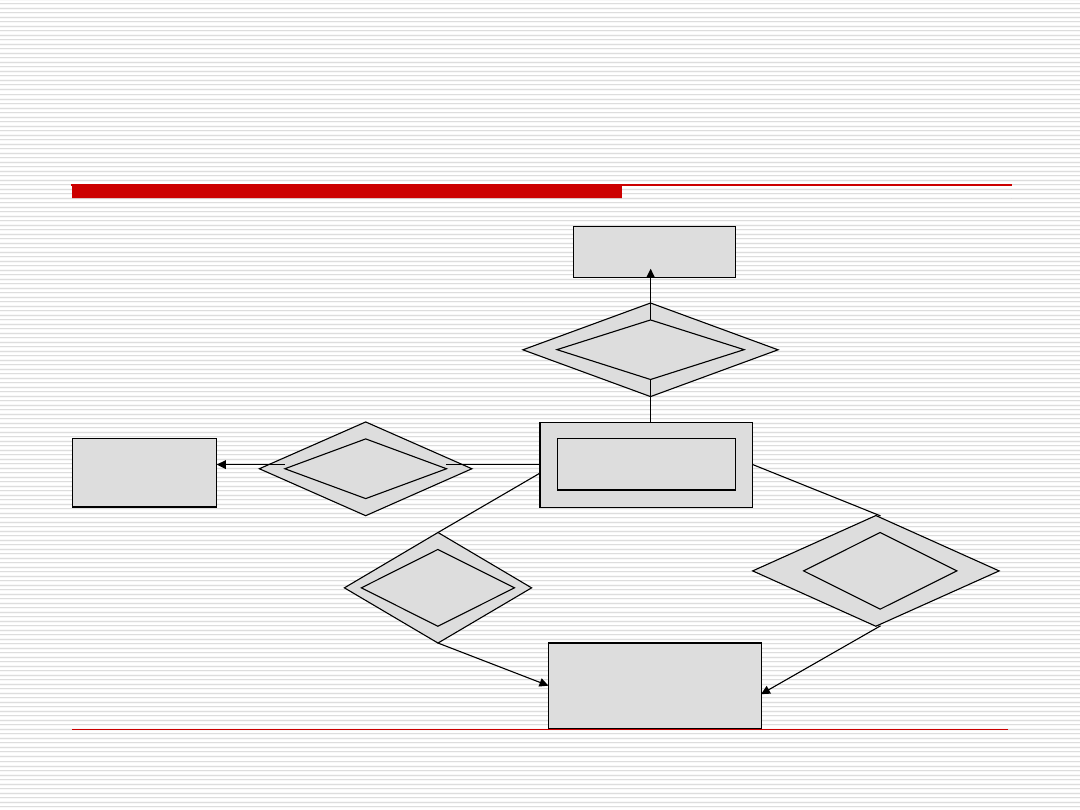
Zbiór słabych encji – przykład(1)

Sala

Znajdujesię

Budynek

Adres

NrSali

dr Paweł Drozda

Zbiór słabych encji – przykład(2)

Stadion

Miejsce

Drużyna

Sędzia

Arbiter

Mecz

Mecz

Goście

Gospodarze

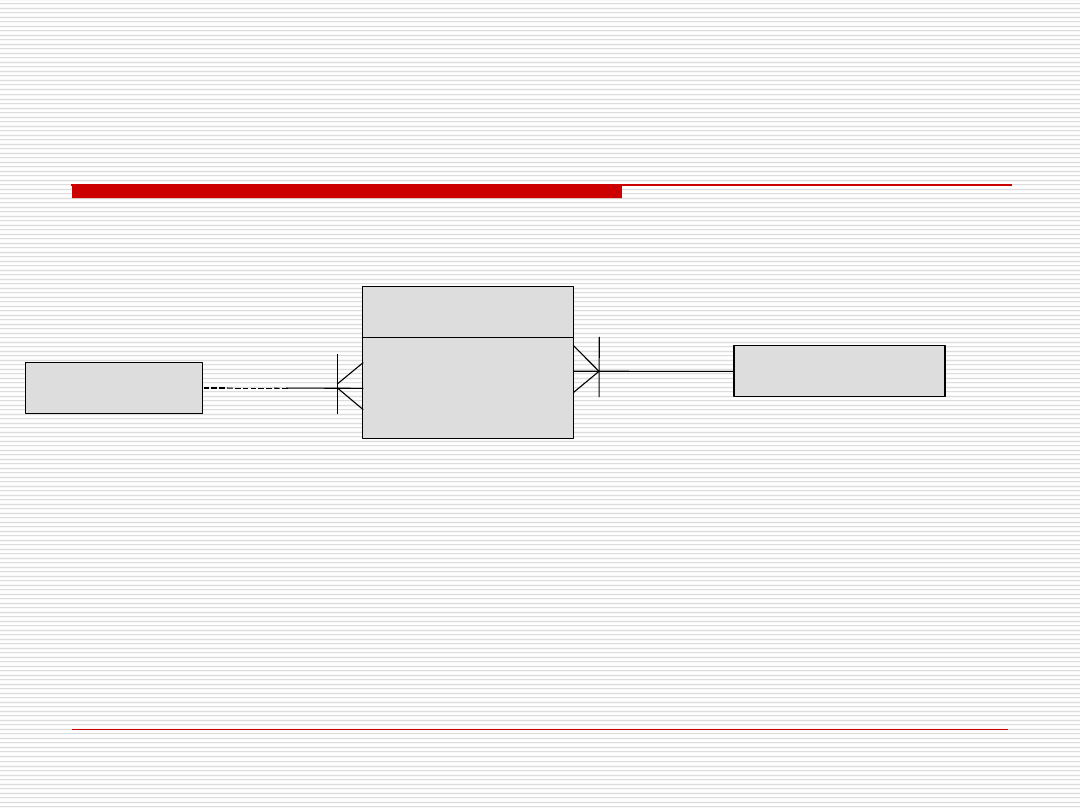
Zbiór słabych encji – przykład,
notacja Berkera

dr Paweł Drozda

Gaża

Występuje

FILM

AKTOR

dr Paweł Drozda

Słabe encje - wymagania



Encje (F) dostarczające klucza muszą być w
związku (R) ze słabą encją (E)



Związek (R) binarny jeden (F) do wielu (E)



Atrybuty klucza E pochodzące z F muszą
być w kluczu F



Gdy F jest słabą encją – atrybut klucza E
może pochodzić z innych encji powiązanych
z F związkiem jeden do wielu

dr Paweł Drozda

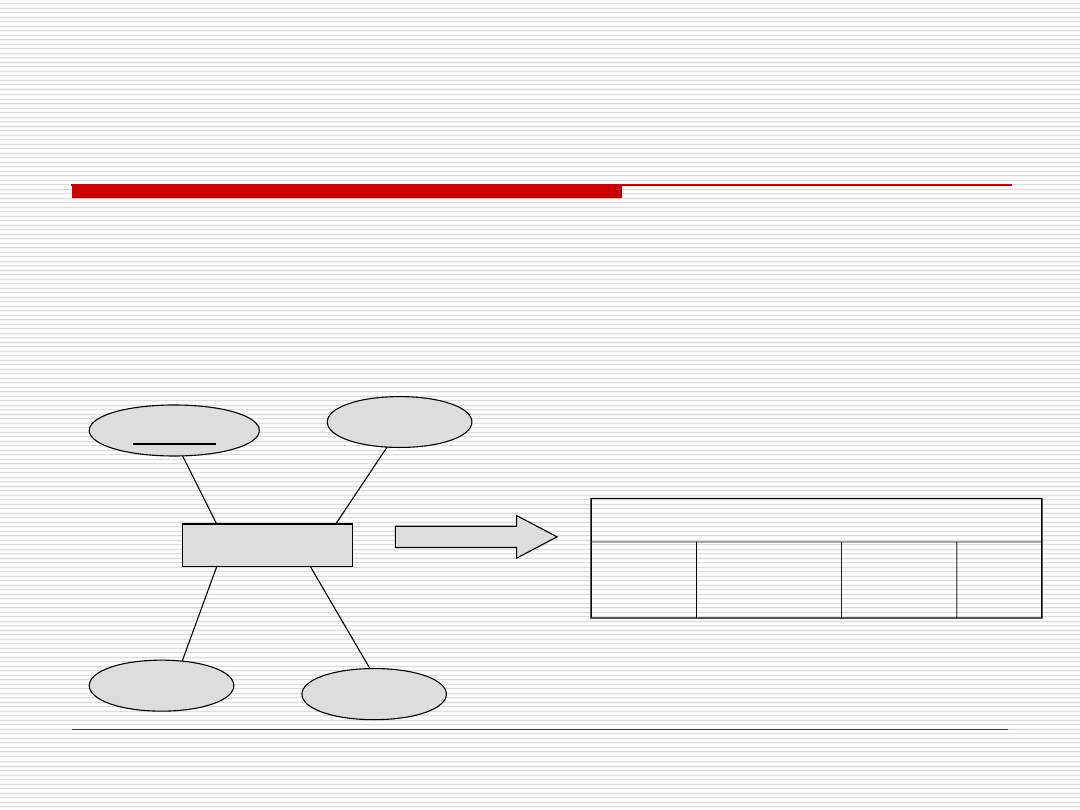
Związki encji => projekty relacyjne



Encja (nie słaba) przekształcana do
relacji z tą samą nazwą oraz tym
samym zbiorem atrybutów

PESEL

Osoba

nazwisko

płeć

telefon

Osoba
PESEL nazwisko telefo

n

płeć

Reguły przekształcania



Encja  Relacja



Atrybut encji  Atrybut relacji



Typ danych atrybutu encji  Typ danych

atrybutu relacji



Identyfikator  klucz podstawowy



Obowiązkowość atrybutu  NOT NULL



Opcjonalność  NULL



Pozostałe ograniczenia atrybutów encji 

ograniczenia integralnościowe relacji

dr Paweł Drozda

Przykład

dr Paweł Drozda

Przekształcanie związków



1:1 – klucz obcy w wybranej tabeli



1:M – klucz obcy w tabeli po stronie
wiele



N:M – nowa tabela

dr Paweł Drozda

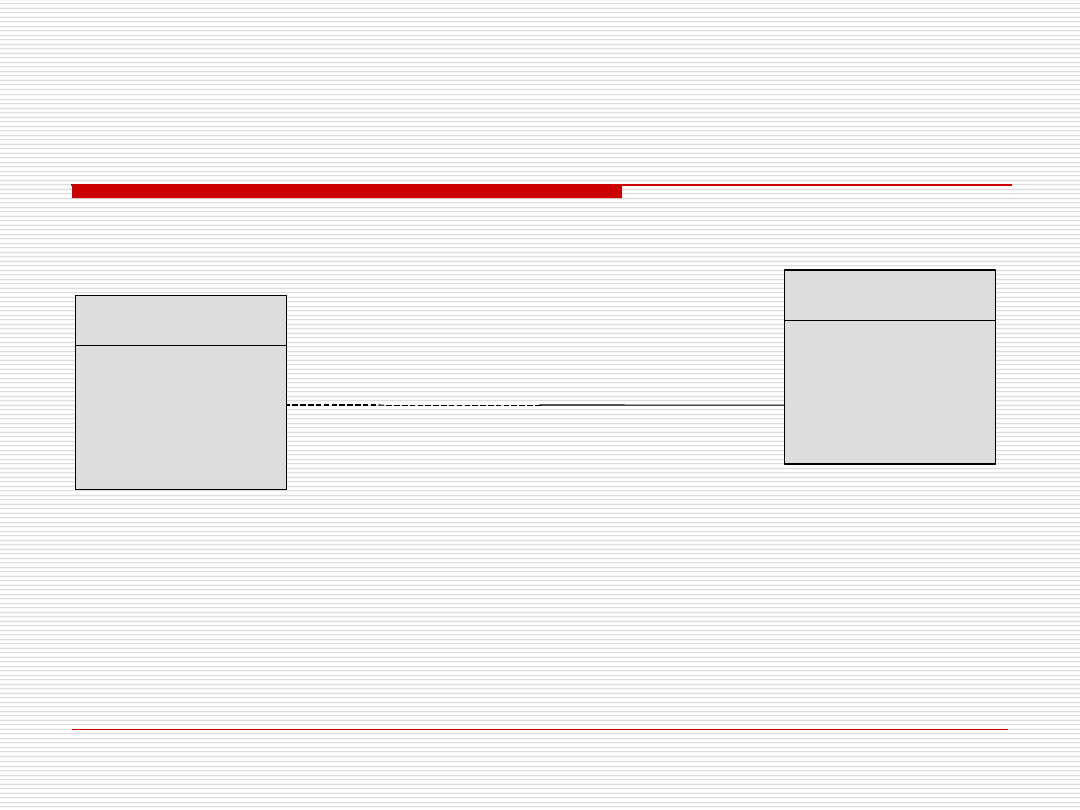
Związek binarny 1:1



Dodany klucz obcy po stronie związku
obowiązkowego

dr Paweł Drozda

Pesel
Nazwisko
Zarobki

NAUCZYCIEL

Id
Nazwa

KLASA

Wychowuje

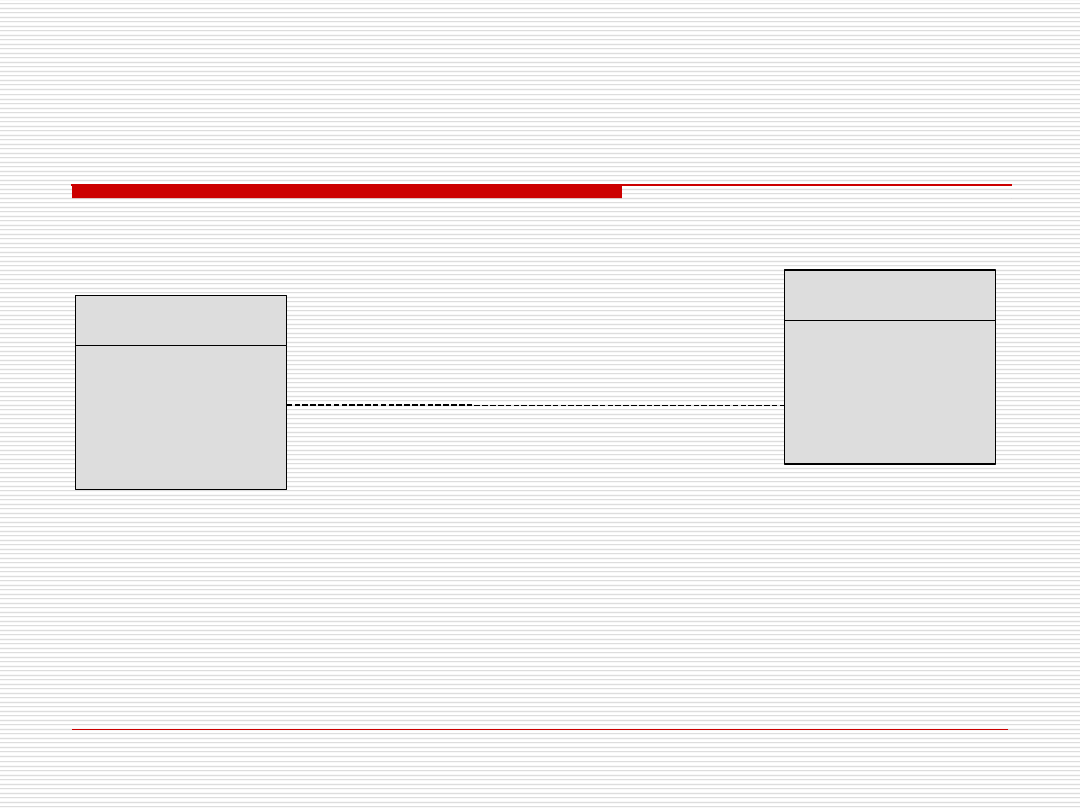
Związek binarny 1:1



Dodany klucz obcy po stronie mniejszej
tabeli

dr Paweł Drozda

Pesel
Nazwisko
Zarobki

PRACOWNIK

Id
IP

KOMPUTER

Uzywa

dr Paweł Drozda

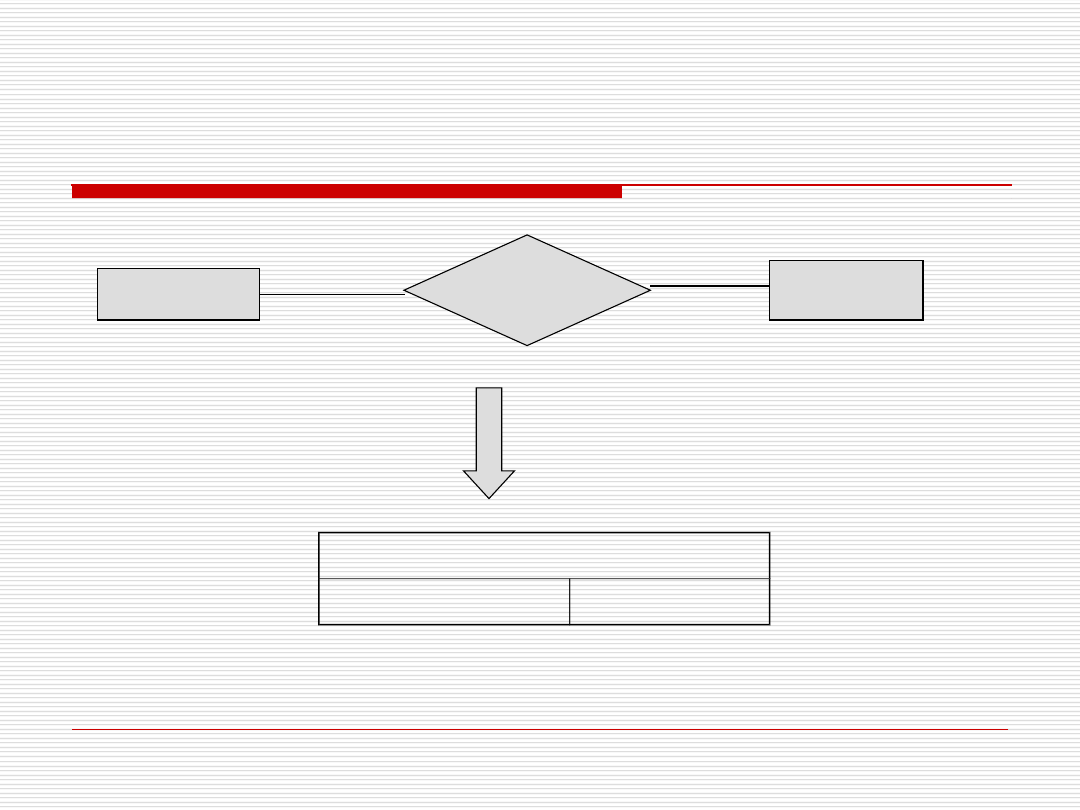
Związek N:M encji do relacji



Związki przyjmują postać relacji



Klucze encji uczestniczących w
związku jako atrybuty relacji



Gdy związek ma własny klucz –
dołączany do atrybutów relacji

dr Paweł Drozda

Przykład

Student

Egzamin

Przedmiot

Egzamin
idprzedmiotu

nrindeksu

dr Paweł Drozda

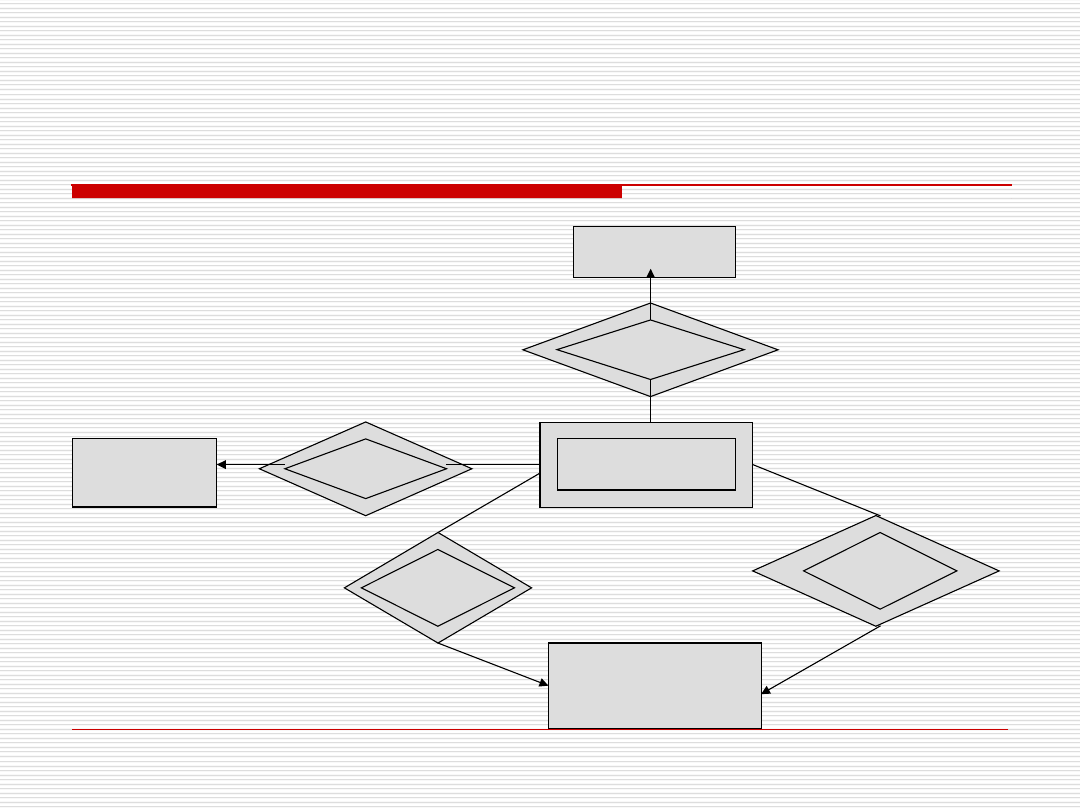
Słabe zbiory encji



Relacja powstała ze słabego zbioru
encji musi zawierać atrybuty tej encji
oraz klucze z encji pozostających w
związku wiele do jeden



Gdy konieczne - przemianowanie
atrybutów (np. gdy atrybut występuje
podwójnie

dr Paweł Drozda

Przykład (1)

Stadion

Miejsce

Drużyna

Sędzia

Arbiter

Mecz

Mecz

Goście

Gospodarze

dr Paweł Drozda

Przykład (2)

Mecz
nrsędziego nazwaStadionu

druzyna1 druzyna2

Wynik przekształcenia

dr Paweł Drozda

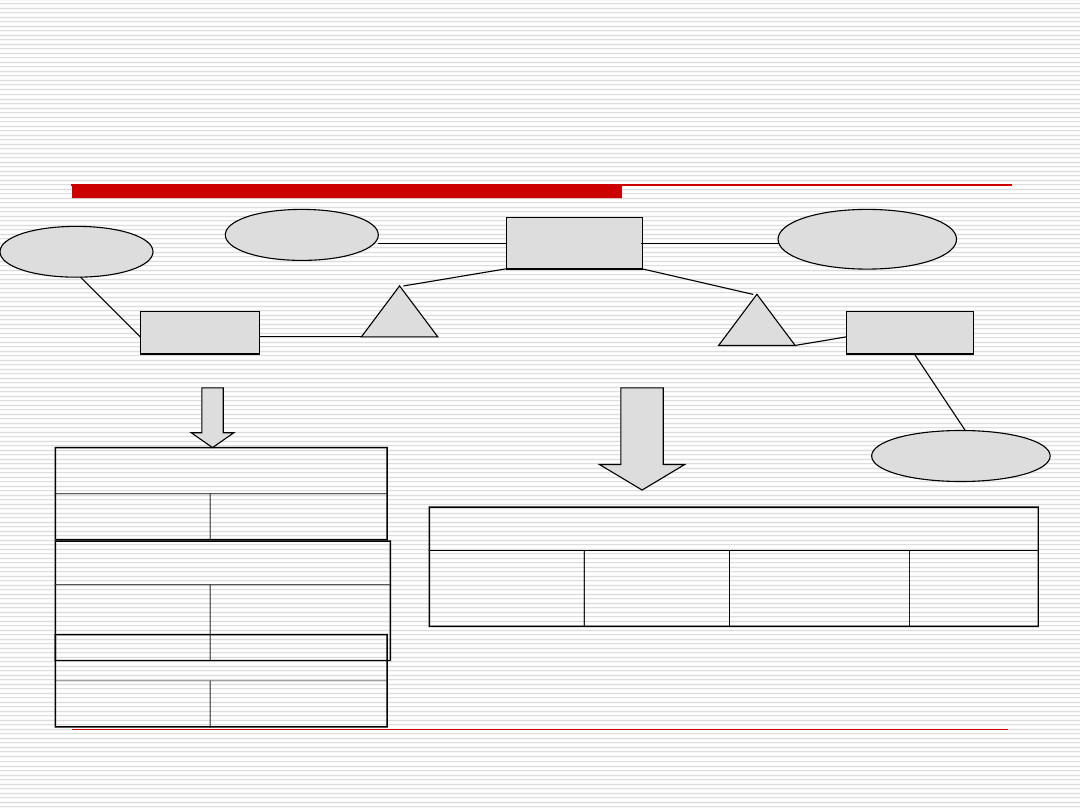
Podklasy do modelu relacyjnego



Trzy możliwości:



Dla każdej podencji tworzona releacja z

atrybutami wspólnymi oraz ze

specyficznymi



Elementy wspólne w jednej tabeli, dla

każdej podencji oddzielna tabela wraz z

ograniczeniami referencyjnymi (klucze

główne dodane do tabel stworzonych dla

podencji)



Stworzenie tylko jednej relacji (atrybuty

mogą przyjmować null)

dr Paweł Drozda

Podklasy przykład

Student

Zaoczny

Dzienny

isa

isa

nrindeksu

nazwisko

stypendium

czesne

Student
nrindeksu nazwisko

Zaoczny
nrindeksu czesne

Student
nrindeksu nazwisko stypendiu

m

czesne

Dzienny
nrindeksu stypendiu

m