©M

Funkcje trygonometryczne

dowolnego kąta.

©M

x

y

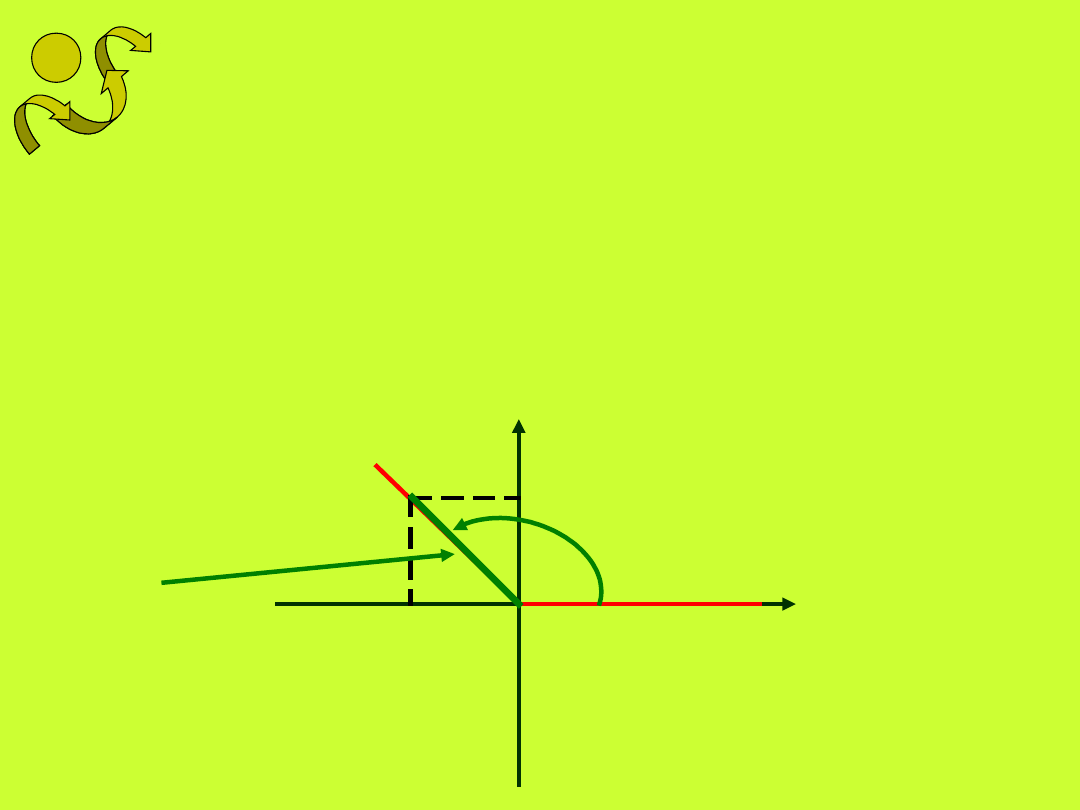
Umieszczamy kąt w układzie współrzędnych

REGUŁY:



wierzchołek kąta  ( 0

0

   360

0

) jest

początkiem układu współrzędnych,



x

p

odcięta

y

p

rzędna

r -
promień
wodzący

P(x

p

,y

p

)

.



pierwsze ramię kąta pokrywa się z dodatnią

półosią x



drugie ramię kąta odkładamy w kierunku

przeciwnym do ruchu wskazówek zegara i
nazywamy ramieniem wodzącym

©M

Jeżeli P(x

p

,y

p

) jest punktem na ramieniu

wodzącym kąta, a r jest promieniem
wodzącym punktu P, to

wartości stosunków nie
zależą od wyboru punktu P.

y

x

,

x

y

,

r

y

,

r

x

p

p

p

p

przykład

Ramię wodzące kata  przechodzi przez punkt A(-

2,-5), to  jest kątem należącym do III ćwiartki.

Promień wodzący a wymienione
stosunki są równe

29

25

4

r







2

5

x

y

,

5

2

y

x

,

29

5

r

y

,

29

2

r

x

A

A

A

A

A

A













Jeżeli P(x

p

,y

p

), to

2

p

2

p

y

x

r





©M

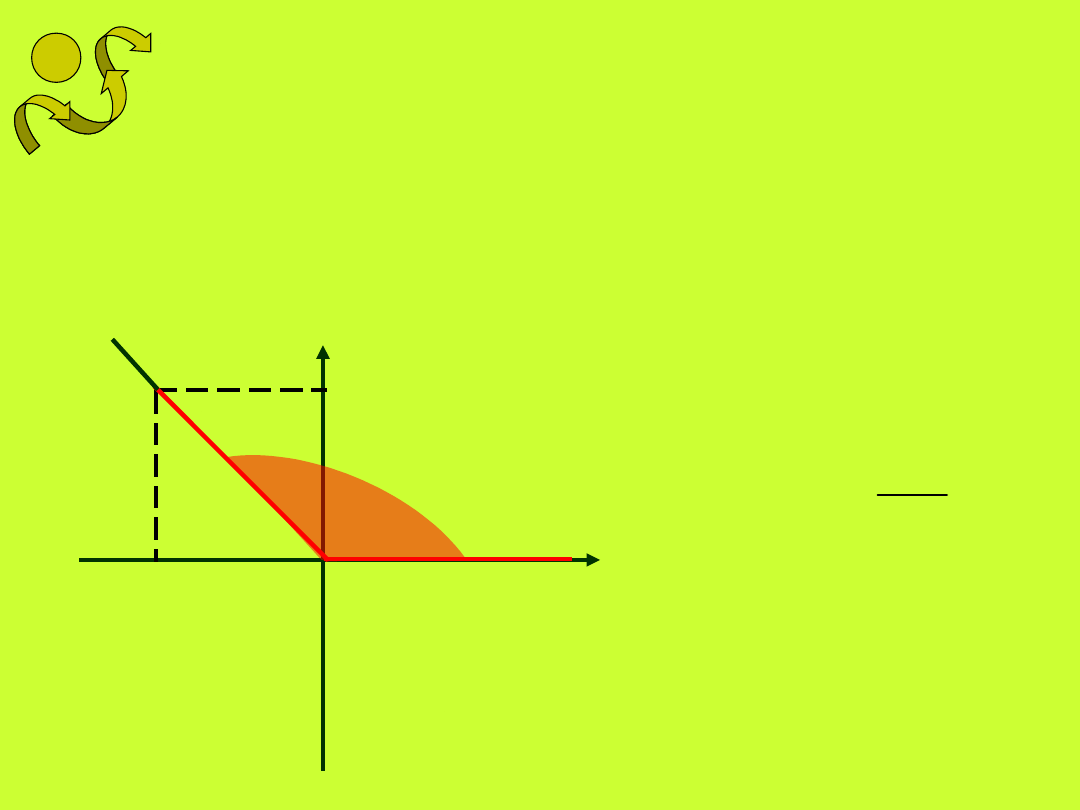
Sinusem kąta  nazywamy

stosunek rzędnej dowolnego
(różnego od wierzchołka) punktu
wybranego na ramieniu wodzącym
kąta do promienia wodzącego tego
punktu.

x

y

x

p

y

p

r

y

sin

p







r

P(x

p

,y

p

)

.

©M

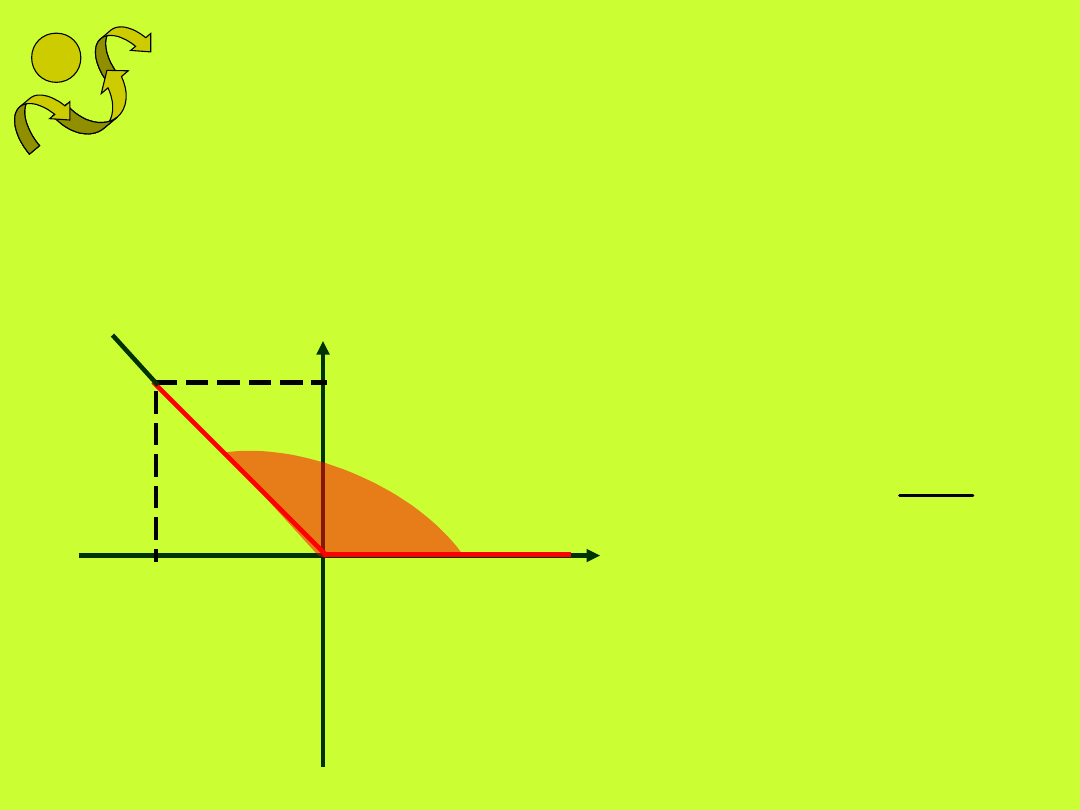
Cosinusem kąta  nazywamy

stosunek odciętej dowolnego
(różnego od wierzchołka) punktu
wybranego na ramieniu wodzącym
kąta do promienia wodzącego tego
punktu.

x

y

x

p

y

p

r

x

cos

p







r

P(x

p

,y

p

)

.

©M

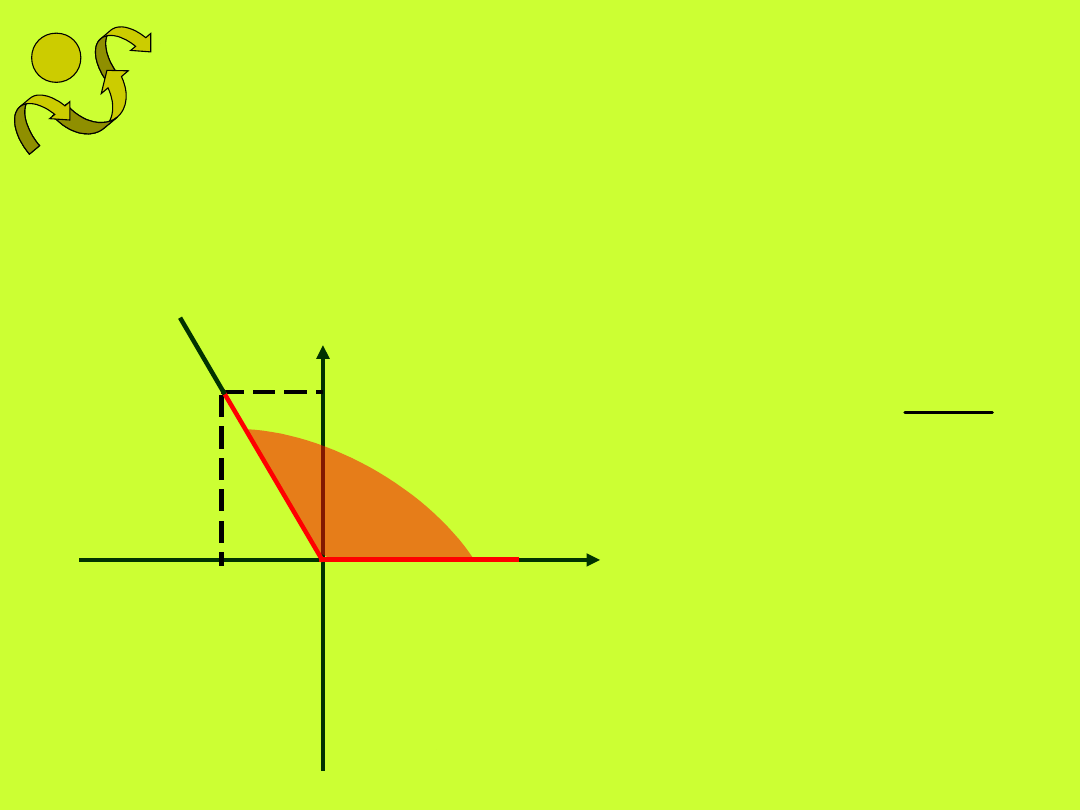
Tangensem kąta  nazywamy

stosunek rzędnej dowolnego
(różnego od wierzchołka) punktu
wybranego na ramieniu wodzącym
kąta do odciętej tego punktu.

x

y

x

p

y

p

p

p

x

y

tg 





r

założenie: x

p

 0, więc funkcja

tangens nie jest określona dla
kątów 90

o

i 270

0

.

P(x

p

,y

p

)

.

©M

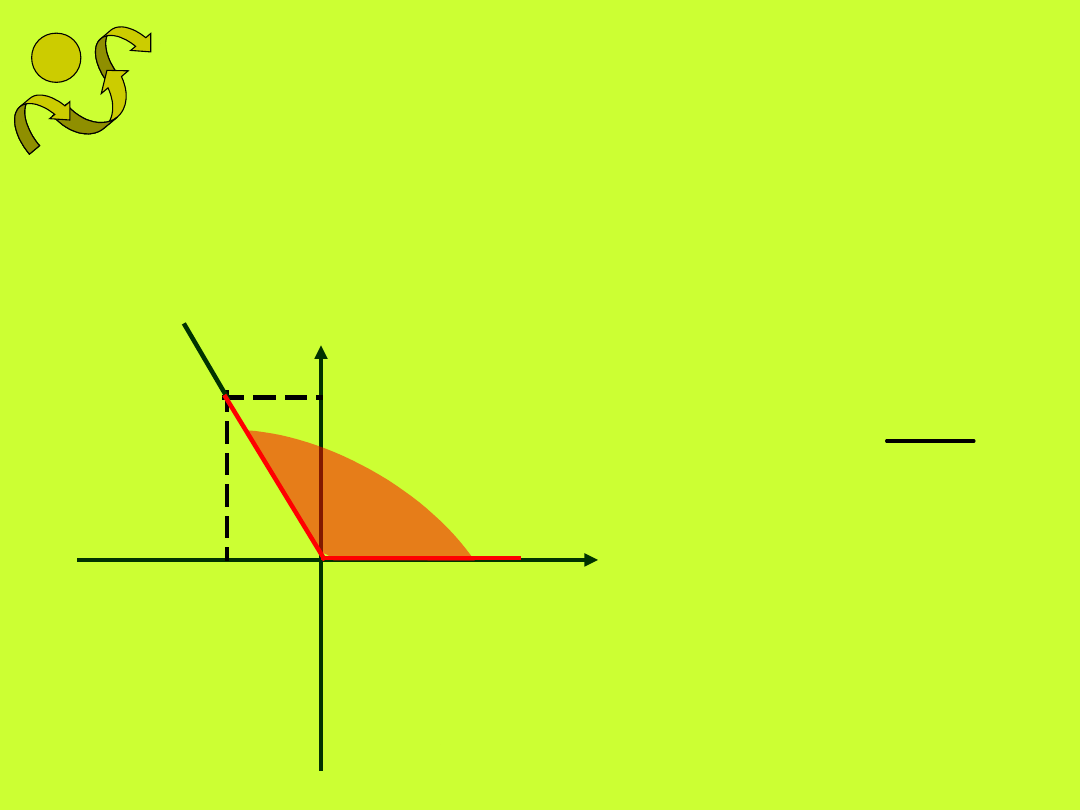
Cotangensem kąta  nazywamy

stosunek odciętej dowolnego
(różnego od wierzchołka) punktu
wybranego na ramieniu wodzącym
kąta do rzędnej tego punktu.

x

y

x

p

y

p

p

p

y

x

ctg 



założenie: y

p

 0, więc

funkcja cotangens nie jest
określona dla kątów 0

o

, 180

0

i

360

0

.

r



P(x

p

,y

p

)

.

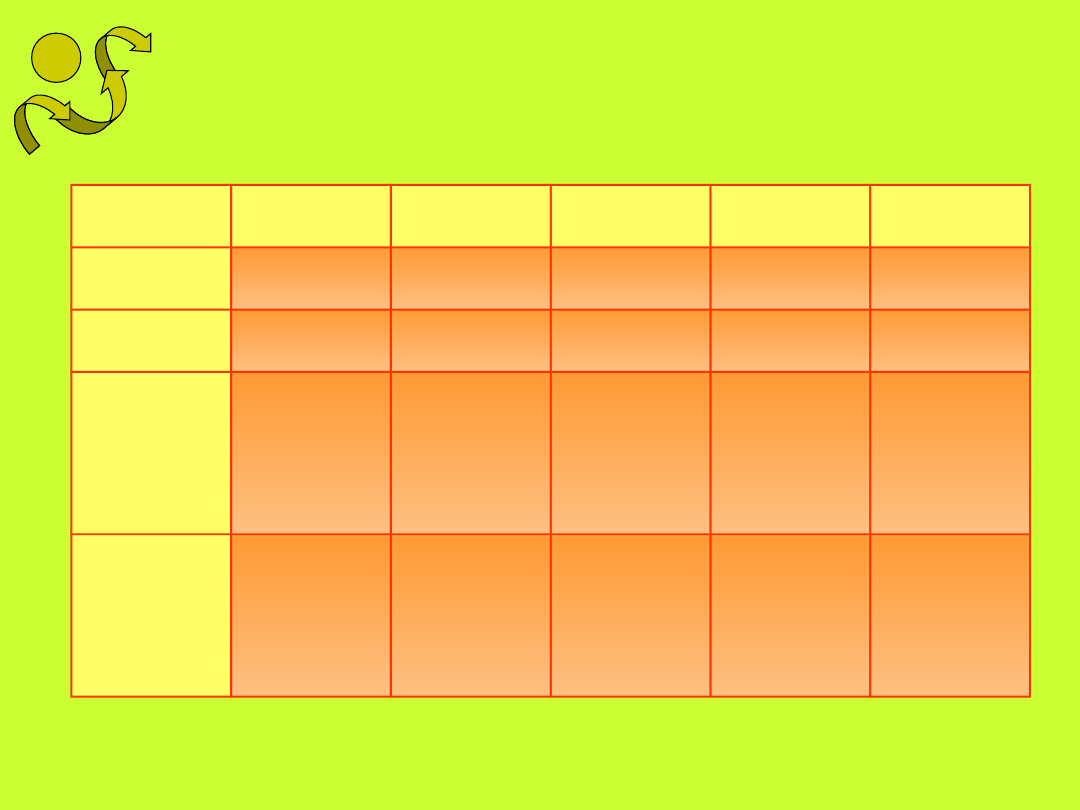
©M

Znaki funkcji trygonometrycznych w
poszczególnych ćwiartkach układu
współrzędnych.



I

II

III

IV

sin

+

+





cos

+





+

tg

+



+



ctg

+



+



W pierwszej ćwiartce same plusy, w drugiej
tylko sinus, w trzeciej tangens i cotangens
a w czwartej cosinus.

©M

Wartości funkcji trygonometrycznych dla

wybranych kątów.



0

0

90

0

180

0

270

0

360

0

sin

0

1

0

-1

0

cos

1

0

-1

0

1

tg

0

nie

istnie

je

0

nie

istnie

je

0

ctg

nie

istnie

je

0

nie

istnie

je

0

nie

istnie

je

©M

x

y

x

y

1

1

.

P

A

60

0

1

1

1

45

0

.

P

x

y

1

1

30

0

.

P

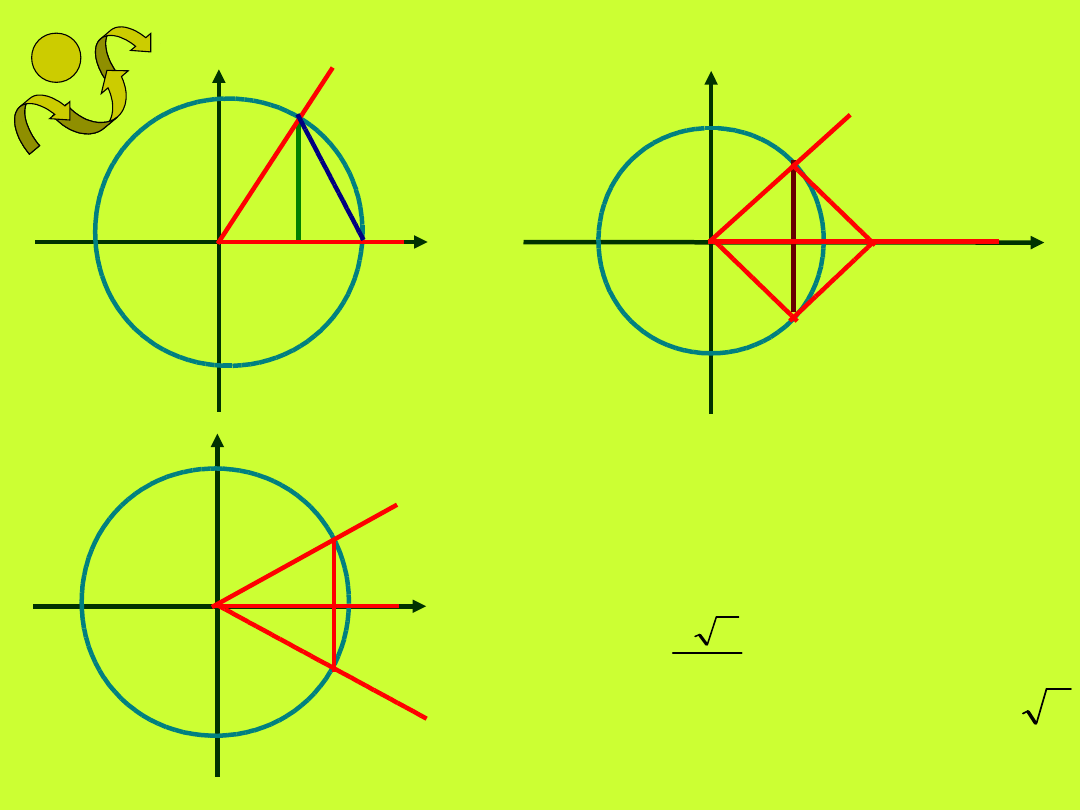
Oblicz wartości funkcji
trygonometrycznych na
podstawie rysunków
wiedząc, że wysokość
trójkąta równobocznego o
boku

a wynosi

natomiast przekątna
kwadratu

2

3

a

2

a

©M



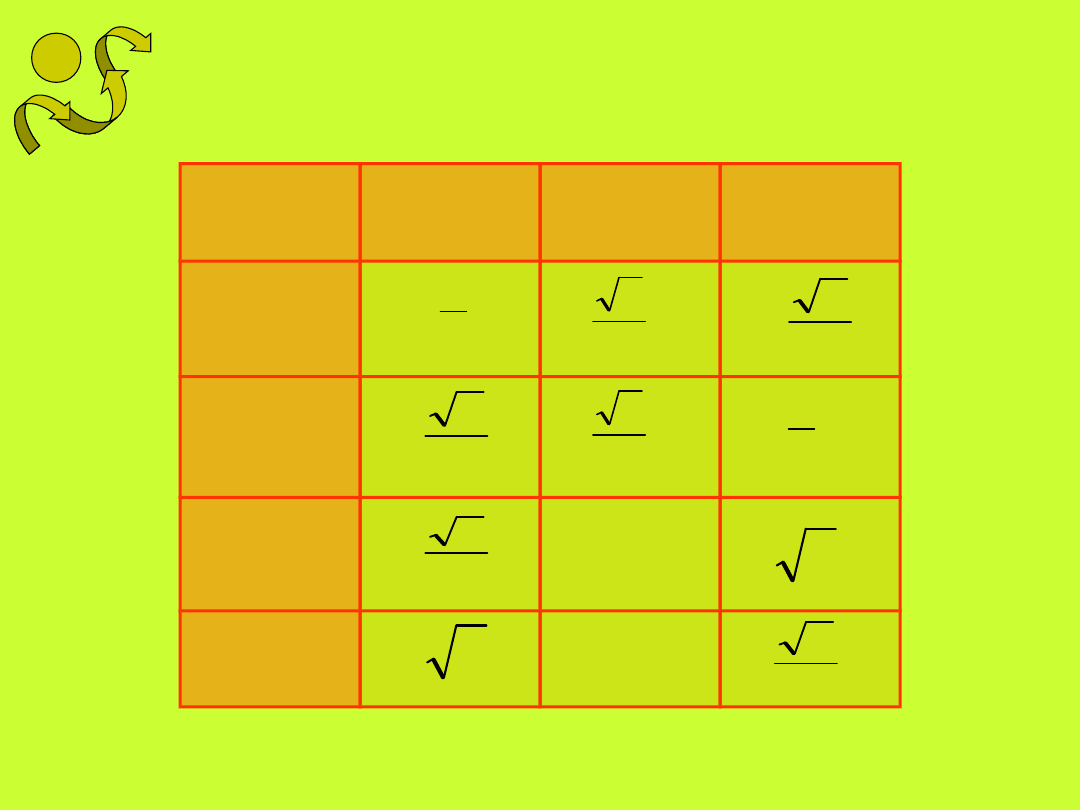
30

0

45

0

60

0

sin

cos

tg

1

ctg

1

2

1

2

1

2

2

2

2

2

3

2

3

3

3

3

3

3

3

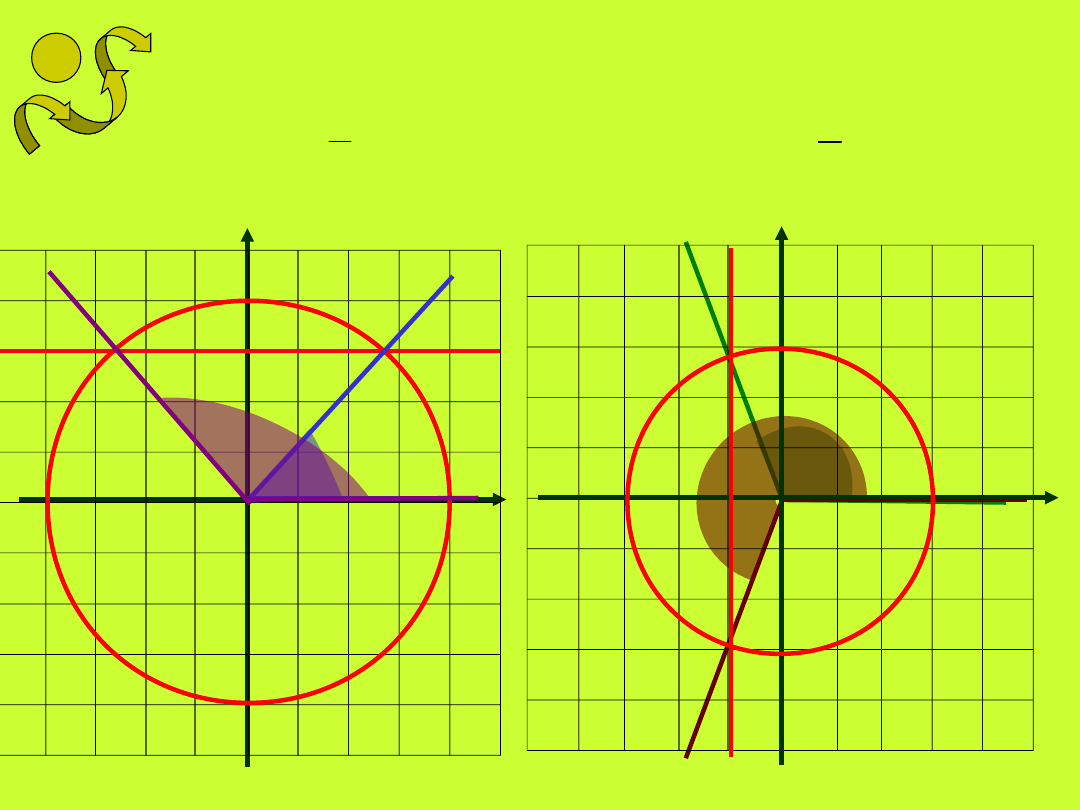
©M



1



2

x

y

1

1

Skonstruować kąt  , wiedząc, że

1.

4

3

sin 



2.

3

1

cos







przyjmujemy, że y

p

= 3 i

r = 4

przyjmujemy, że x

p

= -1 i

r = 3

y =

3

1

x

y

1



1



2

x =

-1

©M

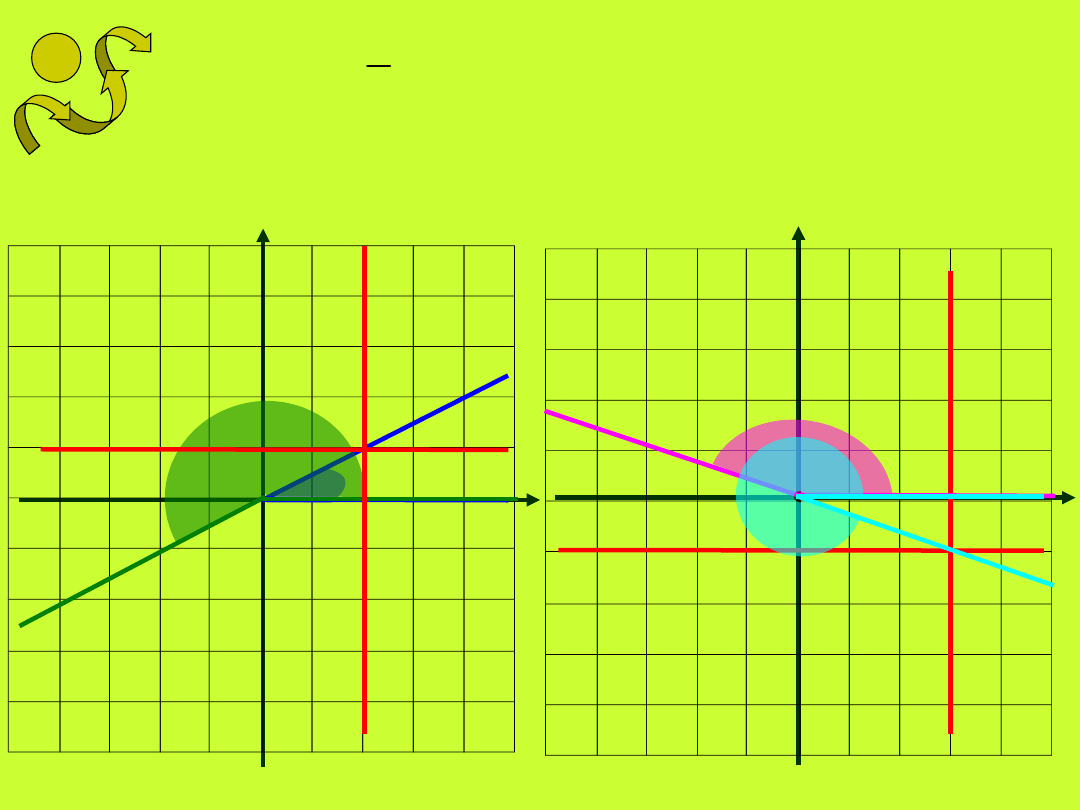
3.

2

1

tg 



4.

3

ctg







1

x

y

1

1

x

y

1

przyjmujemy, że y

p

= 1 i

x

p

= 2

lub

y

p

= -1 i x

p

= -2

przyjmujemy, że x

p

=3 i y

p

= -1

lub

x

p

= -3 i y

p

= 1



1



2

y

=1

x = 2

y =

-1

x =3



1



2

©M