Anna

Pernal

Funkcje

trygonometrycz

ne kąta ostrego

Defin
icje

Zad
ania

Cieka
wostk
i

KONIEC

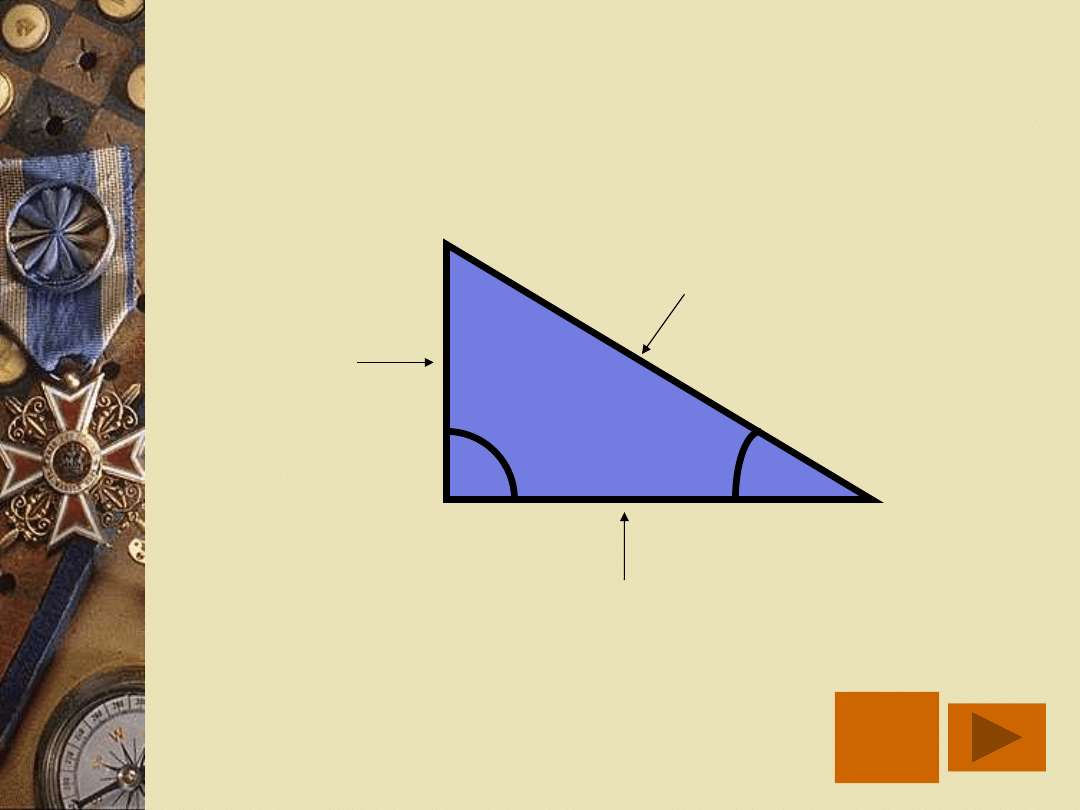
P

rz

y

p

ro

s

to

k

ą

tn

a

p

rz

e

ci

w

le

g

ła

d

o

k

ą

ta



Przyprostokątna

przyległa do kąta 

Prz

eciw

pro

sto

kąt

na





NAZWY BOKÓW TRÓJKĄTA

PROSTOKĄTNEGO

MENU

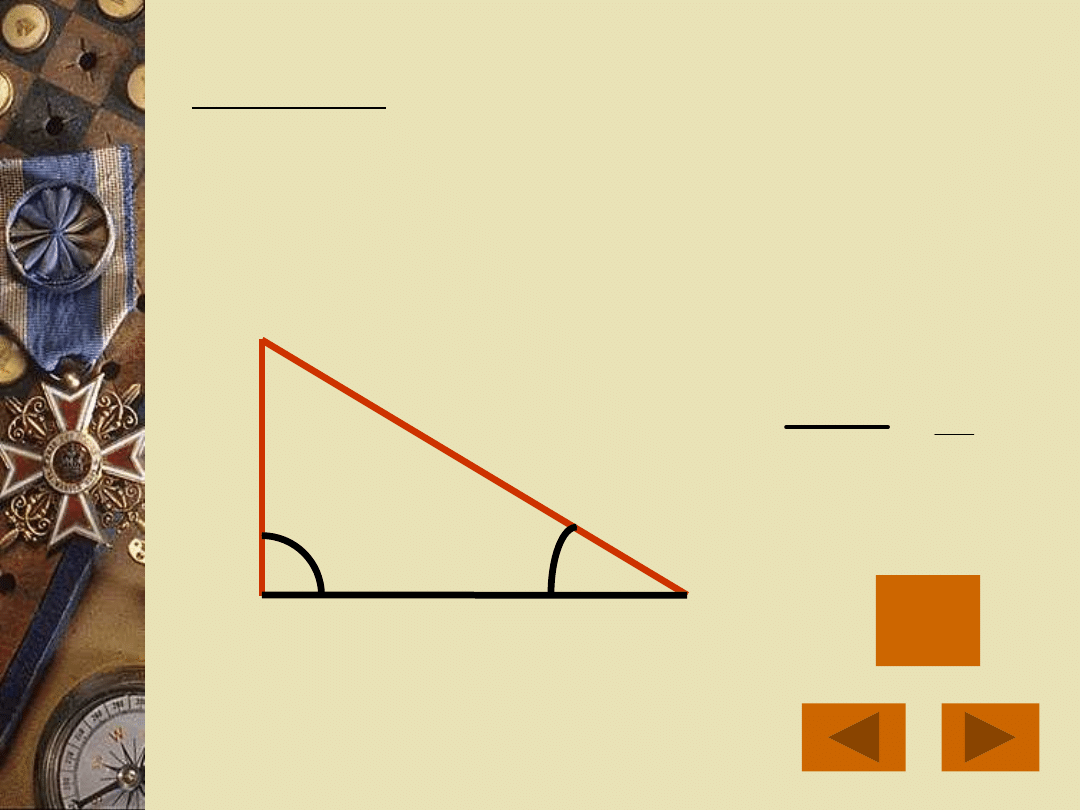
Sinusem kąta ostrego  w trójkącie

prostokątnym nazywamy stosunek

długości przyprostokątnej

przeciwległej do tego kąta do

długości przeciwprostokątnej.

Będziemy go oznaczać sin .





a

b

c

c

a

α

sin 

c

a

α

sin 

MENU

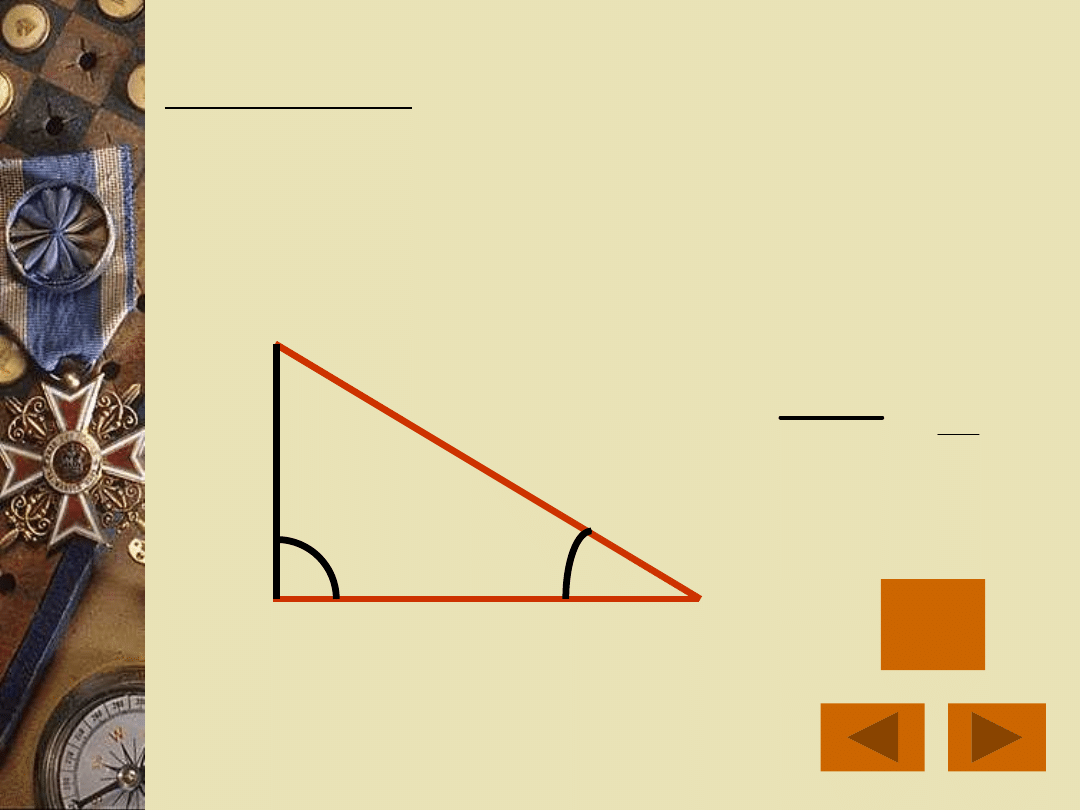
Cosinusem kąta ostrego  w trójkącie

prostokątnym nazywamy stosunek

długości przyprostokątnej przyległej

do tego kąta do długości

przeciwprostokątnej. Będziemy go

oznaczać cos  .





a

b

c

c

a

α

sin 

c

b

α

cos 

MENU

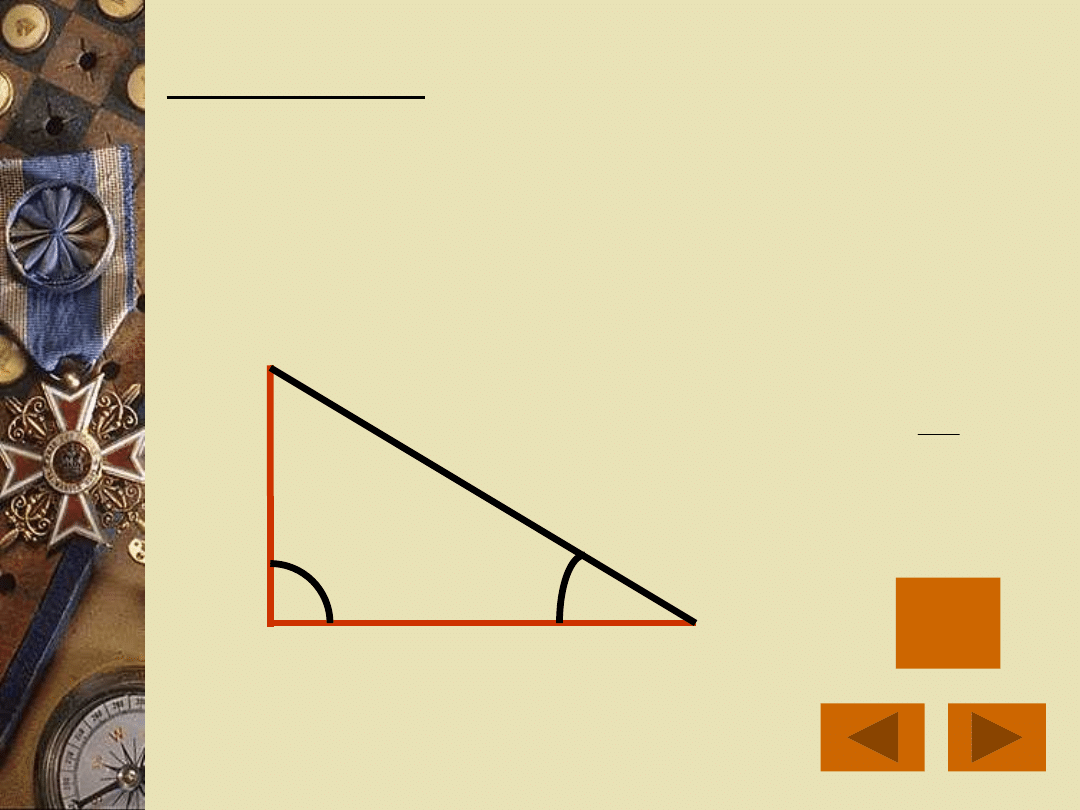
Tangensem kąta ostrego  w trójkącie

prostokątnym nazywamy stosunek

długości przyprostokątnej

przeciwległej do kąta  do długości

drugiej przyprostokątnej. Będziemy

go oznaczać tg  .





a

b

c

b

a

α

tg 

MENU

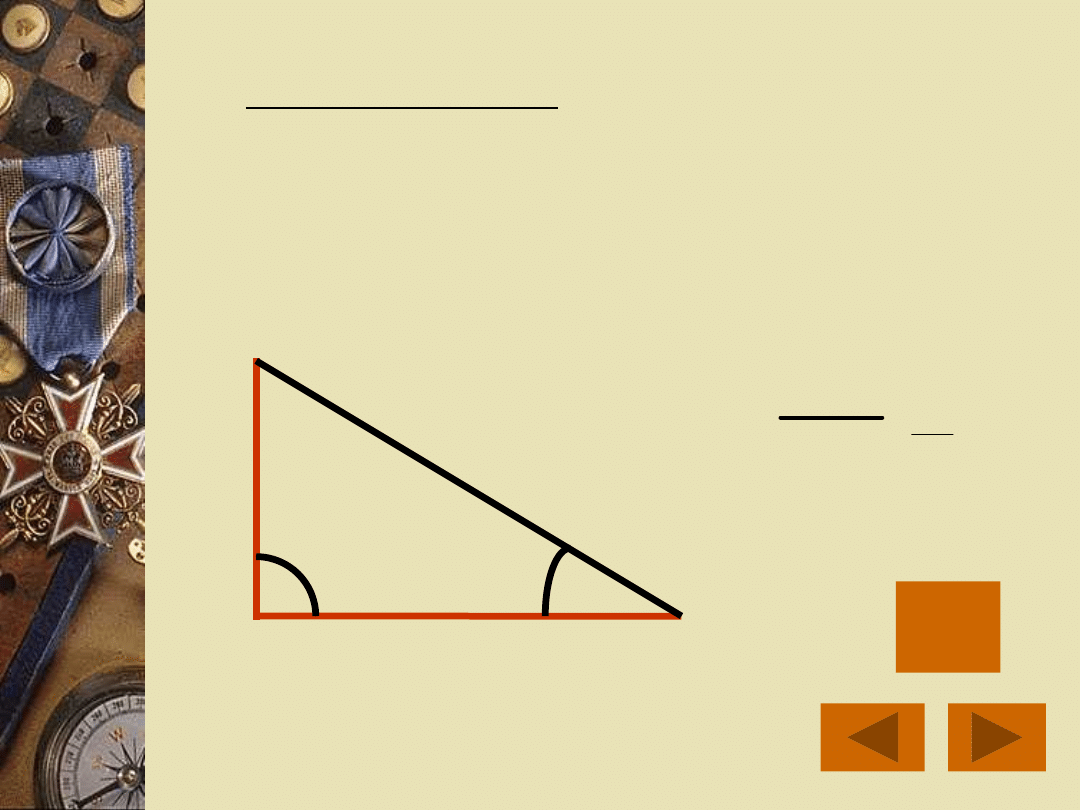
Cotangensem kąta ostrego  w

trójkącie prostokątnym nazywamy

stosunek długości przyprostokątnej

przyległej do kąta  do długości

drugiej przyprostokątnej. Będziemy

go oznaczać ctg  .





a

b

c

c

a

α

sin 

a

b

α

ctg 

MENU

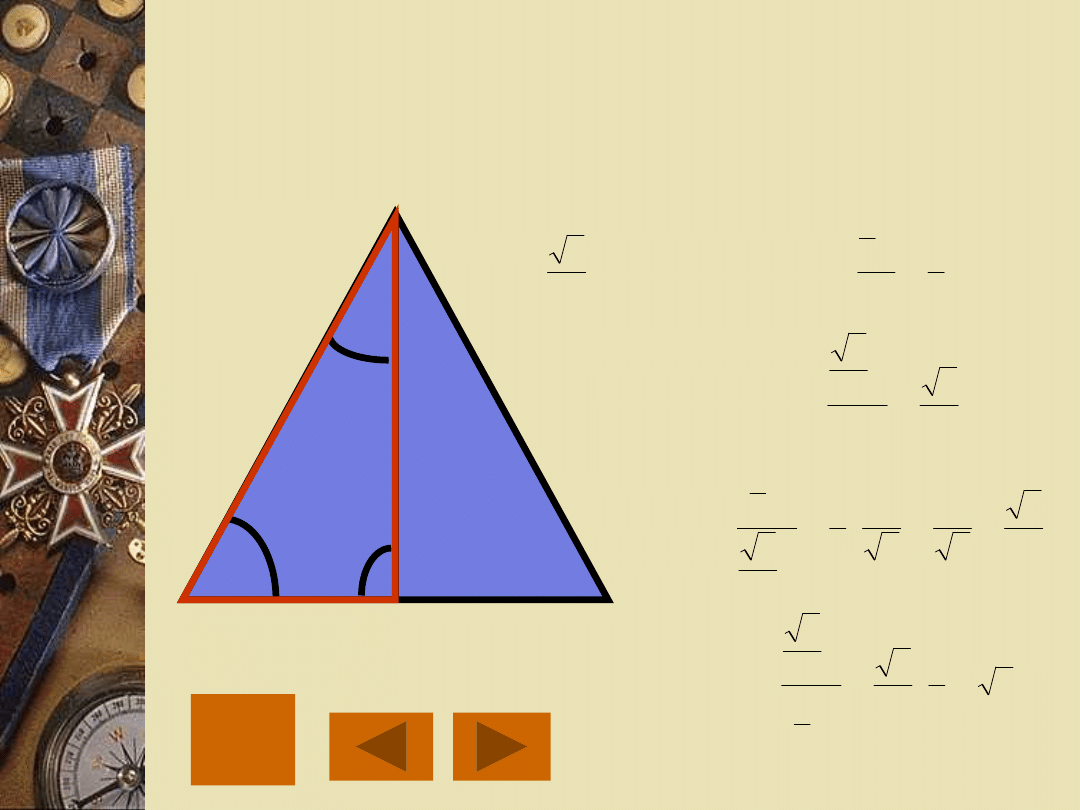
a

a

a

h

60

30

WARTOŚCI FUNKCJI

TRYGONOMETRYCZNYCH KĄTA 30

2

1

a

a

2

1

30

sin







2

3

a

a

2

3

30

cos







3

3

3

1

3

2

2

1

a

2

3

a

2

1

30

tg













3

1

2

2

3

a

2

1

a

2

3

30

ctg











a

2

3

h



MENU

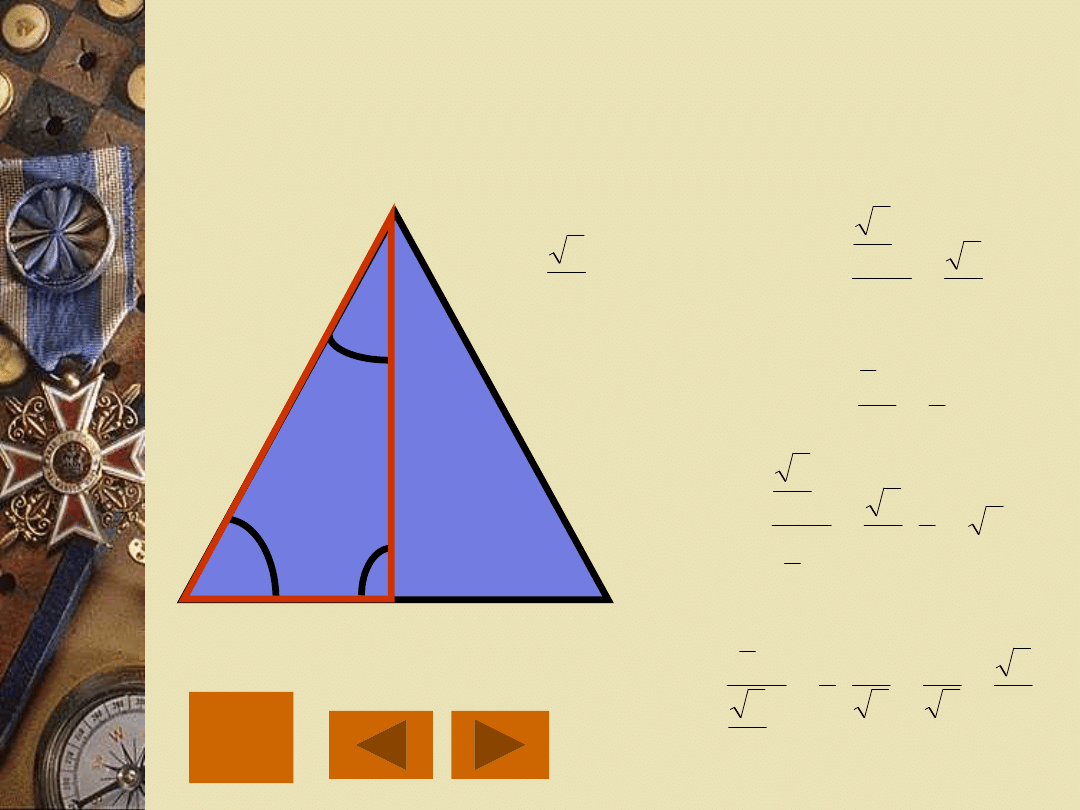
2

3

a

a

2

3

60

sin







2

1

a

a

2

1

60

cos







3

1

2

2

3

a

2

1

a

2

3

60

tg











3

3

3

1

3

2

2

1

a

2

3

a

2

1

60

ctg













MENU

a

a

a

h

60

30

a

2

3

h



WARTOŚCI FUNKCJI

TRYGONOMETRYCZNYCH KĄTA 60



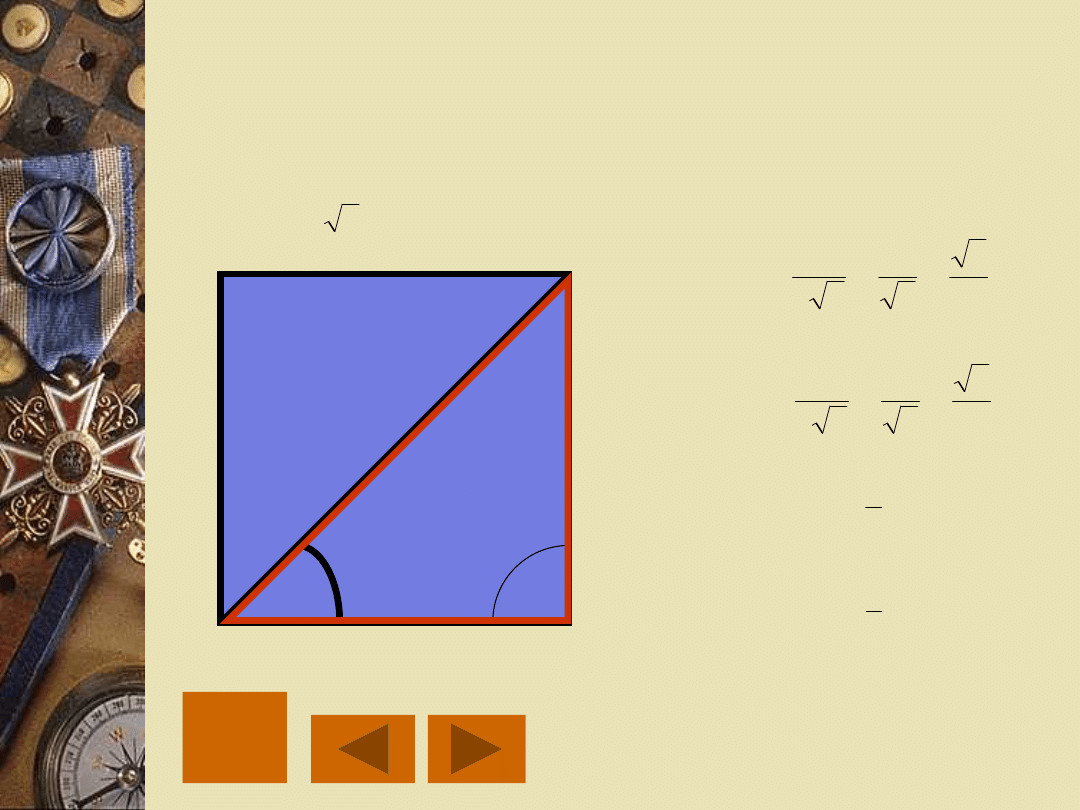
45



d

a

2

2

2

1

2

a

a

45

sin









2

2

2

1

2

a

a

45

cos









1

a

a

45

tg







1

a

a

45

ctg







2

a

d

MENU

a

WARTOŚCI FUNKCJI

TRYGONOMETRYCZNYCH KĄTA 45

WARTOŚCI FUNKCJI

TRYGONOMETRYCZNYCH KĄTÓW



30

45

60

sin 

cos 

tg 

ctg 

2

1

2

2

2

3

2

3

2

2

2

1

3

3

3

3

1

1

3

3

MENU

ZADANIE 1

Boki trójkąta prostokątnego mają

długości a=3, b=8, c=10. Oblicz

wartości funkcji

trygonometrycznych kąta .

MENU

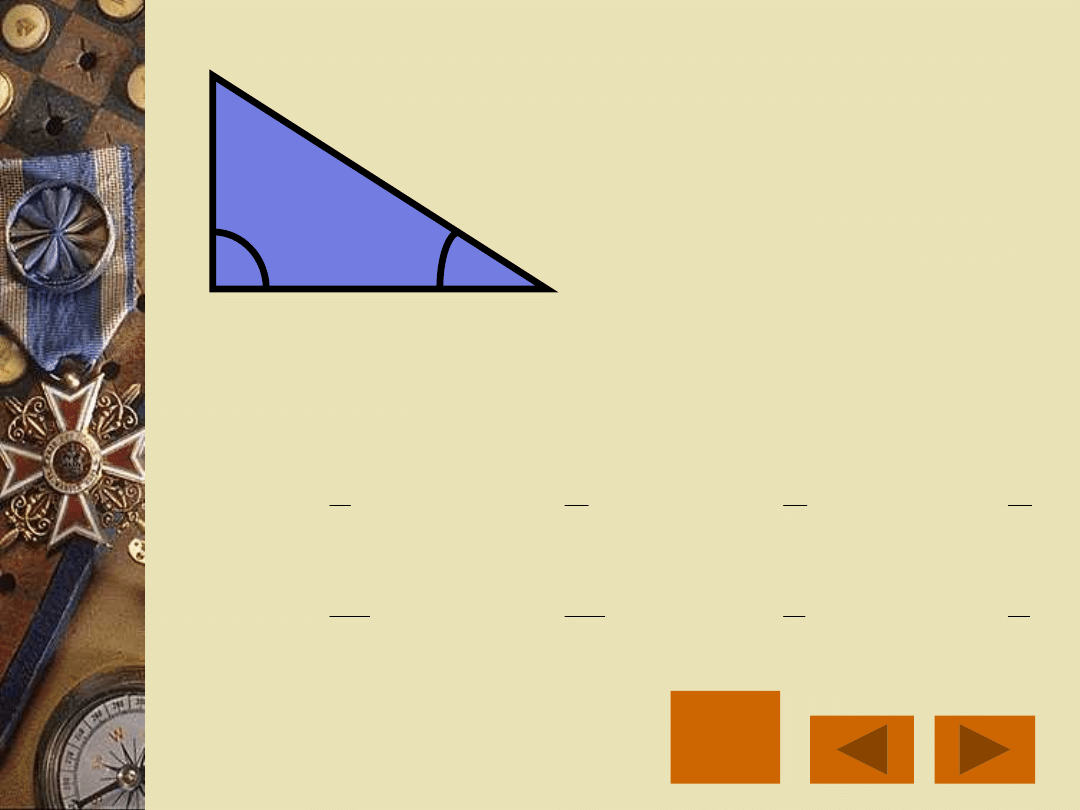
10

c

8

b

3

a

:

Dane







ROZWIĄZANIE

10

3

α

sin

c

a

α

sin





10

8

α

cos

c

b

α

cos





8

3

α

tg

b

a

α

tg





3

8

α

ctg

a

b

α

ctg





?

α

ctg

?

α

tg

?

α

cos

?

α

sin

:

Szukane









MENU



b

a

c



ZADANIE 2

Oblicz wysokość latarni morskiej,

wiedząc, że promienie słoneczne

padają na ziemię pod kątem 45º,

długość jej cienia to 100 Twoich

kroków, a każdy Twój krok to około

75 cm.

MENU

45

º

h

c

MENU

75cm

k

45

α

:

Dane







?

h

:

Szukane



ROZWIĄZANIE

75m

7500cm

75cm

100

c









c

h

α

tg 

75m

h

45

tg





75m

h

1

75m

h

ODPOWIEDŹ

MENU

Wysokość latarni morskiej

wynosi 75 m.

ZADANIE 3

Rozkładaną drabinę o długości 2,5
m możemy rozstawić na szerokość

1 m. Oblicz wysokość h drabiny

oraz miarę kąta  pomiędzy jej

ramionami po rozstawieniu.

MENU

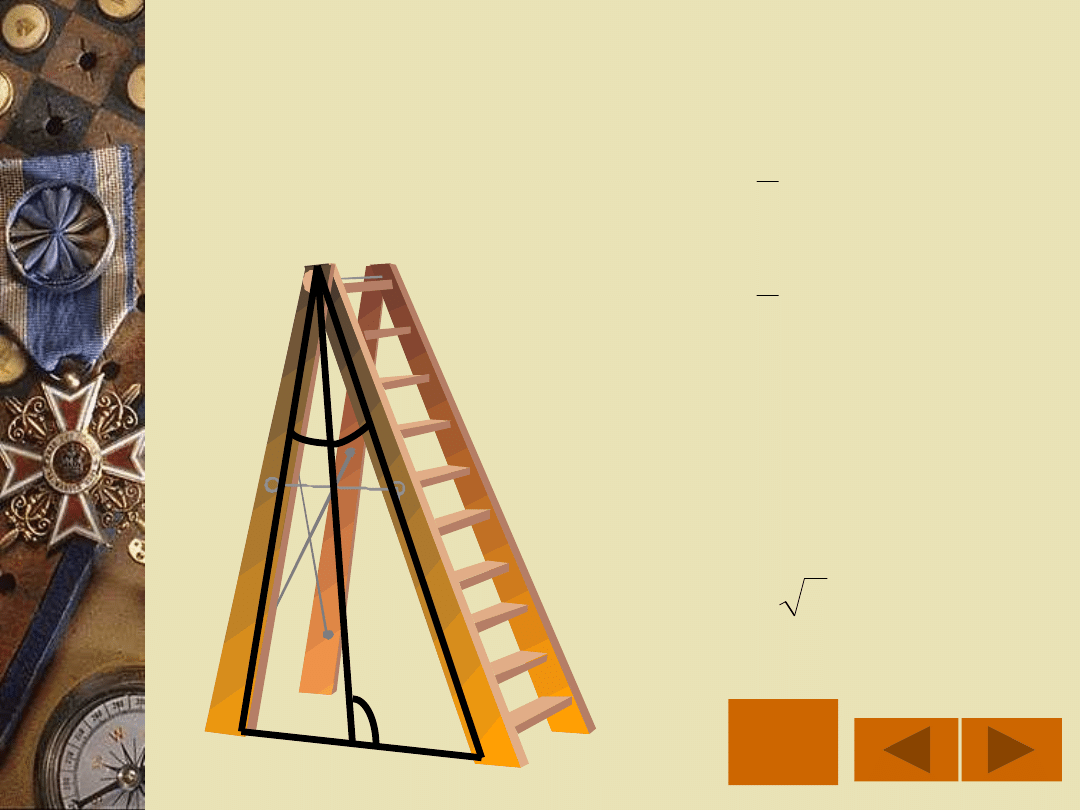
m

1

s

m

2,5

d

:

Dane





ROZWIĄZANIE

?

2α

?

h

:

Szukane





d2

s)

2

1

(

2

h2





(2,5)

2

)

2

1 2

(

h2





6,25

0,25

h2





0,25

6,25

h2





MENU

[m]

6

h

6

h2





h

s

d



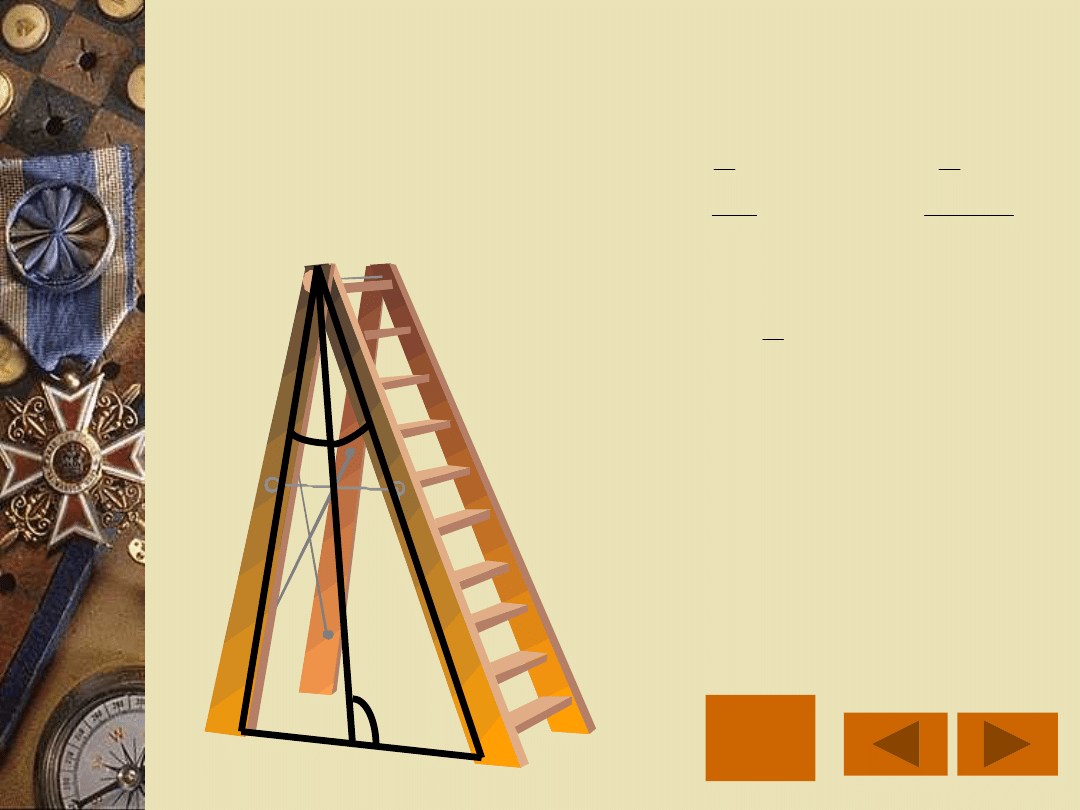
ROZWIĄZANIE

MENU

d

s

2

1

α

sin 

2,5m

m

2

1

α

sin 

5

1

α

sin 



12

α











24

12

2

2α

m

1

s

m

2,5

d

:

Dane





?

2α

?

h

:

Szukane









h

s

d



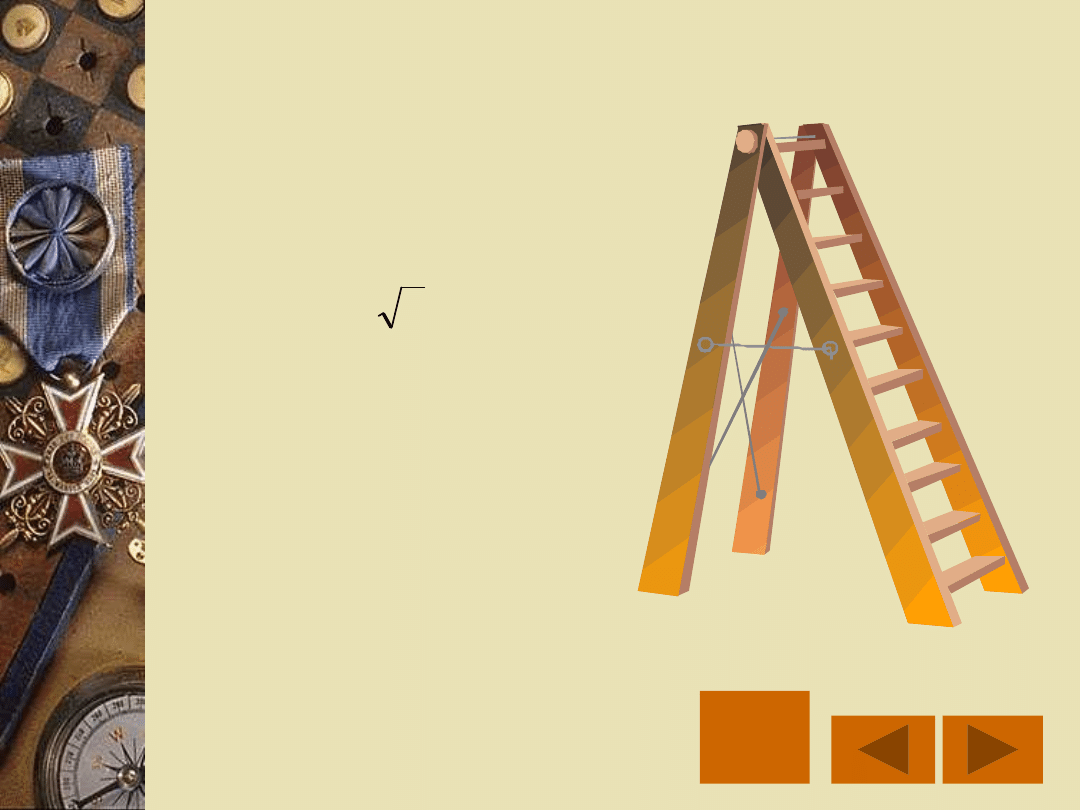
ODPOWIEDŹ

MENU

Wysokość drabiny

wynosi , a kąt

między ramionami

po jej rozstawieniu

ma miarę 24 .

m

6

ZADANIE 4

MENU

Musimy pokonać drogę między

wierzchołkami dwóch pagórków.

Droga do przełęczy ze szczytu

pierwszego pagórka, nachylonego do

poziomu pod kątem 20, wynosi 1 km,

a droga z przełęczy na szczyt

drugiego, nachylonego do poziomu

pod kątem 15 ma długość 1,5 km.
Jaką wysokość, licząc od przełęczy,

mają te pagórki? Wynik zaokrąglij do

metrów.

MENU





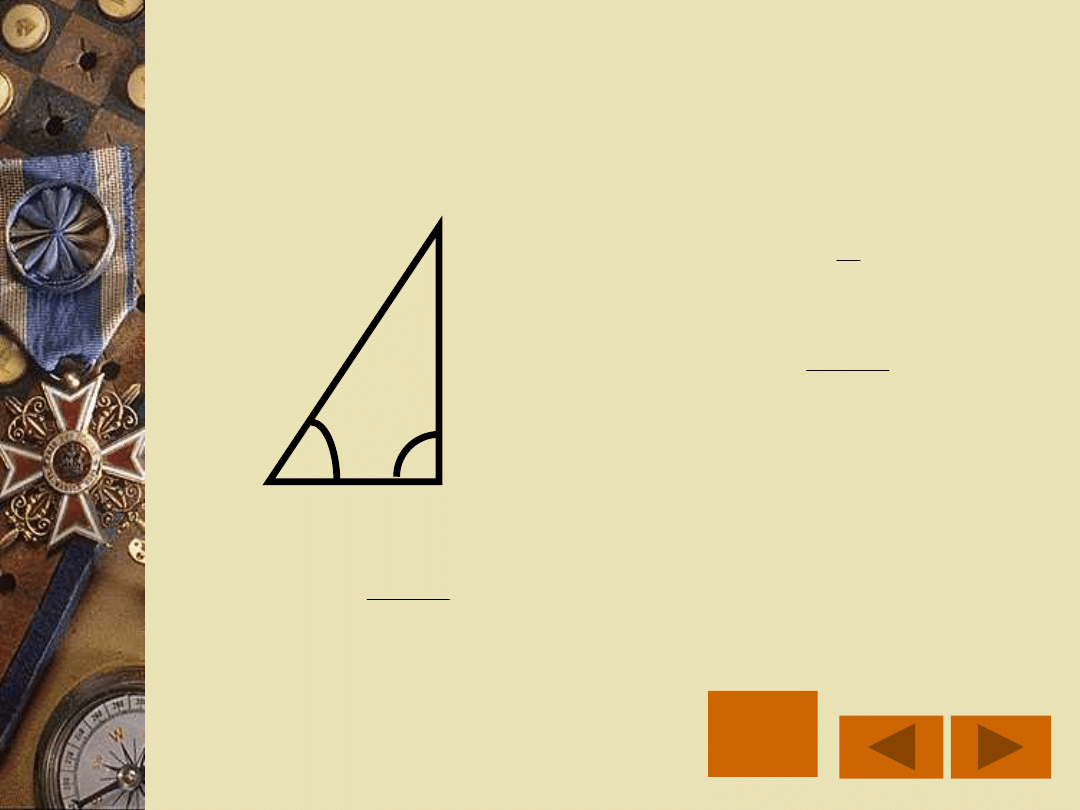
a

h







20

α

km

1

a

:

Dane

?

h

:

Szukane



ROZWIĄZANIE

a

h

α

sin 

MENU

km

1

h

20

sin





km

1

h

0,342



1km

0,342

h





m

342

km

0,342

h





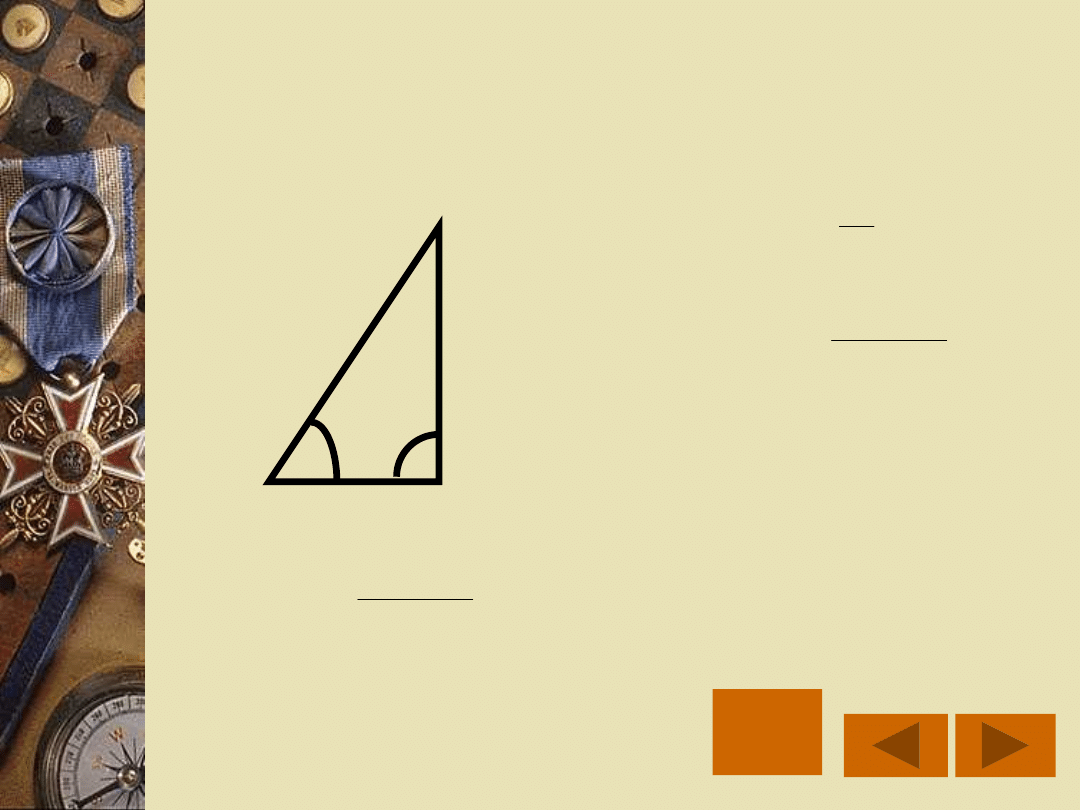
ROZWIĄZANIE

b

H

β

sin 

MENU

km

1,5

H

15

sin





km

1,5

H

0,259



km

1,5

0,259

H





m

389

km

0,3885

H





β



a

H







15

km

1,5

a

:

Dane



?

H

:

Szukane



ODPOWIEDŹ

MENU

Wysokość pierwszego pagórka,

licząc od przełęczy, wynosi 342 m, a

drugiego - 389 m.

Trygonometria (z greckiego "trigonon" - trójkąt i
"metron" - miara) to dział geometrii badający
relacje pomiędzy kątami a bokami początkowo
trójkątów, a później i innych wielokątów.

Trygonometria zaczęła kształtować się już
w starożytności, głównie w związku
z rozwojem astronomii i technik
nawigacyjnych.

Wielki wkład w rozwój trygonometrii
wnieśli uczeni arabscy.

W Europie funkcje trygonometryczne
pojawiły się w XIV wieku.

MENU

Nazwy funkcji trygonometrycznych
pochodzą z języka łacińskiego.

Słowo sinus oznacza zagięcie, zakrzywienie.

Cosinus pochodzi od „complementi sinus”,
czyli sinus dopełnienia.

Słowo tangens oznacza styczną.

Cotangens pochodzi od complementi
tangens czyli tangensa dopełnienia.

MENU

Ko

nie

c

pre

zen

tac

ji