Psychometria 2010

Wykład 2

Klasyczna teoria

testu

Whatever exists, exists in some

amount."

E. L. Thorndike.

Założenia klasycznej teorii testu

(Gulliksen, 1950)

• do psychologii można zaadaptować model

pomiaru pochodzący z fizyki

• podobnie jak każdy obiekt fizyczny ma

określone wartości swoich cech fizycznych,

niezależne od aktu pomiaru i natury

narzędzia badawczego, tak każdy człowiek

ma nieznane prawdziwe wartości cech

psychologicznych

• podczas pomiaru obserwujemy wartości

prawdziwe mierzonej cechy, zakłócone

błędem równym różnicy miedzy

obserwowaną wartością wyniku pomiaru a

nieobserwowalną wartością prawdziwą

mierzonej cechy

Rzetelność

• Klasyczna teoria testu (Gulliksen, 1950)

– „psychometryczne opracowanie
problemu rzetelności i błędu pomiaru”

• Rzetelność jest miarą dokładności

pomiaru

X

t

= X



+ X

e

,

gdzie:

X

t

: wynik otrzymany

X



: wynik prawdziwy

X

e

: składnik błędu

2

2

t

tt

s

s

r







tt

r

gdzie:
r

tt

- rzetelność

s

2



- wariancja wyników

prawdziwych
s

2

t

- wariancja wyników

otrzymanych

var

t

= var



+ var

e

Wynik prawdziwy

(Gulliksen, 1950)

• Wynik prawdziwy to granica, do

jakiej zmierza przeciętna wyników
i-tej osoby w danej liczbie testów
równoległych, jeśli ta liczba
wzrasta nieograniczenie

Wynik prawdziwy

(Guilford, 1954)

• średnia z nieskończenie wielu

badań tym samym testem

• wynik danej osoby otrzymany w

idealnych warunkach idealnym
narzędziem pomiarowym

Składnik błędu (Guilford,

1954)

• różnica między wynikiem

prawdziwym a wynikiem
otrzymanym

• wartość dodatnia lub ujemna

będąca funkcją warunków
testowania konkretnej osoby w
konkretnym badaniu

„Błąd” pomiaru

• Pojęcie ”błędu” nie zawsze

powinno być rozumiane dosłownie,

jako niedokładność

• W metodologii ogólnej: „błąd” to

niedokładność plus wszystko to,

czego nie badamy

• W psychometrii: fluktuacja cechy

może nie być błędem, lecz

przedmiotem pomiaru

• Dwie najbardziej stałe cechy w

psychologii: IQ i… podatność

hipnotyczna

Założenia klasycznej teorii

testów

• Średnia arytmetyczna błędów

wynosi zero

• Korelacja wyniku prawdziwego i

składnika błędu jest zerowa

• Korelacja składników błędu dwóch

testów równoległych (czyli dwóch
kolejnych pomiarów) jest zerowa

• Korelacja składników błędu w

teście i reteście tym samym
testem jest zerowa

• Z założenia o istnieniu wyniku

prawdziwego, niezależnego od

aktu pomiaru, oraz z założenia o

losowości błędów, wynika, że:

– idealne narzędzie badawcze powinno

w dwóch kolejnych pomiarach

przynieść takie same wyniki

– różnice między wynikami dwóch

kolejnych pomiarów są odbiciem

błędów pomiaru i mogą służyć do

jego szacowania

– (podobnie zachowają się wersje

idealnie równoległe)

• Błędy systematyczne

(skorelowane)

• Błędy losowe (nieskorelowane)

– Klasyczna teoria testu i wskaźniki

rzetelności dotyczą wyłącznie błędów
losowych

Szacowanie składnika

błędu

• Z założenia o istnieniu wyniku

prawdziwego, niezależnego od aktu

pomiaru, oraz z założenia o losowości

błędów, wynika, że:

– idealne narzędzie badawcze powinno w

dwóch kolejnych pomiarach przynieść

takie same wyniki

– różnice między wynikami dwóch

kolejnych pomiarów są odbiciem błędów

pomiaru i mogą służyć do jego

szacowania

– (podobnie zachowają się wersje idealnie

równoległe)

• Rzetelność jest zatem równa

teoretycznej wartości współczynnika

korelacji w dwóch kolejnych badaniach

(twierdzenie przydatne empirycznie)

• Rzetelność jest też równa kwadratowi

korelacji między wynikiem prawdziwym

a wynikiem otrzymanym (twierdzenie

mniej przydatne empirycznie)

• Najprościej mówiąc, test rzetelny to

taki, którego wyniki korelują wysoko z

sobą przy powtórzeniu badania

Interpretacja

współczynników

rzetelności

• rzetelność = powtarzalność (stabilność)

wyników testowych (przy założeniu stałości
cechy)

• rzetelność = kwadrat korelacji między

wynikami prawdziwymi a wynikami
uzyskanymi w teście

• rzetelność = odsetek wariancji wyników

prawdziwych w wynikach otrzymanych

• rzetelność = procent wariancji wyników w

teście generowany przez wyniki prawdziwe

• rzetelność = korelacja między testami

równoległymi

• np. alfa Cronbacha = 0,82: 82% wyników w

teście można przypisać wynikom prawdziwym,
18%: składnikowi błędu

Długość testu a jego

rzetelność

• Im dłuższy test (im więcej pozycji

zawiera) tym jest rzetelniejszy, to
jest, tym mniejszym jest obciążony
błędem

• Im więcej składowych znajduje się

w teście, tym bliższy jest on
wynikowi prawdziwemu na mocy
definicji stwierdzającej, że wynik
prawdziwy to średnia z
nieskończenie wielu testów
równoległych

• Rzetelność a wskaźniki rzetelności
• Bezpośrednie badanie rzetelności:

– kalibracja
– seria pomiarów

(w psychologii ani jedno, ani drugie nie jest

możliwe)

• Pośrednie badanie rzetelności:

wskaźniki rzetelności

Krytyka aksjomatyki

Gulliksena

• Thorndike (1964): ponieważ wyniki

prawdziwe nie są mierzalne
bezpośrednio, są one mitem i nie
mogą mieć znaczenia teoretycznego

– przyjęcie tego poglądu odrzucałoby całą

statystykę inferencyjną, która dotyczy
głównie szacowania nieobserwowalnych
parametrów

– wyniki prawdziwe nie są mierzalne

bezpośrednio, ale są szacowalne, z
błędem nie wykluczającym teoretycznej
ani praktycznej użyteczności

Krytyka aksjomatyki

Gulliksena

• Poważniejszy zarzut (Lord i

Novick, 1968): nieweryfikowalność
założenia o losowości błędu
pomiaru, czyli postulatu, że średni
błąd wynosi zero. Stopień
prawdziwości tego założenia nie
jest szacowalny (w
przeciwieństwie do
nieobserwowalnych parametrów)

• Rzetelność odnosi się do:

– stabilności
– równoważności
– spójności

wyników testowych.

Rzetelność – właściwość

testu

czy zbioru wyników?

• Rzetelność jest właściwością zbioru

wyników uzyskanego na konkretnej

populacji, a nie testu

• Stwierdzenie: „rzetelność testu X

wynosi 0,87” jest skrótem

myślowym

• Oszacowanie rzetelności testu może

się różnić w różnych populacjach,

np. IQ szacowane w próbie pobranej

z populacji generalnej i z populacji

studentów

• Wszystkie metody szacowania

rzetelności oparte są na badaniu
zgodności między zbiorami
wyników, dotyczących tej samej
cechy

• Współczynniki rzetelności, jak

wszystkie miary oparte na
korelacji, są wrażliwe na wielkość
wariancji w próbie

• Mogą być generalizowane tylko na

tę populację, z której pobrano
próbę

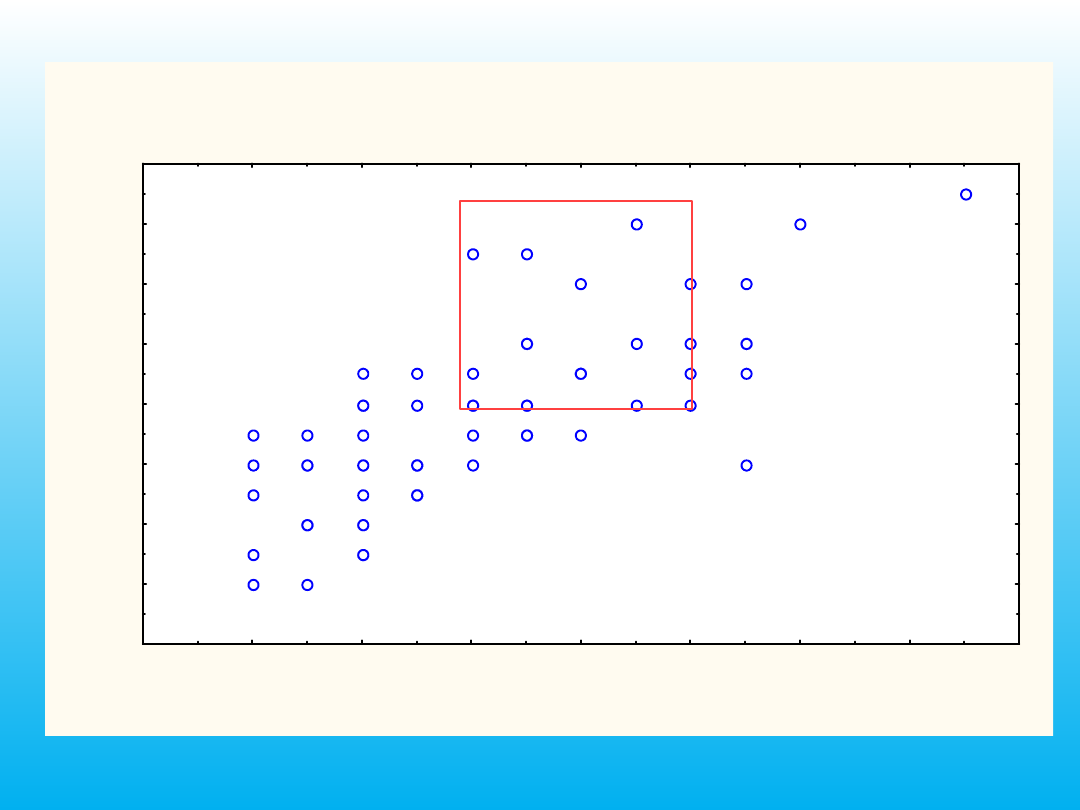
YIELD1 vs. YIELD2

Wsp. korelacji = ,74

YIELD1

Y

IE

LD

2

-2

0

2

4

6

8

10

12

14

-2

0

2

4

6

8

10

12

14