FUZZY

LOGIC

1

• 1

Index

• 2



Brief History



What is fuzzy logic?



Fuzzy Vs Crisp Set



Membership Functions



Fuzzy Logic Vs Probability



Why use Fuzzy Logic?



Fuzzy Linguistic Variables



Operations on Fuzzy Set



Fuzzy Applications



Case Study



Drawbacks



Conclusion



Bibliography

• GEORGE

CANTOR

• George Cantor, in 1870’s,

gave the concept of set
theory which is of great

importance in

mathematics.

SET THEORY

 GEORGE CANTOR:
 His Mathematics and philosophy of infinite,B oston.

Brief History

• 4



Classical logic of Aristotle: Law of Bivalence

“Every proposition is either True or False(no
middle)”



Jan Lukasiewicz proposed three-valued logic :

True, False and Possible



Finally Lofti Zadeh published his paper on fuzzy

logic-a part of set theory that operated over the
range [0.0-1.0]

What is Fuzzy Logic?



Fuzzy logic is a superset of Boolean

(conventional) logic that handles the
concept of partial truth, which is truth
values between "completely true" and
"completely false”.



Fuzzy logic is multivalued. It deals

with degrees of membership and
degrees of truth.



Fuzzy logic uses the continuum of

logical values between 0 (completely
false) and 1 (completely true).

• 5

Boolea

n

(crisp)

Fuzzy

• 6

For example, let a 100 ml glass
contain 30 ml of water. Then we may
consider two concepts: Empty and
Full.

In boolean logic there are two
options for answer i.e. either the
glass is half full or glass is half
empty.

100 ml

30 ml

In fuzzy concept one might define
the glass as being 0.7 empty and
0.3 full.

• 7

Fuzzy Thinking



The concept of a set and set theory are powerful

concepts in mathematics. However, the principal notion
underlying set theory, that an element can (exclusively)
either belong to set or not belong to a set, makes it well
nearly impossible to represent much of human
discourse. How is one to represent notions like:



large profit



high pressure



tall man



moderate temperature



Ordinary set-theoretic representations will require the

maintenance of a crisp differentiation in a very artificial
manner:



high



not quite high



very high … etc.

FUZZY SET THEORY



Fuzzy Set Theory was formalised

by Professor Lotfi Zadeh at the
University of California in 1965
to generalise classical set theory.
Zadeh was almost single
handedly responsible for the
early development in this field.

• LOTFI ZADEH

•

• REFERENCES:

 Zadeh L.A.(1965)Fuzzy sets. Information and

Control,8(1965),338-353.

 Zadeh L.A.(1978)Fuzzy Sets as the Basis for a

Theory of Possibility. Fuzzy Sets and Systems

Fuzzy Vs. Crisp
Set

• 9

A

A’

• a

• a

• b

• b

• c

Fuzzy set

Crisp set

• a: member of

crisp set A

• b: not a member

of set A

• a: full member of fuzzy set

A’

• b: not a member of set A’
• c:partial member of set A’

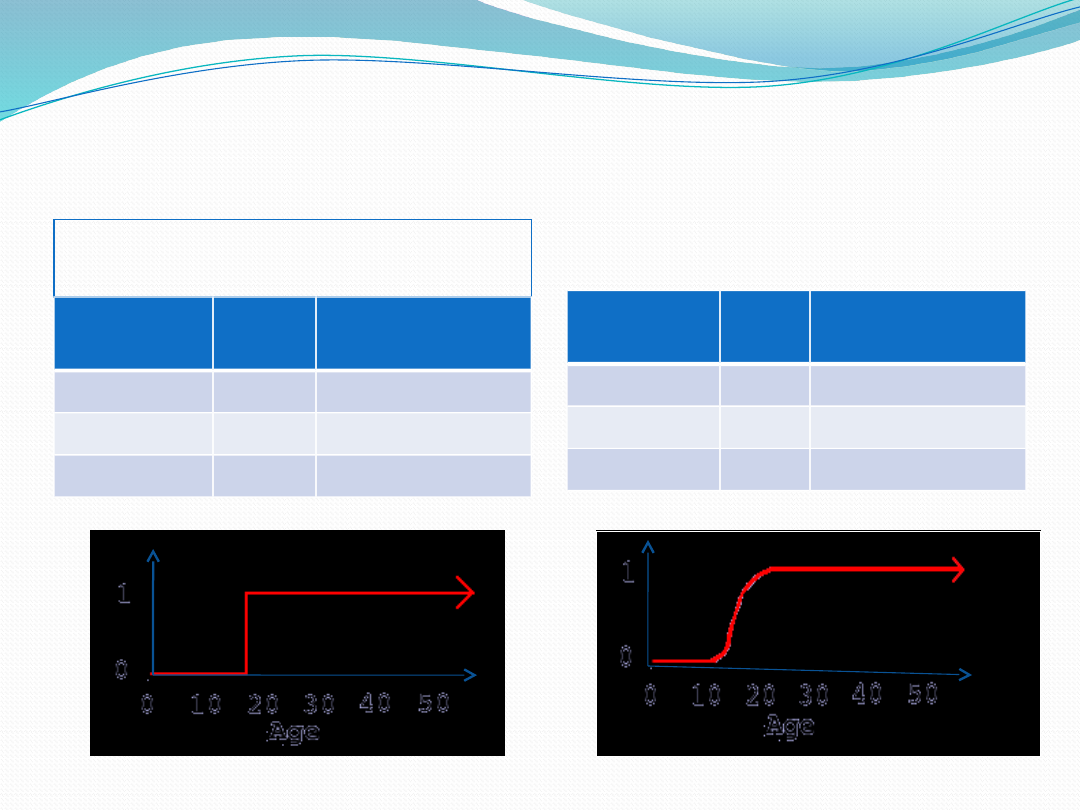
Fuzzy Vs. Crisp Set

Crisp set

Fuzzy set

Name

Age

Degree of

membership

Sally

5

0

Jenny

18

0

Christen

25

1

Name

Age

Degree of

membership

Sally

5

0

Jenny

18

0.75

Christen

25

1

• 10

Crisp Set and Fuzzy Set

• 11

μ

a

(x)={ 1 if element x belongs to the

set A
0 otherwise
}

• Classical set theory enumerates all

element using A={a

1

,a

2

,a

3

,a

4

…,a

n

}

Set A can be represented by Characteristic
function

Example: Consider space X consisting of natural
number<=12
Prime={x contained in X | x is prime
number={2,3,5,7,11}

• Formal definition:

• A fuzzy set

A

in

X

is expressed as a set of

ordered pairs:

• Fuzzy set

• Members

hip

• function

• (MF)

• Universe or

• universe of

discourse

• A fuzzy set is totally characterized

by a

• membership function (MF).

Fuzzy Sets

A

x

x x X

A





{( ,

( ))|

}



{

Membership Functions

• 13

adult(x)= { 0, if age(x) <
16years

(age(x)-16years)/4, if 16years < =
age(x)< = 20years,

1, if age(x) >
20years
}

Crisp Set and Fuzzy Set

• 14

A fuzzy set can be represented by:
A={{ x, A(x) }}
where, A(x) is the membership grade of a element x in
fuzzy set
SMALL={{1,1},{2,1},{3,0.9},{4,0.6},{5,0.4},{6,0.3},
{7,0.2},{8,0.1},{9,0},{10,0},{11,0},{12,0}}

• In fuzzy set theory elements have varying degrees of

membership

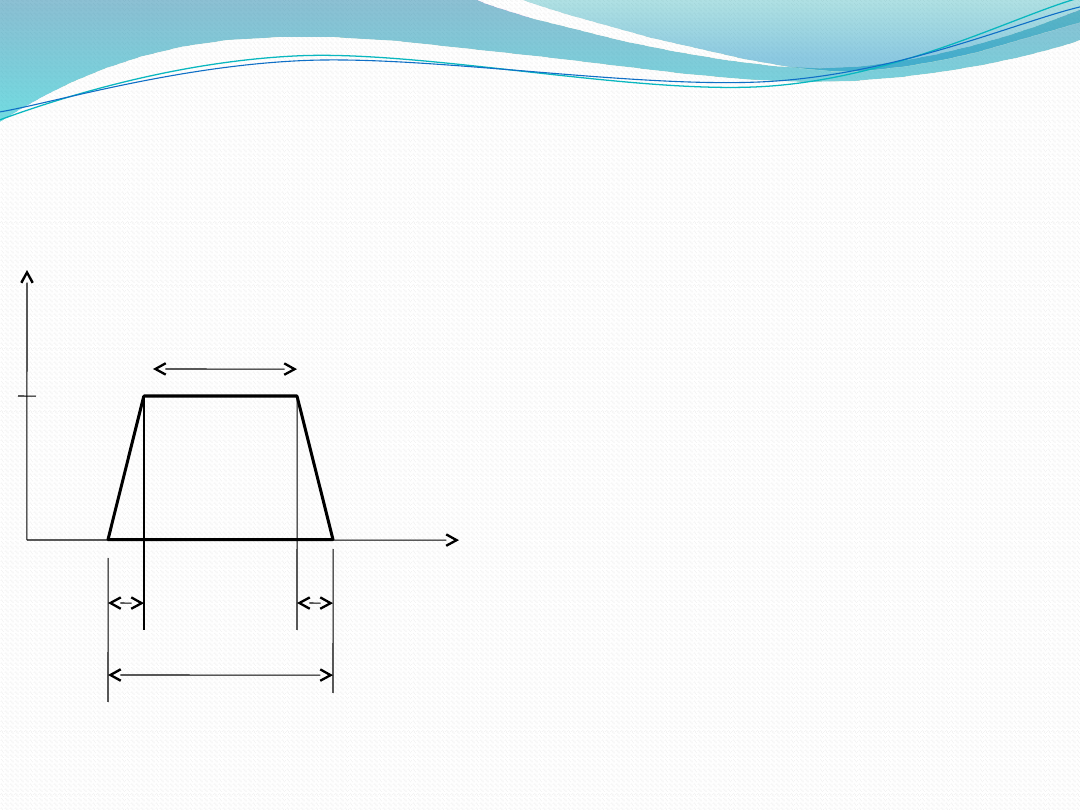
• 15

Features of a membership
function

core

support

boundary

1

0

μ (x)

x



Core: region

characterized by full
membership in set A’
i.e. μ (x)=1.



Support: region

characterized by
nonzero membership in
set A’ i.e. μ(x) >0.



Boundary: region

characterized by partial
membership in set A’
i.e. 0< μ (x) <1

A membership function is a
mathematical function which
defines the degree of an
element's membership in a fuzzy
set.



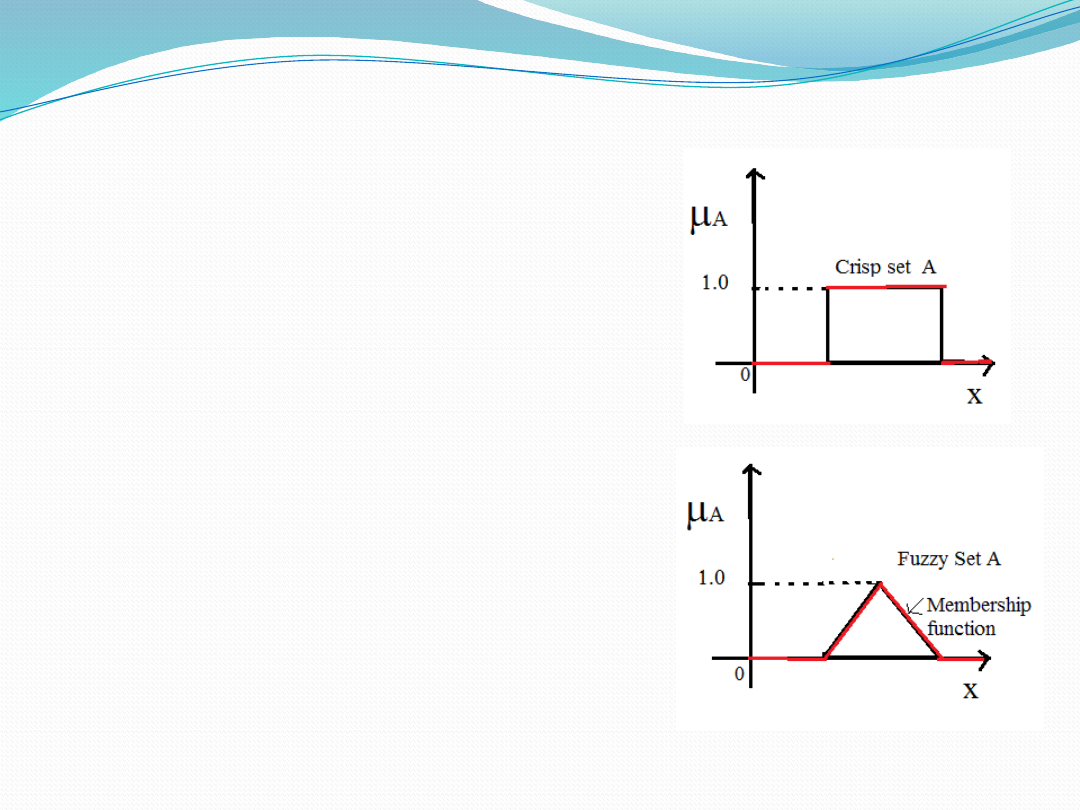
A ‘crisp’ set, A, can be defined

as a set which consists of

elements with either full or no

membership at all in the set.



Each item in its universe is

either in the set, or not.



A “fuzzy set” is defined as a

class

of

objects

with

a

continuum

of

grades

of

membership

. It is characterized

by a “membership function” or
“characteristic function” that
assigns to each member of the
fuzzy

set

a

degree

of

membership in the unit interval
[0,1].

Definition of Crisp Set and

Fuzzy Sets

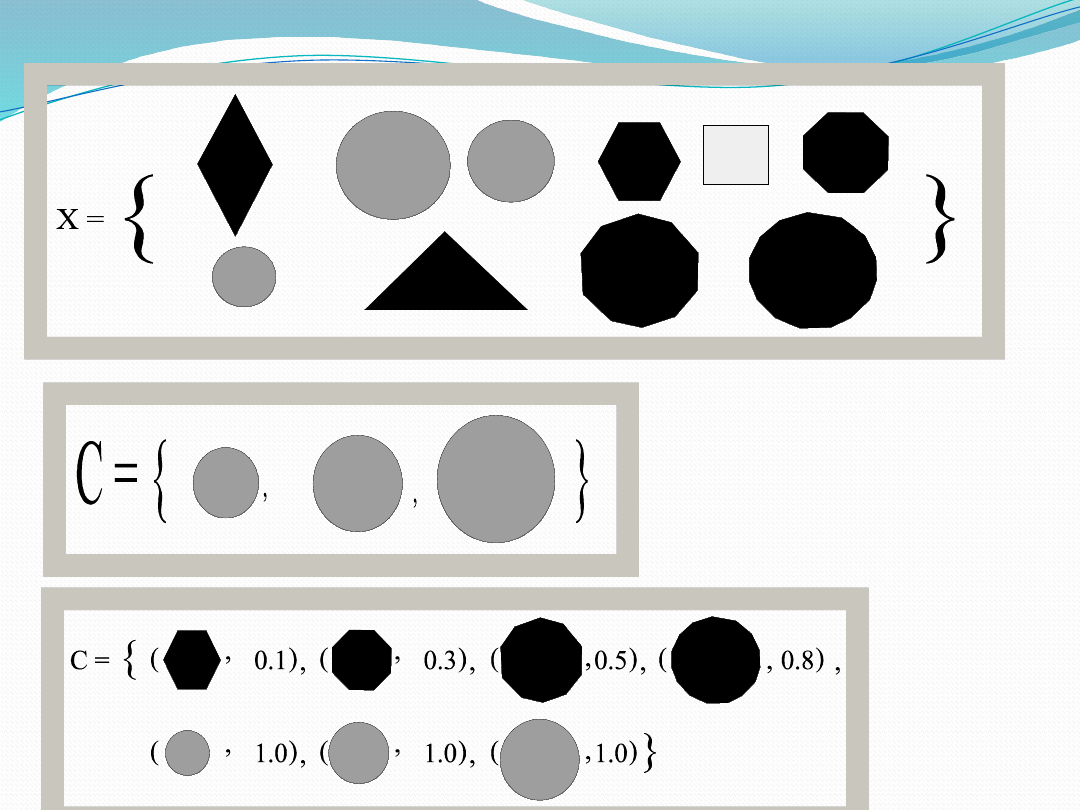
• 17

• One can define the crisp set “circles” as:

• The fuzzy set “circles can be defined as:

Crisp and Fuzzy example

Fuzzy Membership

Functions



One of the key issues in all fuzzy sets is

how to determine fuzzy membership

functions



The membership function fully defines

the fuzzy set



A membership function provides a

measure of the degree of similarity of an

element to a fuzzy set



Membership functions can take any

form, but there are some common

examples that appear in real

applications



Membership functions can:

•

- either be chosen by the user arbitrarily,

based

•

on the user’s experience (MF chosen by two

•

users could be different depending upon

their

•

experiences, perspectives, etc.)

- Or be designed using machine learning

methods (e.g., artificial neural networks,

genetic algorithms, etc.)



There are different shapes of membership

functions; triangular, trapezoidal, piecewise-

linear, Gaussian, bell-shaped, etc

.

Fuzzy Logic Vs Probability

• 20



Both operate over the same numeric range and

at first glance both have similar values:0.0
representing false(or non-membership) and 1.0
representing true.



In terms of probability, the natural language

statement would be ”there is an 80% chance
that Jane is old.”



While the fuzzy terminology corresponds to

“Jane’s degree of membership within the set of
old people is 0.80.’



Fuzzy logic uses truth degrees as a

mathematical model of the vagueness
phenomenon while probability is a mathematical
model of ignorance.

Why use Fuzzy
Logic?

• 21



Fuzzy logic is flexible.



Fuzzy logic is conceptually easy to understand.



Fuzzy logic is tolerant of imprecise data.



Fuzzy logic is based on natural language.

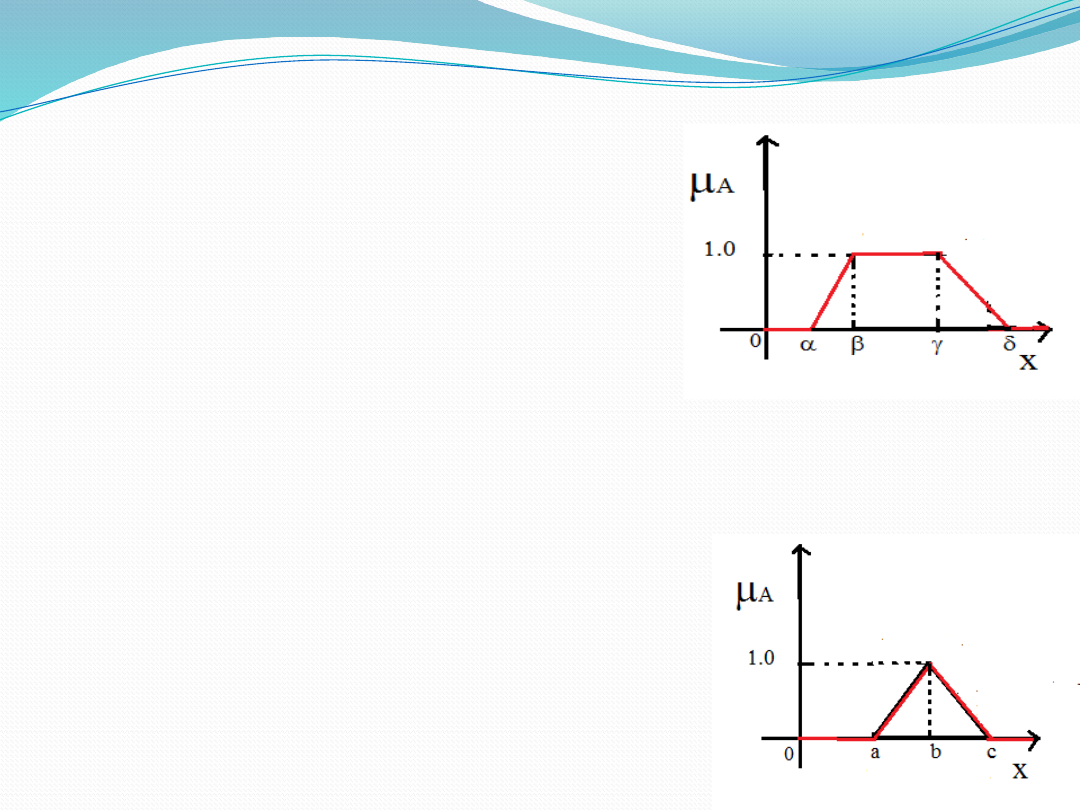
Membership Functions



Trapezoidal Membership

Function



Triangular Membership Function

(

)

0

x<

(

)/(

)

, , , , =

1

(

)/(

)

0

for

x

for

x

X

for

x

x

for

x

for x

a

a

b a

a

b

a b g d

b

g

d

d g

g

d

d

�

� -

-

� �

�

�

� �

�

� -

-

� �

�

>

�

�

�

(

)

0

x< a

(

)/(

)

a

, a, b, c =

(

)/(

)

b

0

for

x a b a for

x b

T X

c x c b

for

x c

for x c

�

� -

-

� �

�

�

-

-

� �

�

�

>

�

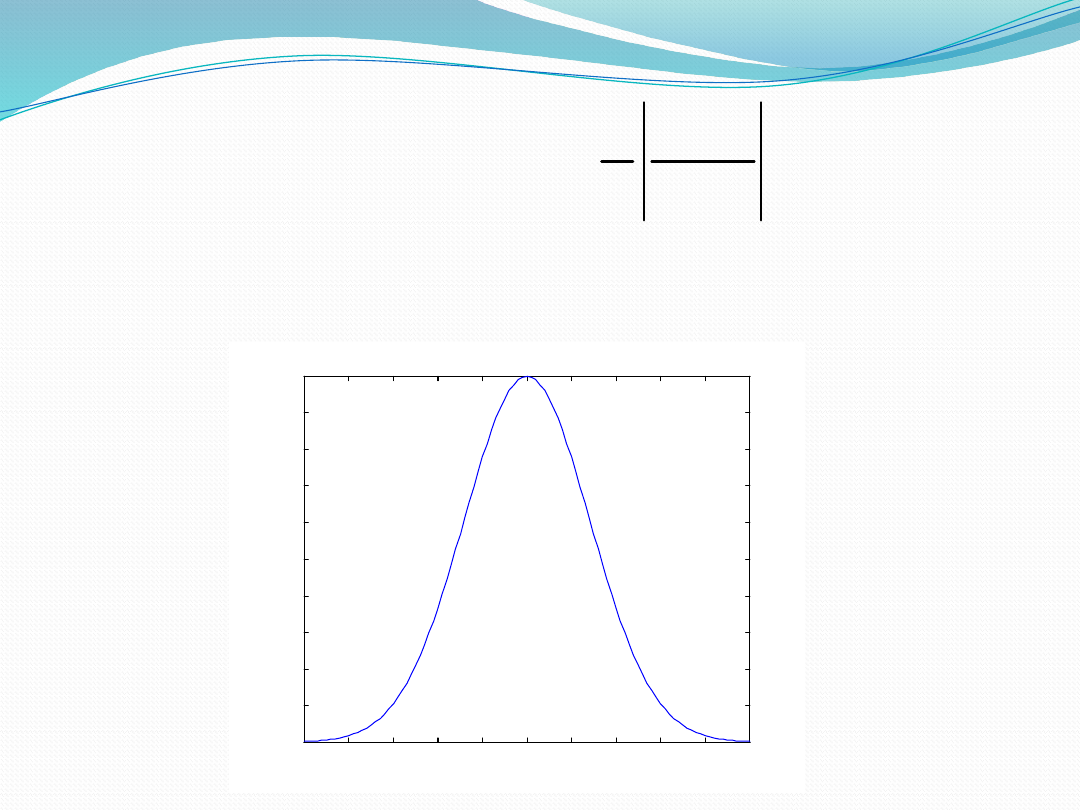
Gaussian membership

function

Where c – centre , s - width and m -

fuzzification factor

0

1

2

3

4

5

6

7

8

9

10

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

•µ

A

(x)

• c=5

• s=2

• m=

2

1

( , , , ) exp

2

m

A

x c

x c s m

s

m

�

�

-

=

-

�

�

�

�

�

�

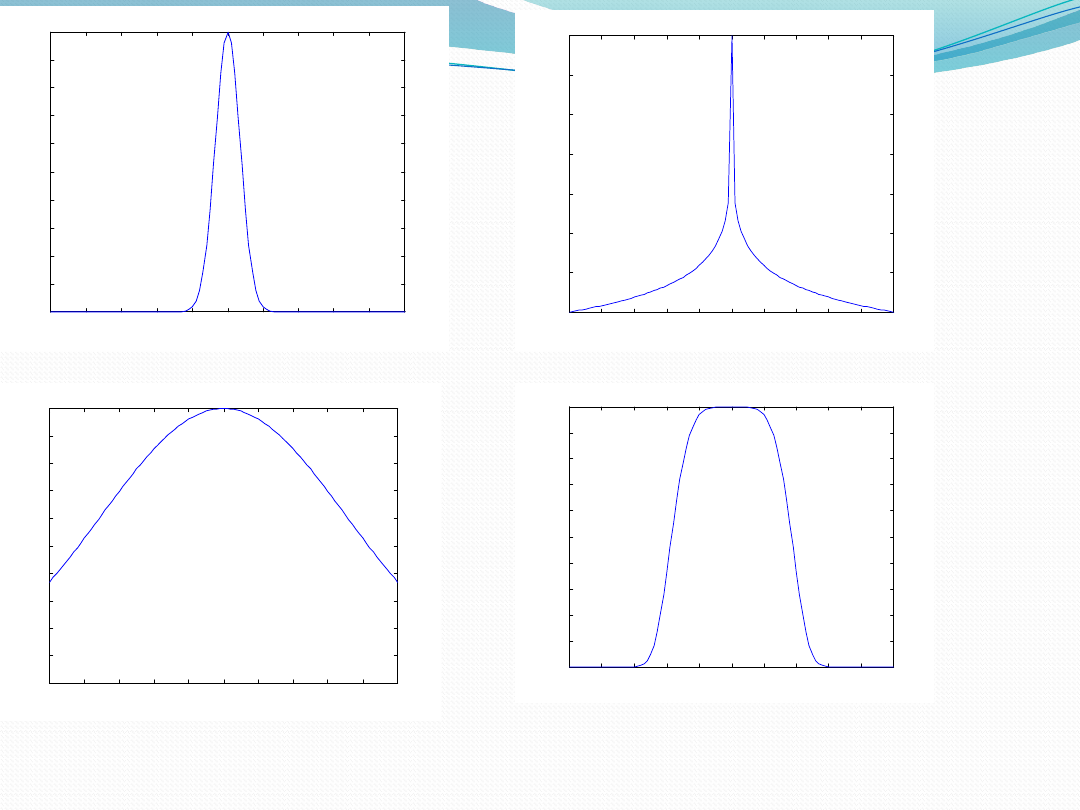
0

1

2

3

4

5

6

7

8

9

10

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

1

2

3

4

5

6

7

8

9

10

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

• c=

5

• s=

0.5

• m=

2

• c=

5

• s=

5

• m

=2

0

1

2

3

4

5

6

7

8

9

10

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

• c=5

• s=2

• m=0

.2

0

1

2

3

4

5

6

7

8

9

10

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

• c=5

• s=5

• m=

5

• 25

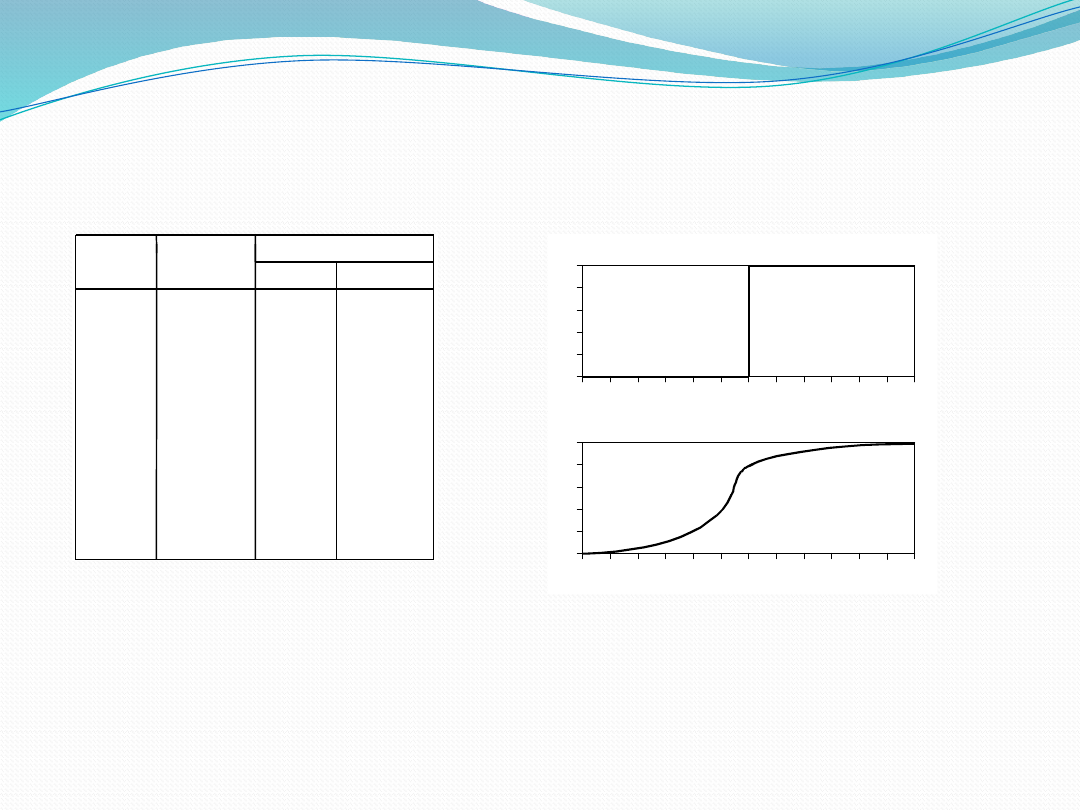
Crisp Sets vs. Fuzzy Sets

• The classical example in fuzzy sets is “

tall men

”. The elements of

the fuzzy set “tall men” are all men, but their degrees of

membership depend on their height.

• The x-axis represents the universe of discourse – the range of all

possible values applicable to a chosen variable. In our case, the

variable is the man height. According to this representation, the

universe of men’s heights consists of all tall men.

• The y-axis represents the membership value of the fuzzy set. In

our case, the fuzzy set of “tall men” maps height values into

corresponding membership values.

150

210

170

180

190

200

160

Height, cm

Degree of

Membership

Tall Men

150

210

180

190

200

1.0

0.0

0.2

0.4

0.6

0.8

160

Degree of

Membership

170

1.0

0.0

0.2

0.4

0.6

0.8

Height, cm

Fuzzy Sets

Crisp Sets

Degree of Membership

Fuzzy

Sham

John

Tom

Bob

Bill

1

1

1

0

0

1.00

1.00

0.98

0.82

0.78

Peter

Steven

Mike

David

Ram

Crisp

1

0

0

0

0

0.24

0.15

0.06

0.01

0.00

Name

Height, cm

205
198
181

167

155
152

158

172

179

208

• 26

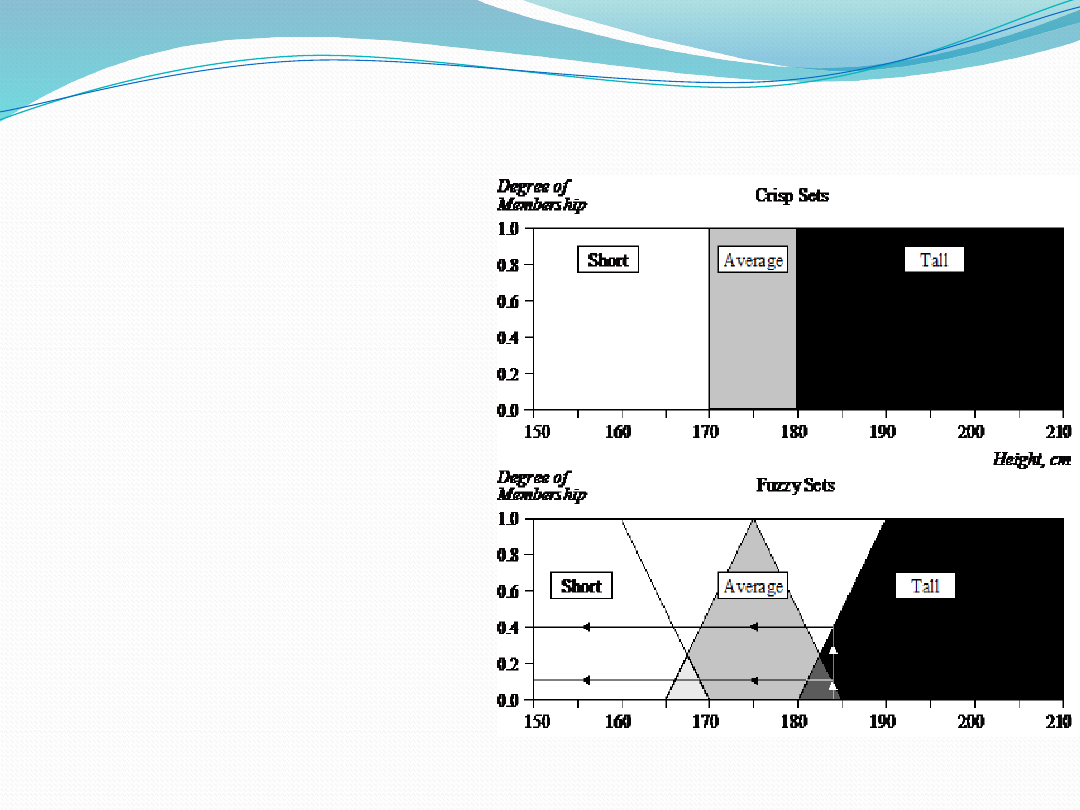
Fuzzy Set Representation



First, we determine the

membership functions. In
our “tall men” example,
we can define fuzzy sets
of tall, short and average
men.



The universe of

discourse for three
defined fuzzy sets consist
of all possible values of
the men’s heights.



For example, a man

who is 184 cm tall is a
member of the average
men set with a degree of
membership of 0.1, and
at the same time, he is
also a member of the tall
men set with a degree of
0.4.

CRISP SET V/S FUZZY SET(Cont.)

The most obvious limiting feature
of bivalent sets that can be seen
clearly from the diagram is that
they are mutually exclusive - it is
not possible to have membership
of more than one set

Fuzzy sets however define
degree of membership.

The Crips set operations of union, intersection and

complementation are defined in terms of characteristic
functions as follows:

•

Union:



A∪B

(x) = max(

A

(x), 

B

(x))  

•

Intersection:



A∩B

(x) = min(

A

(x), 

B

(x))

•

Complement:



not A

(x) = 1- 

A

(x)

 The other set theory constructs that are essential are:

•

Crips Set Inclusion:

A ⊂ B if and only if ∀x (for all x) 

A

(x) =1 implies



B

(x)=1  

•

Crips Set Equality:

A= B if and only if ∀x (for all x) 

A

(x)= 

B

(x).

CRISP SET OPERATIONS

The fuzzy set operations of union, intersection and

complementation are defined in terms of membership
functions as follows:

•

Union:



A∪B

(x) = max(

A

(x), 

B

(x))  

•

Intersection:



A∩B

(x) = min(

A

(x), 

B

(x))

•

Complement:



not A

(x) = 1- 

A

(x)

 The other fuzzy set theory constructs that are essential
are:

•

Fuzzy Set Inclusion:

A ⊂ B if and only if ∀x (for all x) 

A

(x) ≤ 

B

(x)  

•

Fuzzy Set Equality:

A= B if and only if ∀x (for all x) 

A

(x) = 

B

(x).

.

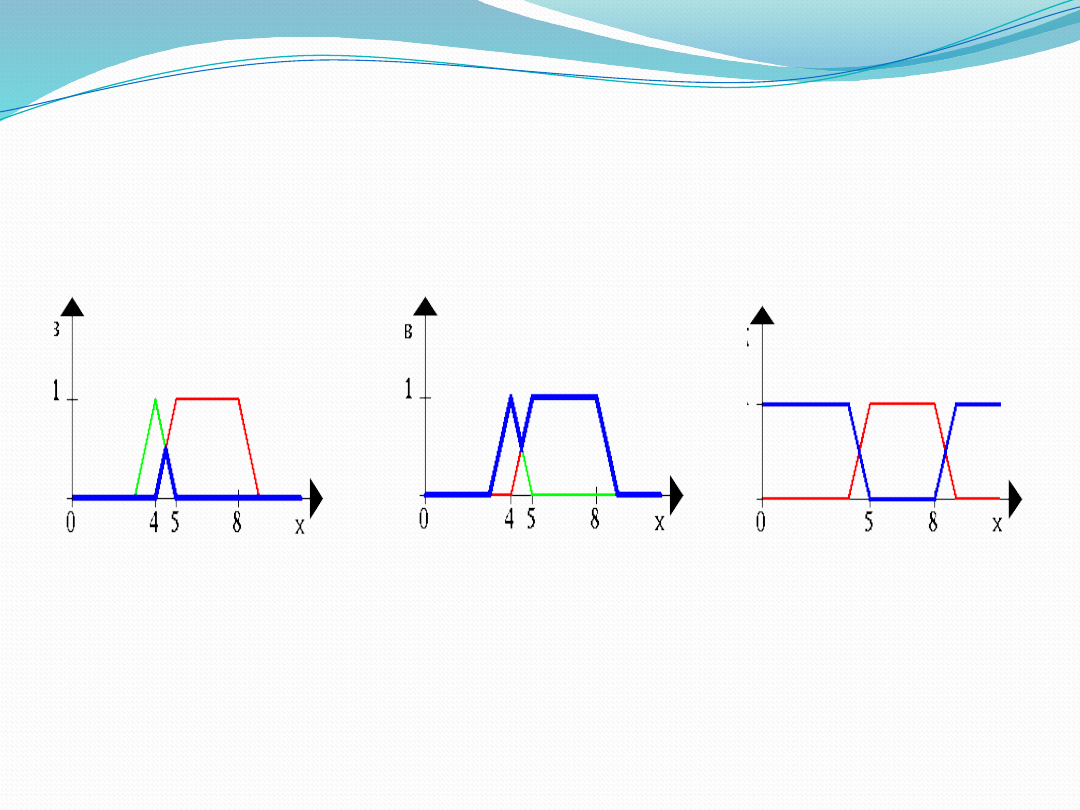
FUZZY SET OPERATIONS

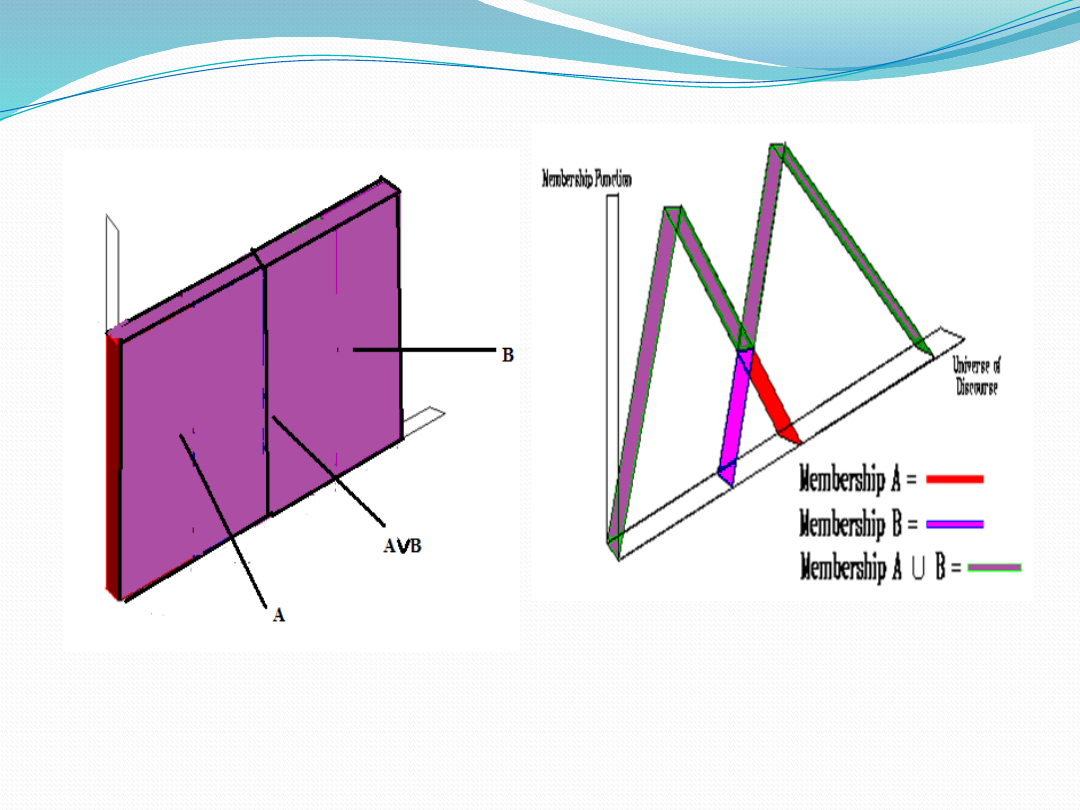
Representation of Union of two

crisp sets and fuzzy sets

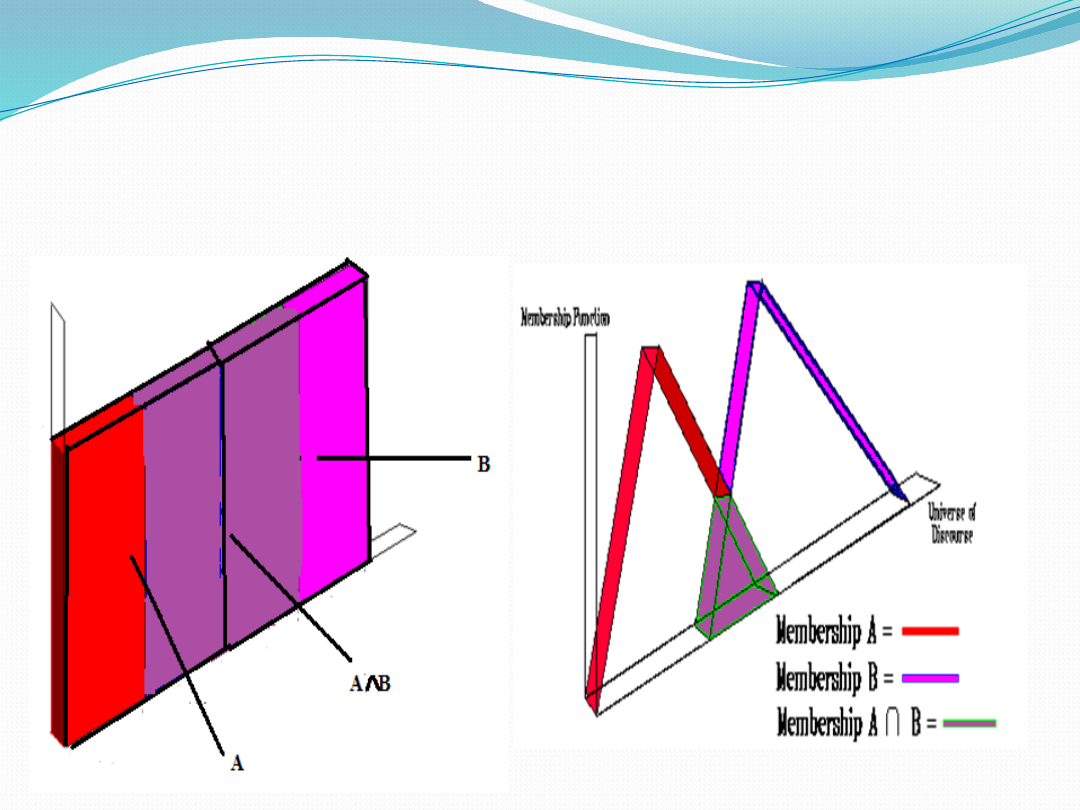
Representation of Intersection

of two crisp sets and fuzzy sets

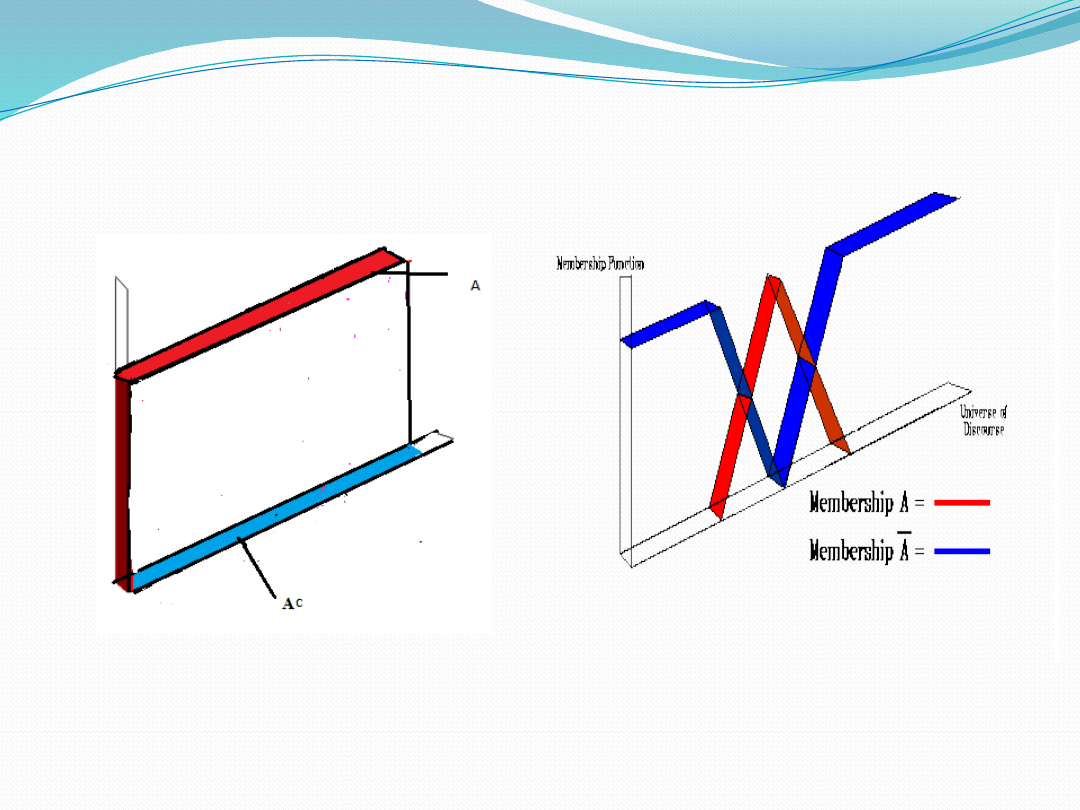
Representation of Complement

of a crisp set and a Fuzzy set

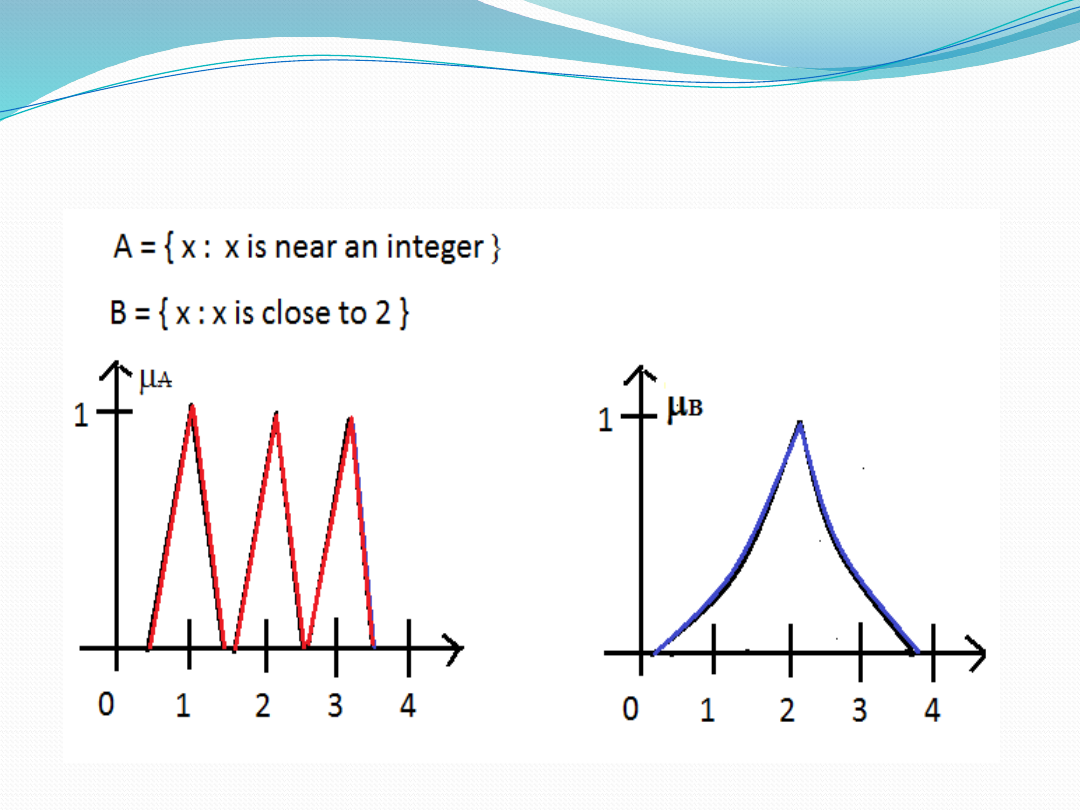
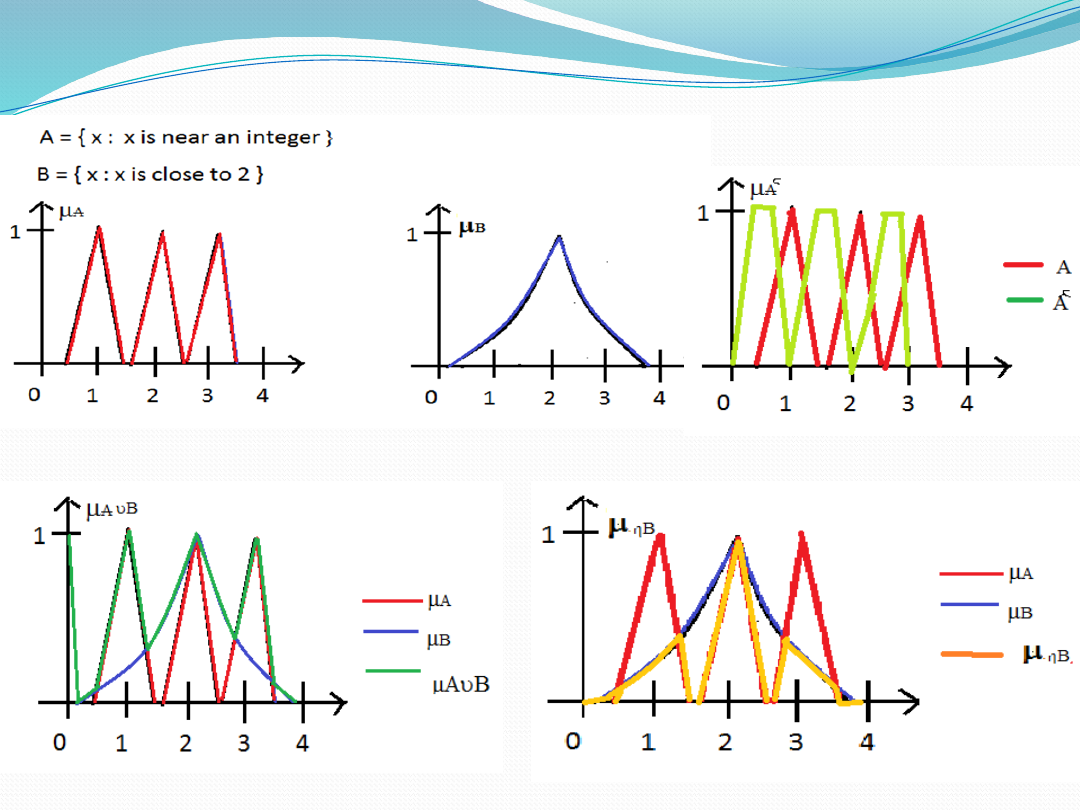
Examples of Fuzzy Sets

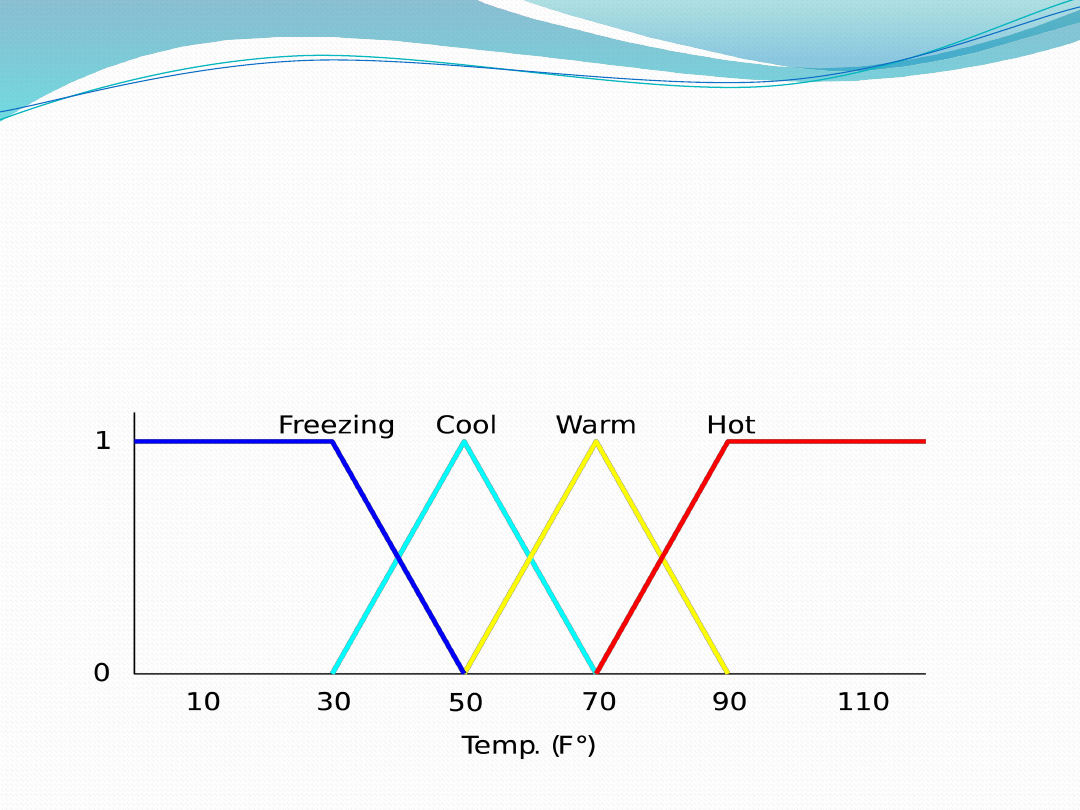
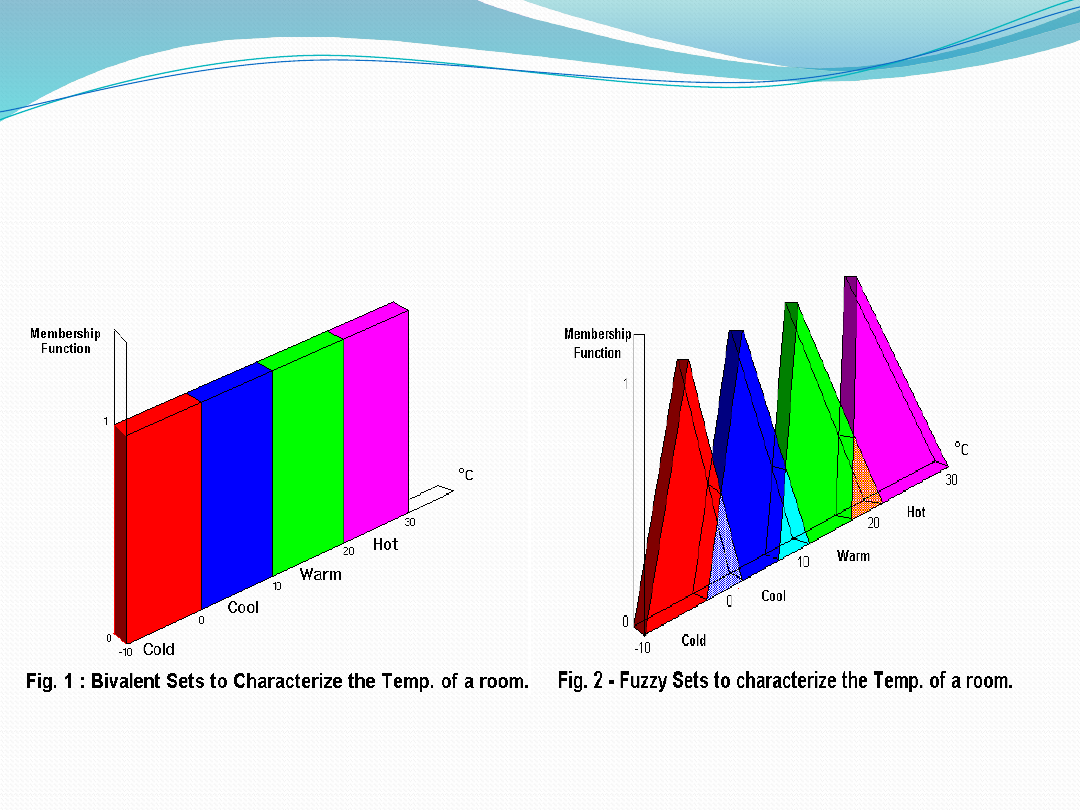
Fuzzy Linguistic Variables



Fuzzy Linguistic Variables are used to represent
qualities spanning a particular spectrum



Temp:

{

Freezing

,

Cool

,

Warm

,

Hot

}

• 35

Operations on Fuzzy
Set

• 36

A

B

μ

A

μ

B

A= {1/2 + .5/3 + .3/4 + .2/5}B= {.5/2 + .7/3 + .2/4 +

.4/5}

Consider:

>Fuzzy set

(A)

>Fuzzy set

(B)

>Resulting operation of fuzzy

sets

INTERSECTIO

N

(A ^ B)

UNION

(A v B)

COMPLEMEN

T

(¬A)

μ

A ∩

B

μ

A

U

μ

A

‘

μ

A∩ B

= min (μ

A

(x),

μ

B

(x))

{.5/2 + .5/3 + .2/4 + .

2/5}

μ

AUB

= max (μ

A

(x),

μ

B

(x))

{1/2 + .7/3 + .3/4 + .

4/5}

μ

A’

= 1-μ

A

(x)

{1/1 + 0/2 + .5/3 + .7/4

+ .8/5}

• 37

Example Speed Calculation

• 38

How fast will I go if it is



65 F°



25 % Cloud Cover ?

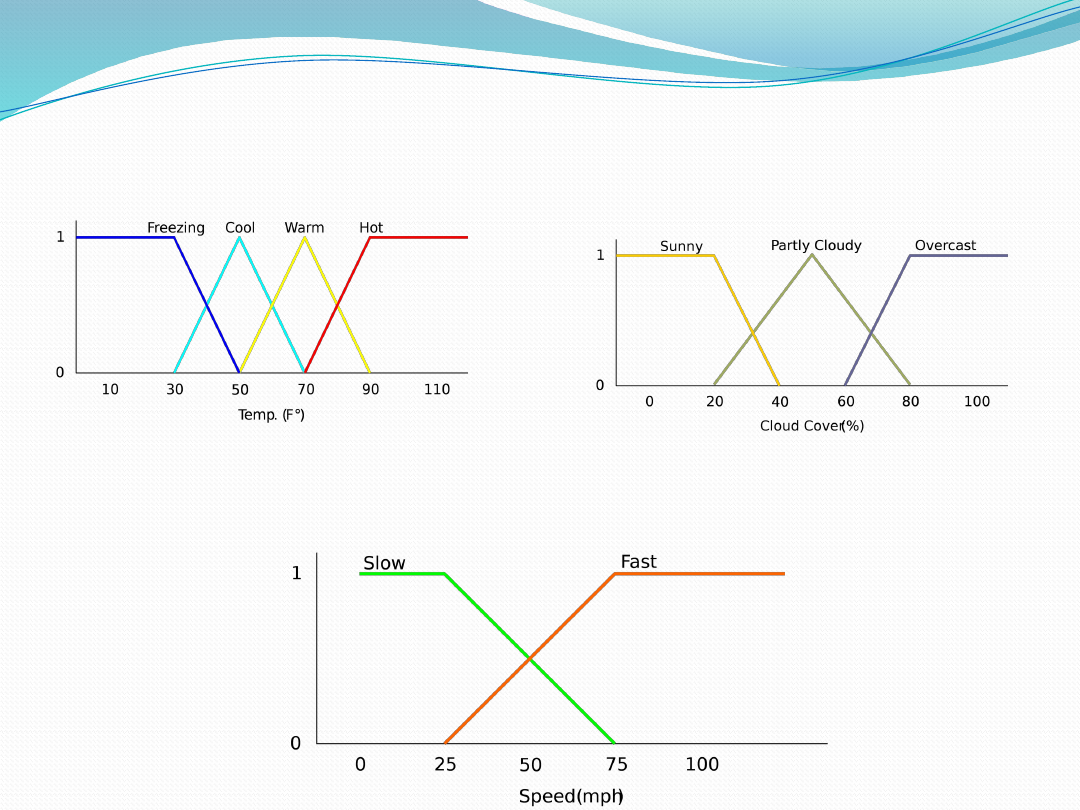
Input
:

Temp: {Freezing, Cool, Warm, Hot}

Cover: {Sunny, Partly

cloudy, Overcast}

Output:

Speed: {Slow, Fast}

• 39



If it's Sunny and Warm, drive Fast

Sunny(Cover)Warm(Temp) Fast(Speed)



If it's Cloudy and Cool, drive Slow

Cloudy(Cover)Cool(Temp) Slow(Speed)



Driving Speed is the combination of output of

these rules...

Rules

• 40



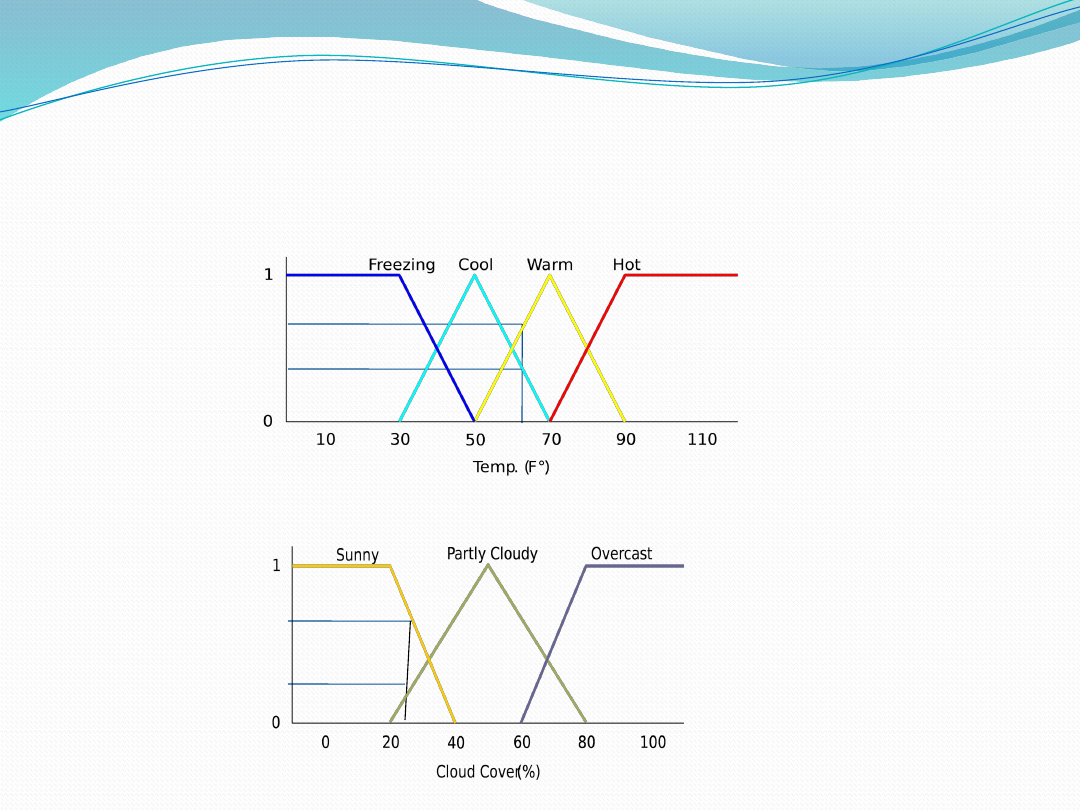
65 F°  Cool = 0.4, Warm= 0.7



25% Cover Sunny = 0.8, Cloudy

= 0.2

Fuzzification:

Calculate Input Membership Levels

• 41

Calculating:



If it's Sunny and Warm, drive Fast

Sunny(Cover)Warm(Temp)Fast(Speed)

0.8



0.7 = 0.7



Fast = 0.7



If it's Cloudy and Cool, drive Slow

Cloudy(Cover)Cool(Temp)Slow(Speed)

0.2  0.4 = 0.2



Slow = 0.2

• 42



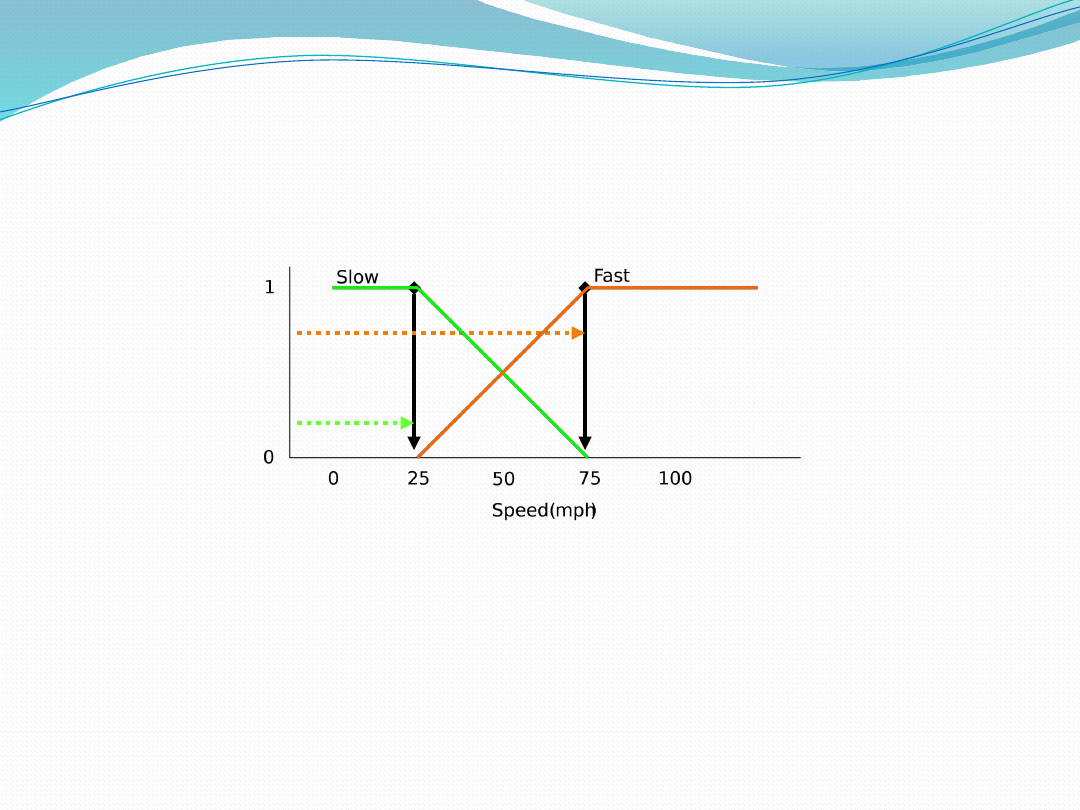
Speed is 20% Slow and 70% Fast



Find centroids: Location where membership

is 100%



Speed = weighted mean

= (2*25+7*75)/(9)
= 63.8 mph

Defuzzification:

Constructing the Output

• 43

Fuzzy Applications

• 44

 Automobile and other vehicle subsystems :

used to control

the speed of vehicles, in Anti Braking System.

 Temperature controllers : Air conditioners,

Refrigerators

 Cameras : for auto-focus

 Home appliances: Rice cookers , Dishwashers ,

Washing

machines and others

 Fuzzy logic is not always accurate. The results are

perceived as

a guess, so it may not be as widely trusted .

Requires tuning of membership functions which is

difficult to

estimate.

 Fuzzy Logic control may not scale well to large or

complex

problems

 Fuzzy logic can be easily confused with

probability theory, and

the terms used interchangeably. While they are
similar concepts,
they do not say the same things.

Drawbacks

• 45



Fuzzy Logic provides way to calculate with

imprecision and

vagueness.



Fuzzy Logic can be used to represent some kinds of

human

expertise .



The control stability, reliability, efficiency, and

durability of fuzzy

logic makes it popular.



The speed and complexity of application production

would not be

possible without systems like fuzzy logic.

Conclusion

• 46

Bibliography

• 47



BOOKS:

• Artificial Intelligence by Elaine Rich, Kelvin Knight and

Shivashankar B Nair

• Fuzzy Thinking by Bart Kosko



WEBSITES :

•

h
ttp://www.seattlerobotics.org/encoder/mar98/fuz/flin
dex.html

•

http://www.dementia.org/~julied/logic/index.html

•

http://mathematica.ludibunda.ch/fuzzy-logic.html