Teoria arbitrażu cenowego

i ocena efektywności

portfela

Teoria arbitrażu cenowego (Arbitrage

pricing Theory – APT)

• Autor Stephen Ross – 1976
• Alternatywa wobec modelu CAPM

– Mniejsza liczba założeń stąd lepszy przy

porównaniach teoretycznych

– Dość trudny do zastosowania w praktyce

Założenia modelu APT

• Rynek

kapitałowy

jest

doskonały

(doskonała konkurencja, brak kosztów
transakcyjnych itp.) – stąd prawo jednej
ceny i arbitraż

• Inwestorzy mają jednolite oczekiwania
• Liczba aktywów dostępnych na rynku jest

bliska nieskończoności

• Stochastyczny proces generowania stóp

zwrotów z aktywów można opisać liniową
funkcją X czynników ryzyka.

Model wieloczynnikowy

1

1

2

2

...

k

k

r

F

F

F

a b

b

b

e

= + � + � + + � +

gdzie:
r –stopa zwrotu akcji (portfela akcji)
α – wyraz wolny równania – oczekiwana stopa zwrotu z akcji

gdy wszystkie czynniki ryzyka równe 0

β

i

– współczynnik wrażliwości stopy zwrotu akcji względem stopy zwrotu i-tego czynnika

F

i

– stopa zwrotu i-go czynnika

ε – składnik losowy

Warunki modelu wieloczynnikowego

[ ]

[ ]
[

]

[

]

0

0

0

0

0

i

i j

k

i k

k m

E

E

E F
E F
E F F

e

ee

e

=

� �=

� �

=

=

=

Warunki modelu wieloczynnikowego

• Wartość oczekiwana ryzyka

specyficznego jest równa zero

• Ryzyka specyficzne różnych aktywów

są nieskorelowane

• Ryzyko specyficznego i-go aktywa

jest nieskorelowane z czynnikami
modelu

• Czynniki modelu są nieskorelowane

Interpretacja modelu

wieloczynnikowego

• Stopa zwrotu z akcji (portfela) zależy w liniowy

sposób od stóp zwrotu pewnych czynników

• Model nie określa jakie to są czynniki
• Czynniki powinny mieć wpływ na stopy zwrotu

z akcji

• O sile zależności decyduje decydują wartości

współczynników wrażliwości

• Model wieloczynnikowy można traktować jako

uogólnienie

modelu

jednoczynnikowego

Sharpe’a

Identyfikacja czynników

modelu

• Wpływ czynnika na ceny aktywów powinien się

przejawiać w ich nieoczekiwanych ruchach

• Powinny

reprezentować

efekt

niedywersyfikowalny

(głównie

czynniki

makroekonomiczne)

• Dostępne regularne i dokładne odczyty wartości

czynników

• Zależność powinna być uzasadniona na gruncie

teorii ekonomii

Propozycje czynników – Chen, Roll,

Ross (1986)

• Nieoczekiwane zmiany inflacji,
• Nieoczekiwane zmiany poziomu GNP mierzone

poziomem indeksu produkcji przemysłowej,

• Nieoczekiwane

zmiany

poziomu

zaufania

inwestorów wywoływane zmiany poziomu premii
za ryzyko kredytowe na

rynku obligacji

korporacyjnych,

• Nieoczekiwane

przesunięcia

krzywej

dochodowości.

Wykorzystanie indeksów oraz cen spot

i futures

• Krótkoterminowe stopy procentowe
• Spread krótko i długoterminowych stóp

procentowych

• Indeksy „szerokiego” rynku akcji (S&P 500,

NYSE Composite, WIG)

• Ceny ropy naftowej
• Ceny złota lub innych metali szlachetnych
• Kursy walut

Arbitraż w modelu APT

Inwestor

dysponując

określonym,

początkowym portfelem papierów
wartościowych

bada

możliwość

budowy portfela arbitrażowego, który
umożliwi mu zwiększenie stopy
zwrotu bez ponoszenia dodatkowego
ryzyka.

Cechy portfela

arbitrażowego

1

1

1

0

0,

1,...,

0

n

i

i

n

i

ij

i

n

i

i

i

x

x

j

k

x

b

e

=

=

=

=

� =

=

� �

�

�

�

Warunek 1 oznacza zerowy nakład netto na budowę portfela, warunek
2 niewrażliwość portfela na działanie wszystkich czynników ryzyka,
warunek 3 (przybliżony)niewrażliwość na ryzyko specyficzne.

Portfel arbitrażowy cd.

Portfel arbitrażowy musi oferować zerową stopę zwrotu, czyli:

Jeśli równanie powyższe dla jakiegoś portfela możliwego do utworzenia

na rynku nie jest spełnione istnieje możliwość dokonywania arbitrażu.

Analogiczne transakcje arbitrażowe będą wykonywane przez

wszystkich inwestorów. W ich efekcie ceny akcji podlegających
sprzedaży będą spadać, a więc ich oczekiwane stopy zwrotu będą
rosnąć. I odwrotnie ceny akcji nabywanych w ramach arbitrażu będą
rosnąć, w wyniku czego ich oczekiwane stopy zwrotu będą spadać.

Aktywność arbitrażowa będzie trwać dopóki wszystkie możliwości

arbitrażu nie zostaną wyeliminowane.

1

0

n

i

i

i

x r

=

� =

�

Ogólna postać modelu APT

W wyniku arbitrażu ustali się liniowa zależność

pomiędzy oczekiwanymi stopami zwrotu a
wrażliwościami, którą można opisać wzorem:

gdzie:
λ

0

– stopa wolna od ryzyka

λ

i

– premia za ryzyko z tytułu działania i-go czynnika

0

1

1

...

k

k

r l

l

b

l

b

= + � + + �

Wyznaczanie parametrów

modelu

Do wyznaczenia parametrów modelu

można wykorzystać ogólną postać
równania modelu odniesioną do
konkretnych portfeli akcji:

0

1

1

...

i

i

k

ik

r l

l

b

l

b

= + � + + �

Budowa k+1 portfeli akcji

Każdy z pierwszych k portfeli to portfel o

jednostkowej wrażliwości na jeden czynnik ryzyka i
zerowej wrażliwości na wszystkie pozostałe
czynniki. Ostatni portfel jest niewrażliwy na
wszystkie czynniki ryzyka (portfel wolny od ryzyka).

11

12

1

21

22

2

1

2

1,1

1,2

1,

1,

0,.....,

0,

0,

1,.....,

0,

...................................................

0,

0,.....,

1,

0,

0,.....,

0

k

k

k

k

kk

k

k

k

k

b

b

b

b

b

b

b

b

b

b

b

b

+

+

+

=

=

=

=

=

=

=

=

=

=

=

=

Wyznaczanie parametrów

modelu

Możemy zbudować następujący układ

równań, którego rozwiązaniem są
wartości parametrów modelu:

1

0

1

2

0

2

0

1

0

..................

k

k

k

r
r

r
r

l

l

l

l

l

l

l

+

= +

= +

= +

=

Zadanie 1

Załóż, że portfele A i B są dobrze zdywersyfikowane, zaś stopa zwrotu z

aktywów wolnych od ryzyka wynosi 4%. Posiadasz następujące dane
o obydwu portfelach:

Portfel Oczekiwana stopa zwrotu Beta
A 8% 1,00
B 6% 0,25

Co na podstawie powyższych informacji, zakładając, że do analizy

można ożyć jednoczynnikowy model arbitrażu cenowego, powiesz o
cenach portfeli A i B

A. Obydwa portfele są właściwie wycenione,
B. Obydwa portfele są zbyt tanie,
C. Obydwa portfele są zbyt drogie,
D. Układ cen pomiędzy portfelami A i B stwarza możliwości arbitrażu.

Zadanie 2

Rynek znajduje się w stanie równowagi opisanym przez

dwuczynnikowy model arbitrażu cenowego. Znane są następujące
informacje o trzech dobrze zdywersyfikowanych portfelach akcji:

Portfel Beta czynnika 1

Beta czynnika 2

Oczekiwana stopa

zwrotu

A

1,0

2,0

18%

B

0,0

1,0

8%

C

1,0

0,0

12%

Na podstawie powyższych danych określ ile wynosi stopa zwrotu z

aktywów wolnych od ryzyka.

Zadanie 3

Na podstawie modelu APT proszę przy pomocy akcji OMV, LOTOS i PKN Orlen

stworzyć syntetyczną pozycję w akcji MOL. Zakładamy, że na cenę spółek
sektora paliwowego wpływ mają tylko dwa czynniki: cena ropy naftowej i
marża rafineryjna zaś inwestorzy mogą bez ograniczeń stosować krótką
sprzedaż i nabywać akcje na kredyt.

Wrażliwość spółek na oba czynniki ryzyka przedstawia się następująco:

OMV

LOTOS PKN Orlen

MOL

Cena ropy

1,5 0,5 0,1 0,6

Marża rafineryjna

0,4 0,9 0,6 0,4

A. Udział OMV (- 46%), udział LOTOS (+ 36%), udział PKN Orlen (+ 110%)
B. Udział OMV (+ 25%), udział LOTOS (+ 36%), udział PKN Orlen (+ 39%)
C. Udział OMV (+ 46%), udział LOTOS (- 36%), udział PKN Orlen (+ 90%)
D. Udział OMV (+ 20%), udział LOTOS (+ 50%), udział PKN Orlen (+ 30%)

21

Wskaźniki oceny efektywności

zarządzania portfelem

• Wskaźnik Sharpe’a

• Wskaźnik Treynora

• Alfa Jensena

Wskaźnik Sharpe’a

• Zwany też wynagrodzenie za zmienność. Wg

Sharpe’a inwestor jest gotów ponosić większe
ryzyko, pod warunkiem że otrzymuje w zamian
relatywnie wyższe zyski. Miara efektywności
wywodzi się więc z równania linii CML:

i

f

i

R R

Sh

s

-

=

Interpretacja wskaźnika

Sharpe’a

Jest to iloraz nadwyżkowej stopy zwrotu oraz

całkowitego ryzyka portfela. Wskaźnik
Sharpe’a udziela trzech zasadniczych
informacji:

- określa nadwyżkowy zwrot na jednostkę

ryzyka,

- im wyższa wartość indeksu Sh tym lepiej

oceniany portfel,

- może służyć do tworzenia rankingów

portfeli.

Przykład

Dane są informacje na temat czterech portfeli inwestycyjnych

stopa zwrotu

odchylenie standardowe

A

0,09

0,16

B

0,10

0,18

C

0,14

0,24

D

0,20

0,30

Wyznacz wskaźniki Sharpe’a i zbuduj ranking portfeli jeśli wiadomo,

że stopa wolna od ryzyka wynosi 8%, stopa zwrotu z portfela
rynkowego 12%, a odchylenie standardowe stopy zwrotu z portfela
rynkowego 20%

0,12 0,08

0, 200

0, 20

0,09 0,08

0,063

0,16

0,10 0,08

0,110

0,18

0,14 0,08

0, 250

0, 24

0, 20 0,08

0, 400

0,30

M

A

B

C

D

S

S

S

S

S

-

=

=

-

=

=

-

=

=

-

=

=

-

=

=

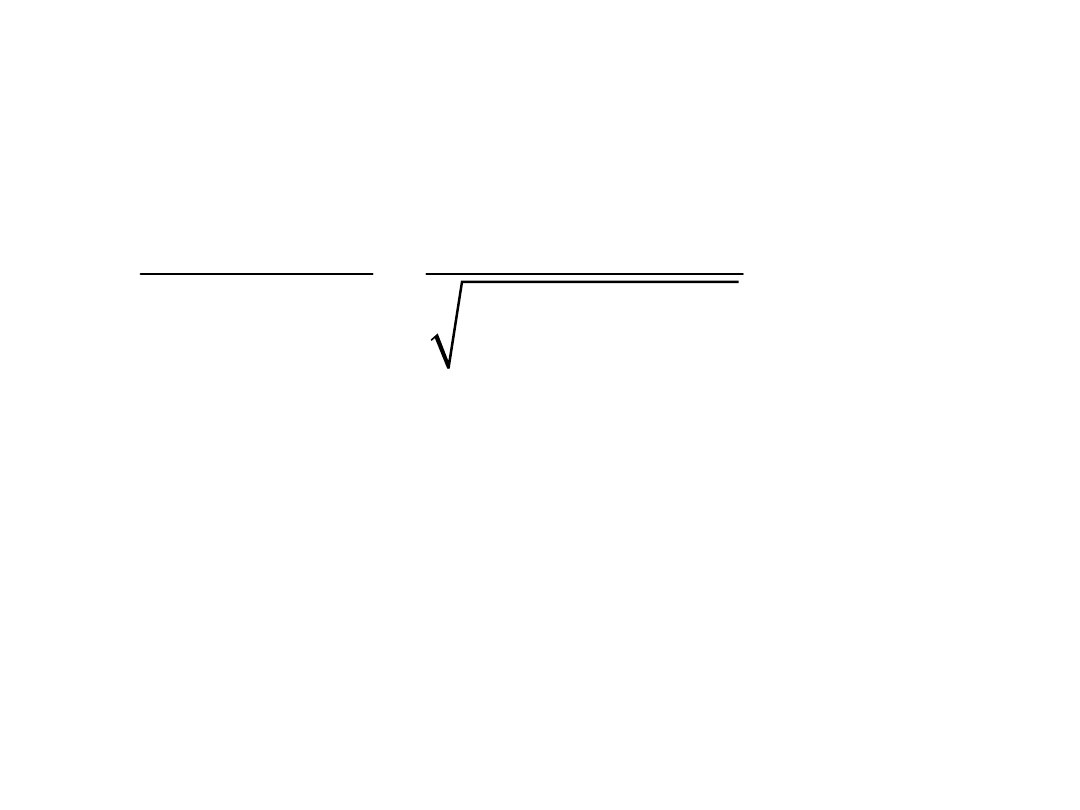
Wskaźnik Sharpe’a ex ante

 

i

f

i

R

R

E

S







Wskaźnik Sharpe’a – rewizja

1994

Rewizja wskaźnika dokonana w 1994

roku

przez

samego

autora

uwzględnia fakt, że stopa wolna od
ryzyka może ulegać zmianie w
okresie inwestycji.

(

)

(

)

i

fi

f

i

f

E R R

E R R

S

Var R R

s

-

-

=

=

�

�

-

�

�

Indeks Sortino

R T

S

DR

-

=

gdzie:
R – stopa zwrotu z akcji (portfela)
T – wymagana stopa zwrotu
DR – downside risk – semiodchylenie standardowe stopy zwrotu z akcji (portfela)

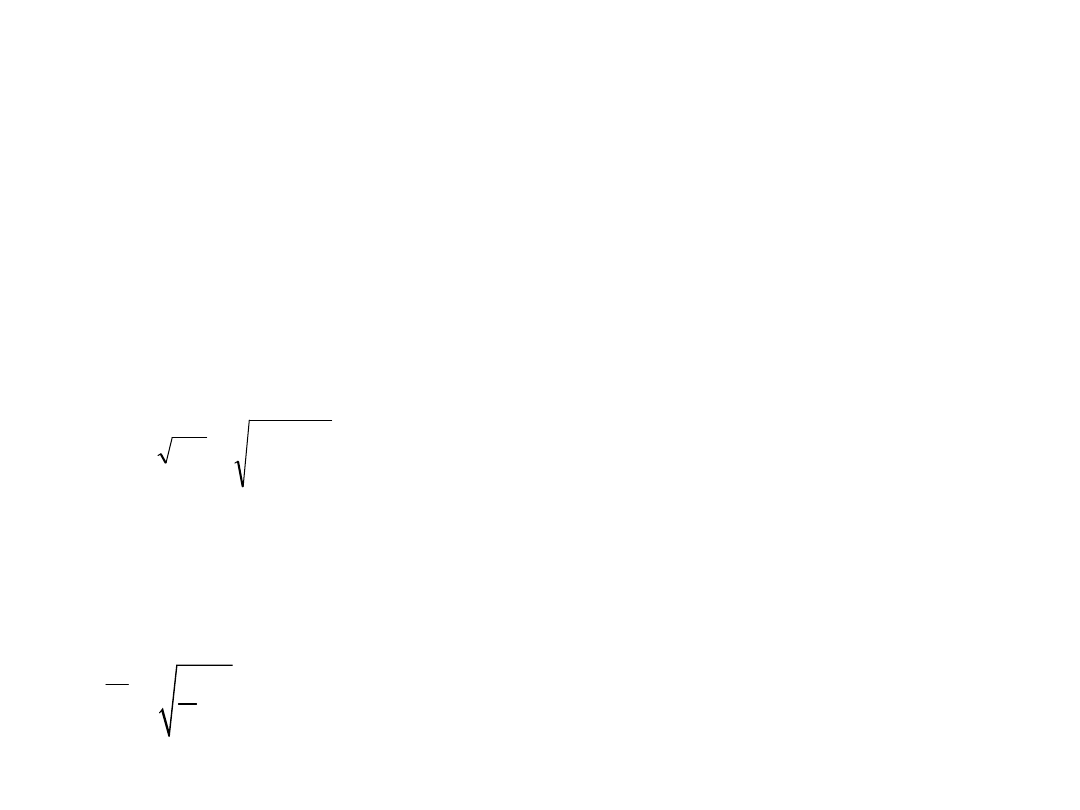
Semiodchylenie

standardowe

Semiodchylenie standardowe interpretowane jest

podobnie jak odchylenie standardowe. Jest to
średnie ważone odchylenie od oczekiwanej stopy
zwrotu, ale w tym przypadku tylko stóp zwrotu
mniejszych od średniej. Inaczej pierwiastek
kwadratowy z semiwariancji









m

i

i

i

d

p

SV

ss

1

2















R

r

gdy

R

r

gdy

R

r

d

i

i

i

i

,

0

,

2

1

i

ss

d

n

=

Wskaźnik Treynora

Miernik zaprezentowany w 1965 roku

przez Jacka Treynora. Wynagrodzenie
za wrażliwość. Wywodzi się z modelu
CAPM. Bazą jest linia SML:

p

f

p

R

R

T







Interpretacja wskaźnika

Treynora

Miara Treynora jest ilorazem dodatkowej stopy

zwrotu ponad stopę wolną od ryzyka i ryzyka
portfela mierzonego betą.

Wyższe wartości wskaźnika oznaczają lepsze

wyniki

zarządzania

portfelem.

Dodatnie

wartości wskaźnika wskazują portfele o stopie
zwrotu wyższej od stopy wolnej od ryzyka.

Treynor uwzględnia więc w odróżnieniu od

Sharpe’a tylko ryzyko systematyczne, co
wynika z przyjęcia założenia o doskonałej
dywersyfikacji portfela.

Przykład

Dane są informacje na temat czterech portfeli

inwestycyjnych
stopa zwrotu Beta

A 0,09 0,80
B 0,10 0,95
C 0,14 1,20
D0,20 1,50

Wyznacz wskaźniki Treynora jeśli wiadomo, że stopa

wolna od ryzyka wynosi 8% a stopa zwrotu z
portfela rynkowego 12%.

0,12 0,08

0,040

1

0,09 0,08

0,013

0,80

0,10 0,08

0,021

0,95

0,14 0,08

0,050

1,20

0,20 0,08

0,080

1,5

M

A

B

C

D

T

T

T

T

T

-

=

=

-

=

=

-

=

=

-

=

=

-

=

=

Interpretacja ujemnych wartości

wskaźnika Treynora

Ujemne wartości wskaźnika Treynora

mogą świadczyć o bardzo złych
wynikach

zarządzania,

albo…..o

bardzo

dobrych

wynikach

osiągniętych w trudnych warunkach
rynkowych.

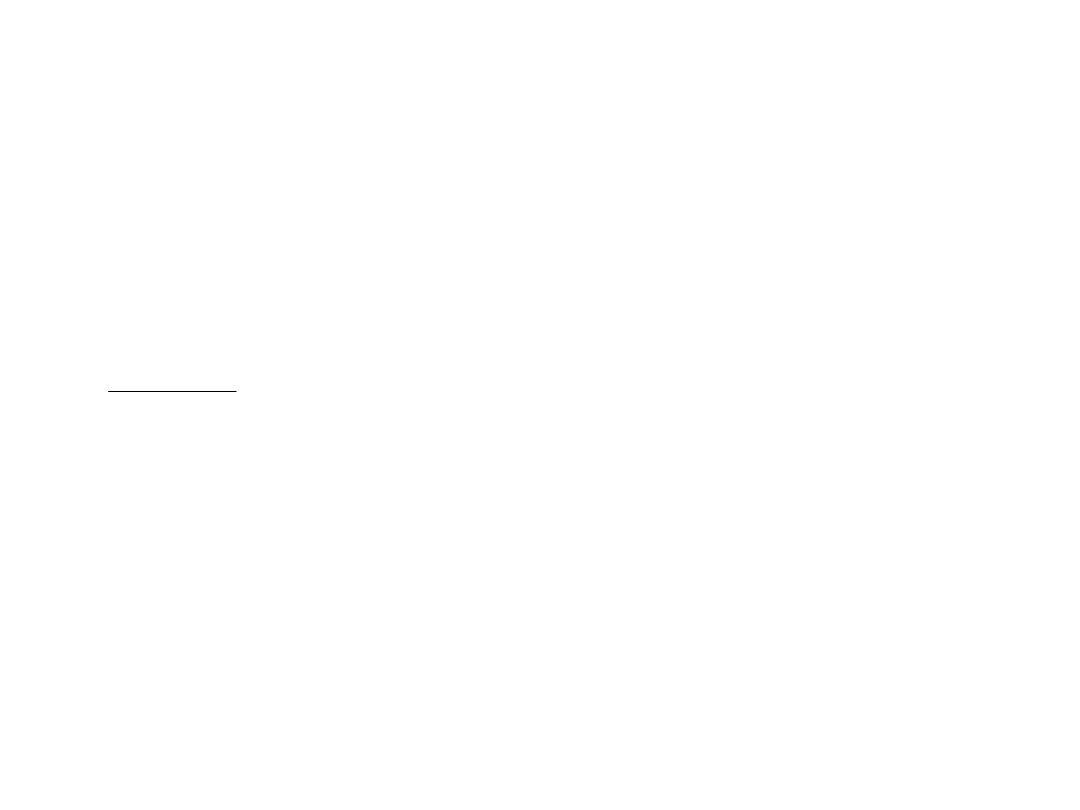
Przykład

stopa zwrotu

Beta

E

0,06

0,60

0,06 0,08

( 0,033)

0,60

E

T

-

=

= -

Zarządzający osiągnął wynik gorszy niż stopa zwrotu wolna od
ryzyka więc wskaźnik Treynora przyjmuje wartość ujemną.

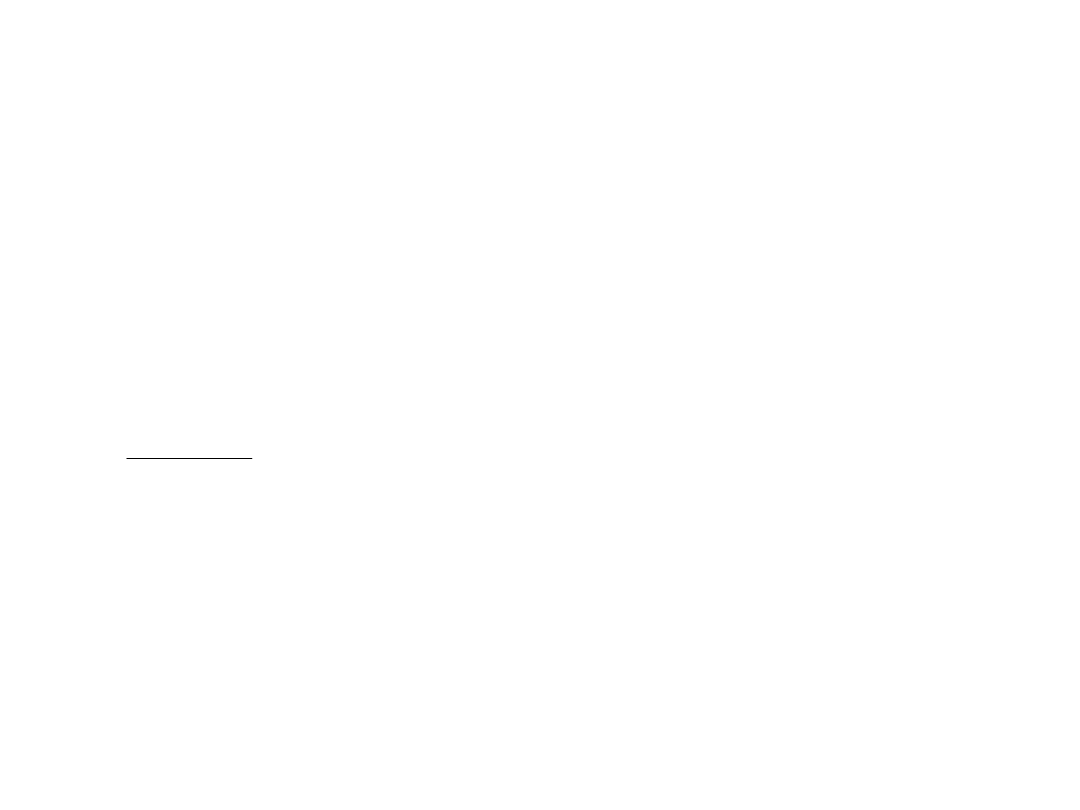
Przykład

Zarządzający zainwestował znaczną część kapitału w metale szlachetne,

których ceny charakteryzują się ujemną korelacją z cenami akcji.

stopa zwrotu

Beta

F 0,10

-0,40

0,10 0,08

( 0,05)

0,40

F

T

-

=

= -

-

Mimo, iż wskaźnik Treynora jest ujemny to osiągnięty wynik jest zupełnie dobry,
a portfel jest szczególnie atrakcyjny w warunkach recesji na rynku akcji.

37

Porównanie wskaźników

• Współczynnik Treynora wyznacza się w oparciu o

współczynnik beta, co oznacza, że uwzględnia się

ryzyko systematyczne

• Współczynnik Sharpe’a ocenia rentowność na

podstawie stopy zwrotu oraz dywersyfikacji

• Dla idealnie zdywersyfikowanego (pozbawionego

ryzyka niesystematycznego) portfela obydwa te

wskaźniki powinny dawać takie same rankingi

portfeli

• Słabo zdywersyfikowany portfel mógłby mieć

wysoki ranking według wskaźnika Treynora, a

niski według wskaźnika Sharpe’a

38

Porównanie wskaźników cd.

Wadą obu wskaźników jest to, że

nie pokazują absolutnych, a jedynie
względne,

wartości

rentowności

portfela. Można na ich podstawie
stworzyć ranking portfeli, ale nie da
się określić dokładnych różnic w ich
rentowności.

Alfa Jensena

Alfa Jensena opracowana w roku 1968,

również na bazie modelu CAPM.
Miernik dany jest następującym
wzorem:

(

)

f

M

f

r

r

r

r

a

b

�

�

= -

+ �

-

�

�

Interpretacja alfy Jensena

• Miara Jensena jest różnicą pomiędzy stopą zwrotu

osiągniętą przez zarządzającego portfelem a stopą
zwrotu z portfela (na linii SML) o takim samym ryzyku
systematycznym, utworzonego z portfela rynkowego z
instrumentem wolnym od ryzyka.

• Dla inwestora najlepszy jest portfel o najwyższej alfie

Jensena.

• Miara Jensena nie jest odpowiednia do porównywania

różnych portfeli. Największą wartość poznawczą ma ten
miernik dla porównania dwóch inwestycji o takich
samych lub zbliżonych wartościach bety.

• Dla celów porównawczych można stosować miernik

zmodyfikowany – iloraz alfy Jensena i Bety.

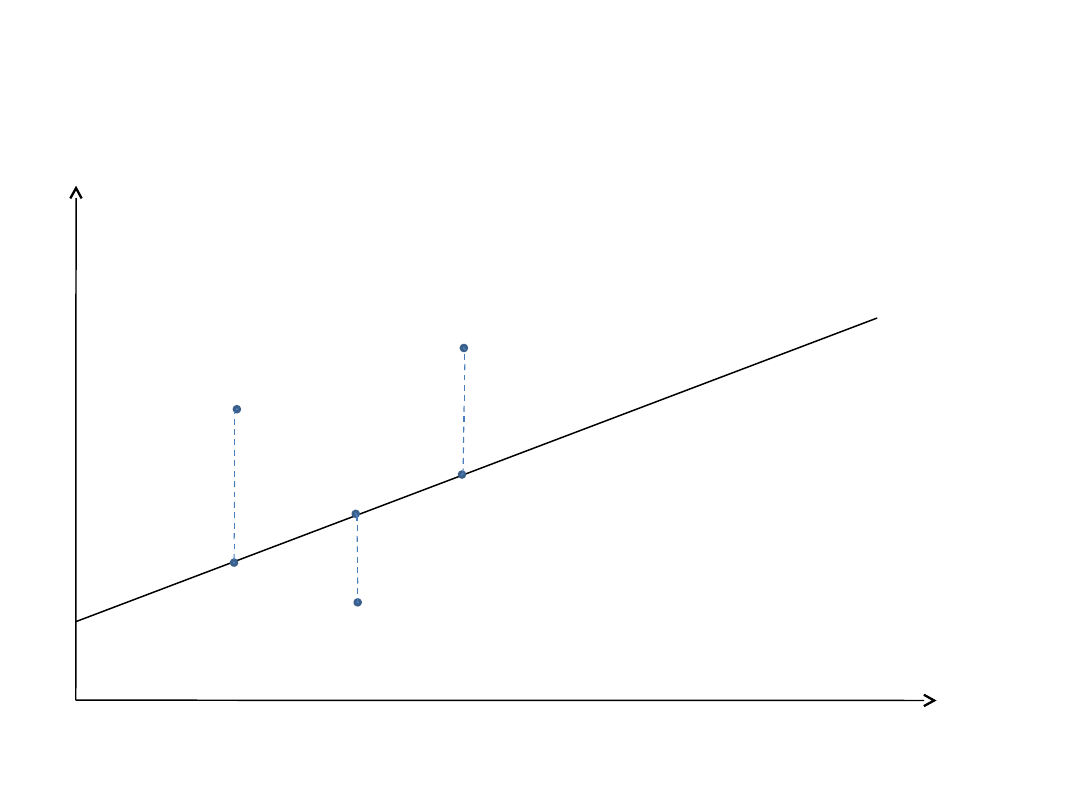
Ilustracja alfy Jensena

A’

A

B

B’

β

r

C

C’

Zadanie 4

Odchylenie standardowe stopy zwrotu z portfela P

wynosi s = 0,12, współczynnika beta tego portfela
wynosi b = 1,1, a wskaźnik Sharpe’a wynosi S =
0,8732. Ile wynosi wskaźnik Treynora dla tego
portfela?

Zadanie 5

Wskaźnik Jensena dla zarządzanego portfela akcji

wynosi 3%. Stopa zwrotu z tego portfela to 18%,
a jego współczynnik beta 1,5. Ile wynosi stopa
zwrotu z portfela rynkowego jeśli wiadomo, że
stopa zwrotu z aktywów wolnych od ryzyka
wynosi 6%?