Wykład z fizyki

I semestr

(dla Wydziału Wiertniczego G i G, rok akademicki

2012/13)

W1 - WSTĘP

dr inż. Jerzy Ostachowicz

WFiIS AGH, D-11, p.26

[e-mail]

Literatura

J. Wolny - Podstawy fizyki
Z. Kąkol - Fizyka dla inżynierów

Cz. Bobrowski FIZYKA- KRÓTKI

KURS

R. Resnick, D.Halliday t.I

FIZYKA 1

……..

INTERNET

WWW.FIS.AGH.EDU.PL

Tematyka wykładów w semestrze letnim ( 1-szy
semestr zajęć)

W1: WSTĘP: wielkości fizyczne, skalary-wektory
(21S)
W2: KINEMATYKA
(19S)
W3: DYNAMIKA PUNKTU MATERIALNEGO
(14S)
W4: DYNAMIKA BRYŁY SZTYWNEJ
(24S)
W5: STATYKA
(3S)
W6: GRAWITACJA
(8S)
W7: MECHANIKA PŁYNÓW
(10S)
W8: DRGANIA
(9S)
W9: FALE
(13S)
W10: TERMODYNAMIKA
(14S)

Wymiar zajęć: 23 godziny lekcyjne (6 terminów:4-3-4-3-
4-5 h)
Rygory: egzamin (po uzyskaniu zaliczenia ćwiczeń)

ĆWICZENIA RACHUNKOWE: wymiar 22 godziny lekcyjne
–udział obowiązkowy; tematyka - możliwie ściśle
powiązana z treścią wykładu
Rygory: zaliczenie na podstawie rezultatów „kartkówek”

WYKŁAD 1: Wielkości fizyczne - skalarne i wektorowe
Podstawowy matematyczny aparat fizyki

Opis świata wymaga zdefiniowania tzw. wielkości fizycznych;
Dzielimy je na podstawowe (długość, czas, masa,….)
i złożone, budowane z wielkości podstawowych według rozpoznanych i

sprawdzonych doświadczalnie zależności (np. prędkość, siła, ciśnienie..).

Działanie w nauce: hipoteza + doświadczenie → teoria ; zbieranie danych

→ korekta

Niezbędne jest określenie jednostki wielkości fizycznej, co pozwala

na porównywanie wyników pomiarów i na operacje liczbowe. Jednostki te
mogą być definiowane w różnych układach jednostek, np. historycznym
układzie CGS; obecnie w nauce i technice obowiązuje układ SI (Systeme
Internationale , fr.), dawniej zwany MKSA.

W zależności od liczby parametrów niezbędnych do ich opisu -

wielkości fizyczne dzielimy na skalary (opis- jedną liczbą) i wektory
(opis kilkoma liczbami –np. siły w przestrzeni kartezjańskiej)

Operacje na zależnościach między wielkościami fizycznymi

podstawowymi i złożonymi wymagają umiejętności zastosowania reguł i
technik zaczerpniętych z matematyki, to jest arytmetyki, algebry,
geometrii, rachunku wektorowego, rachunku różniczkowego i całkowego.

Matematyka uczy przetwarzania danych bez określenia ich związku z

rzeczywistością materialną. – W fizyce każda operacja na wielkościach
fizycznych musi mieć odniesienie to świata materialnego, co m.in. oznacza,
że obliczona czy zmierzona wielkość fizyczna ma wartość liczbową i
jednostkę.

WIELKOŚCI PODSTAWOWE I UZUPEŁNIAJĄCE , układ SI

Wielkość

Jednostka

Symbol

Wielkości

podstawowe
Długość

metr

m

Masa

kilogram

kg

Czas

sekunda

s

Liczność materii

mol

mol

Natężenie prądu

elektrycznego

amper

A

Temperatura

termodynamiczna

kelwin

K

Światłość

kandela

cd

Wielkości

uzupełniające
Kąt płaski

radian

rad

Kąt bryłowy

steradian

sr

Jednostki wtórne

(„Krotności”):

Przedros

tek

Oznacze

nie

Mnożnik

eksa

E

10

18

penta

P

10

15

tera

T

10

12

giga

G

10

9

mega

M

10

6

kilo

k

10

3

hekto

h

10

2

deka

da

10

1

-------

------

10

0

decy

d

10

-1

centy

c

10

-2

mili

m

10

-3

mikro

µ

10

-6

nano

n

10

-9

piko

p

10

-12

femto

f

10

-15

atto

a

10

-18

Definicje jednostek podstawowych (metr, kilogram,
sekunda, amper..)

• Metr (m) jest to długość drogi przebytej w

próżni przez światło w czasie 1/299792458 s
(Genewska Konferencja Miar 1983 r)

• Kilogram (kg) jest to masa

międzynarodowego wzorca tej jednostki masy
przechowywanego w Międzynarodowym
Biurze Miar w Sevres pod Paryżem
(Genewska Konferencja Miar 1901 r

)

• Sekunda (s) jest to czas równy 9 192 631

770 okresom promieniowania
odpowiadającego przejściu między dwoma
nadsubtelnymi poziomami stanu
podstawowego atomu cezu

133

Cs (Genewska

Konferencja Miar 1967 r)

Definicje , c.d.

• Amper (A) jest natężeniem prądu nie zmieniającego

się, który płynąc w dwóch równoległych
prostoliniowych przewodach nieskończenie długich o
przekroju kołowym znikomo małym, umieszczonych w
próżni w odległości 1 m, wywołuje między tymi
przewodami siłę równą 2*10

-7

niutona na każdy metr

długości przewodu (Genewska Konferencja Miar
1948 r)

• Kelwin (K) jest to 1/273,16 część temperatury

termodynamicznej punktu potrójnego wody
(Genewska Konferencja Miar 1967 r)

• Mol jest to liczność materii występująca, gdy liczba

cząstek jest równa liczbie atomów zawartych w masie
0,012 kg

12

C (Genewska Konferencja Miar 1971 r)

• Kandela (cd) jest to światłość, jaką ma w określonym

kierunku źródło emitujące promieniowanie
monochromatyczne o częstotliwości 540*10

12

Hz i

którego natężenie w tym kierunku jest równe 1/681
W/sr (Genewska Konferencja Miar 1979 r)

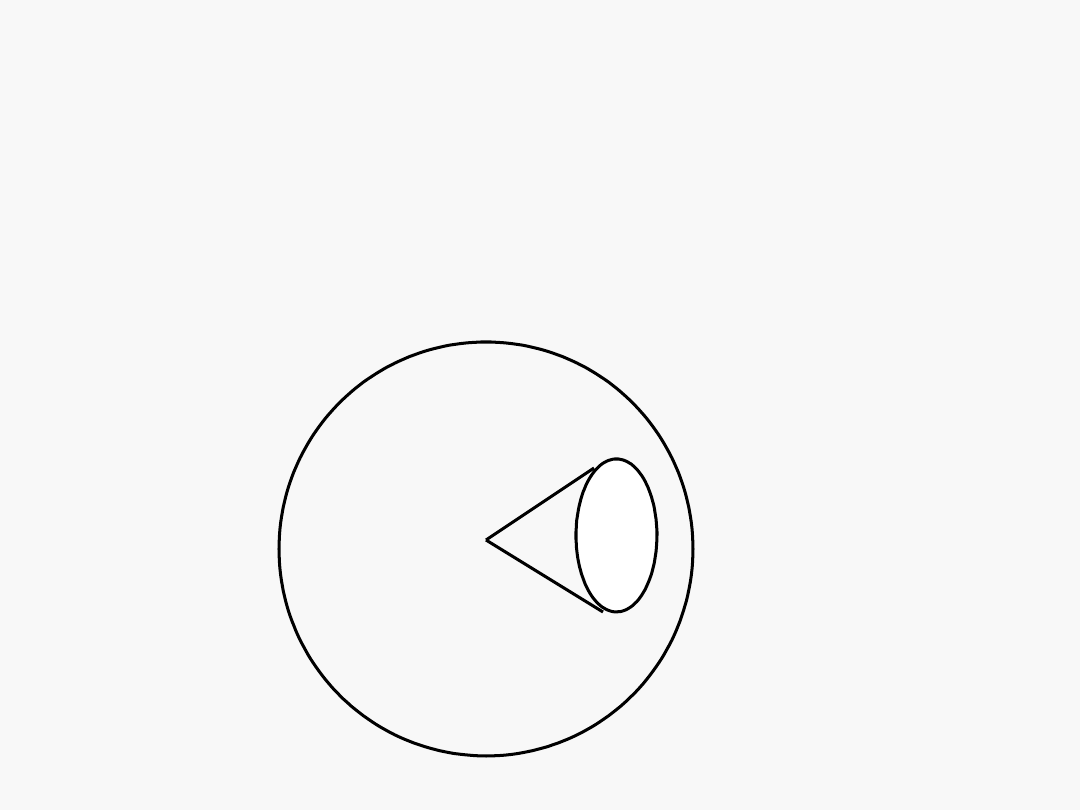
Definicje, c.d.
• Steradian jest kątem bryłowym o wierzchołku w środku

kuli, wycinającym z jej powierzchni część równą
powierzchni kwadratu o boku równym promieniowi tej kuli

• Radian jest to kąt płaski zawarty między dwoma

promieniami koła, wycinającymi z jego okręgu łuk o
długości równej promieniowi tego koła

S

O

=S /r

2

r

W obecnym stanie wiedzy o materii i oddziaływaniach, to jest
wiedzy o budowie atomu, jądra atomowego i sposobów generacji
promieniowania wiemy, że podstawowymi cechami składników
materii jest ich masa i ładunek elektryczny,
a znane oddziaływania to:
- Siły jądrowe oddziaływania pomiędzy nukleonami w jądrze atomu,
- Siły tzw. oddziaływań słabych
- Siły oddziaływania miedzy ładunkami elektrycznymi
(elektromagnetyczne)
- Siły oddziaływania między masami (grawitacyjne)

rodzaj natężenie

zasięg-

grawitacyjne

elektromagnetyc
zne

silne

słabe

2 • 10

-39

7,3 • 10

-9

1
10

-6



10

-15

m

< 10

-15

m

Oddziaływania

Modele

Łatwo spostrzec, że obserwowany świat materialny jest dosyć złożony.

Niezbędne jest jego modelowanie, to znaczy stosowanie uproszczeń z jednej
strony ułatwiających opis a z drugiej niewiele deformujących rzeczywistość,
dostatecznie przydatnych do liczbowych obliczeń i oszacowań.

Przykład 1:
W kinematyce (nauce o ruchu) i dynamice (nauce o efektach działania sił)

przydatne są następujące modele ciał:

- punkt materialny : również dla ciał rozciągłych, np. piłka, kamień,

Ziemia

- bryła sztywna zdefiniowana jako obiekt rozciągły, w którym niezależnie

od wartości działających sił odległości dowolnych dwóch punktów nie ulegają
zmianie

- ciało sprężyste, którego odkształcenie znika gdy znika siła

odkształcająca

W zależności od sytuacji wybieramy inne modelowanie tego samego obiektu.

Np. piłka spadająca w polu grawitacyjnym może być modelowana punktem
materialnym – ale gdy obraca się wokół osi (rotuje) - bryłą sztywną.

Przykład 2– prawa dynamiki - (ruch postępowy)

Znane 3 prawa dynamiki dotyczące efektów

działania sił na punkt (-y) materialny (-e) możemy

wyrazić następująco:

• (1) –jeżeli na ciało (punkt materialny) nie działa siła F, lub

suma wektorowa działających sił jest zerowa – to ciało

pozostaje w spoczynku lub kontynuuje ruch ze stałą

prędkością po prostej (v= const,, np. v=0)

• (2) – jeżeli na ciało (punkt materialny o masie m) działa

siła F, która np. jest wypadkową działających sił, to ciało

doznaje przyspieszenia a proporcjonalnego do siły : F=

m a

• (3) – jeżeli ciało A działa na inne ciało B siłą F , to powstaje

siła reakcji -F oddziaływania ciała B na A, równa co do

wartości sile F ale przeciwnie skierowana

ALE:

dla bryły sztywnej musimy zmodyfikować w/w prawa i

uwzględnić możliwość wprowadzenia siłami ciała w ruch

obrotowy i ustalić adekwatne prawa dynamiki dla ruchu

obrotowego (patrz wykład 4)

Skalary i wektory

(Patrz także plik „Sk-Wekt” w

formacie jpg)

Przykłady wielkości skalarnych:
masa, droga, czas, objętość, ładunek, praca,

moc

Skalary posiadają tylko wartość;
matematyczne operacje na skalarach to algebra

Przykłady wielkości wektorowych:
przemieszczenie, prędkość, przyspieszenie, siła,
moment siły, pęd

Wektory posiadają:

wartość, kierunek, zwrot, punkt przyłożenia;

Matematyczne operacje na wektorach w przestrzeni

kartezjańskiej (x,y,z) zdefiniowane następująco:

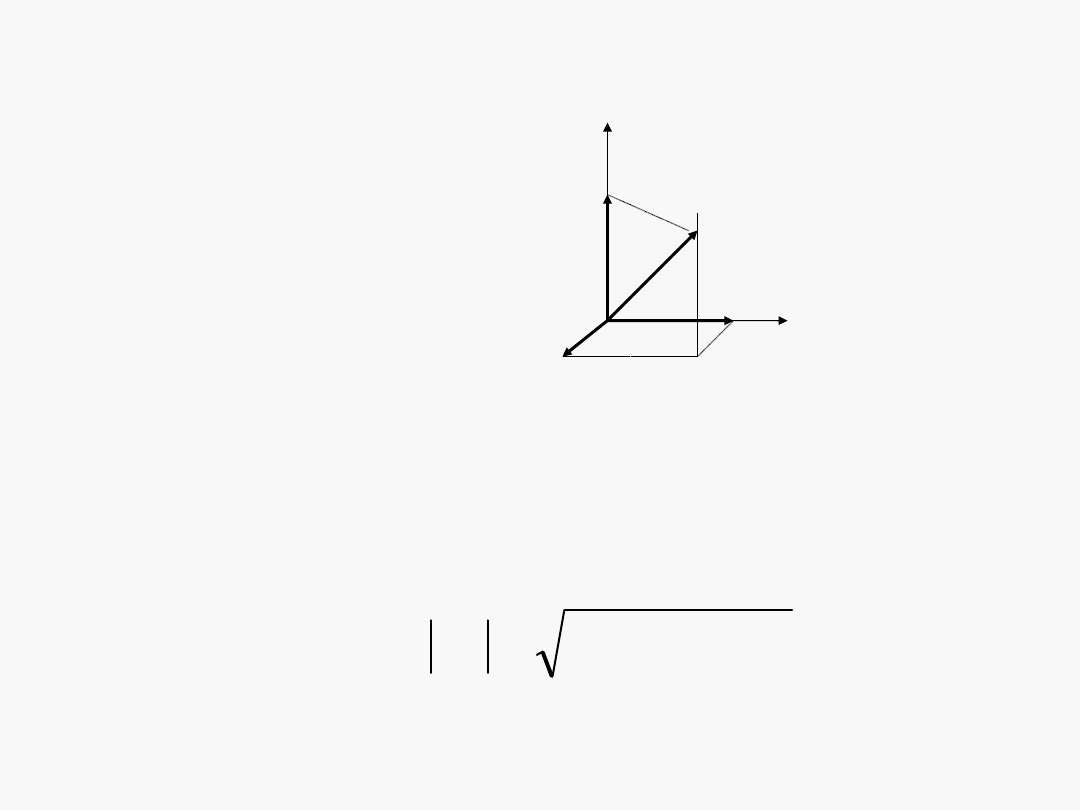
Wektor, składowe wektora

a = (a

x,

,a

y

,a

z

)

2

2

2

z

y

x

a

a

a







a

y

a

a

x

a

z

a

y

Wartość
wektora:

a = i a

x

+ j a

y

+ k a

z

gdzie:

i, j, k -

tzw. wersory osi

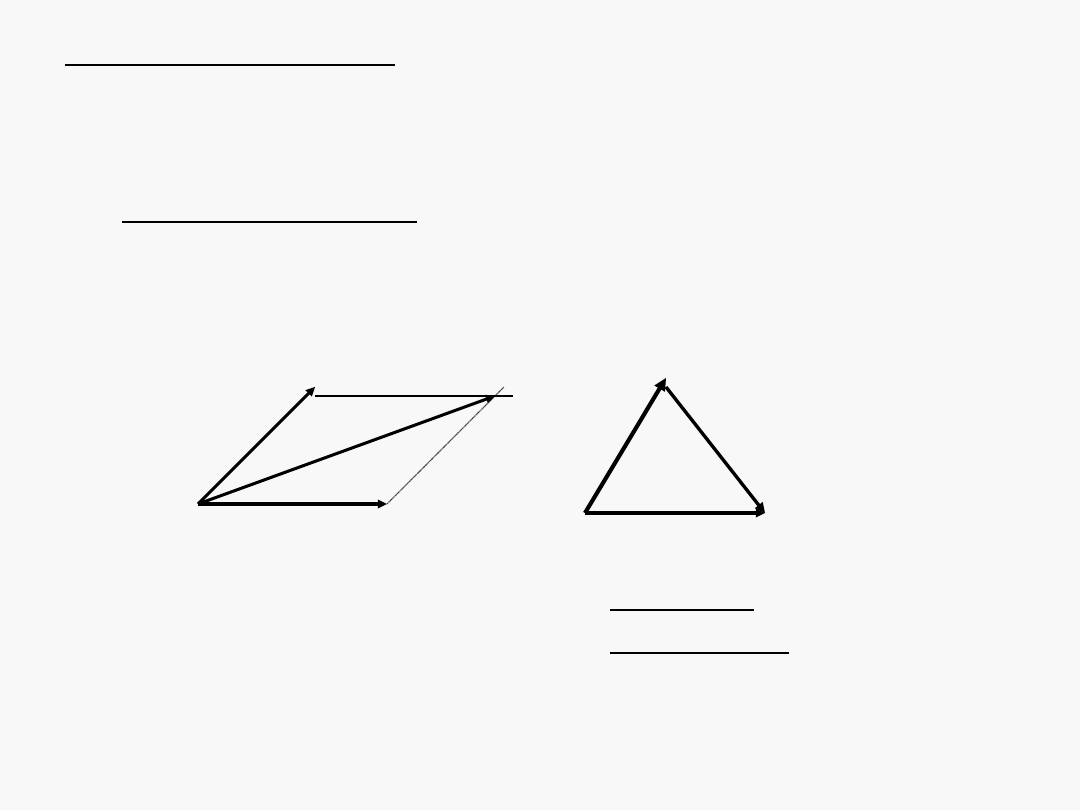
Sumowanie wektorów

Suma wektorów: c = a + b

a + b = (a

x

+ b

x

,a

y

+ b

y

,a

z

+ b

z

)

a

b

c=
a+b

b

a

k=a-b

Różnica
wektorów
k = a - b

Mnożenie skalar ∙ wektor: w = s ∙ a
w

x

= s a

x

, w

y

=s

a

y

, w

z

= s a

z

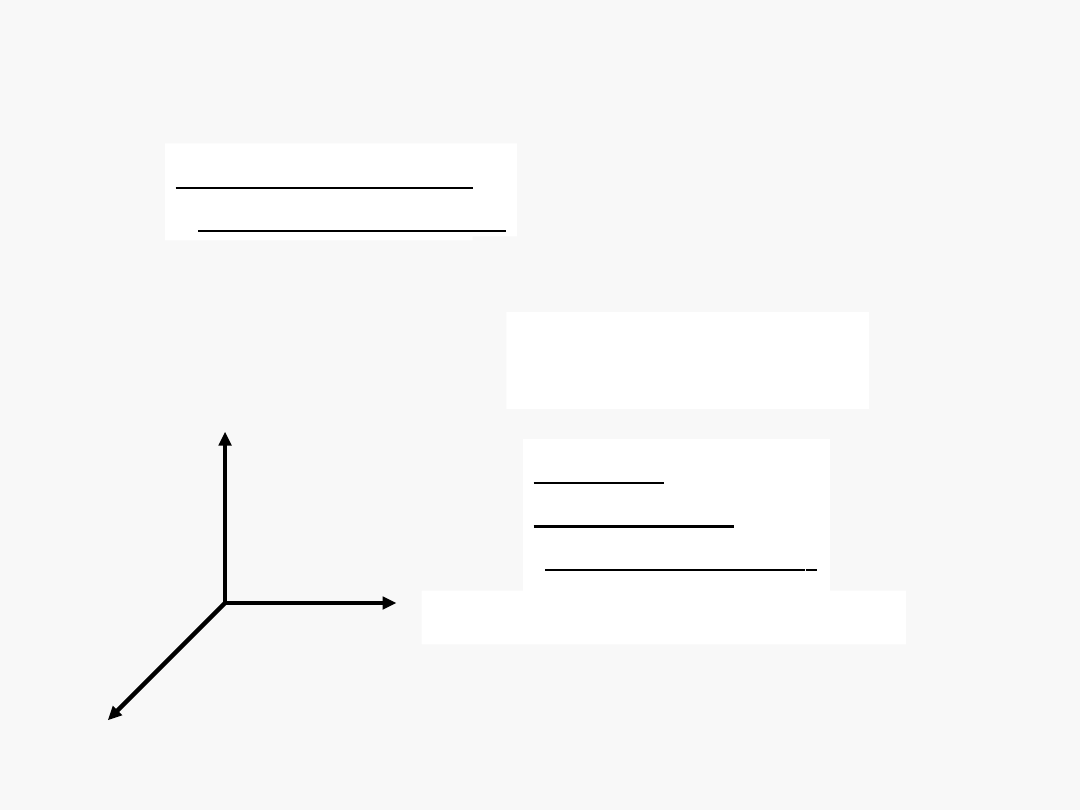
Iloczyny wektorów : skalarny i wektorowy

Iloczyn skalarny
skalar s = a ∙ b

s = a • b  a

x

b

x

+a

y

b

y

+ a

z

b

z

| a • b |  a• b •
cos ( )

Iloczyn
wektorowy
wektor c = a
x b

a

b

c = a x b

| a x b | = a • b • sin ( )

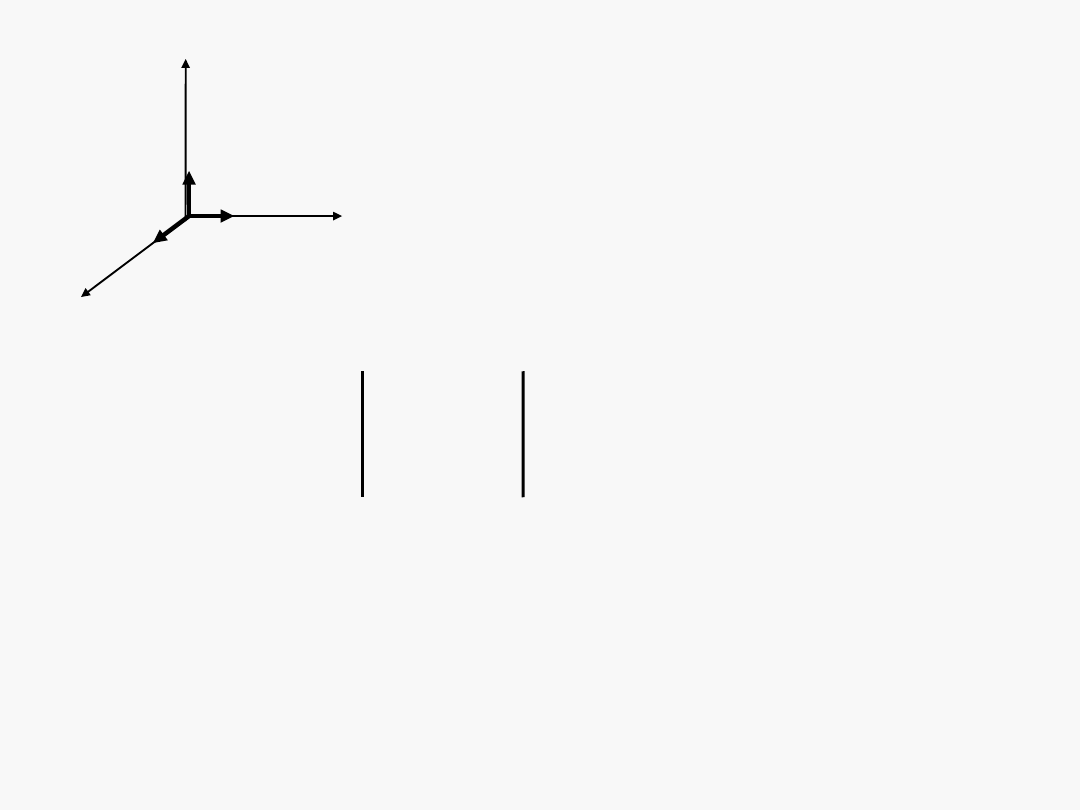
Iloczyn wektorowy, interpretacja:

•

obliczenie

- gdy wektory

• zadane są

współrzędnymi:

y

i

j

k

| i |= | j |= | k |=1

i j
k
a

x

a

y

a

z

b

x

b

y

b

z

a x b
=

=

=

i ( a

y

b

z

- a

z

b

y

) + j ( a

z

b

x

- a

x

b

z

) +k ( a

x

b

y

-

a

y

b

x

)

wersory osi

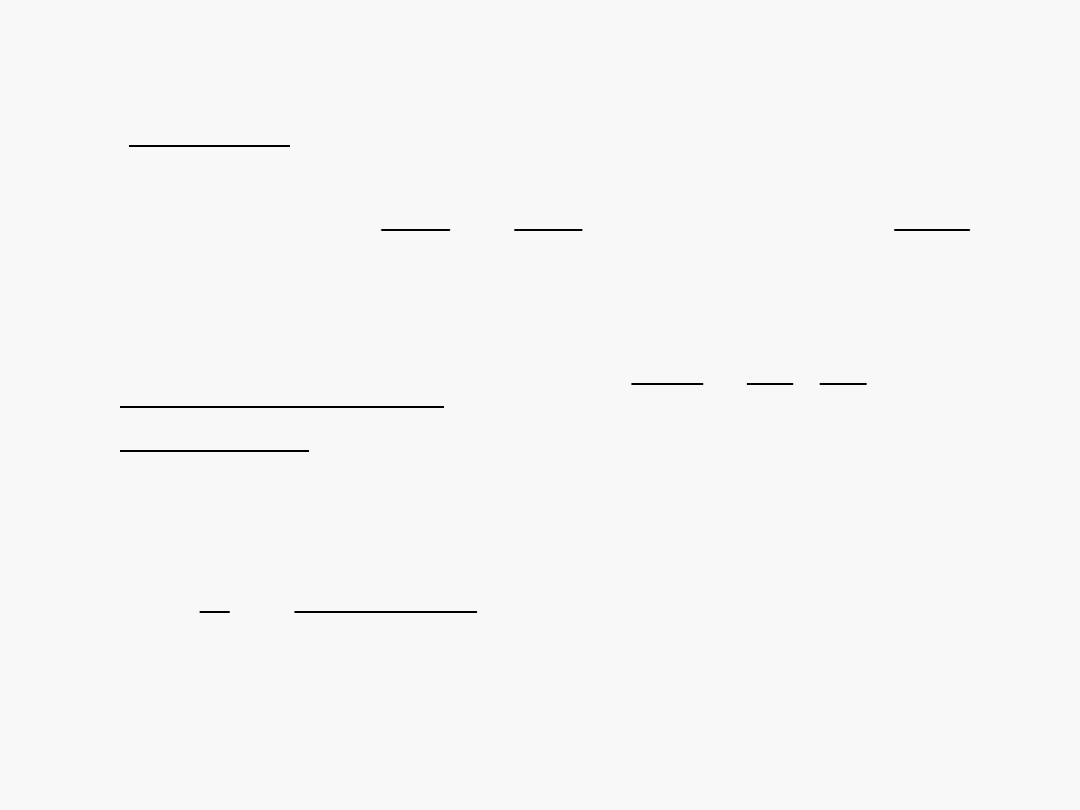
Przydatna matematyka: Pochodna funkcji

x

y

lim

(x)

f

dx

d

dx

dy

y

X















0

'

( f +g )’ = f ’ + g’

( f · g )’ = f ’· g
+f · g’

[f(g(x))]’ = f ’( g (x)) · g’(x

)

2

g

g

f

g

f

g

f















































dx

dy

dx

d

dx

y

d

y

2

2

Definicje:

reguły obliczania
pochodnej:

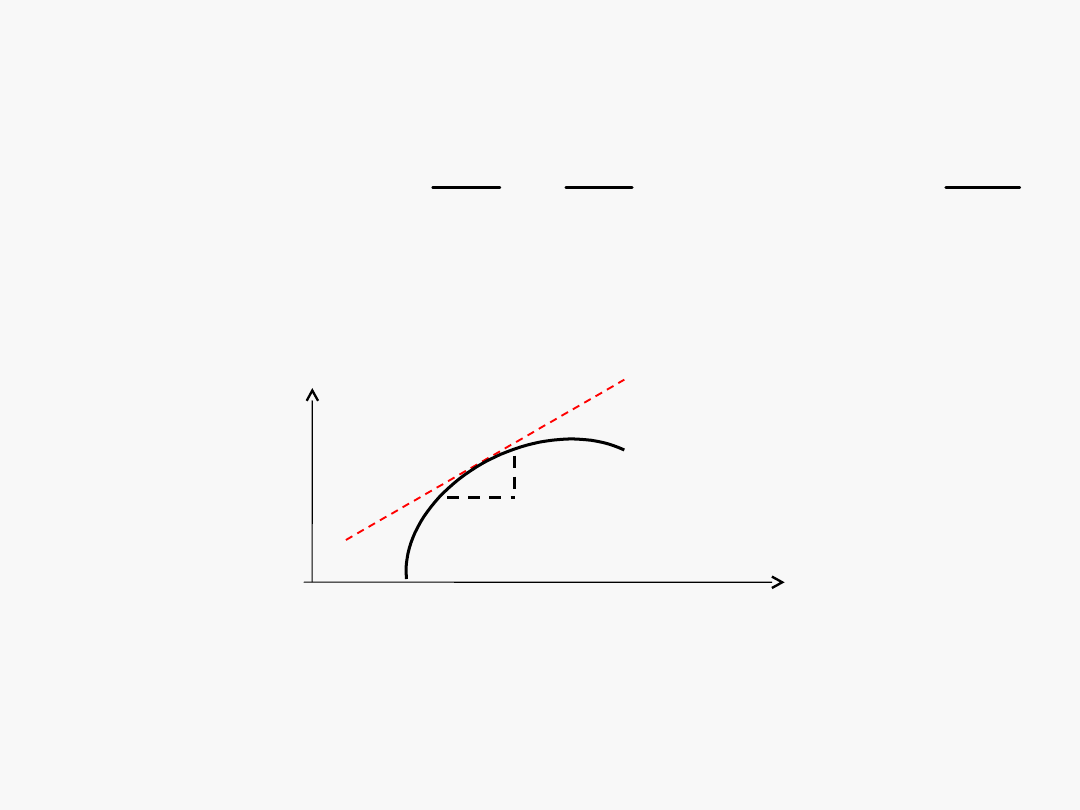
Interpretacja graficzna pochodnej

• Pochodna funkcji

y

st

= a x + b ; a = dy/dx

x

y

lim

(x)

f

dx

d

dx

dy

y

X















0

'

f(x)

X

∆ x

∆ y

styczna

Całki nieoznaczona i oznaczona

• całki

całka nieoznaczona

 

 

 

dx

dF

x

f

x

x

f

x

F









d

całka oznaczona

 

 

 

 

1

2

d

2

1

2

1

x

F

x

F

x

F

x

x

f

x

x

x

x









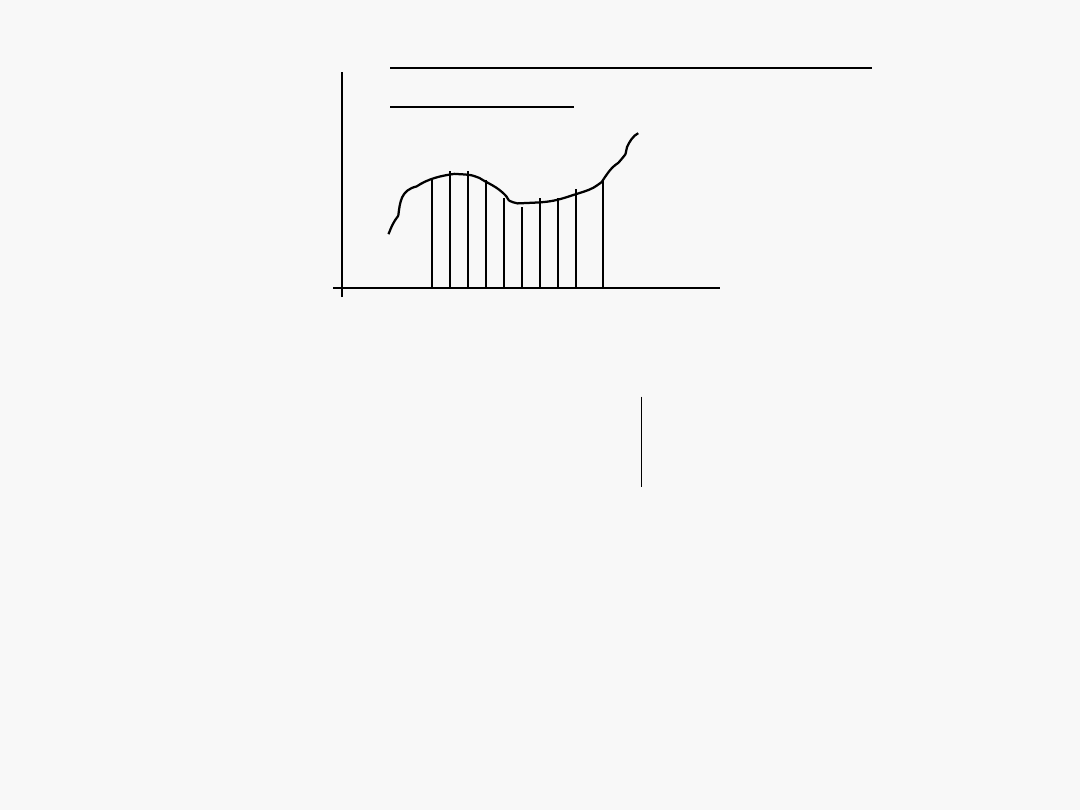
Interpretacja graficzna całki
oznaczone

j

S

x

1

x

2

f(x)

S =

 

 

 

 

1

2

d

2

1

2

1

x

F

x

F

x

F

x

x

f

x

x

x

x









Przykłady obliczania pochodnych niektórych
funkcji:

y= x y

’

= dy/dx = 1 - różniczka dy= dx

y= ax y

’

=dy/dx= a - różniczka dy = a dx , …. itd

y= x

n

y

’

=

dy/dx= nx

n-1

np. y= x

-1/2

dy/dx= -1/2 x

-1/2 - 1

= -1/2 x

-3/2

y= e

x

y

’

=

dy/dx= e

x

y= lnx y

’

=dy/dx= 1/x

y= sin x y

’

= dy/dx= cos x

y= cos x y

’

= dy/dx= - sin x

ekstremum funkcji y= f(x) y

extr

dla y

’

= dy/dx = 0

y

max

dla y

’’

= d

2

y/dx

2

< 0 ; y

min

dla y

’’

=

d

2

y/dx

2

> 0

funkcja ilorazu: np.: y = tg x = sin x/cos x y

’

= (1/cos

2

x)[(cos x cos x – sin

x(-sin x)]=
=1/cos

2

x

funkcja iloczynu: np. y= x tg x y

’

= 1 tg x + x (tg x)

’

=

tg x + x/ cos

2

x

Przykłady obliczania całek niektórych funkcji:

 dx = x + C bo dy=1 dx + 0 ; (dalej stała całkowania C - opuszczona)
 x

n

dx = x

n+1

/(n+1)

 e

x

dx = e

x

 dx/x = ln x
 sin x dx= - cosx
Zastosowania:
E

p

=  (k x) dx = k x

2

/2 (energia potencjalna przy odkształceniu

sprężystym)
s =  v dt = v t ( droga s jeżeli v=const - ruch jednostajny)
s =  v dt =  (v

o

+ at) dt = v

o

t + at

2

/2 (droga s w ruchu ze stałym

przyspieszeniem a)