Bartosz Puchalski 4.V.2005

Ćwiczenie nr 6

Wyznaczanie stałej szybkości reakcji

rozkładu nadtlenku wodoru na katalizatorze węglowym

Po uruchomieniu termostatu przygotowałem 100 ml ok. 0,3% roztworu nadtlenku wodoru i oznaczyłem jego stężenie miareczkując 5 ml próbkę z dodatkiem 1 ml 4 M H₂SO₄ nadmanganianem potasu (VII). Przygotowałem naważkę węgla aktywnego bezpośrednio na łopatce naczyńka reakcyjnego. Wprowadziłem 50 ml roztworu H₂O₂ do naczyńka reakcyjnego i umieściłem w nim łopatkę z węglem aktywnym, tak, by nie dotykała roztworu. Wyrównałem poziomy w biurecie gazowej z podziałką. Po 15 minutach termostatowania wprowadziłem węgiel aktywny do roztworu nadtlenku wodoru, uruchomiłem mieszadło, włączyłem stoper. Odczytywałem poziomy w biurecie gazowej w odpowiednich odstępach minutowych.

1. Obliczam początkową liczbę moli H₂O₂
:

• ponieważ podczas miareczkowania zeszło średnio 5,033 ml KMnO₄ o stężeniu 0,009 mol/l to:

w 1000 ml KMnO₄ było - 0,009 mola KMnO₄

to w 5,033 ml było - x moli KMnO₄

x = 0,0000453 mola KMnO₄

• biorąc pod uwagę stechiometrię reakcji nadtlenku wodoru z nadmanganianem:

2MnO₄^- + 5H₂O₂ + 6H⁺ ↔ 6Mn²⁺ + 5O₂ + 8H₂O

widać, że 2 mole KMnO₄ reagują z - 5 molami H₂O₂

więc 0,0000453 mola KMnO₄ reaguje z - x molami H₂O₂

x = 0,00011325 mola H₂O₂

• ponieważ do miareczkowania wzięto 5 ml próbkę a w naczyńku pomiarowym było 50 ml roztworu H₂O₂:

w 5 ml roztworu H₂O₂ było - 0,00011325 mola H₂O₂

to w 50 ml tego roztworu będzie - x moli H₂O₂

x = 0,0011325 mola H₂O₂ =

2. Obliczam liczbę moli wydzielonego tlenu
:

• korzystam z równania gazu doskonałego Clapeyrona:

; gdzie p - prężność parcjalna O₂ [N m^-2] (równa różnicy P_całkowite - P_{pary wodnej}), V - objętość odczytana z biurety gazowej [m³], T - temperatura [K], R - stała gazowa równa 8,314 [J mol^-1 K^-1]

• przekształcając tak, aby uzyskać wzór na liczbę moli:

• obliczam prężność pary wodnej interpolując odpowiednią wartość z wykresu P_{pary wodnej} = f(T) na podstawie tabeli zamieszczonej w skrypcie:

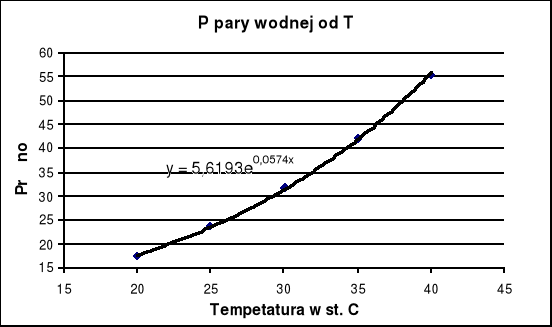
• po podstawianiu do równania y = 5,6193e^0,0574x za x wartość odczytanej przeze mnie temperatury równą 23,7 ^oC uzyskałem:

P_{pary wodnej} = 21,9022 [mm Hg] = 2919,33 [N m^-2]

• prężność parcjalna tlenu pod ciśnieniem 1008 [hPa] wynosi więc:

P_całkowite - P_{pary wodnej} = 100800 - 2919,33 = 97880,67 [N m^-2]

• po podstawieniu wszystkich danych liczba moli tlenu dla pierwszej zanotowanej objętości równej 0,8 ml (0,0000008 m³) wynosi:

3. Wyniki obliczeń zbieram w tabeli:

Czas [s]	V [cm^3]	V [m^3]			W		k [1/s]
120	0,8	0,0000008	3,174E-05	1,069E-03	5,606E-02	0,0576963	0,0004808
240	2	0,0000020	7,936E-05	9,737E-04	1,402E-01	0,1510074	0,0006292
360	2,5	0,0000025	9,920E-05	9,340E-04	1,752E-01	0,1926123	0,000535
480	3	0,0000030	1,190E-04	8,943E-04	2,102E-01	0,2360236	0,0004917
600	3,7	0,0000037	1,468E-04	8,388E-04	2,593E-01	0,3001508	0,0005003
720	4,1	0,0000041	1,627E-04	8,071E-04	2,873E-01	0,3387301	0,0004705
840	4,65	0,0000047	1,845E-04	7,634E-04	3,259E-01	0,3943306	0,0004694
960	5,15	0,0000052	2,044E-04	7,237E-04	3,609E-01	0,4477077	0,0004664
1200	6,1	0,0000061	2,420E-04	6,483E-04	4,275E-01	0,5577144	0,0004648
1500	7,15	0,0000072	2,837E-04	5,650E-04	5,011E-01	0,6952838	0,0004635
1800	8,1	0,0000081	3,214E-04	4,896E-04	5,676E-01	0,8385026	0,0004658
2100	9	0,0000090	3,571E-04	4,182E-04	6,307E-01	0,9961837	0,0004744
2400	9,9	0,0000099	3,928E-04	3,468E-04	6,938E-01	1,1834689	0,0004931

W =
/

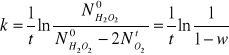
Masa węgla aktywnego = 0,08235 g

4. Obliczam wartość stałej szybkości rozkładu H₂O₂ w katalizatorze węglowym posługując się metodą najmniejszych kwadratów oraz arkuszem kalkulacyjnym excel.

• na podstawie wykresu ln(1/(1-W)) = f(t) wyznaczyłem równanie linii trendu:

y = 0,0005x + 0,0076

• na podstawie równania
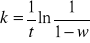
  widać, że dla wartości t = 1 [s] wartość stałej jest równa wartości logarytmu naturalnego podstawiając do powyższego równania:

k = y = 0,0005 * 1 + 0,0076 = 0,0081 [1/s]

Wnioski.

Jak widać wartość stałej jest niewielka, więc reakcja zachodzi powoli. Wykres posiada współczynnik R² = 0,9969 co obrazuje w miarę dokładne wykonanie ćwiczenia. Stałe wyznaczone dla poszczególnych ilości moli tlenu i nadtlenku wodoru są znacznie mniejsze od stałej wyznaczonej na podstawie wykresu prawdopodobnie na skutek różnicy w czasie, który dla drugiego przypadku wnosił 1 s. Reakcja rozkładu nadtlenku wodoru w katalizatorze węglowym jest dobrym przykładem reakcji kinetycznej pierwszego rzędu.

---