Modelowanie i Symulacja Komputerowa

M A T L A B – S i mu l i n k

Simulink

Wprowadzenie: http://me-www.colorado.edu/matlab/simulink/simulink.htm

– interaktywny pakiet przeznaczony do modelowania, symulacji, analizy dynamicznych układów ciągłych, dyskretnych,

dyskretno-ciągłych w czasie

– zintegrowany z MATLAB-em (nie jest możliwe korzystanie z Simulink-a bez zainstalowania MATLAB-a)

– stosowany do projektowania i testowania urządzeń oraz systemów sterujących. Badanie układów metodami symulacyjnymi

znacznie zmniejsza koszty i czas, niezbędny do przygotowania lub modernizacji prototypów urządzeń i systemów sterowania

CEL ĆWICZEŃ LABORATORYJNYCH: zdefiniowanie modelu matematycznego rozważanego układu/procesu

dynamicznego poprzez opis za pomocą równań różniczkowych zwyczajnych, zbudowanie graficznego modelu (schematu

blokowego z wykorzystaniem bloków bibliotecznych Simulink-a), wykonanie eksperymentu symulacyjnego przy

zadanych parametrach symulacji, tworzenie graficznego interfejsu użytkownika umożliwiającego poprawne i wygodne

wprowadzanie danych oraz prezentację rezultatów obliczeń w postaci wykresów

Przykład modelowania 1

1)

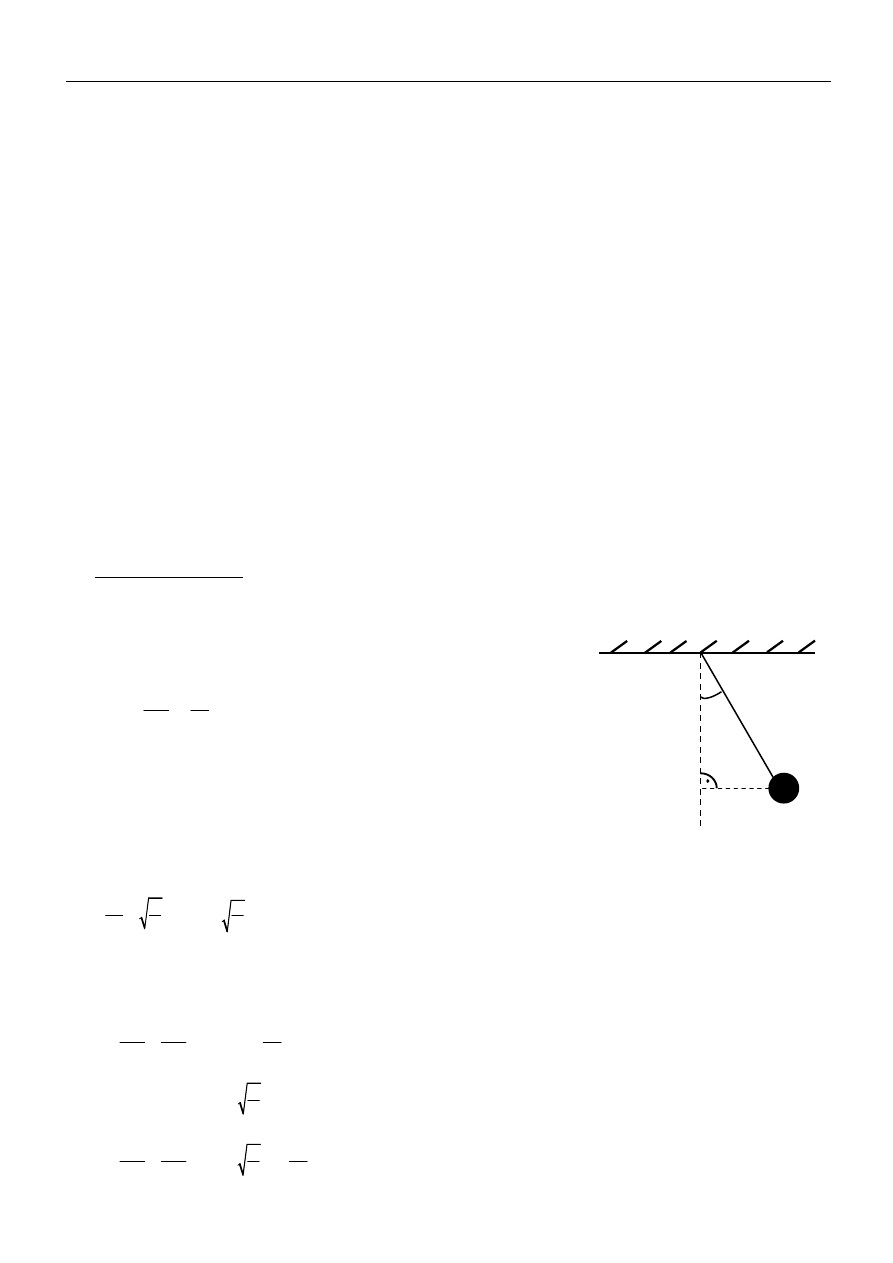
Wahadło matematyczne - ciało wykonujące drgania pod wpływem siły grawitacji.

Zmienność kąta wychylenia wahadła przy uwzględnieniu oporów ośrodka,

siły grawitacji oraz działającej na nie siły wymuszającej opisuje równanie

postaci

2

2

2

sin

cos

d θ

dθ

ml

γ

mgl

θ

A

ωt

dt

dt

+

+

=

gdzie

θ ‒ kąt odchylenia wahadła od położenia w stanie równowagi

l ‒ długość wahadła
m ‒ masa wahadła
g ‒ przyspieszenie ziemskie (

2

9,80665

/

g

m s

=

)

A ‒ amplituda siły wymuszającej
ϖ ‒ częstotliwość siły wymuszającej, gdzie

2

;

2

g

π

l

ω

T

π

T

l

g

=

=

=

(ϖ jest częstością kołową drgań; T – okresem)

γ ‒ współczynnik oporu ośrodka

Z powyższego równania różniczkowego opisującego ruch wahadła wyprowadzić można następującą zależność

2

2

2

1

cos

sin

d θ

dθ

A

ωt

γ

mgl

θ

dt

dt

ml





=

−

−









Po podstawieniu za

g

ω

l

=

otrzymujemy

2

2

2

1

cos

sin

g

d θ

dθ

A

t

γ

mgl

θ

l

dt

dt

ml









=

−

−

















θ

m

l

sinθ

y = l

cosθ

x = l

Modelowanie i Symulacja Komputerowa

M A T L A B – S i mu l i n k

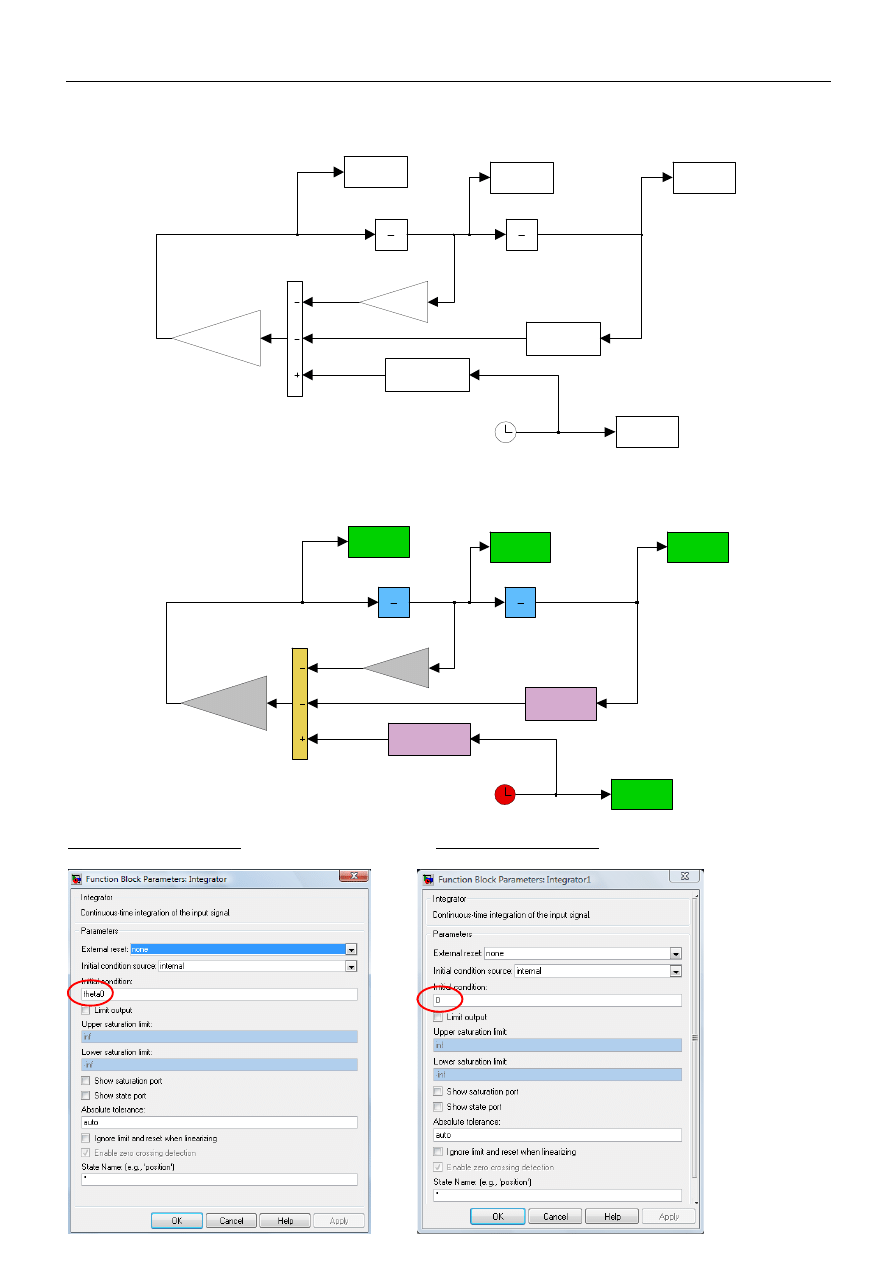
Schemat blokowy powyższego układu zbudowany w oparciu o równanie różniczkowe z wykorzystaniem bloków

bibliotecznych Simulink-a ma następującą postać:

To Workspace 3

d2theta

To Workspace2

t

To Workspace1

dtheta

To Workspace

theta

Sum

Integrator 1

1

s

Integrator

1

s

Gain 2

1/(m*(l^2))

Gain 1

gamma

Fcn1

A *cos(u*sqrt(g/l))

Fcn

m*g*l*sin(u)

Clock

Co można uczynić bardziej przejrzystym edytując teksty oraz wprowadzając odpowiednią kolorystykę

k

ą

t wychylenia

wahadła

d2theta

t

dtheta

theta

1

s

1

s

1/(m*(l^2))

gamma

A *cos(u*sqrt(g/l))

m *g*l*sin(u)

początkowe wychylenie wahadła :

początkowa prędkość wahadła :

Modelowanie i Symulacja Komputerowa

M A T L A B – S i mu l i n k

Przykład modelowania 2

Rozważmy obiekt opisany za pomocą równania różniczkowego drugiego rzędu

( )

( )

( )

( )

2

2

1,5

2

2,5

d y t

dy t

y t

z t

dt

dt

+

+

=

(1)

gdzie y(t) oznacza wyjście układu (odpowiedź) na sygnał wejściowy (zadany)

z(t), przy warunkach początkowych określających stan układu w chwili

początkowej (rozpoczęcia procesu sterowania, t = 0)

( )

( )

' 0

2

0

1

y

y

= −

=

oraz zadanym sygnale wejściowym postaci

( )

(

)

2.3

sin

t

z t

t e

−

=

⋅

Z równania (1) należy wyznaczyć wzór na drugą pochodną

( )

( )

( )

( )

2

2

2,5

1,5

2

d y t

dy t

z t

y t

dt

dt

=

−

−

Na schemacie blokowym blok całkowania odpowiada uzyskaniu sygnałów będących pochodnymi niższego rzędu, co wynika z

odwrotności operacji całkowania względem różniczkowania, tj.

( )

( )

( )

( )

2

2

dy t

d y t

dy t

dt

y t

dt

dt

dt

dt

=

=

∫

∫

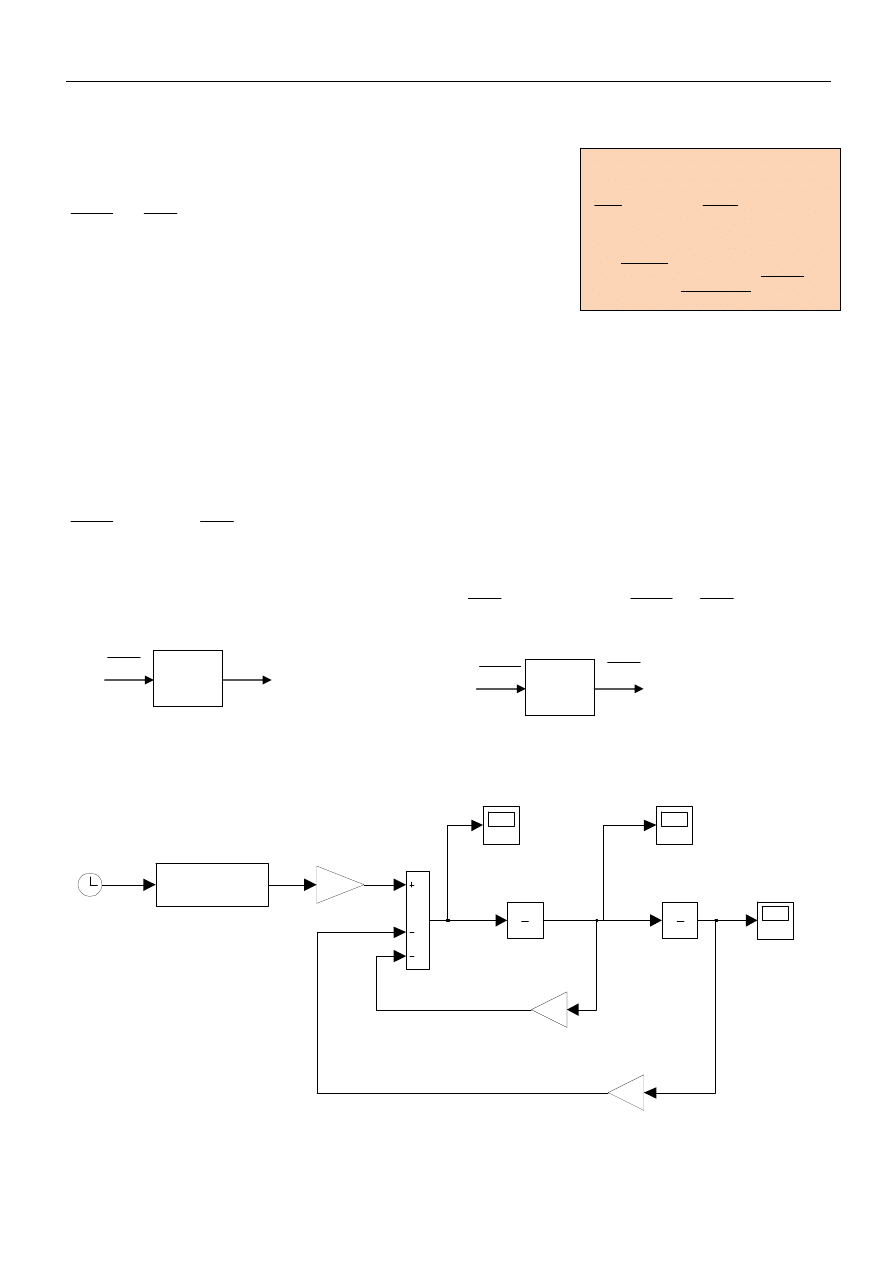
Schemat modelu układu w Simulinku

Sum

Scope 2

Scope 1

Scope

Integrator 1

1

s

Integrator

1

s

Gain 2

2.5

Gain 1

2

Gain

1.5

Fcn

sin(u*exp(-2.3*u))

Clock

∫

( )

2

2

d y t

dt

( )

dy t

dt

( )

''

y t

( )

'

y t

∫

( )

dy t

dt

( )

y t

( )

'

y t

( )

y t

Równoważnym oznaczeniem pochodnych po
czasie

są

( ) ( )

( ) ( )

2

2

dy t

d y t

y t

y t

dt

dt

=

=

ɺ

ɺɺ

W fizyce najczęstszą interpretacją sygnału y(t)
jest położenie obserwowanego ciała, jego
pierwsza pochodna reprezentuje prędkość, zaś
druga pochodna – przyspieszenie.

Modelowanie i Symulacja Komputerowa

M A T L A B – S i mu l i n k

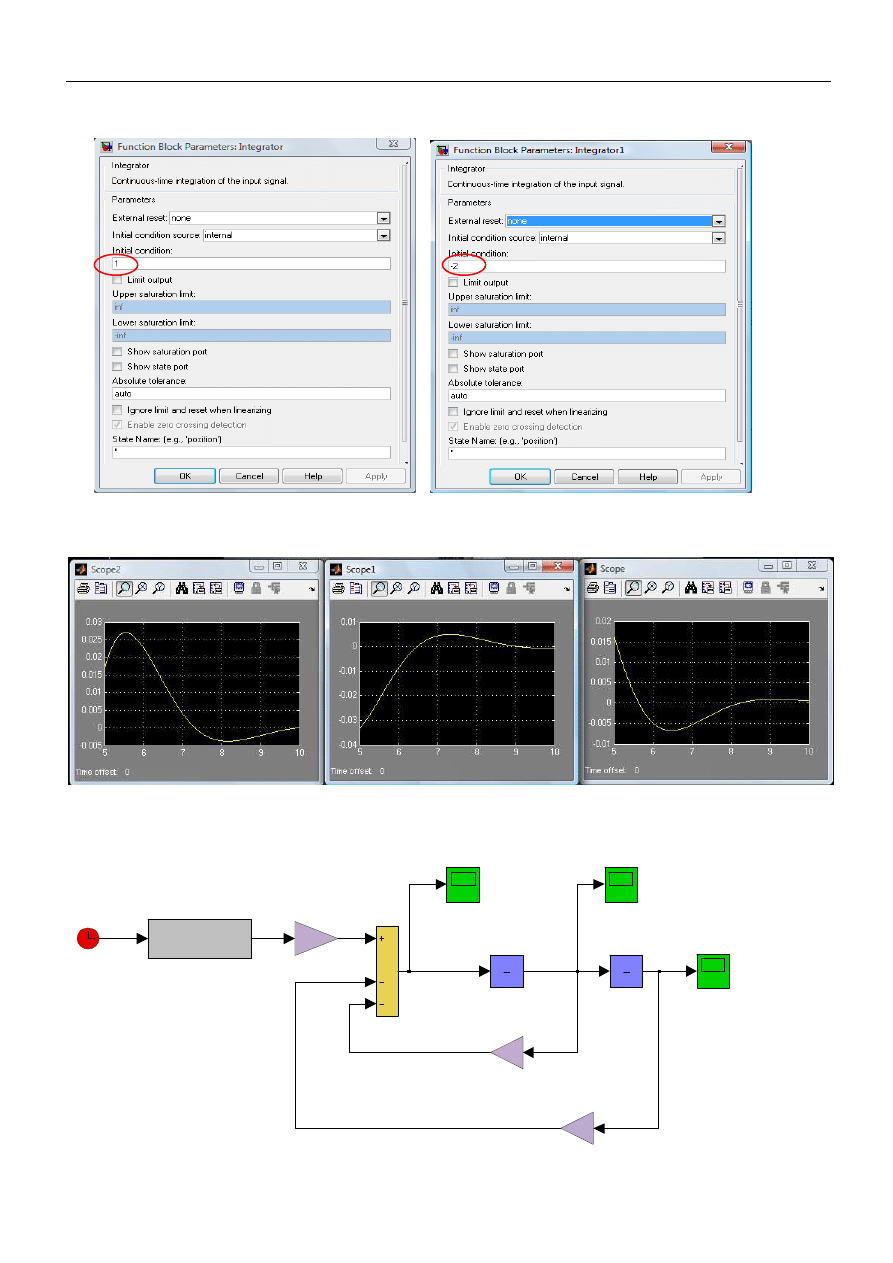
Warunki początkowe

( )

( )

' 0

2

0

1

y

y

= −

=

są ustawiane w integratorach w polu „initial condition”

Przebiegi widoczne na oscyloskopach (po dwukrotnym kliknięciu na dany oscyloskop i wyborze ikony ozn. lornetką)

Schemat można uczynić bardziej przejrzystym edytując teksty oraz wprowadzając odpowiednią kolorystykę

(Menu podręczne: Format, Foreground Color, Bacground Color )

2.5z(t)

y(t)

dy(t)/dt

d2y(t)/dt2

z(t)

sin(u*exp(-2.3*u))

Suma

Scope 2

Scope 1

Scope

1

s

1

s

Clock

2.5

2 y(t)

2

1.5 dy (t)/dt

1.5

Modelowanie i Symulacja Komputerowa

M A T L A B – S i mu l i n k

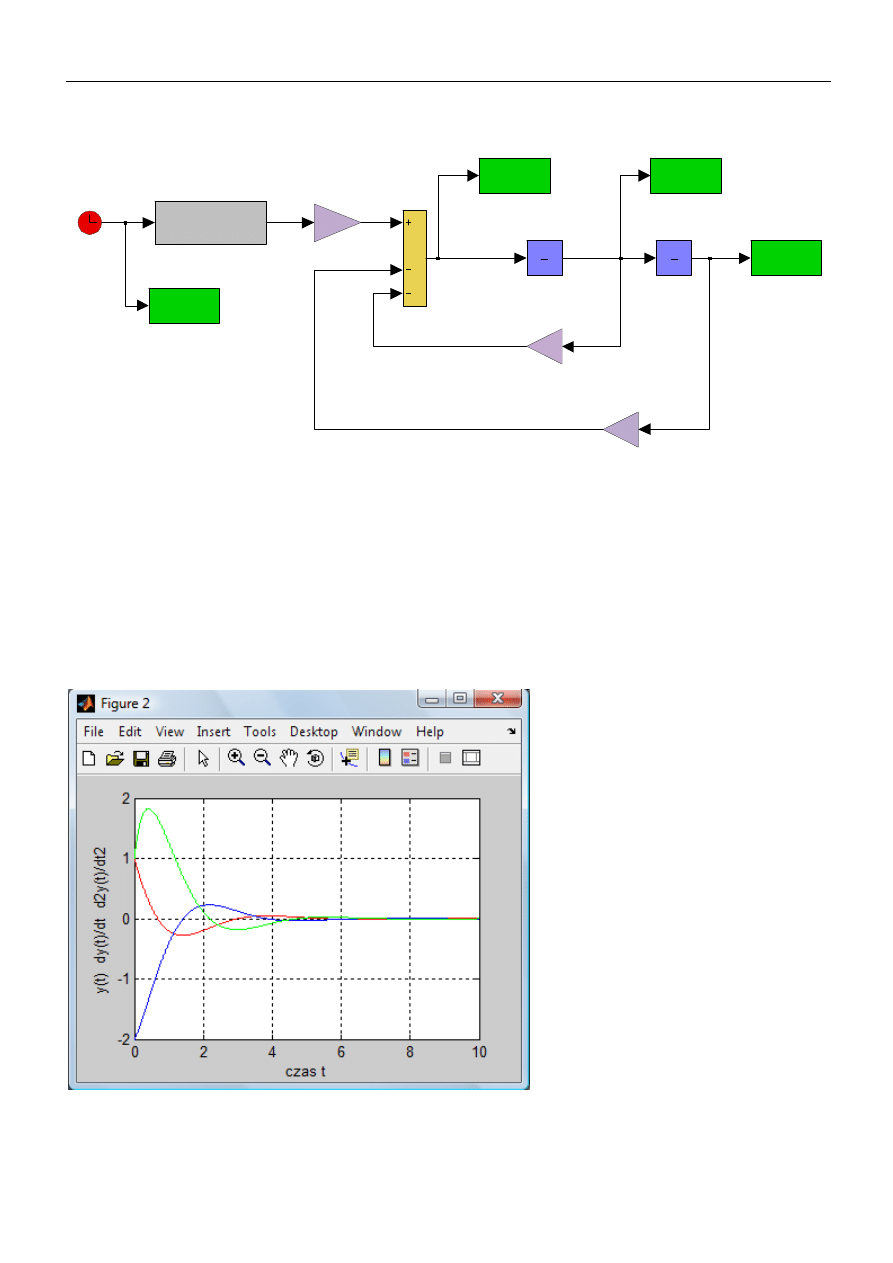
Oscyloskopy mona zastąpić blokami To workspace (kategoria Sinks w bibliotece Simulinka) (zapis wyników pomiarów do

przestrzeni roboczej w formacie tablicowym - Array)

2.5z(t)

y(t)

dy(t)/dt

d2y(t)/dt2

z(t)

sin(u*exp(-2.3*u))

t

d2y

dy

y

Suma

1

s

1

s

Clock

2.5

2 y(t)

2

1.5 dy (t)/dt

1.5

I wówczas na podstawie zgromadzonych danych zilustrować dynamikę obiektu sterowania - położenia, prędkości oraz

przyspieszenia (y(t), dy(t)/dt, d2y(t)/dt2)

Polecenia Matlaba wprowadzane w Command window

>> plot(t,y,’red’,t,dy,’blue’,t,d2y,’green’)
>>grid on
>> title('zmiana polozenia w czasie')
>> xlabel('czas t')
>> ylabel('y(t) dy(t)/dt d2y(t)/dt2')

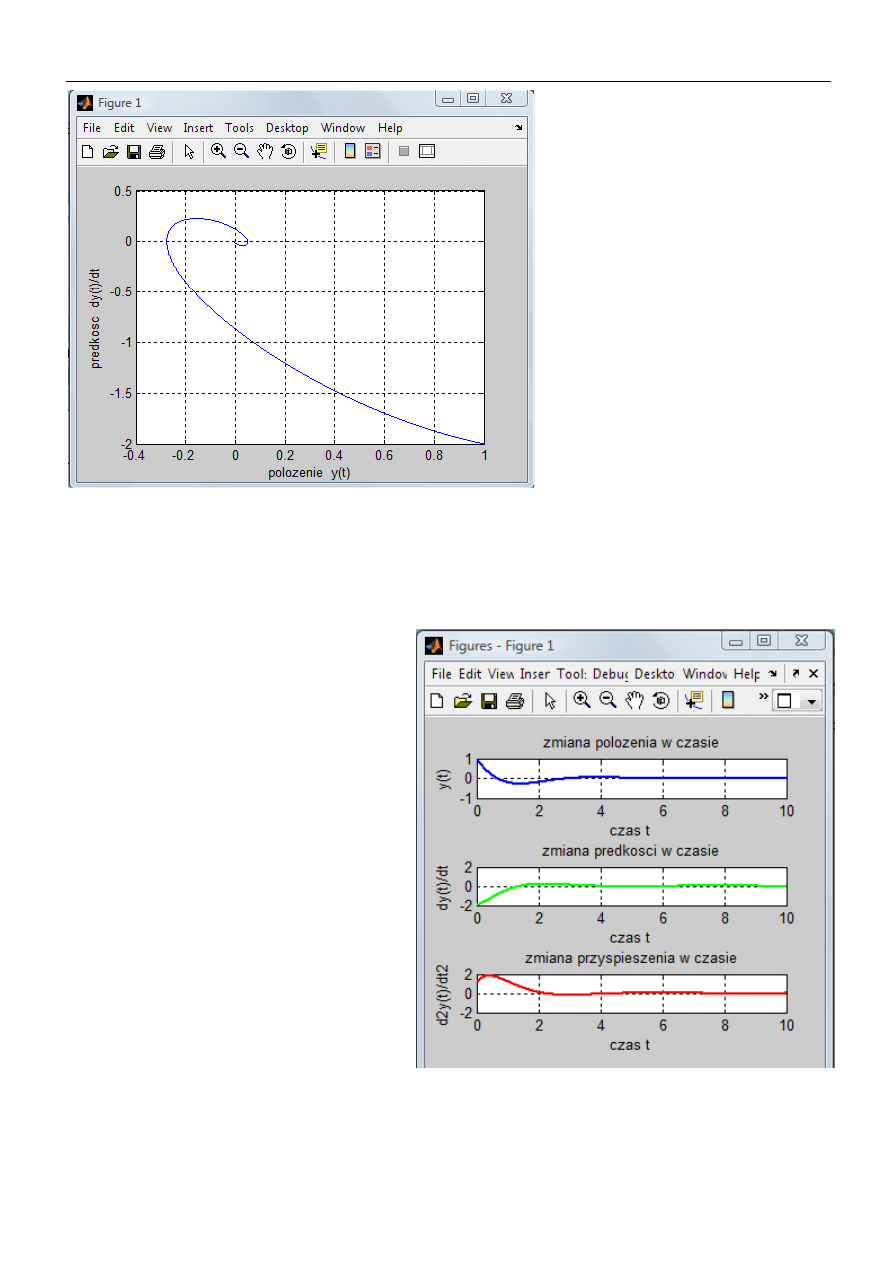
>> plot(y,dy,'blue')

// tak zwany portret fazowy

>> grid
>> xlabel('polozenie')
>> ylabel('predkosc')

Modelowanie i Symulacja Komputerowa

M A T L A B – S i mu l i n k

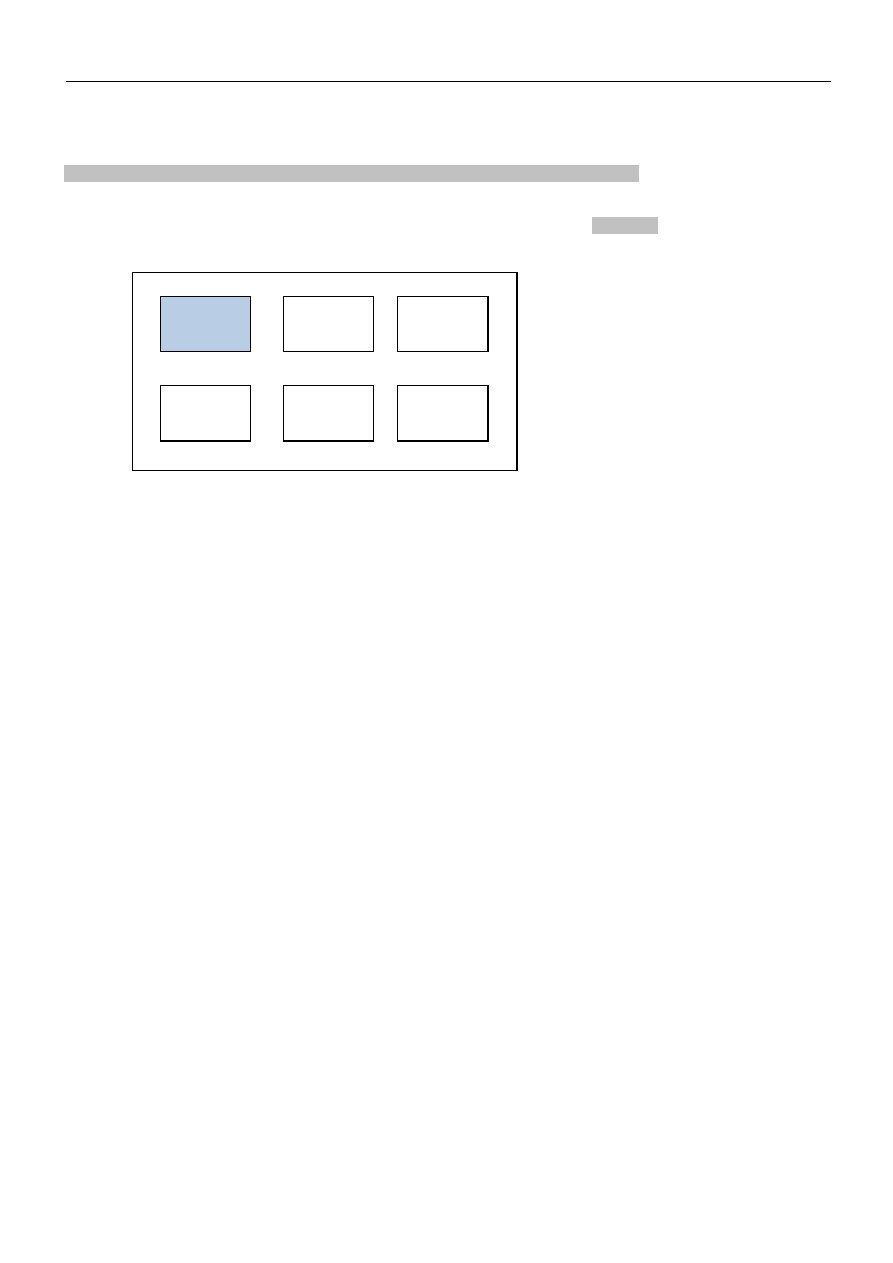
Polecenia Matlaba wprowadzane w Command window
(prezentacja uzyskanych wyników obliczeń w postaci wykresów umieszczonych w jednym oknie w układzie 3x1)

>> subplot(3,1,1)
>> plot(t,y)
>> grid on
>> title('zmiana polozenia w czasie')
>> xlabel('czas t')
>> ylabel('y(t)')

>> subplot(3,1,2)
>> plot(t,dy)
>> grid on
>> title('zmiana predkosci w czasie')
>> xlabel('czas t')
>> ylabel('dy'(t)/dt')

>> subplot(3,1,3)
>> plot(t,d2y)
>> grid on
>> title('zmiana przyspieszenia w czasie')
>> xlabel('czas t')
>> ylabel('d2y(t)/dt2')

Modelowanie i Symulacja Komputerowa

M A T L A B – S i mu l i n k

Ogólnie o tworzeniu podwykresów w jednym oknie wykresu

Polecenie w oknie poleceń Matlab-a

>>subplot(liczba_wierszy, liczba_kolumn, numer pola_wykresu_liczone_od_lewej_do_prawej)

stanowi odwołanie do zadanego pola wykresu w oknie, w którym utworzona została określona liczba okien równa
liczbie_wierszy x liczba_kolumn , np. subplot(2,3,1). Dopiero wówczas poleceniem >>plot(t,y) można wykonać wykres w
tym właśnie oknie

1

2

3

4

5

6